An Inverse Kinematics Solution for Mobile Manipulators in Textile Workshops Based on an Improved Particle Swarm Optimization

Abstract

To enhance the operational performance of mobile manipulators in textile workshops and address the difficulty of inverse kinematics (IK) for this class of redundant manipulators, this paper leverages the robot’s structural symmetries and proposes a chaotic-mutation particle swarm optimization (CMPSO)-based IK algorithm for mobile manipulators, thus simplifying the solution process and ensuring balanced exploration of the search space. First, the coordinate–transformation relationships of the mobile manipulator are analyzed to establish its forward kinematic model. Then, a multi-objective constrained IK model is formulated according to the manipulator’s operating characteristics. The model incorporates a pose-error function, the ‘compliance’ principle, and joint-limit avoidance. To solve this model accurately, we refine the population initialization and boundary-violation handling of the particle swarm algorithm and introduce an asymmetric mechanism via an adaptive mutation strategy, culminating in a CMPSO-based IK solver. On this basis, single-pose IK tests and trajectory-planning experiments are conducted, and simulation results verify the effectiveness and stability of the proposed algorithm.

1. Introduction

With advances in science and technology and growing production demands, the industrial sector is entering a new era—Industry 4.0 [1]. As a traditional manufacturing sector, the textile industry is also experiencing a transformation towards automation and informatization. However, the contemporary textile industry is confronted with challenges such as overcapacity and intense competition, which necessitate the development of smart textile factories as a pivotal pathway for its transformation [2]. The introduction of intelligent equipment such as mobile manipulators in processes like transportation and spinning in textile factories not only reduces labor costs and enhances productivity but also helps to ensure product quality, playing a significant role in the intelligent transformation of textile factories [3].

In recent years, symmetry has assumed an increasingly important role in the modeling and control of robotic systems. Many redundant robots—particularly mobile manipulators—employ asymmetric mechanical architectures to enhance operational flexibility. Mobile manipulators combine the planar mobility of a mobile base with the precise operational capabilities of a multi-degree-of-freedom manipulator, greatly expanding the workspace and adapting to the complex and dynamic environments in textile factories. The study of inverse kinematics for manipulators involves, given a desired end-effector pose, calculating the joint angles of the manipulator. Such problems are often computationally intensive, have non-unique solutions, and require optimization of the results [4]. However, incorporating a mobile base introduces nonholonomic constraints and additional redundant degrees of freedom. This substantially increases model complexity and makes the inverse kinematics problem more challenging [5]. Thus, how to accurately and efficiently solve the inverse kinematics of mobile manipulators has become an important research topic in the field of robotics.

R. Raja et al. proposed an improved KSOM learning framework to learn the mapping between the joint angle space and Cartesian space, addressing the inverse kinematics problem of mobile manipulators and maximizing the operability of the manipulator during the solution process [6]. Khan et al. transformed the tracking problem of mobile manipulators into a constrained position-level optimization problem and employed an improved recurrent neural network algorithm to solve the inverse kinematics under nonholonomic constraints, verifying the stability and convergence of the algorithm [7]. Zhao et al., by integrating task space constraints, joint limit constraints, and collision-free constraints with obstacles, proposed a novel algorithm based on Newton’s method and first-order techniques to generate collision-free inverse kinematics solutions, achieving dynamic obstacle avoidance for spherical obstacles [8]. Abbireddy et al. formulated the IK problem of a redundant manipulator as a nonlinear constrained optimization problem, whose objective is to minimize the position and orientation errors while avoiding obstacles. The classical nonlinear optimization method SQP, together with obstacle-avoidance techniques, was employed to determine the joint variables, and a bounding-box-based method was used to achieve collision avoidance [9]. Zhang et al. introduced a fast solving framework for mobile manipulators with unique domain constraints, along with a real-time obstacle avoidance strategy for the manipulator [10]. Li et al. introduced six parameters to characterize the motion redundancy and transformed the inverse kinematics of dual mobile manipulators into a non-redundant inverse kinematics problem. Subsequently, a weighted product form of normalized ideal redundant behaviors was constructed as the objective function. Finally, the Nelder–Mead simplex method was employed to optimize the redundancy parameters, thereby obtaining the desired joint configuration [11]. Jin et al. treated the mobile base and the manipulator as an integrated system and designed a fully connected network (FCN) to predict the positions and joint configurations of all degrees of freedom based on the target pose, achieving an online optimization for the whole-body inverse kinematics of the mobile manipulator. However, compared to the commonly used NNO algorithm, this method requires a longer computation time and its optimization speed needs improvement [12]. Xu et al. simplifies the inverse kinematics problem of the nine-axis gantry robot into that of a six-axis robotic arm. Through simulation experiments and specific experiments on the Staubli RX160L robotic arm, the accuracy of the inverse kinematics analysis of the robot was confirmed [13]. However, the aforementioned algorithms often rely on complex computations or extensive data training, thereby increasing the cost of solving the inverse kinematics. In response to these shortcomings, an increasing number of researchers have begun to employ intelligent optimization algorithms that do not rely on data training and have lower computational complexity to solve the inverse kinematics problem of mobile manipulators. Algorithms such as Differential Evolution [14], Fruit Fly Optimization [15], Artificial Fish Swarm Algorithm [16], Particle Swarm Optimization [17] and Bald Eagle Search Optimization Algorithm [18] have all been validated for their effectiveness in solving these problems.

Among the intelligent optimization algorithms previously referenced, Particle Swarm Optimization is distinguished by its simple structure and ease of implementation, and is frequently employed to solve complex constrained problems. It has been extensively applied to the inverse kinematics problem of mobile manipulators. Ram et al., targeting mobile manipulators in complex environments, formulated a multi-objective optimization problem with objectives of minimizing pose error and total joint movement, and with obstacle avoidance as a constraint, thereby achieving joint decoupling and an inverse kinematics solution for the mobile manipulator [19]. For SSRMS-type redundant manipulators, Jin et al. introduced the elbow joint posture and derived the algebraic relationship between the elbow posture and joint angles. By incorporating obstacle avoidance and singularity avoidance as additional tasks to constrain the particle swarm algorithm, the approach demonstrated satisfactory performance in terms of accuracy, efficiency, and operability, although it did not account for joint limit issues [20]. Liu et al., for general manipulators that do not satisfy the Pieper criterion, employed an improved particle swarm algorithm to solve their inverse kinematics. They introduced a nonlinear dynamic inertia weight adjustment method based on the concept of similarity and simultaneously utilized multiple populations for the search, thereby enhancing the stability of the inverse solution [21]. Cao et al. presents an improved quantum particle swarm optimization algorithm (IQPSO), which is used to solve the inverse kinematics problems. In this algorithm, quantum behavior is added to the particle swarm optimization algorithm, improve the convergence speed and solution accuracy [22]. Ning et al. proposed an adaptive transfer particle swarm algorithm (VDMAT-PSO) based on measures of velocity and directional manipulability, providing a solution for the inverse kinematics of mobile manipulators [23]. These approaches demonstrate the effectiveness of PSO-based solvers, but each focuses on specific aspects of performance. Challenges such as ensuring a well-distributed search in the high-dimensional solution space and avoiding premature convergence remain unsolved in many cases. In particular, no prior work has integrated multiple advanced PSO strategies into a unified solver for the IK problem of mobile manipulators. This gap means that existing methods may still suffer from uneven exploration of the redundant solution space or early stagnation in local optima.

In recent years, researchers have increasingly leveraged system symmetry in kinematic modeling, controller architectures, and optimization algorithms to simplify computation and improve performance. Correspondingly, deliberately introduced asymmetries—such as nonuniform gains or perturbations in control strategies—have become a growing trend for enhancing robustness and adaptability. By jointly exploiting symmetry and asymmetry in algorithmic and control design, robotic systems achieve improved stability and performance in complex, uncertain environments. To address the limitations of PSO solvers mentioned above, we propose a targeted integrated optimization strategy for IK, which combines several techniques in a novel way. We refer to this improved algorithm as Chaotic Mutation PSO (CMPSO). The integration of these three strategies is specifically designed to balance solution-set distribution and convergence quality in the redundant, high-dimensional search space of a mobile manipulator. We highlight the synergy of the integrated strategies: Sobol initialization ensures a high-quality, uniformly distributed starting population. The logistic chaotic perturbation introduces asymmetry in the swarm’s evolution, preventing synchronized premature convergence by re-diversifying particles when they approach boundaries. The Gaussian–Cauchy mutation adaptively balances local fine-tuning and global exploration, helping particles escape local optima while maintaining convergence precision. Together, these mechanisms complement each other to significantly improve the algorithm’s global search ability, population diversity, and solution accuracy. We apply the proposed CMPSO to a 9-DOF mobile manipulator’s IK problem and conduct extensive simulations, including single-point IK solving and continuous trajectory planning. Comparative experiments against the standard PSO and other enhanced variants demonstrate that our integrated approach achieves superior accuracy, stability, and efficiency.

2. Materials and Methods

2.1. Problem Description of the Inverse Kinematics for Mobile Manipulators

Due to the combination of a mobile platform and a robotic arm, mobile manipulators exhibit highly redundant degrees of freedom, and the relationship between structural symmetry and redundancy cannot be overlooked. Mobile manipulators typically adopt asymmetric configurations; for example, coupling a six-DOF arm with a symmetrically distributed joint layout to a two-wheel chassis yields multiple equivalent inverse solutions for a given end-effector pose. This multiplicity arising from structural asymmetry highlights the presence of redundancy: an asymmetric mechanical architecture allows the manipulator to reach the same end-effector pose via different joint combinations. This redundancy increases motion flexibility but also requires extra constraints to obtain a unique solution.

In our fitness-function design, asymmetric constraints are introduced to select the preferred inverse-kinematics (IK) solution. On the one hand, following the “compliance” principle, candidate solutions are evaluated to favor configurations in which joints stay away from singular postures and the overall posture is relaxed and well conditioned; on the other hand, a joint-limit-avoidance penalty is added to reduce the fitness of solutions whose joint angles approach their admissible bounds. By embedding these asymmetric constraints into the fitness function, we break the equivalence among the multiple solutions induced by the asymmetric structure and, while maintaining end-effector positioning accuracy, prioritize IK solutions that satisfy compliance and safety requirements, thereby improving the robustness of motion planning in redundant systems.

2.1.1. Mobile Manipulator Forward Kinematics

The mobile manipulator studied in this paper consists of a mobile base with three planar degrees of freedom and an Elite collaborative manipulator with six spatial degrees of freedom; its three-dimensional model is shown in Figure 1. The manipulator is rigidly mounted on the mobile base, and no relative motion exists between the manipulator base and the mobile platform. The end-effector is equipped with a gripper to perform pick-and-place tasks in the textile workshop.

Since the floor in a textile workshop is almost flat, it can be assumed that the wheels of the mobile base always remain perpendicular to the ground. The mobile base thus possesses three planar degrees of freedom relative to the world coordinate system, which are the x-axis coordinates $x_p$, the y-axis coordinates $y_p$, and the direction of the mobile base ${\alpha }_p$. Accordingly, the homogeneous transformation matrix of the mobile base coordinate system $\left\{{\mathsf{\Sigma }}_p\right\}$ with respect to the world coordinate system $\left\{{\mathsf{\Sigma }}_w\right\}$ is given by ${}_p{}^{w}T$.

$${}_p{}^{w}T=\left[\begin{array}{cccc}\cos {\alpha }_p& -\sin {\alpha }_p& 0& x_p\\ \sin {\alpha }_p& \cos {\alpha }_p& 0& y_p\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

(1)

The distances between the installation point of the manipulator base and the center of the mobile base along three specified directions are $d_x$, $d_y$ and $d_z$ respectively. As there is no relative motion between the manipulator base and the mobile base, the homogeneous transformation matrix ${}_m{}^{p}T$ of the manipulator base coordinate system $\left\{{\mathsf{\Sigma }}_m\right\}$ with respect to the mobile base coordinate system $\left\{{\mathsf{\Sigma }}_p\right\}$ is expressed as:

$${}_m{}^{p}T=\left[\begin{array}{cccc}1& 0& 0& d_x\\ 0& 1& 0& d_y\\ 0& 0& 1& d_z\\ 0& 0& 0& 1\end{array}\right]$$

(2)

The kinematic model of the Elite robotic arm is established using the Modified Denavit–Hartenberg (MD-H) coordinate representation. For the links connected by rotational joints, the relationship between the adjacent coordinate systems at any given position is shown in Figure 2. In the figure, $a_i$ represents the link length, ${\alpha }_i$ represents the link twist angle, $d_i$ represents the link offset, and ${\theta }_i$ represents the link angle.

The joint coordinate allocation of the Elite manipulator is shown in Figure 3.

Thus, the D–H parameter table for the Elite manipulator is presented in

Table 1. D–H table for the Elite manipulator.

Link i	${\mathit{\alpha }}_{\mathit{i}-1}$ (º)	${\mathit{a}}_{\mathit{i}-1}$ (mm)	${\mathit{d}}_{\mathit{i}}$ (mm)	${\mathit{\theta }}_{\mathit{i}}$ (º)	Joint Angle Range (º)
1	0	0	96	${\theta }_1$	±360
2	90	0	138	${\theta }_2$	±360
3	0	418	114	${\theta }_3$	±360
4	0	398	98	${\theta }_4$	±360
5	−90	0	98	${\theta }_5$	±360
6	90	0	89	${\theta }_6$	±360

.

By combining Figure 2 and Table 1, and based on the transformation relationships between the links, the transformation matrix ${}_i{}^{i-1}T$ between two adjacent links can be constructed as:

$$\begin{array}{c}{}_i{}^{i-1}T=Trans\left(a_{i-1},0,0\right)Rot\left(X_{i-1},{\alpha }_{i-1}\right)Trans\left(0,0,d_i\right)Rot\left(Z_i,{\theta }_i\right)\\ \begin{array}{c}=\left[\begin{array}{cccc}c{\theta }_i& -s{\theta }_i& 0& a_{i-1}\\ s{\theta }_{i}c{\alpha }_{i-1}& c{\theta }_{i}c{\alpha }_{i-1}& -s{\alpha }_{i-1}& -d_{i}s{\alpha }_{i-1}\\ s{\theta }_{i}s{\alpha }_{i-1}& c{\theta }_{i}s{\alpha }_{i-1}& c{\alpha }_{i-1}& d_{i}c{\alpha }_{i-1}\\ 0& 0& 0& 1\end{array}\right]\end{array}\end{array}$$

(3)

where $s{\theta }_i$ represents $\sin {\theta }_i$, $c{\theta }_i$ represents $\cos {\theta }_i$, $s{\alpha }_{i-1}$ represents $\sin {\alpha }_{i-1}$, $c{\alpha }_{i-1}$ represents $\cos {\alpha }_{i-1}$.

Consequently, the homogeneous transformation matrix ${}_t{}^{m}T$ of the tool coordinate system $\left\{{\mathsf{\Sigma }}_t\right\}$ with respect to the manipulator base coordinate system $\left\{{\mathsf{\Sigma }}_m\right\}$ is given by

$${}_t{}^{m}T={}_1{}^{0}T{}_2{}^{1}T{}_3{}^{2}T{}_4{}^{3}T{}_5{}^{4}T{}_6{}^{5}T$$

(4)

According to the chain rule, the forward kinematics of the mobile manipulator in the textile workshop can be expressed as:

$${}_t{}^{w}T={}_p{}^{w}T{}_m{}^{p}T{}_t{}^{m}T=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& p_1\\ r_{21}& r_{22}& r_{23}& p_2\\ r_{31}& r_{32}& r_{33}& p_3\\ 0& 0& 0& 1\end{array}\right]$$

(5)

where $r_{ij}(i,j=1,2,3)$ is the rotation matrix representing the orientation transformation of the end-effector with respect to the world coordinate system, and $p_k\left(k=1,2,3\right)$ is the position vector representing the position transformation of the end-effector with respect to the world coordinate system.

2.1.2. Inverse Kinematics for the Mobile Manipulator

Define the generalized degrees of freedom of the mobile manipulator as:

$$X^{*}=\left[x_p^{*} & y_p^{*} & {\alpha }_p^{*} & {\theta }_1^{\mathrm{*}} & {\theta }_2^{\mathrm{*}} & {\theta }_3^{\mathrm{*}} & {\theta }_4^{\mathrm{*}} & {\theta }_5^{\mathrm{*}} & {\theta }_6^{\mathrm{*}}\right]$$

(6)

From the forward kinematics in Section 2.1.1, the inverse kinematics problem for the mobile manipulator is to find a set of joint variables $X^{*}$ such that its forward kinematics meets the requirements of Equation (5). The fitness function based on orientation error and position error is defined as the sum of the square of the Frobenius norm of the orientation matrix error and the square of the 2-norm of the position error vector:

$$f_1={\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^3{(r_{ij}-r_{ij,tar})}^2}+{\displaystyle \sum _{k=1}^3{(p_k-p_{k,tar})}^2}}$$

(7)

Here, $r_{ij}$ and $r_{ij,tar}$ denote the actual and desired orientation matrices of the mobile manipulator, respectively, $p_k$ and $p_{k,tar}$ denote the corresponding position vectors of the mobile manipulator. To obtain a high-precision pose, the value of the fitness function should be as small as possible.

However, as a manipulator with redundant degrees of freedom, the mobile manipulator generally has multiple inverse kinematics solutions for a given end-effector pose in the world coordinate system. Therefore, constraints are necessary in the solving process to obtain an optimal solution. By introducing the “pliancy” principle into the inverse kinematics formulation, the fitness function is modified to ensure that the solution also minimizes energy consumption of the mobile manipulator. The pliancy principle guarantees that during the transition from the current pose to the desired pose, the joints closer to the manipulator base move as little as possible while the joints farther away move more, thus achieving the goal of reducing energy consumption in joints. For the mobile manipulator used in this paper, assuming the initial generalized joint configuration is $X_{init}$, a “pliancy principle”-based objective function is established as:

$$f_2={(x_p^{*}-x_{p,init})}^2+{(y_p^{*}-y_{p,init})}^2+{({\alpha }_p^{*}-{\alpha }_{p,init})}^2+{\displaystyle \sum _{i=1}^6{\omega }_i{({\theta }_i^{*}-{\theta }_{i,init})}^2}$$

(8)

where the weighting coefficient ${\omega }_i$ for the $i$-th joint is positive and larger for joints near the base and smaller for joints farther away. To minimize joint motion and energy consumption during mobile manipulator operation, the value of the objective function should be minimized.

In addition, if any joint angle nears its limit during motion, the stiffness of the manipulator may deteriorate, thereby affecting subsequent trajectory tracking. Thus, an objective function based on joint limit avoidance is defined to further constrain the solution:

$$f_3={\displaystyle \sum _{i=1}^6\frac{1}{\gamma }\frac{{({\theta }_{\max ,i}-{\theta }_{\min ,i})}^2}{({\theta }_{\max ,i}-{\theta }_i)\left({\theta }_i-{\theta }_{\min ,i}\right)}}$$

(9)

Here, ${\theta }_{\max ,i}$ represents the upper limit of the motion range for the $i$-th joint of the robotic arm, ${\theta }_{\min ,i}$ represents the lower limit of the motion range for the $i$-th joint, and $\gamma$ is a positive scalar gain. To ensure that the joints of the manipulator remain as close as possible to the middle value of their motion range, the value of the obtained solution $f_3$ should be minimized.

Based on the above constraints, the final fitness function of the inverse kinematics model for the mobile manipulator is expressed as:

$$\left\{\begin{array}{c}F={\lambda }_1{f}_1+{\lambda }_2{f}_2+{\lambda }_3{f}_3,{\displaystyle \sum _{i=1}^3{\lambda }_i=1}\\ x_{i,\min }\le x_i\le x_{i,\max }\end{array}\right.$$

(10)

2.2. Chaotic Mutation Particle Swarm Optimization

2.2.1. Basic Principles of Particle Swarm Optimization

Particle Swarm Optimization (PSO) was originally proposed by Kennedy and Eberhart [24]. It simulates the flocking behavior of birds, where each particle represents a potential solution flying through the search space. In PSO, a fitness function is used to evaluate the quality of each solution, and every particle has an associated fitness value. Once the population is initialized, particles begin to search the flying space by following the current best particle. During the iterative process, particles update themselves primarily by tracking two extreme values: the individual best (the best solution each particle has found so far) and the global best (the best solution found by any particle in the population). In some PSO variants, a subset of particles is chosen as neighbors, and the best solution found among these is referred to as the local best.

For a D-dimensional optimization problem, assume the population size is N; each particle thus exists in a D-dimensional space. Let the following vectors be defined:

• The position of a particle at time t is represented as a D-dimensional vector:

  $$X_i\left(t\right)={(x_{i1}\left(t\right),x_{i2}\left(t\right),\dots ,x_{iD}\left(t\right))}^T,i=1,2,3\dots N;$$

  where $x_{id}\left(t\right)\in \left[lb,ub\right]$, with the lower and upper bounds for the d-th dimension being $lb,ub$ respectively.
• The velocity of a particle at time t is represented as a D-dimensional vector:

  $$V_i\left(t\right)={(v_{i1}\left(t\right),v_{i2}\left(t\right),\dots ,v_{iD}\left(t\right))}^T,i=1,2,3\dots N;$$

  where $v_{id}\left(t\right)\in \left[V_{max,d},V_{min,d}\right]$,$V_{max,d}, V_{min,d}$ are the maximum and minimum velocity of the particle respectively.
• The individual best solution encountered by each particle so far is denoted as:

  $$P_{ibest}\left(t\right)={(p_{i1}\left(t\right),p_{i2}\left(t\right),\dots ,p_{iD}\left(t\right))}^T;$$
• The global best solution found by the entire swarm is denoted as:

  $$P_{gbest}\left(t\right)={(p_{g1}\left(t\right),p_{g2}\left(t\right),\dots ,p_{gD}\left(t\right))}^T;$$

After initializing the swarm, the PSO algorithm iteratively updates the particles. In each iteration, the particles determine their individual and global bests based on their fitness values and update their velocities and positions according to the following equations:

$$\begin{array}{c}{V}_{id}\left(t+1\right)={\omega }_i{V}_{id}\left(t\right)+c_1{r}_1\left[p_{id}\left(t\right)-x_{id}\left(t\right)\right]+c_2{r}_2\left[p_{gd}\left(t\right)-x_{id}\left(t\right)\right]\end{array}$$

(11)

$$\begin{array}{c}{x}_{id}\left(t+1\right)=x_{id}\left(t\right)+V_{id}\left(t+1\right)\end{array}$$

(12)

In Equation (11), the inertia weight ${\omega }_i$ determines the influence of the particle’s velocity at time t. A larger ${\omega }_i$ strengthens the global search ability of the algorithm while weakening its local search capability, leading to faster convergence but lower solution accuracy. Conversely, a smaller ${\omega }_i$ enhances the local search ability and improves accuracy, but makes it more difficult for the algorithm to escape local optima. In this study, a linear decreasing inertia weight (LDW) strategy is adopted, which is expressed as follows:

$$\omega \begin{array}{c}={\omega }_{\max }-\left({\omega }_{\max }-{\omega }_{\min }\right)\cdot {\displaystyle \frac{\mathrm{T}}{{\mathrm{T}}_{\max }}}\end{array}$$

(13)

In Equation (13), ${\omega }_{\max }$ represents the initial value of the inertia weight, which is also its maximum value, typically set to 0.9; ${\omega }_{\min }$ denotes the final value of the inertia weight, which is its minimum value, typically set to 0.2. In this way, the inertia weight linearly decreases from 0.9 to 0.2 during the iterations, significantly enhancing the optimization performance of the algorithm. In Equation (11), $c_1$ and $c_2$ are acceleration coefficients (also called learning factors) that indicate the weights of the individual and global best influences. Smaller coefficients allow particles to wander near the target region, while larger coefficients can cause sudden movements toward or away from the target; hence, excessively large or small coefficients are detrimental to the search, and typical values are chosen as $c_1=c_2=2$. The random numbers $r_1$ and $r_2$ are uniformly distributed in the interval $[0, 1]$.

2.2.2. Uniform Particle Swarm Optimization Based on Chaotic Mapping and Mutation

Although PSO is favored in academia for its simple structure and ease of implementation across various optimization problems, deeper research has revealed that it suffers from premature convergence, low precision, and a tendency to fall into local optima [25]. To address the foregoing issues, we propose a chaotic-mutation particle swarm optimization (CMPSO) algorithm that fuses symmetric and asymmetric design principles. First, during population initialization we adopt a uniform-distribution strategy to achieve as even, symmetric coverage of the search space as possible. This symmetric population layout helps avoid search bias, ensures that regions near the global optimum are not overlooked, and thereby improves the quality of the algorithm’s starting point for global optimization. Subsequently, we perturb the swarm with a logistic-map–based chaotic sequence and, together with an adaptive mutation mechanism, randomly adjust particle velocities and positions. Compared with the near-synchronous convergence typical of standard PSO, this chaotic perturbation and mutation act as an asymmetric stochastic excitation: they disrupt symmetric convergence patterns that may emerge during evolution, drive a subset of particles to escape local minima in a nonuniform manner, and enhance global exploration. By combining symmetric uniform initialization with an asymmetric chaotic-mutation strategy, the algorithm maintains population diversity while accelerating convergence, significantly improving the robustness and efficiency of IK computation.

• Population Initialization Based on Sobol Sequences

In PSO, the initial distribution of particles significantly influences the final accuracy and convergence of the algorithm. For the inverse kinematics problem of the mobile manipulator—which is characterized by a large search space and high dimensionality—the initial particles should be uniformly distributed within the search space to enhance diversity and ensure that the global optimum can be located. Traditional PSO methods generate the initial population using pseudo-random numbers, which tend to have low uniformity and may lower both the search efficiency and solution precision.

In contrast to the sequences of pseudo-random numbers, the Quasi-Monte Carlo (QMC) method uses deterministic low-discrepancy sequences (also called quasi-random or sub-random sequences) instead of pseudo-random sequences [26]. The Sobol sequence is a typical low-discrepancy sequence and, compared with pseudo-random numbers, distributes points more evenly within the unit hypercube. This property makes it more efficient in exploring the search space in numerical integration, global optimization, and Monte Carlo simulation problems. Figure 4 compares sample points generated by pseudo-random sequences and Sobol sequences in a two-dimensional space, clearly illustrating that the Sobol sequence provides more comprehensive coverage.

In this paper, the Sobol sequence is employed to generate the initial population. Suppose the search boundaries for a particle are given as $[lb,ub]$, the Sobol-generated points $u\in [0,1]$, then the position of the initial population of particles can be mapped to:

$$x=lb+(ub-lb)\times u$$

(14)

This mapping translates the uniform distribution within the unit hypercube to the actual search space, ensuring that the population covers the entire search interval at initialization. Although the Sobol sequence inherently has low discrepancy, in high-dimensional problems it may exhibit structural regularity leading to insufficient sampling in certain areas. Therefore, a random perturbation is added to break the structure, thereby providing a more random yet low-discrepancy initial population.

2.

Boundary Handling Based on the Logistic Map

In standard PSO, when particles exceed the search boundaries, a simple method is used where the boundary value is assigned to the out-of-bound particle’s position or velocity. Although this method is straightforward, it often diminishes the performance of the particle in subsequent searches and may cause the algorithm to get trapped in local optima. Owing to the inherent randomness and ergodicity of chaotic maps, this paper utilizes the Logistic map to regenerate the positions of out-of-bound particles instead of simply truncating them to the boundary, thereby preserving the particle’s search capability. The Logistic map was first proposed by May [27], and its chaotic mapping equation is given by:

$$x_{n+1}=r\times x_n\times (1-x_n)$$

(15)

In Equation (15), $x_n\in [0,1]$, $n$ is the number of chaotic mapping iterations, and $r\in [0,4]$ is the chaotic coefficient. When $3.5699456\le r\le 4$, Logistic map is in a chaotic state; when the chaotic coefficient is close to 4 the map behaves like a pseudo-random sequence; for lower values, the function converges to a fixed point. In this paper, out-of-bound particles are remapped back into the feasible domain using the Logistic map, avoiding the loss of population diversity that a simple boundary truncation might cause. The implementation procedure is as follows:

• Record the particle’s position in the dimensions where it exceeds the boundary $x_{id}$;
• Map the out-of-bound position $x_{id}$ into the interval $[0,1]$ by Equation (16), where $lb$, $ub$ are the lower and upper bounds;

  $$x_{id}^0=\left\{\begin{array}{c}\left|{\displaystyle \frac{x_{id}-lb}{ub-lb}}\right|,\left|x_{id}-lb\right|<\left|ub-lb\right|\\ \left|{\displaystyle \frac{ub-lb}{x_{id}-lb}}\right|,\left|x_{id}-lb\right|\ge \left|ub-lb\right|\end{array}\right.$$

  (16)
• According to Equation (15) iteration $n$ times to get $x_{id}^n$;
• Use the inverse operation of Equation (16) to place the chaotic state particle back into the solution space;
• Evaluate the fitness of the remapped particle to determine whether to update its individual best.

3.

Adaptive Mutation Strategy for Particles

In standard PSO, as the particles converge toward the global best, the swarm tends to lose diversity and becomes prone to local optima. To increase diversity and enhance the search ability in later stages, this paper designs a selective adaptive weighted mutation strategy: for particles with fitness values worse than the population average, weighted Cauchy mutation and Gaussian mutation are applied, with the mutation weight depending on the fitness of the particle.

Gaussian mutation utilizes normally distributed random numbers to perturb the particle’s position. Due to the property of the normal distribution where most values are concentrated around the mean and the probability density quickly decreases with distance, Gaussian mutation typically results in small perturbations, aiding in local search and fine-tuning. The Gaussian mutation is defined as Equation (17):

$$x_{guassian}=p_{ibest}+N(0,1)$$

(17)

Gaussian mutation has good local search capabilities but is not effective in helping particles escape from local optima. Therefore, Cauchy mutation—with its heavy-tailed characteristics—is also introduced. Cauchy mutation, based on the Cauchy distribution, can not only generate small disturbances but also has a higher probability of generating larger perturbations, facilitating global search. The Cauchy mutation is defined as Equation (18):

$$x_{cauchy}=p_{ibest}+Cauchy\left(0,1\right)$$

(18)

After mutation, the new position of a particle is given by:

$$x_{mutation}=(1-\gamma )\times x_{gaussian}+\gamma \times x_{cauchy}$$

(19)

where $\gamma \in [0,1]$ is the adaptive mutation factor calculated by:

$$\left\{\begin{array}{c}\gamma ={\displaystyle \frac{{\displaystyle \sum _{i=1}^N{q}_i\left(t\right)}}{N}}\\ q_i\left(t\right)=\left\{\begin{array}{c}1,f(P_{ibest}\left(t\right))<f\left(P_{ibest}\left(t-1\right)\right)\\ 0,f(P_{ibest}\left(t\right))\ge f\left(P_{ibest}\left(t-1\right)\right)\end{array}\right.\end{array}\right.$$

(20)

In the early stages of the algorithm, $\gamma$ is large so that inferior particles are more likely to undergo Cauchy mutation, thereby expanding the search space and enhancing the algorithm’s ability to perform wide-range exploration in the initial phase; in later stages, as $\gamma$ approaches zero, the algorithm has already converged near the global optimum. At this stage, inferior particles are more likely to undergo Gaussian mutation, which strengthens the local search capability of the particles. This fitness-based weighted mutation method thus increases population diversity and improves overall performance.

2.2.3. Algorithm Flow of the Chaotic Mutation Particle Swarm for Inverse Kinematics

For the inverse kinematics model described in Section 2.2.2, each particle is composed of 9 joint variables, its position vector is defined as $X^i=\left[x_p^i & y_p^i & {\alpha }_p^i & {\theta }_1^i & {\theta }_2^i & {\theta }_3^i & {\theta }_4^i & {\theta }_5^i & {\theta }_6^i\right]$, its velocity vector is defined as $V^i=\left[v_1^i & v_2^i & v_3^i & v_4^i & v_5^i & v_6^i & v_7^i & v_8^i & v_9^i\right]$, with each position vector representing one feasible inverse kinematics solution.

Based on the above strategies, the main steps of the chaotic mutation particle swarm algorithm (CMPSO) for solving the inverse kinematics are as follows:

• Algorithm Initialization: Set the population size $N$, maximum number of iterations $T$, problem dimension $D$, learning factors $c_1$, $c_2$, the velocity boundaries $\left[V_{min,d},V_{max,d}\right]$, the position boundaries $\left[L_d,U_d\right]$.
• Initial State: Generate a uniformly distributed initial population using the Sobol sequence as described in Equation (14) and calculate the fitness value for each particle. Store each particle’s initial position and fitness value in vector $P_{ibest}$, and record the particle with the best fitness value as the initial global best in $P_{gbest}$.
• State Update: Update the velocity and position of each particle using Equations (11) and (12) and check for boundary violations. If a particle’s position exceeds the boundaries, remap the particle back into the search space using Equations (15) and (16).
• Evaluation and Mutation: Compute the fitness value for each particle in the current iteration and compare it with the individual best fitness value. If the current fitness is better, update $P_{ibest}$ accordingly. For those particles whose fitness is worse than the population average, apply the adaptive weighted mutation as given in Equation (19) and evaluate whether an update of $P_{ibest}$ is necessary.
• Swarm Update: Compare the individual best fitness values with the global best. If an individual value is superior, update the global best $P_{gbest}$ accordingly.
• Termination Check: Determine whether the maximum number of iterations has been reached. If so, terminate the algorithm; otherwise, proceed to the next iteration starting from step (3) until $T$ is reached.
• Output: Return the optimal solution $P_{gbest}$ of the fitness function.

3. Simulation and Results

All experiments in this study were conducted on a computer running Windows 11 and equipped with a 13th Gen Intel^® Core™ i7-13620H processor (Intel Corporation, Santa Clara, CA, USA) at 2.40 GHz. Python 3.13.0 was used as the simulation environment. Inverse kinematics tests were performed for both single-point and continuous-point cases.

3.1. Single-Point Inverse Kinematics Ablation Experiment

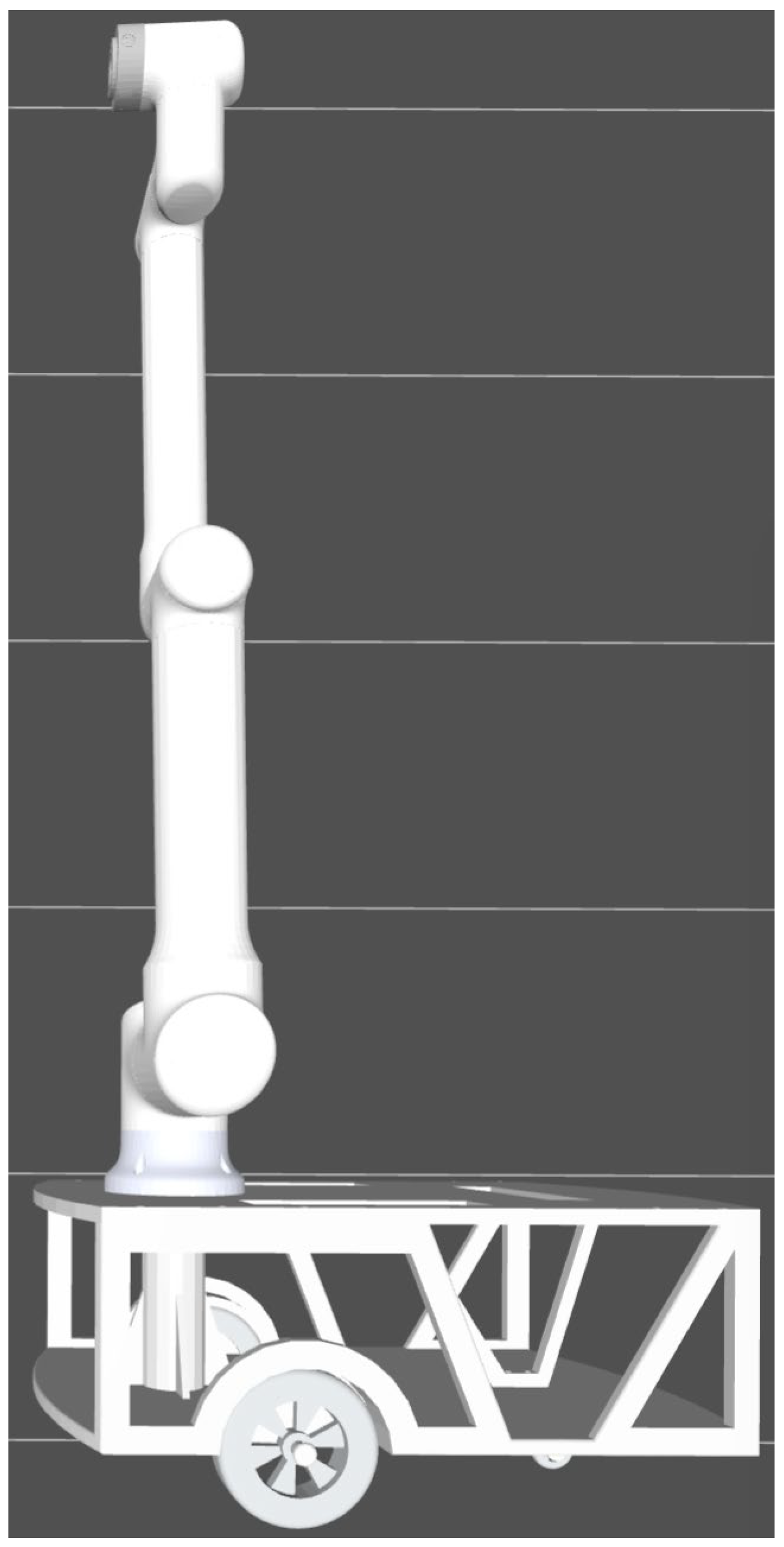
To thoroughly verify the effectiveness of the CMPSO improvement strategies, ablation experiments are first conducted. For the mobile manipulator in the textile workshop shown in Figure 1, ablation tests of inverse kinematics based on the chaotic-mutated particle swarm optimization algorithm are performed following the algorithm flow described in Section 2.2.3. The specific procedure is as follows: given the desired end-effector pose and the initial pose of the mobile manipulator, the improvement strategies of CMPSO are removed individually, and the nine joint variables of the mobile manipulator are solved accordingly. The obtained joint solutions are then substituted into the forward kinematics to compute the actual end-effector pose, and the error relative to the desired pose is evaluated. The algorithm parameters are set as follows: the maximum number of iterations is T = 500, and the population size is N = 30; the extrema of the inertia weight are ${\omega }_{\max }=0.9$ and ${\omega }_{\min }=0.2$; acceleration coefficients $c_1=c_2=2$; to ensure that the particles remain in a fully chaotic state, the chaotic coefficient is chosen as r = 4. The initial configuration of the mobile manipulator is set as:

$$X_0={[0 & 0 & 0 & 0 & pi/2 & 0 & 0 & -pi/2 & 0\\ ]}^T$$

(21)

The desired homogeneous transformation matrix corresponding to the end-effector is given by:

$$T_{\mathit{target}}=\left[\begin{array}{cccc}{r}_{11,tar}& r_{12,tar}& r_{13,tar}& x_{tar}\\ r_{21,tar}& r_{22,tar}& r_{23,tar}& y_{tar}\\ r_{31,tar}& r_{32,tar}& r_{33,tar}& z_{tar}\\ 0& 0& 0& 1\end{array}\right]=\left[\begin{array}{cccc}0.9998& -0.0183& 0.0091& 0.5000\\ 0.0184& 0.9997& -0.0137& 0.5000\\ -0.0089& 0.0139& 0.9999& 0.4000\\ 0& 0& 0& 1.0000\end{array}\right]$$

(22)

The position error for the single-point inverse kinematics solution is defined as:

$$E_{pos}={(x_p-x_{\mathit{target}})}^2+{(y_p-y_{\mathit{target}})}^2+{(z_p-z_{\mathit{target}})}^2$$

(23)

and the orientation error is defined as:

$$E_{ori}={\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^3{(r_{ij}-r_{ij,tar})}^2}}$$

(24)

• Ablation Experiment on Population Initialization Method

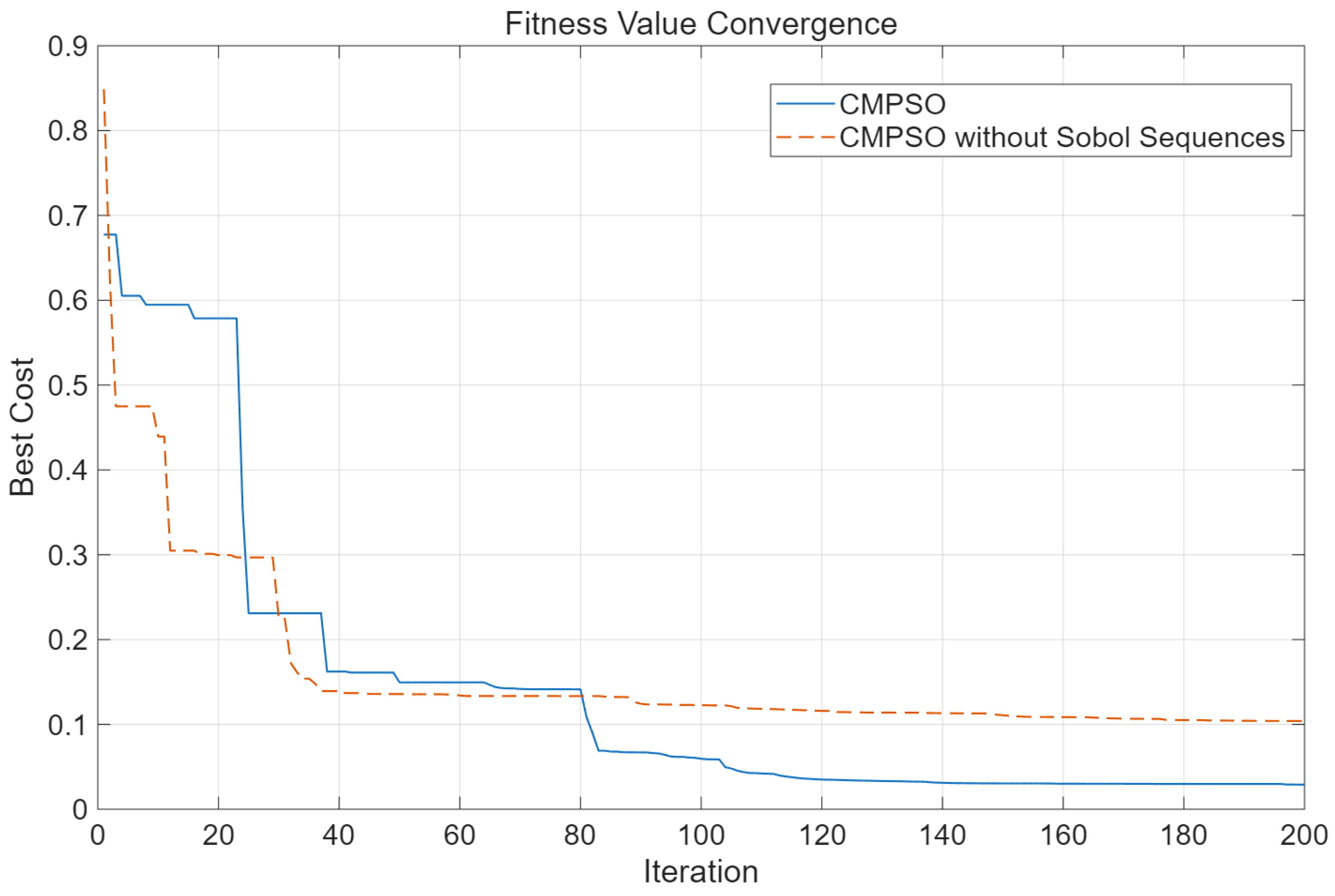
In this experiment, the Sobol sequence-based population initialization method in CMPSO was removed. The convergence curves of the fitness values are shown in Figure 5.

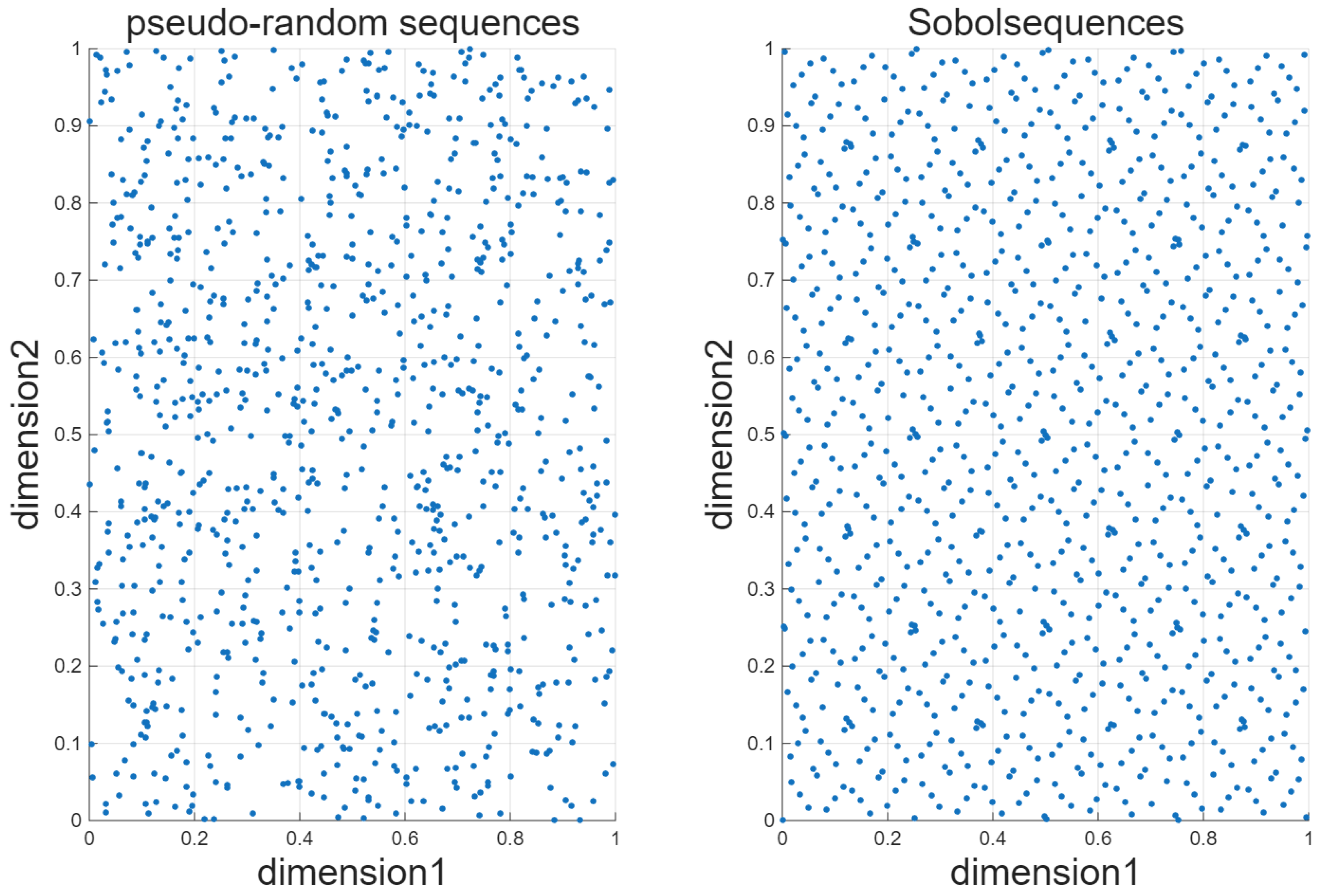
It can be observed that the original CMPSO (before removal) exhibits a lower initial fitness value. This is because the Sobol sequence-based initialization distributes particles more uniformly within the feasible domain, resulting in a higher-quality global optimum in the initial state. Moreover, due to this uniformly distributed starting condition, the algorithm is able to converge toward a better solution in the later stages.

2.

Ablation Experiment on Particle Boundary-Handling Strategy

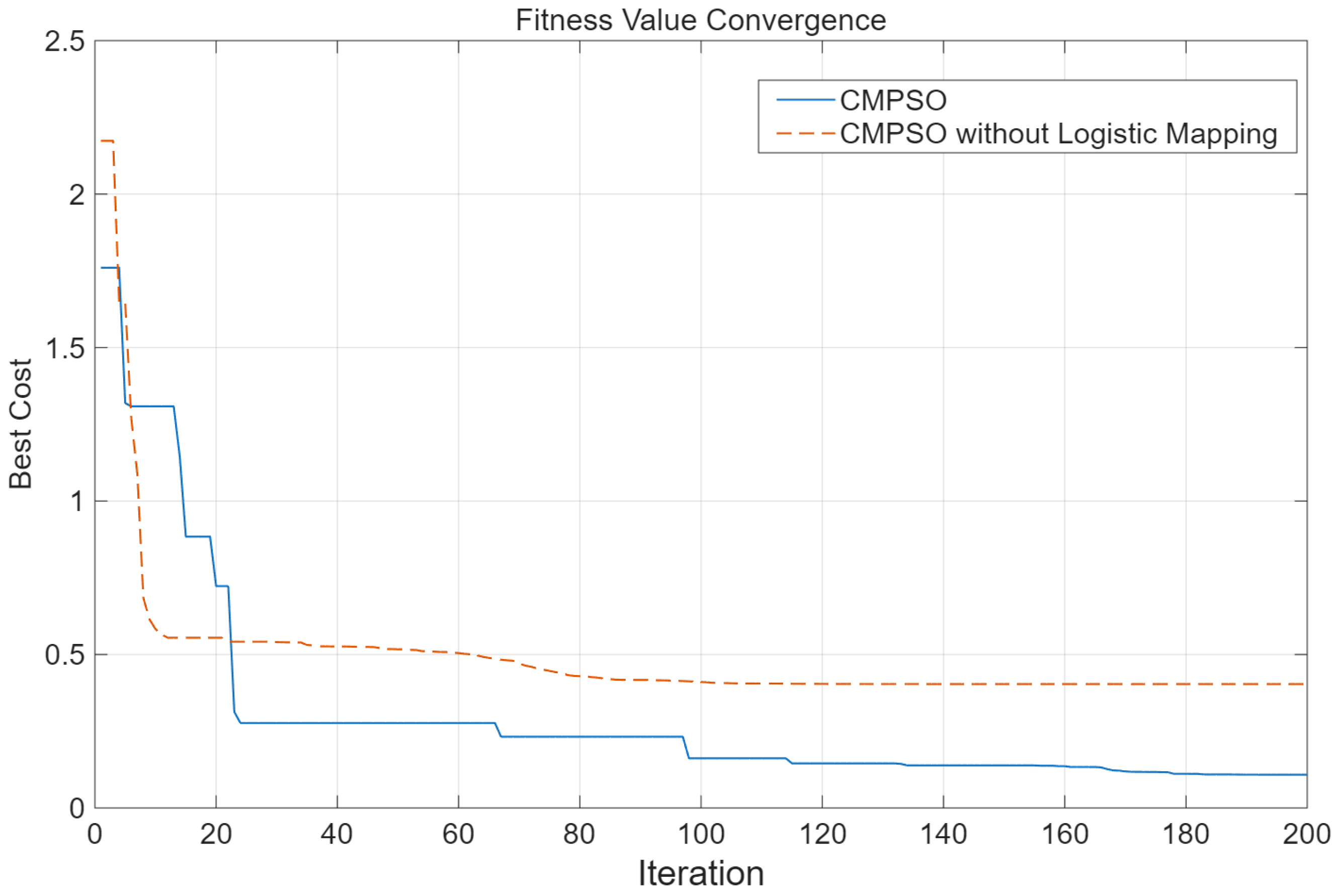
In this experiment, the Logistic mapping-based boundary-handling method in CMPSO was removed. The convergence curves of the fitness values are shown in Figure 6.

It can be observed that when a simple truncation method is used for boundary handling, the algorithm falls into a local optimum during the early and middle stages of iteration and fails to escape. In contrast, the CMPSO algorithm maintains a consistent convergence trend throughout the iterative process. This is because the Logistic mapping-based boundary-handling strategy allows particles that move outside the feasible domain to return uniformly to the feasible region rather than being fixed at the boundary, thereby enhancing their ability to re-explore the search space.

3.

Ablation Experiment on Particle Mutation Strategy

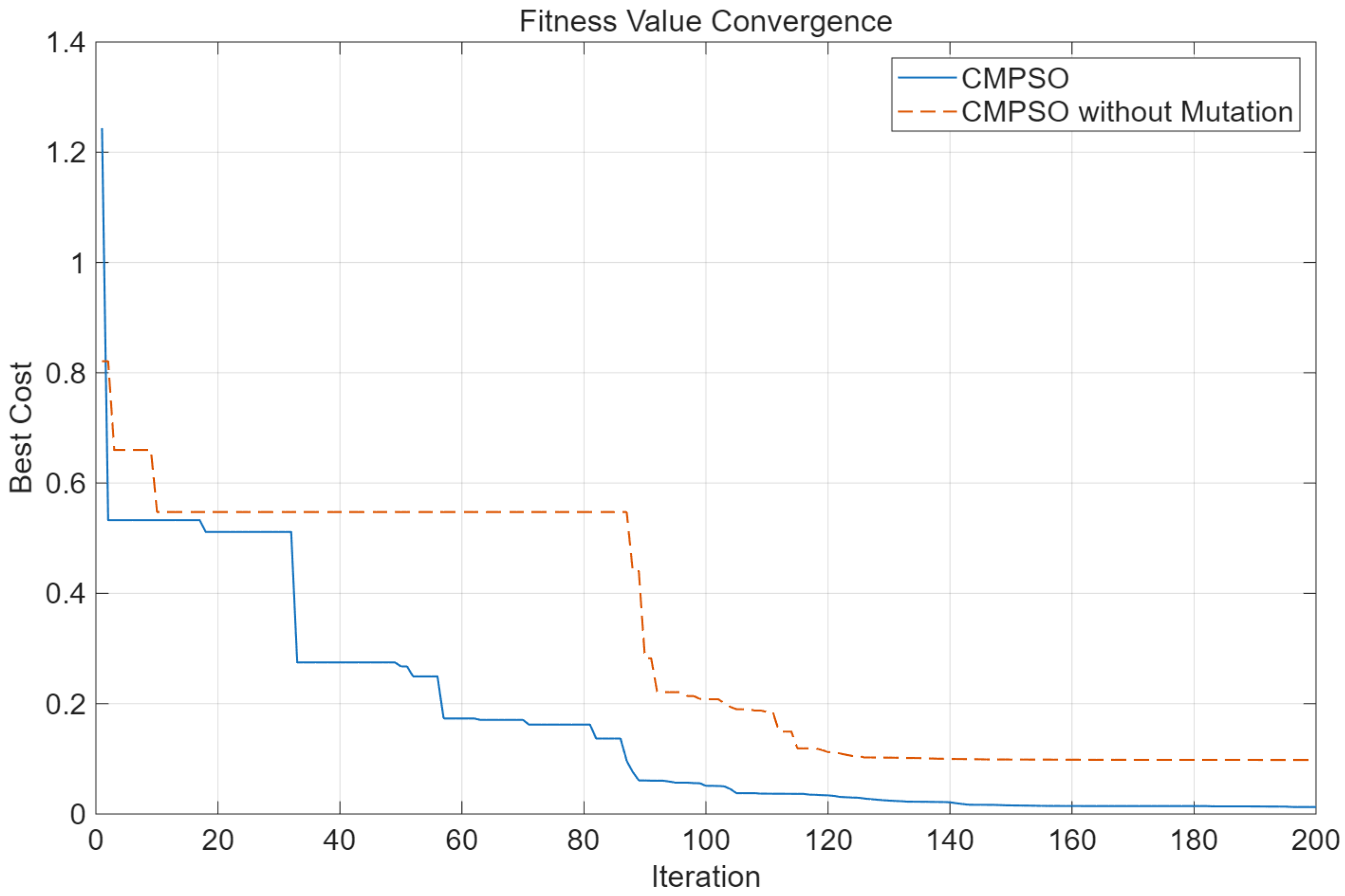
In this experiment, the adaptive mutation strategy of particles was removed. The convergence curves of the fitness values are shown in Figure 7.

It can be observed that CMPSO exhibits more pronounced and frequent stepwise convergence behavior and ultimately finds a better feasible solution. This is because, with the adaptive mutation strategy, particles selectively undergo Gaussian mutation or Cauchy mutation based on their current fitness values, which greatly enhances their ability to escape local optima. As a result, the fitness curve demonstrates stepwise changes. This mutation mechanism significantly improves the search capability of particles, enabling CMPSO to achieve higher solution accuracy in inverse kinematics computation.

3.2. Single-Point Inverse Kinematics Comparison Experiment

The proposed CMPSO is compared with the standard PSO, Adaptive PSO (APSO) [17], and Quantum-behaved PSO (QPSO) [28] in inverse kinematics experiments. The basic algorithm parameters are the same as those in Section 3.1, and the remaining algorithm parameters are set as follows: acceleration coefficient range for APSO as $[1.5,2]$, and contraction–expansion factors for QPSO as ${\beta }_1=0.5$, ${\beta }_2=1.0$. 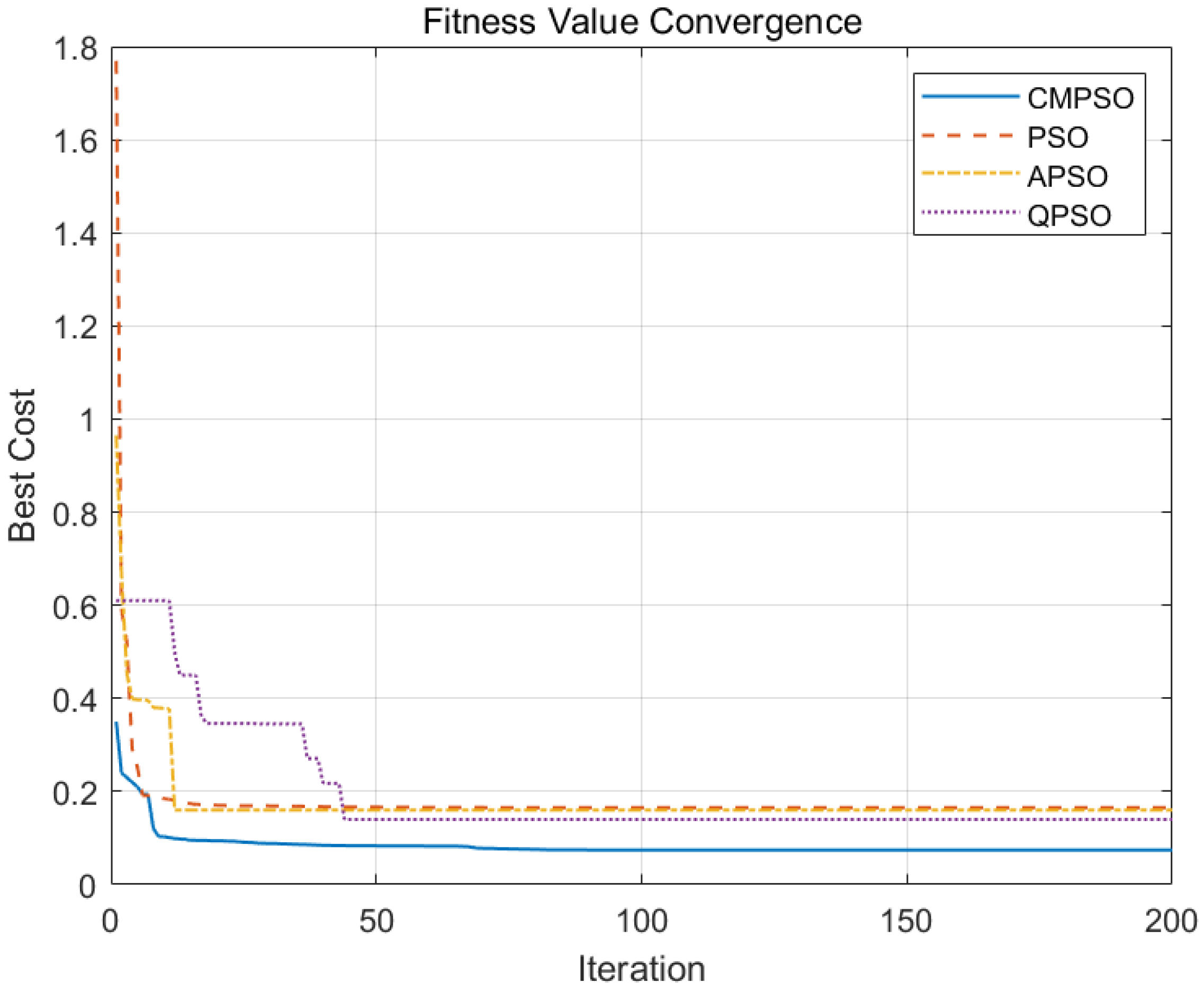The convergence curves depicting the variation in the fitness value with iteration are shown in Figure 8.

Analysis of the convergence curves shows that compared with the other three algorithms, CMPSO starts with a lower initial fitness value due to the use of the Sobol sequence for population initialization, which results in a more uniform distribution of particles in the search space. As the iterations proceed, CMPSO converges the fastest and achieves the highest solution accuracy.

Fifty independent runs were conducted for each algorithm, recording the best fitness value, worst fitness value, mean fitness value, fitness variance, and the average pose error. The pose error is defined as $E=E_{ori}+E_{pos}$. The stability of the algorithms was analyzed, and the results are summarized in

Table 2. Statistical performance data of the algorithms.

Algorithms	PSO	APSO	QPSO	CMPSO
Best Fitness Value	$3.364\times {10}^{-3}$	$6.344\times {10}^{-4}$	$9.101\times {10}^{-4}$	2.478 $\times {10}^{-4}$
Worst Fitness Value	$5.062\times {10}^{-1}$	$1.694\times {10}^{-2}$	$7.042\times {10}^{-3}$	$8.260\times {10}^{-3}$
Mean Fitness Value	$8.429\times {10}^{-3}$	$6.316\times {10}^{-3}$	$4.291\times {10}^{-3}$	$3.175\times {10}^{-3}$
Fitness Value Variance	$1.469\times {10}^{-2}$	$9.264\times {10}^{-3}$	$4.822\times {10}^{-4}$	$1.773\times {10}^{-4}$
Average Pose Error	$1.332\times {10}^{-2}$	$8.716\times {10}^{-3}$	$6.216\times {10}^{-3}$	$3.975\times {10}^{-3}$

.

From Table 2, it can be seen that compared with PSO, APSO, and QPSO, the proposed CMPSO exhibits the smallest mean fitness value and variance, indicating superior stability and convergence, with the average pose error reduced by 70.15%, 54.39%, and 36.05%, respectively. This significantly enhances the accuracy of the inverse kinematics solution.

Inverse kinematics serves as the foundation for subsequent trajectory planning. The time performance of the algorithm determines whether the mobile manipulator can achieve real-time trajectory planning; therefore, it is necessary to evaluate the computational efficiency of the algorithm and further optimize its time complexity when required. According to our previous research, the mobile manipulator studied in this work must operate at a control frequency of at least 250 Hz in the textile workshop. Thus, the solution time of the inverse kinematics algorithm should be less than 4 ms. A total of 1000 inverse kinematics computations were randomly performed within the workspace of the mobile manipulator, and the computation times of the proposed CMPSO as well as PSO, APSO, and QPSO are summarized in

Table 3. Statistical Results of Solution Time Based on Fixed Iteration Count.

Algorithms	PSO	APSO	QPSO	CMPSO
Maximum time (ms)	2.015	2.159	1.900	1.117
Minimum time (ms)	1.664	1.353	1.106	0.874
Average time (ms)	1.932	1.502	1.631	0.971
Variance (ms)	0.049	0.054	0.041	0.003

.

As shown in Table 3, the proposed CMPSO-based inverse kinematics algorithm exhibits significantly superior time performance compared with the other three PSO variants in the random experiments. This improvement is attributed to the designed joint-limit-avoidance constraint, which keeps the manipulator joints away from singular configurations, enhances manipulability, and reduces the computational cost of matrix operations. Based on the maximum and average computation times of CMPSO, the proposed inverse kinematics algorithm can almost satisfy a 1 kHz control frequency, which is much higher than the required 250 Hz. Furthermore, the low variance indicates that the computation efficiency of CMPSO is highly stable, fulfilling the requirements of real-time trajectory planning.

We define successful computation as the case in which the solution error converges to within 1% of the desired pose, upon which the algorithm terminates; otherwise, the computation is considered a failure. Similarly, 1000 random solution experiments were conducted within the workspace of the mobile manipulator, and the computation times for successful solutions are summarized in

Table 4. Statistical Results of Solution Time Based on Convergence Error.

Algorithms	PSO	APSO	QPSO	CMPSO
Maximum time (ms)	1.844	1.311	1.206	0.406
Minimum time (ms)	1.305	0.755	0.634	0.319
Average time (ms)	1.574	1.032	0.920	0.362
Variance (ms)	0.024	0.015	0.009	1.42 × 10−3
Success rate	52%	65%	77%	96%

.

As shown in Table 4, when convergence error rather than iteration count is used as the termination criterion (a criterion that is evidently more consistent with real robot operation and commonly adopted in robotic control), the computational efficiency advantage of the proposed CMPSO-based inverse kinematics algorithm becomes even more significant, consistent with the results shown in Figure 8. Due to the more uniform population initialization, the algorithm uniformly covers the feasible domain in the initial phase, reducing the difficulty of convergence. Additionally, the adaptive mutation strategy greatly improves the success rate of the algorithm.

3.3. Trajectory Planning Experiment

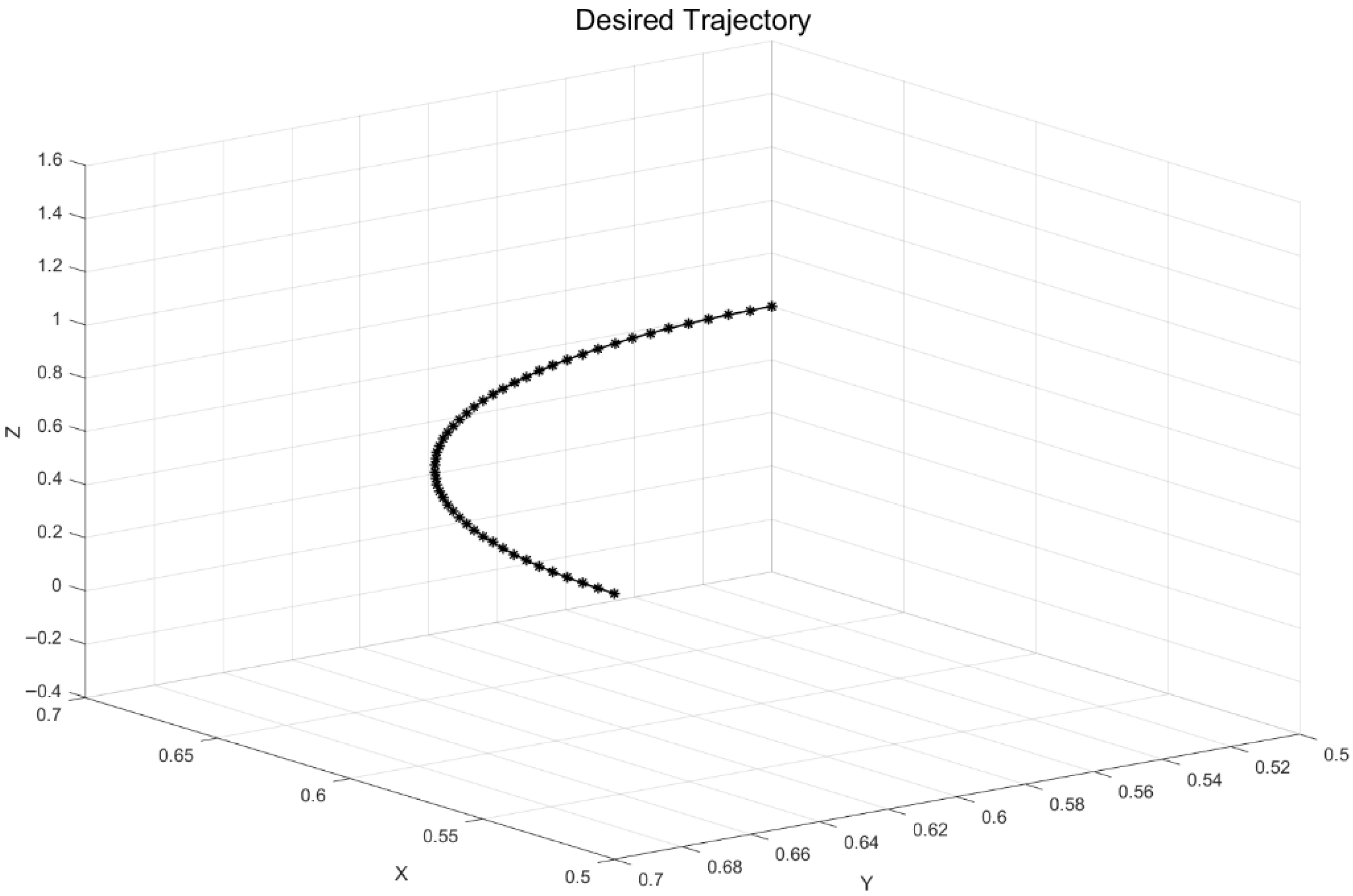
Section 3.1 has verified the feasibility of the algorithm in solving single-point inverse kinematics. On this basis, a trajectory planning test for the mobile manipulator is conducted to further validate the algorithm’s performance in motion control. The specific method is as follows: two points in the manipulator’s workspace $\left(0.5,0.7,0.5\right)$ and $(0.7,0.5,0.5)$, representing a pick-up point and a placement point in the textile workshop, are given. A circular arc in space with a center at $(0.5,0.5,0.5)$ and a radius of 0.2 is planned between these two points. A fifth-order polynomial is used for trajectory planning along the circular arc, and 50 interpolation points are obtained based on the interpolation period, as shown in Figure 9.

In this study, the circular end-effector path is discretized into 50 interpolation points. This number of waypoints provides a sufficiently fine spatial resolution for the given radius and workspace scale, so that the discrete points closely approximate a smooth continuous trajectory while keeping the experimental setup and figures concise. It should be noted that the proposed CMPSO-based inverse kinematics solver treats each interpolation point as an independent optimization problem. Therefore, the algorithm can be directly applied to trajectories with a larger number of interpolation points or to longer and more complex paths without any modification of the optimization framework. Combined with the timing results reported in Table 3 and Table 4, where the average computation time per IK query remains well below the 4 ms budget required by a 250 Hz control frequency, this indicates that the proposed method is suitable for real-time trajectory generation even for significantly denser discretizations.

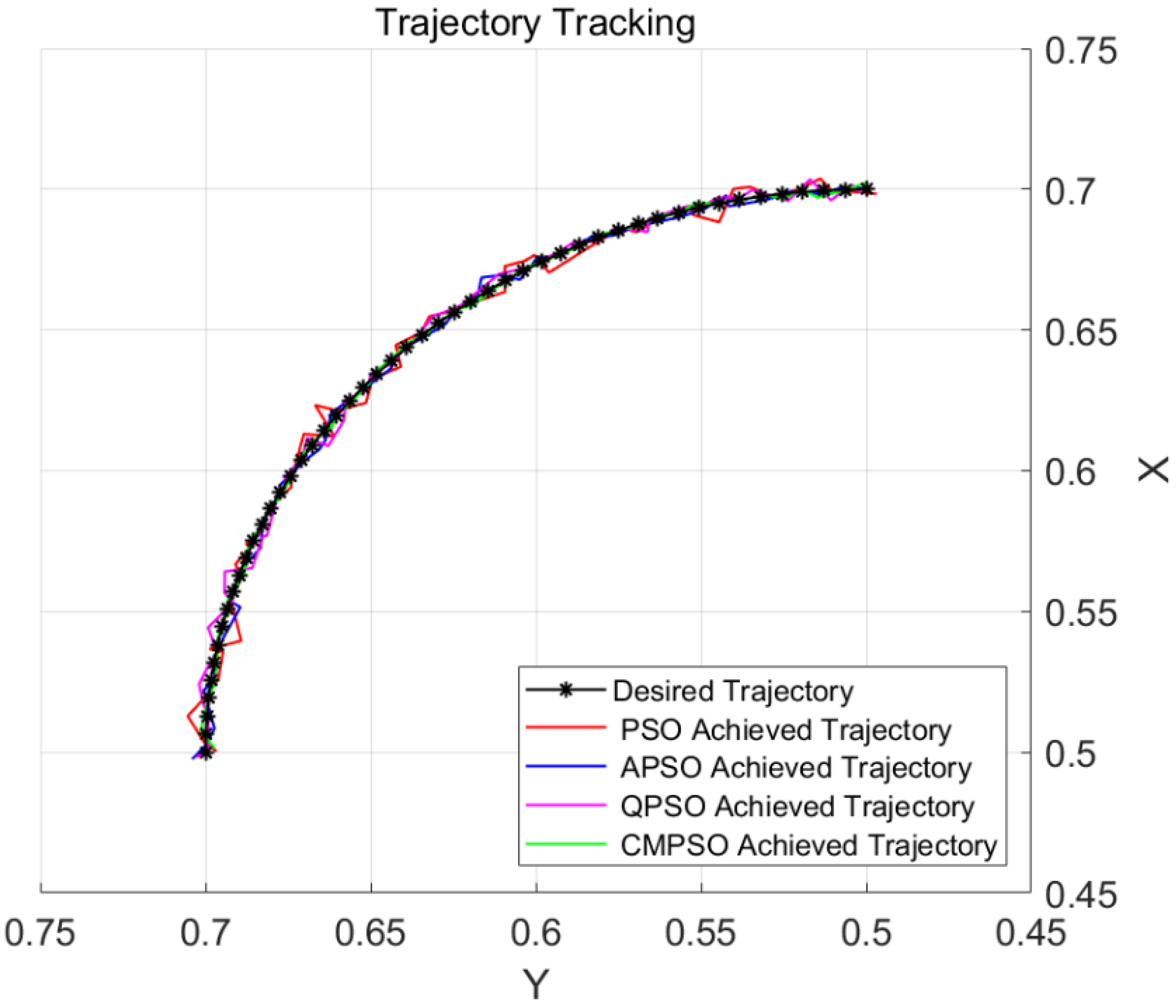
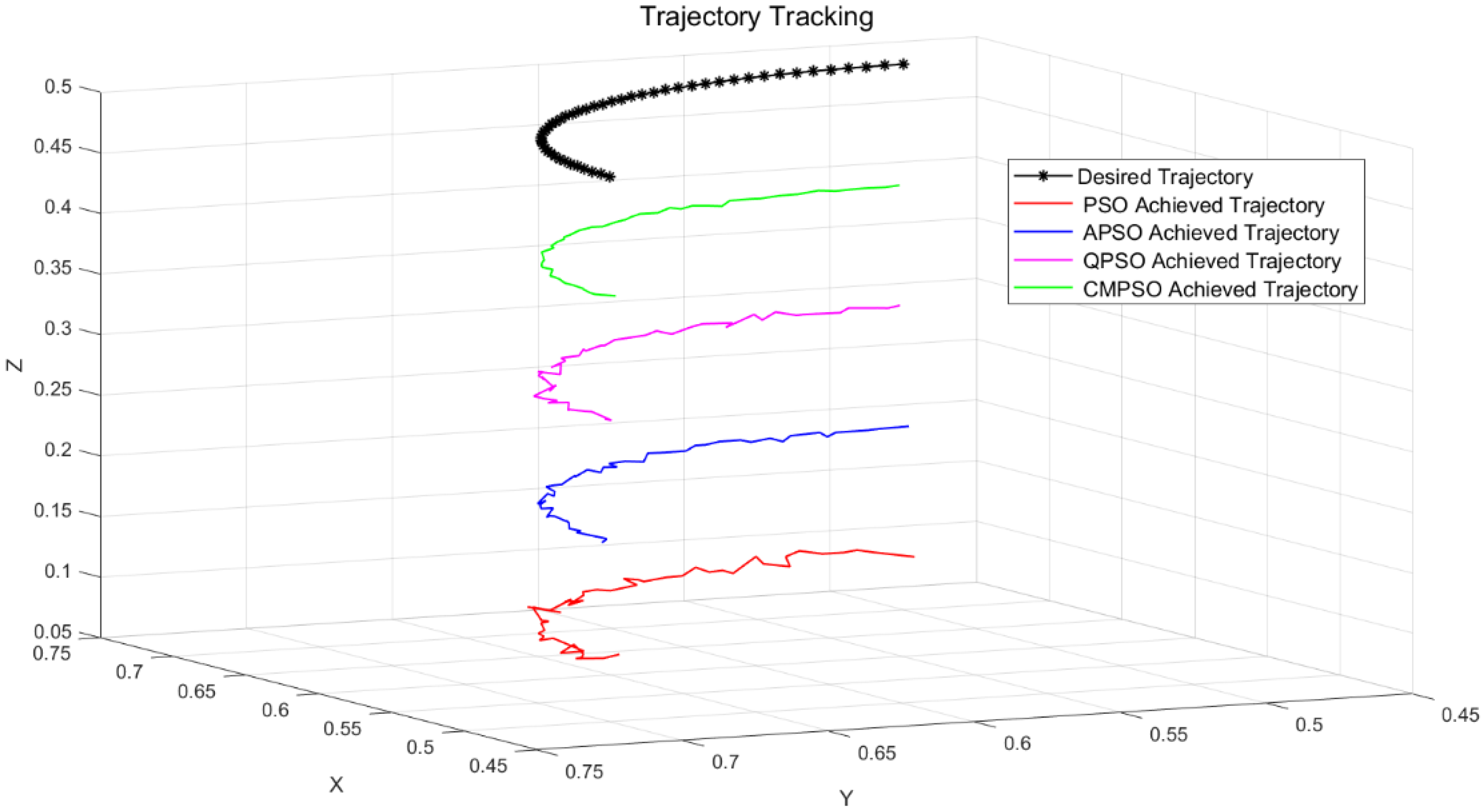
During the trajectory planning process, the PSO algorithm uses the previously computed trajectory point as the starting pose for the current iteration. The first starting pose is the same as that in Equation (21). The pose solutions computed by the algorithm are substituted into Equation (5) to extract and plot the position vectors ${[p_1,p_2,p_3]}^T$. Two-dimensional and three-dimensional comparisons are presented in Figure 10 and Figure 11 (in the three-dimensional view, the trajectory has been translated in the z-direction for visual clarity).

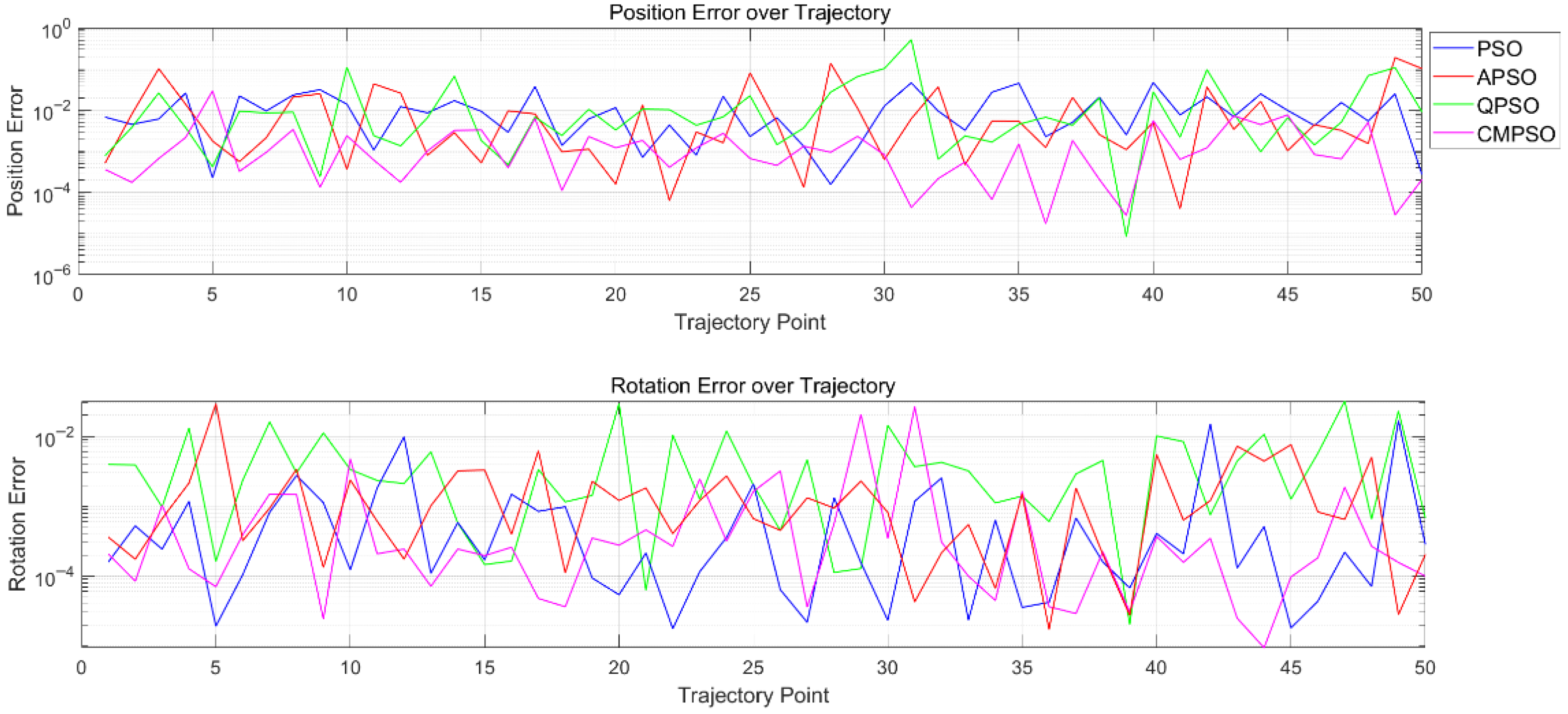
For the 50 trajectory points obtained, the position and orientation errors are calculated based on the definitions in Equations (23) and (24), respectively. The results are illustrated in Figure 12.

Analysis of Figure 8 reveals that the pose error curve obtained by the proposed CMPSO is lower in value and smoother compared to the other three algorithms. The error remains within a limited range $[1\times {10}^{-5},1\times {10}^{-3}]$, indicating a high degree of solution accuracy. These experimental results are consistent with those presented in Section 3.1 and demonstrate that CMPSO has superior precision and stability in solving the inverse kinematics problem.

4. Discussion

In this paper, we addressed the inverse kinematics problem of a mobile manipulator operating in a textile workshop and proposed a CMPSO-based solution capable of achieving high accuracy. By analyzing the coordinate transformation relationships of the mobile manipulator system and adopting the D–H convention, we first established the forward kinematic model of the 9-DOF mobile manipulator. Based on pose error, a “compliance” principle, and joint-limit avoidance, a multi-objective inverse kinematics model was formulated. To overcome the shortcomings of the standard PSO, such as uneven initial population distribution, premature convergence, and a tendency to be trapped in local optima, we introduced three enhancements: Sobol-sequence-based population initialization, logistic-map-based chaotic handling of boundary violations, and a weighted adaptive Gaussian–Cauchy mutation for inferior particles. These components were integrated into a chaotic mutation PSO (CMPSO) algorithm and applied to the multi-objective IK model.

Extensive simulations, including single-point IK solving and trajectory-planning experiments, demonstrated that the proposed CMPSO achieves higher precision and stability compared with the standard PSO and two other enhanced PSO variants (APSO and QPSO). CMPSO consistently yielded the smallest average pose error and variance, indicating superior solution quality and robustness. Moreover, the timing analysis showed that the average computation time per IK query is well below 1 ms, and even the worst-case runtimes satisfy the 4 ms budget required by a 250 Hz control frequency. This implies that the proposed solver is not only suitable for off-line planning, but also has strong potential for real-time control applications, such as online trajectory tracking and whole-body motion generation of mobile manipulators in textile production lines.

Beyond the textile manipulator studied here, the proposed CMPSO framework is largely independent of specific kinematic structures. It requires only the forward kinematics and task-space error definition. As such, it can be extended to other redundant robot systems, including different types of wheeled mobile manipulators and fixed-base manipulators that do not satisfy the Pieper criterion. For these systems, the integrated Sobol initialization, chaotic boundary handling, and adaptive Gaussian–Cauchy mutation are expected to provide similar benefits in terms of maintaining solution-set diversity and improving convergence accuracy in high-dimensional redundant spaces.

From a deployment perspective, several practical considerations will be important for industrial adoption. These include implementing the CMPSO-based IK solver on embedded or industrial controllers with limited computational resources, coping with model uncertainties and sensor noise, and enforcing strict joint, velocity, and workspace constraints to ensure safe operation in cluttered textile factory environments. While the current work focuses on detailed simulations, future research will investigate real-robot validation on a mobile manipulator platform in a textile workshop, integrating the proposed solver with low-level motion controllers and perception modules. This will allow us to evaluate the algorithm under real-world disturbances and hardware limitations and to further refine the method for long-term, reliable deployment in industrial scenarios.