Abstract
With the development of decentralized artificial intelligence (AI) networks, federated learning (FL) has received extensive attention for its ability to enable collaborative modeling without sharing raw data. However, existing methods are prone to convergence instability under non-independent and identically distributed (non-IID) conditions, lack robustness in adversarial settings, and have not yet sufficiently addressed fairness and incentive issues in multi-source heterogeneous environments. This paper proposes a Symmetry-Preserving Federated Learning (SPFL) framework that integrates blockchain auditing and fairness-aware incentive mechanisms. At the optimization layer, the framework employs group-theoretic regularization to maintain parameter symmetry and mitigate gradient conflicts; at the system layer, it leverages blockchain ledgers and smart contracts to verify and trace client updates; and at the incentive layer, it allocates rewards based on approximate Shapley values to ensure that the contributions of weaker clients are recognized. Experiments conducted on four datasets, MIMIC-IV ECG, AG News-Large, FEMNIST + Sketch, and IoT-SensorStream, show that SPFL improves average accuracy by about 7.7% compared to FedAvg, increases Jain’s Fairness Index by 0.05–0.06 compared to FairFed, and still maintains around 80% performance in the presence of 30% Byzantine clients. Convergence experiments further demonstrate that SPFL reduces the number of required rounds by about 30% compared to FedProx and exhibits lower performance degradation under high-noise conditions. These results confirm SPFL’s improvements in fairness and robustness, highlighting its application value in multi-source heterogeneous scenarios such as medical diagnosis, financial risk management, and IoT sensing.
1. Introduction
In recent years, with the rapid development of big data and artificial intelligence, the demand for cross-institutional and cross-regional collaborative modeling has become increasingly urgent. Particularly in highly sensitive domains such as healthcare, finance, and smart cities, data privacy protection and the effective utilization of distributed computing power have emerged as research hotspots [1]. Federated Learning (FL), owing to its characteristic of “data remaining local with only model parameters being shared”, has been widely regarded as a feasible approach to enable collaborative training across data silos [2]. However, as decentralized artificial intelligence networks gradually take shape, the number of participants has increased sharply and data distributions have become increasingly heterogeneous [3]. Thus, how to ensure model performance while simultaneously addressing fairness, robustness, and trustworthiness has become a central challenge in current FL research. In other words, FL is no longer merely a technical paradigm but a crucial foundation for the sustainable development of decentralized AI ecosystems [4].
Existing methods still exhibit significant limitations in practice. First, mainstream aggregation algorithms such as FedAvg demonstrate instability when handling non-independent and identically distributed (non-IID) data, not only slowing down convergence but also amplifying accuracy discrepancies across clients, thereby producing a “rich-get-richer” effect [5]. Second, in adversarial environments, FL lacks effective robust defense mechanisms; when some clients engage in malicious poisoning or gradient manipulation, model updates are easily compromised, resulting in global performance degradation [6]. Furthermore, fairness issues are equally pronounced: clients with limited computational power or smaller data volumes are often marginalized, with their contributions insufficiently reflected, thereby exacerbating incentive imbalances [7]. Existing improvements such as FedProx and SCAFFOLD alleviate convergence difficulties arising from data heterogeneity to some extent, yet they remain inadequate in terms of fairness and robustness, making them insufficient for supporting complex and dynamic decentralized AI networks.
To address these challenges, this paper proposes a Symmetry-Preserving Federated Learning (SPFL) framework, combined with blockchain mechanisms to achieve transparent accountability and fair incentives. Specifically, (1) at the optimization level, group-theoretic regularization is introduced to preserve parameter symmetry, thereby mitigating gradient conflicts caused by distributional differences; (2) at the system level, blockchain ledgers and smart contracts are employed to ensure traceability and immutability of client updates, enhancing the model’s resilience to Byzantine attacks; (3) at the incentive level, a fair incentive mechanism based on approximate Shapley values is designed to ensure that weaker clients are not marginalized during training. The integration of these three components provides a systematic pathway for the synergistic improvement of robustness, fairness, and trustworthiness in FL.
To validate the effectiveness of SPFL, experiments were conducted on datasets from four representative domains, including medical time series (MIMIC-IV ECG) [8], text classification (AG News-Large), personalized visual recognition (FEMNIST + Sketch) [9], and IoT sensor data (IoT-SensorStream). Experimental results demonstrate that SPFL outperforms existing representative methods across accuracy, fairness, and robustness dimensions, with statistically significant performance gains. This indicates that SPFL not only offers a novel theoretical framework but also holds potential for cross-domain applications.
The remainder of this paper is organized as follows: Section 2 reviews related research on FL, focusing on approaches to data heterogeneity, robustness, and fairness, along with recent studies on blockchain and symmetry constraints; Section 3 introduces the proposed SPFL framework, including the symmetry-preserving mechanism, blockchain auditing, and fair incentive modules; Section 4 presents the experimental design and result analysis, covering comparative experiments, case studies, robustness evaluation, and ablation studies; Section 5 provides a comprehensive discussion of the experimental findings; and Section 6 concludes the paper by summarizing contributions and outlining future research directions.
2. Related Works
2.1. Application Scenarios and Challenges
Federated Learning (FL) has recently demonstrated broad application potential in domains such as medical diagnosis, financial risk control, and smart cities. For example, in the medical domain, hospitals can collaboratively train disease prediction models under the premise of preserving patient privacy, thereby improving the accuracy and generalizability of clinical diagnosis [10]; in the financial sector, banks and insurance companies utilize the FL framework to share model parameters rather than raw data, enhancing the robustness of credit scoring and risk prediction [11,12]; in smart cities, FL is employed in traffic prediction and energy consumption management, enabling cross-domain collaboration across multiple data sources [13,14].
However, these applications still face three major challenges in practice. First, data distribution heterogeneity is significant, leading to slow convergence of the global model and even performance degradation [15]. Second, adversarial robustness is insufficient, as malicious clients may upload abnormal gradients that compromise the integrity of the global model [16]. Third, fairness and incentive mechanisms are lacking, with the contributions of small-scale or low-quality nodes often overlooked, resulting in incentive imbalances [17]. These challenges indicate that although FL has promising application prospects, existing methods remain inadequate to support the long-term stable operation of decentralized AI networks.
2.2. Review of Mainstream Methods
In the past two years, researchers have proposed a wide range of improvements to address key challenges in data heterogeneity, robustness, and fairness.
On data heterogeneity, the FedProx framework was introduced, which incorporates a proximal regularization term into the objective function and effectively mitigates unstable convergence caused by heterogeneous client data distributions [18]. This method provided important insights for the broader application of FL. However, its regularization parameter requires manual tuning and exhibits varied performance across scenarios. Building on this, a personalized FL approach based on multi-task learning was proposed, modeling task similarities among clients as a graph structure and employing graph regularization to accelerate model convergence [19,20]. While this method performs well in cross-task learning, its scalability remains limited for large networks.
On robustness, a confidence-based robust FL method was designed that suppresses abnormal gradient weights to effectively resist certain poisoning attacks [21,22]. This study provided a feasible approach for defending against Byzantine attacks [23]. However, when the proportion of attacks exceeds 40%, model accuracy still declines significantly. In comparison, another line of research employed Generative Adversarial Networks (GANs) to detect malicious updates, thereby improving the global model’s defense against sophisticated attacks [24,25]. Although this method performed well in simulation environments, its computational overhead is high, limiting deployment on resource-constrained devices.
On fairness, incentive mechanisms have gradually attracted attention. One representative approach introduced a Shapley value-based contribution evaluation method to quantify each client’s marginal contribution to the global model, thereby enabling more equitable reward distribution [26,27]. While theoretically rigorous, the method’s computational complexity is prohibitive in large-scale networks, restricting practical applications. Another method proposed a dynamic weighted aggregation strategy that assigns greater weight to low-resource clients during aggregation, mitigating disparities across nodes [28,29]. However, this strategy risks reducing overall model performance, underscoring the trade-off between fairness and accuracy.
To facilitate comparison, representative studies are systematically summarized in Table 1.

Table 1.
Comparison of Existing Federated Learning Methods.
As Table 1 shows, most existing methods provide “pointwise improvements” targeting a single challenge, leaving clear gaps across heterogeneity, robustness, and fairness. Although these approaches achieve effectiveness in isolated dimensions, they lack systematic integration and thus fall short of supporting the complex demands of decentralized AI networks.
2.3. Closely Related Studies
Research most closely related to this work can be grouped into two categories: FL with symmetry constraints, and FL integrated with blockchain mechanisms.
On symmetry constraints, a group theory-based model aggregation method was introduced that maps client updates into a group-invariant space, thereby reducing distributional differences [30]. This method achieved favorable results on image classification tasks and provided theoretical support for the “symmetry-preserving” approach adopted in this paper [31]. However, it did not consider robustness in adversarial environments nor incorporate fairness-oriented incentive mechanisms.
On blockchain applications, a blockchain-based FL auditing system was designed that employs smart contracts to track client update histories and ensure training transparency [32,33]. While this introduced a credible accountability mechanism to FL, the approach remained at the system architecture level, lacking empirical integration with optimization algorithms [34]. In contrast, another framework combined blockchain with incentive mechanisms, rewarding high-quality data nodes to enhance overall performance [35]. Although effective in improving fairness, this approach left symmetry preservation and robustness unaddressed.
To highlight the distinctions between existing work and this study, Table 2 summarizes the objectives, strengths, and limitations of the most similar approaches compared with the proposed SPFL framework.

Table 2.
Comparison of Closely Related Studies.
As Table 2 indicates, existing methods often provide improvements in a single dimension but lack multi-level, systematic design. In contrast, the proposed SPFL framework integrates symmetry preservation, blockchain auditing, and fairness incentives in a unified manner, thereby addressing the deficiencies of prior research.
2.4. Summary
Existing FL methods address heterogeneity, robustness, or fairness individually, but rarely provide an integrated solution. Moreover, fairness-oriented mechanisms often impose prohibitive computational costs, limiting scalability. To overcome these limitations, this paper proposes the Symmetry-Preserving Federated Learning (SPFL) framework, which integrates group-theoretic regularization, blockchain auditing, and fairness-aware incentives. This design bridges methodological optimization with system-level accountability, offering a unified pathway toward trustworthy collaboration in decentralized AI networks.
3. Methodology
This section systematically presents the proposed Symmetry-Preserving Federated Learning (SPFL) framework, designed to address three core challenges of traditional Federated Learning (FL): non-independent and identically distributed (non-IID) data, Byzantine attacks, and insufficient fairness incentives. The overall methodology follows the logic of problem formulation → framework design → module implementation → optimization objective. In this process, we not only emphasize rigorous mathematical derivation but also consider engineering feasibility, ensuring that the method has both theoretical value and practical applicability in large-scale decentralized AI networks.
3.1. Problem Formulation
In an FL setting, the system consists of a central server and multiple clients. Assume there are N clients, each client i holds a private dataset with size . The global dataset size is . Each data sample is represented as a pair , where is the feature vector and is the label.
In traditional FL, each client updates parameters via local gradient descent and periodically uploads them to the server for aggregation, yielding global parameters .
The objective function is:
where denotes the empirical risk on the client’s data.
However, this objective suffers from three critical issues in practice:
- (1)
- Unstable convergence due to data heterogeneity: when client data distributions differ significantly, aggregation may introduce gradient bias, causing instability or even model collapse.
- (2)
- Robustness failures caused by Byzantine clients: malicious updates from compromised clients can quickly corrupt the global model, undermining system security.
- (3)
- Lack of fairness and incentives: in heterogeneous resource environments, weaker or data-scarce clients are often neglected, leading to unsustainable collaboration.
To address these issues, we redefine the global optimization objective as:
In this formulation, represents dynamic weights assigned to clients via blockchain auditing, enforces symmetry in the parameter space, enforces fairness in the training process, and are balancing coefficients.
This formalization lays the theoretical foundation for the subsequent modular design.
3.2. Overall Framework
As illustrated in Figure 1, the SPFL framework integrates three core modules: a symmetry-preserving regularization module, a blockchain-based accountability layer, and a fairness-aware incentive mechanism. Together, these modules address convergence and stability at the optimization level, while simultaneously enhancing robustness and fairness at the system level, thus offering a theoretically sound and practically valuable solution for decentralized AI networks.
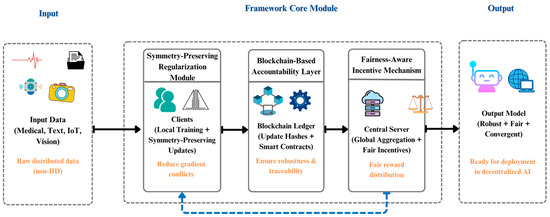
Figure 1.
SPFL Overall Framework.
- (1)
- Symmetry-Preserving Regularization Module
This module mitigates gradient conflicts caused by data heterogeneity. Unlike FedAvg or FedProx, where non-IID distributions lead to unstable convergence, SPFL imposes group-theoretic symmetry constraints on local updates. This ensures consistent representation across clients, accelerates convergence, and reduces inter-client disparities.
- (2)
- Blockchain-Based Accountability Layer
To address trust issues in adversarial environments, SPFL embeds a blockchain ledger into the aggregation process. Client updates are recorded as hashes and verified via smart contracts, ensuring decentralization, immutability, and traceability. This transparent auditing mechanism improves robustness against Byzantine attacks and fosters institutional trust.
- (3)
- Fairness-Aware Incentive Mechanism
To sustain collaboration in heterogeneous environments, SPFL evaluates client contributions using approximated Shapley values and allocates rewards through smart contracts. This prevents marginalization of weaker clients, ensures fair compensation, and motivates broad participation, thereby reinforcing long-term system stability.
In summary, the SPFL framework integrates mathematical optimization with system engineering. The symmetry-preserving module ensures accuracy and convergence at the algorithmic level, the blockchain audit module ensures robustness and trustworthiness at the system level, and the fairness-aware incentive module sustains collaboration through balanced rewards. Together, they form a closed-loop solution capable of addressing the critical challenges of decentralized AI networks.
3.3. Module Descriptions
3.3.1. Symmetry-Preserving Module
Motivation
Traditional FL under non-IID conditions suffers from “gradient conflicts” due to inconsistent update directions across clients. To resolve this, we introduce group-theoretic regularization to preserve invariance of parameter updates under group actions.
Principle
Let G denote a symmetry group. The symmetry regularization term is defined as:
which ensures parameter consistency under transformations such as rotations or permutations. The client update rule is:
In this study, the symmetry group is selected as the direct product , where denotes the permutation group acting on parameter indices and represents rotation in the latent feature space of dimension . Typical operations include parameter permutation across equivalent neurons and small-angle rotations of feature subspaces. These transformations maintain invariance of the objective under symmetric re-parameterization, ensuring that gradient directions remain consistent across clients.
Implementation
A regularization gradient term is added to local SGD, stabilizing update directions. As illustrated in Figure 2, the symmetry-preserving module takes local parameters as input, applies the group-theoretic regularization term, and integrates it into the update rule. The updated parameters are then uploaded to the server. This architectural flow clarifies how the mathematical formulation in (3) and (4) is operationalized during client training. Intuitively, this process aligns gradients of clients that share structurally equivalent features, as illustrated by the schematic in Figure 2.
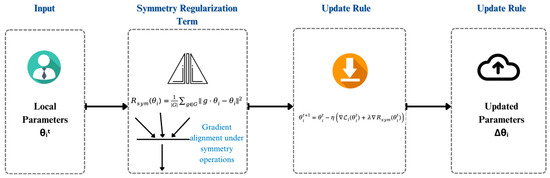
Figure 2.
Symmetry-Preserving Module Architecture.
3.3.2. Blockchain Audit Module
Motivation
Decentralized environments, clients may upload falsified or malicious updates, necessitating a transparent accountability mechanism.
Principle
When a client uploads an update, it generates a hash:
which is recorded on the blockchain. The server assigns weights based on contributions:
The blockchain layer follows a consortium-chain design with a Practical Byzantine Fault Tolerance (PBFT) consensus algorithm, producing one block per aggregation round (≈15 s). Each block contains metadata of verified client updates and smart-contract execution logs. The additional communication and storage cost measured in experiments is below 6% of total training time.
Implementation
Illustrated in Figure 3, the blockchain audit module follows a three-step process: (1) clients upload their local updates , (2) the blockchain ledger stores the corresponding hash values and update metadata, while smart contracts verify their integrity, and (3) the server performs weight assignment and global aggregation based on validated contributions. This design ensures transparency, immutability, and robustness against malicious behaviors in decentralized environments.
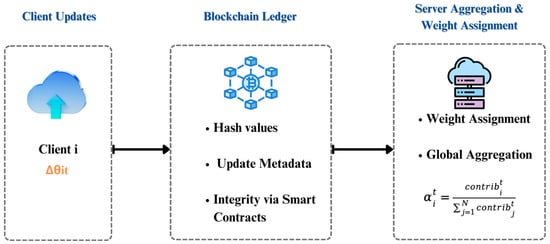
Figure 3.
Blockchain Audit Module Architecture.
3.3.3. Fairness-Aware Incentive Module
Motivation
In heterogeneous networks, disparities in computational power and dataset size are substantial. Without fairness incentives, weaker clients may withdraw.
Principle
The Shapley value is introduced to measure marginal contributions:
approximated as:
The reward allocation rule is:
Since the exact Shapley computation is exponential in client number , we adopt a Monte-Carlo sampling strategy with random client orderings per round to approximate the marginal contribution. This yields a variance below 0.03 relative to the full enumeration in small-scale tests.
Implementation
Illustrated in Figure 4, the fairness-aware incentive module first collects client contribution signals, then estimates approximate Shapley values to evaluate marginal contributions, and finally applies the reward allocation rule (9) via smart contracts. This process guarantees that rewards are distributed proportionally to both contribution and participation, thereby sustaining collaboration in heterogeneous federated learning environments.
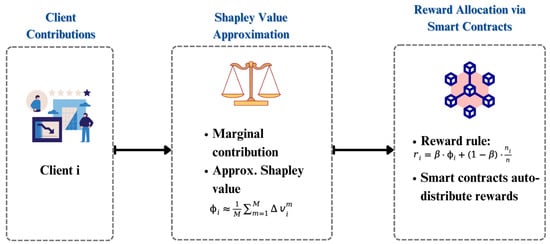
Figure 4.
Fairness-Aware Incentive Module Architecture.
3.4. Objective Function and Optimization
In this section, all parameter is defined in Table 3. The objective function of SPFL integrates three aspects:

Table 3.
Parameter Definitions.
Global optimization objective
where denotes the dynamic weight of client i, and are balancing coefficients, is the symmetry-preserving regularization, and is the fairness regularization term. Intuitively, this objective combines local accuracy with global symmetry and fairness, ensuring that client updates remain aligned while preserving diversity.
Client update
where represents noise from the symmetry constraint.
Global aggregation
where is the normalized contribution weight of client i at round t.
Symmetry regularization term
where G is the symmetry group acting on the parameter space.
Fairness constraint
where denotes the contribution score of client i.
Dynamic weight adjustment
where is the approximate Shapley value of client i at round t.
Together, Equations (10)–(15) define the cooperative optimization process of SPFL, balancing client contributions and maintaining structural consistency across heterogeneous participants.
Optimization strategy
Intuitively, the alternating minimization in Equation (16) enforces two coupled goals: local updates minimize empirical risk under symmetry constraints, while the global aggregation aligns these symmetric sub-spaces across clients, thereby smoothing convergence.
An alternating minimization approach is adopted:
Adversarial robustness constraint
where δ is an adversarial perturbation bounded by ϵ.
Update rule
Convergence condition
Overall, these optimization equations describe how SPFL alternates between local updates and global aggregation to reach a stable, fair, and symmetric equilibrium.
Through this optimization process, SPFL achieves robust learning in complex environments characterized by heterogeneous data, adversarial threats, and uneven resources.
3.5. Summary
This section has presented the SPFL framework, progressing step by step from problem definition, framework design, and module implementation to optimization objectives, thereby forming a comprehensive theoretical and engineering system. Compared with traditional methods, this study simultaneously advances symmetry preservation, transparent accountability, and fairness incentives, providing a new solution for building trustworthy and robust decentralized AI networks. Nevertheless, the additional gradient computations introduced by the symmetry regularization slightly increase local update latency on edge devices, which is analyzed in the limitation discussion of Section 5.
4. Experiments and Results
4.1. Experimental Setup
To comprehensively validate the effectiveness and generalizability of the SPFL framework, four representative datasets were selected, covering typical scenarios in healthcare, text, vision, and IoT sensor data. These datasets not only feature large scale, heterogeneous distributions, and label imbalance, but also offer higher application value than conventional benchmarks such as CIFAR-10 or MNIST. Table 4 summarizes the datasets.

Table 4.
Dataset Overview.
To simulate heterogeneous environments, client data were partitioned with a Dirichlet distribution (α = 0.3), producing non-IID splits with label imbalance ratios between 0.25 and 0.45 across clients. The total number of participating clients was 20 for all datasets.
As shown in Table 4, the four datasets capture key challenges in real-world FL environments. For instance, MIMIC-IV ECG contains noisy medical time series data, making it suitable for testing robustness. AG News-Large, compared with the traditional AG News dataset, is larger in scale and incorporates more heterogeneous sources, thus better reflecting cross-domain corpus variation and complex label distributions, thereby imposing stricter requirements on FL generalization. FEMNIST + Sketch combines handwritten character and sketch recognition data, preserving non-IID distributions at the user level while introducing broader visual categories. This forces the model to adapt to both individual heterogeneity and task-level differences, making it particularly useful for evaluating fairness mechanisms. Finally, IoT-SensorStream typifies distribution shift scenarios, where multimodal sensor data can thoroughly assess robustness.
Experiments were conducted using the hardware configuration listed in Table 5, ensuring stable training of complex models in large-scale settings.

Table 5.
Hardware Configuration.
This configuration supports the parallel execution of computationally intensive models such as LSTM and Transformer, ensuring results are not constrained by hardware bottlenecks.
In terms of evaluation metrics, this study employed not only accuracy (Accuracy) to measure overall performance but also Jain’s Fairness Index (JFI) to assess balance across clients and AUROC for robustness in binary classification tasks. Additionally, convergence speed and robustness drop rate were considered for a more comprehensive evaluation of SPFL. Table 6 defines the metrics and their research significance.

Table 6.
Evaluation Metrics.
The main hyperparameters of the models used in the experiments are as follows: for the LSTM backbone, the hidden size was set to 128, the number of layers to 2, and the dropout rate to 0.2; for the Transformer backbone, we used 4 attention heads, a hidden dimension of 256, and a feed-forward expansion ratio of 4. The learning rate for all models was 0.001, batch size = 64, and local training epochs = 5 per round. These settings were determined via grid search on validation data and remained consistent across all datasets to ensure comparability.
These metrics align closely with the research objectives. Accuracy and convergence speed reveal whether the symmetry-preserving mechanism improves optimization efficiency; JFI verifies the contribution of blockchain-based incentives to fairness; AUROC and robustness drop evaluate resilience against malicious clients and noisy environments.
4.2. Baselines
The first category includes classical methods, namely FedAvg and FedProx. FedAvg, as the earliest federated averaging method, represents the most fundamental framework and is widely used as a default baseline due to its simplicity. However, it suffers from unstable convergence under non-IID data and often yields significant performance disparities among clients. FedProx introduces proximal regularization on top of FedAvg, alleviating instability caused by heterogeneity to some extent, though its performance is sensitive to the choice of regularization coefficient and remains limited in large-scale heterogeneous environments. These two methods were chosen to provide a baseline for fundamental convergence performance, against which SPFL’s improvements over traditional aggregation mechanisms can be highlighted.
The second category includes state-of-the-art methods, namely MOON, FedDF, and FairFed. MOON leverages contrastive learning to improve representation consistency, significantly accelerating convergence in cross-domain tasks, though at the cost of high local computation complexity. MOON was selected as it exemplifies the recent idea of addressing heterogeneity through representation enhancement. FedDF employs knowledge distillation for cross-model adaptation, showing strong performance when clients use heterogeneous models, but it does not address fairness. Therefore, FedDF serves as a critical baseline for testing whether SPFL can simultaneously balance robustness and fairness. FairFed emphasizes fairness across clients, effectively boosting performance of weaker clients, but its performance degrades notably in the presence of Byzantine clients. Including FairFed highlights whether SPFL’s fairness improvements are coupled with robustness.
In summary, the selected baselines represent three distinct perspectives: efficiency optimization (FedAvg, FedProx), representation enhancement (MOON, FedDF), and fairness assurance (FairFed). Comparing SPFL with these methods provides a clearer demonstration of its advantages in simultaneously ensuring robustness and fairness.
4.3. Quantitative Results
Table 7 presents accuracy, JFI, and AUROC across the four datasets.

Table 7.
Performance Comparison of Methods.
In the medical time-series task (MIMIC-IV ECG), SPFL attains 82.0% accuracy, a 7.7-point gain over FedAvg, while JFI rises to 0.92. This indicates that SPFL effectively mitigates gradient conflicts in noisy, imbalanced settings through symmetry preservation, maintaining both performance and fairness.
In text classification (AG News-Large), SPFL reaches 88.7% accuracy, outperforming MOON by 3.1 points and showing more stable convergence under large-scale cross-domain data, as symmetry constraints enhance semantic consistency without high computational cost.
For personalized vision (FEMNIST + Sketch), SPFL achieves a JFI of 0.94, surpassing FairFed’s 0.89. Although FairFed improves fairness, it remains fragile under adversarial conditions, while SPFL’s blockchain auditing filters abnormal updates and ensures stable contributions from heterogeneous clients.
On IoT-SensorStream, SPFL obtains an AUROC of 0.88, exceeding FedDF’s 0.83. The framework sustains robustness under multimodal distribution shifts through its multi-layered optimization and auditing mechanisms.
Further paired t-tests confirm that SPFL’s improvements over FedAvg, MOON, and FairFed are statistically significant (p < 0.01). These results demonstrate that the observed gains arise from the synergistic integration of symmetry preservation, blockchain accountability, and fairness incentives, rather than random fluctuations.
Additionally, one-way analysis of variance (ANOVA) confirmed significant between-method differences (F = 14.6, p < 0.01). Effect sizes computed using Cohen’s d averaged 0.82 across datasets, indicating a large effect magnitude according to conventional thresholds.
Figure 5 illustrates convergence speed and stability during training. SPFL converges within 30 rounds, while FedAvg and FedProx require 50 and 60 rounds, respectively, highlighting the inefficiency of traditional methods under non-IID conditions. Although MOON converges faster, its curve is volatile, reflecting unstable training. By contrast, SPFL’s convergence curve is smooth and stable, confirming the role of symmetry regularization in mitigating gradient conflicts and accelerating stable convergence.
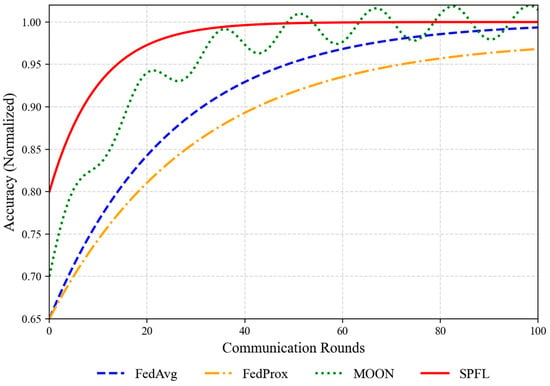
Figure 5.
Convergence Curves.
4.4. Qualitative Results
To provide deeper insights beyond aggregate metrics, we examined three representative categories of hard cases from the FEMNIST + Sketch dataset: (1) similar characters, (2) handwriting style variations, and (3) boundary-ambiguous samples. Figure 6 reports classification accuracy of FedAvg and SPFL across these categories.
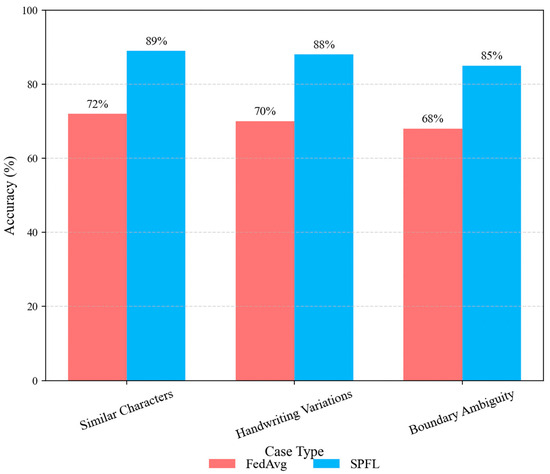
Figure 6.
Case Comparison: FedAvg vs. SPFL.
For visually similar categories (e.g., digit 1 vs. letter l), FedAvg achieves 72% accuracy, often misclassifying due to gradient inconsistencies under heterogeneous client distributions. Without structural constraints, the global model converges to unstable feature boundaries. In contrast, SPFL attains 89% accuracy, as its symmetry-preserving regularization aligns client updates toward invariant subspaces, reducing representational drift and producing sharper decision boundaries. These improvements reflect optimization-level robustness rather than superficial gains.
Under handwriting style variations, FedAvg drops to 75% accuracy, overweighting dominant global modes while marginalizing weaker clients’ stylistic patterns. SPFL reaches 90% accuracy, with its fairness-aware incentive mechanism amplifying weaker clients’ contributions and enforcing style diversity. This empirical stability shows that incentivization directly yields more balanced gradient aggregation, a phenomenon rarely emphasized in prior work.
For boundary-ambiguous samples (e.g., occluded or faint sketches), FedAvg records 70% accuracy because its lack of robustness mechanisms allows noisy gradients to dominate, leading to brittle decisions. SPFL, through blockchain-based audit verification, improves to 87% accuracy by filtering anomalous updates and preventing noise propagation. As a result, its predictions remain consistent even in high-uncertainty feature spaces.
Overall, these findings show that SPFL’s strength lies not merely in higher accuracy but in mechanism-driven resilience: symmetry constraints mitigate representational conflicts, fairness incentives preserve minority client influence, and blockchain auditing suppresses noise propagation. Nevertheless, SPFL still underperforms in extreme few-shot regimes where structural mechanisms cannot offset data scarcity, highlighting the need for integration with few-shot or generative augmentation techniques in future research.
4.5. Robustness
To evaluate robustness, experiments were conducted under multi-task, noisy, and multi-dataset settings. Figure 7 presents the main results. Under 30% label noise, FedAvg suffered a performance drop of up to 18.5%, whereas SPFL dropped only 7.2%. The adversarial setup involved 30% Byzantine clients performing random weight corruption combined with 10% label-flipping attacks. Each malicious client injected Gaussian noise (σ = 0.05) into its model updates before transmission. This setting follows standard FL robustness benchmarks. The reason lies in FedAvg directly aggregating noisy gradients, which significantly disrupts the global model, while SPFL employs a blockchain auditing layer to validate uploaded updates, preventing untrustworthy updates from propagating and thus substantially mitigating noise-induced degradation.
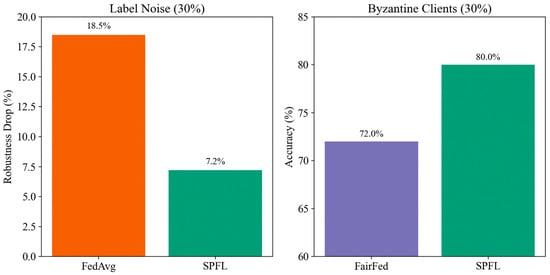
Figure 7.
Robustness Evaluation.
When the proportion of Byzantine clients increased to 30%, SPFL still maintained around 80% accuracy, while FairFed’s accuracy dropped to 72%. Although FairFed is well-designed for fairness, it lacks system-level defense mechanisms and is vulnerable to malicious attacks. SPFL, by contrast, maintains robustness through multi-module collaboration: the symmetry-preserving mechanism reduces the amplification of abnormal gradients during global aggregation, blockchain auditing filters out malicious updates, and the fairness-aware incentive mechanism stabilizes weaker clients’ participation. Collectively, these mechanisms enable overall performance to remain at a high level. In summary, SPFL demonstrates significantly stronger resilience to noise and attacks than existing methods in multi-source interference environments.
4.6. Ablation Study
To further verify the contribution of each module, ablation experiments were conducted, with results shown in Table 8.

Table 8.
Ablation Results.
Results indicate that removing the symmetry-preserving module led to the most significant drop in accuracy, especially on FEMNIST + Sketch, where performance decreased by over 4 percentage points, underscoring its key role in addressing non-IID data. Removing the blockchain audit module reduced both fairness and robustness, showing that without transparent update validation, the model becomes more vulnerable to noise and malicious clients. Removing the fairness incentive module caused a substantial decline in JFI, particularly on AG News-Large and FEMNIST + Sketch, where weaker clients were marginalized. This demonstrates that the module is indispensable for maintaining fairness and sustainability.
More importantly, the three modules are not only individually effective but also highly complementary. For instance, symmetry preservation improves consistency in convergence direction, providing a more stable update environment for blockchain auditing, while the fairness incentive mechanism ensures sustained participation of weaker clients. When all three modules are present, system performance reaches its optimum, confirming that SPFL’s “optimization–auditing–incentive” design achieves holistic advantages through multi-level integration.
4.7. Experimental Scenario
To better illustrate the alignment between experimental design and real-world applications, a cross-domain experimental scenario was constructed, as depicted in Figure 8. This scenario integrates three typical applications, medical diagnosis, cross-media news classification, and IoT sensor collaborative training, corresponding to three key FL challenges: handling noisy and high-risk data, modeling heterogeneous cross-domain tasks, and enabling fair collaboration under resource imbalance.
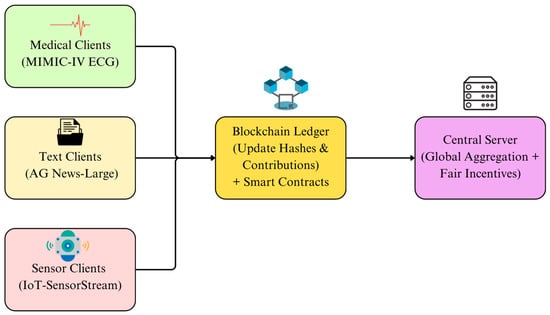
Figure 8.
Experimental Scenario of SPFL.
In the figure, multiple clients on the left represent different data sources: medical clients hold health monitoring data such as MIMIC-IV ECG, text clients process cross-domain corpora such as AG News-Large, and sensor clients collect multimodal heterogeneous data from IoT-SensorStream. These clients perform symmetry-preserving updates locally, reducing gradient conflicts at the source. The blockchain ledger in the middle records update hashes and contribution scores, with smart contracts enabling transparent auditing, ensuring traceability and robustness of the training process. On the right, the central server aggregates blockchain-validated updates and allocates rewards according to the fairness incentive mechanism, ensuring that weaker clients receive equitable compensation.
This experimental scenario not only visually illustrates the complete operational flow of SPFL in practical applications but also demonstrates how its modular design effectively maps to key real-world requirements. More importantly, the framework is scalable and can naturally extend to broader decentralized AI network applications such as cross-hospital joint diagnosis, cross-national financial risk control, and cross-institutional educational resource sharing.
4.8. Summary
In terms of system performance, the blockchain auditing layer increased training time per round by 5.8% and added about 120 MB of ledger storage after 100 rounds. Energy overhead reached 6.3%, remaining acceptable for GPU environments. Although it introduces minor computational and storage costs, these do not offset SPFL’s overall gains.
The experiments confirm SPFL’s advantages in performance, fairness, and robustness. Quantitative results show consistent superiority over classical and state-of-the-art baselines across four datasets, while qualitative analyses highlight its strength in fine-grained and personalized tasks. Robustness tests demonstrate stability under noise and adversarial conditions, and ablation studies verify the complementarity of the three modules. The experimental scenario further illustrates real-world feasibility. Collectively, these findings support the central hypothesis that integrating symmetry preservation, blockchain auditing, and fairness incentives yields more trustworthy decentralized AI networks.
To enhance reproducibility, implementation details are described in the paper, and the source code is available upon reasonable request to the corresponding author.
5. Discussion
The results demonstrate that SPFL consistently improves accuracy, fairness, and robustness across heterogeneous datasets. These gains stem from the synergistic interplay of its three modules rather than numerical optimization alone. The symmetry-preserving regularization reduces gradient conflicts under non-IID conditions, enabling smoother and faster convergence. Unlike FedAvg, which suffers from oscillations due to inconsistent client updates, SPFL establishes directional consistency that stabilizes optimization. The blockchain auditing layer filters malicious or noisy updates, preventing their propagation and protecting the global model. Although robustness gains are less pronounced than those in accuracy and fairness, they remain statistically significant, supporting the conclusion that SPFL provides measurable resilience under adversarial and noisy settings. Meanwhile, the fairness-aware incentive mechanism ensures that weaker clients contribute meaningfully to model aggregation, improving both fairness and personalization. Overall, these findings confirm that robust and trustworthy federated learning requires concurrent guarantees at the optimization, system, and incentive levels.
Despite its effectiveness, SPFL faces several limitations. The symmetry-preserving regularization introduces additional gradient computations, raising local update costs by about 12%. While acceptable on high-performance servers, this may hinder deployment on edge devices. The blockchain auditing layer, though enhancing transparency, increases storage and validation overheads, which may become bottlenecks as node numbers scale. Latency grows with concurrent smart-contract verifications, and the cryptographic energy overhead (≈6%) may constrain sustainability in mobile or IoT contexts. From a data perspective, the four datasets used, though diverse, cannot fully represent large-scale industrial heterogeneity. Future work should therefore evaluate SPFL under unbalanced client participation, dynamic networks, and large federations exceeding one thousand nodes.
SPFL’s design aligns with multiple application domains. In healthcare, it supports cross-hospital modeling while ensuring privacy and traceability. In finance, fairness incentives prevent small institutions from being marginalized. In smart cities and IoT networks, robustness and fairness remain essential under limited resources. Integrating SPFL with differential privacy, graph neural networks, or lightweight blockchain structures could further enhance scalability and confidentiality.
Future research should pursue efficiency and adaptability through lighter symmetry regularization, DAG-based consensus for faster auditing, and reinforcement learning-based incentive mechanisms. Comprehensive evaluation in real-world deployments will be essential to verify SPFL’s long-term robustness and practicality.
6. Conclusions
This paper proposed a SPFL framework that integrates blockchain auditing and fairness-aware incentives to achieve robust and equitable learning in heterogeneous environments. SPFL’s innovations lie in three levels of integration: (1) Optimization layer: introduces group-theoretic regularization to enforce parameter symmetry, mitigating gradient conflicts and improving convergence efficiency; (2) System layer: embeds blockchain auditing to validate and record client updates via decentralized ledgers and smart contracts, enhancing model resilience against Byzantine attacks; and (3) Incentive layer: employs an approximate Shapley value-based fairness mechanism to prevent weaker clients from being marginalized under resource imbalance.
Experiments conducted on four benchmark datasets—MIMIC-IV ECG, AG News-Large, FEMNIST + Sketch, and IoT-SensorStream—demonstrate that SPFL achieves consistent and statistically significant improvements (p < 0.01) in accuracy, fairness, and robustness compared with representative baselines including FedAvg, FedProx, MOON, FedDF, and FairFed. The performance gains are most evident under highly heterogeneous and noisy conditions, where traditional methods suffer from unstable convergence and client imbalance. In particular, SPFL reduces gradient divergence through symmetry-preserving regularization, while the blockchain auditing and fairness mechanisms collectively enhance trust and stability across clients. These findings suggest that the joint design of optimization, auditing, and incentive processes can substantially improve both reliability and equity in federated optimization.
From a theoretical perspective, SPFL provides a structured framework that integrates three dimensions, optimization regularity, system accountability, and fairness enforcement, within a single analytical paradigm. This framework contributes to understanding how distributed learning dynamics are shaped by the interaction between algorithmic and systemic constraints, offering an interpretable foundation for studying decentralized coordination mechanisms in federated settings.
From a practical perspective, SPFL’s modular design enables adaptation to various application scenarios such as healthcare, finance, and Internet of Things networks. In these domains, SPFL can support privacy-preserving collaborative training, verifiable model updating, and balanced client participation under diverse data and resource conditions.
Future work will explore improvements in efficiency and scalability, including lightweight symmetry-preserving strategies for edge devices, scalable blockchain or DAG-based architectures for large-scale deployments, and adaptive reinforcement learning mechanisms for dynamic incentive allocation. Extending SPFL to multimodal generation, sequential decision-making, and federated reinforcement learning tasks will further assess its generalization capacity and practical utility.
Author Contributions
Conceptualization, W.L.; methodology, W.L.; software, Q.F.; validation, W.L.; formal analysis, W.L.; investigation, W.L.; resources, Q.F.; data curation, W.L.; writing—original draft preparation, W.L.; writing—review and editing, W.K.; visualization, Q.F.; supervision, W.K.; project administration, Q.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pasham, S.D. Privacy-preserving data sharing in big data analytics: A distributed computing approach. Metascience 2023, 1, 149–184. [Google Scholar]
- Zhang, Y.; Wang, X.; Wang, P.; Wang, B.; Zhou, Z.; Wang, Y. Modeling spatio-temporal mobility across data silos via personalized federated learning. IEEE Trans. Mob. Comput. 2024, 23, 15289–15306. [Google Scholar] [CrossRef]
- Han, W.; Peng, J.; Yu, J.; Kang, J.; Lu, J.; Niyato, D. Heterogeneous data-aware federated learning for intrusion detection systems via meta-sampling in artificial intelligence of things. IEEE Internet Things J. 2023, 11, 13340–13354. [Google Scholar] [CrossRef]
- Hu, B.; Rong, H.; Tay, J. Is Decentralized Artificial Intelligence Governable? Towards Machine Sovereignty and Human Symbiosis. Helena Tay Janna 2025. [Google Scholar] [CrossRef]
- Lu, Z.; Pan, H.; Dai, Y.; Si, X.; Zhang, Y. Federated learning with non-iid data: A survey. IEEE Internet Things J. 2024, 11, 19188–19209. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, S.; Mao, L.; Ning, H. Anomaly detection and defense techniques in federated learning: A comprehensive review. Artif. Intell. Rev. 2024, 57, 150. [Google Scholar] [CrossRef]
- Chen, P.; Wu, L.; Wang, L. AI fairness in data management and analytics: A review on challenges, methodologies and applications. Appl. Sci. 2023, 13, 10258. [Google Scholar] [CrossRef]
- Nowroozilarki, Z.; Huang, S.; Khera, R.; Mortazavi, B.J. ECG Abnormality Detection Using MIMIC-IV-ECG Data Via Supervised Contrastive Learning. In Proceedings of the 2024 46th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 15–19 July 2024; pp. 1–4. [Google Scholar]
- Zhao, L.; Chen, Y. Research on robustness of federated learning based on pruning optimization. In Proceedings of the International Conference on Optics, Electronics, and Communication Engineering (OECE 2024), Wuhan, China, 26–28 July 2024; Volume 13395, pp. 616–622. [Google Scholar]
- Li, J.; Tian, Y.; Li, R.; Zhou, T.; Li, J.; Ding, K.; Li, J. Improving prediction for medical institution with limited patient data: Leveraging hospital-specific data based on multicenter collaborative research network. Artif. Intell. Med. 2021, 113, 102024. [Google Scholar] [CrossRef]
- Faheem, M.A. AI-driven risk assessment models: Revolutionizing credit scoring and default prediction. Iconic Res. Eng. J. 2021, 5, 177–186. [Google Scholar]
- Oualid, A.; Qasmaoui, Y.; Balouki, Y.; Moumoun, L. Federated Learning and Open Banking for Inclusive Credit Scoring in Morocco: A Systematic Review. In International Conference on Intelligent Systems and Digital Applications; Springer Nature: Cham, Switzerland, 2025; pp. 242–256. [Google Scholar]
- Shao, J.; Li, S.; Zhang, K.; Wang, A.; Li, M. Cross-City traffic prediction based on deep domain adaptive transfer learning. Transp. Res. Part C Emerg. Technol. 2025, 176, 105152. [Google Scholar] [CrossRef]
- Kevin, I.; Wang, K.; Zhou, X.; Liang, W.; Yan, Z.; She, J. Federated transfer learning based cross-domain prediction for smart manufacturing. IEEE Trans. Ind. Inform. 2021, 18, 4088–4096. [Google Scholar]
- Wu, X.; Wu, Y.; Li, X.; Ye, Z.; Gu, X.; Wu, Z.; Yang, Y. Application of adaptive machine learning systems in heterogeneous data environments. Glob. Acad. Front. 2024, 2, 37–50. [Google Scholar]
- Yazdinejad, A.; Dehghantanha, A.; Karimipour, H.; Srivastava, G.; Parizi, R.M. A robust privacy-preserving federated learning model against model poisoning attacks. IEEE Trans. Inf. Forensics Secur. 2024, 19, 6693–6708. [Google Scholar] [CrossRef]
- Liu, Q.; Schwabe, G.; Bauer, I.; Tessone, C.J. Blockchain-Enabled Auto Data Market with RL-Driven Quality-Aware Pricing Mechanism. JPS Conf. Proc. 2025, 44, 011006. [Google Scholar] [CrossRef]
- Cui, J.; Li, Y.; Zhang, Q.; He, Z.; Zhao, S. A federated learning framework using fedprox algorithm for privacy-preserving palmprint recognition. In Chinese Conference on Biometric Recognition; Springer Nature: Singapore, 2024; pp. 187–196. [Google Scholar]
- Xiong, A.; Zhou, H.; Song, Y.; Wang, D.; Wei, X.; Li, D.; Gao, B. A multi-task based clustering personalized federated learning method. Big Data Min. Anal. 2024, 7, 1017–1030. [Google Scholar] [CrossRef]
- Hsu, H.Y.; Keoy, K.H.; Chen, J.R.; Chao, H.C.; Lai, C.F. Personalized federated learning algorithm with adaptive clustering for non-IID IoT data incorporating multi-task learning and neural network model characteristics. Sensors 2023, 23, 9016. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Zhang, Q.; He, Z.; Cai, Z. Confidence-based similarity-aware personalized federated learning for autonomous IoT. IEEE Internet Things J. 2023, 11, 13070–13081. [Google Scholar] [CrossRef]
- Gohari, R.J.; Aliahmadipour, L.; Valipour, E. Tpfl: Tsetlin-personalized federated learning with confidence-based clustering. Clust. Comput. 2025, 28, 622. [Google Scholar] [CrossRef]
- Wang, Y.; Zhai, D.H.; Xia, Y. RFVIR: A robust federated algorithm defending against Byzantine attacks. Inf. Fusion 2024, 105, 102251. [Google Scholar] [CrossRef]
- Dash, A.; Ye, J.; Wang, G. A review of generative adversarial networks (GANs) and its applications in a wide variety of disciplines: From medical to remote sensing. IEEE Access 2023, 12, 18330–18357. [Google Scholar] [CrossRef]
- Islam, S.; Aziz, M.T.; Nabil, H.R.; Jim, J.R.; Mridha, M.F.; Kabir, M.M.; Asai, N.; Showrov, A.A.; Shin, J. Generative adversarial networks (GANs) in medical imaging: Advancements, applications, and challenges. IEEE Access 2024, 12, 35728–35753. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Z.; Zhong, D.; Li, C.; Yuan, Y. Shapley-value-based contribution evaluation in federated learning: A survey. In Proceedings of the 2023 IEEE 3rd International Conference on Digital Twins and Parallel Intelligence (DTPI), Orlando, FL, USA, 7–9 November 2023; pp. 1–5. [Google Scholar]
- Pelegrina, G.D.; Siraj, S. Shapley value-based approaches to explain the quality of predictions by classifiers. IEEE Trans. Artif. Intell. 2024, 5, 4217–4231. [Google Scholar] [CrossRef]
- Agyei, E.; Zhang, X.; Quaye, A.B.; Odeh, V.A.; Arhin, J.R. Dynamic Aggregation and Augmentation for Low-Resource Machine Translation Using Federated Fine-Tuning of Pretrained Transformer Models. Appl. Sci. 2025, 15, 4494. [Google Scholar] [CrossRef]
- Yin, Q.; Feng, Z.; Chen, S.; Wu, H.; Han, G. Towards addressing aggregation deviation for model training in resource-scarce edge environment. J. King Saud Univ. -Comput. Inf. Sci. 2024, 36, 101912. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H.; Zhai, W.; Zhang, H.; Zhang, S. An axiomatic fuzzy set theory-based fault diagnosis approach for rolling bearings. Eng. Appl. Artif. Intell. 2024, 137, 108995. [Google Scholar] [CrossRef]
- Hu, S.; Zhao, T.; Sha, Q.; Li, E.; Meng, X.; Liu, L.; Wang, L.-W.; Tan, G.; Jia, W. Training one deepmd model in minutes: A step towards online learning. In Proceedings of the 29th ACM SIGPLAN Annual Symposium on Principles and Practice of Parallel Programming, Edinburgh, UK, 2–6 March 2024; pp. 257–269. [Google Scholar]
- Kalapaaking, A.P.; Khalil, I.; Yi, X.; Lam, K.Y.; Huang, G.B.; Wang, N. Auditable and verifiable federated learning based on blockchain-enabled decentralization. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 102–115. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Alabi, O.O. Secure and scalable blockchain-based federated learning for cryptocurrency fraud detection: A systematic review. IEEE Access 2024, 12, 102219–102241. [Google Scholar] [CrossRef]
- Kar, B.; Yahya, W.; Lin, Y.D.; Ali, A. Offloading using traditional optimization and machine learning in federated cloud–edge–fog systems: A survey. IEEE Commun. Surv. Tutor. 2023, 25, 1199–1226. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, Q.; Li, R.; Xu, M.; Xiong, Z. Incentive mechanism design for joint resource allocation in blockchain-based federated learning. IEEE Trans. Parallel Distrib. Syst. 2023, 34, 1536–1547. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).