Taylor-Type Direct-Discrete-Time Integral Recurrent Neural Network with Noise Tolerance for Discrete-Time-Varying Linear Matrix Problems with Symmetric Boundary Constraints
Abstract
1. Introduction
- (1)
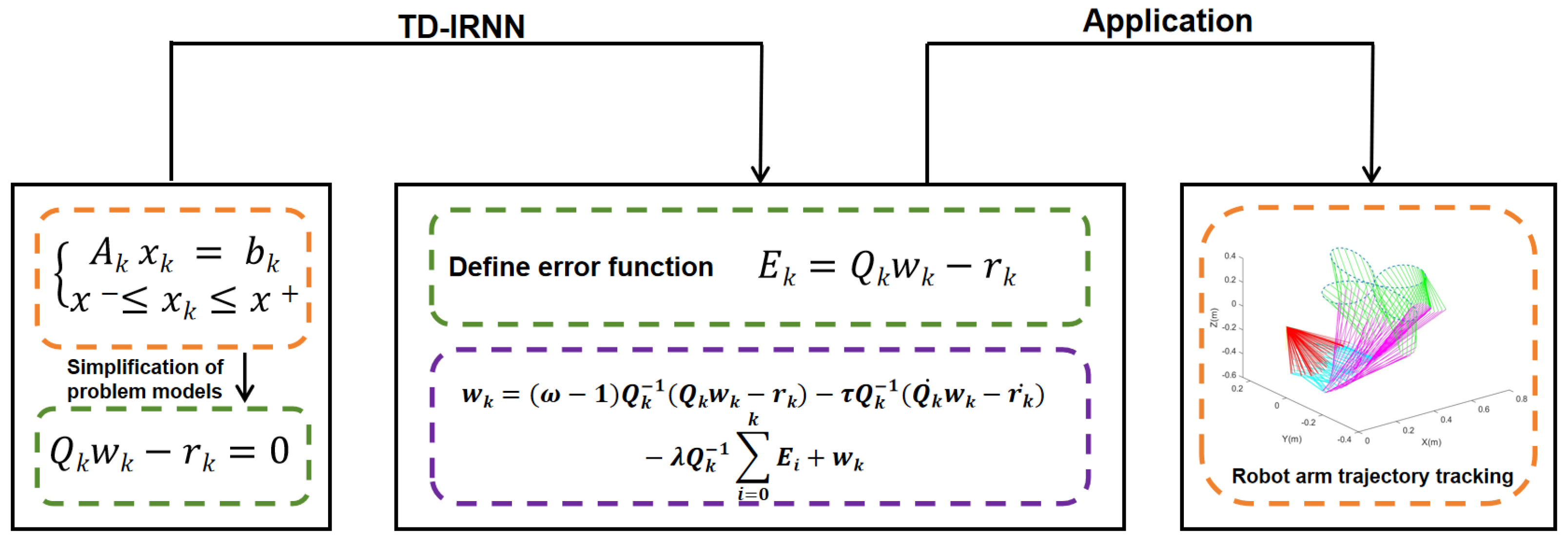
- A novel TD-IRNN model is proposed for solving discrete time-varying linear matrix problem with boundary constraints without relying on continuous-time theory. The complete model formulation and detailed derivation process are provided.
- (2)
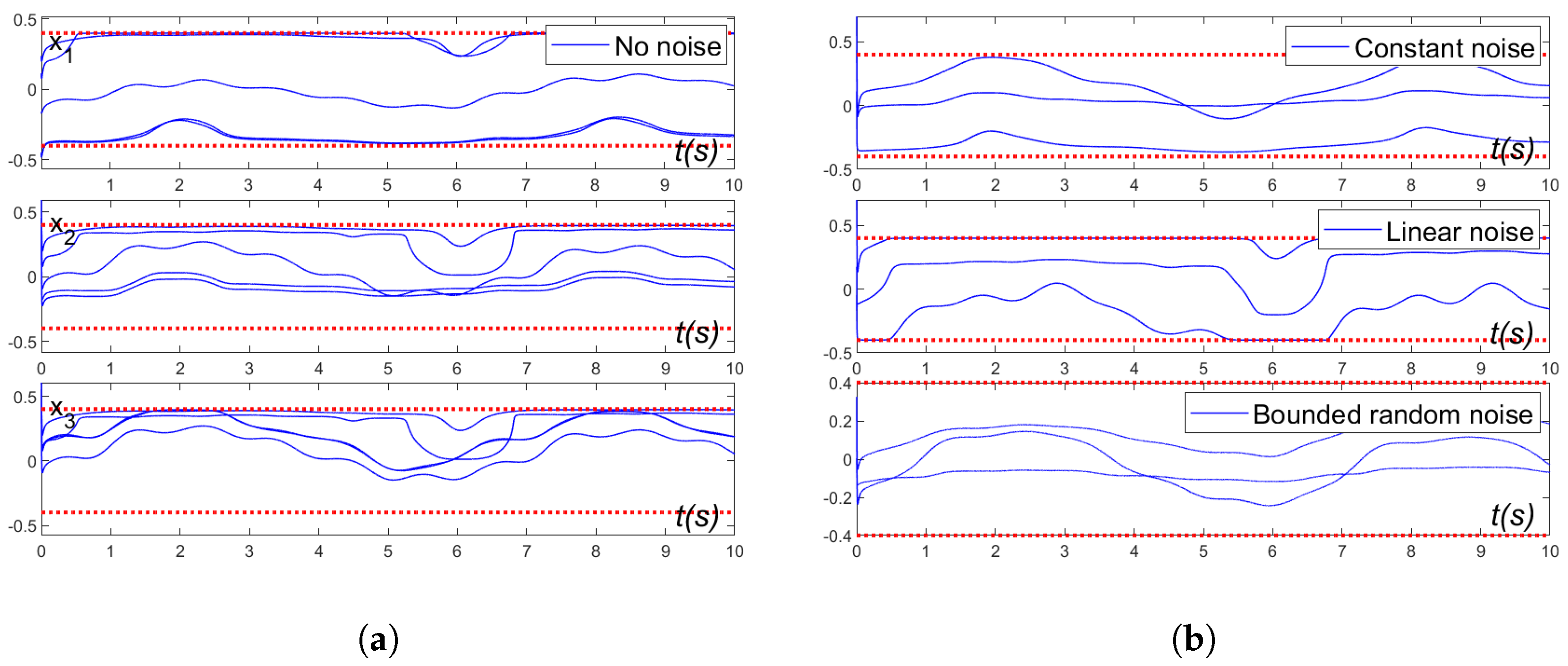
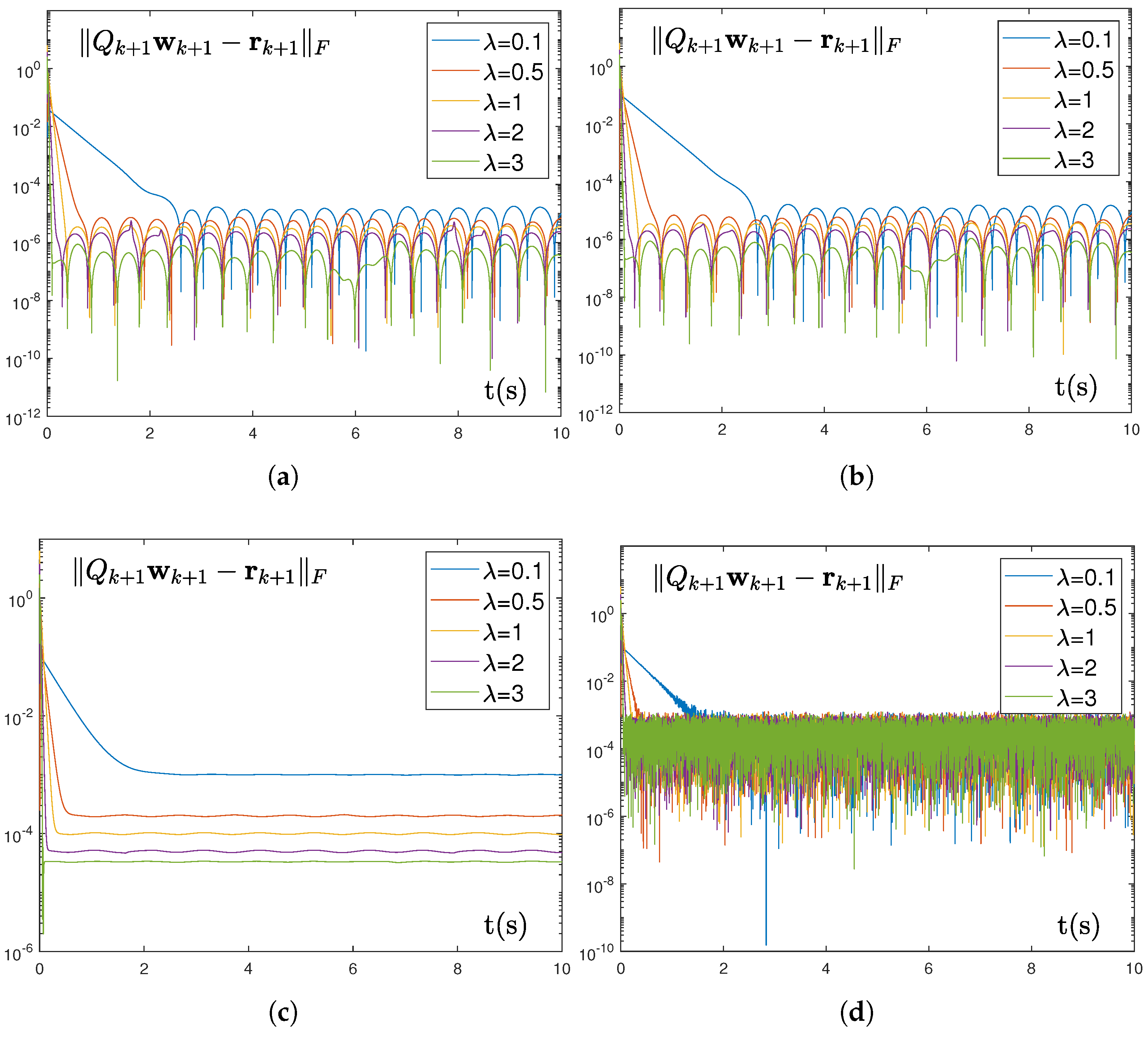
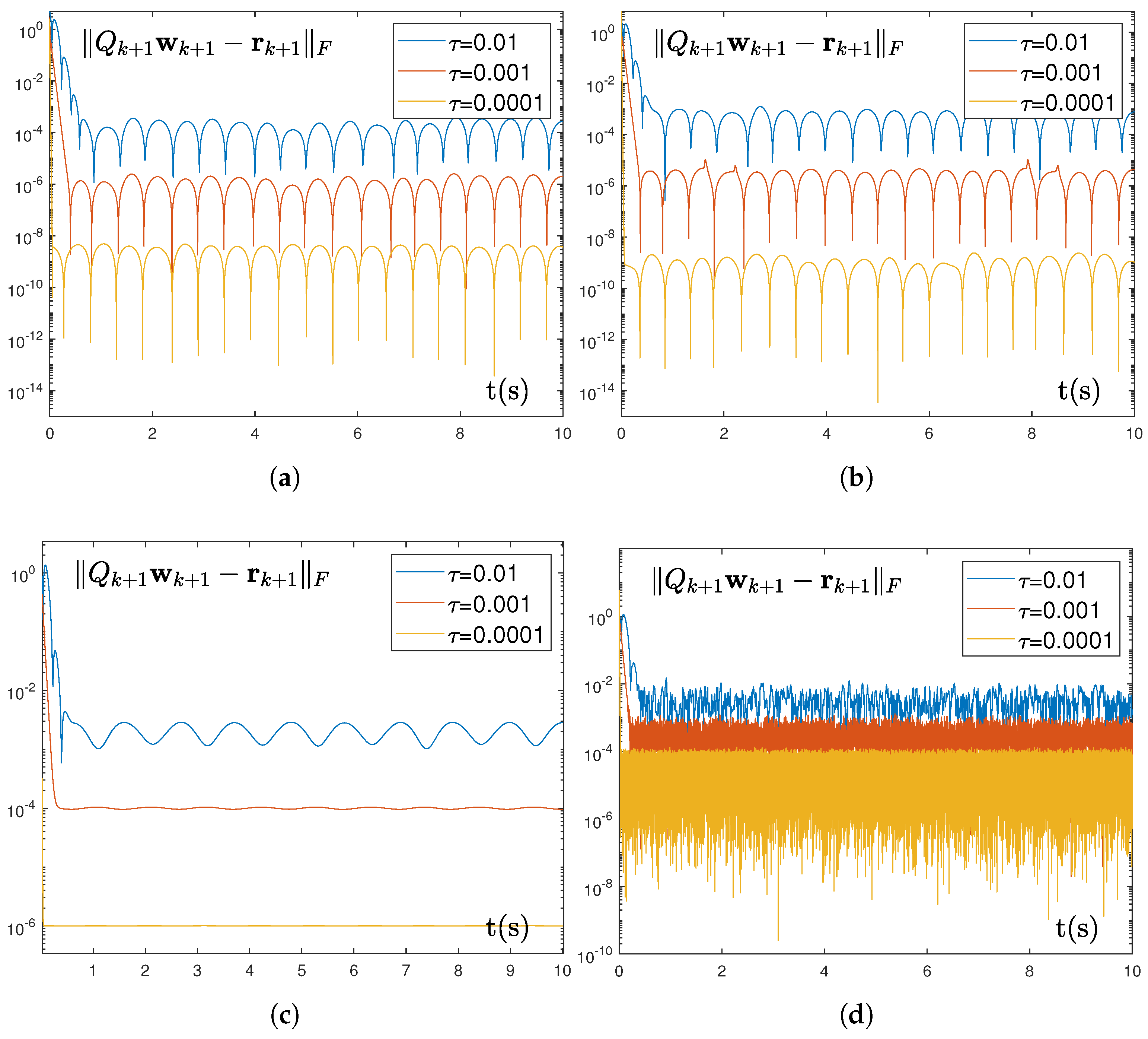
- The convergence and robustness properties of the TD-IRNN model are rigorously proven through theoretical derivations. Specifically, the enhanced model achieves exact convergence when solving discrete time-varying linear matrix problem with boundary constraints and maintains convergence under three distinct types of noise interference.
- (3)
- Comparative numerical experiments with three discrete models confirm the convergence performance of the TD-IRNN model in solving the target problem. Meanwhile, the model demonstrates consistent convergence while satisfying boundary constraints under constant, linear, and bounded random noise conditions. Furthermore, two robotic arm trajectory tracking experiments validate the practicality and effectiveness of the TD-IRNN model in practical applications.
2. Problem Formulation and Existing Discrete Model
| Time-varying augmented matrix | |
| Time-varying augmented matrix | |
| Time-varying vector | |
| The upper bound of the variable | |
| The lower bound of the variable | |
| Time-varying augmented matrix | |
| the pseudoinverse of matrix | |
| Sampling gap | |
| Design parameter | |
| Integral parameter of the TD-IRNN model | |
| Error function | |
| Error state vector | |
| The jth element of | |
| Truncation error vector |
2.1. Problem Formulation
2.2. EDTZNN Model
2.3. TDTZNN Model
2.4. TDRNN Model
3. Novel TD-IRNN Model
4. Theoretical Analyses
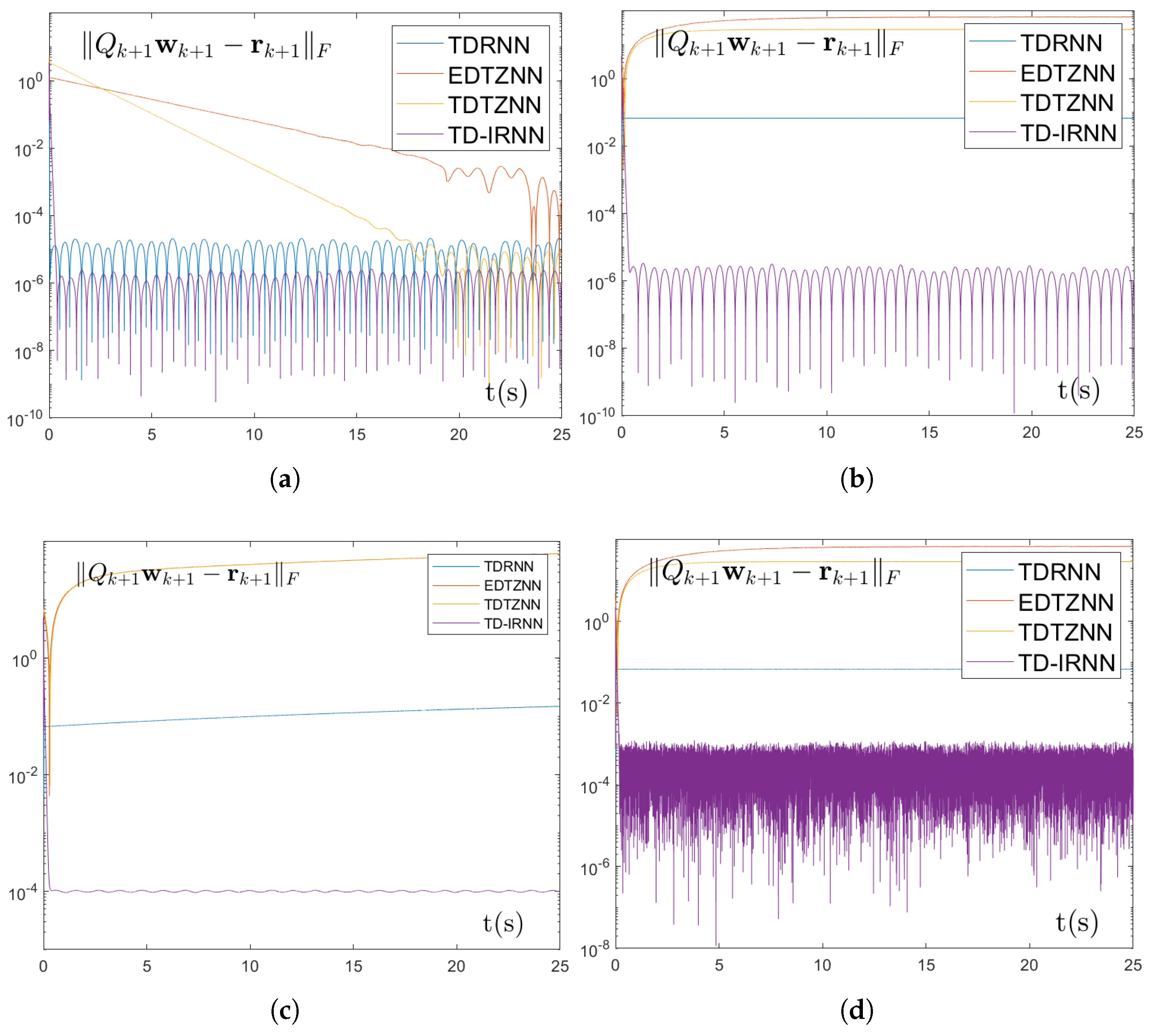
5. Simulation Experiment
5.1. Numerical Experiment
| Algorithm 1 Numerical Implementation of TD-IRNN Model (12) |
|
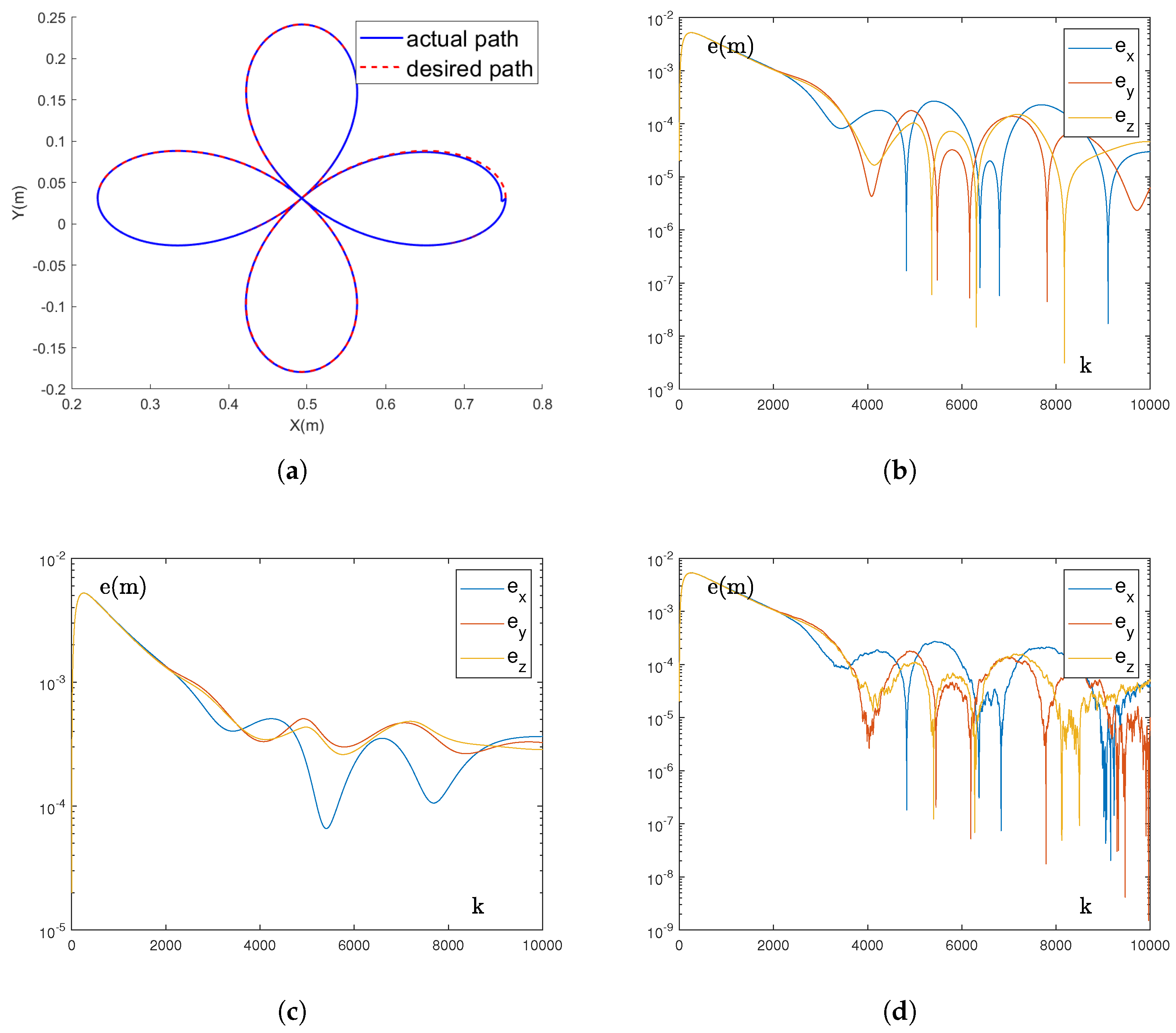
5.2. Application of Robotic Arm
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, T.; Xu, S.; Zhang, W. New Approach to Feedback Stabilization of Linear Discrete Time-Varying Stochastic Systems. IEEE Trans. Autom. Control 2025, 70, 2004–2011. [Google Scholar] [CrossRef]
- Cui, Y.; Song, Z.; Wu, K.; Yan, J.; Chen, C.; Zhu, D. A Discrete-Time Neurodynamics Scheme for Time-Varying Nonlinear Optimization with Equation Constraints and Application to Acoustic Source Localization. Symmetry 2025, 17, 932. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, J.; Yi, C. A pre-defined finite time neural solver for the time-variant matrix equation E (t) X (t) G (t) = D (t). J. Frankl. Inst. 2024, 361, 106710. [Google Scholar] [CrossRef]
- Zhou, B.; Dong, J.; Cai, G. Normal Forms of Linear Time-Varying Systems with Applications to Output-Feedback Stabilization and Tracking. IEEE Trans. Cybern. 2025, 55, 2671–2683. [Google Scholar] [CrossRef]
- Hu, K.; Liu, T. Robust Data-Driven Predictive Control for Linear Time-Varying Systems. IEEE Control Syst. Lett. 2024, 8, 910–915. [Google Scholar] [CrossRef]
- Tang, W.; Cai, H.; Xiao, L.; He, Y.; Li, L.; Zuo, Q.; Li, J. A Predefined-Time Adaptive Zeroing Neural Network for Solving Time-Varying Linear Equations and Its Application to UR5 Robot. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 4703–4712. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, Y.; Luo, B.; Pan, W.; Xu, X.; Xie, H. Model-based safe reinforcement learning with time-varying constraints: Applications to Intelligent vehicles. IEEE Trans. Ind. Electron. 2024, 71, 12744–12753. [Google Scholar] [CrossRef]
- Han, F.; Wang, Z.; Liu, H.; Dong, H.; Lu, G. Local Design of Distributed State Estimators for Linear Discrete Time-Varying Systems Over Binary Sensor Networks: A Set-Membership Approach. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5641–5654. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, Y.; Zhang, Q.; Tang, W.; Shen, Y. Interval Estimation for Time-Varying Descriptor Systems via Simultaneous Optimizations of Multiple Interval Widths. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3774–3782. [Google Scholar] [CrossRef]
- Liu, Q.; Yue, Y. Distributed Multiagent System for Time-Varying Quadratic Programming with Application to Target Encirclement of Multirobot System. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5339–5351. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, Y.; Ming, L. Novel Snap-Layer MMPC Scheme via Neural Dynamics Equivalency and Solver for Redundant Robot Arms with Five-Layer Physical Limits. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 3534–3546. [Google Scholar] [CrossRef]
- Lei, Y.; Xu, L.; Chen, J. Parameter-Gain Accelerated ZNN Model for Solving Time-Variant Nonlinear Inequality-Equation Systems and Application on Tracking Symmetrical Trajectory. Symmetry 2025, 17, 1342. [Google Scholar] [CrossRef]
- Chen, G.; Du, G.; Xia, J.; Xie, X.; Wang, Z. Aperiodic Sampled-Data H∞ Control of Vehicle Active Suspension System: An Uncertain Discrete-Time Model Approach. IEEE Trans. Ind. Inform. 2024, 20, 6739–6750. [Google Scholar] [CrossRef]
- Yang, H.; Yang, L.; Ivanov, I.G. Controller Design for Continuous-Time Linear Control Systems with Time-Varying Delay. Mathematics 2025, 13, 2519. [Google Scholar] [CrossRef]
- Liufu, Y.; Jin, L.; Li, S. Adaptive Noise-Learning Differential Neural Solution for Time-Dependent Equality-Constrained Quadratic Optimization. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 17253–17264. [Google Scholar] [CrossRef]
- Lin, C.; Jiang, Z.; Cong, J.; Zou, L. RNN with High Precision and Noise Immunity: A Robust and Learning-Free Method for Beamforming. IEEE Internet Things J. 2025, 12, 15779–15791. [Google Scholar] [CrossRef]
- Tan, J.; Shang, M.; Jin, L. Metaheuristic-Based RNN for Manipulability Optimization of Redundant Manipulators. IEEE Trans. Ind. Inform. 2024, 20, 6489–6498. [Google Scholar] [CrossRef]
- Li, X.; Lin, F.; Wang, H.; Zhang, X.; Ma, H.; Wen, C.; Blaabjerg, F. Temporal Modeling for Power Converters with Physics-in-Architecture Recurrent Neural Network. IEEE Trans. Ind. Electron. 2024, 71, 14111–14123. [Google Scholar] [CrossRef]
- Abdul Aziz, M.; Rahman, M.H.; Abrar Shakil Sejan, M.; Tabassum, R.; Hwang, D.D.; Song, H.K. Deep Recurrent Neural Network Based Detector for OFDM with Index Modulation. IEEE Access 2024, 12, 89538–89547. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, W.; Zhong, S.; Yi, C. A super-twisting algorithm combined zeroing neural network with noise tolerance and finite-time convergence for solving time-variant Sylvester equation. Expert Syst. Appl. 2024, 248, 123380. [Google Scholar] [CrossRef]
- Zhang, Y.; Yi, C. Zhang Neural Networks and Neural-Dynamic Method; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2011. [Google Scholar]
- Seo, J.H.; Kim, K.D. An RNN-Based Adaptive Hybrid Time Series Forecasting Model for Driving Data Prediction. IEEE Access 2025, 13, 54177–54191. [Google Scholar] [CrossRef]
- Zheng, B.; Li, C.; Zhang, Z.; Yu, J.; Liu, P.X. An Arbitrarily Predefined-Time Convergent RNN for Dynamic LMVE with Its Applications in UR3 Robotic Arm Control and Multiagent Systems. IEEE Trans. Cybern. 2025, 55, 1789–1800. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Li, Z.; Nie, Z.; Shao, H.; Guo, D. New recurrent neural network for online solution of time-dependent underdetermined linear system with bound constraint. IEEE Trans. Ind. Inform. 2018, 15, 2167–2176. [Google Scholar] [CrossRef]
- Shi, Y.; Chong, W.; Cao, X.; Jiang, C.; Zhao, R.; Gerontitis, D.K. A New Double-Integration-Enhanced RNN Algorithm for Discrete Time-Variant Equation Systems with Robot Manipulator Applications. IEEE Trans. Autom. Sci. Eng. 2025, 22, 8856–8869. [Google Scholar] [CrossRef]
- Li, J.; Pan, S.; Chen, K.; Zhu, X.; Yang, M. Inverse-Free discrete ZNN models for solving future nonlinear equality and inequality system with robot manipulator control. IEEE Trans. Ind. Electron. 2025. Early Access. [Google Scholar] [CrossRef]
- Cang, N.; Qiu, F.; Xue, S.; Jia, Z.; Guo, D.; Zhang, Z.; Li, W. New discrete-time zeroing neural network for solving time-dependent linear equation with boundary constraint. Artif. Intell. Rev. 2024, 57, 140. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, Y.; Li, S.; Zhang, Y. Modified ZNN for time-varying quadratic programming with inherent tolerance to noises and its application to kinematic redundancy resolution of robot manipulators. IEEE Trans. Ind. Electron. 2016, 63, 6978–6988. [Google Scholar] [CrossRef]
- Zheng, L.; Yu, W.; Xu, Z.; Zhang, Z.; Deng, F. Design, Analysis, and Application of a Discrete Error Redefinition Neural Network for Time-Varying Quadratic Programming. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 13646–13657. [Google Scholar] [CrossRef]
- Shi, Y.; Sheng, W.; Wang, J.; Jin, L.; Li, B.; Sun, X. Real-Time Tracking Control and Efficiency Analyses for Stewart Platform Based on Discrete-Time Recurrent Neural Network. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5099–5111. [Google Scholar] [CrossRef]
- Shi, Y.; Ding, C.; Li, S.; Li, B.; Sun, X. Discrete generalized-Sylvester matrix equation solved by RNN with a novel direct discretization numerical method. Numer. Algorithms 2023, 93, 971–992. [Google Scholar] [CrossRef]
- Lu, H.; Jin, L.; Luo, X.; Liao, B.; Guo, D.; Xiao, L. RNN for solving perturbed time-varying underdetermined linear system with double bound limits on residual errors and state variables. IEEE Trans. Ind. Inform. 2019, 15, 5931–5942. [Google Scholar] [CrossRef]
- Shi, Y.; Ding, C.; Li, S.; Li, B.; Sun, X. New RNN Algorithms for Different Time-Variant Matrix Inequalities Solving Under Discrete-Time Framework. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 5244–5257. [Google Scholar] [CrossRef]
- Shi, Y.; Chong, W.; Zhao, W.; Li, S.; Li, B.; Sun, X. A new recurrent neural network based on direct discretization method for solving discrete time-variant matrix inversion with application. Inf. Sci. 2024, 652, 119729. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, C.; Wang, B.; Zhao, J.; Gong, X.; Gao, J.; Chen, H. Noise-tolerant znn-based data-driven iterative learning control for discrete nonaffine nonlinear mimo repetitive systems. IEEE/CAA J. Autom. Sin. 2024, 11, 344–361. [Google Scholar] [CrossRef]
- Huang, S.; Ma, Z.; Yu, S.; Han, Y. New discrete-time zeroing neural network for solving time-variant underdetermined nonlinear systems under bound constraint. Neurocomputing 2022, 487, 214–227. [Google Scholar] [CrossRef]

| Model | Construction Paradigm | Core Mechanism for Noise Robustness |
|---|---|---|
| EDTZNN | continuous-time discretization (Euler) | none (highly susceptible to noise) |
| TDTZNN | continuous-time discretization (Taylor) | none (highly susceptible to noise) |
| TDRNN | direct-discrete-time | none (susceptible to noise) |
| TD-IRNN (This work) | direct discrete-time | integral-enhanced error dynamics |
| Integral Parameter | Different Noises | Mean Squared Error |
|---|---|---|
| 0.1 | No noise | |
| linear noise | ||
| random noise | ||
| constant noise | ||
| 0.5 | No noise | |
| linear noise | ||
| random noise | ||
| constant noise | ||
| 1 | No noise | |
| linear noise | ||
| random noise | ||
| constant noise | ||
| 2 | No noise | |
| linear noise | ||
| random noise | ||
| constant noise | ||
| 3 | No noise | |
| linear noise | ||
| random noise | ||
| constant noise |
| Sampling Gap | Different Noises | Steady-State Error |
|---|---|---|
| 0.01 | linear noise | |
| random noise | ||
| constant noise | ||
| 0.001 | linear noise | |
| random noise | ||
| constant noise | ||
| 0.0001 | linear noise | |
| random noise | ||
| constant noise |
| CN | LN | RBN | |
|---|---|---|---|
| EDTZNN model | |||
| TDTZNN model | |||
| TDRNN model | 6.6655 | 1.1398 | 6.8604 |
| TD-IRNN model | 2.0715 | 1.002 | 7.5244 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Li, X.; Chen, J.; Yi, C.; Li, Y. Taylor-Type Direct-Discrete-Time Integral Recurrent Neural Network with Noise Tolerance for Discrete-Time-Varying Linear Matrix Problems with Symmetric Boundary Constraints. Symmetry 2025, 17, 1975. https://doi.org/10.3390/sym17111975
Chen Y, Li X, Chen J, Yi C, Li Y. Taylor-Type Direct-Discrete-Time Integral Recurrent Neural Network with Noise Tolerance for Discrete-Time-Varying Linear Matrix Problems with Symmetric Boundary Constraints. Symmetry. 2025; 17(11):1975. https://doi.org/10.3390/sym17111975
Chicago/Turabian StyleChen, Yuhuan, Xuan Li, Jie Chen, Chenfu Yi, and Yang Li. 2025. "Taylor-Type Direct-Discrete-Time Integral Recurrent Neural Network with Noise Tolerance for Discrete-Time-Varying Linear Matrix Problems with Symmetric Boundary Constraints" Symmetry 17, no. 11: 1975. https://doi.org/10.3390/sym17111975
APA StyleChen, Y., Li, X., Chen, J., Yi, C., & Li, Y. (2025). Taylor-Type Direct-Discrete-Time Integral Recurrent Neural Network with Noise Tolerance for Discrete-Time-Varying Linear Matrix Problems with Symmetric Boundary Constraints. Symmetry, 17(11), 1975. https://doi.org/10.3390/sym17111975





