A Derivative-Free Method with the Symmetric Rank-One Update for Constrained Nonlinear Systems of Monotone Equations

Abstract

This paper presents a new derivative-free method with a symmetric rank-one (SR1) update for handling constrained nonlinear systems of monotone equations. Distinctively, the approach employs a revised SR1 update formula that leverages information from the latest three iterates and their corresponding function values—a key improvement over existing SR1 variants relying only on two-point information. Derived from this revised formula, the approach integrates projection techniques for performance enhancement. One of its key advantages lies in the search direction: it exhibits sufficient descent and trust-region properties while eliminating the need for line search techniques. Theoretical analysis shows that the algorithm converges globally under specified conditions. Furthermore, numerical experiments are conducted to compare the proposed algorithm with two other existing approaches; results demonstrate that it exhibits superior reliability and robustness in terms of the number of iterations, function evaluations, and CPU runtime.

1. Introduction

This paper focuses on solving the constrained system of nonlinear equations formulated as follows:

$$F\left(x\right)=0,x\in \Omega ,$$

(1)

where $F:{\mathbb{R}}^n\to {\mathbb{R}}^n$ denotes a monotone and continuously differentiable mapping, and $\Omega \subseteq {\mathbb{R}}^n$ represents a nonempty closed convex set.

Formally, the monotonicity of the mapping F is characterized by the following inequality:

$${(F\left(x\right)-F\left(y\right))}^T(x-y)\ge 0,\forall x,y\in {\mathbb{R}}^n.$$

(2)

Systems of nonlinear monotone equations originate from numerous practical problems and are widely applied in interdisciplinary fields. Typical application scenarios include automatic control systems [1], optimal power flow calculations [2], and compressive sensing [3,4,5]. Given the broad scope of application fields for nonlinear monotone equations, a multitude of researchers have developed an array of iterative numerical techniques to solve Problem (1). Examples of such methods include the Newton algorithm [6], the Gauss–Newton algorithm [7], the BFGS algorithm [8], the quasi-Newton algorithm [9], and gradient-based algorithms [10,11,12,13].

In recent years, several optimization methods, which were developed based on the projection and proximal point approach initially proposed by Solodov and Svaiter [14], have been extended to tackle Problem (1). Among these extended approaches are conjugate gradient methods—originally developed for solving large-scale unconstrained optimization problems, owing to their advantages of low memory requirements and a simple structural design. For instance, Li and Zheng [15] developed two derivative-free approaches for solving nonlinear monotone equations. Dai and Zhu [16] integrated a projection technique into the modified HS conjugate gradient approach and proposed a derivative-free projection approach to tackle high-dimensional nonlinear monotonic equations. Additionally, Kimiaei et al. [17] established a subspace inertial algorithm specifically tailored for derivative-free nonlinear monotone equations. Meanwhile, Liu et al. [18] developed an accelerated Dai-Yuan conjugate gradient projection approach, which incorporates an optimal parameter selection strategy to enhance performance. P.Kumam et al. [19] proposed another hybrid approach for solving monotone operator equations and applied it to signal processing problems. Xia et al. [20] proposed a modified two-term conjugate gradient-based projection algorithm for constrained nonlinear equations. Fang [21] presented a derivative-free RMIL conjugate gradient approach for constrained nonlinear systems of monotone equations. Zhang et al. [22] developed a three-term projection approach specifically formulated for solving nonlinear monotone equations, with subsequent extension of this approach to address practical problems in signal processing, thereby validating its applicability.

Another class of widely used iterative methods for solving nonlinear equations is the quasi-Newton approach. For example, Abubakar et al. [23] proposed a scaled memoryless quasi-Newton approach based on the SR1 update formula for solving systems of nonlinear monotone operator equations. Awwal et al. [24] proposed a new derivative-free spectral projection approach for addressing Problem (1), with the aid of a modified SR1 updating formula. Rao and Huang [25] developed a novel sufficient descent direction based on a scaled memoryless DFP updating formula and proposed a derivative-free approach for solving systems of nonlinear monotone equations. Tang and Zhou [26] proposed a two-step Broyden-like approach for solving nonlinear equations, which is designed to compute an additional approximate quasi-Newton step formed by using the previous Broyden-like matrix when the iterates are close to the solution set. Ullah et al. [27] introduces a two-parameter scaled memoryless BFGS approach with scaling for solving systems of monotone nonlinear equations, in which the optimal scaling parameters are determined by minimizing a measure function that incorporates all eigenvalues of the memoryless BFGS matrix.

Inspired by the studies mentioned above, a new quasi-Newton method is proposed in this paper for solving nonlinear equations, with a revised SR1 updating formula as its technical support. The proposed approach in this paper has the following advantages: (1) The search direction is constructed based on the revised SR1 update formula and utilizes information from the latest three iterates ($x_{k-2},x_{k-1},x_k$) and their corresponding function values. This three-point information captures richer curvature characteristics, outperforming two-point approaches by enhancing direction reliability. (2) Under the framework of the Lipschitz condition and convex constraints, this approach demonstrates global convergence when applied to monotone nonlinear equations. (3) The search direction of our proposed approach possesses the properties of both sufficient descent and the trust region, with no reliance on line search techniques.

The remainder of this paper is structured as follows: Section 2 elaborates on the motivation behind the proposed approach and presents the corresponding algorithm. Section 3 analyzes the global convergence of the proposed approach. Section 4 conducts comparative numerical experiments to evaluate the method’s performance. Section 5 provides a summary.

2. Algorithm

In this section, we first revisit the quasi-Newton iterative methods, which produce $\left\{x_k\right\}$ using the following iterative formula:

$$x_{k+1}=x_k+{\alpha }_k{d}_k.$$

(3)

Within this framework, the step length ${\alpha }_k$ is obtained using line search methods, and the search direction $d_k$ is computed based on

$$d_k=-M_{k}F\left(x_k\right),$$

(4)

in which $M_k$ is an approximation of the inverse of the Hessian matrix at the k-th iteration. One well-known quasi-Newton matrix update formula, specifically the Symmetric Rank-One (SR1) approach, is presented as follows:

$$M_k=M_{k-1}+{\displaystyle \frac{(s_{k-1}-M_{k-1}{y}_{k-1}){(s_{k-1}-M_{k-1}{y}_{k-1})}^T}{{(s_{k-1}-M_{k-1}{y}_{k-1})}^T{y}_{k-1}}},$$

(5)

where $s_{k-1}=x_k-x_{k-1}$, $y_{k-1}=F\left(x_k\right)-F\left(x_{k-1}\right)$. In the iterative process of the SR1 approach, the iterative matrix $M_k$ can hardly maintain positive definiteness consistently. Meanwhile, the denominator may tend to zero, resulting in the failure of the algorithm.

To enhance the performance of the original SR1 approach, two modified formulations have been proposed in existing studies. One is by Abubakar et al. [23], who adjusted (5) to introduce a parameter $\theta$, and the modified formula is given by:

$$M_k=M_{k-1}+{\displaystyle \frac{(s_{k-1}-M_{k-1}\theta y_{k-1}){(s_{k-1}-M_{k-1}\theta y_{k-1})}^T}{s_{k-1}^T(y_{k-1}+w{s}_{k-1})}}.$$

(6)

The other is by Awwal et al. [24], who improved the denominator of (5) using a max function to avoid singularity. Their modified formula reads:

$$M_k=M_{k-1}+{\displaystyle \frac{(s_{k-1}-M_{k-1}{y}_{k-1}){(s_{k-1}-M_{k-1}{y}_{k-1})}^T}{\max \{s_{k-1}^T(y_{k-1}+w{s}_{k-1}),\parallel y_{k-1}+w{s}_{k-1}{\parallel }^2\}}}.$$

(7)

The SR1 improvement formulas (6) and (7) relying only on the latest two points have two key flaws. First, heavy dependence on the recent $s_{k-1}$ and $y_{k-1}$ causes information singularity. Limited local data fails to capture the global curvature of the function, leading to inaccurate Hessian inverse approximations and unstable convergence paths—especially in strongly nonlinear problems. Second, they underperform in high-dimensional or tightly constrained scenarios: two vectors cannot fully represent multi-dimensional curvature, and the tiny $s_{k-1}$ from tight constraints reduces information distinguishability, rendering matrix updates ineffective and causing algorithm stagnation.

In [28], Broyden put forward the following update formula:

$$B_k=B_{k-1}+{\displaystyle \frac{(y_{k-1}-B_{k-1}{s}_{k-1})s_{k-1}^T}{s_{k-1}^T{s}_{k-1}^T}},$$

(8)

where $B_k$ is an approximation of the Jacobian matrix at the k-th iteration. Based on Broyden’s work, Fang et al. [9] proposes a modified quasi-Newton method, whose update formula is

$$B_k=B_{k-1}+{\displaystyle \frac{({\overline{y}}_{k-1}-B_{k-1}{\overline{s}}_{k-1}){\overline{s}}_{k-1}^T}{{\overline{s}}_{k-1}^T{\overline{s}}_{k-1}^T}},$$

(9)

where ${\overline{s}}_{k-1}=s_{k-1}-{\delta }_{k-1}{s}_{k-2}$, ${\overline{y}}_{k-1}=y_{k-1}-{\delta }_{k-1}{y}_{k-2}$, ${\delta }_{k-1}={\displaystyle \frac{\parallel s_{k-1}{\parallel }^2}{\parallel s_{k-2}\parallel (2\parallel s_{k-1}\parallel +\parallel s_{k-2}\parallel )}}$.

Numerical experiments indicate that the modified quasi-Newton method holds considerable promise. Inspired by Equation (9), this paper proposes a revised SR1 update formula as follows:

$$M_k={\mu }_k{M}_{k-1}+{\displaystyle \frac{(s_{k-1}-M_{k-1}{y}_{k-1}){(s_{k-1}-M_{k-1}{y}_{k-1})}^T}{{({\tilde{s}}_{k-1}-M_{k-1}{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}}},$$

(10)

where ${\mu }_k>0$, ${\tilde{s}}_{k-1}=s_{k-1}-{\delta }_{k-1}{s}_{k-2}+t_{k-1}{\tilde{y}}_{k-1}$, ${\tilde{y}}_{k-1}=y_{k-1}-{\delta }_{k-1}{y}_{k-2}$, ${\delta }_{k-1}={\displaystyle \frac{\parallel s_{k-1}{\parallel }^2}{\parallel s_{k-2}\parallel (2\parallel s_{k-1}\parallel +\parallel s_{k-2}\parallel )}}$, $t_{k-1}=1+{\displaystyle \frac{\parallel F_{k-1}{\parallel }^2+{\delta }_{k-1}(s_{k-1}^T{y}_{k-2}+s_{k-2}^T{y}_{k-1})}{\parallel {\tilde{y}}_{k-1}{\parallel }^2}}$. If we set ${\mu }_k=1,{\delta }_{k-1}=0,t_{k-1}=0$ for all k, then the SR1 update given by (10) reduces to the classical version.

According to the definitions of ${\tilde{s}}_{k-1}$ and ${\tilde{y}}_{k-1}$, we have

$$\begin{array}{cc}\hfill {({\tilde{s}}_{k-1}-M_{k-1}{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}& ={(s_{k-1}-{\delta }_{k-1}{s}_{k-2}+t_{k-1}{\tilde{y}}_{k-1}-M_{k-1}{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}\hfill \\ \hfill & =s_{k-1}^T{\tilde{y}}_{k-1}-{\delta }_{k-1}{s}_{k-2}^T{\tilde{y}}_{k-1}+t_{k-1}{\tilde{y}}_{k-1}^T{\tilde{y}}_{k-1}-{\tilde{y}}_{k-1}^T{M}_{k-1}{\tilde{y}}_{k-1}\hfill \\ \hfill & =s_{k-1}^T(y_{k-1}-{\delta }_{k-1}{y}_{k-2})-{\delta }_{k-1}{s}_{k-2}^T(y_{k-1}-{\delta }_{k-1}{y}_{k-2})+{\parallel F_{k-1}\parallel }^2\hfill \\ \hfill & +{\delta }_{k-1}(s_{k-1}^T{y}_{k-2}+s_{k-2}^T{y}_{k-1})+{\tilde{y}}_{k-1}^T(I-M_{k-1}){\tilde{y}}_{k-1}\hfill \\ \hfill & =s_{k-1}^T{y}_{k-1}+{\delta }_{k-1}^2{s}_{k-2}^T{y}_{k-2}+{\parallel F_{k-1}\parallel }^2+{\tilde{y}}_{k-1}^T(I-M_{k-1}){\tilde{y}}_{k-1},\hfill \end{array}$$

(11)

where I is an identity matrix with the same dimension as $M_{k-1}$. If we set $M_{k-1}=I$ and use (10), we have

$$M_k={\mu }_{k}I+{\displaystyle \frac{(s_{k-1}-y_{k-1}){(s_{k-1}-y_{k-1})}^T}{s_{k-1}^T{y}_{k-1}+{\delta }_{k-1}^2{s}_{k-2}^T{y}_{k-2}+{\parallel F_{k-1}\parallel }^2}},$$

(12)

Based on the monotonicity of F and ${\mu }_k>0$, we conclude that $M_k$ is a symmetric positive definite matrix.

Combining with (4) and (10), we have

$$d_k=\left\{\begin{array}{cc}-F_k\hfill & \mathrm{if}k=0\hfill \\ -{\mu }_k{F}_k-{\displaystyle \frac{(s_{k-1}-y_{k-1}){(s_{k-1}-y_{k-1})}^T{F}_k}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}}}\hfill & \mathrm{if}k\ge 1\hfill \end{array}\right..$$

(13)

From the definition of $d_k$, it is easy to see that for $k\in \mathbb{N}$, we have

$$\begin{array}{cc}\hfill F_k^T{d}_k& =-{\mu }_k{F}_k^T{F}_k-{\displaystyle \frac{F_k^T(s_{k-1}-y_{k-1}){(s_{k-1}-y_{k-1})}^T{F}_k}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}}}\hfill \\ \hfill & =-\left({\mu }_k+{\displaystyle \frac{\parallel F_k^T(s_{k-1}-y_{k-1}){\parallel }^2}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}{\parallel F_k\parallel }^2}}\right){\parallel F_k\parallel }^2\hfill \end{array}$$

(14)

For $c>0$, we set

$${\mu }_k=c-{\displaystyle \frac{\parallel F_k^T(s_{k-1}-y_{k-1}){\parallel }^2}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}{\parallel F_k\parallel }^2}},$$

(15)

and then we get $F_k^T{d}_k=-c{\parallel F_k\parallel }^2$. When $k=0$, we have $F_0^T{d}_0=-{\mu }_0{\parallel F_0\parallel }^2.$ In addition, inspired by the BB method [29], we propose the following parameter:

$${\lambda }_k={\displaystyle \frac{s_{k-1}^T{s}_{k-1}}{{\tilde{s}}_{k-1}^T{\tilde{y}}_{k-1}}}.$$

(16)

Furthermore, using (13), (15) and (16), this paper proposes the modified search direction as follows:

$$d_k=\left\{\begin{array}{cc}-F_k\hfill & \mathrm{if}k=0\hfill \\ -max\{{\mu }_k,{\lambda }_k\}{F}_k-{\beta }_k{\eta }_k\hfill & \mathrm{if}k\ge 1\hfill \end{array}\right.$$

(17)

where ${\beta }_k={\displaystyle \frac{{(s_{k-1}-y_{k-1})}^T{F}_k}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}}}$, ${\eta }_k=s_{k-1}-y_{k-1}$. ${\tilde{s}}_{k-1}=s_{k-1}-{\delta }_{k-1}{s}_{k-2}+t_{k-1}{\tilde{y}}_{k-1}$, ${\tilde{y}}_{k-1}=y_{k-1}-{\delta }_{k-1}{y}_{k-2}$, ${\delta }_{k-1}={\displaystyle \frac{\parallel s_{k-1}{\parallel }^2}{\parallel s_{k-2}\parallel (2\parallel s_{k-1}\parallel +\parallel s_{k-2}\parallel )}}$, $t_{k-1}=1+{\displaystyle \frac{\parallel F_{k-1}{\parallel }^2+{\delta }_{k-1}(s_{k-1}^T{y}_{k-2}+s_{k-2}^T{y}_{k-1})}{\parallel {\tilde{y}}_{k-1}{\parallel }^2}}$.

Next, we introduce the projection operator $P_{\Omega }[·]$, defined as follows:

$$P_{\Omega }\left[x\right]=argmin\{\parallel x-y\parallel \mid y\in \Omega \},\forall x\in {\mathbb{R}}^n.$$

(18)

This operator corresponds to projecting the vector x onto the closed convex set $\Omega$. Such a projection ensures that the subsequent iterative points generated by our algorithm stay within the domain $\Omega$. It is well known that the projection operator satisfies the non-expansive property, which is expressed as

$$\parallel P_{\Omega }\left[x\right]-P_{\Omega }\left[y\right]\parallel \le \parallel x-y\parallel ,\forall x,y\in {\mathbb{R}}^n.$$

(19)

Next, we present the detailed steps of our proposed algorithm (Algorithm 1).

Algorithm 1 Revised SR1 update Method (RSR1M)

$\mathbf{Step}\mathbf{0}:$ Select $\theta >0,\sigma >0,ϵ>0,{\zeta }_2>{\zeta }_1>0,1>\rho >0,2>\gamma >0.$ along with an initial point $x_0\in {\mathbb{R}}^n$. Let $k=0$. $\mathbf{Step}\mathbf{1}:$ If $\parallel F\left(x_k\right)\parallel <ϵ$, terminate the algorithm; Otherwise, proceed to step 2. $\mathbf{Step}\mathbf{2}:$ Determine the search direction $d_k$ via (17). $\mathbf{Step}\mathbf{3}:$ Define the step-length ${\alpha }_k=\theta {\rho }^m$, m is the smallest natural number that makes ${\alpha }_k$ satisfy the following inequality: $$-F{(x_k+{\alpha }_k{d}_k)}^T{d}_k\ge \sigma {\alpha }_k{P}_{[{\zeta }_1,{\zeta }_2]}\left[\left|\right|F(x_k+{\alpha }_k{d}_k)\left|\right|\right]·\left|\right|d_k{\left|\right|}^2.$$ (20) The definition of the projection operator P for $\forall z\in \mathbb{R}$ is $$P_{[{\zeta }_1,{\zeta }_2]}\left[z\right]=\left\{\begin{array}{c}{\zeta }_2\mathrm{if}z\ge {\zeta }_2\hfill \\ {\zeta }_1\mathrm{if}z\le {\zeta }_1\hfill \\ z\mathrm{otherwise}.\hfill \end{array}\right.$$ (21) Moreover, set $h_k=x_k+{\alpha }_k{d}_k$ and proceed to step 4. $\mathbf{Step}\mathbf{4}:$ If $h_k\in \Omega$ and $\parallel F\left(h_k\right)\parallel <ϵ$, set $x_{k+1}=h_k$, terminate the algorithm; Otherwise compute $$x_{k+1}=P_{\Omega }[x_k-\gamma {\displaystyle \frac{F{\left(h_k\right)}^T(x_k-h_k)}{\parallel F\left(h_k\right){\parallel }^2}}F\left(h_k\right)]$$ (22) and set $k:=k+1$, proceed to step 1.

3. Convergence Analysis

Next, we analyze the convergence of the proposed algorithm. The following assumptions are required:

Assumption 1.

The solution set Ω corresponding to Problem (1) is nonempty.

Assumption 2.

F is Lipschitz continuous on ${\mathbb{R}}^n$, meaning that

$$\left|\right|F\left(x_1\right)-F\left(x_2\right)\left|\right|\le L\left|\right|x_1-x_2\left|\right|,\forall x_1,x_2\in {\mathbb{R}}^n.$$

Lemma 1.

Assume that Assumptions 1 and 2 hold. Then, the sequences $\left\{{\alpha }_k\right\}$ and $\left\{F_k\right\}$ are generated by following the update rules of Algorithm 1, and we further have

$${\alpha }_k\ge min\left\{\theta ,{\displaystyle \frac{\rho c\parallel F_k{\parallel }^2}{(L+\sigma {\zeta }_2){\parallel d_k\parallel }^2}}\right\}.$$

(23)

Proof. 

When ${\alpha }_k\ne \theta$, the line search mechanism of Algorithm 1 shows that ${\rho }^{-1}{\alpha }_k$ violates the condition (20), implying that

$$\begin{array}{cc}\hfill -F{(x_k+{\rho }^{-1}{\alpha }_k{d}_k)}^T{d}_k& \le \sigma {\rho }^{-1}{\alpha }_k{P}_{[{\zeta }_1,{\zeta }_2]}\left[\left|\right|F(x_k+{\rho }^{-1}{\alpha }_k{d}_k)\left|\right|\right]\left|\right|d_k{\left|\right|}^2\hfill \\ \hfill & \le \sigma {\rho }^{-1}{\alpha }_k{\zeta }_2\left|\right|d_k{\left|\right|}^2.\hfill \end{array}$$

(24)

Combining the above equation, (15)–(17) and Assumption 2, we obtain

$$\begin{array}{cc}\hfill c\left|\right|F_k{\left|\right|}^2& \le {\left(F(x_k+{\rho }^{-1}{\alpha }_k{d}_k)-F_k\right)}^T{d}_k-F{(x_k+{\rho }^{-1}{\alpha }_k{d}_k)}^T{d}_k\hfill \\ \hfill & \le {\rho }^{-1}{\alpha }_k(L+\sigma {\zeta }_2)\left|\right|d_k{\left|\right|}^2.\hfill \end{array}$$

(25)

The above inequation indicates that

$${\alpha }_k\ge {\displaystyle \frac{\rho c\parallel F_k{\parallel }^2}{(L+\sigma {\zeta }_2){\parallel d_k\parallel }^2}},$$

which implies (23). □

To address the estimation of the Lipschitz constant L (which is often unknown in practical applications), we introduce a recursive formula to adaptively estimate L:

$$L_k=max\left\{L_{k-1},{\displaystyle \frac{\parallel F\left(x_k\right)-F\left(x_{k-1}\right)\parallel }{\parallel x_k-x_{k-1}\parallel }}\right\},$$

where $L_0$ is initialized to a small positive value (e.g., $L_0=1.0$ in our experiments)—a common choice in numerical optimization to avoid overestimation of initial smoothness. This formula leverages the Lipschitz continuity property $\parallel F\left(x\right)-F\left(y\right)\parallel \le L\parallel x-y\parallel$ and updates L iteratively based on successive function evaluations and iterate values, ensuring it captures the local smoothness of F during iterations.

Lemma 2.

Assume that Assumptions 1 and 2 hold. Then, the sequences $\left\{x_k\right\}$, $\left\{{\alpha }_k\right\}$, $\left\{d_k\right\}$ and $\left\{h_k\right\}$ are generated by following the update rules of Algorithm 1. Based on this, for any $x^{*}$ that satisfies $F\left(x^{*}\right)=0$, we can conclude that the sequence $\{\parallel x_k-x^{*}\parallel \}$ converges, and the sequence $\left\{x_k\right\}$ is bounded. In addition, we have

$$\underset{k\to \infty }{lim}{\alpha }_k\left|\right|d_k\left|\right|=0.$$

(26)

Proof. 

By virtue of the monotonicity of $F\left(x\right)$ and the condition $F\left(x^{*}\right)=0$, we have

$$\begin{array}{cc}\hfill F{\left(h_k\right)}^T(x_k-x^{*})& =F{\left(h_k\right)}^T(x_k-h_k)+F{\left(h_k\right)}^T(h_k-x^{*})\hfill \\ \hfill & \ge F{\left(h_k\right)}^T(x_k-h_k)+F{\left(x^{*}\right)}^T(h_k-x^{*})\hfill \\ \hfill & =F{\left(h_k\right)}^T(x_k-h_k).\hfill \end{array}$$

(27)

Combining with (19), (21), (22) and (27), we have

$$\begin{array}{cc}\hfill \left|\right|x_{k+1}-x^{*}\left|\right|-\left|\right|x_k-x^{*}{\left|\right|}^2& =\left|\right|P_{\Omega }[x_k-\gamma {\displaystyle \frac{F{\left(h_k\right)}^T(x_k-h_k)}{\parallel F\left(h_k\right){\parallel }^2}}F\left(h_k\right)]-P_{\Omega }\left[x^{*}\right]{\left|\right|}^2-\left|\right|x_k-x^{*}{\left|\right|}^2\hfill \\ \hfill & \le \left|\right|x_k-\gamma {\displaystyle \frac{F{\left(h_k\right)}^T(x_k-h_k)}{\parallel F\left(h_k\right){\parallel }^2}}F\left(h_k\right)-x^{*}{\left|\right|}^2-\left|\right|x_k-x^{*}{\left|\right|}^2\hfill \\ \hfill & ={\gamma }^2{\displaystyle \frac{{\left(F{\left(h_k\right)}^T(x_k-h_k)\right)}^2}{\parallel F\left(h_k\right){\parallel }^4}}\left|\right|F\left(h_k\right){\left|\right|}^2-2\gamma {\displaystyle \frac{{\left(F{\left(h_k\right)}^T(x_k-h_k)\right)}^2}{\parallel F\left(h_k\right){\parallel }^2}}\hfill \\ \hfill & =-\gamma (2-\gamma ){\displaystyle \frac{{\left[F{\left(h_k\right)}^T\left({\alpha }_k{d}_k\right)\right]}^2}{\left|\right|F\left(h_k\right){\left|\right|}^2}}\hfill \\ \hfill & =-\gamma (2-\gamma ){\displaystyle \frac{{\alpha }_k^2{\left[F{(x_k+{\alpha }_k{d}_k)}^T{d}_k\right]}^2}{\left|\right|F\left(h_k\right){\left|\right|}^2}}\hfill \\ \hfill & \le -\gamma (2-\gamma ){\displaystyle \frac{{\alpha }_k^2{[\sigma {\alpha }_k{P}_{[{\zeta }_1,{\zeta }_2]}\left[\left|\right|F(x_k+{\alpha }_k{d}_k)\left|\right|\right]·|\left|d_k\right|{|}^2]}^2}{\left|\right|F\left(h_k\right){\left|\right|}^2}}\hfill \\ \hfill & \le -\gamma (2-\gamma ){\displaystyle \frac{{\sigma }^2{\zeta }_1^2\left|\right|{\alpha }_k{d}_k{\left|\right|}^4}{\left|\right|F\left(h_k\right){\left|\right|}^2}}\hfill \end{array}$$

(28)

where $0<\gamma <2$. The above inequality shows that the sequence $\left\{x_k-x^{*}\right\}$ is monotonically decreasing and bounded below, so it converges. This directly implies the boundedness of $\left\{x_k\right\}$. In addition, we have

$$\begin{array}{cc}\hfill \parallel F\left(h_k\right)\parallel & \le \parallel F\left(h_k\right)-F\left(x_k\right)\parallel +\parallel F\left(x_k\right)-F\left(x^{*}\right)\parallel \hfill \\ \hfill & \le L(\parallel h_k-x_k\parallel +\parallel x_k-x^{*}\parallel )\hfill \\ \hfill & =L(\parallel {\alpha }_k{d}_k\parallel +\parallel x_k-x^{*}\parallel ),\hfill \end{array}$$

(29)

Furthermore, using (28) and (29), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\gamma (2-\gamma ){\sigma }^2{\zeta }_1^2}{L^2}}\sum _{k=0}^{\infty }{\displaystyle \frac{\left|\right|{\alpha }_k{d}_k{\left|\right|}^4}{(\parallel {\alpha }_k{d}_k\parallel +\parallel x_k-x^{*}{\parallel )}^2}}& \le \gamma (2-\gamma ){\sigma }^2{\zeta }_1^2\sum _{k=0}^{\infty }{\displaystyle \frac{\left|\right|{\alpha }_k{d}_k{\left|\right|}^4}{\parallel F\left(h_k\right){\parallel }^2}}\hfill \\ \hfill & \le \sum _{k=0}^{\infty }\left(\right||x_k-x^{*}{\left|\right|}^2-\left|\right|x_{k+1}-x^{*}{\left|\right|}^2)\hfill \\ \hfill & \le \left|\right|x_0-x^{*}{\left|\right|}^2,\hfill \end{array}$$

(30)

which shows that

$$\underset{k\to \infty }{lim}{\alpha }_k\left|\right|d_k\left|\right|=0.$$

□

Lemma 3.

Suppose the sequences $\left\{d_k\right\}$ and $\left\{F_k\right\}$ are obtained by Algorithm 1. If there exists a positive constant ϖ such that

$$\parallel F_k\parallel \ge \varpi ,\forall k\ge 0,$$

(31)

then we obtain

$$min\left\{1,c\right\}\parallel F_k\parallel \le \left|\right|d_k\left|\right|\le max\left\{1,c+{\displaystyle \frac{8{\phi }^2{(1+L)}^2}{{\varpi }^2}},{\displaystyle \frac{4{\phi }^2(2+2L+L^2)}{{\varpi }^2}}\right\}\left|\right|F_k\left|\right|.$$

(32)

Proof. 

When $k=0$, it is not difficult to obtain that $\parallel d_0\parallel =\parallel F_0\parallel$. Clearly, this result satisfies (32). When $k\ge 1$, from Lemma 2, it follows that the sequence $\left\{x_k\right\}$ is bounded, so there exists a positive constant $\phi$ such that $\parallel x_k\parallel \le \phi$, $k\ge 0$. Then, we get

$$\parallel s_{k-1}\parallel =\parallel x_k-x_{k-1}\parallel \le \parallel x_k\parallel +\parallel x_{k-1}\parallel \le 2\phi$$

(33)

Furthermore, according to (33) and Assumption 2, we have

$$\parallel s_{k-1}-y_{k-1}\parallel \le (1+L)\parallel s_{k-1}\parallel \le 2(1+L)\phi$$

(34)

Then, we have two cases.

Case 1: If $max\{{\lambda }_k,{\mu }_k\}={\mu }_k$, then by using (15), (17), (31) and (34), it can be concluded that

$$\begin{array}{cc}\hfill \parallel d_k\parallel & \le |{\mu }_k|\parallel F_k\parallel +|{\beta }_k|\parallel {\eta }_k\parallel \hfill \\ \hfill & \le \left(c+{\displaystyle \frac{\parallel F_k^T(s_{k-1}-y_{k-1}){\parallel }^2}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}{\parallel F_k\parallel }^2}}\right)\parallel F_k\parallel +{\displaystyle \frac{|{(s_{k-1}-y_{k-1})}^T{F}_k|}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}}}\parallel s_{k-1}-y_{k-1}\parallel \hfill \\ \hfill & \le \left(c+{\displaystyle \frac{2\parallel (s_{k-1}-y_{k-1}){\parallel }^2}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}}}\right)\parallel F_k\parallel \hfill \\ \hfill & =\left(c+{\displaystyle \frac{2\parallel (s_{k-1}-y_{k-1}){\parallel }^2}{s_{k-1}^T{y}_{k-1}+{\delta }_{k-1}^2{s}_{k-2}^T{y}_{k-2}+{\parallel F_{k-1}\parallel }^2}}\right)\parallel F_k\parallel \hfill \\ \hfill & \le \left(c+{\displaystyle \frac{2\parallel (s_{k-1}-y_{k-1}){\parallel }^2}{\parallel F_{k-1}{\parallel }^2}}\right)\parallel F_k\parallel \hfill \\ \hfill & \le \left(c+{\displaystyle \frac{8{\phi }^2{(1+L)}^2}{{\varpi }^2}}\right)\parallel F_k\parallel ,\hfill \end{array}$$

(35)

and

Case 2: If $max\{{\lambda }_k,{\mu }_k\}={\lambda }_k$, then by using (16), (17), (31), (33) and (34), it can be concluded that

$$\begin{array}{cc}\hfill \parallel d_k\parallel & \le |{\lambda }_k|\parallel F_k\parallel +|{\beta }_k|\parallel {\eta }_k\parallel \hfill \\ \hfill & \le {\displaystyle \frac{s_{k-1}^T{s}_{k-1}}{{\tilde{s}}_{k-1}^T{\tilde{y}}_{k-1}}}\parallel F_k\parallel +{\displaystyle \frac{|{(s_{k-1}-y_{k-1})}^T{F}_k|}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}}}\parallel s_{k-1}-y_{k-1}\parallel \hfill \\ \hfill & \le {\displaystyle \frac{s_{k-1}^T{s}_{k-1}}{s_{k-1}^T{y}_{k-1}+{\delta }_{k-1}^2{s}_{k-2}^T{y}_{k-2}+{\tilde{y}}_{k-1}^T{\tilde{y}}_{k-1}+{\parallel F_{k-1}\parallel }^2}}+{\displaystyle \frac{\parallel (s_{k-1}-y_{k-1}){\parallel }^2}{\parallel F_{k-1}{\parallel }^2}}\parallel F_k\parallel \hfill \\ \hfill & \le {\displaystyle \frac{\parallel s_{k-1}{\parallel }^2+{\parallel (s_{k-1}-y_{k-1})\parallel }^2}{\parallel F_{k-1}{\parallel }^2}}\parallel F_k\parallel \hfill \\ \hfill & \le {\displaystyle \frac{4{\phi }^2(2+2L+L^2)}{{\varpi }^2}}\parallel F_k\parallel .\hfill \end{array}$$

(36)

Using (35) and (36), we show that the right-hand side of (32) holds.

Next, from (15) and (17), we get

$$\begin{array}{cc}\hfill F_k^T{d}_k& =-max\{{\mu }_k,{\lambda }_k\}{\parallel F_k\parallel }^2-{\displaystyle \frac{F_k^T(s_{k-1}-y_{k-1}){(s_{k-1}-y_{k-1})}^T{F}_k}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}}}\hfill \\ \hfill & \le -{\mu }_k{\parallel F_k\parallel }^2-{\displaystyle \frac{F_k^T(s_{k-1}-y_{k-1}){(s_{k-1}-y_{k-1})}^T{F}_k}{{({\tilde{s}}_{k-1}-{\tilde{y}}_{k-1})}^T{\tilde{y}}_{k-1}}}\hfill \\ \hfill & =-c\parallel F_k{\parallel }^2\hfill \end{array}$$

(37)

Based on (37), we obtain

$$\parallel d_k\parallel \ge {\displaystyle \frac{\parallel F_k^T{d}_k\parallel }{\parallel F_k\parallel }}\ge c\parallel F_k\parallel ,$$

(38)

which shows that the left-hand side of (32) holds. □

Theorem 1.

Assume that Assumptions 1 and 2 hold. Then, the sequences $\left\{x_k\right\}$ and $\left\{F_k\right\}$ are generated by following the update rules of Algorithm 1, and we further have

$$\underset{k\to \infty }{lim\; inf}\parallel F_k\parallel =0.$$

(39)

Proof. 

Assume that (39) is false. Then, there is a positive constant k for which

$$\parallel F_k\parallel \ge \varpi ,$$

(40)

where $\varpi$ is a positive constant. This together with (23) and (32), we obtain

$$\begin{array}{cc}\hfill {\alpha }_k\parallel d_k\parallel & \ge min\left\{\theta \parallel d_k\parallel ,{\displaystyle \frac{\rho c\parallel F_k{\parallel }^2}{(L+\sigma {\zeta }_2)\parallel d_k\parallel }}\right\}\hfill \\ \hfill & \ge min\left\{\theta min\{1,c\}\parallel F_k\parallel ,{\displaystyle \frac{\rho c\parallel F_k{\parallel }^2}{(L+\sigma {\zeta }_2)max\left\{1,c+\frac{8{\phi }^2{(1+L)}^2}{{\varpi }^2},\frac{4{\phi }^2(2+2L+L^2)}{{\varpi }^2}\right\}\left|\right|F_k\left|\right|}}\right\}\hfill \\ \hfill & \ge min\left\{\theta min\{1,c\}\varpi ,{\displaystyle \frac{\rho c\varpi }{(L+\sigma {\zeta }_2)max\left\{1,c+\frac{8{\phi }^2{(1+L)}^2}{{\varpi }^2},\frac{4{\phi }^2(2+2L+L^2)}{{\varpi }^2}\right\}}}\right\}\hfill \\ \\ & >0,\hfill \end{array}$$

(41)

which contradicts with the conclusion of Lemma 2, then (39) is hold. □

While the proof of Theorem 1 relies on the global Lipschitz continuity of F (to ensure strict mathematical rigor in establishing global convergence), this assumption does not contradict its practical applicability to engineering problems. We bridge this gap through the following engineering-oriented reasoning: (1) Practical engineering problems implicitly satisfy effective global Lipschitz continuity: The domain of interest for F in engineering (e.g., voltage, pixel values) is bounded. Locally Lipschitz functions can meet the theoretical assumption by domain extension or selecting a sufficiently large global L. (2) Though the proof uses global L, the algorithm calculates step size via iteratively updated local $L_k$, avoiding conservatism from global assumptions and ensuring practical efficiency.

4. Numerical Experiments

The present section is devoted to conducting a series of numerical experiments to assess the performance of Algorithm 1, which we compare with the following two algorithms: (1) The three-term projection approach based on spectral secant equation (TTPM) [22]; (2) The derivative-free approach involving symmetric rank-one update (DFSR1) [24]. The core mechanism of TTPM relies on its three-term search direction, which integrates a projection-based feasible direction and a conjugate gradient-driven correction term. The projection-based direction uses the Solodov-Svaiter operator to keep iterates within the convex constraint set, while the correction term leverages historical direction data to prevent stagnation. This design enables effective constraint handling without derivative information, making TTPM a representative projection-based derivative-free approach for constrained nonlinear monotone equations. DFSR1 extends the SR1 quasi-Newton update to derivative-free scenarios via a modified correction term (with a positive tuning parameter) instead of Jacobian approximation. This modification, paired with a max-value denominator, avoids numerical singularity while preserving the symmetric rank-one structure for efficient updates. Its key strength is adaptive adjustment of the approximation matrix using a spectral parameter, ensuring the search direction meets the sufficient descent property.

These methods are chosen as benchmarks for three reasons: (1) Both are derivative-free and tailored for convex constrained monotone equations, aligning with the proposed method for fair comparison; (2) They represent dominant design philosophies and are widely validated in recent studies; (3) Their performance has been validated in prior studies: TTPM exhibits reliable stability in constraint handling, and DFSR1 outperforms approaches like PDY in convergence speed. These dual strengths provide a well-rounded reference to assess the proposed method’s merits across key performance metrics.

All algorithms were implemented in MATLAB 2018a and executed on an Lenovo computer equipped with an 11th-Generation Intel Core i7-11700K processor. To ensure fairness in the comparison, all algorithms were run using the parameters specified in their respective original papers, with same initial points applied consistently across all tests. We evaluated the algorithms on thirteen problems commonly adopted in existing literature, with dimensions set to 10,000 and 50,000. All test problems were initialized using the following eight starting points:

$$\begin{array}{cccc}\hfill x_1& ={(10,10,\dots ,10)}^T,\hfill & \hfill x_2& ={(-10,-10,\dots ,-10)}^T,\hfill \\ \hfill x_3& ={(-1,-1,\dots ,-1)}^T,\hfill & \hfill x_4& ={(1,1,\dots ,1)}^T,\hfill \\ \hfill x_5& ={(0.1,0.1,\dots ,0.1)}^T,\hfill & \hfill x_6& ={(-0.1,-0.1,\dots ,-0.1)}^T,\hfill \\ \hfill x_7& ={\left({\displaystyle \frac{1}{n}},{\displaystyle \frac{2}{n}},\dots ,1\right)}^T,\hfill & \hfill x_8& ={\left(1-{\displaystyle \frac{1}{n}},1-{\displaystyle \frac{2}{n}},\dots ,1-{\displaystyle \frac{n}{n}}\right)}^T.\hfill \end{array}$$

For Algorithm 1, the parameter settings were as follows: We define $\theta =1, \sigma ={10}^{-4},ϵ={10}^{-6}, {\zeta }_1=0.001, {\zeta }_2=0.8, \rho =0.5, \gamma =1.2, c=0.1.$ The stopping criteria for the numerical experiments were defined as either of the two conditions below being satisfied: (1) The number of iterations exceeds 1000; (2) The residual norm meets $\parallel F\left(x_k\right)\parallel \le {10}^{-6}$ or $\parallel F\left(h_k\right)\parallel \le {10}^{-6}$.

We now list the test problems, where the mapping F is defined as follows: $F\left(x\right)={(f_1\left(x\right),f_2\left(x\right),\dots ,f_n\left(x\right))}^T.$

Problem 1.

This problem drawn from [30] is

$$\begin{array}{cc}\hfill f_i\left(x\right)& =x_i-sin\left(\right|x_i|-1),i=1,2,\dots ,n,\hfill \\ \hfill \Omega & =\{x\in {\mathbb{R}}^n|x_i|\ge -1,\sum _{i=1}^n{x}_i\le n,i=1,2,\dots ,n\}.\hfill \end{array}$$

Problem 2.

This problem drawn from [30] is

$$\begin{array}{cc}\hfill f_i\left(x\right)& =e^{x_i}-1,i=1,2,\dots ,n,\hfill \\ \hfill \Omega & ={\mathbb{R}}_{+}^n.\hfill \end{array}$$

Problem 3.

This problem drawn from [30] is

$$\begin{array}{cc}\hfill f_i\left(x\right)& =2x_i-sin\left(x_i\right),i=1,2,\dots ,n,\hfill \\ \hfill \Omega & ={\mathbb{R}}_{+}^n.\hfill \end{array}$$

Problem 4.

This problem drawn from [31] is

$$\begin{array}{cc}\hfill f_1\left(x\right)& =x_1,\hfill \\ \hfill f_i\left(x\right)& =cos\left(x_{i-1}\right)+x_i-1,i=2,3,\dots ,n,\hfill \\ \hfill \Omega & ={\mathbb{R}}_{+}^n.\hfill \end{array}$$

Problem 5.

This problem drawn from [31] is

$$\begin{array}{cc}\hfill f_i\left(x\right)& =2x_i+x_{i+1}-{\displaystyle \frac{1}{3}}{x}_{i+1},i=1,2,\dots ,n-1,\hfill \\ \hfill f_n\left(x\right)& =2x_n-{\displaystyle \frac{1}{3}}{x}_{n-1},\hfill \\ \hfill \Omega & ={\mathbb{R}}_{+}^n.\hfill \end{array}$$

Problem 6.

This problem drawn from [31] is

$$\begin{array}{cc}\hfill f_1\left(x\right)& ={\displaystyle \frac{1}{{(x_1+1)}^2}}-exp\left(x_i\right),\hfill \\ \hfill f_i\left(x\right)& ={\displaystyle \frac{1}{{(x_i+1)}^2}}+cos\left(x_{i+1}\right)-2exp\left(x_i\right),i=2,3,\dots ,n-1,\hfill \\ \hfill f_n\left(x\right)& ={\displaystyle \frac{1}{{(x_n+1)}^2}}-exp\left(x_n\right),\hfill \\ \hfill \Omega & ={\mathbb{R}}_{+}^n.\hfill \end{array}$$

Problem 7.

This problem drawn from [31] is

$$\begin{array}{cc}\hfill f_i\left(x\right)& =log\left(\right|x_i|+1)-{\displaystyle \frac{x_i}{n}},i=1,2,\dots ,n,\hfill \\ \hfill \Omega & ={\mathbb{R}}_{+}^n.\hfill \end{array}$$

Problem 8.

This problem drawn from [22] is

$$\begin{array}{cc}\hfill f_i\left(x\right)& =x_i-3x_i\left({\displaystyle \frac{sin\left(x_i\right)}{3}}-0.66\right)+2,i=1,2,\dots ,n,\hfill \\ \hfill \Omega & =\{x\in {\mathbb{R}}^n|x_i|\ge -5,i=1,2,\dots ,n\}.\hfill \end{array}$$

Problem 9.

This problem drawn from [22] is

$$\begin{array}{cc}\hfill f_i\left(x\right)& ={\left(e^{x_i}\right)}^2+3sin\left(x_i\right)cos\left(x_i\right)-1,i=1,2,\dots ,n,\hfill \\ \hfill \Omega & =\{x\in {\mathbb{R}}^n|x_i|\ge -5,i=1,2,\dots ,n\}.\hfill \end{array}$$

Problem 10.

This problem drawn from [22] is

$$\begin{array}{cc}\hfill f_i\left(x\right)& ={\displaystyle \frac{i}{n}}{e}^{x_i}-1,i=1,2,\dots ,n,\hfill \\ \hfill \Omega & ={\mathbb{R}}_{+}^n.\hfill \end{array}$$

Problem 11.

This problem drawn from [31] is

$$\begin{array}{cc}\hfill f_1\left(x\right)& =cos\left(x_1\right)-9+3x_1+8exp\left(x_2\right),\hfill \\ \hfill f_i\left(x\right)& =cos\left(x_i\right)-9+3x_i+8exp\left(x_{i-1}\right),i=2,3,\dots ,n,\hfill \\ \hfill \Omega & ={\mathbb{R}}_{+}^n.\hfill \end{array}$$

Problem 12.

This problem drawn from [31] is

$$\begin{array}{cc}\hfill f_i\left(x\right)& =min\{min\{|x_i|,x_i^2\},max\{|x_i|,x_i^3\left\}\right\},i=1,2,\dots ,n,\hfill \\ \hfill \Omega & ={\mathbb{R}}_{+}^n.\hfill \end{array}$$

Problem 13.

This problem drawn from [31] is

$$\begin{array}{cc}\hfill f_i\left(x\right)& ={\displaystyle \frac{i}{10}}(1-x_i^2-e^{-x_i^2}),i=1,2,\dots ,n-1,\hfill \\ \hfill f_n\left(x\right)& ={\displaystyle \frac{n}{10}}(1-e^{-x_n^2}),\hfill \\ \hfill \Omega & ={\mathbb{R}}_{+}^n.\hfill \end{array}$$

Detailed outcomes of the experiments are presented in

Table 1. The results of three algorithms for Problems 1–5.

Prob	Dim	Sta		TTPM					DFSR1					Alg.1
			Niter	Nfun	Tcpu	$\parallel {\mathit{F}}^{*}\parallel$		Niter	Nfun	Tcpu	$\parallel {\mathit{F}}^{*}\parallel$		Niter	Nfun	Tcpu	$\parallel {\mathit{F}}^{*}\parallel$
P1	10,000	$x_1$	18	53	0.0135	$4.36\times {10}^{-7}$		19	39	0.0118	$8.97\times {10}^{-7}$		10	28	0.0063	$2.25\times {10}^{-7}$
		$x_2$	18	54	0.0093	$4.36\times {10}^{-7}$		18	39	0.0100	$7.75\times {10}^{-7}$		9	26	0.0045	$2.34\times {10}^{-7}$
		$x_3$	17	52	0.0092	$4.36\times {10}^{-7}$		18	38	0.0064	$6.69\times {10}^{-7}$		9	26	0.0045	$2.21\times {10}^{-7}$
		$x_4$	17	49	0.0073	$5.00\times {10}^{-7}$		18	37	0.0072	$7.72\times {10}^{-7}$		8	28	0.0045	$3.09\times {10}^{-7}$
		$x_5$	14	42	0.0064	$5.74\times {10}^{-7}$		18	38	0.0073	$6.60\times {10}^{-7}$		9	33	0.0056	$7.41\times {10}^{-7}$
		$x_6$	16	48	0.0076	$5.89\times {10}^{-7}$		19	40	0.0082	$9.70\times {10}^{-7}$		8	23	0.0042	$4.59\times {10}^{-7}$
		$x_7$	20	55	0.0083	$7.53\times {10}^{-7}$		15	32	0.0061	$9.41\times {10}^{-7}$		13	52	0.0089	$1.72\times {10}^{-7}$
		$x_8$	20	55	0.0089	$7.99\times {10}^{-7}$		15	32	0.0056	$9.40\times {10}^{-7}$		13	52	0.0088	$1.72\times {10}^{-7}$
	50,000	$x_1$	18	53	0.0316	$9.76\times {10}^{-7}$		24	57	0.0394	$5.12\times {10}^{-7}$		10	28	0.0220	$5.04\times {10}^{-7}$
		$x_2$	18	54	0.0291	$9.76\times {10}^{-7}$		19	41	0.0302	$6.91\times {10}^{-7}$		9	26	0.0154	$5.24\times {10}^{-7}$
		$x_3$	17	52	0.0328	$9.76\times {10}^{-7}$		19	40	0.0240	$5.97\times {10}^{-7}$		9	26	0.0165	$4.94\times {10}^{-7}$
		$x_4$	17	49	0.0318	$8.26\times {10}^{-7}$		21	44	0.0376	$6.12\times {10}^{-7}$		8	28	0.0167	$6.92\times {10}^{-7}$
		$x_5$	14	42	0.0231	$9.48\times {10}^{-7}$		19	41	0.0258	$6.78\times {10}^{-7}$		10	37	0.0227	$2.69\times {10}^{-7}$
		$x_6$	16	48	0.0309	$9.73\times {10}^{-7}$		18	39	0.0239	$4.71\times {10}^{-7}$		9	26	0.0159	$1.23\times {10}^{-7}$
		$x_7$	21	58	0.0356	$5.74\times {10}^{-7}$		16	33	0.0257	$1.12\times {10}^{-8}$		13	52	0.0327	$3.85\times {10}^{-7}$
		$x_8$	21	58	0.0356	$5.81\times {10}^{-7}$		16	33	0.0207	$1.12\times {10}^{-8}$		13	52	0.0353	$3.85\times {10}^{-7}$
P2	10,000	$x_1$	1	15	0.0021	0		1	12	0.0013	0		1	12	0.0015	0
		$x_2$	1	2	0.0004	0		1	2	0.0004	0		1	2	0.0004	0
		$x_3$	1	2	0.0004	0		2	4	0.0006	0		1	2	0.0003	0
		$x_4$	1	3	0.0004	0		2	6	0.0009	0		1	3	0.0005	0
		$x_5$	15	31	0.0060	$8.06\times {10}^{-7}$		1	3	0.0004	0		3	9	0.0018	0
		$x_6$	15	30	0.0040	$5.08\times {10}^{-7}$		2	4	0.0005	0		4	12	0.0016	0
		$x_7$	19	39	0.0069	$4.93\times {10}^{-7}$		2	5	0.0006	0		13	49	0.0059	$7.07\times {10}^{-7}$
		$x_8$	19	39	0.0073	$4.93\times {10}^{-7}$		2	5	0.0005	0		13	49	0.0053	$7.06\times {10}^{-7}$
	50,000	$x_1$	1	15	0.0094	0		1	12	0.0078	0		1	12	0.0067	0
		$x_2$	1	2	0.0013	0		1	4	0.0024	0		1	2	0.0013	0
		$x_3$	1	2	0.0013	0		1	3	0.0026	0		1	2	0.0018	0
		$x_4$	1	3	0.0016	0		2	6	0.0042	0		1	3	0.0023	0
		$x_5$	16	33	0.0250	$8.11\times {10}^{-7}$		1	3	0.0014	0		3	9	0.0060	0
		$x_6$	15	30	0.0220	$8.57\times {10}^{-7}$		2	4	0.0022	0		4	12	0.0062	0
		$x_7$	19	39	0.0268	$8.34\times {10}^{-7}$		2	6	0.0043	0		14	53	0.0280	$5.41\times {10}^{-7}$
		$x_8$	19	39	0.0210	$8.33\times {10}^{-7}$		2	6	0.0028	0		14	53	0.0245	$5.40\times {10}^{-7}$
P3	10,000	$x_1$	2	6	0.0018	0		7	30	0.0067	0		5	20	0.0040	0
		$x_2$	1	4	0.0010	0		1	7	0.0019	0		1	4	0.0010	0
		$x_3$	1	3	0.0004	0		3	6	0.0009	0		1	3	0.0004	0
		$x_4$	17	35	0.0056	$9.73\times {10}^{-7}$		1	3	0.0004	0		3	9	0.0016	0
		$x_5$	15	31	0.0050	$9.35\times {10}^{-7}$		3	6	0.0007	0		3	9	0.0010	0
		$x_6$	1	3	0.0004	0		1	3	0.0003	0		1	3	0.0004	0
		$x_7$	17	35	0.0055	$7.25\times {10}^{-7}$		1	3	0.0005	0		3	9	0.0016	0
		$x_8$	17	35	0.0049	$7.25\times {10}^{-7}$		1	3	0.0003	0		3	9	0.0011	0
	50,000	$x_1$	2	6	0.0069	0		10	53	0.0464	0		5	20	0.0151	0
		$x_2$	1	4	0.004	0		1	8	0.0094	0		1	4	0.0041	0
		$x_3$	1	3	0.002	0		3	6	0.0039	0		1	3	0.0021	0
		$x_4$	18	37	0.024	$7.40\times {10}^{-7}$		1	3	0.0021	0		3	9	0.0060	0
		$x_5$	16	33	0.019	$9.40\times {10}^{-7}$		3	6	0.0040	0		3	9	0.0052	0
		$x_6$	1	3	0.001	0		1	3	0.0011	0		1	3	0.0014	0
		$x_7$	18	37	0.020	$5.51\times {10}^{-7}$		1	3	0.0016	0		3	9	0.0038	0
		$x_8$	18	37	0.019	$5.51\times {10}^{-7}$		1	3	0.0013	0		3	9	0.0043	0
P4	10,000	$x_1$	65	129	0.045	$5.57\times {10}^{-7}$		37	107	0.0320	$5.92\times {10}^{-7}$		39	194	0.0513	$3.57\times {10}^{-7}$
		$x_2$	62	123	0.039	$8.00\times {10}^{-7}$		24	50	0.0159	$7.53\times {10}^{-7}$		40	203	0.0580	$3.13\times {10}^{-7}$
		$x_3$	58	115	0.037	$9.80\times {10}^{-7}$		25	51	0.0160	$1.66\times {10}^{-7}$		53	304	0.0777	$5.93\times {10}^{-7}$
		$x_4$	63	125	0.039	$9.92\times {10}^{-7}$		23	46	0.0149	$6.82\times {10}^{-7}$		43	223	0.0576	$3.90\times {10}^{-7}$
		$x_5$	56	112	0.043	$6.24\times {10}^{-7}$		28	59	0.0191	$5.96\times {10}^{-7}$		44	222	0.0589	$4.09\times {10}^{-7}$
		$x_6$	59	119	0.044	$6.39\times {10}^{-7}$		24	48	0.0149	$4.37\times {10}^{-7}$		48	236	0.0673	$6.37\times {10}^{-7}$
		$x_7$	64	130	0.042	$7.85\times {10}^{-7}$		25	52	0.0166	$4.37\times {10}^{-7}$		48	261	0.0736	$4.73\times {10}^{-7}$
		$x_8$	53	106	0.037	$8.30\times {10}^{-7}$		25	52	0.0192	$9.19\times {10}^{-7}$		66	344	0.0948	$6.78\times {10}^{-7}$
	50,000	$x_1$	58	114	0.165	$8.06\times {10}^{-7}$		148	972	1.1514	$9.24\times {10}^{-7}$		42	217	0.2666	$3.18\times {10}^{-7}$
		$x_2$	57	112	0.163	$6.96\times {10}^{-7}$		148	972	1.1459	$7.82\times {10}^{-7}$		43	218	0.2650	$4.99\times {10}^{-7}$
		$x_3$	60	118	0.167	$8.95\times {10}^{-7}$		149	974	1.1507	$3.91\times {10}^{-7}$		33	153	0.1984	$8.18\times {10}^{-7}$
		$x_4$	55	108	0.153	$8.74\times {10}^{-7}$		149	974	1.1705	$5.57\times {10}^{-7}$		51	256	0.3231	$9.14\times {10}^{-7}$
		$x_5$	59	117	0.166	$9.32\times {10}^{-7}$		149	974	1.1812	$3.60\times {10}^{-7}$		35	163	0.2110	$4.80\times {10}^{-7}$
		$x_6$	59	116	0.166	$7.86\times {10}^{-7}$		149	974	1.1622	$3.83\times {10}^{-7}$		49	258	0.3151	$4.09\times {10}^{-7}$
		$x_7$	59	116	0.165	$8.32\times {10}^{-7}$		149	974	1.1511	$7.77\times {10}^{-7}$		42	207	0.2585	$9.92\times {10}^{-7}$
		$x_8$	60	118	0.167	$6.59\times {10}^{-7}$		149	974	1.1449	$3.51\times {10}^{-7}$		41	212	0.2644	$9.79\times {10}^{-7}$
P5	10,000	$x_1$	27	82	0.009	$9.86\times {10}^{-7}$		20	72	0.0069	$6.04\times {10}^{-7}$		15	72	0.0070	$7.38\times {10}^{-7}$
		$x_2$	28	85	0.010	$7.36\times {10}^{-7}$		1	8	0.0006	0		1	4	0.0004	0
		$x_3$	24	73	0.008	$7.51\times {10}^{-7}$		1	5	0.0004	0		1	4	0.0004	0
		$x_4$	23	70	0.008	$7.36\times {10}^{-7}$		11	27	0.0031	$8.82\times {10}^{-7}$		14	67	0.0064	$4.67\times {10}^{-7}$
		$x_5$	19	58	0.006	$5.80\times {10}^{-7}$		1	4	0.0004	0		12	57	0.0055	$8.98\times {10}^{-7}$
		$x_6$	19	58	0.006	$7.82\times {10}^{-7}$		2	7	0.0007	0		1	4	0.0004	0
		$x_7$	21	64	0.007	$7.05\times {10}^{-7}$		3	9	0.0009	$9.02\times {10}^{-11}$		13	62	0.0057	$6.82\times {10}^{-7}$
		$x_8$	23	70	0.008	$6.17\times {10}^{-7}$		2	8	0.0006	0		13	62	0.0059	$6.81\times {10}^{-7}$
	50,000	$x_1$	25	76	0.026	$7.05\times {10}^{-7}$		29	138	0.0460	$5.20\times {10}^{-7}$		16	77	0.0232	$5.73\times {10}^{-7}$
		$x_2$	30	91	0.030	$4.36\times {10}^{-7}$		1	9	0.0024	0		1	4	0.0010	0
		$x_3$	25	76	0.027	$6.75\times {10}^{-7}$		1	6	0.0018	0		1	4	0.0014	0
		$x_4$	21	64	0.023	$7.84\times {10}^{-7}$		13	35	0.0121	$4.92\times {10}^{-7}$		14	67	0.0215	$7.24\times {10}^{-7}$
		$x_5$	17	52	0.017	$9.14\times {10}^{-7}$		1	4	0.0012	0		13	62	0.0207	$4.40\times {10}^{-7}$
		$x_6$	19	58	0.019	$8.08\times {10}^{-7}$		2	7	0.0019	0		1	4	0.0010	0
		$x_7$	26	79	0.028	$8.18\times {10}^{-7}$		11	28	0.0106	$8.06\times {10}^{-7}$		14	67	0.0215	$6.02\times {10}^{-7}$
		$x_8$	20	61	0.020	$9.45\times {10}^{-7}$		3	13	0.0041	$1.80\times {10}^{-7}$		14	67	0.0214	$6.02\times {10}^{-7}$

,

Table 2. The results of three algorithms for Problems 6–10.

Prob	Dim	Sta		TTPM					DFSR1					Alg.1
			Niter	Nfun	Tcpu	$\parallel {\mathit{F}}^{*}\parallel$		Niter	Nfun	Tcpu	$\parallel {\mathit{F}}^{*}\parallel$		Niter	Nfun	Tcpu	$\parallel {\mathit{F}}^{*}\parallel$
P6	10,000	$x_1$	1	2	0.002	0		1	2	0.0013	0		1	2	0.0012	0
		$x_2$	1	2	0.001	0		1	2	0.0009	0		1	2	0.0008	0
		$x_3$	1	2	0.002	0		1	2	0.0022	0		1	2	0.0022	0
		$x_4$	2	3	0.002	0		93	1014	0.3296	0		2	3	0.0018	0
		$x_5$	3	4	0.004	0		104	1123	0.3377	0		3	4	0.0022	0
		$x_6$	1	2	0.001	0		1	2	0.0005	0		1	2	0.0005	0
		$x_7$	2	3	0.003	0		90	977	0.2625	0		2	3	0.0012	0
		$x_8$	2	3	0.003	0		89	966	0.2465	0		2	3	0.0014	0
	50,000	$x_1$	1	2	0.005	0		1	2	0.0038	0		1	2	0.0036	0
		$x_2$	1	2	0.004	0		1	3	0.0060	0		1	2	0.0041	0
		$x_3$	1	2	0.006	0		1	2	0.0063	0		1	2	0.0060	0
		$x_4$	2	3	0.006	0		93	1014	1.3388	0		2	3	0.0055	0
		$x_5$	3	4	0.014	0		106	1146	1.4721	0		3	4	0.0082	0
		$x_6$	1	2	0.002	0		1	2	0.0019	0		1	2	0.0022	0
		$x_7$	2	3	0.011	0		93	1012	1.1441	0		2	3	0.0054	0
		$x_8$	2	3	0.012	0		93	1012	1.1158	0		2	3	0.0053	0
P7	10,000	$x_1$	6	7	0.005	0		11	55	0.0206	0		3	4	0.0021	0
		$x_2$	1	2	0.001	0		1	4	0.0013	0		1	2	0.0008	0
		$x_3$	1	2	0.001	0		1	2	0.0006	0		1	2	0.0006	0
		$x_4$	2	3	0.001	0		1	2	0.0006	0		2	3	0.0012	0
		$x_5$	1	2	0.001	0		1	2	0.0007	0		1	2	0.0007	0
		$x_6$	1	2	0.001	0		1	2	0.0007	0		1	2	0.0007	0
		$x_7$	nan	nan	nan	$1.81\times {10}^{-3}$		3	4	0.0016	0		3	4	0.0019	0
		$x_8$	nan	nan	nan	$2.50\times {10}^{-3}$		3	4	0.0016	0		3	4	0.0020	0
	50,000	$x_1$	6	7	0.019	0		22	139	0.2329	0		3	4	0.0097	0
		$x_2$	1	2	0.004	0		1	5	0.0077	0		1	2	0.0033	0
		$x_3$	1	2	0.002	0		1	3	0.0044	0		1	2	0.0025	0
		$x_4$	2	3	0.006	0		2	4	0.0064	0		2	3	0.0050	0
		$x_5$	1	2	0.004	0		1	2	0.0032	0		1	2	0.0032	0
		$x_6$	1	2	0.003	0		1	2	0.0031	0		1	2	0.0031	0
		$x_7$	nan	nan	nan	$2.18\times {10}^{-2}$		3	4	0.0067	0		4	5	0.0096	$5.41\times {10}^{-29}$
		$x_8$	nan	nan	nan	$2.32\times {10}^{-2}$		3	4	0.0066	0		3	4	0.0083	0
P8	10,000	$x_1$	14	56	0.011	$4.84\times {10}^{-7}$		47	187	0.0413	$9.36\times {10}^{-7}$		11	53	0.0079	$2.53\times {10}^{-7}$
		$x_2$	14	56	0.008	$5.97\times {10}^{-7}$		43	157	0.0329	$9.25\times {10}^{-7}$		12	58	0.0105	$9.70\times {10}^{-7}$
		$x_3$	12	49	0.007	$9.68\times {10}^{-7}$		30	94	0.0138	$8.40\times {10}^{-7}$		11	53	0.0085	$7.28\times {10}^{-7}$
		$x_4$	12	48	0.009	$6.37\times {10}^{-7}$		37	118	0.0246	$7.81\times {10}^{-7}$		12	55	0.0098	$5.31\times {10}^{-7}$
		$x_5$	13	53	0.009	$7.80\times {10}^{-7}$		34	106	0.0190	$6.89\times {10}^{-7}$		9	43	0.0066	$8.20\times {10}^{-7}$
		$x_6$	13	53	0.008	$4.47\times {10}^{-7}$		32	100	0.0157	$8.33\times {10}^{-7}$		11	53	0.0081	$6.68\times {10}^{-7}$
		$x_7$	28	112	0.016	$9.00\times {10}^{-7}$		46	127	0.0214	$9.56\times {10}^{-7}$		10	47	0.0077	$9.19\times {10}^{-7}$
		$x_8$	28	112	0.017	$9.01\times {10}^{-7}$		46	127	0.0262	$9.75\times {10}^{-7}$		10	47	0.0077	$8.84\times {10}^{-7}$
	50,000	$x_1$	14	56	0.044	$6.53\times {10}^{-7}$		66	355	0.3356	$7.73\times {10}^{-7}$		11	53	0.0397	$5.66\times {10}^{-7}$
		$x_2$	14	56	0.040	$8.05\times {10}^{-7}$		45	175	0.1563	$8.48\times {10}^{-7}$		13	63	0.0408	$2.57\times {10}^{-7}$
		$x_3$	13	53	0.029	$4.37\times {10}^{-7}$		35	111	0.0661	$8.93\times {10}^{-7}$		12	58	0.0329	$7.43\times {10}^{-7}$
		$x_4$	13	52	0.037	$4.77\times {10}^{-7}$		40	135	0.0962	$6.45\times {10}^{-7}$		14	65	0.0446	$2.97\times {10}^{-7}$
		$x_5$	14	57	0.035	$3.52\times {10}^{-7}$		36	116	0.0720	$8.18\times {10}^{-7}$		10	48	0.0278	$8.45\times {10}^{-7}$
		$x_6$	13	53	0.031	$9.99\times {10}^{-7}$		36	114	0.0771	$9.29\times {10}^{-7}$		11	53	0.0342	$7.24\times {10}^{-8}$
		$x_7$	30	120	0.082	$5.15\times {10}^{-7}$		42	121	0.0846	$5.79\times {10}^{-7}$		11	52	0.0299	$3.82\times {10}^{-7}$
		$x_8$	30	120	0.072	$5.15\times {10}^{-7}$		42	121	0.0930	$6.08\times {10}^{-7}$		11	52	0.0354	$3.79\times {10}^{-7}$
P9	10,000	$x_1$	8	41	0.044	$4.86\times {10}^{-7}$		36	83	0.0955	$7.04\times {10}^{-7}$		13	60	0.0404	$4.88\times {10}^{-7}$
		$x_2$	8	20	0.010	$4.86\times {10}^{-7}$		36	76	0.0720	$7.04\times {10}^{-7}$		16	81	0.0235	$7.84\times {10}^{-7}$
		$x_3$	5	20	0.006	$2.06\times {10}^{-7}$		10	45	0.0153	$1.65\times {10}^{-7}$		16	92	0.0220	$8.46\times {10}^{-7}$
		$x_4$	5	22	0.006	$6.38\times {10}^{-8}$		7	30	0.0077	$8.14\times {10}^{-7}$		11	54	0.0125	$1.00\times {10}^{-7}$
		$x_5$	4	17	0.004	$1.83\times {10}^{-8}$		7	29	0.0063	$6.43\times {10}^{-7}$		14	81	0.0156	$6.80\times {10}^{-7}$
		$x_6$	4	17	0.003	$2.30\times {10}^{-8}$		7	29	0.0068	$4.38\times {10}^{-7}$		14	81	0.0172	$8.01\times {10}^{-7}$
		$x_7$	34	152	0.036	$7.70\times {10}^{-7}$		53	162	0.0386	$9.71\times {10}^{-7}$		17	97	0.0211	$4.42\times {10}^{-7}$
		$x_8$	35	146	0.034	$7.14\times {10}^{-7}$		53	162	0.0389	$9.73\times {10}^{-7}$		17	97	0.0199	$4.27\times {10}^{-7}$
	50,000	$x_1$	9	45	0.192	$1.83\times {10}^{-7}$		38	87	0.4673	$7.43\times {10}^{-7}$		15	70	0.1919	$9.10\times {10}^{-7}$
		$x_2$	9	24	0.043	$1.83\times {10}^{-7}$		38	80	0.3674	$7.43\times {10}^{-7}$		17	87	0.1117	$4.93\times {10}^{-7}$
		$x_3$	5	20	0.023	$4.60\times {10}^{-7}$		17	107	0.1340	$4.13\times {10}^{-7}$		17	98	0.0888	$7.71\times {10}^{-7}$
		$x_4$	5	22	0.027	$1.43\times {10}^{-7}$		8	34	0.0359	$8.64\times {10}^{-7}$		11	54	0.0525	$2.24\times {10}^{-7}$
		$x_5$	4	17	0.015	$4.10\times {10}^{-8}$		8	34	0.0306	$8.56\times {10}^{-7}$		15	87	0.0787	$4.05\times {10}^{-7}$
		$x_6$	4	17	0.016	$5.15\times {10}^{-8}$		8	34	0.0294	$9.31\times {10}^{-7}$		15	87	0.0825	$7.08\times {10}^{-7}$
		$x_7$	38	167	0.148	$5.33\times {10}^{-7}$		54	169	0.1662	$8.32\times {10}^{-7}$		17	97	0.0865	$9.81\times {10}^{-7}$
		$x_8$	37	164	0.150	$4.46\times {10}^{-7}$		54	169	0.1639	$8.32\times {10}^{-7}$		17	97	0.0877	$9.74\times {10}^{-7}$
P10	10,000	$x_1$	44	436	0.071	$4.55\times {10}^{-7}$		176	270	0.082	$9.81\times {10}^{-7}$		20	103	0.018	$8.13\times {10}^{-7}$
		$x_2$	26	44	0.011	$6.36\times {10}^{-7}$		58	67	0.020	$9.73\times {10}^{-7}$		23	97	0.019	$6.60\times {10}^{-7}$
		$x_3$	30	49	0.012	$4.76\times {10}^{-7}$		161	167	0.056	$9.89\times {10}^{-7}$		16	65	0.012	$6.48\times {10}^{-7}$
		$x_4$	20	41	0.012	$7.36\times {10}^{-7}$		122	130	0.046	$9.76\times {10}^{-7}$		16	66	0.015	$6.91\times {10}^{-7}$
		$x_5$	30	48	0.013	$8.22\times {10}^{-7}$		68	74	0.023	$9.86\times {10}^{-7}$		16	61	0.015	$5.23\times {10}^{-7}$
		$x_6$	26	44	0.010	$8.51\times {10}^{-7}$		108	114	0.037	$9.81\times {10}^{-7}$		19	77	0.016	$6.43\times {10}^{-7}$
		$x_7$	32	54	0.016	$5.52\times {10}^{-7}$		215	224	0.073	$9.93\times {10}^{-7}$		21	99	0.019	$4.38\times {10}^{-7}$
		$x_8$	23	46	0.013	$9.70\times {10}^{-7}$		96	101	0.036	$9.76\times {10}^{-7}$		14	52	0.011	$7.02\times {10}^{-7}$
	50,000	$x_1$	52	460	0.347	$4.79\times {10}^{-7}$		223	365	0.396	$9.76\times {10}^{-7}$		20	104	0.081	$9.68\times {10}^{-7}$
		$x_2$	28	51	0.050	$9.68\times {10}^{-7}$		208	243	0.322	$9.75\times {10}^{-7}$		18	72	0.056	$9.44\times {10}^{-7}$
		$x_3$	29	48	0.052	$4.81\times {10}^{-7}$		223	257	0.349	$9.90\times {10}^{-7}$		18	76	0.070	$3.51\times {10}^{-7}$
		$x_4$	28	50	0.051	$9.91\times {10}^{-7}$		167	181	0.232	$9.99\times {10}^{-7}$		16	66	0.065	$9.02\times {10}^{-7}$
		$x_5$	28	47	0.053	$7.66\times {10}^{-7}$		97	108	0.148	$9.94\times {10}^{-7}$		16	61	0.057	$6.45\times {10}^{-7}$
		$x_6$	25	50	0.046	$9.95\times {10}^{-7}$		212	231	0.320	$9.80\times {10}^{-7}$		14	50	0.045	$3.10\times {10}^{-7}$
		$x_7$	40	62	0.068	$9.36\times {10}^{-7}$		176	186	0.259	$9.86\times {10}^{-7}$		24	143	0.109	$8.85\times {10}^{-7}$
		$x_8$	24	50	0.052	$5.40\times {10}^{-7}$		62	68	0.086	$9.76\times {10}^{-7}$		16	60	0.055	$5.72\times {10}^{-7}$

and

Table 3. The results of three algorithms for Problems 11–13.

Prob	Dim	Sta		TTPM					DFSR1					Alg.1
			Niter	Nfun	Tcpu	$\parallel {\mathit{F}}^{*}\parallel$		Niter	Nfun	Tcpu	$\parallel {\mathit{F}}^{*}\parallel$		Niter	Nfun	Tcpu	$\parallel {\mathit{F}}^{*}\parallel$
P11	10,000	$x_1$	20	134	0.031	$9.11\times {10}^{-7}$		1	12	0.004	0		1	12	0.004	0
		$x_2$	1	5	0.002	0		1	12	0.005	0		2	10	0.004	0
		$x_3$	1	6	0.002	0		1	12	0.003	0		1	6	0.001	0
		$x_4$	17	103	0.022	$6.13\times {10}^{-7}$		6	40	0.010	0		4	25	0.006	0
		$x_5$	17	103	0.021	$8.70\times {10}^{-7}$		2	12	0.002	0		3	17	0.003	0
		$x_6$	17	102	0.018	$6.39\times {10}^{-7}$		1	7	0.001	0		1	6	0.001	0
		$x_7$	304	1904	0.389	0		nan	nan	nan	$7.17\times {10}^{+2}$		27	209	0.028	0
		$x_8$	492	3636	0.892	0		nan	nan	nan	$9.54\times {10}^{+2}$		12	72	0.011	0
	50,000	$x_1$	21	140	0.133	$6.84\times {10}^{-7}$		1	12	0.020	0		1	12	0.020	0
		$x_2$	1	5	0.009	0		1	12	0.021	0		2	10	0.016	0
		$x_3$	1	6	0.008	0		1	12	0.012	0		1	6	0.007	0
		$x_4$	18	109	0.099	$4.60\times {10}^{-7}$		10	72	0.085	0		4	25	0.029	0
		$x_5$	18	109	0.083	$8.68\times {10}^{-7}$		3	18	0.018	0		3	17	0.013	0
		$x_6$	18	108	0.079	$4.79\times {10}^{-7}$		1	8	0.007	0		1	6	0.005	0
		$x_7$	284	1640	1.464	0		nan	nan	nan	$9.89\times {10}^{+2}$		21	156	0.089	0
		$x_8$	300	1714	1.637	0		11	64	0.060	$8.10\times {10}^{-7}$		24	175	0.097	0
P12	10,000	$x_1$	nan	nan	nan	$6.87\times {10}^{-5}$		1	2	0.001	0		3	6	0.008	0
		$x_2$	1	2	0.003	0		1	7	0.008	0		1	2	0.002	0
		$x_3$	1	2	0.002	0		1	2	0.002	0		1	2	0.001	0
		$x_4$	nan	nan	nan	$6.84\times {10}^{-5}$		1	2	0.000	0		3	5	0.006	0
		$x_5$	nan	nan	nan	$6.76\times {10}^{-5}$		3	4	0.008	0		3	4	0.007	0
		$x_6$	1	2	0.002	0		1	2	0.002	0		1	2	0.002	0
		$x_7$	nan	nan	nan	$4.50\times {10}^{-5}$		22	23	0.018	$9.61\times {10}^{-7}$		19	20	0.020	$5.51\times {10}^{-7}$
		$x_8$	nan	nan	nan	$4.50\times {10}^{-5}$		22	23	0.018	$9.61\times {10}^{-7}$		19	21	0.023	$9.26\times {10}^{-7}$
	50,000	$x_1$	nan	nan	nan	$1.54\times {10}^{-4}$		1	2	0.006	0		3	6	0.034	0
		$x_2$	1	2	0.012	0		1	8	0.043	0		1	2	0.011	0
		$x_3$	1	2	0.007	0		1	4	0.017	0		1	2	0.007	0
		$x_4$	nan	nan	nan	$1.53\times {10}^{-4}$		1	2	0.001	0		3	5	0.029	0
		$x_5$	nan	nan	nan	$1.51\times {10}^{-4}$		3	4	0.033	0		3	4	0.033	0
		$x_6$	1	2	0.012	0		1	2	0.011	0		1	2	0.011	0
		$x_7$	nan	nan	nan	$1.01\times {10}^{-4}$		39	41	0.386	$9.86\times {10}^{-7}$		22	23	0.099	$2.03\times {10}^{-7}$
		$x_8$	nan	nan	nan	$1.01\times {10}^{-4}$		39	41	0.386	$9.86\times {10}^{-7}$		21	23	0.097	$5.66\times {10}^{-7}$
P13	10,000	$x_1$	5	158	0.013	0		7	68	0.009	0		6	27	0.003	0
		$x_2$	5	159	0.013	0		7	68	0.009	0		6	27	0.003	0
		$x_3$	7	324	0.025	0		1	12	0.002	0		4	15	0.002	0
		$x_4$	4	5	0.001	0		9	90	0.018	0		4	15	0.002	0
		$x_5$	nan	nan	nan	$1.56\times {10}^{+1}$		10	71	0.010	0		9	40	0.006	0
		$x_6$	1	2	0.000	0		1	2	0.000	0		1	2	0.000	0
		$x_7$	4	5	0.001	0		9	90	0.014	0		4	15	0.002	0
		$x_8$	7	254	0.020	0		15	156	0.024	0		5	16	0.003	0
	50,000	$x_1$	5	176	0.048	0		6	57	0.021	0		6	27	0.012	0
		$x_2$	5	174	0.051	0		6	57	0.019	0		6	27	0.010	0
		$x_3$	nan	nan	nan	$3.53\times {10}^{+1}$		7	68	0.029	0		4	15	0.020	0
		$x_4$	5	164	0.051	0		7	68	0.049	0		4	15	0.021	0
		$x_5$	6	59	0.020	0		8	69	0.042	0		7	28	0.014	0
		$x_6$	1	2	0.001	0		1	2	0.001	0		1	2	0.001	0
		$x_7$	5	161	0.048	0		7	68	0.041	0		4	15	0.016	0
		$x_8$	7	311	0.094	0		9	90	0.055	0		4	15	0.007	0

, following the format “Niter Nfun Tcpu $\parallel F^{*}\parallel$”. Specifically, “Niter” refers to the number of iterations, “Nfun” denotes the count of function value calculations, and “Tcpu” represents the CPU time (unit: seconds), $\parallel F^{*}\parallel$ indicates the final value of $\parallel F\left(x_k\right)\parallel$ upon program termination. Meanwhile, “Dim” indicates the dimension of each test problem, and “Sta” stands for the starting points. By analyzing these tables comprehensively, it can be clearly observed that for the given test problems, Algorithm 1 demonstrates consistent advantages over TTPM and DFSR1. Specifically, Algorithm 1 exhibits the minimum Niter and Nfun values in a large number of test instances. Meanwhile, Algorithm 1 also consumes less CPU time: in the vast majority of the test problems, its CPU time is consistently the smallest.

To investigate the impact of parameter variations on the performance of Algorithm 1, we conduct sensitivity analyses for key parameters ($\gamma$, $\rho$, c, ${\zeta }_1$, and ${\zeta }_2$). The evaluation metrics used include: average number of iterations ($\overline{\mathrm{Niter}}$), average number of function evaluations ($\overline{\mathrm{Nfun}}$), average CPU time ($\overline{\mathrm{Tcpu}}$, unit: seconds), and average optimal residual ($\overline{\parallel F^{*}\parallel }$, representing the final value of $\parallel F\left(x_k\right)\parallel$ when the program terminates). The results are presented in

Table 4. Sensitivity analysis of parameter $\gamma$ for Algorithm 1.

		$\mathit{\gamma }=1$					$\mathit{\gamma }=1.2$					$\mathit{\gamma }=1.4$
	$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$		$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$		$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$
	14.457	72.188	0.044	$3.088\times {10}^{-7}$		10.529	48.183	0.030	$2.710\times {10}^{-7}$		10.565	49.909	0.033	$2.872\times {10}^{-7}$

,

Table 5. Sensitivity analysis of parameter $\rho$ for Algorithm 1.

		$\mathit{\rho }=0.4$					$\mathit{\rho }=0.5$					$\mathit{\rho }=0.6$
	$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$		$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$		$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$
	15.087	65.519	0.038	$3.574\times {10}^{-7}$		10.529	48.183	0.030	$2.710\times {10}^{-7}$		10.856	52.375	0.035	$2.790\times {10}^{-7}$

,

Table 6. Sensitivity analysis of parameter c for Algorithm 1.

		c = 0.05					c = 0.1					c = 0.2
	$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$		$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$		$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$
	10.590	48.913	0.031	$2.708\times {10}^{-7}$		10.529	48.183	0.030	$2.710\times {10}^{-7}$		10.861	52.385	0.035	$2.478\times {10}^{-7}$

and

Table 7. Sensitivity analysis of parameter ${\zeta }_1$ and ${\zeta }_2$ for Algorithm 1.

	${\mathit{\zeta }}_1$ = 0.01		${\mathit{\zeta }}_2$ = 0.8			${\mathit{\zeta }}_1$ = 0.001		${\mathit{\zeta }}_2$ = 0.8			${\mathit{\zeta }}_1$ = 0.001		${\mathit{\zeta }}_2$ = 8
	$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$		$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$		$\overline{\mathrm{Niter}}$	$\overline{\mathrm{Nfun}}$	$\overline{\mathrm{Tcpu}}$	$\overline{\parallel {\mathit{F}}^{*}\parallel }$
	10.529	48.183	0.031	$2.710\times {10}^{-7}$		10.529	48.183	0.030	$2.710\times {10}^{-7}$		10.532	49.043	0.031	$2.699\times {10}^{-7}$

.

Table 4 focuses on the sensitivity analysis of parameter $\gamma$, with three tested values: $\gamma =1$, $\gamma =1.2$, and $\gamma =1.4$. The results show that the best performance is achieved when $\gamma =1.2$, with the minimum average number of iterations (10.529), average number of function evaluations (48.183), average CPU time (0.030), and average optimal residual (2.710 × 10⁻⁷). Compared to $\gamma =1.2$, when $\gamma =1.0$, the average number of iterations increases by 37.3%, the average number of function evaluations by 49.8%, the average CPU time by 13.3%, and the average optimal residual by 13.9%. In contrast, the differences between $\gamma =1.4$ and $\gamma =1.2$ are negligible: the average number of iterations increases by only 0.34%, the average number of function evaluations by 3.58%, the average CPU time by 10%, and the average optimal residual by 5.98%. This indicates that $\gamma =1.2$ is the optimal choice, $\gamma =1.4$ is still acceptable, but $\gamma =1.0$ leads to significant performance degradation.

Table 5 analyzes the sensitivity of parameter $\rho$, with tested values of 0.4, 0.5, and 0.6. The best performance is observed when $\rho =0.5$, with all metrics minimized (average iterations 10.529, average function evaluations 48.183, average CPU time 0.030, average optimal residual 2.710 × 10 ⁻⁷). When $\rho =0.4$, the average number of iterations increases by 43.3%, the average number of function evaluations by 36.3%, the average CPU time by 26.67%, and the average optimal residual by 31.88%. For $\rho =0.6$, the average number of iterations increases by 3.07%, the average number of function evaluations by 8.74%, the average CPU time by 16.67%, and the average optimal residual by 2.95%. It is evident that $\rho =0.5$ is the optimal balance point, with deviations to 0.4 causing severe performance loss and deviations to 0.6 leading to moderate degradation.

Table 6 examines the sensitivity of parameter c, with tested values of 0.05, 0.1, and 0.2. The optimal performance is achieved when c = 0.1, with all metrics minimized. Compared to c = 0.1, when c = 0.05, the average number of iterations increases by 0.58%, the average number of function evaluations by 1.51%, the average CPU time by 3.33%, and the average optimal residual by 0.07%. For c = 0.2, the average number of iterations increases by 3.12%, the average number of function evaluations by 8.72%, the average CPU time by 16.67%, and the average optimal residual by 8.12%. This demonstrates that c = 0.1 is the optimal choice, c = 0.05 is slightly inferior, and c = 0.2 leads to noticeable performance decline.

Table 7 investigates the sensitivity of parameters ${\zeta }_1$ and ${\zeta }_2$, with three tested combinations: ${\zeta }_1=0.01,{\zeta }_2=0.8$; ${\zeta }_1=0.001,{\zeta }_2=0.8$; and ${\zeta }_1=0.001,{\zeta }_2=8$. The combination ${\zeta }_1=0.001,{\zeta }_2=0.8$ performs the best, with the minimum average number of iterations (10.529), average number of function evaluations (48.183), average CPU time (0.030), and average optimal residual (2.710 × 10⁻⁷). When ${\zeta }_1=0.01,{\zeta }_2=0.8$, the average number of iterations remains unchanged, the average number of function evaluations shows no change, the average CPU time increases by 3.33%, and the average optimal residual remains unchanged. For ${\zeta }_1=0.001,{\zeta }_2=8$, the average number of iterations increases by 0.03%, the average number of function evaluations by 1.78%, the average CPU time by 3.33%, and the average optimal residual by 0.4%. This indicates that ${\zeta }_1=0.001,{\zeta }_2=0.8$ is the optimal parameter pair, with other combinations causing only minor performance fluctuations.

These sensitivity analyses identify the optimal ranges for the key parameters of Algorithm 1, enhancing its practical guidance in real-world applications by quantifying the extent of performance changes caused by parameter variations.

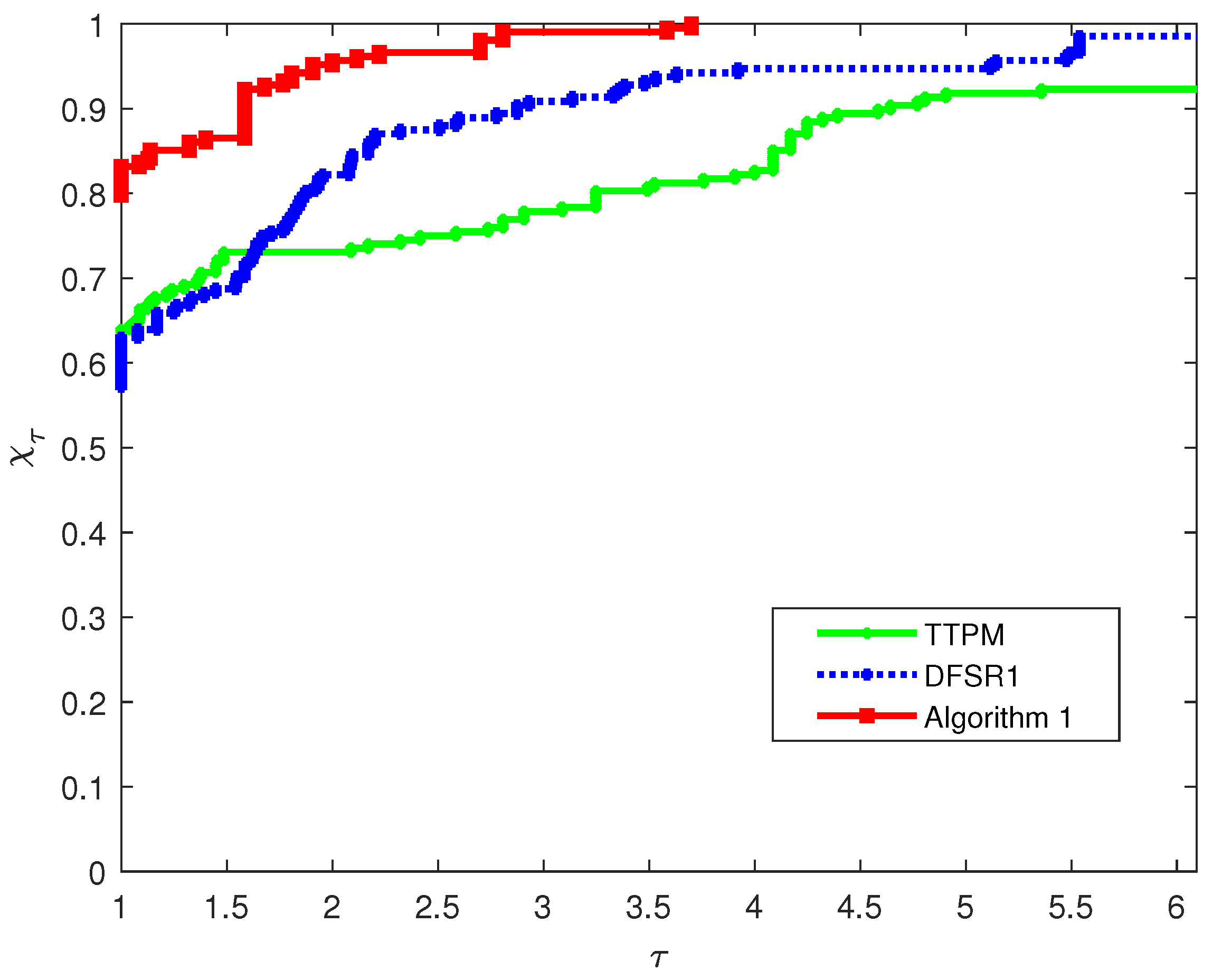
In order to conduct a comprehensive comparison across all algorithms, we make use of the performance profile framework developed by Dolan and Mor’e [32], which is standard in the field of numerical optimization for algorithmic performance assessment. Figure 1 illustrates the performance profiles for the number of iterations on a ${log}_2$-scale, involving three algorithms: TTPM, DFSR1, and Algorithm 1.

In Figure 1, it can be observed that as $\tau$ increases, Algorithm 1 consistently achieves a higher proportion of solved problems than TTPM and DFSR1. Specifically, when $\tau$ reaches around 1.5, the curve of Algorithm 1 rises significantly faster and remains at the top afterward—this clearly demonstrates its notable advantage in iteration efficiency. In contrast, the proportion of solved problems for DFSR1 grows relatively slowly, while TTPM is less competitive in iteration performance compared to the other two algorithms.

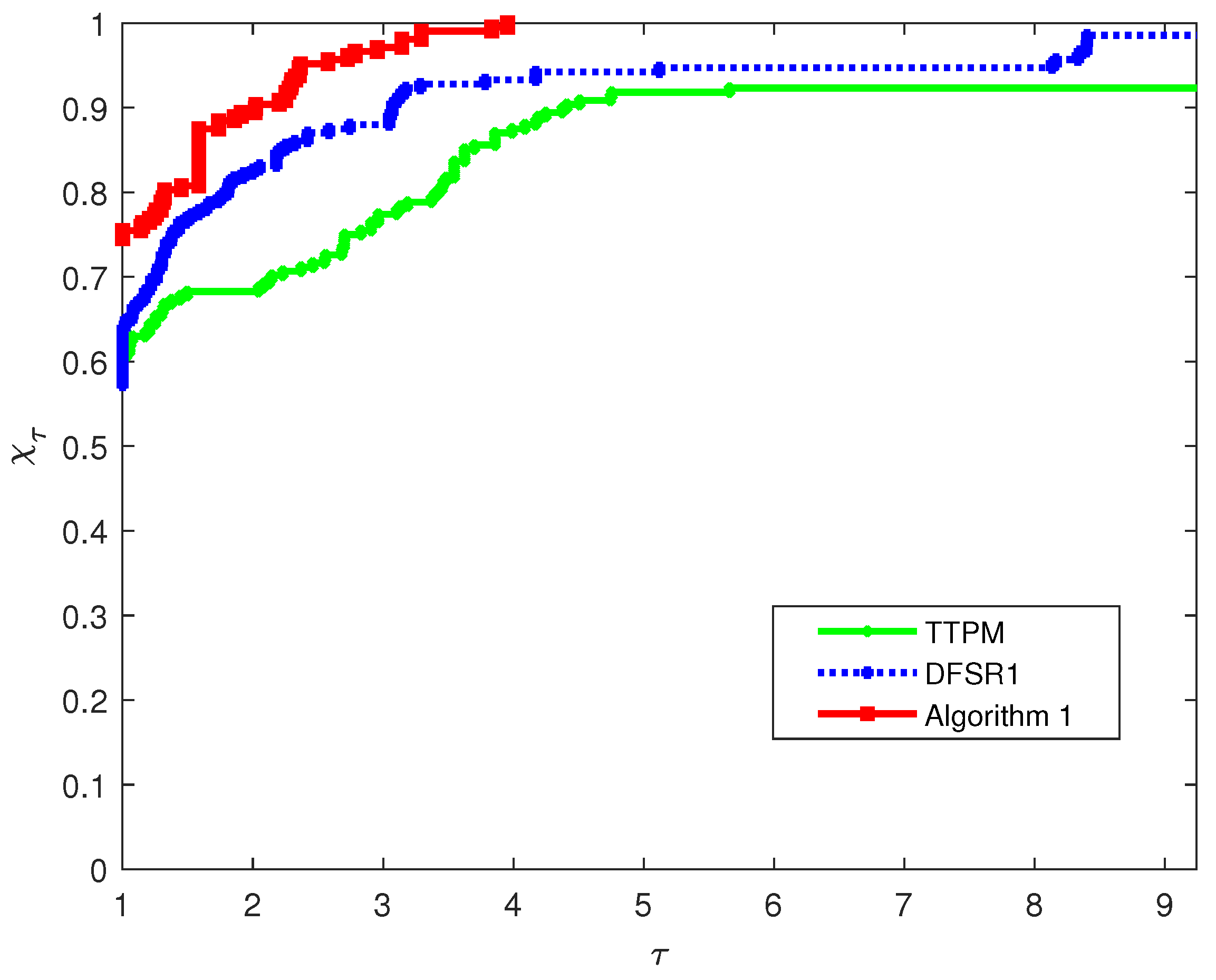
Figure 2 presents the performance regarding function evaluations. It is evident that Algorithm 1 solves the largest proportion of problems no matter what value $\tau$ takes. Consistent with the iteration results, Algorithm 1 performs exceptionally well, even when $\tau$ is small, the proportion of problems it solves already surpasses that of TTPM and DFSR1. Additionally, TTPM and DFSR1 show similar performance in function evaluations, but both are less efficient than Algorithm 1.

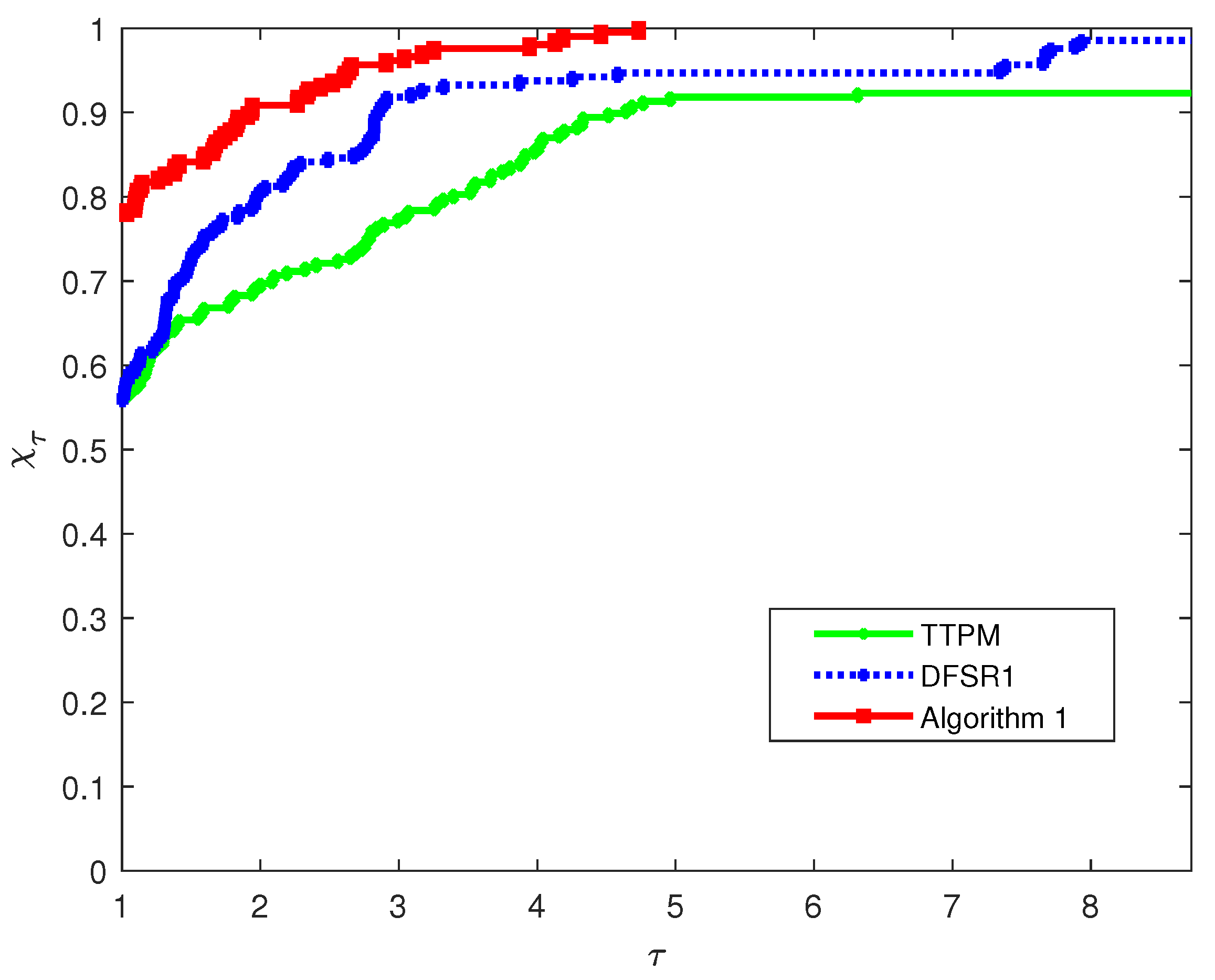
Figure 3 illustrates the performance differences in CPU time. As can be seen from the figure, the curve of Algorithm 1 takes the lead from the very beginning and stays at the highest level as $\tau$ increases. This means that within the entire range of $\tau$ values, Algorithm 1 outperforms DFSR1 and TTPM in CPU time efficiency. Whether it is the basic efficiency when $\tau$ is small or the ability to cover more problems when $\tau$ increases, Algorithm 1 can solve a higher proportion of test problems with shorter CPU time, fully demonstrating its stable advantage in computational speed.

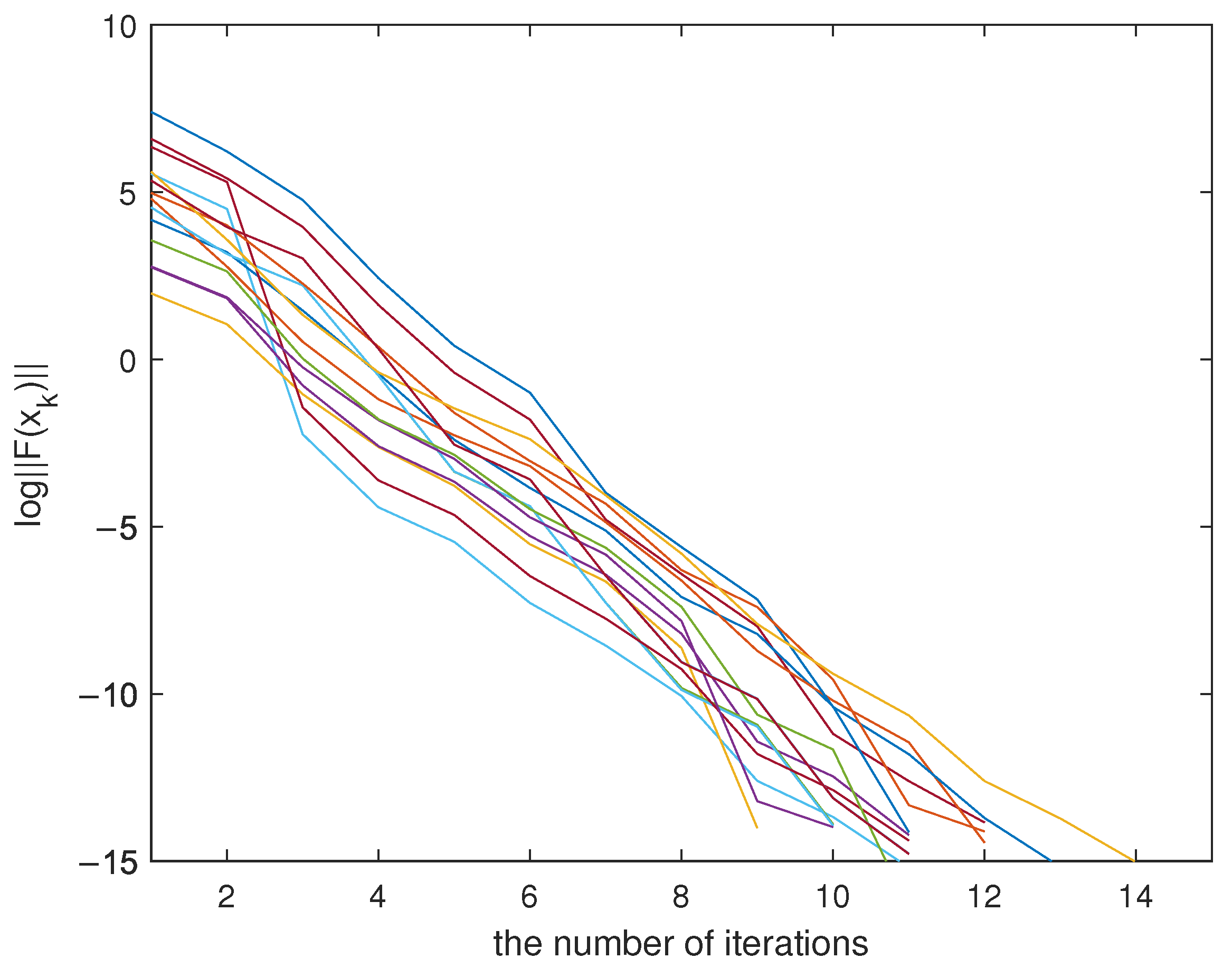
Moreover, we verify the convergence rate of Algorithm 1 through numerical experiments. Specifically, for Problem 8, we consider scenarios with two dimensions and eight initial points, resulting in 16 problem instances in total. We plot the curve of $log\parallel F\left(x_k\right)\parallel$ versus the number of iterations, as shown in Figure 4. It is evident that the curves of $log\parallel F\left(x_k\right)\parallel$ decrease linearly with the number of iterations, indicating that the Algorithm 1 exhibits linear convergence for Problem 8.

5. Results

In conclusion, this paper presents a new derivative-free method integrated with a symmetric rank-one update for solving constrained nonlinear systems of monotone equations. Rooted in the revised SR1 update formula and enhanced by projection techniques, the method exhibits distinct advantages: its search direction inherently satisfies sufficient descent and trust-region properties, eliminating reliance on line search techniques—a feature that simplifies practical implementation. Theoretical results confirm its global convergence under specified conditions, laying a solid foundation for its theoretical reliability. Comparative numerical experiments with two existing approaches further validate that the proposed method outperforms competitors in terms of iteration count, function evaluations, and CPU runtime, demonstrating superior reliability and robustness. These findings highlight the method’s potential as an efficient and stable tool for addressing constrained nonlinear monotone equations, with promising applications in related engineering and scientific computing fields.