Multi-Physics Coupling Mechanism of the Dynamic Sealing Performance of the O-Ring at the Neck of a Type IV Hydrogen Storage Cylinder Under Linearly Decreasing Filling Conditions
Abstract
1. Introduction
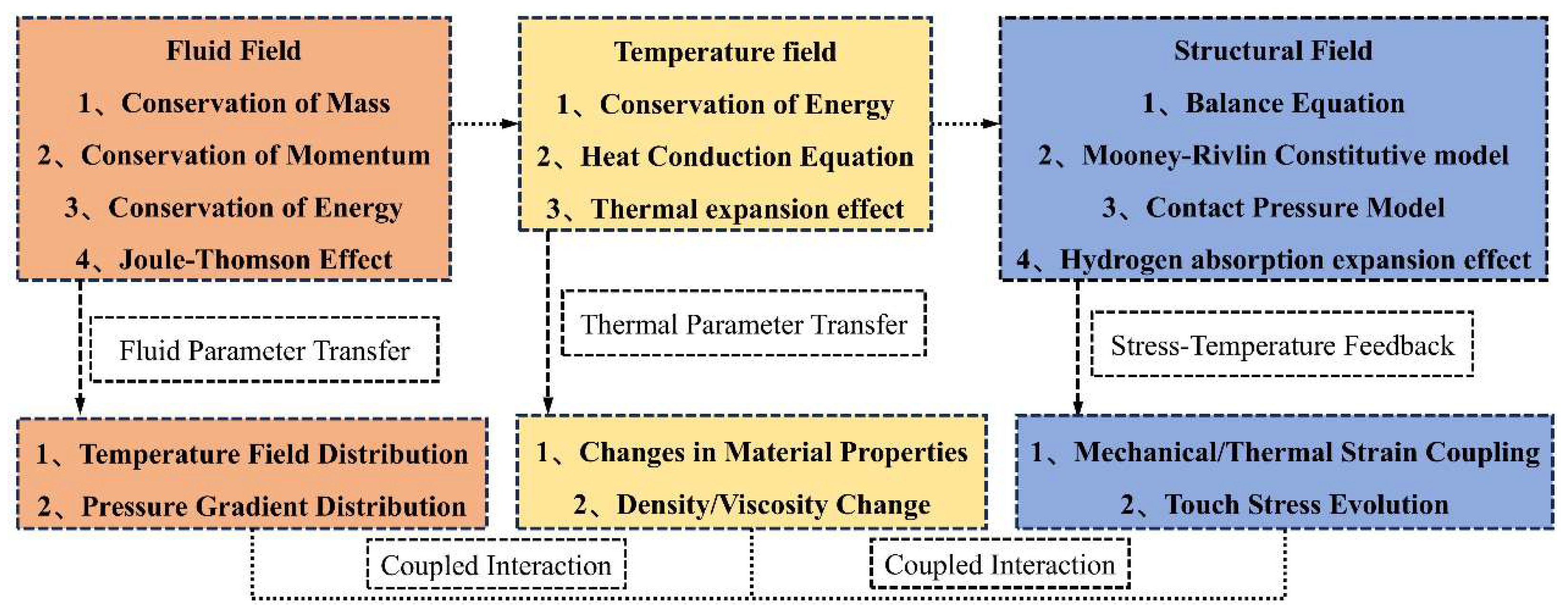
2. Mathematical Model
2.1. Basic Assumptions
- The ambient temperature change is assumed to remain constant, and the heat transfer coefficient between the metal valve seat and the external environment is assumed to remain constant.
- During hydrogen filling, due to the short duration, the Type IV cylinder is assumed to undergo an adiabatic process with the external environment, with hydrogen heat exchange occurring only with the valve and O-ring [14].
- It is assumed that heat generated inside the hydrogen storage vessel does not affect the mechanical properties of any components.
- During hydrogen refueling, the primary heat sources are gas compression and the Joule–Thomson effect. Heat generated by the viscoelastic properties of the O-ring is two to three orders of magnitude lower, and thus the heat from the O-ring is neglected [31].
2.2. Heat Transfer Model
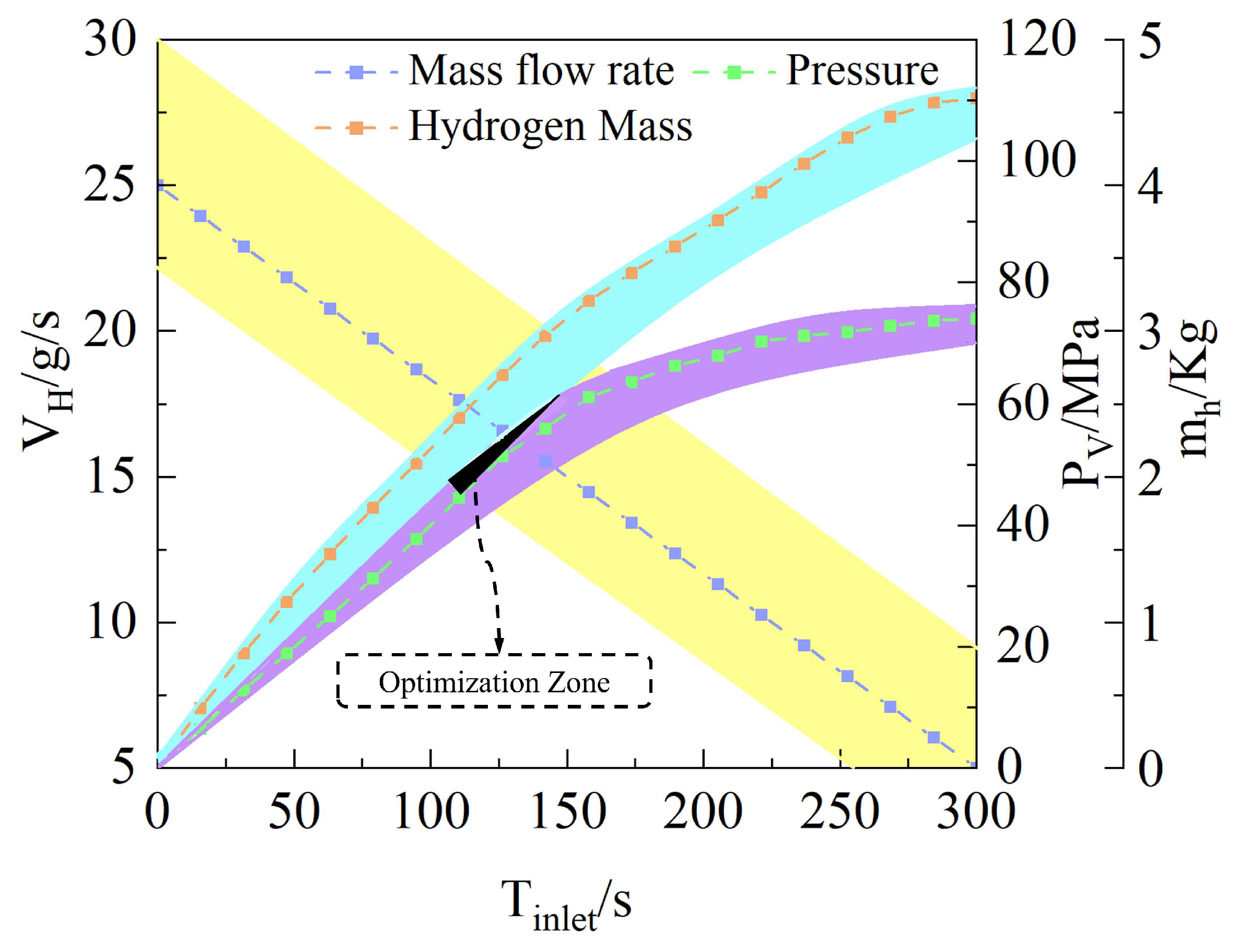
2.3. Linear Decreasing Hydrogen Filling Strategy
3. Numerical Analysis Model
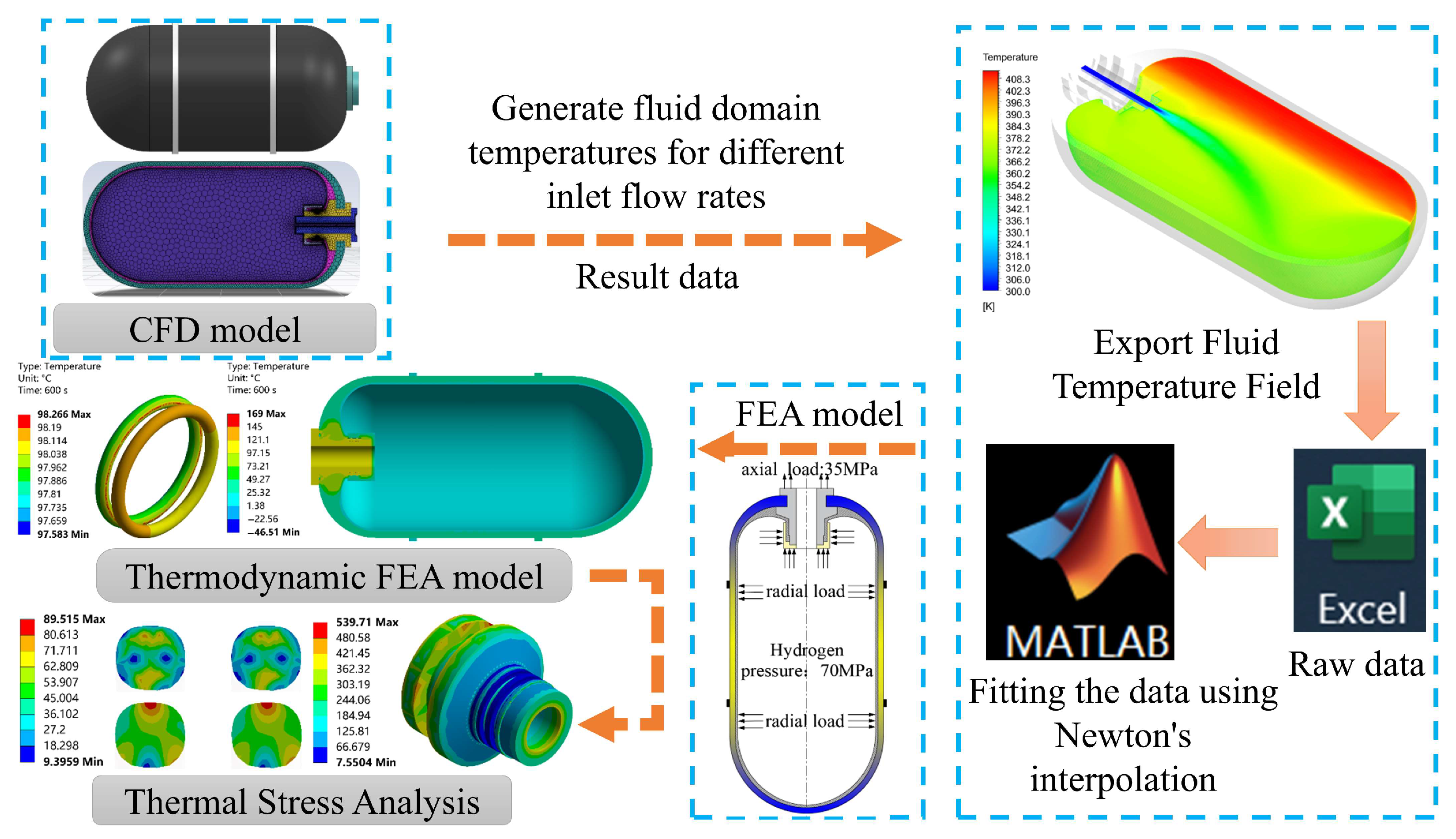
3.1. Analysis Process
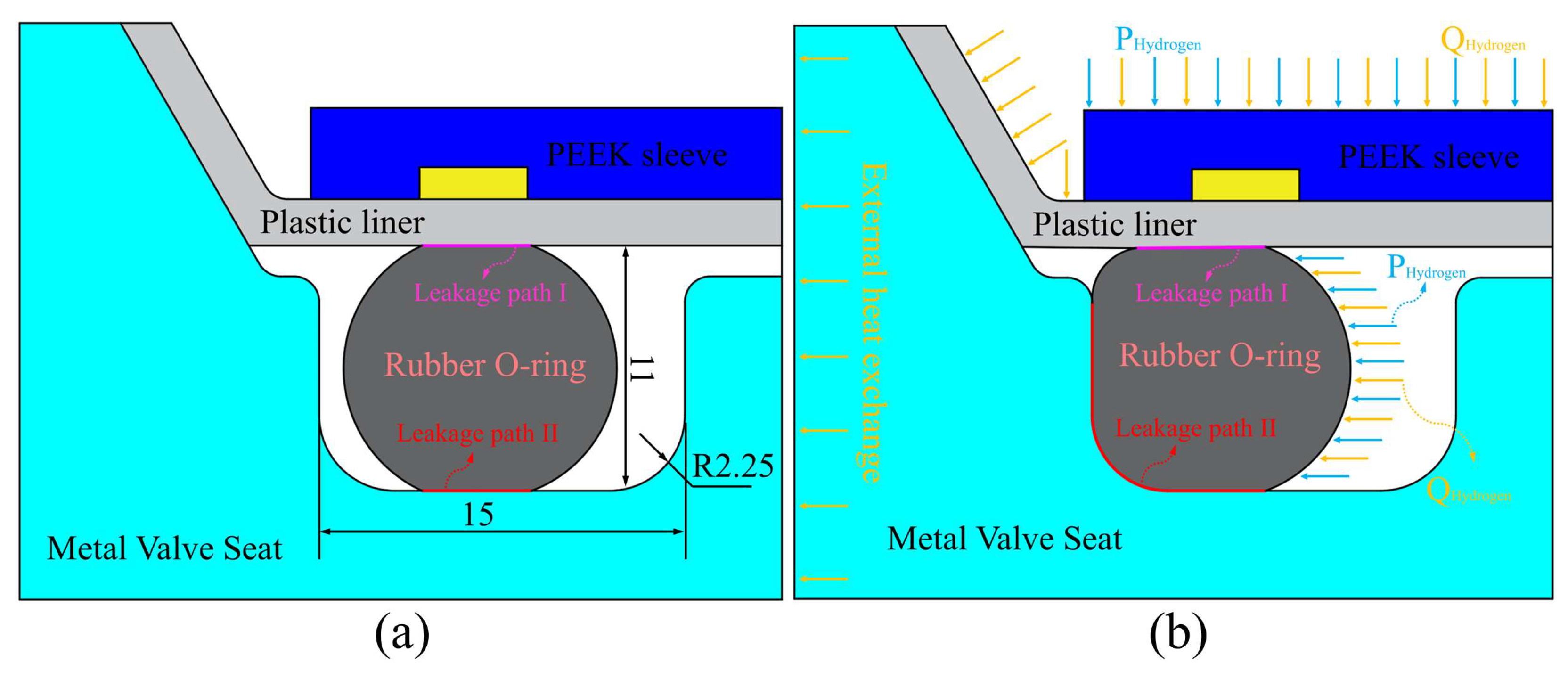
3.2. Model Settings
3.3. Boundary Conditions and Solution Method
3.4. Verification
4. Results Analysis and Discussion
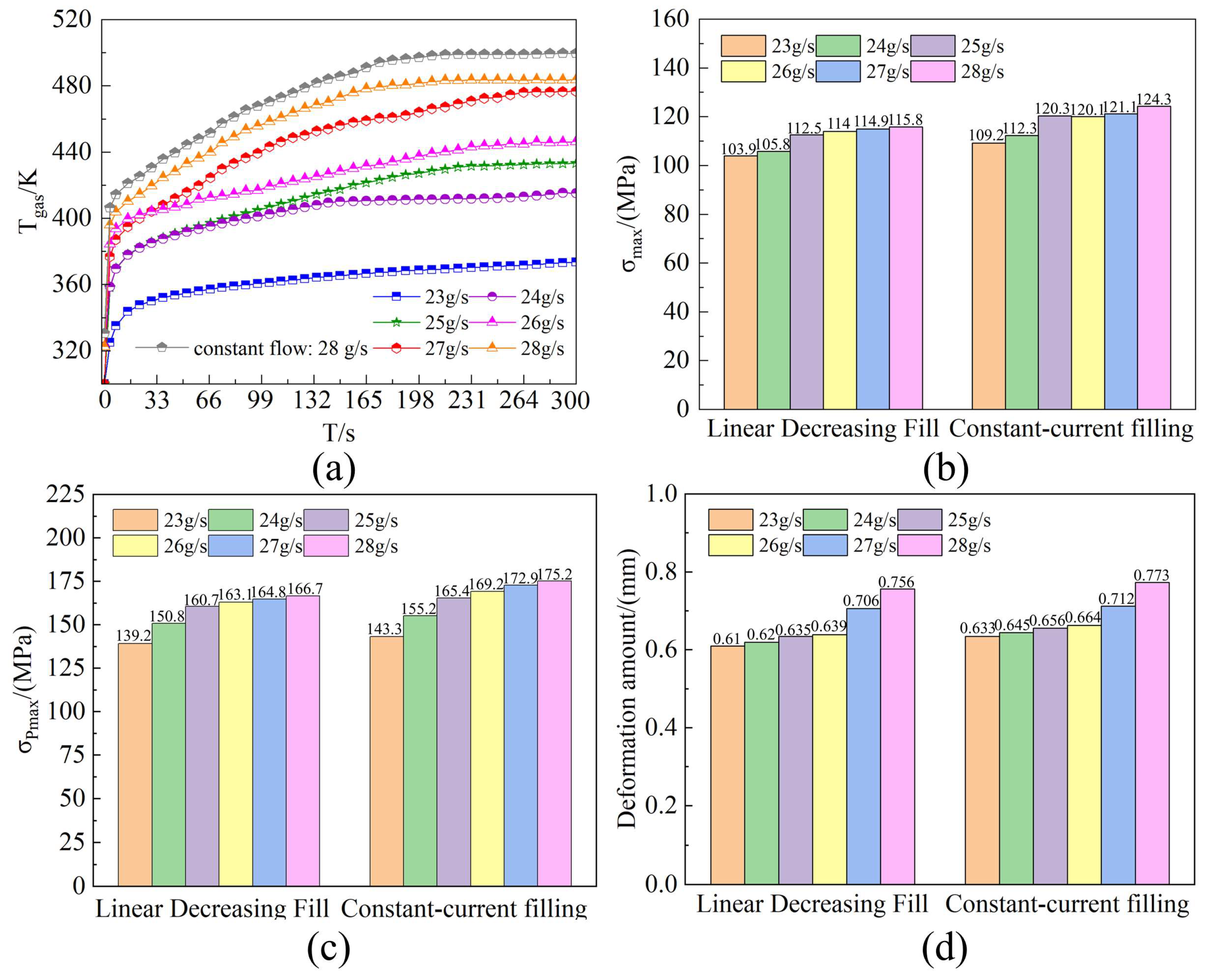
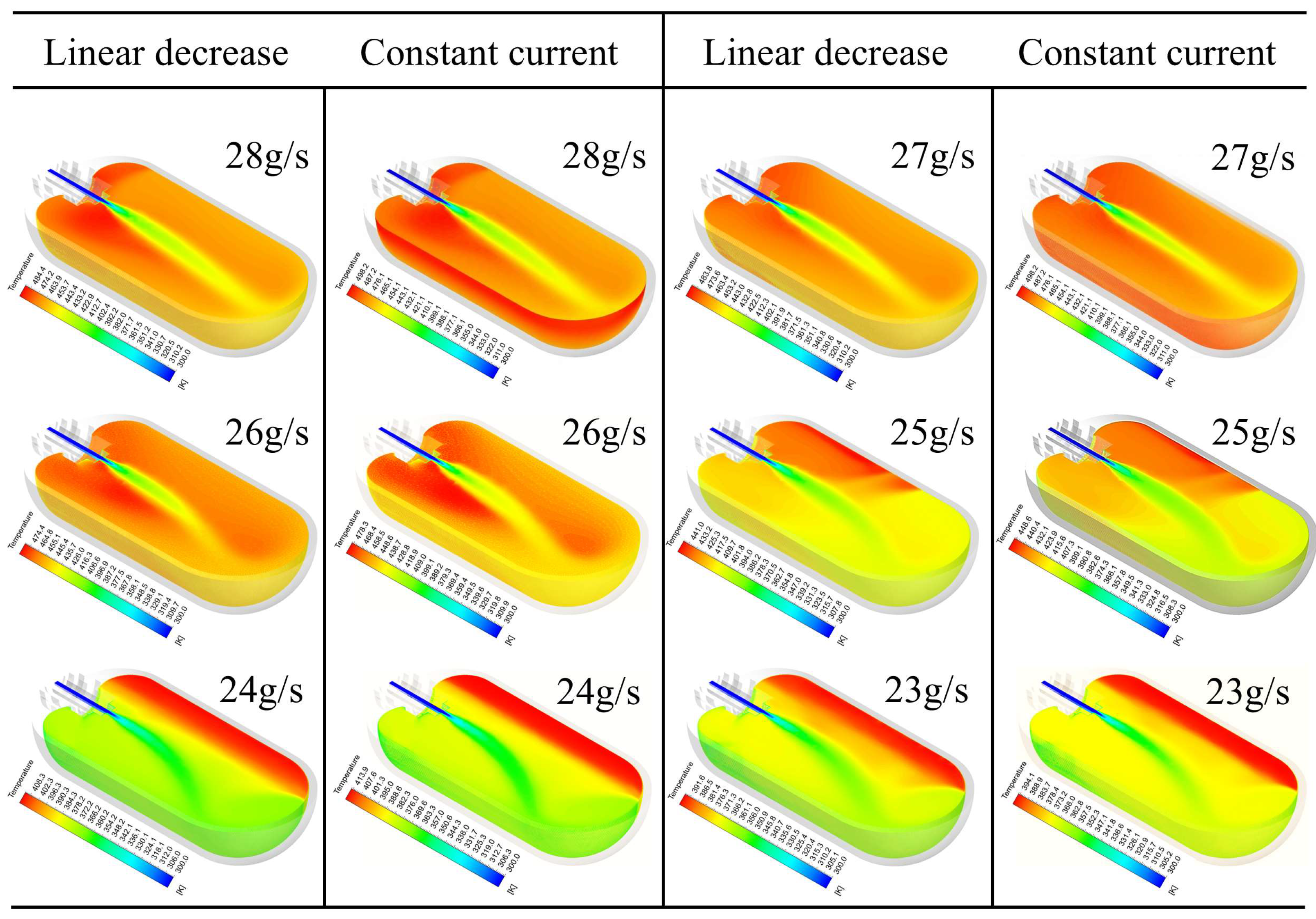
4.1. Comparative Analysis of System-Level Thermodynamic Responses
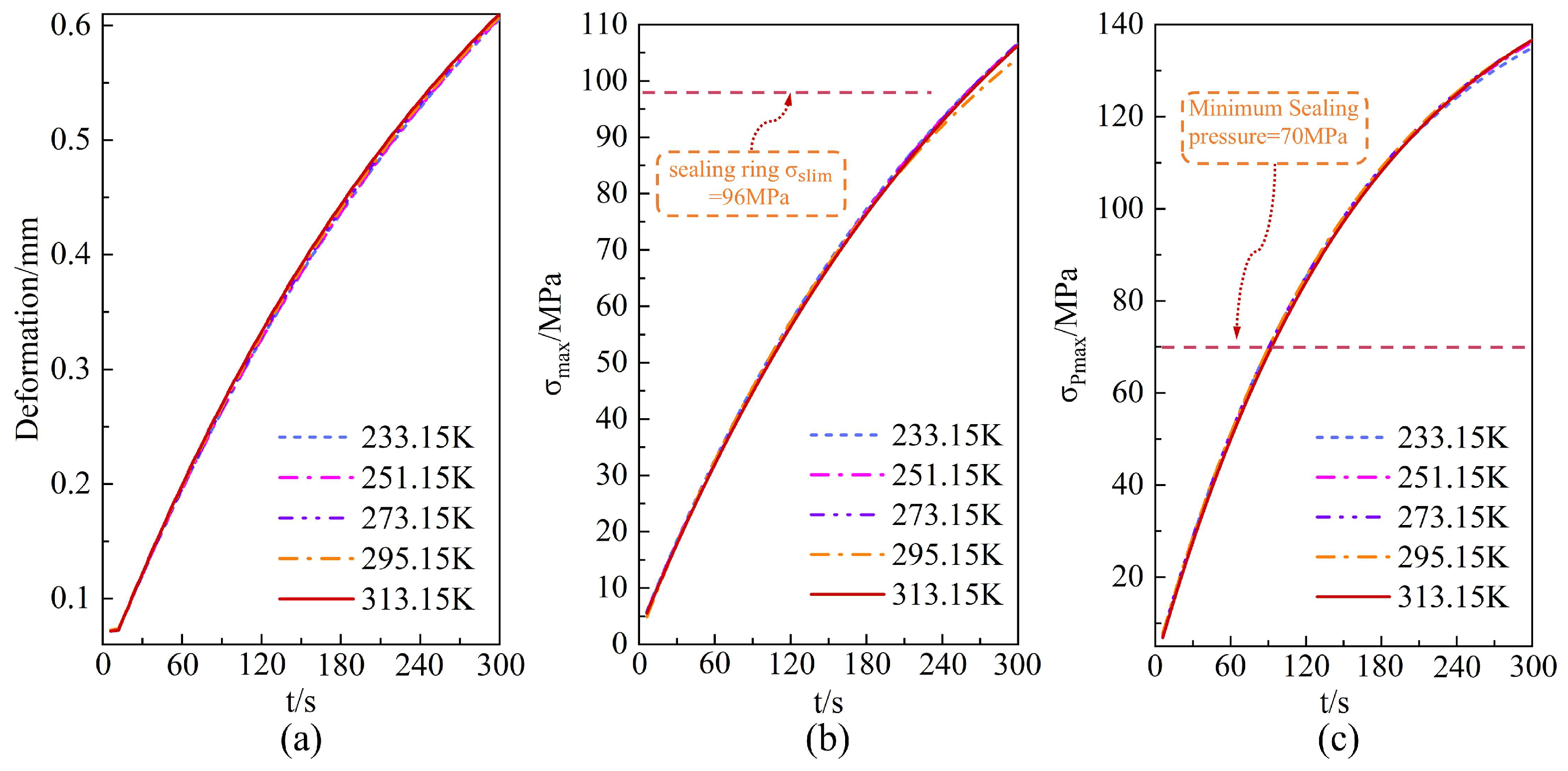
4.2. Environment Temperature Impact Assessment and Contribution Analysis
4.3. Thermal–Mechanical Coupling Mechanism and the Dominant Role of Sealing Performance
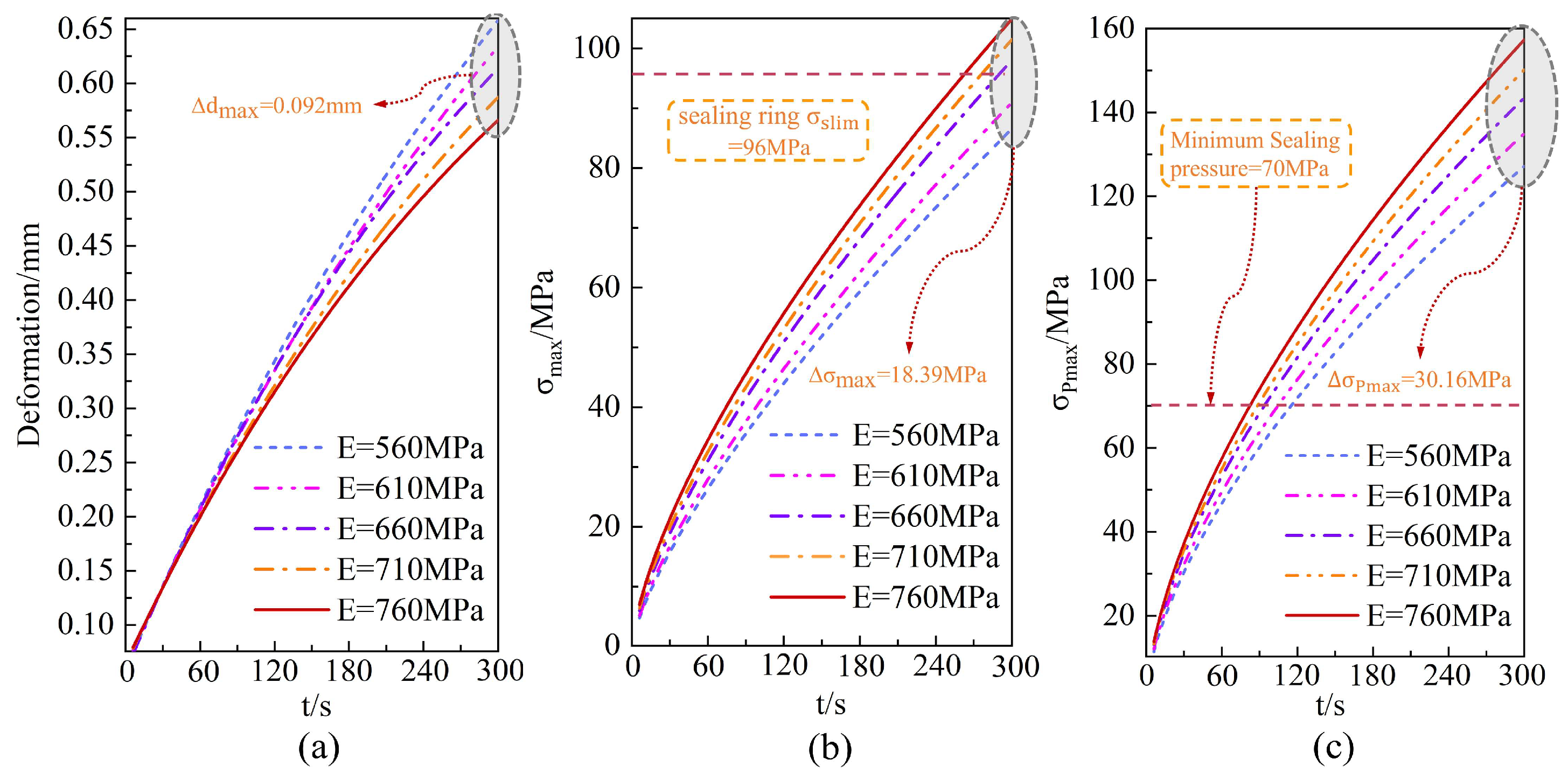
4.4. The Micro-Mechanisms of Material Nonlinear Behavior
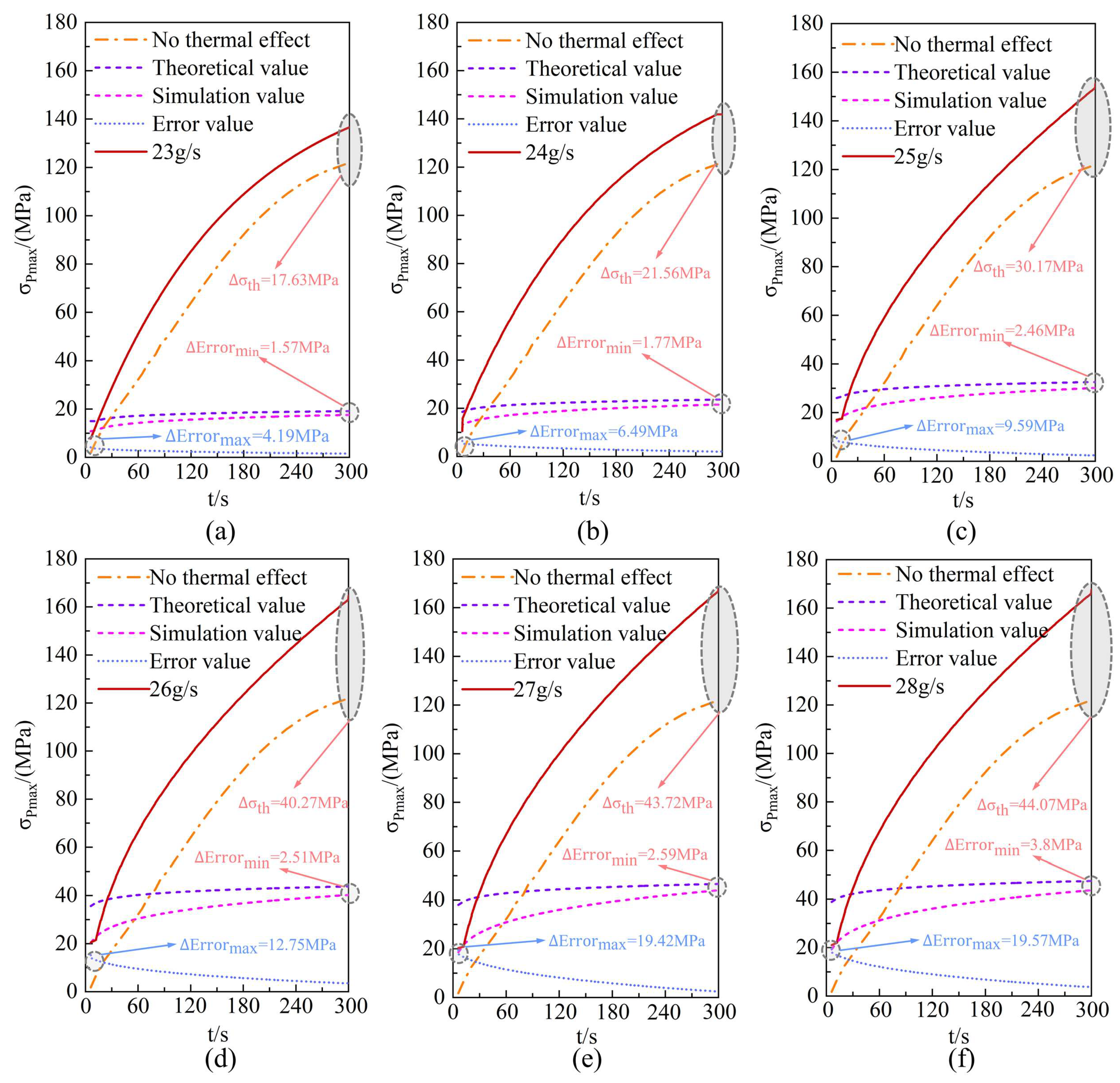
4.5. Multi-Physics Coupling Model Validation and Error Analysis
5. Conclusions and Future Work
- (1)
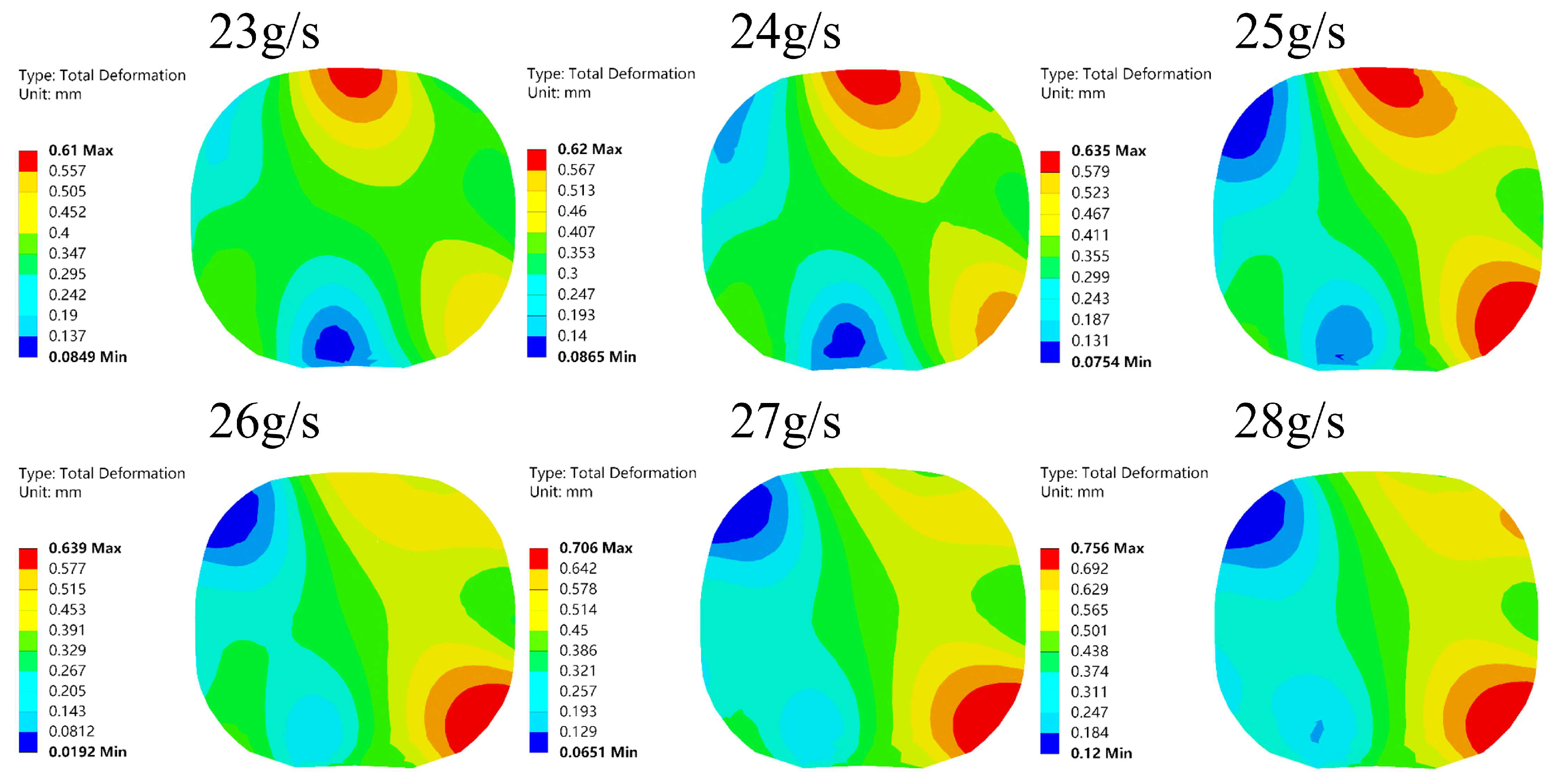
- The hydrogen filling rate significantly influences hydrogen temperature rise, with the temperature exhibiting nonlinear behavior as the filling rate increases. For each 1 g/s increment in filling rate, the maximum hydrogen temperature rises by approximately 2.062 K on average, while the O-ring at the cylinder neck experiences average increases in deformation, internal stress, and contact stress of 0.00157 mm, 0.128 MPa, and 0.296 MPa, respectively, resulting in a marked reduction in sealing performance. The high-temperature region within the cylinder is concentrated at the dome–valve seat junction, causing pronounced lateral displacement and torsional deformation of the O-ring contact points.
- (2)
- Increasing the elastic modulus of O-rings enhances structural rigidity and suppresses deformation, but also elevates stress levels, posing a risk of exceeding the material’s yield strength. When environment temperatures fluctuate within the range of 233.15–313.15 K, the impact on the dynamic performance of sealing systems is negligible, with contact stress variations remaining below 1%. This effect is significantly weaker than the temperature rise dominated by hydrogen during the filling process.
- (3)
- Comparison reveals that the maximum temperature at completion of the linear decreasing filling strategy is approximately 5.3% lower than that of the constant-flow rate strategy, with contact stress fluctuations reduced by 4.6%. For every 0.1 g/s increase in the initial hydrogen filling flow rate, the error between the theoretical and experimental values of the O-ring thermal contact stress increases by 0.3076 MPa. This heat transfer model effectively predicts the evolution of O-ring thermal contact stress during filling at initial flow rates below 25 g/s. The deviation between its predictions and simulation results is only 2.905 MPa. It also effectively controls hydrogen temperature rise, thereby enhancing the sealing performance of the hydrogen storage vessel inlet.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, J.; Kim, J. Balancing hydrogen and nuclear: How nuclear expansion reshapes power-to-gas and hydrogen storage in a carbon neutral energy system. Energy 2025, 336, 138437. [Google Scholar] [CrossRef]
- Muhammed, N.S.; Gbadamosi, A.O.; Epelle, E.I.; Abdulrasheed, A.A.; Haq, B.; Patil, S.; Al-Shehri, D.; Kamal, M.S. Hydrogen production, transportation, utilization, and storage: Recent advances towards sustainable. J. Energy Storage 2023, 73, 109207. [Google Scholar] [CrossRef]
- Liu, P.F.; Chu, J.K.; Hou, S.J.; Xu, P.; Zheng, J.Y. Numerical simulation and optimal design for composite high-pressure hydrogen storage vessel: A review. Renew. Sustain. Energy Rev. 2012, 16, 1817–1827. [Google Scholar] [CrossRef]
- Chen, M.; Hu, Z.; Jia, X.; Yang, Q.; Shen, A.L. Research Progress. on Key Technologies for Type IV Vehicle Hydrogen Storage Cylinders. Press. Vessel. Technol. 2020, 37, 39–50. [Google Scholar] [CrossRef]
- Ueda, M.; Hidaka, T.; Ichihara, N.; Yang, H.; Iwase, W.; Matsuda, T.; Morita, N.; Aoki, R.; Yokozeki, T. Voids in type-IV composite pressure vessels manufactured by a dry filament-winding process. Int. J. Press. Vessels Pip. 2024, 208, 105154. [Google Scholar] [CrossRef]
- Sebők, B.; Schülke, M.; Réti, F.; Kiss, G. Diffusivity, permeability and solubility of H2, Ar, N2, and CO2 in poly(tetrafluoroethylene) between room temperature and 180 °C. Polym. Test. 2016, 49, 66–72. [Google Scholar] [CrossRef]
- Melideo, D.; Desideri, U.; Andreas, J.; Kalisch, T. Zero-Dimensional modeling and optimization of hydrogen refueling for type IV tanks: From validation to large-scale applications. Energy 2025, 332, 137254. [Google Scholar] [CrossRef]
- Fragiacomo, P.; Martorelli, M.; Genovese, M. Numerical modeling for analysis and improvement of hydrogen refueling process for heavy-duty vehicles. Appl. Energy 2025, 380, 125092. [Google Scholar] [CrossRef]
- Miguel, N.; Cebolla, R.O.; Acosta, B.; Moretto, P.; Harskamp, F.; Bonato, C. Compressed hydrogen tanks for on-board application: Thermal behaviour during cycling. Int. J. Hydrogen Energy 2015, 40, 6449–6458. [Google Scholar] [CrossRef]
- Melideo, D.; Baraldi, D.; Galassi, M.C.; Cebolla, R.O.; Iborra, B.A.; Moretto, P. CFD model performance benchmark of fast filling simulations of hydrogen tanks with pre-cooling. Int. J. Hydrogen Energy 2014, 39, 4389–4395. [Google Scholar] [CrossRef]
- Dicken, C.J.B.; Mérida, W. Measured effects of filling time and initial mass on the temperature distribution within a hydrogen cylinder during refuelling. J. Power Sources 2007, 165, 324–336. [Google Scholar] [CrossRef]
- Li, M.X.; Yang, Q.; Zhang, C.Z.; Huang, S.; Zhang, M.J.; Zhang, G.; Zhao, L.; Jiang, S. Experimental and numerical study of the temperature evolution in hydrogen cylinder under fast-refueling process. Int. J. Heat Mass Transf. 2023, 211, 124220. [Google Scholar] [CrossRef]
- Simonovski, I.; Baraldi, D.; Melideo, D.; Acosta-Iborra, B. Thermal simulations of a hydrogen storage tank during fast filling. Int. J. Hydrogen Energy 2015, 40, 12560–12571. [Google Scholar] [CrossRef]
- Zhang, E.H.; Zhao, Y.C.; Zhang, J.H.; Wang, W.C.; Yu, W.H. Numerical Analysis of Hydrogen Behavior Inside Hydrogen Storage Cylinders under Rapid Refueling Conditions Based on Different Shapes of Hydrogen Inlet Ports. Energies 2024, 17, 5116. [Google Scholar] [CrossRef]
- Wu, Q.G.; Zu, L.; Wang, P.C.; Liu, Z.; Zhang, Q.; Zhang, G.; Chen, S.; Fu, J.; Zhou, L.; Wang, H.; et al. Design and fabrication of carbon-fiber-wound composite pressure vessel with HDPE liner. Int. J. Press. Vessels Pip. 2022, 200, 104851. [Google Scholar] [CrossRef]
- Wu, E.Q.; Zhao, Y.; Zhao, B.; Xu, W.P. Fatigue life prediction and verification of high-pressure hydrogen storage vessel. Int. J. Hydrogen Energy 2021, 46, 30412–30422. [Google Scholar] [CrossRef]
- Tomioka, J.; Kiguchi, K.; Tamura, Y.; Mitsuishi, H. Influence of temperature on the fatigue strength of compressed-hydrogen tanks for vehicles. Int. J. Hydrogen Energy 2011, 36, 2513–2519. [Google Scholar] [CrossRef]
- Ramirez, J.; Halm, D.; Grandidier, J.; Villalong, S.; Nony, F. 700 bar type IV high pressure hydrogen storage vessel burst-Simulation and experimental validation. Int. J. Hydrogen Energy 2015, 40, 13183–13192. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Gu, J.F.; Pan, S.; Yang, W.X.; Li, Z.; Ruan, S.; Shen, C. Numerical study on the influence of liner geometry and lay-up sequence on the fatigue life of composite hydrogen storage vessel. Int. J. Press. Vessels Pip. 2023, 205, 104986. [Google Scholar] [CrossRef]
- Pépin, J.; Lainé, E.; Grandidier, J.; Benoit, G.; Mellier, D. Replication of liner collapse phenomenon observed in hyperbaric type IV hydrogen storage vessel by explosive decompression experiments. Int. J. Hydrogen Energy 2018, 43, 4671–4680. [Google Scholar] [CrossRef]
- Li, Q.; Huang, G.; Qi, L.; Jin, C.; Zhao, Y.; Qiu, S.; Gu, C.; Hua, Z. Thermal-fluid-structure coupling progressive failure analysis for the type III composite cylinder under localized fire. Int. J. Hydrogen Energy 2023, 139, 868–880. [Google Scholar] [CrossRef]
- Xu, B.P.; Cheng, C.L.; Wen, J.X. Numerical modelling of transient heat transfer of hydrogen composite cylinders subjected to fire impingement. Int. J. Hydrogen Energy 2019, 44, 11247–11258. [Google Scholar] [CrossRef]
- Hupp, N.; Stahl, U.; Kunze, K.; Wilde, P.; Sinske, H.; Hinrichsen, O. Influence of fire intensity, fire impingement area and internal pressure on the fire resistance of composite pressure vessels for the storage of hydrogen in automobile applications. Fire Saf. J. 2019, 104, 1–7. [Google Scholar] [CrossRef]
- Zheng, J.; Ou, K.; Bie, H.; Xu, P.; Zhao, Y.; Liu, X.; He, Y. Heat transfer analysis of high-pressure hydrogen storage tanks subjected to localized fire. Int. J. Hydrogen Energy 2012, 37, 13125–13131. [Google Scholar] [CrossRef]
- Jaca, R.C.; Godoy, L.A.; Calabró, H.D.; Espinosa, S.N. Thermal post-buckling behavior of oil storage tanks under a nearby fire. Int. J. Press. Vessel. Pip. 2021, 189, 104289. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, G.; Liu, P. Finite Element Analysis of Sealing Performance of Rubber D-Ring Seal in High-Pressure Hydrogen Storage Vessel. J. Fail. Anal. Prev. 2018, 18, 846–855. [Google Scholar] [CrossRef]
- Zhou, C.; He, M.; Chen, G.; Jiang, S. Numerical study on sealing characteristic of rubber X-ring exposed to high-pressure hydrogen by considering swelling effect. Ind. Lubr. Tribol. 2019, 71, 133–138. [Google Scholar] [CrossRef]
- Yamabe, J.; Koga, A.; Nishimura, S. Failure behavior of rubber Oring under cyclic exposure to high-pressure hydrogen gas. Eng. Fail. Anal. 2013, 35, 193–205. [Google Scholar] [CrossRef]
- Yamabe, J.; Fujiwara, H.; Nishimura, S. Fracture analysis of rubber sealing material for high pressure hydrogen vessel. J. Environ. Eng. 2011, 6, 53–68. [Google Scholar] [CrossRef]
- Fujiwara, H.; Ono, H.; Nishimura, S. Degradation behavior of acrylonitrile butadiene rubber after cyclic high-pressure hydrogen exposure. Int. J. Hydrogen Energy 2015, 40, 2025–2034. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, L.; Li, C.; Meng, X.K.; Peng, X.; Jiang, J. Thermal-mechanical-diffusion multi-field coupling behavior of rubber seals in high-pressure hydrogen environment. Int. J. Hydrogen Energy 2025, 112, 333–346. [Google Scholar] [CrossRef]
- Wang, B.; Li, X.; Peng, X.; Li, Y.; Li, X.; Chen, Y.; Jin, J. Influence of Nitrile Butadiene Rubber (NBR) Shore Hardness and Polytetrafluoroethylene (PTFE) Elastic Modulus on the Sealing Characteristics of Step Rod Seals. Lubricants 2023, 11, 367. [Google Scholar] [CrossRef]
- Li, X.; Wang, B.; Peng, X.; Li, Y.; Li, X.; Chen, Y. Effect of nitrile butadiene rubber hardness on the sealing characteristics of hydraulic O-ring rod seals. J. Zhejiang Univ. Sci. A 2024, 25, 63–78. [Google Scholar] [CrossRef]
- Li, J.; Liu, J.; Zhao, B.; Wang, D.; Guo, S.; Song, J.; Li, X. Research on Temperature Rise of Type IV Composite Hydrogen Storage Cylinders in Hydrogen Fast-Filling Process. Energies 2023, 16, 2918. [Google Scholar] [CrossRef]
- GB/T 1040.1-2018; Plastics-Determination of Tensile Properties-Part 1. National Technical Committee on Plastics Standardization, Subcommittee on General Methods and Products (SAC/TC 15/SC 4). China Standards Press: Beijing, China, 2018.
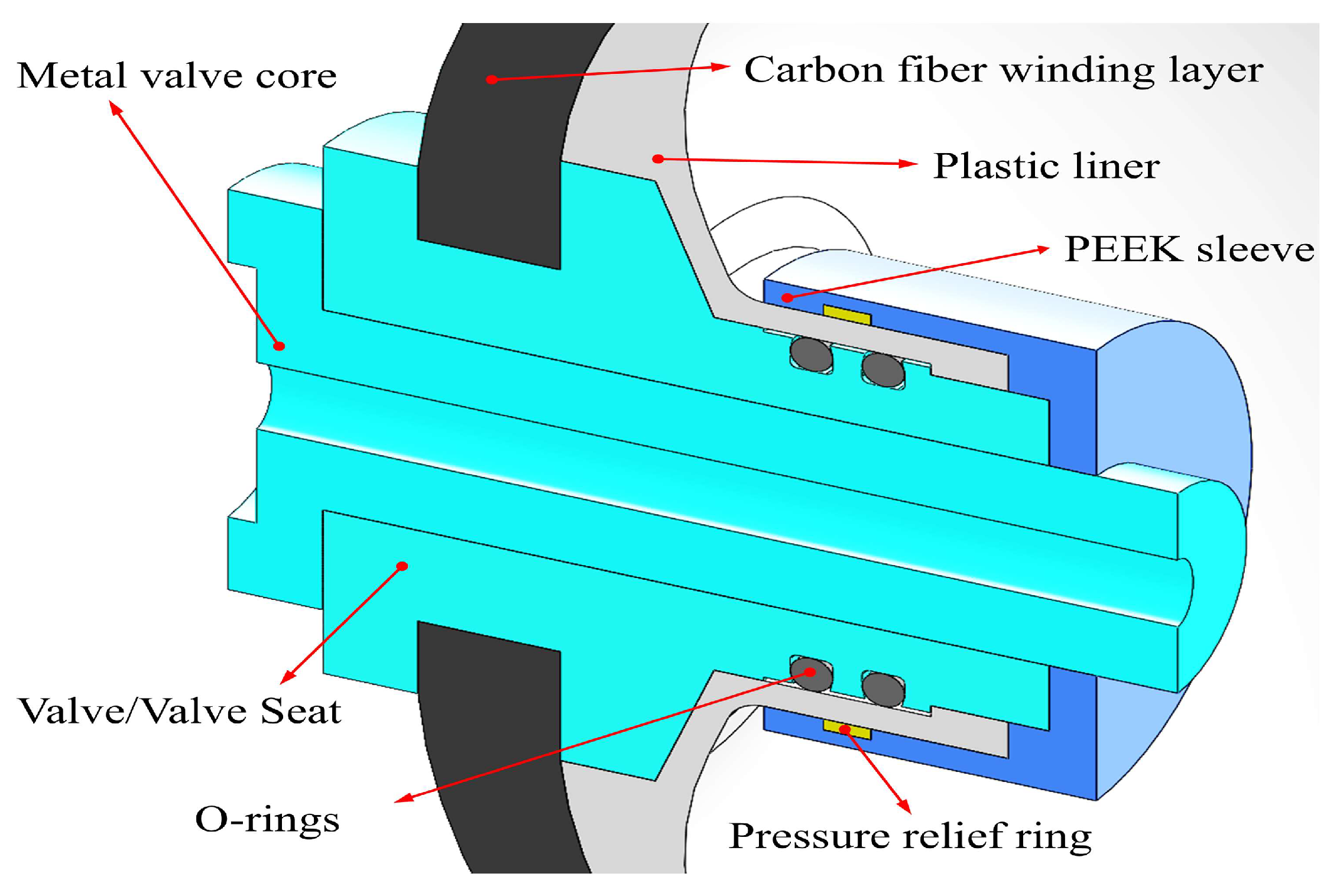
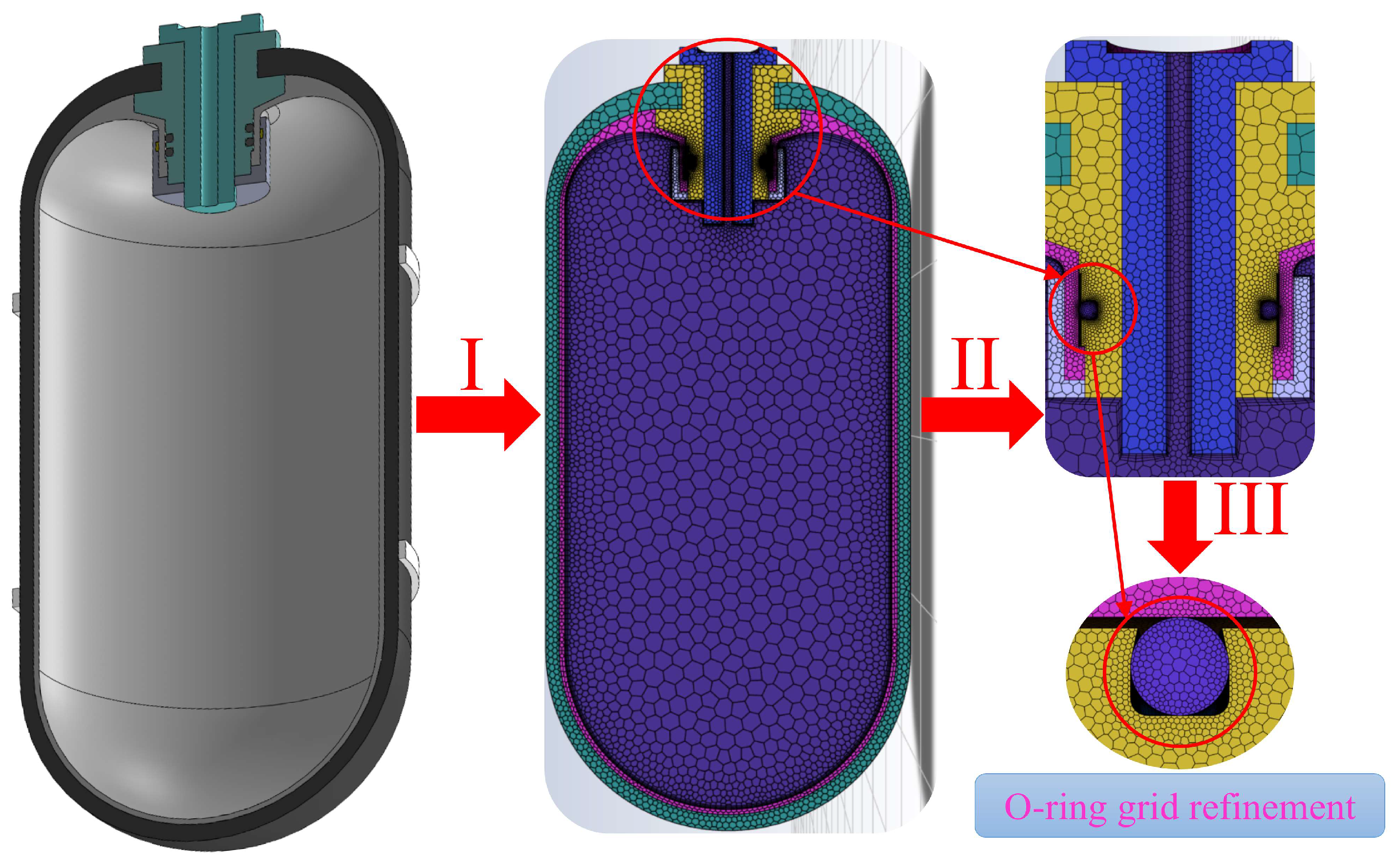
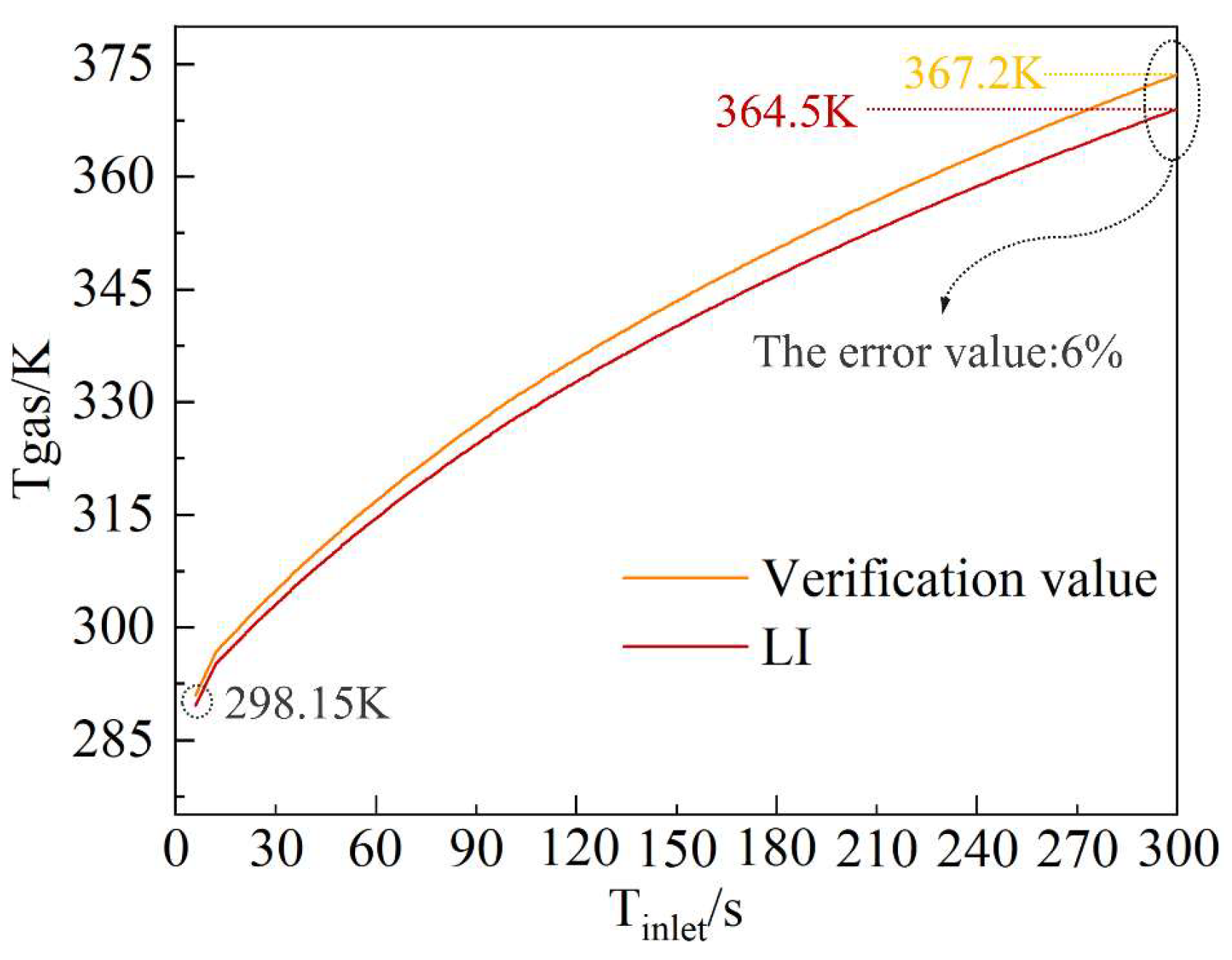
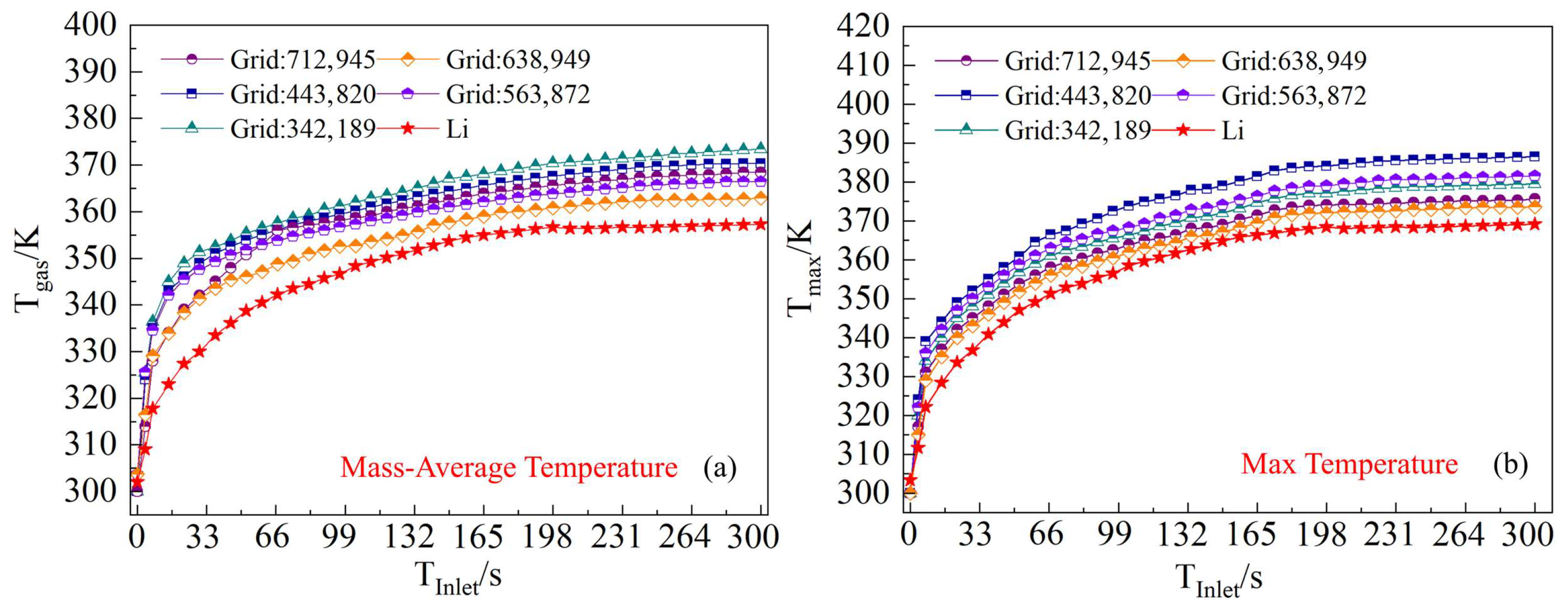


| Initial mass flow rate, g/s | 23–30 |
| Slope of the decreasing filling rate | −6.10 × 10−5 |
| Refill time, s | 300 |
| Final pressure, MPa | 70.2–76.6 |
| Hydrogen refueling quality, kg | 4.312–4.632 |
| Parameters | Value | Reference [34] |
|---|---|---|
| Hydrogen storage cylinder capacity V, L | 80.2 | 24 |
| Total length of hydrogen storage cylinder L1, mm | 891 | 918 |
| Total length of plastic inner cylinder L2, mm | 803 | - |
| Outer diameter of plastic inner cylinder D0, mm | 384 | 203 |
| Plastic inner cylinder thickness δ1, mm | 6 | 3 |
| Thickness of carbon fiber winding Layer δ2, mm | 15 | 20 |
| Seal diameter D1, mm | 9 | - |
| Work pressureP0, MPa | 70 | 70 |
| Name | O-Ring (PTFE) | Valve (6061) | Plastic Liner (HDPE) | Carbon Fiber |
|---|---|---|---|---|
| Density (g/cm3) | 2.2 | 2.7 | 0.97 | 1.8 |
| Modulus of elasticity (MPa) | 660 | 69,000 | 1080 | - |
| Poisson ratio μ | 0.4532 | 0.33 | 0.4183 | - |
| Coefficient of thermal expansion (K−1) | 0.00015 | 0.000023 | 0.000145 | - |
| Specific heat capacity (kg·K) | 1300 | 900 | 2200 | 1300 |
| Thermal conductivity (W/(m·K)) | 0.25 | 170 | 0.5 | 1.5 |
| Initial Conditions and Boundary Conditions | Value | Reference [34] |
|---|---|---|
| Initial temperature T0, K | 298.15 | 298.15 |
| Environment temperature Te, K | 295.15 | 289 |
| Initial pressure P0, MPa | 2 | 7 |
| Refilling method | Linear decrease | Constant pressure |
| Convective heat transfer coefficient hout, W/(m2⋅K) | 6 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, E.; Shi, X.; Wang, W.; Wang, Z. Multi-Physics Coupling Mechanism of the Dynamic Sealing Performance of the O-Ring at the Neck of a Type IV Hydrogen Storage Cylinder Under Linearly Decreasing Filling Conditions. Symmetry 2025, 17, 1921. https://doi.org/10.3390/sym17111921
Zhang E, Shi X, Wang W, Wang Z. Multi-Physics Coupling Mechanism of the Dynamic Sealing Performance of the O-Ring at the Neck of a Type IV Hydrogen Storage Cylinder Under Linearly Decreasing Filling Conditions. Symmetry. 2025; 17(11):1921. https://doi.org/10.3390/sym17111921
Chicago/Turabian StyleZhang, Enhui, Xiaolong Shi, Wenchao Wang, and Zhiqiang Wang. 2025. "Multi-Physics Coupling Mechanism of the Dynamic Sealing Performance of the O-Ring at the Neck of a Type IV Hydrogen Storage Cylinder Under Linearly Decreasing Filling Conditions" Symmetry 17, no. 11: 1921. https://doi.org/10.3390/sym17111921
APA StyleZhang, E., Shi, X., Wang, W., & Wang, Z. (2025). Multi-Physics Coupling Mechanism of the Dynamic Sealing Performance of the O-Ring at the Neck of a Type IV Hydrogen Storage Cylinder Under Linearly Decreasing Filling Conditions. Symmetry, 17(11), 1921. https://doi.org/10.3390/sym17111921






