A Note on Schrödinger Operator Relations and Power-Law Energies
Abstract
1. Introduction
2. Schrödinger’s Operator Relations
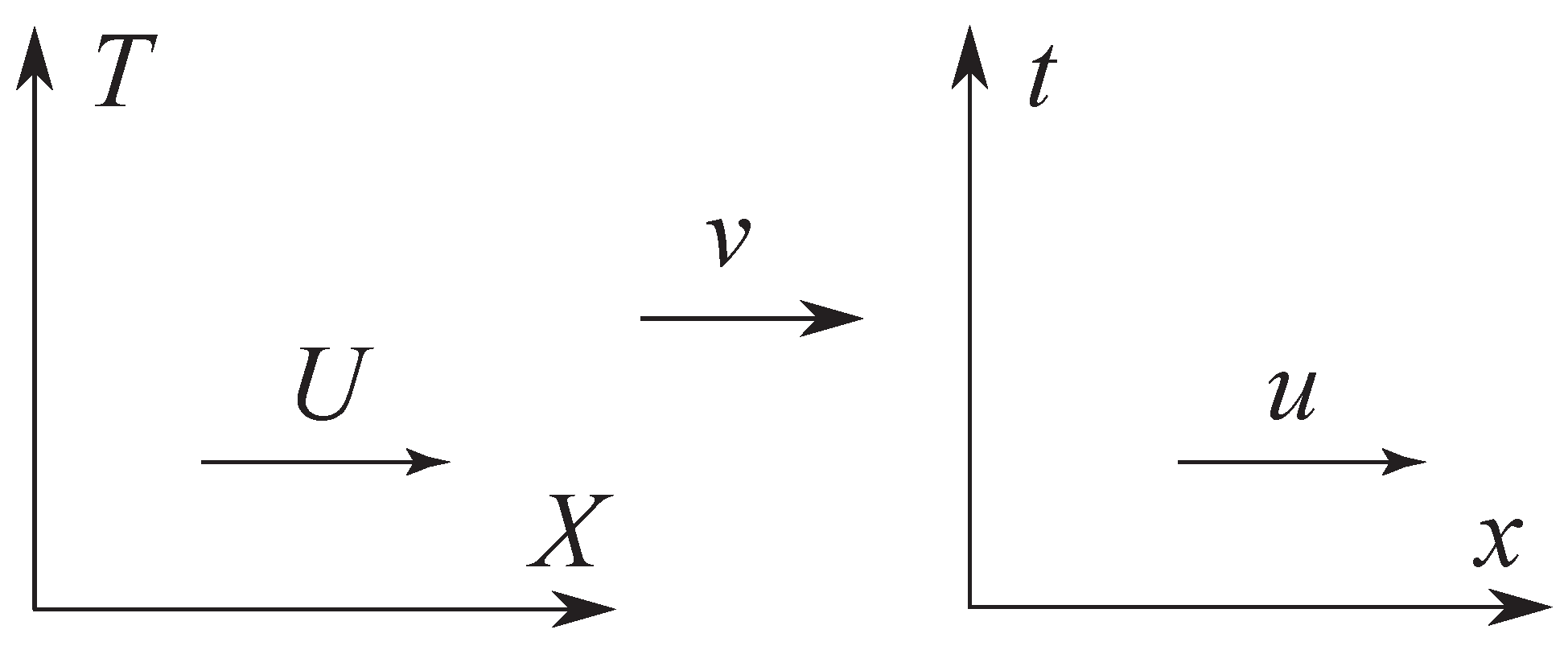
2.1. Special Relativity and Lorentz Transformations
2.2. Lorentz Invariant Extended Newton’s Second Law
2.3. Invariants Invariants and
2.4. Klein–Gordon Partial Differential Equation
3. Elementary Particle Power-Law Energy-Momenta Relations
4. Generalised Schrödinger Operator Relations
4.1. Generalised Operator Relations
4.2. Some Standard Operator Relations
4.3. Invariant Operators and
4.4. Operator Interpretation for
4.5. Operator Interpretation for
5. Some Solutions for
5.1. Separable Solution for
5.2. Travelling Wave Solution for
5.3. Self-Similar Solution for
6. Summary and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Reduction to First-Order Differential Equation
References
- Bjorken, J.D.; Drell, S.D. Relativistic Quantum Fields (Pure and Applied Physics); McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Dirac, P.A.M. Lectures on Quantum Mechanics; Courier Dover Publications: New York, NY, USA, 1964. [Google Scholar]
- Dirac, P.A.M. Principles of Quantum Mechanics; Clarendon Press: Oxford, UK, 1981. [Google Scholar]
- Gross, F. Relativistic Quantum Mechanics and Field Theory; John Wiley and Sons: New York, NY, USA, 2008. [Google Scholar]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Addison-Wesley Advanced Book Program: New York, NY, USA, 1995. [Google Scholar]
- Roman, P. Introduction to Quantum Field Theory; John Wiley and Sons: New York, NY, USA, 1969. [Google Scholar]
- Hagan, K. Particles and Quantum Fields; World Scientific: New York, NY, USA, 2016. [Google Scholar]
- de Broglie, L. Waves and quanta. Nature 1923, 112, 540. [Google Scholar] [CrossRef]
- de Broglie, L. Ondes et quanta. Comptes Rendus 1923, 177, 507–510. [Google Scholar]
- de Broglie, L. Recherches sur la Theorie des Quanta. Ph.D. Thesis, Sorbonne University of Paris, Paris, France, 1924. [Google Scholar]
- Bohm, D.J.; Hiley, B.J. The de Broglie pilot wave theory and the further development of new insights arising out of it. Found. Phys. 1982, 12, 1001–1016. [Google Scholar] [CrossRef]
- Guemez, J.; Fiolhais, M.; Fernandez, L.A. The principle of relativity and the de Broglie relation. Am. J. Phys. 2016, 84, 443–447. [Google Scholar] [CrossRef]
- Houlik, J.M.; Rousseaux, G. “Non-relativistic” kinematics: Particles or waves. arXiv 2010, arXiv:1005.1762. [Google Scholar]
- Weinberger, P. Revisiting Louis de Broglie’s famous 1924 paper in the Philosophical Magazine. Philos. Mag. Lett. 2006, 86, 405–410. [Google Scholar] [CrossRef]
- Hill, J.M. A consistent extension of the Planck-de Broglie relations. Z. Fur Angew. Math. Und Phys. 2025, 76, 239. [Google Scholar] [CrossRef]
- Hill, J.M. Einstein’s energy and space isotropy. Z. Fur Angew. Math. Und Phys. 2022, 73, 65. [Google Scholar] [CrossRef]
- Hill, J.M. Mathematics of Particle-Wave Mechanical Systems; Springer: Berlin/Heidelberg, Germany, 2022; ISBN 978-3-031-19792-5/978-3-031-19793-2. [Google Scholar] [CrossRef]
- Aspect, A.; Villain, J. The birth of wave mechanics (1923–1926). Comptes Rendus Phys. 2017, 18, 583–585. [Google Scholar] [CrossRef]
- Sommerfeld, A. Wave Mechanics; Brose, H.L., Translator; Methuen Co., Ltd.: London, UK, 1930. [Google Scholar]
- Hill, J.M. On the formal origins of dark energy. Z. Fur Angew. Math. Und Phys. 2018, 69, 133–145. [Google Scholar] [CrossRef]
- Hill, J.M. Some further comments on special relativity and dark energy. Z. Fur Angew. Math. Und Phys. 2019, 70, 5–14. [Google Scholar] [CrossRef]
- Clark, H. A First Course in Quantum Mechanics; Van Nostrand Reinhold Co., Ltd.: London, UK, 1982; pp. 313–317. [Google Scholar]
- Migkas, K.; Schellenberger, G.; Reiprich, T.H.; Pacaud, F.; Ramos-Ceja, M.E.; Lovisari, L. Probing cosmic isotropy with a new X-ray galaxy cluster sample through the LX − T scaling relation. Astron. Astrophys. 2020, 636, A15. [Google Scholar] [CrossRef]
- Wilczynska, M.R.; Webb, J.K.; Bainbridge, M.; Barrow, J.D.; Bosman, S.E.; Carswell, R.F.; Dąbrowski, M.P.; Dumont, V.; Lee, C.-C.; Leite, A.C.; et al. Four direct measurements of the fine structure constant 13 billion years ago. Sci. Adv. Astrophys. 2020, 6, 9672. [Google Scholar] [CrossRef] [PubMed]
- Suto, K. The Planck constant was not a universal constant. J. Appl. Math. Phys. 2020, 8, 456–463. [Google Scholar] [CrossRef][Green Version]
- Barrow, J.D.; Magueijo, J. A contextual Planck parameter and the classical limit in quantum cosmology. Found. Phys. 2021, 51, 22. [Google Scholar] [CrossRef]
- Ames, W.F. Nonlinear Partial Differential Equations in Engineering I; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Ames, W.F. Nonlinear Partial Differential Equations in Engineering II; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Hill, J.M. Differential Equations and Group Methods for Scientists and Engineers; Studies in Advanced Mathematics; CRC Press: Boca Raton, FL, USA, 1992; ISBN 0-8493-4442-5. [Google Scholar]
- Hill, J.M. One-Dimensional Stefan Problems: An Introduction; Pitman Monographs and Surveys in Pure and Applied Mathematics; Longman: London, UK, 1987; ISBN 0-582-98823-3. [Google Scholar]
- Howison, S. Practical Applied Mathematics: Modelling, Analysis, Approximation; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2005; ISBN 10-0-521-84274-3. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hill, J.M. A Note on Schrödinger Operator Relations and Power-Law Energies. Symmetry 2025, 17, 1887. https://doi.org/10.3390/sym17111887
Hill JM. A Note on Schrödinger Operator Relations and Power-Law Energies. Symmetry. 2025; 17(11):1887. https://doi.org/10.3390/sym17111887
Chicago/Turabian StyleHill, James M. 2025. "A Note on Schrödinger Operator Relations and Power-Law Energies" Symmetry 17, no. 11: 1887. https://doi.org/10.3390/sym17111887
APA StyleHill, J. M. (2025). A Note on Schrödinger Operator Relations and Power-Law Energies. Symmetry, 17(11), 1887. https://doi.org/10.3390/sym17111887





