Positron Production by Runaway Electrons in Lorentzian Plasmas
Abstract
1. Introduction
2. Theory and Methods
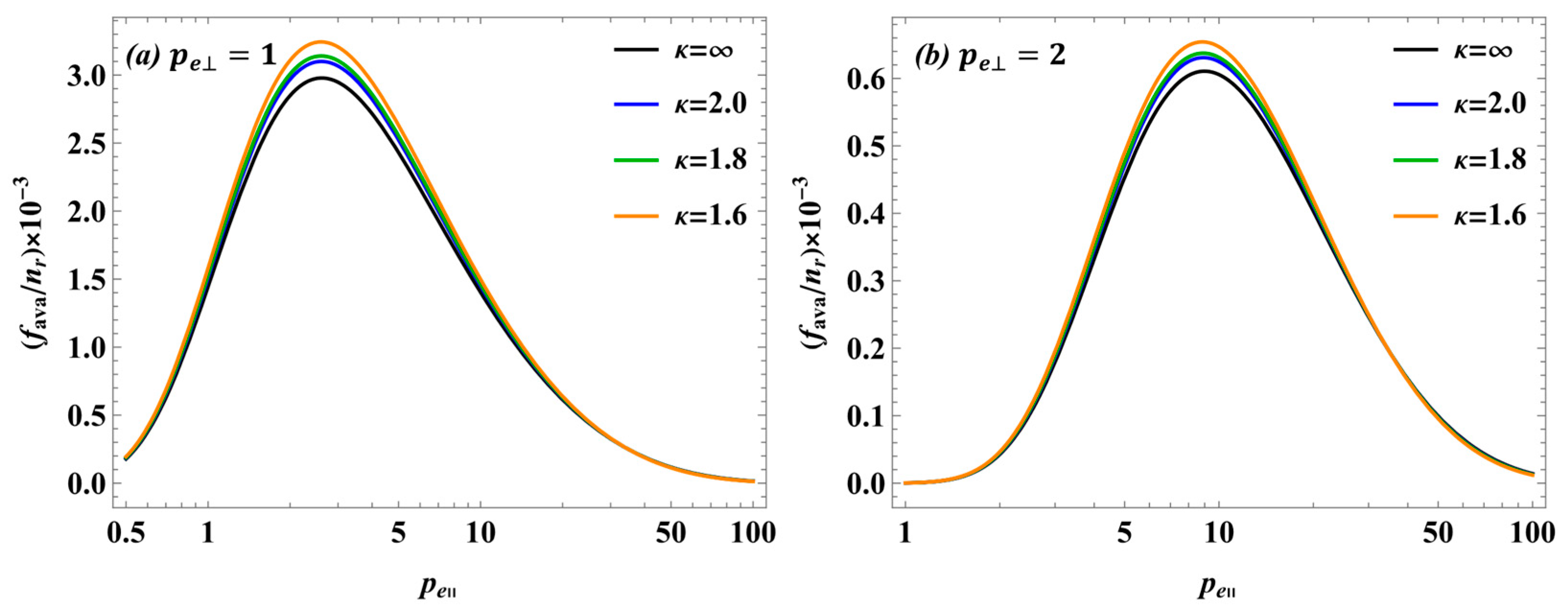
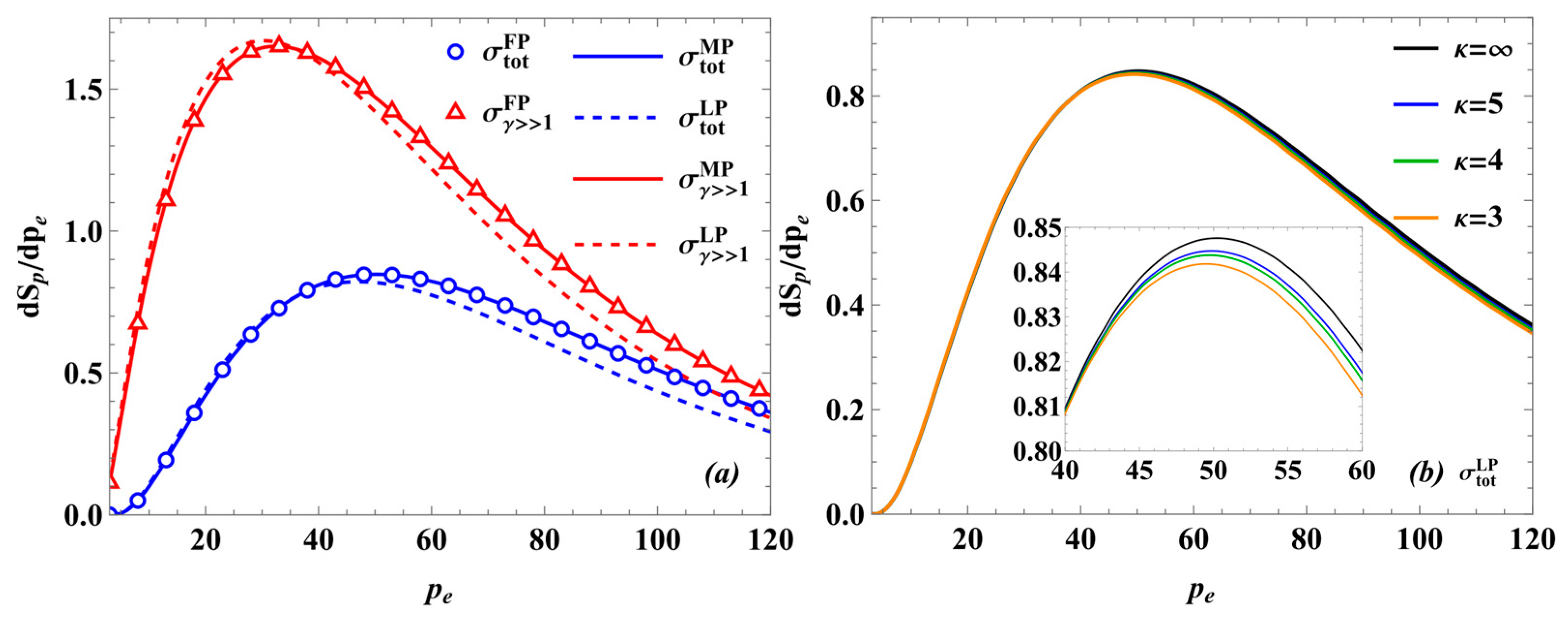
2.1. Positron Production and Distribution Functions
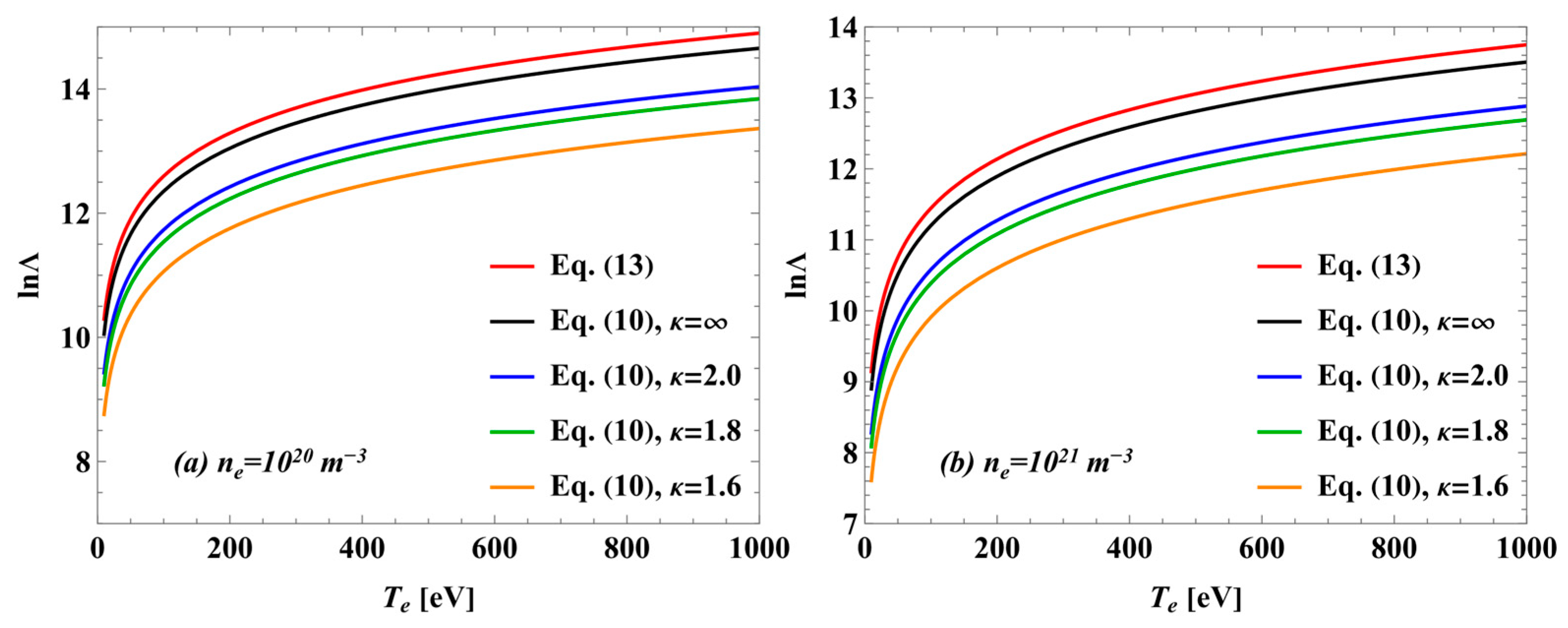
2.2. Kappa Distribution and Coulomb Logarithm
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hoppe, M.; Embreus, O.; Fülöp, T. DREAM: A fluid-kinetic framework for tokamak disruption runaway electron simulations. Comput. Phys. Commun. 2021, 268, 108098. [Google Scholar] [CrossRef]
- Bergström, H.; Särkimäki, K.; Bandaru, V.; Skyllas, M.M.; Hoelzl, M. Assessment of the runaway electron load distribution in ITER during 3D MHD induced beam termination. Plasma Phys. Control. Fusion 2024, 66, 095001. [Google Scholar] [CrossRef]
- Helander, P.; Ward, D.J. Positron Creation and Annihilation in Tokamak Plasmas with Runaway Electrons. Phys. Rev. Lett. 2003, 90, 135004. [Google Scholar] [CrossRef]
- Fülöp, T.; Papp, G. Runaway Positrons in Fusion Plasmas. Phys. Rev. Lett. 2012, 108, 225003. [Google Scholar] [CrossRef]
- Liu, J.; Qin, H.; Fisch, N.J.; Teng, Q.; Wang, X. What Is the Fate of Runaway Positrons in Tokamaks? Phys. Plasmas 2014, 21, 064503. [Google Scholar] [CrossRef]
- Del-Castillo-Negrete, D.; Carbajal, L.; Spong, D.; Izzo, V. Numerical Simulation of Runaway Electrons: 3-D Effects on Synchrotron Radiation and Impurity-Based Runaway Current Dissipation. Phys. Plasmas 2018, 25, 056104. [Google Scholar] [CrossRef]
- Guanying, Y.; Liu, J.; Xie, J.; Li, J. Detection of Tokamak Plasma Positrons Using Annihilation Photons. Fusion Eng. Des. 2017, 118, 124–128. [Google Scholar] [CrossRef]
- Vasyliunas, V.M. A Survey of Low-Energy Electrons in the Evening Sector of the Magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. Atmos. 1968, 73, 2839. [Google Scholar] [CrossRef]
- Pierrard, V.; Lazar, M.; Stverak, S. Implications of Kappa Suprathermal Halo of the Solar Wind Electrons. Front. Astron. Space Sci. 2022, 9, 892236. [Google Scholar] [CrossRef]
- Livadiotis, G. Kappa Distributions Theory and Applications in Plasmas, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2017; p. 724. [Google Scholar]
- Livadiotis, G.; McComas, D.J. Understanding Kappa Distributions: A Toolbox for Space Science and Astrophysics. Space Sci. Rev. 2013, 175, 183–214. [Google Scholar] [CrossRef]
- Mirza, A.M.; Masood, W.; Iqbal, J.; Batool, N. Toroidal ion-temperature-gradient driven vortices in an inhomogeneous magnetoplasma with non-Maxwellian electrons. Phys. Plasmas 2015, 22, 092313. [Google Scholar] [CrossRef]
- Mendis, D.A.; Rosenberg, M. Cosmic Dusty Plasma. Annu. Rev. Astron. Astrophys. 1994, 32, 419. [Google Scholar] [CrossRef]
- Leubner, M.P. Fundamental Issues on Kappa-Distributions in Space Plasmas and Interplanetary Proton Distributions. Phys. Plasmas 2004, 11, 1308. [Google Scholar] [CrossRef]
- Peigney, B.E.; Larroche, O.; Tikhonchuk, V. Fokker–Planck Kinetic Modeling of Suprathermal α -Particles in a Fusion Plasma. J. Comput. Phys. 2014, 278, 416. [Google Scholar] [CrossRef]
- Gupta, N.; Johari, R.; Bhardwaj, S.B. Generation of Superthermal Electrons by Self-Focused Cosh Gaussian Laser Beams in Inertial Confinement Fusion Plasma. J. Opt. 2022, 52, 1094. [Google Scholar] [CrossRef]
- Singh, K.; Kakad, A.; Kakad, B.; Saini, N.S. Evolution of Ion Acoustic Solitary Waves in Pulsar Wind. Mon. Not. R. Astron. Soc. 2020, 500, 1612. [Google Scholar] [CrossRef]
- El-Awady, E.I.; El-Tantawy, S.A.; Moslem, W.M.; Shukla, P.K. Electron–Positron–Ion Plasma with Kappa Distribution: Ion Acoustic Soliton Propagation. Phys. Lett. A 2010, 374, 3216. [Google Scholar] [CrossRef]
- Lui, A.T.Y.; Krimigis, S.M. Earthward Transport of Energetic Protons in the Earth’s Plasma Sheet. Geophys. Res. Lett. 1981, 8, 527. [Google Scholar] [CrossRef]
- Leubner, M.P. On Jupiter’s Whistler Emission. J. Geophys. Res. Atmos. 1982, 87, 6335. [Google Scholar] [CrossRef]
- Seisembayeva, M.M.; Reinholz, H.; Shalenov, E.O.; Jumagulov, M.N.; Dzhumagulova, K.N. Coulomb Logarithm and the Dreicer Field in a Dense Semiclassical Plasma. Contrib. Plasma Phys. 2022, 62, e202200014. [Google Scholar] [CrossRef]
- Bishovatyi-Kogan, G.S.; Zeldovich, Y.B.; Syunyaev, R.A. Physical Processes in a Low-Density Relativistic Plasma. Sov. Astron. 1971, 15, 17. [Google Scholar]
- Heitler, W. The Quantum Theory of Radiation, 3rd ed.; Oxford University Press: Oxford, UK, 1953; p. 464. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Electrodynamics. In Course of Theoretical Physics, 2nd ed.; Pergamon: Oxford, UK, 1975; Volume 4, p. 652. [Google Scholar]
- Gryaznykh, D.A. Cross section for the production of electron-positron pairs by electrons in the field of a nucleus. Phys. At. Nucl. 1998, 61, 394. [Google Scholar]
- Fülöp, T.; Pokol, G.; Helander, P.; Lisak, M. Destabilization of Magnetosonic-Whistler Waves by a Relativistic Runaway Beam. Phys. Plasmas 2006, 13, 062506. [Google Scholar] [CrossRef]
- Rubab, N.; Murtaza, G. Debye Length in Non-Maxwellian Plasmas. Phys. Scr. 2006, 74, 145. [Google Scholar] [CrossRef]
- Bryant, D.A. Debye Length in a Kappa-Distribution Plasma. J. Plasma Phys. 1996, 56, 87. [Google Scholar] [CrossRef]
- Hesslow, L.; Embréus, O.; Hoppe, M.; DuBois, T.C.; Papp, G.; Rahm, M.; Fülöp, T. Generalized Collision Operator for Fast Electrons Interacting with Partially Ionized Impurities. J. Plasma Phys. 2018, 84, 905840605. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shalenov, E.O.; Myrzali, M.A.; Seitkozhanov, Y.S.; Dzhumagulova, K.N.; Masheyeva, R.U.; Jumagulov, M.N. Positron Production by Runaway Electrons in Lorentzian Plasmas. Symmetry 2025, 17, 1843. https://doi.org/10.3390/sym17111843
Shalenov EO, Myrzali MA, Seitkozhanov YS, Dzhumagulova KN, Masheyeva RU, Jumagulov MN. Positron Production by Runaway Electrons in Lorentzian Plasmas. Symmetry. 2025; 17(11):1843. https://doi.org/10.3390/sym17111843
Chicago/Turabian StyleShalenov, Erik O., Murat A. Myrzali, Yeldos S. Seitkozhanov, Karlygash N. Dzhumagulova, Ranna U. Masheyeva, and Murat N. Jumagulov. 2025. "Positron Production by Runaway Electrons in Lorentzian Plasmas" Symmetry 17, no. 11: 1843. https://doi.org/10.3390/sym17111843
APA StyleShalenov, E. O., Myrzali, M. A., Seitkozhanov, Y. S., Dzhumagulova, K. N., Masheyeva, R. U., & Jumagulov, M. N. (2025). Positron Production by Runaway Electrons in Lorentzian Plasmas. Symmetry, 17(11), 1843. https://doi.org/10.3390/sym17111843





