Global Dynamics and Bifurcation of an Evolutionary Beverton-Holt Model with the Allee Effect
Abstract
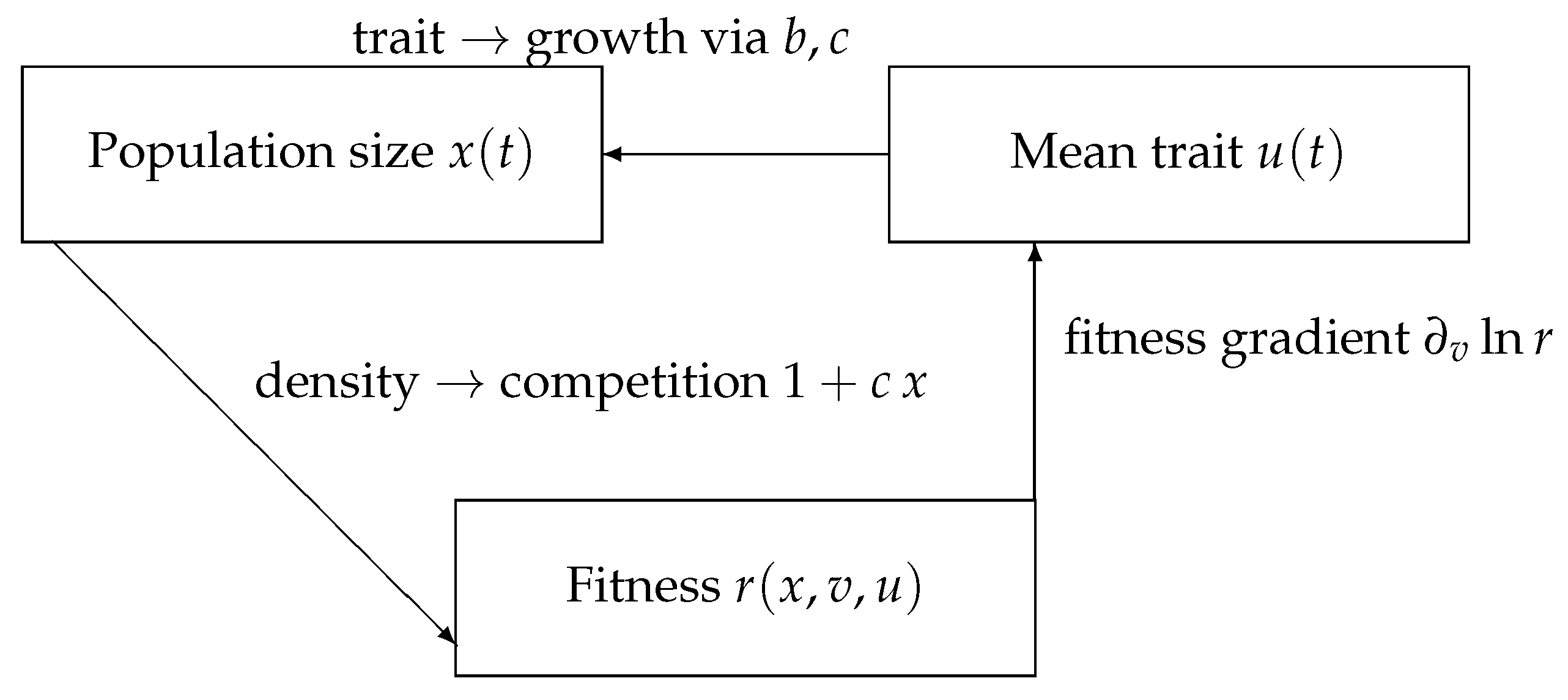
1. Introduction
- density-dependent growth via the Beverton-Holt mechanism;
- mate limitation via a saturating reproductive term;
- predator saturation as an Allee-inducing mortality factor;
- evolution of a quantitative trait under selection.
Objectives of This Study
- Understand how mate limitation and predator saturation induce Allee effects in trait-structured populations;
- Determine the conditions under which the system exhibits multiple attractors, extinction thresholds, and complex dynamics;
- Investigate the influence of evolutionary rates () on persistence and bifurcation behavior;
- Provide rigorous mathematical analysis and numerical simulations to reveal the long-term outcomes of eco-evolutionary feedbacks in populations subject to Allee effects.
2. Fixed Points
3. Stability
3.1. Trivial Fixed Point
- Case 1: Suppose . We prove the result in the case without loss of generality. We partition the right half plane into two disjoint regions separated by the u isocline:
- 1.
- .
- 2.
- .
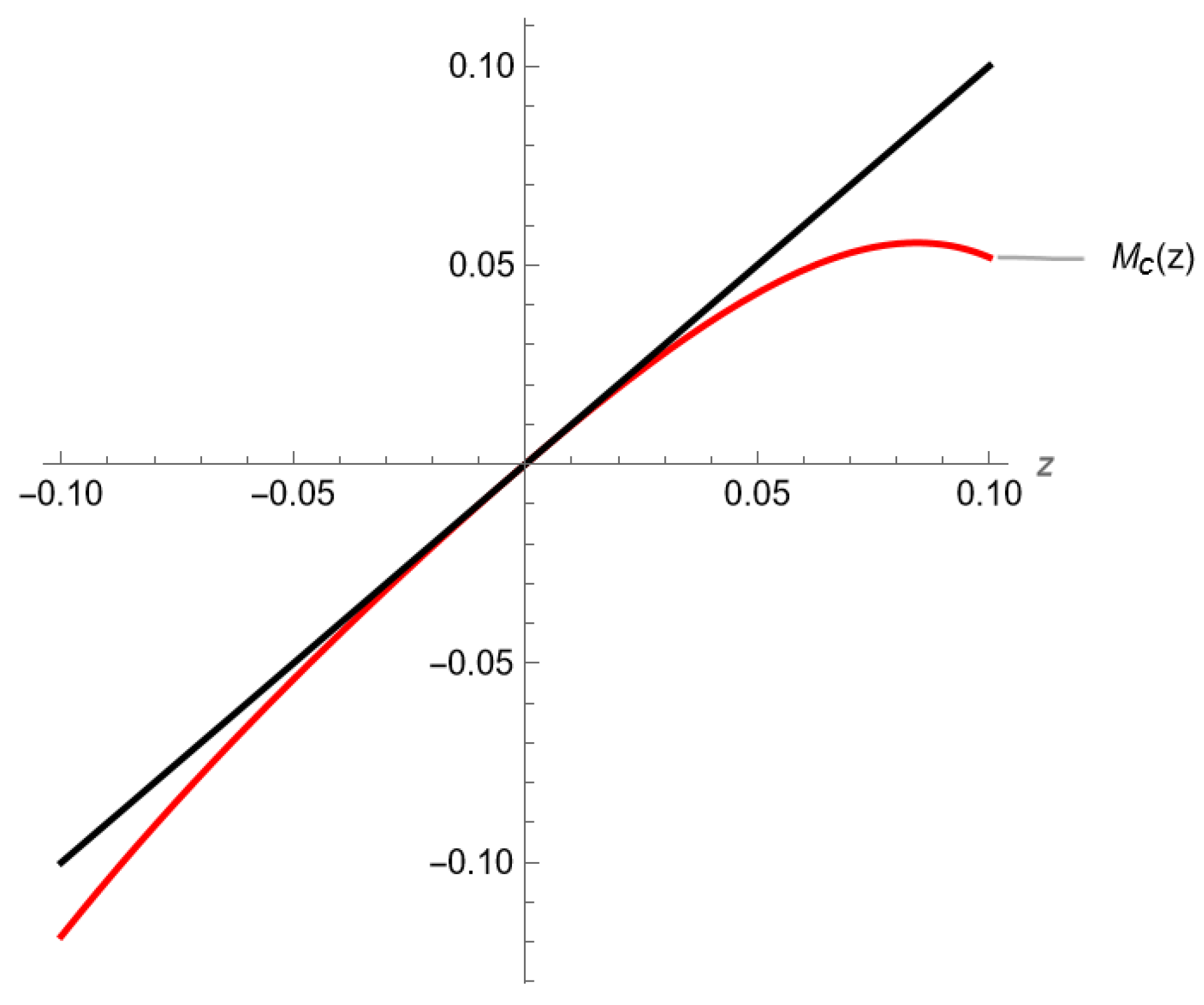
Note that .If , observe first that since the isoclines for the mapping do not intersect for , we must have . Thenwhere the last inequality follows since and is strictly increasing in y. Thus, . Inductively, for all . From above, we knowSince for and , the argument of the exponential is negative. Thus, in this case we have . Taking limits, the result follows since .Finally, let . Observe then that as the point lies above the u isocline. If for some we have , then we may proceed as before. Otherwise, for all positive integers t. In that case, is a monotone decreasing sequence that is bounded below by , so converges to a value . Sinceand , we have as , so also converges. Since F has a unique fixed point for , we have .If instead , then now is decreasing in y instead of increasing, and we reverse the roles of the sets L and H in the proof to obtain a symmetrical argument. - Case 2: Now consider . It suffices to prove thatcan be bounded above independently of t. For brevity, define and . Observe thatand thatThenSince , this impliesas the sum telescopes.It remains to bound . Since , we haveThenSince , we havewhich is independent of t. Thus, we may writefor some constant c and the result follows as since .
3.2. Nontrivial Fixed Points
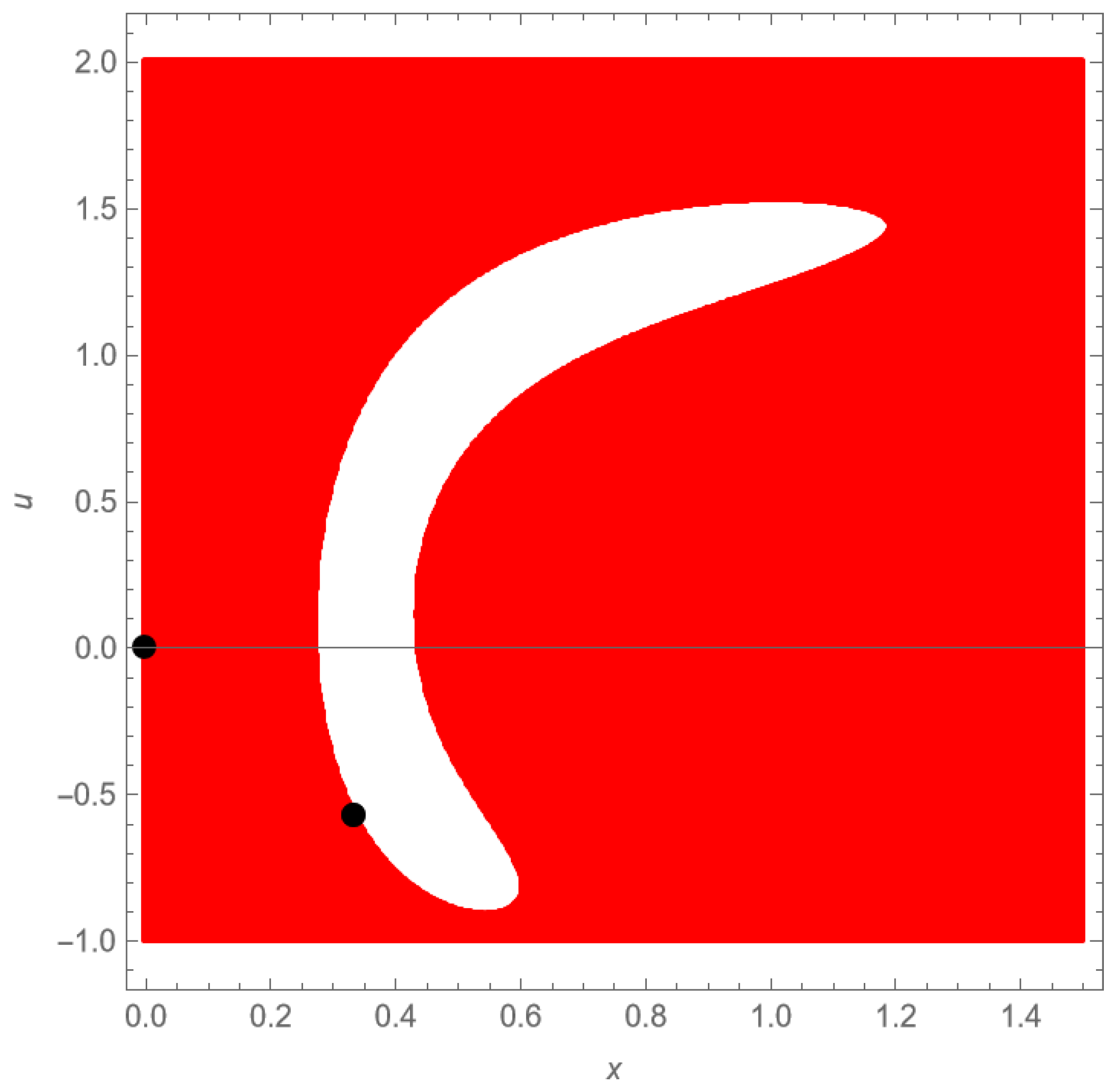
3.2.1. Invariant Sets
- 1.
- the rectangle is forward invariant under F if ;
- 2.
- the rectangle is forward invariant under F if .
- 1.
- Let . We need to show that with implies that . We observe thatestablishing the result.
- 2.
- Let . The partial derivatives of arewith if and if . Consequently, g is strictly monotone in each coordinate and there are no critical points in the interior, so the minimum and maximum must occur on the boundary U.Similarly to the precedent case, using the triangle inequality and the fact that is monotone increasing in x, we haveestablishing forward invariance.
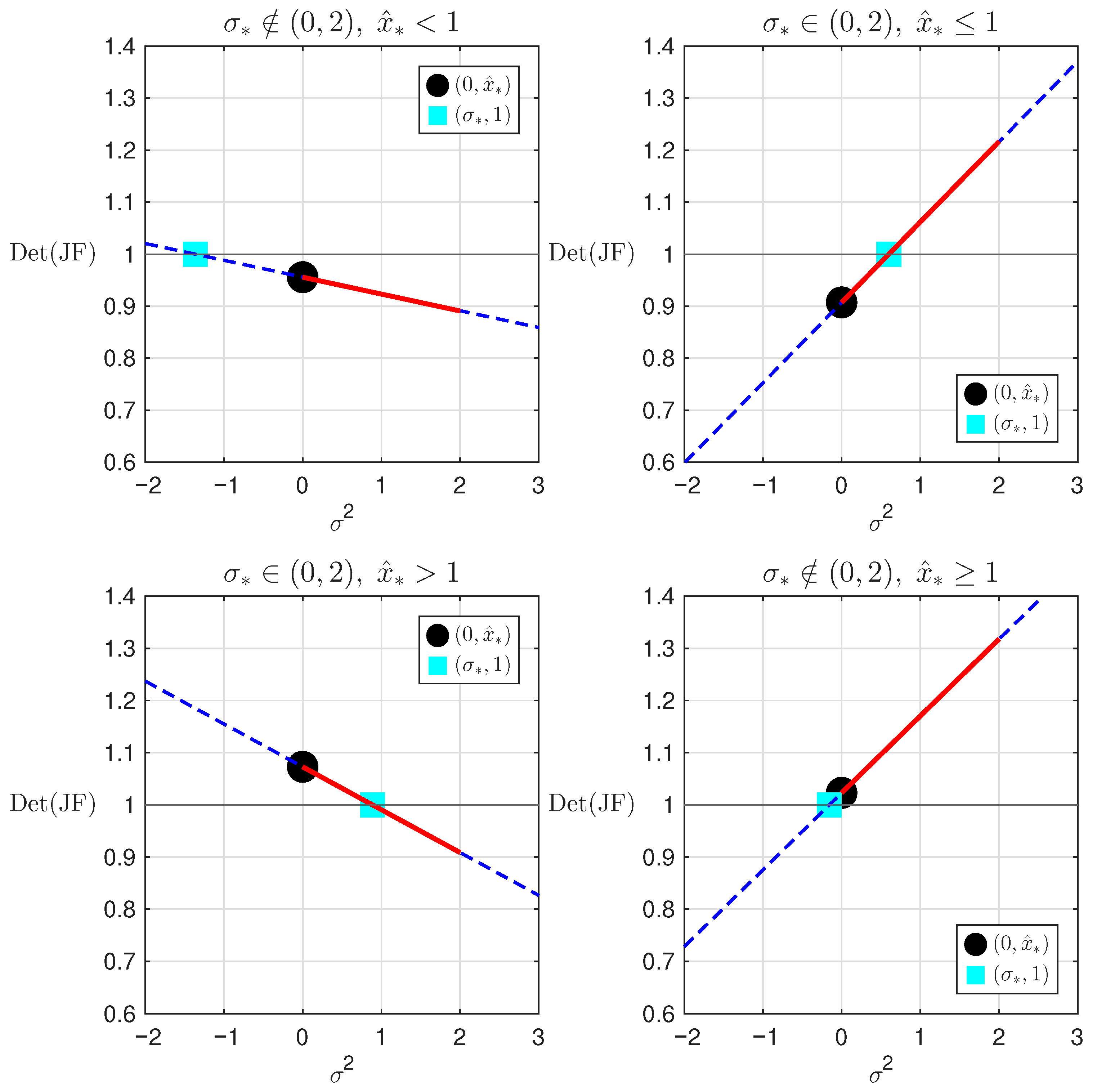
3.2.2. Week Allee Effect
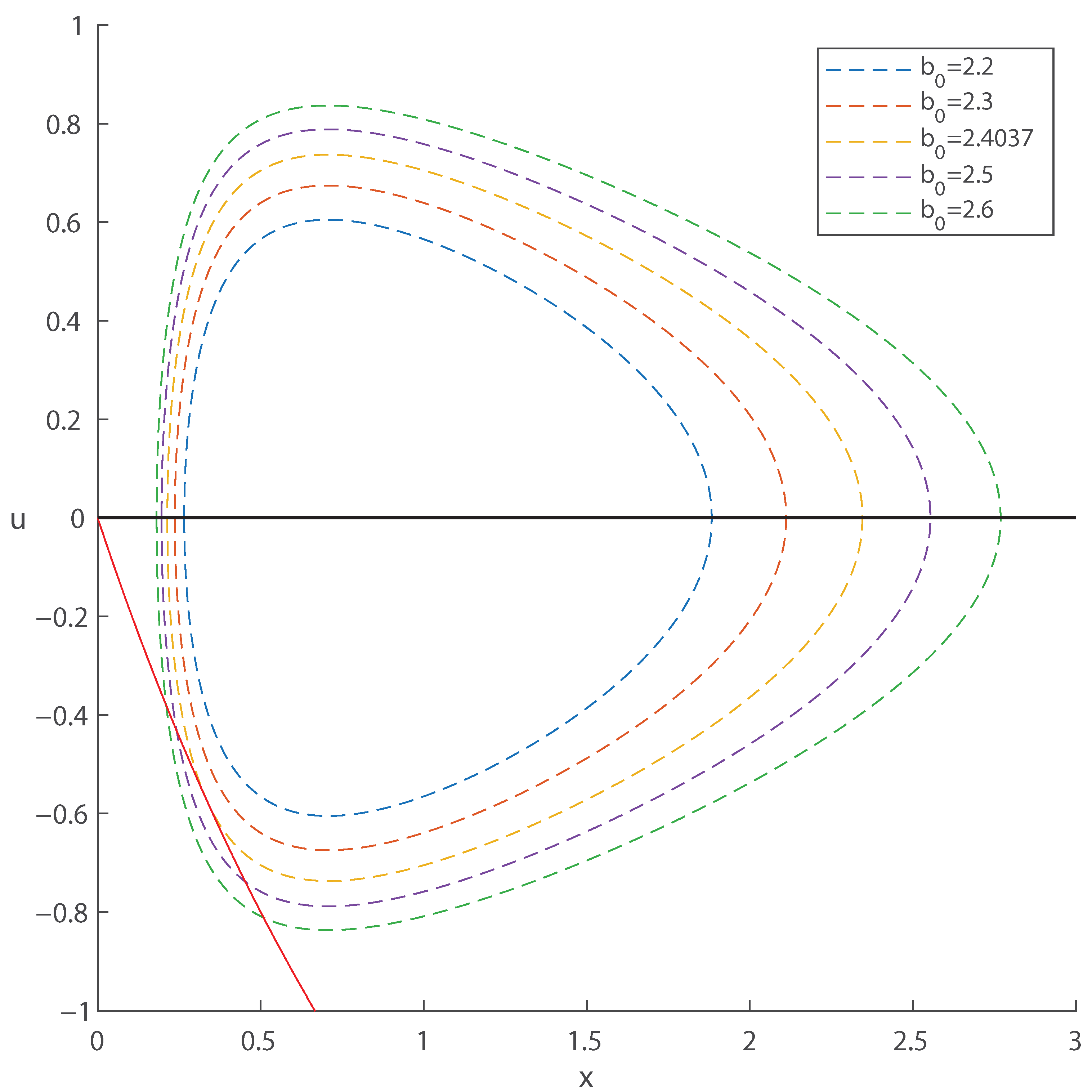
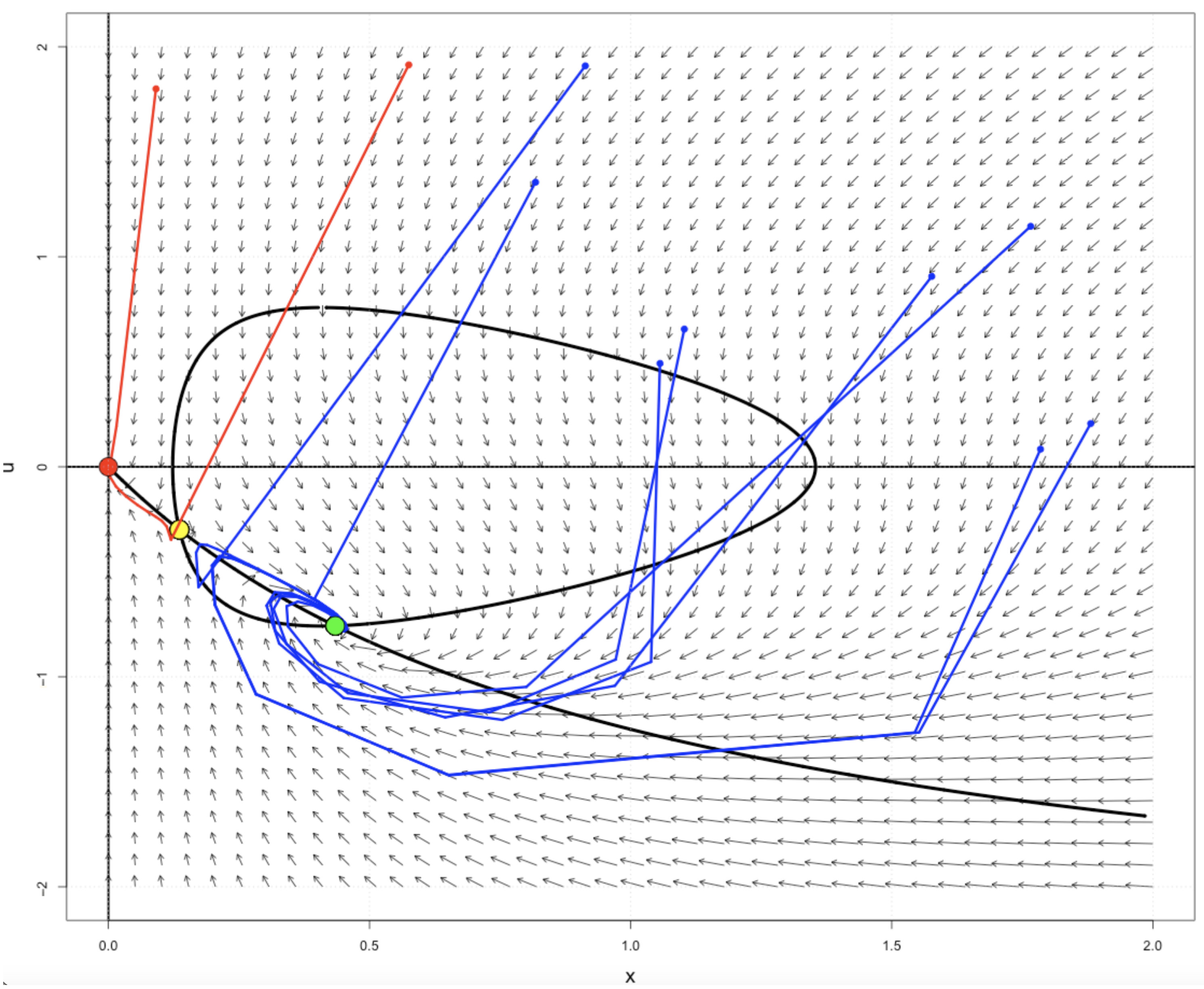
3.2.3. Strong Allee Effect
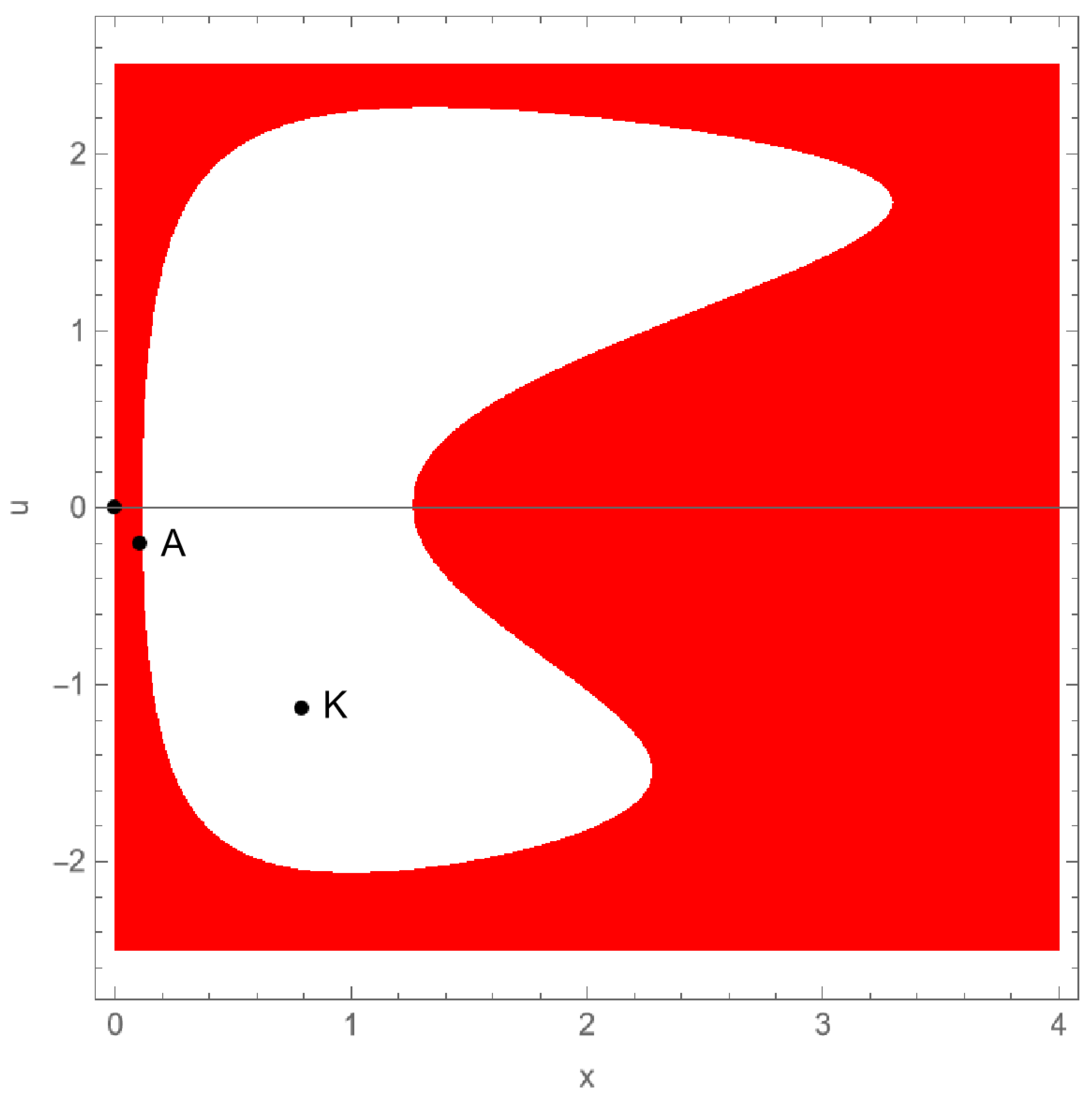
- 1.
- If and , then for .
- 2.
- If and , then for and for .
- 3.
- If and , then for and for .
- 4.
- If and , then for .
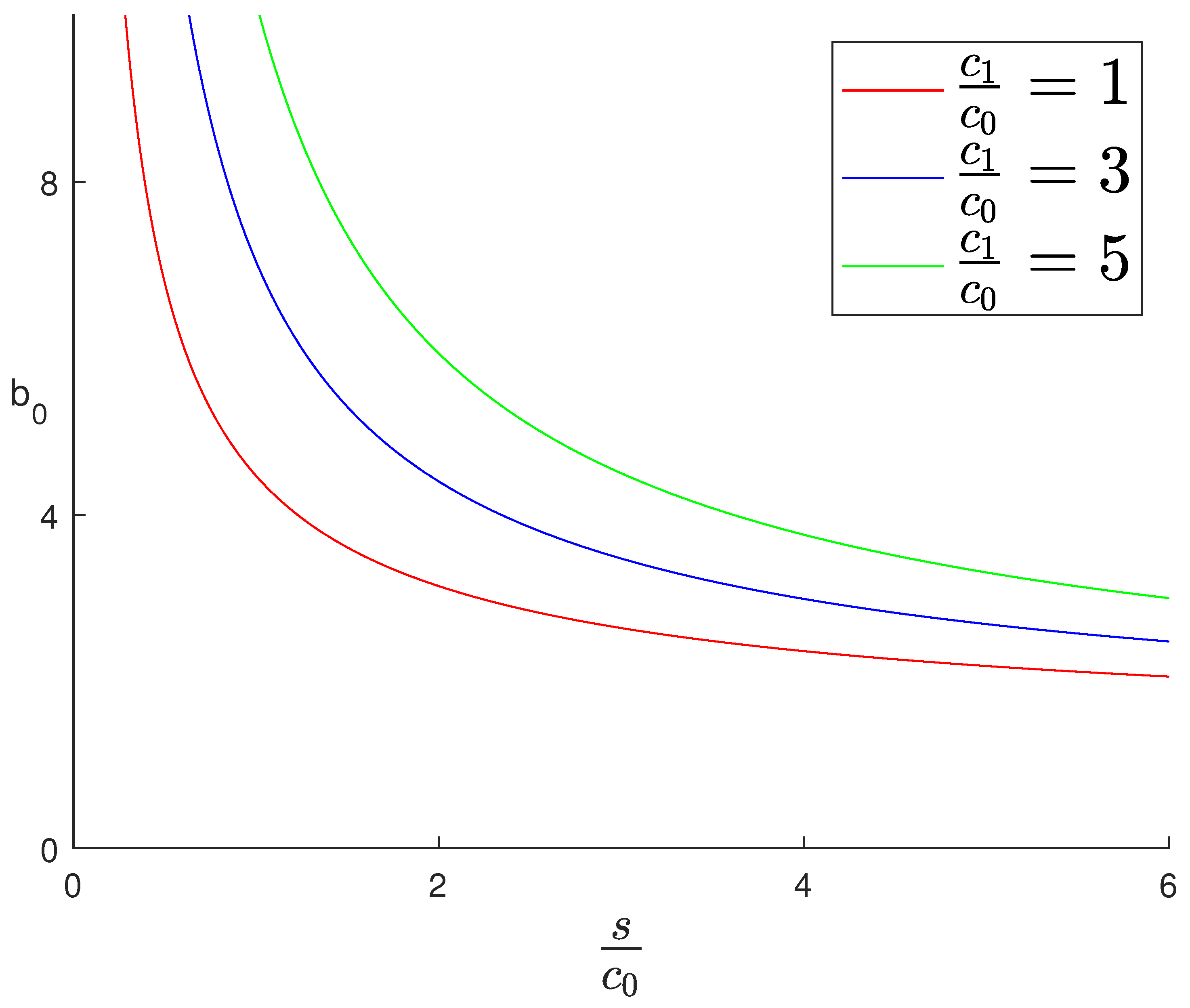
4. The Effect of Evolution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beverton, R.J.H.; Holt, S.J. On the dynamics of exploited fish populations. Fish. Investig. 1957, 19, 1–533. [Google Scholar]
- Leslie, P.H. Some further notes on the use of matrices in certain population mathematics. Biometrika 1948, 35, 213–245. [Google Scholar] [CrossRef]
- Elaydi, S.; Cushing, J.M. Discrete Mathematical Models in Population Biology; Springer: Berlin/Heidelberg, Germany, 2025. [Google Scholar]
- Elaydi, S.N. Discrete Chaos, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Elaydi, S.N. An Introduction to Difference Equations, 3rd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Lande, R. Natural selection and random genetic drift in phenotypic evolution. Evolution 1976, 30, 314–334. [Google Scholar] [CrossRef]
- Lande, R. A quantitative genetic theory of life history evolution. Ecology 1982, 63, 607–615. [Google Scholar] [CrossRef]
- Abrams, P.A. Modelling the dynamics of life history evolution. Theor. Popul. Biol. 2001, 59, 345–357. [Google Scholar]
- D’Aniello, E.; Elaydi, S.; Kwessi, E.; Luís, R.; Ryals, B. Global Asymptotic Stability and Bifurcation of an Evolutionary Beverton-Holt Model. J. Differ. Equ. Appl. 2025, 1–39. [Google Scholar] [CrossRef]
- Dercole, F.; Rinaldi, S. Analysis of Evolutionary Processes; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Brown, J.S.; Vincent, T.L. Evolutionary Game Theory, Natural Selection, and Darwinian Dynamics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Assas, L.; Dennis, B.; Elaydi, S.; Kwessi, E.; Livadiotis, G. A stochastic modified Beverton-Holt model with Allee effects. J. Differ. Equ. Appl. 2016, 22, 37–54. [Google Scholar] [CrossRef]
- Assas, L.; Elaydi, S.; Kwessi, E.; Livadiotis, G.; Ribble, D. Hierarchical competition models with Allee effect. J. Biol. Dyn. 2014, 9, 34–51. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Assas, L.; Elaydi, S.; Kwessi, E.; Livadiotis, G.; Dennis, B. Hierarchical competition models with Allee effect II: The case of immigration. J. Biol. Dyn. 2015, 9, 288–316. [Google Scholar] [CrossRef]
- Courchamp, F.; Berec, L.; Gascoigne, J. Allee Effects in Ecology and Conservation; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Cushing, J.M. The Allee effect in age-structured population dynamics. In Mathematical Ecology; Hallam, S.L.T., Gross, L., Eds.; Springer: Berlin, Germany, 1988; pp. 479–505. [Google Scholar]
- Cushing, J.M. Oscillations in age-structured population models with an Allee effect. J. Comput. Appl. Math. 1994, 52, 71–80. [Google Scholar] [CrossRef]
- Cushing, J.M. The evolutionary dynamics of a population model with a strong Allee effect. Math. Biosci. Eng. 2015, 12, 643–660. [Google Scholar] [CrossRef] [PubMed]
- Cushing, J.M. Difference equations as models of evolutionary dynamics. J. Biol. Dyn. 2019, 13, 103–127. [Google Scholar] [CrossRef] [PubMed]
- Elaydi, S.N.; Sacker, R.J. Population models with Allee effect: A new model. J. Biol. Dyn. 2010, 4, 397–408. [Google Scholar] [CrossRef]
- Livadiotis, G.; Assas, L.; Elaydi, S.; Kwessi, E.; Ribble, D. Competition models with Allee effects. J. Differ. Equ. Appl. 2014, 20, 1127–1151. [Google Scholar] [CrossRef]
- Livadiotis, G.; Elaydi, S. General Allee effect in two-species population biology. J. Biol. Dyn. 2012, 6, 959–973. [Google Scholar] [CrossRef]
- Ch-Chaoui, M.; Mokni, K. A discrete evolutionary Beverton–Holt population model. Int. J. Dyn. Control 2023, 11, 1060–1075. [Google Scholar] [CrossRef]
- Mokni, K.; Elaydi, S.; Ch-Chaoui, M.; Eladdadi, A. Discrete evolutionary population models: A new approach. J. Biol. Dyn. 2020, 14, 454–478. [Google Scholar] [CrossRef]
- Allee, W.C. Animal Aggregations: A Study in General Sociology; University of Chicago Press: Chicago, IL, USA, 1931. [Google Scholar] [CrossRef]
- Taylor, C.M. Allee Effects. In Encyclopedia of Theoretical Ecology; Hastings, A., Gross, L.J., Eds.; University of California Press: Berkeley, CA, USA, 2012; pp. 13–19. [Google Scholar] [CrossRef]
- Dennis, B. Allee effects: Population growth, critical density, and the Allee effect. Ecology 1989, 70, 1066–1072. [Google Scholar] [CrossRef]
- Adamson, P.T.; Morozov, A.Y. Bifurcation analysis of the predator–prey model with the Allee effect in the predator population. Math. Biol. 2021, 63, 1–24. [Google Scholar] [CrossRef]
- Ackleh, A.S.; Cushing, J.M.; Salceanu, P.L. On the dynamics of ecolutionary competition models. Nat. Resurce Model. 2015, 28, 380–397. [Google Scholar] [CrossRef]
- Cushing, J.M. An Evolutionary Beverton-Holt Model. In Theory and Applications of Difference Equations and Discrete Dynamical Systems; AlSharawi, E.S., Cushing, J.Z., Eds.; Springer Proceedings in Mathematics and Statistics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Cushing, J.M. A darwinian Ricker equation. In Progress on Difference Equations and Discrete Dynamical Systems; Baigent, S.E.S., Bhoner, M., Eds.; Springer Proceedings in Mathematics and Statistics; Springer: Cham, Switzerland, 2020; Volume 341, pp. 231–243. [Google Scholar]
- Mokni, K.; Ch-Chaoui, M. Strong Allee Effect and Evolutionary Dynamics in a Single-Species Ricker Population Model. J. Biol. Syst. 2023, 31, 1341–1370. [Google Scholar] [CrossRef]
- Mokni, K.; Ch-Chaoui, M. Exploring persistence, stability, and bifurcations: A Darwinian Ricker–Cushing model. Int. J. Dyn. Control 2025, 13, 34. [Google Scholar] [CrossRef]
- Mokni, K.; Ben, A.H.; Ghosh, B.; Ch-Chaoui, M. Nonlinear dynamics of a Darwinian Ricker system with strong Allee effect and immigration. Math. Comput. Simul. 2025, 229, 789–813. [Google Scholar] [CrossRef]
- Rael, R.C.; Vincent, T.L.; Cushing, J.M. Competitive outcomes changed by evolution. J. Biol. Dyn. 2011, 5, 227–252. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB, R2025a; The MathWorks, Inc.: Natick, MA, USA, 2025; Available online: https://www.mathworks.com (accessed on 1 June 2025).
- Carr, J. Applications of Center Manifold Theory; Springer: New York, NY, USA, 1982. [Google Scholar]
- Luís, R.; Elaydi, S.; Oliveira, H. Stability of a Ricker-type competition model and the competitive exclusion principle. J. Biol. Dyn. 2011, 5, 636–660. [Google Scholar] [CrossRef]
- Wolfram Research Inc. Mathematica, Version 14.3; Wolfram Research: Champaign, IL, USA, 2025; Available online: https://www.wolfram.com/mathematica/ (accessed on 1 June 2025).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 1 June 2025).
- Jury, E. On the roots of a real polynomial inside the unit circle and a stability criterion for linear discrete systems. IFAC Proc. Vol. 1963, 1, 142–153. [Google Scholar] [CrossRef]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: New York, NY, USA, 2015. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology, 2nd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Allen, L.J.S. An Introduction to Stochastic Processes with Applications to Biology; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- D’Aniello, E.; Elaydi, S. The structure of ω-limit sets of asymptotically non-autonomous discrete dynamical systems. DCDS-B 2020, 25, 903–915. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Kot, M. Elements of Mathematical Ecology; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Aniello, E.; Elaydi, S.; Kwessi, E.; Luís, R.; Ryals, B. Global Dynamics and Bifurcation of an Evolutionary Beverton-Holt Model with the Allee Effect. Symmetry 2025, 17, 1811. https://doi.org/10.3390/sym17111811
D’Aniello E, Elaydi S, Kwessi E, Luís R, Ryals B. Global Dynamics and Bifurcation of an Evolutionary Beverton-Holt Model with the Allee Effect. Symmetry. 2025; 17(11):1811. https://doi.org/10.3390/sym17111811
Chicago/Turabian StyleD’Aniello, Emma, Saber Elaydi, Eddy Kwessi, Rafael Luís, and Brian Ryals. 2025. "Global Dynamics and Bifurcation of an Evolutionary Beverton-Holt Model with the Allee Effect" Symmetry 17, no. 11: 1811. https://doi.org/10.3390/sym17111811
APA StyleD’Aniello, E., Elaydi, S., Kwessi, E., Luís, R., & Ryals, B. (2025). Global Dynamics and Bifurcation of an Evolutionary Beverton-Holt Model with the Allee Effect. Symmetry, 17(11), 1811. https://doi.org/10.3390/sym17111811





