Abstract
The line contact behavior of multiscale meshing interfaces necessitates synergistic investigation spanning nano-to centimeter-scale ranges. When nominally smooth gear teeth surfaces come into contact, the mechanical–thermal coupling effect at the meshing interface actually occurs over a collection of microscale asperities (roughness peaks) exhibiting hierarchical distribution characteristics. The emergent deformation phenomena across multiple asperity scales govern the self-organized evolution of interface conformity, thereby regulating both the load transfer efficiency and thermal transport properties within the contact zone. The fractal nature of the roughness topography on actual meshing interfaces calls for the development of a cross-scale theoretical framework that integrates micro-texture optimization with multi-physics coupling contact behavior. Conventional roughness characterization methods based on statistical parameters suffer from inherent limitations: their parameter values are highly dependent on measurement scale, lacking uniqueness under varying sampling intervals and instrument resolutions, and failing to capture the scale-invariant nature of meshing interface topography. A scale-independent parameter system grounded in fractal geometry theory enables essential feature extraction and quantitative characterization of three-dimensional interface morphology. This study establishes a progressive deformation theory for gear line contact interfaces with fractal geometric characteristics, encompassing elastic, elastoplastic transition, and perfectly plastic stages. By systematically investigating the force–thermal coupling mechanisms in textured meshing interfaces under multiscale conditions, the research provides a theoretical foundation and numerical implementation pathways for high-precision multiscale thermo-mechanical analysis of meshing interfaces.
1. Introduction
Meshing interface engineering has emerged as a distinct interdisciplinary domain dedicated to resolving multiscale contact challenges inherent in gear surface topographies. This necessitates the development of scale-bridging computational frameworks to decode the intricate interplay between interfacial mechanics and thermal transfer phenomena. This research field carries significant academic importance, as interfacial contact behavior profoundly impacts the global performance of marine power rear transmission components under coupled thermo-mechanical loading conditions. The meshing interface, specifically defined as the contact boundary region formed under the mode loading conditions, exhibits fundamentally distinct deformation mechanisms compared to bulk materials. This divergence originates from the marked differences between the interfacial microstructure and bulk material properties, along with their abrupt physical property transitions. Hence, a fundamental understanding of the governing thermo-mechanical contact behavior at the meshing interface is required, it is essential to establish a multiscale research framework specifically tailored for non-smooth line-contact interface topographies.
The pioneering work in the study of meshing interface mechanics can be traced back to the Hertzian elastic contact theory [1,2]. This groundbreaking work laid the foundation for contact mechanics, a field devoted to the deformation of rigid contacts whose macroscopic geometry obeys Euclidean symmetry. Ever since Hertz’s seminal study, the elastoplastic deformation of rotationally symmetric bodies in contact has remained a focal point of research. This is primarily due to the significant impact of meshing interface mechanics on the durability of gear transmission systems containing contact elements. In the early studies of quasi-static contact, the deformation response of an ideal elastoplastic half-space subjected to indentation by a rigid sphere was a fundamental problem. In another early study, the process of a rigid cylinder indenting into a linearly hardening elastic half-space is analyzed, and it is found that the contact pressure distribution exhibited a flattening characteristic, with the material having the weakest strain hardening capability showing the most significant deviation from the Hertzian pressure distribution [3,4,5]. In subsequent research, a power law strain hardening nonlinear elastic model will be employed to simulate the deformation response induced by a rigid spherical indenter penetrating a semi-infinite medium within the perfectly plastic regime. A comprehensive investigation into the quasi-static spherical indentation problem will be conducted.
The continuous advancement of numerical computation methods, including the finite element, finite difference, finite volume, and boundary element methods, along with substantial gains in computational efficiency, has led to groundbreaking progress in the theoretical modeling and numerical simulation of meshing interface mechanics. In contact-mechanics modeling, researchers have built a finite-element model of rolling contact between a cylindrical body and an elastoplastic half-space. To represent the cylindrical load, they introduce, for the first time, a moving pressure patch whose shape is elliptical or adaptively modified from an ellipse [6,7,8]. The three-dimensional frictionless contact between a rigid sphere and a linear kinematic hardening half-space has been systematically investigated using a moving Hertzian pressure distribution [9,10,11]. In the realm of elastoplastic contact theory, scholars have conducted in-depth analyses of the mechanical responses of isotropic strain-hardening and non-hardening elastoplastic half-spaces under cyclic loading by spherical indenters, obtaining for the first time an exact interfacial mechanical solution for the first loading cycle in the perfectly plastic contact deformation stage. Based on extensive numerical calculations, the research team has mapped out characteristic diagrams of average contact pressure versus deformation mechanisms, covering elastic, perfectly plastic, and elastic-hardening materials [12,13,14]. Notably, studies on the contact behavior between a rigid sphere and a fully elastoplastic half-space reveal that as the number of loading cycles increases, the contact interface pressure distribution gradually deviates from the classical Hertzian theory solution [15]. Regarding the influence of material parameters, numerous researchers have systematically examined the multiple loading-unloading processes of elastoplastic spherical contact under various material parameter conditions and proposed a universal solution for average contact pressure based on normalized indentation strain parameters for perfect plastic materials [16]. Recent dynamic contact studies have expanded this theoretical framework to encompass spherical indentation of elastoplastic half-spaces, both with and without strain hardening as well as with strain-rate-dependent constitutive behavior [17]. Critically, the analysis reveals that a normalized strain parameter, explicitly identified as the product of the yield strain and the indentation strain, functions as a universal descriptor. This parameter serves as a universal descriptor that consistently characterizes global dimensionless parameters of the field, such as the dimensionless mean pressure, across the entire contact interface [18]. This theoretical breakthrough provides a foundational basis for predicting the mechanical contact behavior of meshing interfaces under complex working conditions. Although the aforementioned studies and numerous relevant findings in recent years have provided a vital theoretical foundation for the macroscopic contact mechanics of meshing interfaces under various loading conditions, it must be pointed out that real gear surfaces in mesh are not ideally smooth, but are composed of complex geometric features spanning multiple scales [19]. Therefore, to accurately characterize the local deformation behavior of surface asperities (roughness peaks) during actual contact processes, a multi-scale analysis framework must be established. Against this backdrop, the microcontact theory has emerged. Its core objective is to reveal the deformation evolution mechanism of the contact region of asperities. In the field of rough surface contact theory research, a milestone is the earliest proposed probabilistic contact model. The innovation of this model lies in its first recognition that nominally smooth surfaces are actually composed of asperities distributed over multiple scales, and its pioneering use of the normal distribution to describe the height distribution characteristics of asperities [20]. However, this model has obvious theoretical limitations: it postulates that all asperities share the same curvature radius for all asperities and a fixed center-to-center distance, which is significantly different from the actual topography of rough surfaces. It is precisely this idealized assumption that gives rise to the fundamental theoretical shortcomings inherent in all contact interface mechanics analyses derived from this model.
The morphological characteristics of real meshing gear interfaces are conventionally quantified by statistical height descriptors, most notably, the Root-Mean-Square (RMS) roughness, the RMS slope of the micro-asperities, and their mean summit curvature. However, due to the significant non-stationary and random characteristics of the actual meshing surface morphology, these statistical parameters will fluctuate significantly with changes in the measurement sampling area size and instrument resolution, making them unsuitable as deterministic parameters [21]. Therefore, to achieve precise characterization of gear meshing surface morphology, it is necessary to establish an analysis method based on scale-invariant parameters that are independent of measurement scale and instrument resolution. The representation methods of scale invariance of geometric similarity features under different magnifications (i.e., self-affine characteristics) have gradually attracted the attention of the academic community [22]. This, in turn, has spurred the use of fractal geometry in contact interface mechanics. Fractals offer a powerful tool for describing, quantifying, and ultimately predicting these natural phenomena: it clarifies how materials respond to external stimuli and faithfully characterizes the true topography of meshing gear surfaces [23]. High-resolution microscopy has experimentally verified that the vast majority of real contact interfaces display fractal behavior. The fact that the power spectrum of most contact surfaces follows a power-law characteristic over a wide range of scales has led to the introduction of fractal geometry into contact mechanics research, giving birth to the emerging sub-discipline of fractal surface contact mechanics, a field that focuses on studying the multi-scale deformation behavior induced by meshing interfaces with fractal characteristics over a wide range of scales.
The analysis demonstrates that the multi-scale nature of meshing interfaces introduces complexity to contact-related physical phenomena (including deformation and thermal conduction), which substantially complicates the performance assessment of thermo-mechanical systems. The present work proposes to: (1) establish a multi-scale theoretical contact model for meshing interfaces subject to mechanical-thermal coupling effects; and (2) develop correlations between dimensionless parameters characterizing the contact behavior of fractal-based multi-scale meshing interfaces.
Our main contributions are: (1) Moving beyond the scale limitations of conventional statistical descriptors, we introduce a fractal-based formalism that provides a scale-invariant representation of real surface topography. This framework unifies the fully elastic, elastoplastic, and perfectly plastic evolution of asperities across scales from nanometer-scale roughness peaks to centimeter-scale macroscopic contacts yielding a continuous-scale description of the self-organizing behavior of multi-asperity systems. It establishes a theoretical foundation for optimizing surface topography and analyzing deformation mechanisms in line contact interfaces. (2) By considering the tiered distribution of micro-topography and the cross-scale correlation of contact states, we systematically clarify how the hierarchical architecture of interfacial asperities collectively governs both load-transfer efficiency and thermal transport behavior. This work elucidates the scaling law that connects localized thermo-mechanical concentrations at individual asperity summits to the global thermo-mechanical response of the macroscopic contact zone, thereby providing a theoretical basis for thermal management design and contact fatigue life prediction in high-power-density transmission systems. (3) Integrating geometric attributes of microscale surface textures with macroscopic mechanical and thermal contact responses, a fractal-parameter-driven optimization framework for micro-texture design is developed. This approach coordinates multi-scale asperity deformation modes with conductive heat-flow pathways, enabling simultaneous control of interfacial contact stress and frictional heat dissipation. It offers a practical numerical pathway for integrated multi-scale, multi-physics simulation and surface engineering in high-precision gear transmission systems.
2. Multiscale Characterization of Real Meshing Interface Morphology
The interfacial contact properties of meshing surfaces exhibiting fractal roughness are characterized by mathematical invariants, continuity, non-differentiability, and self-affinity, that are rigorously captured by the two-dimensional Weierstrass–Mandelbrot (W–M) function. Retaining dimensional consistency, the function superposes cosine spectra whose frequencies follow a geometric progression, as expressed in Equation (1). This mathematical structure reflects the self-similarity characteristics of multi-scale features in fractal profiles, where the frequencies exhibit geometric progression growth [18,24,25].
where represents the two-dimensional projected length of the meshing interface profile, characterizes the roughness, which is dependent on the fractal dimension, is the fractal dimension, constrained to the range of (1, 2), serves as the characteristic scaling parameter for asperity distribution at meshing interfaces (), which determines the self-affine properties by governing the spectral component density in contact profiles, and is the frequency index whose value determines the weighting contribution of multi-scale features in meshing interface profiles. The domain of the frequency index is defined as the integers from 0 to , where denotes the rounding of the bracketed value to the largest integer, and represents the minimum wavelength in the meshing interface profile. To ensure the applicability of continuum medium description, is typically set at 5 to 6 times the material’s lattice spacing. The selection of parameter must satisfy both phase randomization and high spectral density conditions. Research indicates that represents an optimal balance between interface flatness and contact frequency distribution density. The scaling parameter serves an even more fundamental role in fractal characterization of quantifying the magnification of the lateral dimension , the height will be scaled by , expressed as . This self-affine relationship constitutes a fundamental characteristic of self-affine fractals, whose physical essence stems from scale-invariant fundamental physical laws governing specific geometric domains.
The modeling of higher-dimensional random processes can be formulated through a generalization of the Weierstrass–Mandelbrot (W-M) function within a framework of multiple variables [26]. This extension retains the original function’s essential properties, homogeneity, scaling behavior, and self-affinity, as defined in Equation (1). A bivariate formulation enables the simulation of a 3D fractal meshing interface, accurately representing its undulating topography in all directions. By taking the real part of the function, we obtain a height profile that exhibits stochastic variations across any planar orientation.
In the polar coordinate system describing the contact points of a meshing interface at height , the transformation relationship with Cartesian coordinates is expressed as: , . Wherein, the physical interpretations and dimensional units of parameters and are consistent with those specified in Equation (1). is a random phase, uniformly distributed over [0, 2π] and drawn from a random-number generator; it prevents the spectral components of the meshing-interface profile from aliasing in the spatial domain. The parameter represents the wavenumber associated with the characteristic sample size, defined as . The angle describes the ridge offset in the azimuthal direction (under uniform angular offset conditions, ). is a morphological construction parameter indicating the number of superimposed ridges, and its optimum value can be chosen from the power-spectral signature of the meshing-interface topography. For a two-dimensional interface characterized by cylindrical undulations, , whereas for a three-dimensional isotropic fractal interface defined by axisymmetric power spectral properties, the condition must be satisfied.
The height characterization function of a three-dimensional isotropic interface () is obtained by introducing the roughness parameter satisfying the relation into Equation (2), and substituting the relational expressions of , , , as well as the value range of into Equation (2).
Classical geometry and fractal geometry differ fundamentally in their conceptualization of dimension. Classical geometry employs an integer-based dimensional framework, where the concept of dimension builds from a zero-dimensional point to a one-dimensional line, a two-dimensional plane, and finally a three-dimensional solid. In contrast, fractal geometry introduces the innovative concept of fractional dimensions [27,28,29]. Consider a straight line segment: while its classical dimension is unequivocally 1, in fractal geometry, a surface composed of intricately interconnected line segments may exhibit a non-integer dimension between 1 and 2 (for a two-dimensional surface) or between 2 and 3 (for a three-dimensional structure). This fractional dimension quantifies the spatial filling efficiency of the surface’s complex structure [30,31,32]. If a surface that macroscopically resembles a tall mountain but is microscopically composed of countless tiny valleys will have a fractal dimension approaching 2. Conversely, a surface that appears flat at macroscopic scales but exhibits extreme microscopic complexity, such as being covered with nanoscale roughness peaks and valleys, will have a fractal dimension closer to 3. Thus, fractal dimension serves as a quantitative measure of morphological complexity across multiple scales, bridging macroscopic observations with microscopic intricacies. The physical significance of fractal interface roughness can be elucidated as follows: Equations (1) and (3) show that R modulates the amplitude of each frequency component that constitutes the meshing interface profile. The equations further demonstrate that fractal interface roughness is a frequency-independent height-scaling parameter. It is possible to generate random rough-interface profiles using the two- and three-dimensional functions described by Equations (1) and (3). The only unknowns are the scale-independent parameters and , which can be obtained from experiment. Fractal geometry possesses an inherent capability to characterize meshing interfaces across multiple scales (even those differing from the measurement scale), and its characterization is not limited by the resolution of imaging instruments or the scale of measurement [33]. A fractal interface is fully characterized by three independent, scale-invariant parameters: , , and .
The length scale range over which an interface exhibits fractal characteristics depends on its morphological structure, with different machining processes contributing to the final contact morphology in distinct ways [34,35]. Taking polishing as an example: at scales less than or equal to the average abrasive particle size, the process behaves as a stochastic process; however, at larger scales (such as wafer planarization), its effects can be described as deterministic. While fractal descriptions are widely adopted for engineering surfaces at micro/nano scales, their macro/mesoscopic morphology still adheres to Euclidean geometry. If the contact interface morphology itself is formed by stochastic processes (thin-film devices fabricated via photolithography), fractal descriptions remain valid even at macroscopic scales, requiring the determination of distinct fractal parameters for different scale ranges to ensure the applicability of the aforementioned fractal surface theory. This implies that a single set of fractal parameters is not applicable across the entire scale range where fractal behavior holds true. Such interfaces are termed as exhibiting multifractal characteristics.
3. Multiscale Analysis of Meshing Interface Micro-Asperity Contact Mechanics Characteristics
The mechanical properties of the meshing interface are a comprehensive reflection of the interactions between the deformations of multiple micro-asperities, which are triggered by the inherent multi-scale roughness of the contact interface, as shown in Figure 1. In the study of meshing interface mechanics, it is essential to incorporate the deformation of micro-asperities with the multi-scale characterization of the contact interface. As mentioned earlier, the contact interface of two fractal surfaces can be modeled using Equations (1)–(3). The model typically employs fractal parameters that dominate the power spectrum of the contact surface within a target frequency or specific wavelength range, and often adopts a multifractal description approach. Based on this, the problem can be simplified under the action of the global surface interference amount , when a deformable fractal interface contacts a rigid flat plane, multi-scale micro-asperity contact is formed, which exhibits a distinct scale effect (as shown in Figure 2).
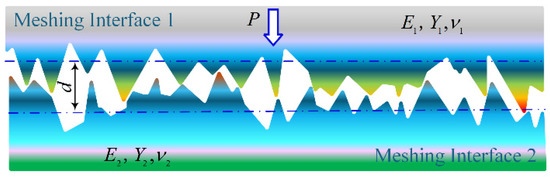
Figure 1.
Asperity-scale confined micro-contacts of meshing interface.
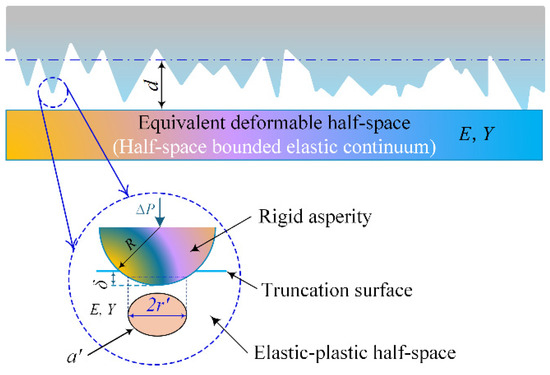
Figure 2.
A micro-contact model is developed for rigid spherical asperities interacting with an elastoplastic half-space, incorporating equivalent elastoplastic material parameters and a fractal-based representation of the rigid rough meshing interface (where the power spectral density dominates within the target frequency range). The model describes the contact configuration between the deformable half-space and the truncated asperities.
In Figure 2, each micro-asperity is modeled as a truncated sphere, where the truncation is a function of the local contact surface interference distance , thereby forming a circular truncated contact domain of radius . Therefore, the key to the analysis of interface contact mechanics is to accurately grasp the distribution patterns of micro-asperity contact under a given global surface interference amount, as well as the deformation behavior characteristics at the micro-asperity scale.
For relatively small interferences of the meshing interface, the textured meshing interface only involves several discrete microcontact points of varying sizes. As the meshing interface interference increases, more microcontact points will form, and some of the previously formed microcontact points will grow larger by merging with adjacent microcontact points. Figure 3 shows a similar model, that is, the microcontact points formed when two non-smooth interfaces are brought into real-time contact under a normal load . These microcontact points are approximately circular spots. Therefore, the real area of contact , defined as the sum of the contact areas of all micro asperity contact points, is significantly less than the nominal contact area . The microcontact model of the textured meshing interface is simplified as shown in Figure 3.
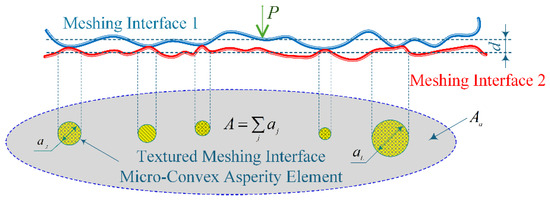
Figure 3.
A non-smooth contact model of two meshing interfaces underload indicates that the actual meshing occurs at micro-asperities contacts points of varying sizes.
The distribution of truncated areas for the resulting micro-asperity contacts is characterized by a power law. The model describes the non-smooth contact behavior between two meshing interfaces under load, with its distinctive feature being that actual meshing only occurs at discretely distributed asperity contact points, where these micro-contact points exhibit multi-scale distribution characteristics.
where is the count of micro-asperities, within the meshing domain, that have a contact area exceeding , and is the largest micro-element contact area exhibited by any micro-element within the meshing domain. According to Equation (4), the distribution function of micro-asperity contact areas within the meshing domain is written as
where is derived from the truncated interface contact area of the meshing gear profile, as given by the following formula
where represents the minimum microcontact area within the meshing domain, which indicates the truncated microcontact area below which the continuous medium mechanics cannot be applied to describe. Due to the existence of , Equation (6) is expressed in the following simplified form.
The total micro-contact asperity area, denoted as , of the textured-element meshing interface is determined by the fractal distribution of the surface heights (as shown in Equation (3)), which is the sum of the areas of all pixels greater than the truncated interface height. Correspondingly, and is obtained through Equations (6), (7) and Equation (5), respectively. The spatial distribution of surface micro-asperities roughness across the textured meshing interface has been fully characterized for the specified contact profile. However, since is dependent on the contact interference amount (or contact load ) of the meshing domain textured interface through , the micro-contact behavior may show significant inconsistency. After the non-smooth interface is truncated by a rigid plane to a certain meshing domain interference amount and the contact area distribution of the textured interface micro-roughness asperities is established (as shown in Equation (5)), it is necessary to further investigate the deformation modes of each micro-contact. A rigorous treatment of this problem demands the introduction of contact deformation equations to accurately capture the micromechanical response of interacting roughness asperities.
The deformation problems of sphere-plane contact (point contact) and cylinder-plane contact (line contact) have become core research topics in three-dimensional and two-dimensional mechanics, respectively. In the study of three-dimensional contact problems, the commonly used approach is to simplify the microscopic interfacial contact between two deformable and rough surfaces as a micro-asperity contact model between two spheres with different radii of curvature (, ), elastic properties (, ), poison’s ratios (, ), and yield strengths (, ). Through equivalent transformation analysis, a spherical asperity model is established with an equivalent curvature radius and an equivalent elastic modulus . Under normal contact loading, this model determines the critical interference at which yielding occurs, ultimately forming a circular microscopic contact area (radius , denoted ), as illustrated in Figure 1 and Figure 2.
The local dimensionless contact interference , and the asperity curvature radius at the meshing interface , are defined as
For textured meshing interfaces with effective elastoplastic parameters ( and ), a range of deformation modes may manifest at the micro-asperity level, with the predominant mode being determined by the values of and , which are governed by the parameters and as shown in Equation (8). The microcontact meshing behavior of textured interfaces can be modeled through two primary regimes: elastic deformation and perfectly plastic deformation. A more realistic description would include elastic deformation, elastoplastic deformation, and perfectly plastic deformation, while a more precise characterization would involve elastic deformation, linear elastoplastic deformation, nonlinear elastoplastic deformation, perfectly plastic transient deformation, and steady-state perfectly plastic deformation. Even without considering interfacial strain hardening, the correlation between the dimensionless average contact pressure and the actual textured interface meshing contact area is formulated for three micro-asperity deformation modes: elastic, elastoplastic, and perfectly plastic.
Under micro-asperity contact conditions, the deformation mode of a textured meshing interface is governed jointly by the peak local interference, , of the micro-asperities and the effective elastoplastic parameters ( and ) of the material, as illustrated in Figure 2. A single dimensionless parameter () fails to effectively characterize the deformation evolution in the elastoplastic transition regime. Instead, it is advisable to define the ratios and as independent, dimensionless parameters. The micro-contact parameters at the meshing interface, specifically the dimensionless average contact pressure and the ratio of the local micro-asperity contact area to the actual area of meshing contact, should be comprehensively analyzed over a wide range of and values. Figure 4 and Figure 5 respectively present the finite element simulation results in the elastoplastic contact deformation region. When ranges between 12–450, the variation patterns of and the corresponding with are revealed. All simulation cases indicate that yielding begins at . According to Hertz theory, this implies that elastic deformation occurs within the dimensionless range of local micro-asperity meshing interface interference .
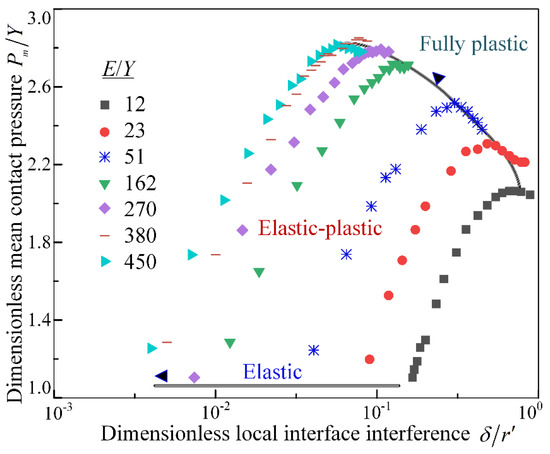
Figure 4.
Correlation between dimensionless contact pressure mean value (), local micro-roughness meshing interface interference (), and ratio () of effective elastic modulus to yield strength.
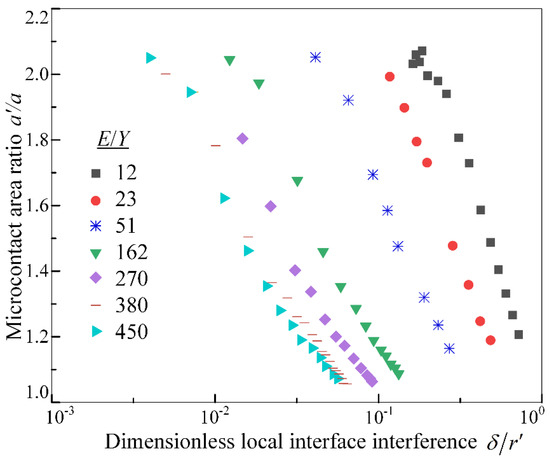
Figure 5.
Correlation between the actual meshing interface contact area ratio (), local micro-roughness meshing interface interference (), and ratio () of effective elastic modulus to yield strength.
Under normal circumstances, as the fractal dimension increases, the micro-texture roughness , contact load, and actual contact area of the meshing interface all exhibit a consistent upward trend. This is attributed to the increased surface complexity associated with a higher fractal dimension , the fractal texture interface will exhibit relatively smooth and dense surface morphological characteristics. This surface morphology significantly enhances the micro-contact load-bearing capacity, thereby leading to an increase in the actual contact area. Meanwhile, as the fractal roughness of micro-textures gradually decreases, the contact interface load and the actual micro-asperity contact area will also show a similar increasing trend. The reason is that a high value means that the surface profile is relatively rough and not dense enough, which directly results in a smaller actual contact interface area, and a correspondingly lower micro-asperity contact load-bearing capacity.
This theoretical analysis elucidates how geometric and material parameters govern the evolution of the real contact area, uncovering the underlying mechanisms in multi-scale fractal interfaces. It presents a framework for the experimental evaluation of the real contact area in meshing interfaces, addressing the constraints imposed by the sampling length and resolution of detection instruments. It is particularly pointed out that the multiscale microcontact mechanics analysis is applied to assess the real contact area detection data of meshing interfaces obtained by various experimental techniques such as optical interferometry, X-ray, and tomography scanning. The multiscale microcontact mechanics analysis framework can also be used to evaluate the reliability of non-smooth meshing interface micro-asperity theory and textured micro-element elastic models in characterizing the contact mechanical behavior of multiscale surface textures. Furthermore, the micro-asperity contact mechanics theory described in this topic can be extended by introducing a more comprehensive theoretical system (micro-contact elastoplastic theory) to incorporate the coupled thermoelastic deformation effects between adjacent micro-asperities of the meshing interface under high-load conditions, where elastoplastic behavior dominates.
4. Multiscale Thermomechanics Characteristics Analysis of Meshing Interface Micro-Asperity Contact
While the meshing interface thermal resistance phenomenon has long been recognized, its inconsistency is intricate and challenging to explain, attributed to the combined influence of factors such as the micro-textured morphology of the meshing interface, applied contact pressure, and the thermomechanics characteristics of micro-contact multiscale elements. The thermal resistance of the meshing interface is a thermal transfer limiting phenomenon dominated by multiscale contact thermo-mechanical coupling effects, which is particularly significant in line contact gear systems with dynamic micro-texture features. As shown in Figure 3, due to the typical multiscale fractal characteristics of the micro-asperities on the meshing interface, the real contact area is comprised of discrete micro-asperities, resulting in an effective area that is much less than the nominal area . The thermal conduction process of the micro-textured meshing interface has the following characteristics: (1) The thermal flow transmission path is strictly limited by the micro-texture morphological features determined by fractal parameters. (2) The efficiency of heat transfer is determined by the characteristics of micro-contact point distribution at the interface in a state of elastoplastic deformation. (3) The thermo-mechanical coupling effect at the microscopic scale causes a significant two-way interaction between thermal conduction and elastic deformation. This complex thermal transfer mechanism requires a multiscale thermodynamic analysis method to accurately characterize its thermal transfer behavior, by considering the micro-contact characteristics and thermo-mechanical coupling effects of the fractal meshing interface.
The distribution characteristics of micro-contact points under elastoplastic deformation determine the thermal transfer efficiency across the interface. Assuming a vacuum environment with negligible radiative heat transfer between the conductive surfaces, heat transfer is dominated by conduction, the thermal contact resistance can be analyzed based on heat conduction through microscopic asperity contacts. The characteristics of microcontact thermal resistance are determined by the mechanical and thermophysical properties of the micro-textured elements, the interface morphology, and the existence of any interstitial films. Assuming a vacuum environment in which convective heat transfer is absent and thermal radiation is negligible compared with conduction, the interfacial thermal resistance characteristics can be analyzed through the thermal conduction of the micro-textured contact points. The contact thermal conductivity coefficient of the textured micro-elements is expressed as
where is the total thermal flux load between the meshing interfaces, and , where and denotes the nominal contact temperature at meshing interfaces (1) and (2), respectively, while and represent the thermal conductivity of the respective interfaces. Under a textured interface interference of , is the resultant total number of micro-asperity contacts. denotes an individual asperity micro-contact area, the value of is determined by , and the specific expression is selected from the equations based on the deformation mode. Determine the fraction of the total heat flux that is conducted through a single asperity micro-contact of area . The corresponding expression is:
In the rolling/sliding line contact meshing interface, micro-asperities not only limit the thermal flux conduction but also cause the gear surface temperature to rise. Based on the two-dimensional fractal thermal conduction theory of line contact interface with the distribution density function of gear surface temperature rise, this study comprehensively accounts for key factors under high-speed and low-speed rolling/sliding line contact conditions, including the proportion of the actual contact area affected by gear surface temperature rise and the maximum temperature rise within the fractal domain, and introduces a three-dimensional fractal method based on the dimensionless average temperature rise . This method is proposed at the micro-asperity contact by simplifying the concept.
where denotes the mean temperature rise during low-speed rolling/sliding, while represents the mean temperature rise during high-speed rolling/sliding. The occurrence of low-speed or high-speed rolling/sliding is determined by the Peclet number , where is defined as the relative sliding velocity at the micro-contact interface, corresponds to the density, and is the specific heat capacity. For low-speed rolling/sliding (), the thermal flux will conduct into both meshing interfaces see Figure 6. Whereas for high-speed rolling/sliding (), the thermal flux will transfer from the hotter micro-interface to the relatively cooler one, as illustrated in Figure 7.
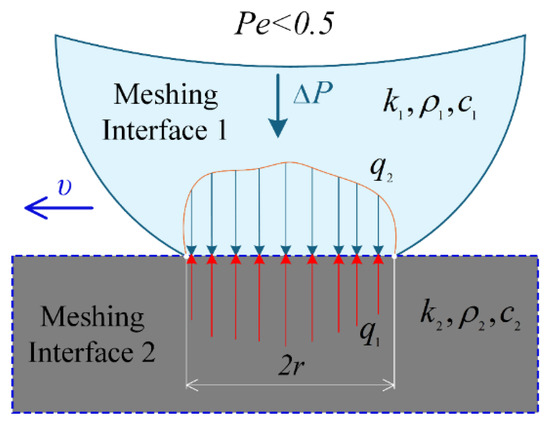
Figure 6.
Thermal conduction models for micro-asperity contact interface: Low-speed rolling and sliding line contact conditions.
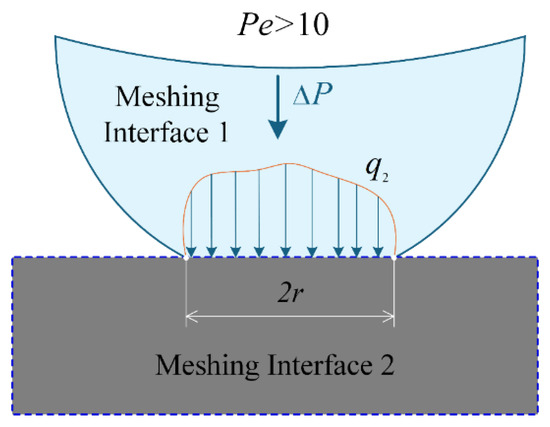
Figure 7.
Thermal conduction models for micro-asperity contact interface: High-speed rolling and sliding line contact conditions.
An iterative optimization framework is employed for the microcontact thermal analysis. The micro-texture morphology and thermo-mechanical properties of the meshing interface are continuously adjusted until the micro-asperity contact size distribution meets the following convergence criterion: under the given contact load, apparent area, rolling/sliding speed, and friction coefficient, the resulting interface temperature rise must fall within the prescribed limits.
This analysis rests on the following set of fundamental assumptions: (1) The influence of the thermoelastic effect on the deformation of micro-asperity contact can be considered a secondary factor; (2) As applied in the temperature calculation, the micro-asperity contact area is calculated via the contact mechanics method described previously. Following the iterative calculations, the resulting micro-asperity contact area that meets the specific temperature rise conditions can be substituted into the pertinent contact mechanics equations to compute the corresponding thermoelastic performance parameters. It should be noted that although this method achieves indirect coupling of thermal and mechanical analyses, it does not explicitly account for the influence of temperature on the dimensions of micro-asperity contact units. For more accurate analysis, a fully coupled thermo-mechanical analysis method can be employed to solve the meshing interface heat conduction process and contact deformation behavior simultaneously.
If the contact temperature distribution at the textured micro-element interface fails to comply with application specifications, the morphology and thermo-mechanical properties of the micro-elements on the meshing interface can be co-adjusted iteratively according to the flowchart shown in Figure 8. This process continues until the contact analysis of the meshing interface yields a size distribution of rough micro-element contact points that satisfies the following requirement: under given meshing load, micro-contact area, rolling-sliding velocity, and friction coefficient, the temperature rise at the meshing interface falls within the predetermined range.
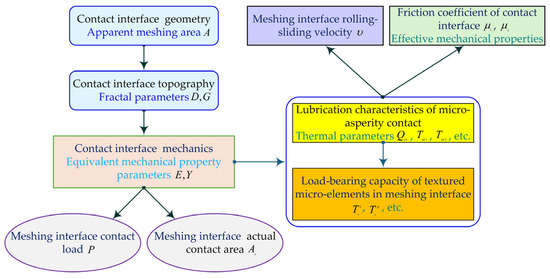
Figure 8.
Schematic flowchart of the process for analyzing meshing load characteristics and optimizing fractal dimension.
5. Analysis of Meshing Load-Bearing Characteristics of Textured Interface Considering Fractal Dimension
This study proposes a novel fractal-based parameter system for characterizing the micro-contact elements of textured interfaces. Through theoretical derivation, the micro-contact load equation and actual contact area equation between textured micro-elements of meshing interfaces are obtained. The influence of mechanisms of critical parameters, including the friction coefficient and the peak-to-valley amplitude of micro-asperities, on the mechanical properties of textured interfaces (including normal stiffness, viscous damping, and average contact load coefficient) are analyzed. A quantitative relationship model between the morphological characteristics of textured micro-elements and the meshing load-bearing characteristics is constructed. Based on the established mathematical analytical model for micro-element contact at textured interfaces, the dynamic evolution laws of meshing load-bearing behavior of textured interfaces evolves with different fractal characterization parameters are studied using MATLAB 2023 version numerical simulation methods. The findings provide a theoretical basis and parameter guidance for optimizing the texture micro-element configuration design of meshing tooth surfaces, thereby enabling the optimal load-bearing performance of textured interfaces.
The relationship between the contact load of textured micro-elements and the actual interfacial contact area in the meshing region is analyzed via MATLAB simulations across a range of fractal dimensions [36]. Figure 9 (left) shows that under a constant meshing load, an increase in the textured interface contact area is accompanied by a decrease in unit micro-element area, resulting in enhanced interface load-bearing capacity.
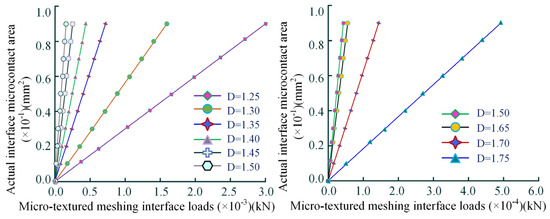
Figure 9.
Correlation of load distribution and actual asperity micro-contact area on textured meshing interfaces under varying fractal parameters (left), and the impact mechanism of actual asperity micro-contact area on dynamic meshing load-bearing capacity of textured interfaces (right).
The results demonstrate that the load on the textured interface is directly proportional to the actual contact area. The analysis reveals that a growth in fractal dimension is accompanied by a steady increase in the slope, which reaches its maximum at a fractal dimension of [], thereby demonstrating that the textured interface exhibits the best average contact load coefficient at this fractal dimension. In Figure 9 (right), the presence of a declining slope in the variation curve at a fractal dimension of [] indicates that an optimal constant exists. The optimal meshing and load-bearing capacity of the micro-contact interface is achieved at a fractal dimension of [] for the textured micro-elements.
The simulation results in Figure 10 reveal a pronounced positive correlation between the micro-asperity contact area of the textured meshing interface and the fraction of purely elastic micro-asperities. As the textured contact area on the tooth surfaces of the gear pair expands, the percentage of purely elastic micro-asperities within the micro-contact zone of the meshing domain increases monotonically.
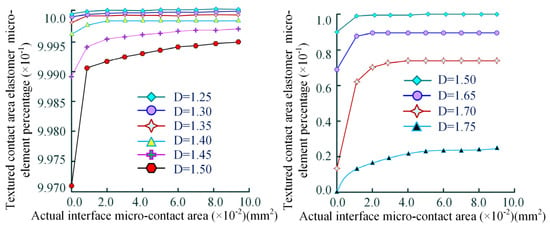
Figure 10.
The influence law of the actual interface micro-element contact area at the textured surface on the meshing load-bearing characteristics (left), and the time-variant characteristics of the purely elastic micro-element contact area ratio throughout the meshing process (right).
The fractal dimension of the micro-texture exhibits a pronounced negative correlation with the percentage of purely elastic micro-elements, which decreases systematically as the fractal dimension increases. The critical fractal dimension value of [] is characterized by a distinct drop in the percentage of purely elastic micro-elements, this downward trend accelerates significantly. This phenomenon underscores the profound impact of fractal dimension on the micro-contact behavior of surface asperities. Specifically, an increased fractal dimension amplifies stress concentration at asperity tips. This heightened stress propagates plastic deformation, substantially diminishing the proportion of elastic micro-elements.
6. Conclusions
This paper presents a universal multi-scale theoretical approach for textured meshing interfaces with self-affine micro-contact behavior of asperities. The core objective is to introduce a mathematically rigorous method for characterizing the fundamental mechanical and thermal properties of micro-contact interfaces that exhibit multi-scale roughness. This analysis can be further extended by introducing more complex contact mechanics treatment methods, covering the deformation of adjacent micro-contacts, rolling and sliding friction, and the influence of thermal effects on contact deformation. This study utilizes dimensionless representations of both the micro-texture morphology at the meshing interface and the associated mechanical and thermal parameters to investigate the mechanothermal characteristics of micro-contact interfaces exhibiting multiscale roughness. The correlations established between various dimensionless quantities in the paper provide an effective means for real-time solution of the rolling and sliding line contact textural micro-element interface parameters (actual contact area and thermal contact conductivity). The contribution of this work is the establishment of a theoretical paradigm for innovative thinking in the investigation of mechanothermal properties at micro-contact textured meshing interfaces.
The in-depth investigation of the mechanical contact behavior and thermal transfer mechanism of micro-texturized meshing interfaces is of great significance in both traditional and modern technological fields. To regulate the complex physical mechanisms behind the micro-contact phenomena of textured meshing interfaces, it is necessary to focus on the hierarchical structure of the textural micro-element morphology and employ a multi-scale approach to handle the textural micro-elements. Combining the fractal geometry-based method, which provides a realistic and scale-invariant description of the interface micro-contact, using a hybrid analytical-numerical method, which employs a constitutive model defined at the level of individual micro-protrusions, is crucial for in-depth research on interface micro-contact phenomena across diverse length scales. The importance of this research method cannot be overstated, as it can influence the design of the configuration of textural micro-elements with rolling and sliding line contact meshing interfaces, which in turn is related to the operating efficiency of Marine Power Rear Transmission Systems (MPRTS).
Based on this research approach, the following three key findings are summarized:
- (1)
- Fractal characterization accurately captures multi-scale interface contact behavior
The application of fractal geometry enables a scale-invariant and physically realistic description of surface topography at micro-textured meshing interfaces. This approach reveals that contact load and real contact area follow fractal scaling laws, which are critical for predicting mechanical response across different size scales, from macroscopic components down to micro-asperities.
- (2)
- Micro-texture morphology hierarchically modulates both thermal and mechanical contact performance
Through a multi-scale analysis of texture micro-elements, it is demonstrated that hierarchical surface structures significantly influence interfacial heat transfer and stress distribution. Specifically, optimized micro-texture configurations can enhance heat dissipation at sliding/rolling contacts while reducing localized stress concentrations, thereby improving the interface’s tribological and thermal performance.
- (3)
- Hybrid analytical-numerical modeling effectively predicts interface behavior under combined rolling-sliding conditions
By combining fractal micro-contact theory with numerical simulation based on a constitutive model for micro-protrusions, this research provides a validated predictive framework for contact pressure, subsurface stress, and thermal field distribution in line-contact meshing interfaces. This method offers critical insights for designing texture parameters that boost the efficiency and durability of MPRTS.
Future research will focus on deepening theoretical investigations, systematically conducting experimental validation, and actively promoting demonstration applications to facilitate the translation and implementation of research outcomes. Gears, serving as the core components for torque transmission, are produced in a wide variety of sizes and are distinguished by their high load-bearing capacity and transmission efficiency. These characteristics are essential for ensuring the reliability and operational precision of MPRTS. When operating in specialized marine environments, MPRTS are subjected to extreme conditions, including but not limited to extreme high and low temperatures; intense pressures (reaching 20–30 MPa, equivalent to 200–300 times atmospheric pressure); and corrosive exposure to weak acids and alkalis. The harsh marine environment poses significant challenges for MPRTS, particularly in terms of material degradation caused by acid-alkali corrosion. Over extended periods, MPRTS are continuously exposed to alternating conditions characterized by high temperature and humidity, coupled with salt fog as well as seawater spray. This leads to severe electrochemical corrosion issues. Gears experience contact fatigue and scuffing during operation under load. Ensuring the load-bearing capacity of gears poses a significant challenge in deep-sea applications, as high-end equipment imposes increasingly stringent demands for greater capacity and operational reliability. Although advanced manufacturing techniques such as contact interface hardening and microtexture precision machining, which have incrementally improved gear meshing load-bearing capacity, these methods still fall short of meeting the ever-increasing demands for extended service life and higher load capacity. Frequent equipment failures due to insufficient gear strength remain a persistent issue, highlighting that gear load-bearing capacity continues to be a critical bottleneck limiting the durability and dependability of marine power rear transmission systems.
This research overcomes previous limitations in characterizing the time-varying frictional contact interface Thermo-Elasto-Hydrodynamic Lubrication (TEHL) characteristics of MPRTS in service performance, which inadequately considers the microscopic morphology of the rolling/sliding transition regions (points/lines) at the meshing interface. It innovatively proposes tuning the multi-scale parameters that characterize Interfacial Micro-Texture (IMT) to simultaneously optimize interfacial lubrication and meshing load-bearing performance. This breakthrough overcomes the application bottleneck of traditional lubrication being ineffective under extremely harsh working conditions. It has been demonstrated that gear tooth surfaces featuring a Micro-Textured Meshing Interface (MTMI) can sustain a stable low-friction characteristic at the line contact interface over extended periods. This offers a potential approach for achieving homogeneous Interface-Enriched Lubrication (IEL) and enhanced Anti-Scuffing Load-Bearing Capacity (ASLBC) in gear surfaces, particularly within the meshing domain of MPRTS under extreme high-speed and heavy-load conditions. By investigating the micro-contact textured interfaces load-bearing evolution mechanism governing TEHL considering the effects of multi-scale characterization parameters, the proposed work forges a cross-scale associative coupling among macroscopic fields (stress, film thickness, temperature) and microscopic features (local geometry, asperity distribution, texture orientation). This integration refines the theoretical scheme for lubrication of meshing interfaces under extreme conditions and provides a rigorous scientific basis, and attendant design guidelines, for enhancing the gear meshing surface ASLBC in MPRTS, offering both high engineering value and distinctive academic innovation.
Author Contributions
Conceptualization, X.W. and Y.W.; methodology, W.Z.; software, J.R.; validation, X.W., Y.W. and J.R.; formal analysis, W.Z.; investigation, J.R.; resources, Y.W.; data curation, W.Z.; writing—original draft preparation, W.Z. and X.W.; writing—review and editing, X.W., Y.W. and J.R.; visualization, J.R.; supervision, J.R. and W.Z.; project administration, Y.W. and W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The research subject was supported by the National Natural Science Foundation Sponsored Project (Project Approval Number: 52475257), the National Key Research and Development Program Project (Grant No. 2023YFB3406301), the Fund Project for Technological Field of National Defense Science and Technology Plan 173 (2024-JCJQ-JJ-2020) and (2024-JCJQ-JJ-2043), the Marine Propulsion Research and Development (MPRD) Program (Grant No. MG20220203) and the Supported by the Scientific Research Funds of Huaqiao University (605-50Y23032).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank Huaqiao University (HQU), Heilongjiang Institute of Technology (HLJIT), and the Harbin Institute of Technology (HIT) for their support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yu, G.; Mao, H.; Jiang, L.; Liu, W.; Valerii, T. Fractal Contact Mechanics Model for the Rough Surface of a Beveloid Gear with Elliptical Asperities. Appl. Sci. 2022, 12, 4071. [Google Scholar] [CrossRef]
- Meng, F.; Xia, H.; Zhang, X.; Wang, J.; Jin, Y. Study on nonlinear dynamic characteristics of gear system with 3D anisotropic rough tooth surface based on fractal theory. Int. J. Non-Linear Mech. 2023, 150, 104366. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, Y.; Han, H.; Ma, H.; Wang, H.; Li, Z. Meshing Characteristics of Spur Gears Considering Three-Dimensional Fractal Rough Surface under Elastohydrodynamic Lubrication. Machines 2022, 10, 705. [Google Scholar] [CrossRef]
- Wang, W.; He, Y.Y.; Zhao, J.; Mao, J.Y.; Hu, Y.T.; Luo, J.B. Optimization of groove texture profile to improve hydrodynamic lubrication performance: Theory and experiments. Friction 2020, 8, 83–94. [Google Scholar] [CrossRef]
- Marques, P.M.T.; Marafona, J.D.M.; Martins, R.C.; Seabra, J.H.O. A continuous analytical solution for the load sharing and friction torque of involute spur and helical gears considering a non-uniform line stiffness and line load. Mech. Mach. Theory 2021, 161, 104320. [Google Scholar] [CrossRef]
- Wang, Y.; Azam, A.; Zhang, G.; Dorgham, A.; Liu, Y.; Wilson, M.C.T.; Neville, A. Understanding the Mechanism of Load-Carrying Capacity between Parallel Rough Surfaces through a Deterministic Mixed Lubrication Model. Lubricants 2022, 10, 12. [Google Scholar] [CrossRef]
- Cao, J.; Yang, S.; Chen, Z.; Sun, H.; Ning, F.; Bao, H. A Fractal Prediction Model for the Friction Coefficient of Wet Clutch Friction Plates. Appl. Sci. 2024, 14, 12075. [Google Scholar] [CrossRef]
- Cai, Z.J.; Zheng, X.Q.; Lan, H.Q.; Wang, L.N.; Yang, S.W.; Sheng, R. Time-Varying Meshing Stiffness and Dynamic Parameter Model of Spiral Bevel Gears with Different Surface Roughness. Appl. Sci. 2024, 14, 1533. [Google Scholar] [CrossRef]
- Liu, W.L.; Ni, H.J.; Wang, P.; Chen, H.L. Investigation on the tribological performance of micro-dimples textured surface combined with longitudinal or transverse vibration under hydrodynamic lubrication. Int. J. Mech. Sci. 2020, 174, 105474. [Google Scholar] [CrossRef]
- Chang, X.; Renqing, D.; Liao, L.; Zhu, P.; Lin, B.; Huang, Y.; Luo, S. Study on hydrodynamic lubrication and friction reduction performance of spur gear with groove texture. Tribol. Int. 2023, 177, 107978. [Google Scholar] [CrossRef]
- Černe, B.; Petkovšek, M.; Duhovnik, J.; Tavčar, J. Thermo-mechanical modeling of polymer spur gears with experimental validation using high-speed infrared thermography. Mech. Mach. Theory 2024, 146, 103734. [Google Scholar] [CrossRef]
- Ni, X.; Sun, J.; Ma, C.; Zhang, Y. Wear Model of a Mechanical Seal Based on Piecewise Fractal Theory. Fractal Fract. 2023, 7, 251. [Google Scholar] [CrossRef]
- Ammosov, L.; Mönkkönen, K.; Suvanto, M. Precise fabrication of microtextured stainless steel surfaces using metal injection moulding. Precis. Eng. 2020, 62, 89–94. [Google Scholar] [CrossRef]
- Zhao, J.; Hou, L.; Li, Z.; Zhang, H.; Zhu, R. Prediction of tribological and dynamical behaviors of spur gear pair considering tooth root crack. Eng. Fail. Anal. 2022, 135, 106145. [Google Scholar] [CrossRef]
- Brown, C.; Nescio, M.; Chadha, V.; Zheng, C.; Abelev, E.; Chmielus, M.; Jacobs, T. The Difficulty of Measuring Surface Topography in Additive Manufacturing: A Comparison Between Measured and True Surface Features of Binder-Jet Printed Samples. J. Tribol. 2025, 147, 091116. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Grützmacher, P.G.; Gachot, C.; Costa, H.L. Surface texturing in machine elements-A critical discussion for rolling and sliding contacts. Adv. Eng. Mater. 2019, 21, 1900194. [Google Scholar] [CrossRef]
- Wang, X.G.; An, S.Y.; Wang, Y.M.; Ruan, J.F.; Ji, S.E. TEM fitting considering TEPs of contact interface of meshing gear. J. Mech. Sci. Technol. 2021, 35, 4443–4457. [Google Scholar] [CrossRef]
- Sivayogan, G.; Dolatabadi, N.; Johns-Rahnejat, P.; Rahmani, R.; Rahnejat, H. Non-Newtonian Thermo-Elastohydrodynamics and Sub-Surface Stress Field of High-Performance Racing Spur Gears. Lubricants 2022, 10, 146. [Google Scholar] [CrossRef]
- Xing, Y.Q.; Li, X.; Hu, R.Y.; Long, X.Y.; Wu, Z.; Liu, L. Numerical analyses of rectangular micro-textures in hydrodynamic lubrication regime for sliding contacts. Meccanica 2019, 56, 365–382. [Google Scholar] [CrossRef]
- Rajput, H.; Atulkar, A.; Porwal, R. Optimization of the surface texture on piston ring in four-stroke IC engine. Mater. Today Proc. 2021, 44 Pt 1, 428–433. [Google Scholar] [CrossRef]
- Zhang, N.; Zhai, W.; Yin, S.; Chen, S.; Xia, J.; Luan, L.; Zhai, A. Deep-sea soft soil and deep-sea mining vehicle interaction: From soil properties to locomotion performance. Appl. Ocean Res. 2025, 154, 104372. [Google Scholar] [CrossRef]
- Li, Z.; Xiao, H.; Tang, Y.; Liang, G.; Wang, L.; Yang, J. A deterministic model of surface profile degradation for evaluating time-varying mesh stiffness and dynamic responses of spur gear considering tooth surface wear evolution. Mech. Syst. Signal Process. 2025, 225, 112313. [Google Scholar] [CrossRef]
- Gupta, N.; Tandon, N.; Pandey, R.; Vidyasagar, K.C.; Kalyanasundaram, D. Tribodynamic studies of textured gearsets lubricated with fresh and MoS2 blended greases. Tribol. Int. 2022, 165, 107247. [Google Scholar] [CrossRef]
- Wang, X.G.; Huang, H.; Song, J.Y.; Wang, Y.M.; Ruan, J.F. Numerical Analysis of Friction Reduction and ATSLB Capacity of Lubricated MTMI with Textured Micro-Elements. Lubricants 2023, 11, 78. [Google Scholar] [CrossRef]
- Wos, S.; Koszela, W.; Pawlus, P. Comparing tribological effects of various chevron-based surface textures under lubricated unidirectional sliding. Tribol. Int. 2020, 146, 106205. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, J.; Hu, N.; Shen, G.; Li, Y.; Zhang, L. Research on the time-varying mesh stiffness method and dynamic analysis of cracked spur gear system considering the crack position. J. Sound Vib. 2023, 548, 117505. [Google Scholar] [CrossRef]
- Kaneta, M.; Matsuda, K.; Nishikawa, H. The Causes of Asymmetric Deformation of Surface Roughness Asperities in Elastohydrodynamic Lubrication Contacts. J. Tribol. 2022, 144, 061601. [Google Scholar] [CrossRef]
- Cheng, G.; Ma, J.; Li, J.; Sun, K.; Wang, K.; Wang, Y. Study on the Dynamic Characteristics of Gears Considering Surface Topography in a Mixed Lubrication State. Lubricants 2024, 12, 7. [Google Scholar] [CrossRef]
- Mu, X.K.; Sun, W.; Liu, C.; Wang, Y.L.; Yuan, B.; Sun, Q.C. Study on rough surfaces: A novel method for high-precision simulation and interface contact performances analysis. Precis. Eng. 2022, 73, 11–22. [Google Scholar] [CrossRef]
- Li, C.; Qiu, X.; Yu, Z.; Li, S.; Niu, Q.; Kurniawan, R.; Ko, T. Novel Environmentally Friendly Manufacturing Method for Micro-Textured Cutting Tools. Int. J. Precis. Eng. Manuf. Green Technol. 2021, 8, 193–204. [Google Scholar] [CrossRef]
- Cao, P.; Li, Q.; Feng, K.; Qin, Y. Dynamic modeling of spur gear transmission system with evolutive coupling fault of fatigue crack and wear. Eng. Fail. Anal. 2024, 156, 107820. [Google Scholar] [CrossRef]
- Wu, J.P.; Yang, C.B.; Liu, C.; Wang, Y.L.; Zhang, H.S.; Wang, L.Y.; Li, H.Y. Numerical analysis of micro-textured friction element interface temperature fields under mixed lubrication. Int. Commun. Heat Mass Transf. 2025, 163, 108743. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, W.Z.; Wu, H.; Chen, T.; Li, S.; Li, H.; Zhou, Z.; Hu, X. Multi-field coupling lubrication interface heat transfer model for hypoid gear transmission. Int. Commun. Heat Mass Transf. 2024, 154, 107451. [Google Scholar] [CrossRef]
- Li, Z.H.; Jiang, M.J.; Guo, X.H.; Zhang, K.D. Improving the frictional properties of the tool/chip interface of micro-textured ceramics tools by using electromagnetic-assisted nanofluids. Mater. Today Commun. 2024, 39, 109017. [Google Scholar] [CrossRef]
- Di, J.; Fan, Z.; Zhang, H.; Wang, C.; Wang, J.; Peng, C. Numerical and experimental studies of cavitation damage characteristics of 17-4PH stainless steel under array groove structure. J. Tribol. 2025, 147, 124602. [Google Scholar] [CrossRef]
- Banerjee, S.; Gowrisankar, A.; Mahipal Reddy, K. Fractals and Dimensions. In Fractal Patterns with MATLAB; Springer Briefs in Complexity; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–18. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).