Biomedical Knowledge Graph Embedding with Hierarchical Capsule Network and Rotational Symmetry for Drug-Drug Interaction Prediction
Abstract
1. Introduction
- We introduce Rot4Cap, which embeds BioKGs in a 4D vector space and leverages geometric symmetry to capture complex relational patterns, including RMPs and hierarchical structures.
- We integrate BERT, CNN, and GNN to obtain molecular and textual representations of drugs, employing capsule networks to model inter-dimensional correlations of entity embeddings.
- We demonstrate the effectiveness of Rot4Cap on three widely used BioKG datasets, where it consistently surpasses both traditional and state-of-the-art DDI prediction models.
2. Related Work
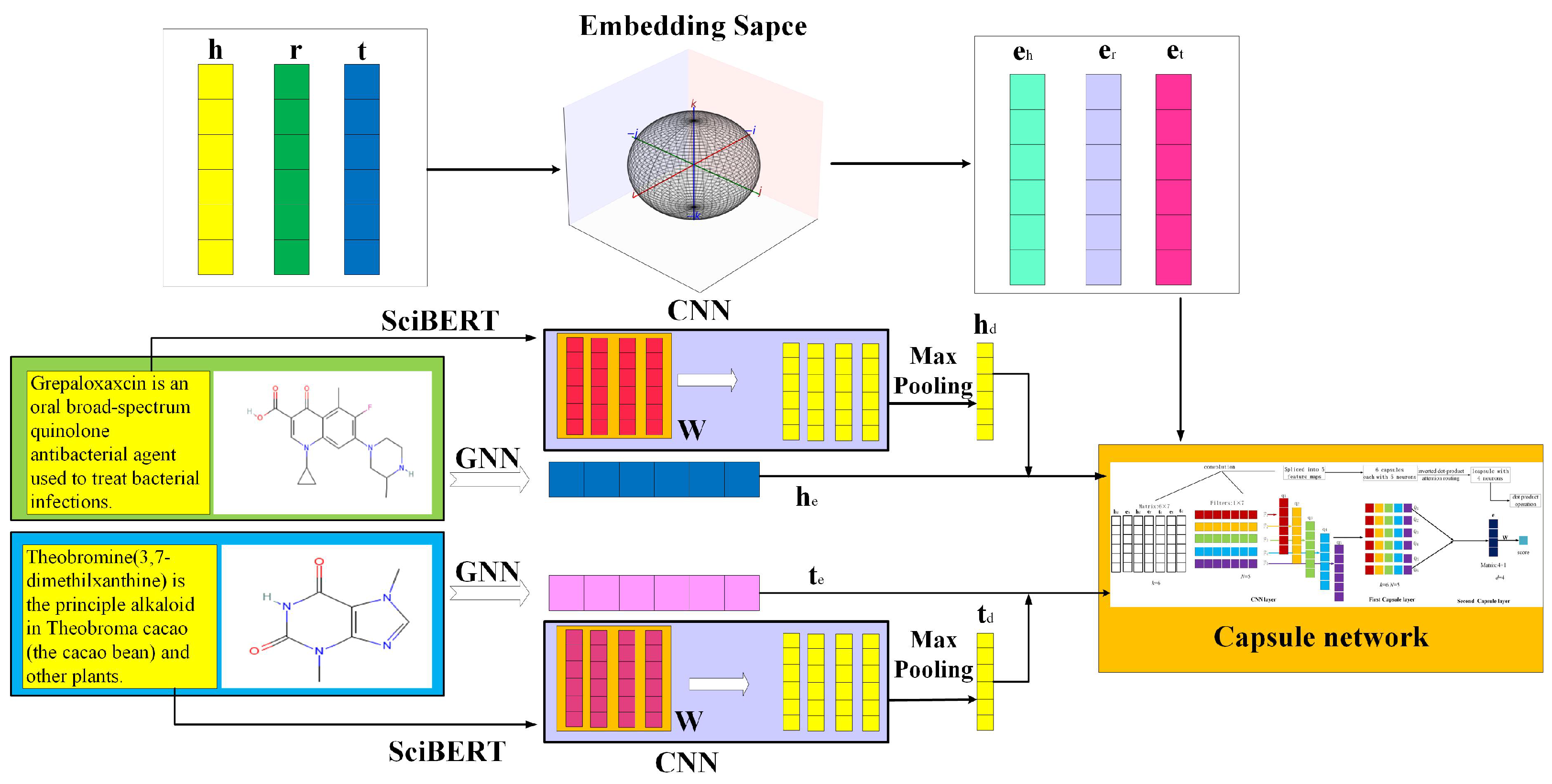
3. Model
3.1. Motivation for Four-Dimensional Embedding
3.2. Entity Embedding Layer
3.3. Molecular Structure Layer
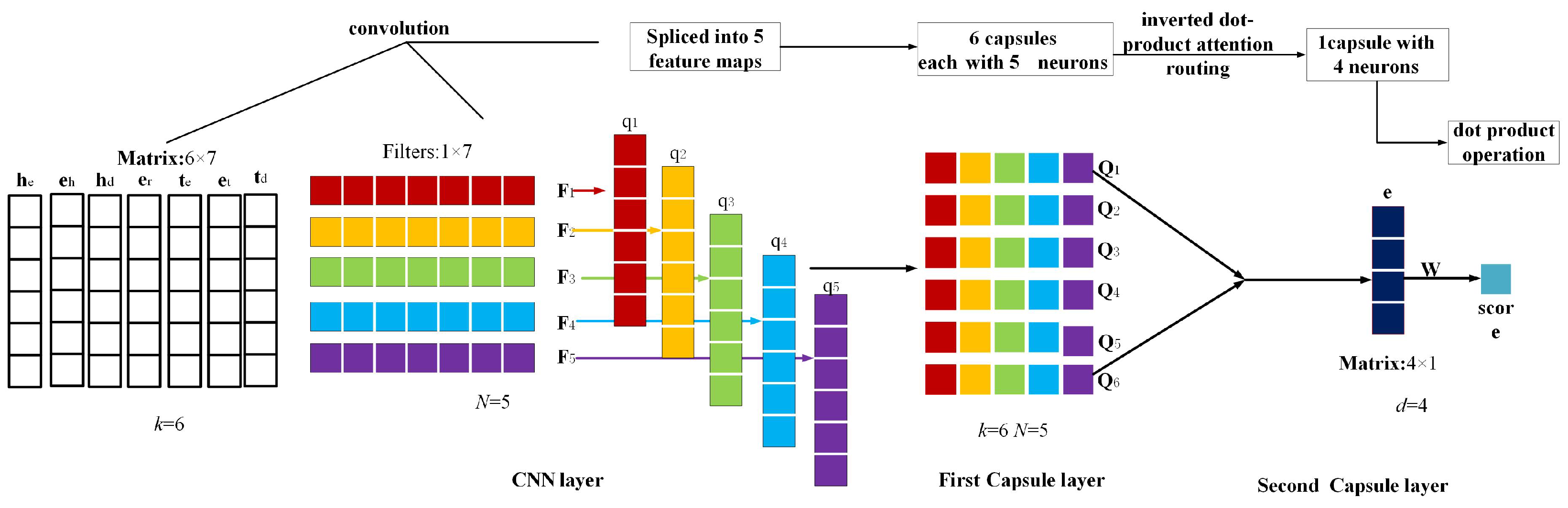
3.4. Capsule Network Layer
4. Experimental Design
4.1. Data Sets
4.2. Baselines and Metrics
- Accuracy (Acc.): Overall correctness.
- Precision (Pre.): Ability to correctly identify positive instances.
- Recall (Rec.): Ability to capture all relevant positive instances.
- F1 Score (F1): Harmonic mean of Precision and Recall.
- Area Under the ROC Curve (Auc): Measures the area under the ROC curve (TPR vs. FPR), with higher values indicating better performance.
- Area Under the Precision–Recall Curve (AUPR): Measures the area under the Precision–Recall curve, particularly useful for imbalanced datasets.
4.3. Implementation Details
4.4. Computational Cost Analysis
4.5. Experiment Results
4.6. Experimental Analysis
4.6.1. The Effect of Different Features
4.6.2. The Effect of Capsule Network
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Finkel, R.; Clark, M.A.; Cubeddu, L.X. Pharmacology; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2009. [Google Scholar]
- Chowdhury, M.F.M.; Lavelli, A. FBK-IRST: A Multi-Phase Approach to Semantic Textual Similarity. In Proceedings of the *Second Joint Conference on Lexical and Computational Semantics* (*#*SEM 2013): Volume 1: Proceedings of the Main Conference and the Shared Task: Semantic Textual Similarity, Atlanta, GA, USA, 13–14 June 2013; pp. 351–355. [Google Scholar]
- Tu, K.; Cui, P.; Wang, X.; Wang, F.; Zhu, W. Structural Deep Embedding for Hyper-Networks. In Proceedings of the AAAI, New Orleans, LA, USA, 2–7 February 2018; AAAI Press: Washington, DC, USA, 2018; pp. 426–433. [Google Scholar]
- Guan, N. Knowledge graph embedding with concepts. Knowl. Based Syst. 2019, 164, 38–44. [Google Scholar] [CrossRef]
- Jin, X.; Sun, X.; Chen, J.; Sutcliffe, R.F.E. Extracting Drug-drug Interactions from Biomedical Texts using Knowledge Graph Embeddings and Multi-focal Loss. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; ACM: New York, NY, USA, 2022; pp. 884–893. [Google Scholar]
- Sun, Z.; Deng, Z.-H.; Nie, J.-Y.; Tang, J. RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space. In Proceedings of the ICLR, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Su, X.; You, Z.-H.; Huang, D.; Wang, L.; Wong, L.; Ji, B.; Zhao, B. Biomedical Knowledge Graph Embedding with Capsule Network for Multi-Label Drug-Drug Interaction Prediction. IEEE Trans. Knowl. Data Eng. 2023, 35, 5640–5651. [Google Scholar] [CrossRef]
- Thomas, P.; Neves, M.L.; Rocktäschel, T.; Leser, U. WBI-DDI: Drug-Drug Interaction Extraction using Majority Voting. In Proceedings of the Association for Computer Linguistics NAACL-HLT, Atlanta, GA, USA, 14–15 June 2013; pp. 628–635. [Google Scholar]
- Bokharaeian, B.; Díaz, A. NIL_UCM: Extracting Drug-Drug interactions from text through combination of sequence and tree kernels. In Proceedings of the Association for Computer Linguistics 7th International Workshop on Semantic Evaluation, SemEval@NAACL-HLT, Atlanta, GA, USA, 14–15 June 2013; pp. 644–650. [Google Scholar]
- Kim, S.; Liu, H.; Yeganova, L.; Wilbur, W.J. Extracting drug-drug interactions from literature using a rich feature-based linear kernel approach. J. Biomed. Inform. 2015, 55, 23–30. [Google Scholar] [CrossRef] [PubMed]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Cao, S.; Lu, W.; Xu, Q. GraRep: Learning Graph Representations with Global Structural Information. In Proceedings of the CIKM 2015, Melbourne, VIC, Australia, 19–23 October 2015; ACM: New York, NY, USA, 2015; pp. 891–900. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. DeepWalk: Online learning of social representations. In Proceedings of the ACM KDD ’14, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 855–864. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. LINE: Large-scale Information Network Embedding. In Proceedings of the ACM WWW 2015, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Wang, D.; Cui, P.; Zhu, W. Structural Deep Network Embedding. In Proceedings of the ACM SIGKDD, San Francisco, CA, USA, 13–17 August 2016; pp. 1225–1234. [Google Scholar]
- Lee, J. BioBERT: A pre-trained biomedical language representation model for biomedical text mining. Bioinformatics 2020, 36, 1234–1240. [Google Scholar] [CrossRef] [PubMed]
- Beltagy, I. SciBERT: A Pretrained Language Model for Scientific Text. In Proceedings of the Association for Computational Linguistic EMNLP-IJCNLP, Hong Kong, China, 3–7 November 2019; pp. 3613–3618. [Google Scholar]
- Asada, M.; Miwa, M.; Sasaki, Y. Using drug descriptions and molecular structures for drug-drug interaction extraction from literature. Bioinformatics 2021, 37, 1739–1746. [Google Scholar] [CrossRef] [PubMed]
- Abdelaziz, I.; Fokoue, A.; Hassanzadeh, O.; Zhang, P.; Sadoghi, M. Large-scale structural and textual similarity-based mining of knowledge graph to predict drug-drug interactions. J. Web Semant. 2017, 44, 104–117. [Google Scholar] [CrossRef]
- Çelebi, R.; Yasar, E.; Uyar, H.; Gümüs, Ö.; Dikenelli, O.; Dumontier, M. Evaluation of knowledge graph embedding approaches for drug-drug interaction prediction using Linked Open Data. In Proceedings of the SWAT4LS 2018, Antwerp, Belgium, 3–6 December 2018; CEUR Workshop Proceedings. Volume 2275. [Google Scholar]
- Bordes, A.; Usunier, N.; García-Durán, A.; Weston, J.; Yakhnenko, O. Translating Embeddings for Modeling Multi-relational Data. In Advances in Neural Information Processing Systems 26, Proceedings of the 27th Annual Conference on Neural Information Processing Systems (NeurIPS 2013), Lake Tahoe, NV, USA, 5–8 December 2013; Burges, C.J.C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; pp. 2787–2795. [Google Scholar]
- Ji, G.; He, S.; Xu, L.; Liu, K.; Zhao, J. Knowledge Graph Embedding via Dynamic Mapping Matrix. In Proceedings of the Association for Computer Linguistics ACL, Beijing, China, 26–31 July 2015; Volume 1: Long Papers. pp. 687–696. [Google Scholar]
- Mondal, I. BERTKG-DDI: Towards Incorporating Entity-specific Knowledge Graph Information in Predicting Drug-Drug Interactions. In Proceedings of the AAAI, SDU@AAAI 2021, Virtual Event, 9 February 2021; CEUR Workshop Proceedings. Volume 2831. [Google Scholar]
- Ma, T.; Xiao, C.; Zhou, J.; Wang, F. Drug Similarity Integration Through Attentive Multi-View Graph Auto-Encoders. In Proceedings of the IJCAI, Stockholm, Sweden, 13–19 July 2018; pp. 3477–3483. [Google Scholar]
- Lin, X.; Quan, Z.; Wang, Z.-J.; Ma, T.; Zeng, X. KGNN: Knowledge Graph Neural Network for Drug-Drug Interaction Prediction. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI 2020, Virtual, 7–15 January 2021; pp. 2739–2745. [Google Scholar]
- Su, X.; Hu, P.; You, Z.-H.; Philip, S.Y.; Hu, L. Dual-Channel Learning Framework for Drug-Drug Interaction Prediction via Relation-Aware Heterogeneous Graph Transformer. In Proceedings of the 38th AAAI Conference on Artificial Intelligence, Vancouver, QC, Canada, 20–27 February 2024; Volume 38, pp. 249–256. [Google Scholar]
- Le, T.; Tran, H.; Le, B. Knowledge graph embedding with the special orthogonal group in quaternion space for link prediction. Knowl. Based Syst. 2023, 266, 110400. [Google Scholar] [CrossRef]
- Landrum, G. RDKit: Open-Source Cheminformatics Software. Available online: http://www.rdkit.org (accessed on 15 March 2025).
- Tsubaki, M.; Tomii, K.; Sese, J. Compound-protein interaction prediction with end-to-end learning of neural networks for graphs and sequences. Bioinformatics 2019, 35, 309–318. [Google Scholar] [CrossRef] [PubMed]
- Hendrycks, D.; Gimpel, K. Bridging Nonlinearities and Stochastic Regularizers with Gaussian Error Linear Units. CoRR 2016, abs/1606.08415. [Google Scholar]
- Ba, L.J.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex Embeddings for Simple Link Prediction. In Proceedings of the ICML, New York, NY, USA, 19–24 June 2016; JMLR Workshop and Conference Proceedings. Volume 48, pp. 2071–2080. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed Representations of Words and Phrases and their Compositionality. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems 2013, Lake Tahoe, NV, USA, 5–8 December 2013; Advances in Neural Information Processing Systems 26. pp. 3111–3119. [Google Scholar]
- Hu, W.; Fey, M.; Zitnik, M.; Dong, Y.; Ren, H.; Liu, B.; Catasta, M.; Leskovec, J. Open Graph Benchmark: Datasets for Machine Learning on Graphs. In Proceedings of the NeurIPS 2020, Virtual, 6–12 December 2020. [Google Scholar]
- Wishart, D.S.; Feunang, Y.D.; Guo, A.C. DrugBank 5.0: A major update to the DrugBank database for 2018. Nucleic Acids Res. 2018, 46, D1074–D1082. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Furumichi, M.; Tanabe, M.; Sato, Y.; Morishima, K. KEGG: New perspectives on genomes, pathways, diseases and drugs. Nucleic Acids Res. 2017, 45, D353–D361. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; He, X.; Cao, Y.; Liu, M.; Chua, T.-S. KGAT: Knowledge Graph Attention Network for Recommendation. In Proceedings of the ACM KDD, Anchorage, AK, USA, 4–8 August 2019; pp. 950–958. [Google Scholar]
- Schlichtkrull, M.S.; Kipf, T.N.; Bloem, P.; van den Berg, R.; Titov, I.; Welling, M. Modeling Relational Data with Graph Convolutional Networks. In Proceedings of the ESWC, Heraklion, Greece, 3–7 June 2018; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2018; Volume 10843, pp. 593–607. [Google Scholar]
- Zhang, S.; Tay, Y.; Yao, L.; Liu, Q. Quaternion knowledge graph embeddings. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Nguyen, D.Q.; Vu, T.; Nguyen, T.D. A Capsule Network-based Embedding Model for Knowledge Graph Completion and Search Personalization. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; pp. 2180–2189. [Google Scholar]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2D Knowledge Graph Embeddings. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; AAAI Press: Washington, DC, USA, 2018; pp. 1811–1818. [Google Scholar]
- Jiang, X.; Wang, Q.; Wang, B. Adaptive Convolution for Multi-Relational Learning. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; pp. 978–987. [Google Scholar]

| Datasets | #Drugs | #Interactions | #Entities | #Relations | #Triples |
|---|---|---|---|---|---|
| OGB-biokg | 10,533 | 1,195,972 | 93,773 | 51 | 5,088,434 |
| DrugBank | 3,797 | 1,236,361 | 2,116,569 | 74 | 7,740,864 |
| KEGG | 1,925 | 56,983 | 129,910 | 168 | 362,870 |
| Datasets | Methods | ACC. | Pre. | Rec. | F1 | Auc | AUPR |
|---|---|---|---|---|---|---|---|
| OGB-Biokg | Laplacian | 0.5710 ± 0.003 | 0.5296 ± 0.005 | 0.5934 ± 0.004 | 0.5597 ± 0.005 | 0.5692 ± 0.0002 | 0.5861 ± 0.0004 |
| DeepWalk | 0.5681 ± 0.004 | 0.5473 ± 0.007 | 0.5223 ± 0.006 | 0.5345 ± 0.005 | 0.5419 ± 0.0002 | 0.5325 ± 0.0003 | |
| LINE | 0.5786 ± 0.007 | 0.5534 ± 0.011 | 0.5386 ± 0.013 | 0.5459 ± 0.011 | 0.5418 ± 0.0002 | 0.5374 ± 0.0003 | |
| KGNN | 0.7389 ± 0.002 | 0.7541 ± 0.006 | 0.7245 ± 0.010 | 0.7390 ± 0.009 | 0.7849 ± 0.0008 | 0.7378 ± 0.0005 | |
| KGAT | 0.7489 ± 0.002 | 0.7559 ± 0.006 | 0.7191 ± 0.006 | 0.7370 ± 0.006 | 0.7962 ± 0.0004 | 0.8011 ± 0.0004 | |
| RGCN | 0.8467 ± 0.004 | 0.8773 ± 0.006 | 0.8063 ± 0.004 | 0.8403 ± 0.005 | 0.9172 ± 0.0006 | 0.9268 ± 0.0005 | |
| BERTKG-DDIs | 0.8326 ± 0.003 | 0.8835 ± 0.004 | 0.8243 ± 0.005 | 0.8529 ± 0.006 | 0.8967 ± 0.0004 | 0.9167 ± 0.0004 | |
| Xin.et al | 0.8627 ± 0.002 | 0.9105 ± 0.008 | 0.8467 ± 0.007 | 0.8774 ± 0.005 | 0.9276 ± 0.0004 | 0.9341 ± 0.0005 | |
| KG2ECapsule | 0.9078 ± 0.002 | 0.9219 ± 0.004 | 0.8914 ± 0.003 | 0.9064 ± 0.003 | 0.9656 ± 0.0002 | 0.9672 ± 0.0002 | |
| TIGER | 0.8791 ± 0.16 | - | - | 0.8754 ± 0.17 | 0.9477 ± 0.14 | 0.9571 ± 0.12 | |
| TransECap | 0.8507 ± 0.004 | 0.9023 ± 0.010 | 0.8357 ± 0.009 | 0.8677 ± 0.002 | 0.9091 ± 0.0010 | 0.9207 ± 0.0009 | |
| RotatECap | 0.8756 ± 0.004 | 0.9143 ± 0.011 | 0.8637 ± 0.004 | 0.8883 ± 0.004 | 0.9308 ± 0.0010 | 0.9509 ± 0.0008 | |
| QuatECap | 0.8904 ± 0.008 | 0.9198 ± 0.004 | 0.8827 ± 0.010 | 0.9009 ± 0.008 | 0.9539 ± 0.0006 | 0.9537 ± 0.0006 | |
| Rot4Cap | 0.9137 ± 0.004 | 0.9286 ± 0.003 | 0.8991 ± 0.006 | 0.9136 ± 0.004 | 0.9703 ± 0.0004 | 0.9731 ± 0.0006 | |
| DrugBank | Laplacian | 0.5923 ± 0.004 | 0.4455 ± 0.006 | 0.3372 ± 0.010 | 0.3838 ± 0.009 | 0.6724 ± 0.0002 | 0.4782 ± 0.0002 |
| DeepWalk | 0.6163 ± 0.004 | 0.6059 ± 0.003 | 0.5904 ± 0.005 | 0.5980 ± 0.008 | 0.6501 ± 0.0002 | 0.4782 ± 0.0002 | |
| LINE | 0.6374 ± 0.005 | 0.6283 ± 0.006 | 0.6189 ± 0.013 | 0.6236 ± 0.005 | 0.6926 ± 0.0002 | 0.4923 ± 0.0003 | |
| KGNN | 0.7947 ± 0.003 | 0.7959 ± 0.004 | 0.7931 ± 0.004 | 0.7945 ± 0.004 | 0.8602 ± 0.0005 | 0.8587 ± 0.0005 | |
| BERTKG-DDIs | 0.8469 ± 0.002 | 0.8524 ± 0.005 | 0.5681 ± 0.002 | 0.6817 ± 0.004 | 0.8925 ± 0.0006 | 0.8726 ± 0.0004 | |
| Xin.et al | 0.87364 ± 0.004 | 0.8672 ± 0.005 | 0.8620 ± 0.005 | 0.8646 ± 0.002 | 0.9224 ± 0.0004 | 0.9341 ± 0.0003 | |
| KG2ECapsule | 0.9078 ± 0.002 | 0.9219 ± 0.004 | 0.8914 ± 0.003 | 0.9064 ± 0.003 | 0.9656 ± 0.0002 | 0.9672 ± 0.0002 | |
| TIGER | 0.7905 ± 0.87 | - | - | 0.8033 ± 0.94 | 0.8662 ± 0.57 | 0.8370 ± 0.68 | |
| TransECap | 0.87327 ± 0.003 | 0.8704 ± 0.005 | 0.8637 ± 0.004 | 0.8670 ± 0.005 | 0.9231 ± 0.0007 | 0.9327 ± 0.0002 | |
| RotatECap | 0.8837 ± 0.002 | 0.8921 ± 0.003 | 0.8732 ± 0.007 | 0.8825 ± 0.005 | 0.9354 ± 0.0009 | 0.9453 ± 0.0007 | |
| QuatECap | 0.8894 ± 0.003 | 0.9107 ± 0.006 | 0.8743 ± 0.004 | 0.8921 ± 0.008 | 0.9509 ± 0.0007 | 0.9601 ± 0.0004 | |
| Rot4Cap | 0.9127 ± 0.005 | 0.9268 ± 0.002 | 0.8967 ± 0.006 | 0.9115 ± 0.006 | 0.9720 ± 0.0009 | 0.9739 ± 0.0012 | |
| KEGG | Laplacian | 0.5694 ± 0.010 | 0.3683 ± 0.021 | 0.3781 ± 0.016 | 0.3731 ± 0.016 | 0.5608 ± 0.010 | 0.2916 ± 0.013 |
| DeepWalk | 0.5800 ± 0.008 | 0.3801 ± 0.008 | 0.3762 ± 0.011 | 0.3781 ± 0.009 | 0.5751 ± 0.009 | 0.3005 ± 0.012 | |
| LINE | 0.5528 ± 0.006 | 0.3546 ± 0.010 | 0.3390 ± 0.016 | 0.3466 ± 0.013 | 0.5462 ± 0.013 | 0.2810 ± 0.015 | |
| KGNN | 0.7282 ± 0.008 | 0.4790 ± 0.024 | 0.4237 ± 0.013 | 0.4497 ± 0.018 | 0.8314 ± 0.009 | 0.4484 ± 0.013 | |
| KGAT | 0.7798 ± 0.008 | 0.5340 ± 0.015 | 0.4185 ± 0.015 | 0.4692 ± 0.015 | 0.8202 ± 0.010 | 0.5382 ± 0.011 | |
| RGCN | 0.8330 ± 0.005 | 0.4969 ± 0.012 | 0.4392 ± 0.018 | 0.4663 ± 0.015 | 0.8358 ± 0.006 | 0.4590 ± 0.010 | |
| BERTKG-DDIs | 0.8216 ± 0.007 | 0.5773 ± 0.008 | 0.4587 ± 0.015 | 0.5112 ± 0.007 | 0.8267 ± 0.004 | 0.4937 ± 0.009 | |
| Xin.et al | 0.8367 ± 0.006 | 0.5837 ± 0.012 | 0.4592 ± 0.017 | 0.5140 ± 0.011 | 0.8426 ± 0.015 | 0.5887 ± 0.009 | |
| KG2ECapsule | 0.8348 ± 0.003 | 0.6278 ± 0.008 | 0.4794 ± 0.011 | 0.5437 ± 0.009 | 0.8505 ± 0.004 | 0.6644 ± 0.007 | |
| TransECap | 0.8302 ± 0.003 | 0.5769 ± 0.011 | 0.4561 ± 0.011 | 0.5094 ± 0.007 | 0.8381 ± 0.007 | 0.5192 ± 0.004 | |
| RotatECap | 0.8402 ± 0.003 | 0.6014 ± 0.007 | 0.4621 ± 0.007 | 0.5226 ± 0.011 | 0.8491 ± 0.005 | 0.5891 ± 0.011 | |
| QuatECap | 0.8439 ± 0.007 | 0.6204 ± 0.005 | 0.4687 ± 0.005 | 0.5340 ± 0.004 | 0.8510 ± 0.007 | 0.6209 ± 0.004 | |
| Rot4Cap | 0.8467 ± 0.008 | 0.6408 ± 0.007 | 0.5012 ± 0.009 | 0.5625 ± 0.006 | 0.8627 ± 0.005 | 0.6821 ± 0.002 |
| Models | Scoring Function | ACC. | Pre. | Rec. | F1 | Auc | AUPR |
|---|---|---|---|---|---|---|---|
| Rot4CovE | 0.8857 | 0.8962 | 0.8734 | 0.8847 | 0.9426 | 0.9507 | |
| Rot4ConvKB | 0.8975 | 0.9037 | 0.8769 | 0.8901 | 0.9521 | 0.9567 | |
| Rot4CapsE, | 0.9034 | 0.9089 | 0.8825 | 0.8955 | 0.9537 | 0.9628 | |
| Rot4Cap | 0.9127 | 0.9268 | 0.8967 | 0.9115 | 0.9720 | 0.9739 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Li, X.; Liu, Y.; Bi, P.; Hu, T. Biomedical Knowledge Graph Embedding with Hierarchical Capsule Network and Rotational Symmetry for Drug-Drug Interaction Prediction. Symmetry 2025, 17, 1793. https://doi.org/10.3390/sym17111793
Zhang S, Li X, Liu Y, Bi P, Hu T. Biomedical Knowledge Graph Embedding with Hierarchical Capsule Network and Rotational Symmetry for Drug-Drug Interaction Prediction. Symmetry. 2025; 17(11):1793. https://doi.org/10.3390/sym17111793
Chicago/Turabian StyleZhang, Sensen, Xia Li, Yang Liu, Peng Bi, and Tiangui Hu. 2025. "Biomedical Knowledge Graph Embedding with Hierarchical Capsule Network and Rotational Symmetry for Drug-Drug Interaction Prediction" Symmetry 17, no. 11: 1793. https://doi.org/10.3390/sym17111793
APA StyleZhang, S., Li, X., Liu, Y., Bi, P., & Hu, T. (2025). Biomedical Knowledge Graph Embedding with Hierarchical Capsule Network and Rotational Symmetry for Drug-Drug Interaction Prediction. Symmetry, 17(11), 1793. https://doi.org/10.3390/sym17111793






