High-Precision Digital Time-Interval Measurement in Dual-Comb Systems via Adaptive Signal Processing and Centroid Localization

Abstract

Time and frequency standards constitute fundamental requirements for diverse applications spanning daily life technologies to advanced scientific research. Among precision time dissemination methods, microwave-clock-based dual comb time transfer has emerged as a promising approach that achieves ultra-precise time interval measurements through linear optical sampling. However, conventional peak detection methodologies employed in such systems exhibit critical limitations: vulnerability to amplitude noise interference and inherent accuracy constraints imposed by analog sampling rates. To address these challenges, we present a novel digital time differential measurement paradigm integrating three key algorithmic innovations: (1) adaptive signal detection and extraction protocols, (2) multi-stage noise suppression processing, and (3) optimized centroid determination techniques. This comprehensive digital processing framework significantly enhances both measurement stability and operational efficiency, demonstrating single-shot temporal resolution at 17.6 fs stability levels. Our method establishes new capabilities for high-precision time-frequency transfer applications requiring robust noise immunity and enhanced sampling dynamics.

1. Introduction

Time is a crucial physical quantity closely related to human society, and it is currently the most accurate and stable physical quantity. Time and frequency standard provide fundamental support for many important applications, such as metrology and calibration, precision timing, modern communication [1,2,3,4], ranging and positioning [5,6,7,8]. High-precision time reference is generated by atomic clocks [9]. However, the cost and complexity of atomic clocks limit their deployment in specific laboratories. Therefore, there is a need to develop high-precision time transfer over long distances.

The emergence of optical frequency combs (OFC) with high precision, high resolution, and wide spectrum has introduced a new method for time transfer known as dual comb time transfer [10,11,12,13,14,15,16]. This method uses dual comb linear optical sampling (LOS) for time-interval measurement. This technology breaks through the limitations of imprecise time-interval measurement in traditional electrical methods [17,18,19,20,21,22,23], and has ultra-high time interval measurement precision, which brings ultra-high time transfer stability to the dual comb time transfer. The current free-space-based dual comb time transfer scheme has achieved a time deviation of less than 1 fs at averaging times between 1 s and 1 h [16], while the fiber based dual comb time transfer scheme has achieved a 6.23-fs residual time deviation between synchronized timescales at 1 s [24].

In the dual comb time transfer of microwave clocks, the time interval measurement technique based on LOS amplifies the time interval information and converts it into the time interval between two interference pulses. The current methods utilize the time interval between the peak values of these two interference pulses in the time domain to calculate the time interval information. However, this approach is susceptible to amplitude noise interference, and its precision is limited by the sampling rate during analog-to-digital conversion. In addition, the time interval information can also be calculated using the phase difference in the frequency domain. The calculation accuracy of this approach is extremely high, but more processing steps are required. Furthermore, the duty cycle of the dual comb interference pulse signal is extremely low in the time domain. When the repetition frequency of the optical comb in LOS is 100 MHz and the repetition frequency difference is 1 kHz, only 0.6% of the double comb interference pulse signal in one cycle is effective, while 99.4% consists of invalid electrical noise signals. The processing of these invalid electrical noise signals results in a waste of computing resources and an accumulation of noise.

In this article, we propose a time difference digital measurement method to address the limitations of peak localization methods, which is achieved by processing digital signals using an efficient post-processing algorithm. Specifically, we have designed an effective signal detection and extraction algorithm to extract the effective parts of the dual comb interference pulse signal, a noise smoothing algorithm to reduce the impact of amplitude noise, and an efficient centroid algorithm to reduce dependence on the sampling rate and improve measurement accuracy. This method uses the envelope centroid of the effective part to locate the time information of the interference pulse. The time interval of the envelope centroid in the time domain is the time difference that needs to be measured. Experimental results show that this method significantly improves the stability and measurement speed of time interval measurement, achieving a stability of 17.6 fs.

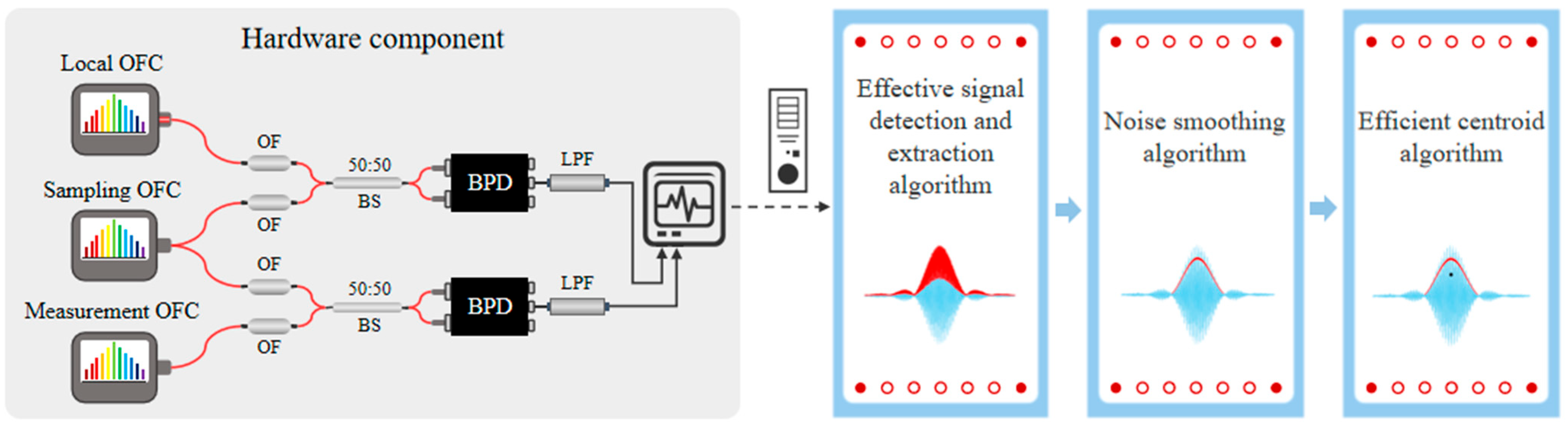
2. Materials and Methods

The system of time difference digital measurement method is shown in Figure 1. This system aims to measure the time difference between the local OFC signal and the measurement OFC signal (with a repetition rate of 100 MHz). To amplify the time information and improve measurement accuracy, we introduce a sampling OFC signal with a repetition rate difference of 1 kHz to perform LOS on these two OFC signals. In the hardware part, the three comb signals interfere in a 2*2 50:50 optical beam splitter (BS, Thorlabs, Newton, NJ, USA) after passing through an optical filter, forming a dual comb interference pulse signal. The balanced photodetectors (BPDs, Thorlabs, Newton, NJ, USA) performs balanced detection on it and converts it into a dual comb interference pulse digital signal by an oscilloscope (Keysight Technologies, Santa Rosa, CA, USA) (400 MSa/s sampling rate, 400 kpts sampling depth). In the software section, the digital dual comb interference pulse signal is subjected to effective signal detection and extraction algorithms, noise smoothing algorithms, and efficient centroid algorithms. Their functions are:

• Effective signal detection and extraction algorithm: The effective signal detection and extraction algorithm searches for the peak position of the signal as the starting point, takes the full width at half maximum (FWHM) of the main pulse of the dual comb interference pulse signal as the extraction unit to discard the ineffective energy that does not contribute to the time estimation results during the entire acquisition process, allowing for the extraction of the effective signal necessary for accurate time estimation;
• Noise smoothing algorithm: The noise smoothing algorithm uses sliding average filtering on the envelope of the effective signal to reduce the impact of amplitude noise on the signal envelope waveform. Additionally, it utilizes feature points of the envelope signal that are less sensitive to noise, thereby minimizing the additional impact of amplitude noise on the centroid position;
• Efficient centroid algorithm: The efficient centroid algorithm calculates the centroid of the effective signal envelope to locate the time information in the dual comb interference pulse signal, and obtains the time difference necessary for dual comb time synchronization by calculating the time interval between the centroids of the two interference pulses in the time domain.

2.1. Effective Signal Detection and Extraction Algorithm

The duty cycle of the dual comb interference pulse signal is very small, attributed to the characteristics of dual comb LOS. In LOS, the electronic noise from the BPDs will overwhelm 99.4% of the interference pulse signal. As a result, the effective part of the dual comb interference pulse signal will be very small, mainly of the main peak and four signal sidelobes distributed on either side. Processing invalid noise data can lead to a waste of computing resources, slow down measurement speed, and even limit the stability of time interval measurements. Measurement speed is the key in time difference digital measurement methods, as it directly impacts the real-time performance of the measurements.

To solve this problem, we designed an effective signal detection and extraction algorithm designed to automatically identify effective signals above electronic detection noise. This algorithm is divided into two main components: effective signal detection and effective signal extraction. The effective signal detection component includes signal acquisition, single-cycle signal extraction, signal maximum value search, energy peak time discrimination, and period correction. To correctly detect each pulse carrying time information in the dual comb interference pulse signal, the detection algorithm first intercepts a signal with a period of data volume. Then, the recognition algorithm detects the position of the effective signal through the maximum value of the signal. In addition, to prevent unexpected situations in the pulse position from affecting the effective signal extraction, the detection algorithm distinguishes the position of the pulse (Figure 2) and automatically corrects it.

The effective signal extraction part consists of full width at half maximum estimation, effective signal range coverage, and Hilbert transform. The data volume of the effective signal will change with the sampling rate, so we select the FWHM of the main peak of the signal as the unit for signal extraction. Once the effective signal is detected, the extraction algorithm extracts the effective part of the dual comb interference pulse signal based on the time position corresponding to the peak and the time range that corresponds to the multiple of the FWHM, defining the effective signal range. Finally, the extraction algorithm obtains the envelope of the effective signal through Hilbert transform and sends it to the noise smoothing algorithm for further processing.

The processing results of the effective signal detection and extraction algorithms are shown in Figure 3c. The effective signal recognition and extraction algorithm successfully extracts the effective signal and its envelope from each pulse of the dual comb interference pulse signal, utilizing only 0.6% of the total data volume for the entire cycle. This algorithm not only eliminates the influence of ineffective electrical noise on the estimation results, but also significantly reduces the waste of computing resources, making it serves as a processing method that effectively balances improved measurement stability with processing speed.

2.2. Noise Smoothing Algorithm

The amplitude noise is one of the main noises that affect the stability of the time difference digital measurement method. This type of noise can cause signal distortion and fluctuations in the envelope signal. In addition, amplitude noise causes a shift in the extraction of effective signals in effective signal recognition and extraction algorithms by affecting the position of the maximum value of the pulse signal. All of these factors can impact the efficient centroid algorithm’s localization of time information in pulses, ultimately resulting in decreased stability of the time difference digital measurement method.

To filter the amplitude noise in the interference pulse signal of the dual comb, we designed a noise smoothing algorithm, as shown in Figure 3d. The noise smoothing algorithm consists of two main components: sliding average and offset correction. The sliding average reduces the impact of amplitude noise on the envelope signal waveform by replacing the current data point with the average value of data collected over a specified time period. Offset correction is further divided into three parts: envelope maximum value search, envelope full width at half maximum estimation, and envelope correction truncation. This correction process addresses the offset introduced by amplitude noise in the extraction algorithm by utilizing envelope signal feature points that are less sensitive to noise. Specifically, the algorithm uses the peak position of the envelope signal as the starting point for the entire process and uses the full width at half maximum of the envelope signal as the extraction unit to re-extract the signal from the envelope signal, in order to correct the offset caused by amplitude noise.

The processing results of the noise smoothing algorithm are shown in Figure 3e. After processing, the signal envelope waveform becomes smooth, indicating that the sliding average used in the noise smoothing algorithm effectively suppresses the influence of amplitude noise on the envelope waveform. While the filtering effect of offset correction is not directly observable in the envelope waveform, it is evident in the fluctuation range of the center of gravity position.

The phase noise is also a non-negligible noise in signals, which can affect the algorithm’s recognition of the maximum value position of pulse signals. However, phase noise is mainly affects on the carrier of the signal and has a relatively small impact on the envelope. In addition, the offset correction filtering effect of the noise smoothing algorithm can effectively reduce the impact of phase noise on the centroid position.

2.3. Efficient Centroid Algorithm

We have designed an efficient centroid positioning algorithm to reduce the dependence of time difference digital measurement methods on the sampling rate of digital acquisition devices, enabling them to achieve extremely high measurement accuracy, even at low sampling rates, as shown in Figure 3f. The efficient centroid algorithm consists of envelope centroid calculation and time difference calculation. The calculation of the envelope centroid is achieved through a discretized centroid calculation formula:

$$t_g={\displaystyle \frac{\sum _0^{N}tE\left(t\right)dt}{\sum _0^{N}E\left(t\right)dt}}.$$

(1)

In the Equation (1), $E\left(t\right)$ is the envelope of the effective signal, and $t_g$ is the time position of the envelope centroid. The center of gravity is obtained by weighted averaging the envelope signal, and its function is to locate the time information of the pulse signal. Consequently, the time difference between the interference pulse signals of two columns of the dual comb can be expressed as the time interval between the centroids of the two corresponding pulse envelopes. The time difference calculation can be expressed as:

$$\tau ={\displaystyle \frac{D_{\mathrm{g}}}{\alpha ·\mathrm{S}\mathrm{a}}}={\displaystyle \frac{\left|t_{g1}-t_{g2}\right|}{\mathrm{S}\mathrm{a}}}·{\displaystyle \frac{{∆f}_r}{f_r}}.$$

(2)

In the Equation (2), $\mathrm{S}\mathrm{a}$ is the sampling rate, $\alpha$ is the scaling factor, which is 10⁵ in this article. The efficient centroid algorithm replaces the signal peak with the centroid of the effective envelope, which has higher positioning accuracy for pulse timing information. In addition, in terms of implementation methods, the efficient centroid algorithm integrates and smooths the energy concentration area, which also reduce the impact of amplitude noise jitter on the time calculation results. The implementation process of the algorithm is shown in Appendix A.

3. Results

To investigate the precision improvement brought by the use of centroid positioning pulse time information method, we simulated the dual comb interference pulse signal using numerical simulation method. In the simulation, we set the repetition rate of the optical frequency comb to 100 MHz, the repetition frequency difference to 1 kHz, and the sampling rate to 400 MSa/s, which are the same parameters as in the experiment. We change the time position of the dual comb interference pulse signal in the time domain in the simulation, so that it moves to the right (in the positive direction of the time axis) at a speed of 10 attoseconds (as) per measurement times. The measurement results of traditional peak positioning method and center of gravity positioning method are shown in the following Figure 4a. The accuracy of traditional peak localization methods is limited by the sampling rate, with a measurement accuracy of 25 fs at a sampling rate of 400 MSa/s. When the change in time is less than 25 fs, traditional peak positioning methods cannot accurately measure, resulting in the situation shown in the yellow curve in the Figure 4a. The weighted average method enables the centroid positioning method to have a measurement accuracy of 10 as or even higher at a sampling rate of 400 MSa/s, as shown in the red curve in the Figure 4a. The ultra-high measurement accuracy enables the time difference digital measurement method to meet the requirements for measuring time jitter in microwave clock dual comb time transmission.

The amplitude noise on the signal can cause positioning jitter, thereby affecting the stability of time interval measurement in time difference digital measurement methods. To investigate in detail the filtering effect of efficient centroid algorithm and noise smoothing algorithm on amplitude noise, we added Gaussian white noise to the dual comb interference pulse simulated signal to simulate the influence of amplitude noise. The power of Gaussian white noise is set to 0.003 W, which is close to the normal amplitude noise level in the laboratory, while other simulation parameters remain unchanged. The time jitter of peak positioning, center of gravity positioning, and center of gravity positioning after noise smoothing is shown in Figure 4b. Among these three sets of measurement data, the centroid positioning method after noise smoothing algorithm has the smallest time jitter. We use standard deviation to evaluate the jitter of three sets of data. The standard deviation of peak positioning measurement results is 860.34 fs, and the standard deviation of center of gravity positioning measurement results is 342.43 fs. After noise smoothing algorithm, the standard deviation of measurement results is reduced to 137.8 fs. Therefore, this time difference digital measurement method has high anti-interference ability against amplitude noise.

In sliding average processing, the size of the window is set to a multiple of its full width at half maximum. The size of the sliding average window affects the filtering quality of sliding average and offset correction. We tested the time jitter of the center of gravity under different sliding average window sizes, as shown in the Figure 5a. As the sliding average window size increases, the filtering effect of sliding average processing increases relatively slowly (gray curve in the Figure 5a), while the filtering effect of offset correction processing increases rapidly (red curve in the Figure 5a). For the noise smoothing algorithm, when the sliding average window size increases from 0.1 times FWHM to 0.4 times FWHM, the time jitter of the center of gravity decreases from 198.81 fs to 93.03 fs, with a faster descent speed. When the sliding average window size increases from 0.4 times FWHM to 0.65 times FWHM, the time jitter of the center of gravity decreases from 93.03 fs to 83.48 fs, and the descent speed is slow (blue curve in the Figure 5a). The increase in sliding average window size brings better amplitude noise filtering effect. Meanwhile, increasing the sliding average window will increase the algorithm processing time. Therefore, we need to balance these two.

In the microwave clock dual comb time transfer system, in addition to amplitude noise, there are other noises that can affect the stability of time interval measurements. We used the experimental structure shown in the Figure 1 to collect 100 sets of time interval data at a sampling rate of 400 MSa/s, and the sampling time for each set of data is 1 s. Time Deviation (TDEV) is a commonly used indicator in time transfer to evaluate time jitter. Therefore, we evaluated the measurement data using TDEV, as shown in Figure 5b. In addition, we use TDEV@1s Evaluate the stability of the time difference digital measurement method. The blue curve is the TDEV curve of the data without the noise smoothing algorithm, with a stability of 97.5 fs. After adding the noise smoothing algorithm, the short-term stability (TDEV) of the time interval data was effectively reduced, achieving a stability of 17.6 fs. The drift of time interval measurement data resulted in an increase at the back end of the curve.

4. Discussion

The time difference digital measurement method is a new way to improve measurement performance through digital processing algorithms. Digital signal processing has the characteristics of convenience, flexibility, programmability, and ease of integration, which greatly reduces the hardware requirements in the time difference measurement of microwave clock dual comb time transfer. In addition, the time difference digital measurement method can also be used in many cutting-edge applications that require time interval measurement, such as optical clock dual comb time transfer and dual comb distance measurement. We believe this will open up new pathway for the application of dual comb. In the next step of our work, we will further discuss the impact of relevant noise and detector noise in the system on the algorithm. Furthermore, we may incorporate Variational Mode Decomposition (VMD) algorithm into the program to process signals and enhance the program’s ability to detect effective signals through machine learning.

5. Conclusions

In this study, we implemented a time difference digital measurement method with high stability and anti-interference performance for microwave clock dual comb time transfer. This method uses algorithms to digitize signals, improving measurement accuracy and speed, and filtering out amplitude noise. Meanwhile, we also demonstrated the significant improvement of this method in terms of time interval measurement accuracy and resistance to amplitude noise interference when compared to traditional methods. In the experiment, we achieved a time measurement stability of 17.6 fs in a one-shot measurement.