Abstract
This work investigates the stability analysis of linear control systems defined on Lie groups, with a particular focus on low-dimensional cases. Unlike their Euclidean counterparts, such systems evolve on manifolds with non-Euclidean geometry, where trajectories respect the group’s intrinsic symmetries. Stability notions, such as inner asymptotic, inner, and input–output (BIBO) stability, are studied. The qualitative behavior of solutions is shown to depend critically on the spectral decomposition of derivations associated with the drift, and on the algebraic structure of the underlying Lie algebra. We study two classes of examples in detail: Abelian and solvable two-dimensional Lie groups, and the three-dimensional nilpotent Heisenberg group. These settings, while mathematically tractable, retain essential features of non-commutativity, geometric non-linearity, and sub-Riemannian geometry, making them canonical models in control theory. The results highlight the interplay between algebraic properties, invariant submanifolds, and trajectory behavior, offering insights applicable to robotic motion planning, quantum control, and signal processing.
1. Introduction
The stability analysis of dynamical control systems defined on Lie groups, particularly linear control systems, is a cornerstone for understanding their long-term behavior under a wide range of inputs and perturbations. These systems evolve according to flows generated by vector fields that are compatible with the underlying group operations, ensuring that the dynamics preserve the intrinsic symmetry of the Lie group. As a consequence, their stability properties are deeply intertwined with the geometric and algebraic structure of the group, including its topology, curvature, and the properties of its Lie algebra.
In the classical setting of linear control systems on the Euclidean space , stability is typically investigated through the spectral analysis of system matrices, through asymptotically inner stable (AIS), inner stable (IS) and BIBO (bounded input bounded output) stability, which also consider an output map, Lyapunov methods, and the qualitative study of solution trajectories. It is possible to prove that stability depends on the controllability and observability properties of the system. Extending these ideas to the more general framework of Lie groups requires additional tools: one must account for the non-Euclidean geometry of the state space, the invariance of trajectories under group translations, and the role of the exponential map linking the Lie algebra to the group manifold. For linear control systems on Lie groups, these properties are well understood [1,2,3,4,5,6].
In this work, we are particularly interested in low-dimensional Lie groups, focusing on the Abelian group including the plane, the cylinder, and the torus, as well as on the solvable case of the second dimension and on the three-dimensional Heisenberg group. These examples are not only mathematically tractable but also serve as canonical models in control theory: two-dimensional solvable Lie groups capture essential features of systems with non-trivial but relatively simple algebraic structures, while the Heisenberg group provides a fundamental non-commutative example with deep connections to sub-Riemannian geometry [7], quantum mechanics [8], and non-linear control [9,10]. Studying stability in these settings allows us to highlight the interplay between the algebraic properties of the group and the qualitative behavior of the associated control systems (see [5,6,11]).
Furthermore, these groups constitute ideal testbeds for future work on the stability analysis regarding arbitrary Lie group structures and dimensions. Their relatively low dimension enables explicit computations and the visualization of trajectories, while their rich algebraic structure preserves the essential challenges of non-commutativity and geometric non-linearity found in higher-dimensional cases. The solvable two-dimensional groups provide a natural bridge between Abelian systems and more complex non-Abelian dynamics, allowing for a clear examination of how non-trivial Lie brackets influence stability. On the other hand, the Heisenberg group, as the simplest example of a nilpotent non-Abelian Lie group, serves as a prototype for understanding drift phenomena, controllability constraints, and the robustness of stability under perturbations in settings where classical Euclidean tools no longer apply [5,12].
For instance, consider the two-dimensional solvable Lie group with the product
and Lie algebra , determined by
Similarly, let the simply connected nilpotent Heisenberg Lie group, with
and Lie algebra , with Lie brackets computed as follows:
Here, is the canonical non-degenerate alternating form on .
A linear control system on these groups depends on the properties of the drift, a linear vector field whose flow is a 1-parameter group of G-automorphisms associated with a derivation of . The control vectors are elements of , considered as right-invariant vector fields. The spectral characteristics of this derivation, along with their influence on the flow trajectories, determine whether solutions tend toward stable submanifolds or diverge over time. The stability properties are fundamentally affected by the non-Abelian, solvable, and nilpotent Lie algebra structure. Analyzing their trajectories involves geometric control methods that consider invariant submanifolds and the stratified structure of the Lie algebra, which in turn determines whether solutions remain confined, approach particular orbits, or diverge [7].
This geometric perspective allows us to assess whether trajectories are attracted to equilibrium points or invariant sets or whether they tend to diverge.
Overall, analyzing linear control systems on Lie groups through their algebraic and geometric structures provides a profound understanding of stability phenomena that naturally arise in areas such as robotic motion planning, quantum control, and signal processing, where Lie group symmetries are fundamental.
Finally, this work presents a control framework for robotic navigation modeled on the Heisenberg Lie group, capturing both positional and internal orientation dynamics. The model integrates environmental influences, actuation inputs, and intrinsic drift effects, providing a geometric perspective on robot motion in a 3D environment. We analyze stability properties—such as asymptotic and bounded-input bounded-output (BIBO) stability—via a spectral analysis of the underlying system matrices and the associated Lie group structure. Additionally, the role of output projections, representing measurable quantities like position or heading, is examined to establish practical conditions ensuring bounded and stable robot behavior under bounded control efforts. The approach highlights how Lie group geometry and algebraic properties directly influence the system’s stability and provides insights applicable to robotic path planning, sensor fusion, and stabilization tasks.
2. Linear Control Systems on Euclidean Spaces
Let be a real matrix of order two, , and . The classical linear control system on the plane is given by the family of ordinary differential equations
parameterized by the class of locally integrable bounded functions , with output map
where is the system solution with control u in , , given by
Definition 1.
The linear control system on is said to be
- 1.
- AIS if , with ,
- 2.
- IS if with ,
- 3.
- The system is BIBO stable if with and thus the solution through the outmapis bounded.
Remark 1.
The algebraic and geometric multiplicity of λ is denoted by , respectively. It is well known [11,13] that
- 1.
- The system is if and only if .
- 2.
- The system is if and only if , and if with then
Although BIBO stability depends on the controls, the spectrum of A still plays a crucial role in determining BIBO stability. Next, we introduce the transition rational function through the quotient
of the polynomials. D and N are monic and coprime polynomials satisfying . Therefore, the system is BIBO stable if and only if the roots of the denominator D, which are also roots of A, have negative real parts [11].
Recall that is controllable if is observable if and only if and are co-prime.
3. Linear Control Systems on Lie Groups
Let G be a connected Lie group with Lie algebra . A linear vector field on G is determined by its flow [1], a 1-parameter group of , and the Lie group of the G-automorphism, as follows:
Similarly, the automorphism group of is the set
Exactly as in the Euclidean case, for any real t, belongs to .
A vector field Y on G is said to be right-invariant [14,15] if, for any ,
By replacing h by the identity element e, any fixed vector determines, through the derivative of the right g-translation , a vector at the tangent space of G at . In particular, generalizes the column vectors b in the classical linear control system.
Definition 2.
A linear control system on the Lie group G is determined by
a family of ODEs parametrized by the admissible control
, as in the classical case [1].
Recall that a derivation on a Lie algebra is a linear map which satisfies the Leibniz rule,
From the Jacobi identity, we can associate a derivation to each , which is determined by
The relationship between and is given through Observe that is a one-parameter subgroup of and . Additionally, the commutative diagram determines a formula allowing the computation of the flow, as follows:
W.l.o.g. assume the Lie algebra rank condition LARC [16] for . Precisely, for any ,
For the classical LCS, LARC is equivalent to the Kalman rank condition [17],
Actually, the brackets are , , and so on. The Cayley–Hamilton Theorem stops the process at the step.
The integral curve of is denoted by with control u and initial condition g at time t. To compute this solution, it is enough to translate the solution starting at the identity element e by the flow of the drift on g, at any time t [1]. In fact, we have the formula
Exactly as in the classical case, .
Next, we introduce the appropriate stability notions on Lie groups. As in the Euclidean space, the BIBO stability of an LCS is considered with respect to an output map h, a homomorphism , where H is a Lie group. We denote this system by .
Definition 3.
Let us consider an LCS on the connected Lie group G.
- 1.
- is AIS if , ; then,
- 2.
- is IS if , ; then, is bounded.
- 3.
- is said to be BIBO stable if the set
Similarly to the Euclidean case, BIBO stability is expected to depend on h and on the spectrum of . The kernel of the output map h is identified as a closed (normal) subgroup of the group G. Rather than focusing directly on the map h, we find it more insightful to analyze the situation by investigating the closed subgroups of G and examining the projection of the original system onto the corresponding homogeneous space. This approach provides a broader perspective that can reveal deeper structural insights into the dynamics of the system.
Let be a homomorphism. By the isomorphism theorem, we know that
Given a control , the image of the orbit under a homomorphism h is bounded if and only if the canonical projection of this orbit onto the quotient space is bounded. Conversely, for a normal subgroup N of a Lie group G, there exists a homomorphism such that . Therefore, BIBO stability is equivalent to studying the stability of the projections of system trajectories onto homogeneous spaces of the Lie group.
By transitioning to this new framework, we can better establish the conditions required for ensuring stability in the original system. Specifically, each right-invariant vector field within this context can be effectively projected onto any quotient space, facilitating the analysis of the system’s behavior in a reduced setting. However, for the Linear vector field, its associated derivation must preserve the Lie algebra of the subgroup during this projection. This preservation is crucial as it ensures the invariance of the algebraic structures throughout the projection process, thereby maintaining the integrity of the system’s dynamics.
Furthermore, it is important to note that when the system is unable to be projected onto a suitable quotient space, the task of guaranteeing bounded-input bounded-output (BIBO) stability becomes significantly more complex. In such cases, the interactions within the system may exhibit behavior that is less tractable, making it imperative to explore alternative methods or frameworks to assess stability. Thus, understanding the intricacies of the subgroup structure and the implications of projection is vital for deriving meaningful conclusions regarding the original system’s stability.
In the sequel, we analyze the different classes of stability on the Abelian and solvable group of dimension two. The last chapter contains a complete analysis of the stability on a simply connected Heisenberg Lie group of dimension three.
4. Stability on the Abelian Group of Dimension Two
- If G is Abelian and simply connected, then and the stability is already characterized any LCS reads as follows:Therefore, the results are well known (see Remark 1, [11,13]).
- If G is Abelian but not simply connected, from the general theory it follows that with is a discrete subgroup. We know that up to the isomorphism,Thus, the possible quotient groups G areWe know that .
- (a)
- The case . Let us consider an invertible general matrixSinceThus, we obtain
- (b)
- The case ; as before, consider an arbitrary invertible matrix,Since , we haveMoreover, .
Stability on
If , we get . From that, we can compute the derivation associated with any linear vector field on G,
Thus, . A linear vector field on G is given by , and any right-invariant vector fields reads .
Any arbitrary linear control system on reads as follows:
It turns out that the flow of the drift is given by
Since the first component is fixed, . So, the system is not AIS.
On the other hand, the first component is bounded; thus, the system is IS if and only if if and only if is bounded if and only if .
In Figure 1, the behavior of the drift flow given by (2) for and some initial conditions is shown. It is observed that the orbits converge to the circle lying on the plane, indicating that the system is IS but not AIS.
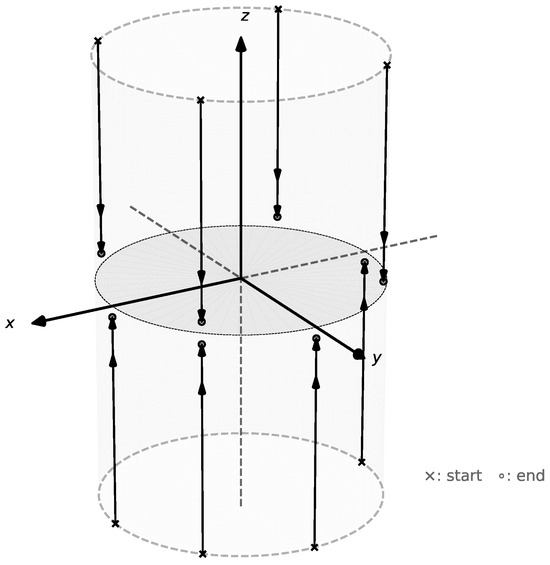
Figure 1.
Geometric description of the behavior of the flow of the drift (2), with .
Let be a homomorphism. By the isomorphism theorem, we know that
So, given a control , the image of h of the orbit is bounded if and only if the canonical projection of this orbit to the quotient
Up to the automorphism, the normal subgroups of of are
with being discrete and of dimension 0, and . The homogeneous spaces are
- (a)
- (b)
- (c)
The cases (a) and (b) with and (c) with are BIBO stable, since the corresponding manifolds of the state space are compact. For the remaining cases, the second component of the projection preserves the second component. Moreover, the first component is projected onto a compact set. Therefore, the BIBO stability depends on the analysis of the second component. The solution of (1) is given by the following flow:
Then, if , the component y is bounded if and only if .
In Figure 2, we observe the geometric behavior of the flow associated with the LCS (1) to visually analyze the BIBO stability of the system. Consider and different initial conditions. When the control is applied, the trajectories converge to the circle located at height (the upper circle). Conversely, when , the trajectories converge to the circle located at (the lower circle). This behavior illustrates the characteristic property of BIBO stability.
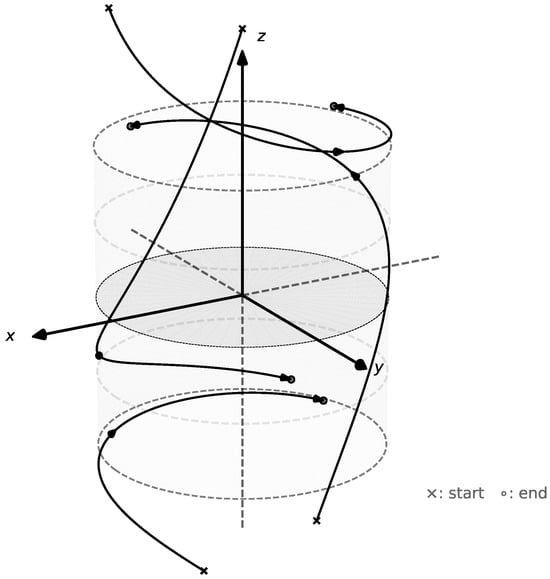
Figure 2.
Geometric description of the flow behavior (3), with .
Stability on
Here, and
Any linear vector field on G is trivial. An LCS turns and invariant control system without drift. Assume ; therefore,
Depending on the coefficients and , the dynamics contain rational and irrational flows. Moreover, the system is never AIS. Since is compact, the system is inner and BIBO stable.
5. Stability on the Solvable Group of Dimension Two
Let us consider the Lie group with the product
and Lie algebra , with the bracket
Any derivation is given by
A linear vector field is
The 1-parameter group of G-automorphism determining the flow is given by
A right-invariant vector field has the face
Then, an arbitrary linear control system on G is given by
5.1. Asymptotic Inner Stable
The system cannot be asymptotic inner-stable. The first component is fixed by the flow.
5.2. Inner Stable
On the other hand, is bounded if and only if the second component is bounded:
- (i)
- .
- (ii)
- , which is never IS.
5.3. BIBO Stability
In analogy with the Abelian case, our interest lies in examining the projections of the system’s solutions onto the quotient spaces. Just observe that
therefore, there are no discrete subgroups other than the trivial one, .
For 1-dimensional subgroups, we have , which is the only ideal if , up to isomorphisms.
In Figure 3, we can observe the behavior of some orbits of the drift flow (4), where it is evident that all the flows are bounded and each orbit converges vertically to a point on the curve . Therefore, the system is IS.
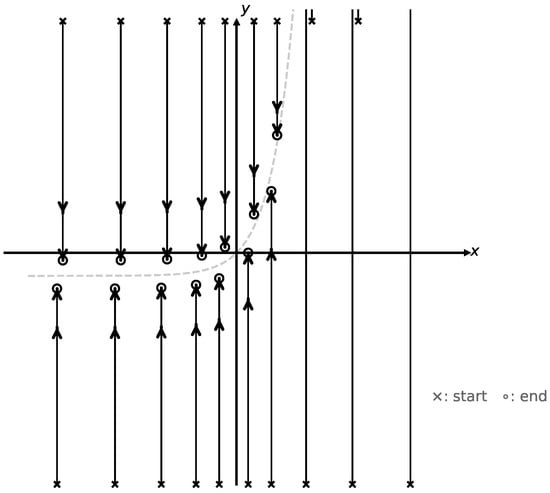
Figure 3.
Geometric description of the flow behavior (4), case .
Consequently, the only normal subgroups of G are precisely of the form , with being discrete. In particular, we obtain
with
Since the first component , we obtain . Thus, the system is BIBO stable, if and only if
6. Stability on the Heisenberg Group of Dimension Three
Let with
the Heisenberg Lie group, with Lie algebra , where
where is the non-degenerate alternating form on . The exponential map
reduces to the identity . From the special structure of the Lie algebra, it turns out that
The right-invariant vector fields are
If , a linear control system on the Heisenberg Lie group is given by
satisfy if if and only if .
6.1. Inner Stability
The flow of is
where , for any .
Thus, , , if and only if
We should have ; then, there exists and such that
Therefore, is AIS . In fact,
On the other hand, the set is bounded if and only if
are bounded. If and only if , A is not nilpotent and P and Q are bounded.
Since is the first case, we have two possibilities:
- (a)
- . . If , we getTherefore, is IS if and only if .In Figure 4, we observe the behavior of the drift flow (5) for the case where . The flow is explicitly given bywhere , , and . We see that as , the first coordinate tends to zero, and the second coordinate approaches . Therefore, the system is IS.
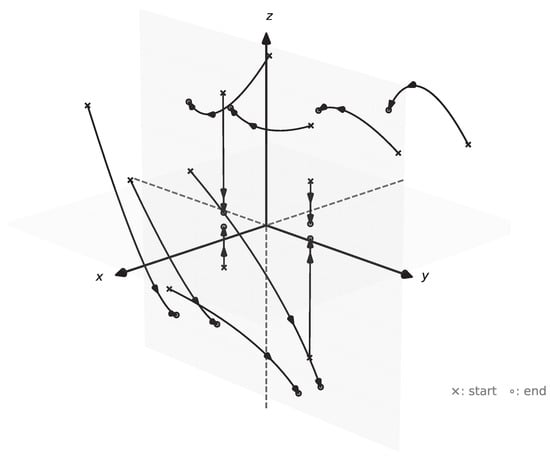 Figure 4. Geometric description of the flow behavior (5), case , , .
Figure 4. Geometric description of the flow behavior (5), case , , . - (b)
- and A is not null. Since the matrix is not nilpotent,Thus, the linear control system is IS.Finally, if , we getwhich is bounded if and only if . So, is IS, if and only if and so ; thus, .In Figure 5, we observe the flow of the drift (5) for the case where and A is not null. In this situation, the behavior is governed by a rotation-type matrix and the flow is given bywhere and . Therefore, the system is IS.
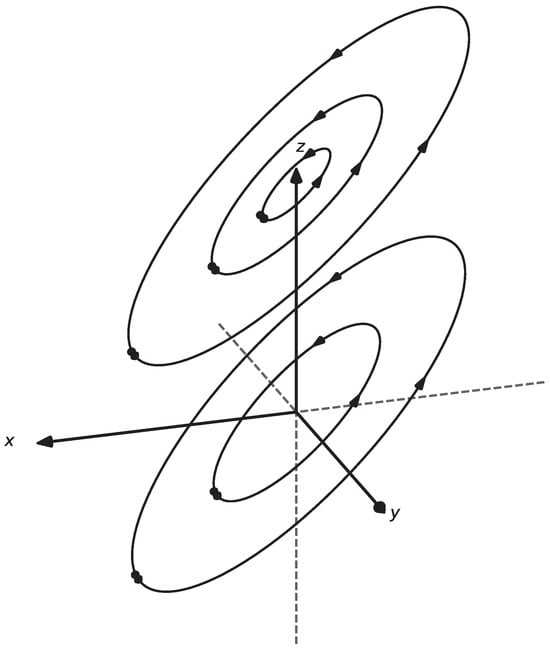 Figure 5. Geometric description of the flow behavior (5), case , .
Figure 5. Geometric description of the flow behavior (5), case , .
6.2. BIBO Stability
The objective now is to analyze BIBO stability. As in the cases, we only need to consider the normal subgroups of and check when the projections of the system orbits starting from the identity are bounded.
The normal subgroups of , up to isomorphisms, are
- and
- and
- and
Since the flow of a linear vector field is given by
it can be seen that the normal subgroups are not necessarily -invariant.
We already know that a linear system in has the form
where .
In particular, due to the compacity of , we have
- If , then and the system is BIBO stable.
- If , then , then the system is BIBO stable.
- If , then .Since the canonical projection isthe z component (which depends on v) is projected to and the component (independent of z) projects onto itself. The system is BIBO stable if and only if the systemsatisfies every orbit of (7) starting from , which is bounded. In this case, it is equivalent to say that .
- If , the system projects onto and, as before, it is BIBO stable if and only if .
- For the cases and , we have
- (a)
- If , then and
- (b)
- If , then andIn both cases, the system will be BIBO stable if the projection of the orbits from the origin under the map is bounded.However, this is the same problem of Euclidean BIBO stability:and its stability is (again) related to the eigenvalues of A.
7. Robotic Control Model
Let us consider an arbitrary LCS on the Heisenberg Lie group, as before:
- Variables and parameters
In particular, this general model captures how a robot navigates in a environment via v, with an internal orientation or phase z, under both environments influencing and controlling inputs. Next, we introduce the variables, parameters, and their physical interpretations.
: Represents the planar position of the robot in the x-y plane. In practice, this corresponds to the robot’s current location relative to a fixed reference point, such as a docking station or starting position.
: Corresponds to an internal state variable such as the robot’s heading angle or an accumulated phase. This variable is crucial for orientation control, path following, or synchronization tasks.
: The control input—for example, a voltage, PWM signal, or torque command—applied to the robot’s actuators. It is a bounded input generated by the control law, representing actual actuation effort.
: A control influence vector, determining how the control input affects the robot’s movement in the plane. For example, means that the control command directly influences forward motion along the x-axis.
: A drift direction vector, modeling environmental effects or undesired biases—such as wind, slopes, or mechanical imperfections—that cause the internal state to evolve even without control input.
: A scalar drift rate influencing the internal state z. Physically, it can represent a natural tendency of the robot’s heading or phase to drift over time due to unmodeled influences.
: The matrix describing the intrinsic dynamics of the planar position v. For example, it models damping (negative eigenvalues) or growth (positive eigenvalues) due to friction, inertia, or other environmental interactions.
: The trace of A affects the growth or decay rate of the internal state z. A negative trace indicates a natural tendency for z to decay, aiding stabilization.
- The dynamical point of view
models the robot’s planar motion, influenced by its dynamics and actuation ;
models how the robot’s heading or internal phase evolves, influenced by drift , control , and coupling with position via the symplectic form ;
is the control effort, modeled as a bounded actuation signal (e.g., voltage, torque);
are constants defining how control inputs influence motion and drift, respectively;
A models the inertial and environmental effects, whose eigenvalues determine whether the system tends to stabilize or diverge.
- Summary
Choosing A with eigenvalues in the left-half plane ensures that the trajectories asymptotically tend to the equilibrium.
A skew-symmetric A induces bounded oscillations, implying inner stability.
The Homomorphism h and BIBO Stability Analysis: In many control problems on Lie groups, the output map is often a projection onto a subgroup or a lower-dimensional manifold within H. Analyzing the BIBO stability via the projection h provides practical insights, especially when the measurable outputs (like position or heading) are of primary interest.
Role of the Projection h Since h is a homomorphism, the projected output trajectories are obtained by applying h to the system’s flow . The dynamics of these projected states often satisfy a lower-dimensional (linear or non-linear) system:
where is derived from the original system matrices and the properties of h.
- Analyzing BIBO Stability via Projection
The eigenvalues of determines stability, as follows:
If all eigenvalues of have negative real parts, the projected system is asymptotically stable.
When the input signal is bounded (), the output remains bounded if and only if the projected system is stable.
- Implication for the Original System
Since is a bounded projection of the original trajectories, the boundedness of the projected output implies that the original system is BIBO stable with respect to h. This means that controlling the system to stabilize the projected states (like position or heading) suffices to ensure the system’s outputs stay bounded under bounded inputs.
- Summary
Projection h simplifies the stability analysis by reducing it to a subsystem.
Eigenvalues of the resulting matrix determine whether the projected output remains bounded under bounded inputs.
Conclusion: If the projected system is asymptotically stable, the original system is BIBO stable with respect to h.
- Choice of Output Map h
In the robotic setting, typical choices include
Position output:
extracting the planar position; this relates to the robot’s location in space.
Orientation or heading:
capturing the robot’s heading angle or internal phase.
Combined output:
providing position and orientation collectively.
Practical Implication
When , BIBO stability ensures that if the control efforts are bounded (e.g., voltage commands in the robot); then, the robot’s position will not diverge, ensuring safe and predictable operation.
Achieving BIBO stability typically requires the system matrix A to have eigenvalues in the half-plane, guaranteeing the boundedness of solutions .
In summary, choosing a suitable output map h, BIBO stability guarantees that the robot’s measurable states (like position or heading) stay bounded when the control inputs are bounded—a crucial requirement in real-world robotic control to prevent unbounded drifts or erratic behavior.
8. Future Work and Research
- Building upon the current analysis, several avenues for future investigation emerge:
Extension to Higher-Dimensional Lie Groups: Expanding the stability analysis to encompass higher-dimensional and more complex Lie groups, particularly those with richer algebraic structures such as semi-simple or reductive groups. This would deepen the understanding of control phenomena in more intricate geometric settings.
Non-Linear Control Systems: Investigating stability properties of non-linear control systems defined on Lie groups, including the role of non-linearities, invariance properties, and the impact of non-quadratic vector fields. This could provide insights into more realistic models with practical applications.
Robustness and Perturbation Analysis: Analyzing the robustness of the stability conditions under perturbations of the drift or control vector fields. This includes the study of system stability under parameter uncertainties and external disturbances within the Lie group framework.
Controllability and Stabilization: Exploring the controllability aspects associated with these systems, especially the design of feedback laws that ensure asymptotic or practical stability, possibly employing Lie algebraic techniques or geometric control methods.
Applications to Robotics and Quantum Systems: Applying the established stability criteria to specific problems in robotic motion planning, such as navigation on Lie group configuration manifolds, as well as in quantum control where Lie groups such as SU(2) and SU(1,1) play a key role.
Advancing research in these directions will significantly enhance the understanding of control dynamics on Lie groups, with potential impacts across mathematics, engineering, and applied sciences.
Author Contributions
V.A., M.L.T.T. and W.E.V.H. were involved in the conception and design of the article. V.A. and M.L.T.T. primarily took charge of drafting and revising the manuscript. J.E.P.M. contributed as a researcher and writer, and edited the final document. All authors have read and agreed to the published version of the manuscript.
Funding
This article was supported by the research project: “Estabilidad de Sistemas de Control Lineales sobre Grupos de Lie”, PI-08-2024-UNSA.
Data Availability Statement
Research analytic methods and study material are freely available.
Acknowledgments
We would like to express our gratitude to Universidad Nacional de San Agustín de Arequipa (UNSA) in Arequipa, Perú.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ayala, V.; Tirao, J. Linear control systems on Lie groups and Controllability. Symp. Pure Math. 1999, 64, 47–64. [Google Scholar] [CrossRef]
- Da Silva, A.; Kizil, E.; Ayala, V. Linear control systems on a 4D solvable Lie group used to model primary visual cortex V1. Math. Control Signals Syst. 2025, Submitted. [Google Scholar]
- Ayala, V.; Da Silva, A. The control set of a linear control system on the two-dimensional Lie group. J. Differ. Equ. 2020, 268, 6683–6701. [Google Scholar] [CrossRef]
- Ayala, V.; Hacibekiroglu, A. Observable Linear Pairs. Comput. Appl. Math. 1997, 16, 205–214. [Google Scholar]
- Jean, F. Control of Nonholonomic Systems: From Sub-Riemannian Geometry to Motion Planning; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Zhang, X. A symmetry group and controllability of nonlinear homogeneous systems. IFAC Proc. Vol. 1999, 32, 2576–2579. [Google Scholar] [CrossRef]
- Agrachev, A.; Barilari, D.; Boscain, U. A Comprehensive Introduction to Sub-Riemannian Geometry; Cambridge University Press: Cambridge, UK, 2019; Volume 181. [Google Scholar] [CrossRef]
- Folland, B. Harmonic Analysis in Phase Space; Annals of Mathematics Studies; Princeton University Press: Princeton, NJ, USA, 1989; Volume 122, ISBN 9780691085289. [Google Scholar]
- Agrachev, A.; Sachkov, Y. Control Theory from the Geometric Viewpoint; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Montgomery, R. A Tour of Subriemannian Geometries, Their Geodesics and Applications. Math. Surv. Monogr. 2002, 91. [Google Scholar] [CrossRef]
- Lewis, A. A Mathematical Approach to Classical Control, PDF Version: 2016/09/21. Available online: https://shorturl.at/eNrWe (accessed on 12 October 2025).
- Brockett, R.W. System Theory on Group Manifolds and Coset Spaces. SIAM J. Control 1972, 10, 265–284. [Google Scholar] [CrossRef]
- Wonham, M.W. Linear Multivariable Control: A Geometric Approach; Applications of Mathematics; Springer: New York, NY, USA, 1979; Volume 10. [Google Scholar] [CrossRef]
- Helgason, S. Differential Geometry, Lie Groups, and Symmetric Spaces; Academic Press: London, UK, 1978; ISBN-13: 978-1470479732. [Google Scholar]
- San Martin, L.A.B. Algebras de Lie, 2nd ed.; Editora Unicamp: Campinas, Brazil, 2010. [Google Scholar]
- Jurdjevic, V. Geometric Control Theory; Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Kalman, R. Lectures on Controllability and Observability. In Controllability and Observability; Evangelisti, E., Ed.; C.I.M.E. Summer Schools; Springer: Berlin/Heidelberg, Germany, 2010; Volume 46. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).