An Iterative Approach for Finding Minimal-Optimal Solutions of the Min-Max Programming Problem with Addition-Overlap Functions

Abstract

Finding an optimal solution of the min-max programming problem with addition-overlap function constraints has been studied in the literature. Since the definition of overlap functions is very general and has no explicit formulations, a bisection method was proposed to yield a uniform-optimal solution for such optimization problems with a general overlap function involved in its constraint part. The uniform-optimal solution could be improved if the system manager wants extra properties such as also yielding lower cost performance. The minimal-optimal solution is proposed other than the uniform-optimal solution to answer manager’s call. In this paper, we propose an iterative method to yield at least one minimal-optimal solution. Our method starts from the uniform-optimal solution and systematically reduces the values of some non-binding variables while preserving the feasibility and optimality. To rigorously establish our method, we specify explicitly a nontrivial “min-shifted” overlap function in place of the general overlap function of the min-max programming problem. The proof of finding a minimal-optimal solution of our algorithm is given. By shifting the searching sequence of decision variables, our algorithm may find other minimal-optimal solutions which provide more flexibility for the system manager to choose. Numerical examples are provided to illustrate the procedures of the algorithm.

1. Introduction

Fuzzy preference modeling has increasingly relied on relational approaches to systematically capture preference relations between alternatives [1]. Within this framework, t-norm-based aggregation functions have emerged as fundamental tools, particularly in the study of fuzzy relational equations that represent preference structures in uncertain environments [2,3]. These t-norms have proven particularly valuable because they satisfy critical properties like associativity and monotonicity, making them suitable for multi-stage decision processes [4,5].

However, as noted by Fodor and Roubens [6], the associativity condition required by t-norms is not essential in many real-world preference scenarios. This theoretical insight led to the development of overlap functions—a more flexible class of aggregation operators that preserves continuity and boundary conditions while relaxing the need for associativity [7]. In particular, the seminal work by Dimuro et al. [8] introduced the concept of additive generator pairs, providing a systematic framework for constructing overlap functions with desirable theoretical properties.

Beyond their theoretical appeal, overlap functions have demonstrated considerable practical value in various application domains. For instance, they have been used to improve image segmentation via advanced thresholding techniques [9] and to facilitate more sophisticated three-way decision-making models in interval-valued fuzzy information systems [10]. Their ability to model situations of indifference, where no clear preference exists between alternatives, has also made them a key component in advanced fuzzy decision-making frameworks [11,12].

Building on this foundation, recent studies have explored the use of overlap functions in optimization frameworks, particularly within the context of min-max programming. The min-max optimization problem has been extensively applied across various domains, including optimal control systems [13], robust machine learning [14], and fuzzy optimization [15].

In fuzzy optimization, significant attention has focused on min-max programming problems with addition-min fuzzy relational inequalities (FRIs), particularly in modeling resource allocation for BitTorrent-like peer-to-peer (BT-P2P) file-sharing systems [16,17]. The general model can be expressed as follows:

$$\begin{array}{ccc}\hfill \mathrm{Minimize}& & Z\left(x\right)=max\{x_1,\cdots ,x_n\}\hfill \\ \hfill \mathrm{subject} \mathrm{to}& & g_i\left(x\right)=\sum _{j=1}^{n}min\{a_{ij},x_j\}\ge b_i,\forall i\in \mathcal{I},\hfill \\ & & x_j\in [0,1],\forall j\in \mathcal{J},\hfill \end{array}$$

(1)

where parameters $a_{ij}\in [0,1]$ and $b_i>0$ for any $i\in \mathcal{I}=\{1,2,\cdots ,m\},j\in \mathcal{J}=\{1,2,\cdots ,n\}$.

Yang et al. [18] demonstrated that the solution set of addition-min FRIs is determined by a unique maximal solution and a convex set of minimal solutions. Building on this structural insight, Yang et al. [19] first proposed the uniform-optimal solution for model (1), where all variables share an identical optimal value. Later, Chiu et al. [20] simplified the solution process by reformulating model (1) as a single-variable optimization problem, thereby enabling the derivation of the uniform-optimal solution through both an analytical and an iterative method. Advancements in solving FRIs—a key tool for optimization under uncertainty—have been comprehensively reviewed by Deo et al. [21]. Specifically, they systematically categorized solution algorithms, ranging from traditional linear programming to modern metaheuristics such as Particle Swarm Optimization, while also exploring advanced topics, including bipolar fuzzy relations and hybrid models. Furthermore, recent advances in max-min optimization models have been developed to evaluate the stability of the widest-interval solution for systems of max-min FRIs [22,23] and addition-min FRIs [24].

While mathematically convenient, the uniform-optimal solution of model (1) may prove suboptimal for practical applications like BT-P2P data transmission. Yang [25] addressed this limitation through an optimal-vector-based (OVB) algorithm to compute so-called minimal-optimal solutions. Guu et al. [26] also proposed a two-phase method optimizing transmission costs under congestion constraints to obtain another minimal-optimal solution, which are strictly better or at least no worse than the uniform-optimal solution in terms of cost. Subsequent studies expanded on this concept, including the exploration of leximax minimal solutions [27], active-set-based methods [28], and iterative approaches for generalized min-max problems [29].

These developments underscore the practical importance of identifying not only optimal but also structurally minimal solutions in min-max optimization models. Motivated by this, the present study extends the concept to a more broader class of problems constrained by addition-overlap functions. Specifically, we consider the following min-max programming model:

$$\begin{array}{ccc}\hfill \mathrm{Minimize}& & Z\left(x\right)=max\{x_1,\cdots ,x_n\}\hfill \\ \hfill \mathrm{subject} \mathrm{to}& & g_i\left(x\right)=\sum _{j=1}^{n}O(a_{ij},x_j)\ge b_i,\forall i\in \mathcal{I},\hfill \\ & & x_j\in [0,1],\forall j\in \mathcal{J},\hfill \end{array}$$

(2)

where parameters $a_{ij}\in [0,1]$ and $b_i>0$ for any $i\in \mathcal{I}=\{1,2,\cdots ,m\},j\in \mathcal{J}=\{1,2,\cdots ,n\}$. $O(a_{ij},x_j)$ is the overlap function, which will be defined later in Definition 1.

When the constraint system in problem (2) is feasible, Wu et al. [30] demonstrated that a uniform-optimal solution is guaranteed to exist. Notably, this result remains valid for the optimization problem (2) regardless of the specific operator chosen from the class of overlap functions. Their approach involves transforming the original problem into an equivalent single-variable optimization problem, which can be efficiently solved using the classical bisection method.

Moreover, Wu et al. [30] extended the min-max optimization problem (2), incorporating a novel overlap function operator (4)—termed the “min-shifted” overlap function. Incorporating this operator, the min-max model becomes

$$\begin{array}{ccc}\hfill \mathrm{Minimize}& & Z\left(x\right)=max\{x_1,\cdots ,x_n\}\hfill \\ \hfill \mathrm{subject} \mathrm{to}& & g_i\left(x\right)=\sum _{j=1}^{n}O(a_{ij},x_j)\ge b_i,\forall i\in \mathcal{I},\hfill \\ & & x_j\in [0,1],\forall j\in \mathcal{J},\hfill \end{array}$$

(3)

where the overlap function $O(a_{ij},x_j)$ is defined as

$$\begin{array}{c}\hfill O(a_{ij},x_j)={\displaystyle \frac{min\{a_{ij},x_j\}}{min\{a_{ij},x_j\}+(1-max\{0,x_j+a_{ij}-1\})}}.\end{array}$$

(4)

Although the classical bisection method can be applied for general overlap functions, including the min-shifted overlap function in (4), Wu et al. [30] adopted a distinct approach for solving model (3) and then derived the uniform-optimal solution using a tailored algorithm.

However, to the best of our knowledge, no existing method provides an effective way to compute minimal-optimal solutions for problem (3). This paper fills this gap by proposing an iterative refinement strategy that starts from the uniform-optimal solution and systematically reduces adjustable variables while preserving both feasibility and optimality. The resulting minimal-optimal solution not only retains global optimality but also satisfies a strong minimality condition, ensuring that no component can be further decreased without violating the problem’s constraints.

The contribution of our approach is demonstrated by its ability to successfully solve a problem that was previously intractable. The primary evidence for its effectiveness lies in the following aspects:

(a).

We have rigorously proven that our method always produces a feasible and minimal-optimal solution (as established in Section 3 and Section 4).

(b).

The numerical examples in Section 5 confirm that the algorithm functions as intended, correctly identifying diverse minimal-optimal solutions for various problem instances.

(c).

By finding minimal-optimal solutions, our method provides decision-makers with superior, structurally efficient alternatives compared to the uniform-optimal solution, which is a significant practical advancement.

The remainder of this paper is organized as follows: Section 2 reviews fundamental concepts of overlap functions and their properties. Section 3 formulates the min-max optimization problem with addition-overlap constraints. Section 4 presents our iterative algorithm for finding minimal-optimal solutions along with its theoretical analysis. Section 5 provides numerical examples demonstrating the method’s effectiveness, and Section 6 concludes with directions for future research.

2. Some Properties of the Min-Shifted Overlap Function

In this section, we review the definition of overlap function and explore the relevant properties of the min-shifted overlap function as defined in (4). This foundational knowledge will aid us to find the minimal-optimal solution for problem (3).

Definition 1.

(See [7,8]). A bivariate function $O:{[0,1]}^2\to [0,1]$ is said to be an overlap function if it satisfies the following conditions:

(O1) 

$O(x,y)=O(y,x)$ for all $x,y\in [0,1]$;

(O2) 

$O(x,y)=0$ if and only if $xy=0$;

(O3) 

$O(x,y)=1$ if and only if $x=y=1$;

(O4) 

O is non-decreasing;

(O5) 

O is continuous.

For convenience, the form of the min-shifted overlap function in (4) is simplified as follows:

$$\begin{array}{c}\hfill O(a,x)={\displaystyle \frac{min\{a,x\}}{min\{a,x\}+(1-max\{0,x+a-1\left\}\right)}},\mathrm{for} \mathrm{all}a,x\in [0,1].\end{array}$$

(5)

Let $D=min\{a,x\}+(1-max\{0,x+a-1\left\}\right)$ be the denominator of (5). Analyzing the value of the overlap function $O(a,x)$ for (5), the following results can be obtained.

Lemma 1

([30], Lemma 1). For (5), there are

(i). 

$O(a,0)=0$ and $O(0,x)=0$;

(ii). 

$O(a,1)=a$ and $O(1,x)=x$;

(iii). 

$D\ge 1$, and if $ax\ne 0$ and $ax\ne 1$, then $D>1$;

(iv). 

$O(a,x)\le min\{a,x\}$;

(v). 

If $0<a$ and $0<x_1\le x_2\le 1$, then ${\displaystyle \frac{O(a,x_2)}{O(a,x_1)}}\le {\displaystyle \frac{x_2}{x_1}}$.

Lemma 2

([30], Lemma 2). For (5), the following results hold:

(i). 

If $x\le a$ and $x+a\le 1$, then $O(a,x)={\displaystyle \frac{x}{x+1}}$.

(ii). 

If $x\le a$ and $x+a\ge 1$, then $O(a,x)={\displaystyle \frac{x}{2-a}}$.

(iii). 

If $x\ge a$ and $x+a\le 1$, then $O(a,x)={\displaystyle \frac{a}{a+1}}$.

(iv). 

If $x\ge a$ and $x+a\ge 1$, then $O(a,x)={\displaystyle \frac{a}{2-x}}$.

When $a\in [0,1]$ is used as a given parameter and $a=0.5$ is the dividing point, then the value of the min-shifted overlap function $O(a,x)$ in (5) can be derived, and the two sets of results are roughly illustrated in Figure 1 and Figure 2.

(1)

When $a\le 0.5$, the value of $O(a,x)$ in (5) is determined by three cases, as detailed below:

• Case 1: $x\le a$

We have $x\le a\le 0.5$ and $x+a\le 1$. It follows that $min\{a,x\}=x$ and $max\{0,x+a-1\}=0$. Substituting these into $O(a,x)$ yields

$$O(a,x)={\displaystyle \frac{x}{x+1}}.$$

• Case 2: $a\le x\le 1-a$

Here, $a\le x$ and $x+a\le 1$. These imply $min\{a,x\}=a$ and $max\{0,x+a-1\}=0$. Substituting into $O(a,x)$ gives

$$O(a,x)={\displaystyle \frac{a}{a+1}}.$$

• Case 3: $x\ge 1-a$

Since $a\le 0.5$, we have $x\ge 0.5\ge a$ and $x+a\ge 1$. Thus, $min\{a,x\}=a$ and $max\{0,x+a-1\}=x+a-1$. Substituting these into $O(a,x)$ results in

$$O(a,x)={\displaystyle \frac{a}{a+[1-(x+a-1\left)\right]}}={\displaystyle \frac{a}{2-x}}.$$

To summarize, when $a\le 0.5$, $O(a,x)$ is given by the piecewise function:

$$\begin{array}{c}\hfill O(a,x)=\left\{\begin{array}{ccc}{\displaystyle \frac{x}{x+1}}\hfill & \mathrm{if}\hfill & x\le a,\hfill \\ {\displaystyle \frac{a}{a+1}}\hfill & \mathrm{if}\hfill & a\le x\le 1-a,\hfill \\ {\displaystyle \frac{a}{2-x}}\hfill & \mathrm{if}\hfill & x\ge 1-a.\hfill \end{array}\right.\end{array}$$

(6)

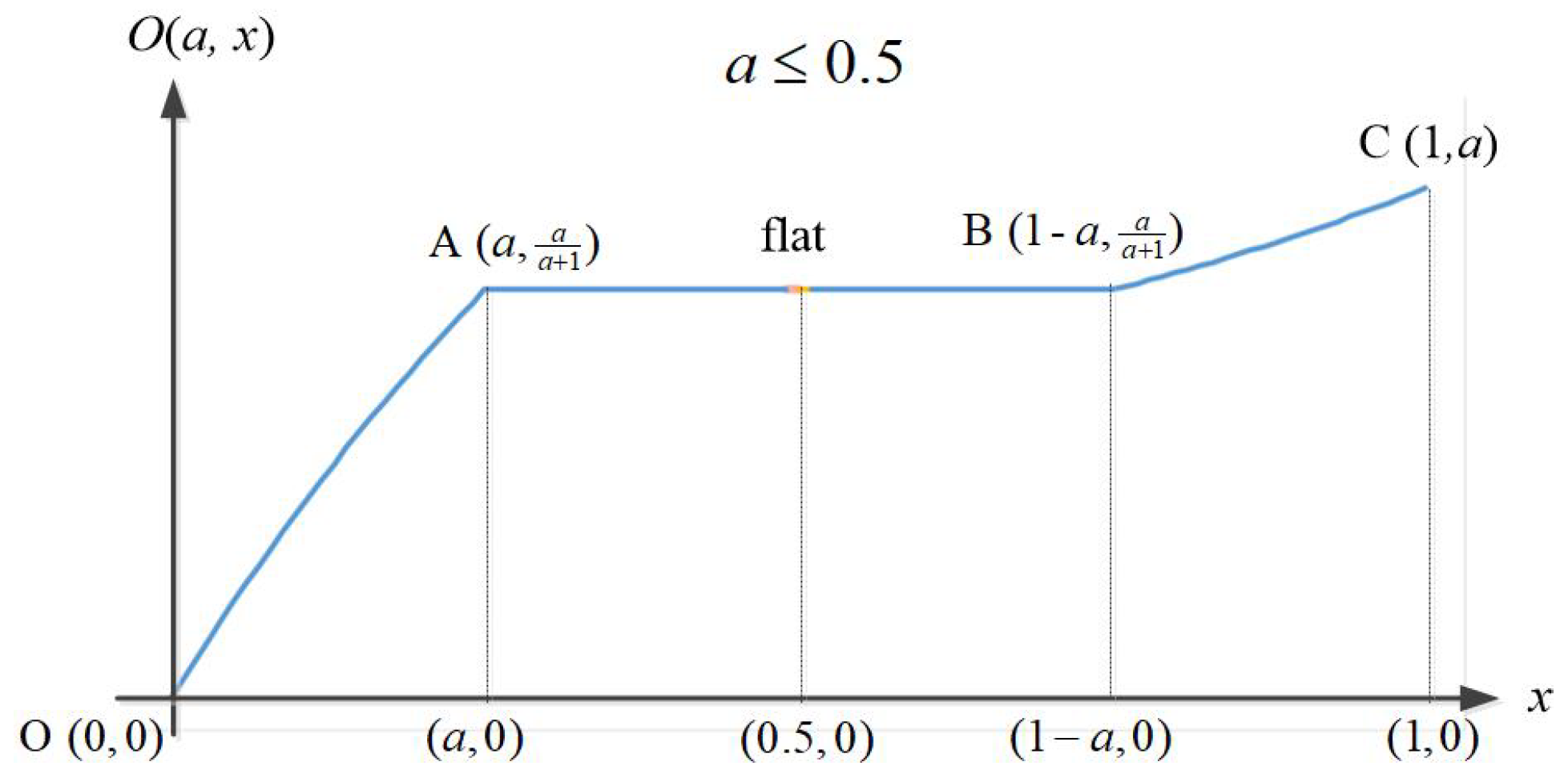
Figure 1 (where $a\le 0.5$) depicts a piecewise function with a flat segment along line AB, where $x\in [a,1-a]$, indicating that the overlap function $O(a,x)$ is continuous and non-decreasing in this case.

(2)

When $a\ge 0.5$, the value of $O(a,x)$ in (5) is determined by three cases, as detailed below:

• Case 1: $x\le 1-a$

We have $x\le 0.5\le a$ and $x+a\le 1$. It follows that $min\{a,x\}=x$ and $max\{0,x+a-1\}=0$. Substituting these into $O(a,x)$ yields

$$O(a,x)={\displaystyle \frac{x}{x+1}}.$$

• Case 2: $1-a\le x\le a$

Here, $x\le a$ and $x+a\ge 1$. These imply $min\{a,x\}=x$ and $max\{0,x+a-1\}=x+a-1$. Substituting into $O(a,x)$ gives

$$O(a,x)={\displaystyle \frac{x}{x+[1-(x+a-1\left)\right]}}={\displaystyle \frac{x}{2-a}}.$$

• Case 3: $a\le x\le 1$

Since $a\ge 0.5$, we have $0.5\le a\le x$ and $x+a\ge 1$. Thus, $min\{a,x\}=a$ and $max\{0,x+a-1\}=x+a-1$. Substituting these into $O(a,x)$ results in

$$O(a,x)={\displaystyle \frac{a}{a+[1-(x+a-1\left)\right]}}={\displaystyle \frac{a}{2-x}}.$$

To summarize, when $a\ge 0.5$, $O(a,x)$ is given by the piecewise function:

$$\begin{array}{c}\hfill O(a,x)=\left\{\begin{array}{ccc}{\displaystyle \frac{x}{x+1}}\hfill & \mathrm{if}\hfill & x\le 1-a,\hfill \\ {\displaystyle \frac{x}{2-a}}\hfill & \mathrm{if}\hfill & 1-a\le x\le a,\hfill \\ {\displaystyle \frac{a}{2-x}}\hfill & \mathrm{if}\hfill & a\le x\le 1.\hfill \end{array}\right.\end{array}$$

(7)

Figure 2 (where $a\ge 0.5$) shows a piecewise function without any flat segment, meaning that $O(a,x)$ is continuous and strictly increasing for all $0\le x\le 1$.

Theorem 1.

For the overlap function $O(a,x)$ defined in (5), when $0\le a\le 0.5$, the following properties hold:

(i).

Strict monotonicity for small x: If $0\le x\le a$, then $O(a,x)$ is a strictly increasing function.

(ii).

Symmetry: If $a\le x\le 1-a$, then $O(a,x)=O(a,1-x)$.

(iii).

Strict monotonicity for large x: If $1-a\le x\le 1$, then $O(a,x)$ is a strictly increasing function.

Proof. 

(i).

Strict monotonicity for small x:

Given $0\le a\le 0.5$ and $0\le x\le a$, we consider two values $0\le x_1<x_2\le a$ and show that $O(a,x_2)-O(a,x_1)>0$ for $a>0$.

From (6), we have $O(a,x_1)={\displaystyle \frac{x_1}{x_1+1}}$ and $O(a,x_2)={\displaystyle \frac{x_2}{x_2+1}}$. Thus,

$$O(a,x_2)-O(a,x_1)={\displaystyle \frac{x_2}{x_2+1}}-{\displaystyle \frac{x_1}{x_1+1}}={\displaystyle \frac{x_2-x_1}{(x_1+1)(x_2+1)}}>0.$$

Since the denominator is always positive, the numerator $x_2-x_1$ ensures the expression remains positive. Hence, $O(a,x)$ is strictly increasing in this interval.

(ii).

Symmetry:

Given $0\le a\le 0.5$ and $a\le x\le 1-a$, we analyze $O(a,x)$ and $O(a,1-x)$ as follows:

• Evaluating $O(a,x)$: Since $a\le x\le 1-a$, we have $a\le x$ and $a+x\le 1$, which implies that $min\{a,x\}=a$, $max\{0,x+a-1\}=0$, and leading to

  $$\begin{array}{c}\hfill O(a,x)={\displaystyle \frac{min\{a,x\}}{min\{a,x\}+(1-max\{0,x+a-1\left\}\right)}}={\displaystyle \frac{a}{a+(1-0)}}={\displaystyle \frac{a}{a+1}}.\end{array}$$
• Evaluating $O(a,1-x)$: Since $a\le x\le 1-a$, we have $a\le 1-x\le 1-a$ and $(1-x)+a\le 1$, which implies that $min\{a,1-x\}=a$, $max\{0,(1-x)+a-1\}=0$, and leading to

$$\begin{array}{c}\hfill O(a,1-x)={\displaystyle \frac{min\{a,1-x\}}{min\{a,1-x\}+(1-max\{0,(1-x)+a-1\left\}\right)}}={\displaystyle \frac{a}{a+(1-0)}}={\displaystyle \frac{a}{a+1}}.\end{array}$$

Since both expressions are identical for all $a\le x\le 1-a$, it follows that $O(a,x)=O(a,1-x)$.

(iii).

Strict monotonicity for large x:

Given $0\le a\le 0.5$ and $1-a\le x\le 1$, we analyze two values $1-a\le x_1<x_2\le 1$ and show that $O(a,x_2)-O(a,x_1)>0$ for $a>0$.

From (6), we have $O(a,x_1)={\displaystyle \frac{a}{2-x_1}}$ and $O(a,x_2)={\displaystyle \frac{a}{2-x_2}}$. Thus,

$$O(a,x_2)-O(a,x_1)={\displaystyle \frac{a}{2-x_2}}-{\displaystyle \frac{a}{2-x_1}}={\displaystyle \frac{a(x_2-x_1)}{(2-x_1)(2-x_2)}}>0.$$

Again, since the denominator is positive and $a(x_2-x_1)>0$, we conclude that $O(a,x)$ is strictly increasing in this interval. □

Theorem 1 states that for $0\le a\le 0.5$, the min-shifted overlap function $O(a,x)$ is strictly increasing in the intervals $0\le x\le a$ and $1-a\le x\le 1$, while remaining symmetry in the middle interval $a\le x\le 1-a$.

For example, when $a=0.45$, the overlap function $O(0.45,x)$ is strictly increasing for $0\le x\le 0.45$ and $0.55\le x\le 1$. However, by Theorem 1, it remains symmetry at $O(0.45,x)=0.310345$ in the middle interval $a=0.45\le x\le 1-a=0.55$.

Theorem 2.

For the overlap function $O(a,x)$ defined in (5), if $0.5\le a\le 1$, then $O(a,x)$ is strictly increasing for all $0\le x\le 1$.

Proof. 

Given $0.5\le a\le 1$ and $0\le x\le 1$, we analyze the following three cases and show that $O(a,x_2)-O(a,x_1)>0$ whenever $x_1<x_2$.

• Case 1: $0\le x_1<x_2\le 1-a$

From (7), we have $O(a,x_1)={\displaystyle \frac{x_1}{x_1+1}}$ and $O(a,x_2)={\displaystyle \frac{x_2}{x_2+1}}$. Thus, the difference is

$$O(a,x_2)-O(a,x_1)={\displaystyle \frac{x_2}{x_2+1}}-{\displaystyle \frac{x_1}{x_1+1}}={\displaystyle \frac{x_2-x_1}{(x_1+1)(x_2+1)}}>0.$$

Since the denominator $(x_1+1)(x_2+1)$ is always positive and the numerator $x_2-x_1$ remains positive, it follows that $O(a,x)$ is strictly increasing in this interval.

• Case 2: $1-a\le x_1<x_2\le a$

From (7), we have $O(a,x_1)={\displaystyle \frac{x_1}{2-a}}$ and $O(a,x_2)={\displaystyle \frac{x_2}{2-a}}$. Thus, the difference is

$$O(a,x_2)-O(a,x_1)={\displaystyle \frac{x_2}{2-a}}-{\displaystyle \frac{x_1}{2-a}}={\displaystyle \frac{x_2-x_1}{2-a}}>0.$$

Since the denominator $2-a$ is always positive and the numerator $x_2-x_1$ is positive. Hence, $O(a,x)$ is strictly increasing in this interval.

• Case 3: $a\le x_1<x_2\le 1$

From (7), we have $O(a,x_1)={\displaystyle \frac{a}{2-x_1}}$ and $O(a,x_2)={\displaystyle \frac{a}{2-x_2}}$. Thus, the difference is

$$O(a,x_2)-O(a,x_1)={\displaystyle \frac{a}{2-x_2}}-{\displaystyle \frac{a}{2-x_1}}={\displaystyle \frac{a(x_2-x_1)}{(2-x_1)(2-x_2)}}>0.$$

Since $a>0$, the denominator is always positive, and the numerator $a(x_2-x_1)$ is positive. Hence, $O(a,x)$ is strictly increasing in this interval.

Since $O(a,x)$ is strictly increasing in all three cases, we conclude that it is strictly increasing for all $0\le x\le 1$. □

Theorem 2 presents a different result from Theorem 1. It states that for $0.5\le a\le 1$, the min-shifted overlap function $O(a,x)$, as defined in (5), is strictly increasing over the entire interval $0\le x\le 1$. For example, when $a=0.55$, the overlap function $O(0.55,x)$ is strictly increasing throughout the interval $0\le x\le 1$. In other words, $O(0.55,x)$ takes unique values for every distinct x in this interval.

Proposition 1.

For the min-shifted overlap function $O(a,x)$ defined as in (5), the following strict quasi-monotonicity property holds:

$$O(a,x_1)<O(a,x_2)\Rightarrow x_1<x_2,\forall a,x_1,x_2\in [0,1].$$

Proof. 

By Definition 1, the function $O(a,x)$ is non-decreasing and continuous in $x\in [0,1]$ for any fixed $a\in [0,1]$. Suppose, for contradiction, that $O(a,x_1)<O(a,x_2)$ but $x_1\ge x_2$. Since $O(a,x)$ is non-decreasing in x, it follows that

$$O(a,x_1)\ge O(a,x_2),$$

which contradicts the initial assumption that $O(a,x_1)<O(a,x_2)$. Therefore, the assumption $x_1\ge x_2$ is false, and it must hold that $x_1<x_2$. □

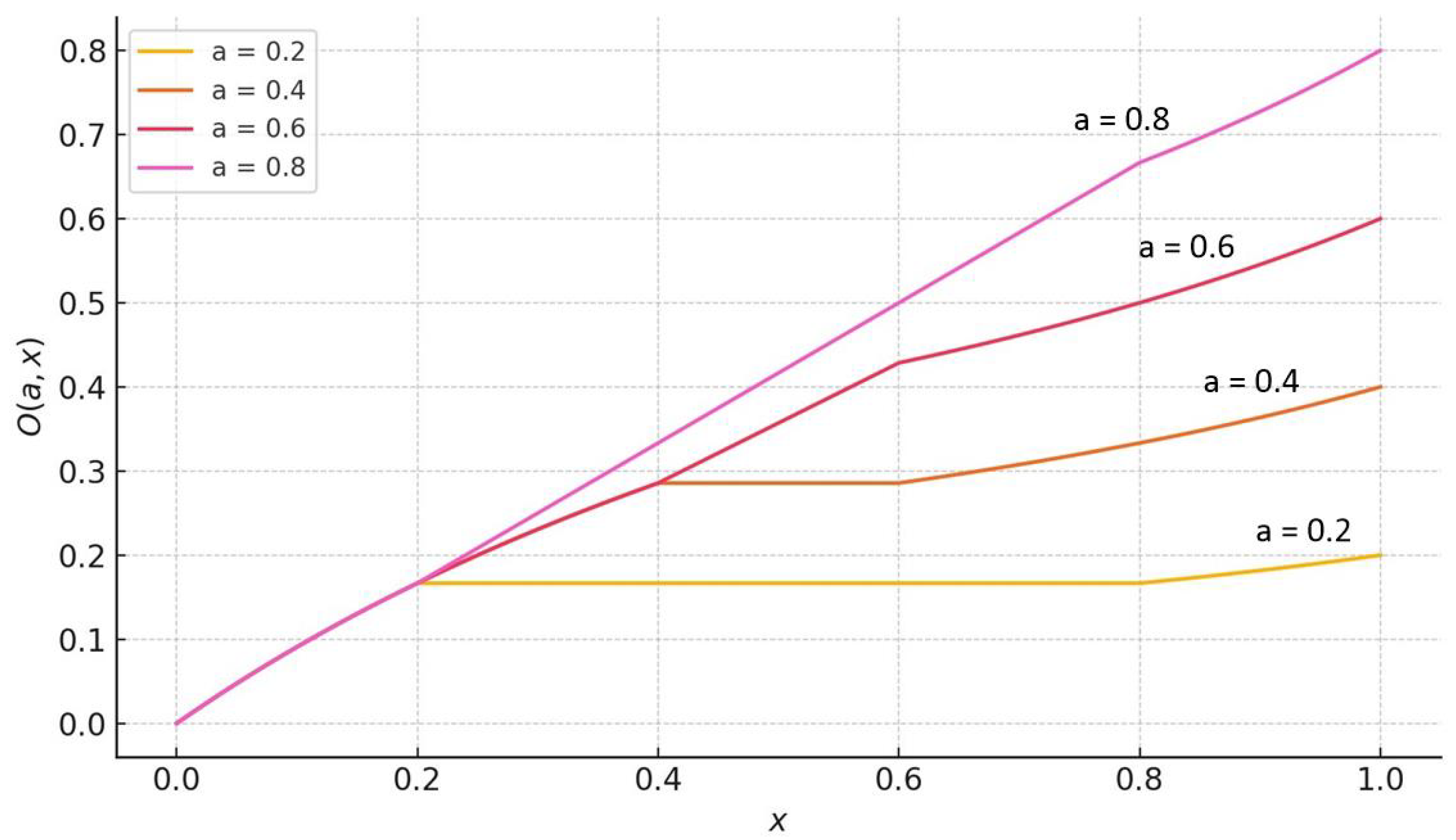
To provide an intuitive understanding of Proposition 1, we examine the graph of the min-shifted overlap function $O(a,x)$ over the domain $x\in [0,1]$ for fixed values of $a\in (0,1)$. As illustrated in Figure 3, the function $O(a,x)$ is strictly increasing with respect to x for any fixed value of a.

For example, consider the case where $a=0.4$. If $O(0.4,x_1)=0.285714<O(0.4,x_2)=0.3$, it follows that $x_1\in [0.4,0.6]$ and $x_1<x_2={\displaystyle \frac{2}{3}}$, which is consistent with the strict quasi-monotonicity of the function.

Proposition 2.

For a given $O(a,x_1)<O(a,x_2)$, the following properties hold:

(i). 

If $a\le 0.5$ and $x_1\in [0,a]\cup [1-a,1]$, or if $0.5\le a\le 1$ and $x_1\in [0,a]$, then $x_1<x_2\le 1$.

(ii). 

If $a\le 0.5$ and $x_1\in [a,1-a]$, then $x_1\le 1-a<x_2\le 1$.

Proof. 

We prove each case separately based on the structure of the min-shifted overlap function $O(a,x)$.

(i).

For $x_1\in [0,a]$ or $x_1\in [1-a,1]$ when $a\le 0.5$, Theorem 1:(i) and (iii) ensure that $O(a,x)$ is strictly increasing in these intervals. Similarly, when $a\ge 0.5$ and $x_1\in [0,a]$, Theorem 2 ensures that $O(a,x)$ is strictly increasing on the entire interval $[0,1]$, which includes $[0,a]$. Thus, in both scenarios, $O(a,x_1)<O(a,x_2)$ implies that $x_1<x_2\le 1$.

(ii).

If $a\le 0.5$ and $x_1\in [a,1-a]$, then by Theorem 1:(ii), the function $O(a,x)$ is symmetric in this interval: $O(a,x)=O(a,1-x)$. This symmetry implies that $O(a,x)$ is not strictly increasing in $[a,1-a]$, so it is possible to have $O(a,x_1)=O(a,x_2)$ even if $x_1\ne x_2$ in this range. Since we are given that $O(a,x_1)<O(a,x_2)$, it must be that $x_2$ lies outside this non-strict region. Because the function resumes strict monotonicity in the interval $(1-a,1]$, it follows that $x_2\in (1-a,1]$. Therefore, we have $x_1\le 1-a<x_2\le 1$.

□

Moreover, based on (6) and (7), the value of x in the equation $O(a,x)=\gamma$ can be obtained via the inverse function method as follows:

(1)

If $a\le 0.5$ and $O(a,x)=\gamma$, then there is

$$\begin{array}{c}\hfill x=\left\{\begin{array}{ccc}{\displaystyle \frac{\gamma }{1-\gamma }}\hfill & \mathrm{if}\hfill & \gamma \le {\displaystyle \frac{a}{a+1}},\hfill \\ [a,1-a]\hfill & \mathrm{if}\hfill & \gamma ={\displaystyle \frac{a}{a+1}},\hfill \\ {\displaystyle \frac{2\gamma -a}{\gamma }}\hfill & \mathrm{if}\hfill & {\displaystyle \frac{a}{a+1}}\le \gamma \le a.\hfill \end{array}\right.\end{array}$$

(8)

(2)

If $0.5\le a\le 1$ and $O(a,x)=\gamma$, then there is

$$\begin{array}{c}\hfill x=\left\{\begin{array}{ccc}{\displaystyle \frac{\gamma }{1-\gamma }}\hfill & \mathrm{if}\hfill & \gamma \le {\displaystyle \frac{1-a}{2-a}},\hfill \\ \gamma (2-a)\hfill & \mathrm{if}\hfill & {\displaystyle \frac{1-a}{2-a}}\le \gamma \le {\displaystyle \frac{a}{2-a}},\hfill \\ {\displaystyle \frac{2\gamma -a}{\gamma }}\hfill & \mathrm{if}\hfill & {\displaystyle \frac{a}{2-a}}\le \gamma \le a.\hfill \end{array}\right.\end{array}$$

(9)

Note that the value of the variable x does not exist if $O(a,x)=\gamma >a$, since we have $O(a,x)\le min\{a,x\}$ according to Lemma 1:(iv).

Why study the min-shifted overlap function? From the above analysis, by adjusting the parameter a, we could obtain different shapes of the figures. This is to illustrate that the min-shifted overlap function has very rich capacity to model different scenarios. Recall that an overlap function is a mathematical tool used to quantify the degree of “overlap” or shared characteristics between two or more objects or concepts. Take Figure 3, for example; if $O(a,x)$ is used to model the “indifference” between a and x, then selecting $a=0.2$ gives a wide range $[0.2,0.8]$ of x, which gives the same low level of indifference. When one increases a to be close to $0.5$, this range shrinks. Another feature is the piecewise property. One can see that the min-shifted overlap function could offer three piecewise segments to capture the features of asymmetric indifference between two objects.

3. A Single-Variable Optimization Problem for the Min-Max Programming Problem (2)

In this section, we review how to find the uniform-optimal solution to the min-max programming problem (2). Some definitions and relevant properties are given.

Definition 2.

Let $x={\left(x_j\right)}_{j\in \mathcal{J}}$ be a vector in ${[0,1]}^n$. The solution set of problems (2) and (3) is denoted by $X(A,b):=\{x\in {[0,1]}^n|g_i\left(x\right)={\sum }_{j=1}^{n}O(a_{ij},x_j)\ge b_i,\forall i\in \mathcal{I}\}$.

Definition 3.

Problem (2) is said to be consistent if $X(A,b)\ne \varnothing$. A solution $x^{*}\in X(A,b)$ is called optimal for problem (2) if $Z\left(x^{*}\right)\le Z\left(x\right)$ for all $x\in X(A,b)$.

Definition 4.

Let $x^1={\left(x_j^1\right)}_{j\in \mathcal{J}}$ and $x^2={\left(x_j^2\right)}_{j\in \mathcal{J}}$ be two vectors. For any vector $x^1$ and $x^2$, $x^1\le x^2$ if and only if $x_j^1\le x_j^2$ for all $j\in \mathcal{J}$. A vector $x\in X(A,b)$ is said to be minimal if $x^{\prime }\le x$ implies $x=x^{\prime }$ for any $x^{\prime }\in X(A,b)$.

Proposition 3.

Problem (2) is consistent, $X(A,b)\ne \varnothing$, if and only if ${\sum }_{j=1}^n{a}_{ij}\ge b_i$ holds for all $i\in \mathcal{I}$.

Proof. 

• (⇒) Since $X(A,b)\ne \varnothing$, and $O(a_{ij},x_j)\le min\{a_{ij},x_j\}$ for all $i\in \mathcal{I},j\in \mathcal{J}$, according to Lemma 1-(iv), we have $g_i\left(x\right)\ge b_i,\forall i\in \mathcal{I}$ such that

  $$\sum _{j=1}^n{a}_{ij}\ge \sum _{j=1}^{n}min\{a_{ij},x_j\}\ge \sum _{j=1}^{n}O(a_{ij},x_j)=g_i\left(x\right)\ge b_i,\mathrm{for}\mathrm{all}i\in \mathcal{I}.$$
• (⇐) Since ${\sum }_{j=1}^n{a}_{ij}\ge b_i,\forall i\in \mathcal{I}$ is given, and Lemma 1:(ii) states $O(a_{ij},1)=a_{ij}$, it follows that $x={\left(x_j\right)}_{j\in \mathcal{J}}$ with $x_j=1$ for all $j\in \mathcal{J}$ is a feasible solution to problem (2). Specifically, we have

  $$\begin{array}{c}\hfill g_i\left(x\right)=\sum _{j=1}^{n}O(a_{ij},1)=\sum _{j=1}^n{a}_{ij}\ge b_i\mathrm{holds},\mathrm{for}\mathrm{all}i\in \mathcal{I}.\end{array}$$

□

Proposition 3 shows that the necessary and sufficient condition of the solution set $X(A,b)\ne \varnothing$ of (2) is ${\sum }_{j=1}^n{a}_{ij}\ge b_i$ for all $i\in \mathcal{I}$. This condition can be used to check the consistency of the problem (2) before finding the optimal solution.

As previously mentioned, to find a uniform-optimal solution of the problem (2), Wu et al. [30] have shown that it can be transformed into a single-variable optimization problem, as follows:

$$\begin{array}{ccc}\hfill \mathrm{Minimize}& & Z\left(y\right)=y\hfill \\ \hfill \mathrm{subject} \mathrm{to}& & G_i\left(y\right)=\sum _{j=1}^{n}O(a_{ij},y)\ge b_i,\forall i\in \mathcal{I},\hfill \\ & & y\in [0,1],\hfill \end{array}$$

(10)

where parameters $a_{ij}\in [0,1]$ and $b_i>0$, for all $i\in \mathcal{I}=\{1,2,\cdots ,m\},j\in \mathcal{J}=\{1,2,\cdots ,n\}$.

Theorem 3

([30], Theorem 2). Suppose $y^{*}$ is the optimal solution to problem (10), and let $x^{*}=(x_1^{*},\cdots ,x_n^{*})$ be an optimal solution to problem (2) with optimal value $Z\left(x^{*}\right)=max\{x_1^{*},\cdots ,x_n^{*}\}$. Then, $max\{x_1^{*},\cdots ,x_n^{*}\}=y^{*}$ holds.

Theorem 3 demonstrates that the min-max programming problem (2), when constrained by a solvable general addition-overlap function, can be reformulated as a single-variable optimization problem (10). This transformation enables the use of the bisection method to determine the optimal value $y^{*}$. This methodology also applies to problem (3), which is subject to the min-shifted overlap function. Consequently, a uniform-optimal solution $x^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}$ for problem (3), where all variables take the same value, $x_j^{*}=y^{*}$ for all $j\in \mathcal{J}$, can be expressed as

$$x^{*}=(x_1^{*},x_2^{*},\cdots ,x_n^{*})=(y^{*},y^{*},\cdots ,y^{*}).$$

Example 1.

Find the optimal solution to the following min-max programming problem, which is subject to a system of addition-overlap functions as defined in problem (3).

$$\begin{array}{ccc}\hfill \mathrm{Minimize}& & Z\left(x\right)=max\{x_1,x_2,x_3,x_4,x_5,x_6\}\hfill \\ \hfill \mathrm{subject} \mathrm{to}& & g_1\left(x\right)\ge 1.8,\hfill \\ & & g_2\left(x\right)\ge 0.6,\hfill \\ & & g_3\left(x\right)\ge 2.0,\hfill \\ & & g_4\left(x\right)\ge 1.8,\hfill \\ & & x_j\in [0,1],j\in \mathcal{J}=\{1,2,3,4,5,6\},\hfill \end{array}$$

(11)

where

$$\begin{array}{ccc}& & g_1\left(x\right)=O(0.35,x_1)+O(0.6,x_2)+O(0.3,x_3)+O(0.4,x_4)+O(0.42,x_5)+O(0.45,x_6),\hfill \\ & & g_2\left(x\right)=O(0.2,x_1)+O(0.3,x_2)+O(0.68,x_3)+O(0.4,x_4)+O(0.8,x_5)+O(0.6,x_6),\hfill \\ & & g_3\left(x\right)=O(0.25,x_1)+O(0.4,x_2)+O(0.32,x_3)+O(0.3,x_4)+O(0.7,x_5)+O(0.8,x_6),\hfill \\ & & g_4\left(x\right)=O(0.26,x_1)+O(0.3,x_2)+O(0.45,x_3)+O(0.6,x_4)+O(0.42,x_5)+O(0.9,x_6),\hfill \end{array}$$

and the operator $O(a_{ij},x_j)$ is the min-shifted overlap function with

$$\begin{array}{c}\hfill O(a_{ij},x_j)={\displaystyle \frac{min\{a_{ij},x_j\}}{min\{a_{ij},x_j\}+(1-max\{0,x_j+a_{ij}-1\})}}.\end{array}$$

According to Theorem 3, to solve the optimal solution of problem (11), it can be transformed into the following single-variable problem.

$$\begin{array}{ccc}\hfill \mathrm{Minimize}& & Z\left(y\right)=y\hfill \\ \hfill \mathrm{subject} \mathrm{to}& & G_1\left(y\right)\ge 1.8,\hfill \\ & & G_2\left(y\right)\ge 0.6,\hfill \\ & & G_3\left(y\right)\ge 2.0,\hfill \\ & & G_4\left(y\right)\ge 1.8,\hfill \\ & & y\in [0,1],\hfill \end{array}$$

(12)

where

$$\begin{array}{ccc}& & G_1\left(y\right)=O(0.35,y)+O(0.6,y)+O(0.3,y)+O(0.4,y)+O(0.42,y)+O(0.45,y),\hfill \\ & & G_2\left(y\right)=O(0.2,y)+O(0.3,y)+O(0.68,y)+O(0.4,y)+O(0.8,y)+O(0.6,y),\hfill \\ & & G_3\left(y\right)=O(0.25,y)+O(0.4,y)+O(0.32,y)+O(0.3,y)+O(0.7,y)+O(0.8,y),\hfill \\ & & G_4\left(y\right)=O(0.26,y)+O(0.3,y)+O(0.45,y)+O(0.6,y)+O(0.42,y)+O(0.9,y).\hfill \end{array}$$

By applying either the method proposed in [30] or the classical bisection method to solve problem (12), we obtain the optimal value $y^{*}=0.643875$. According to Theorem 3, the corresponding uniform-optimal solution $x^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}$ for problem (11) is

$$\begin{array}{c}\hfill x^{*}=(x_1^{*},\cdots ,x_6^{*})=(0.643875,\cdots ,0.643875).\end{array}$$

In Example 1, the uniform-optimal solution $x^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}$, where $x_j^{*}=y^{*}=0.643875$ for all $j\in \mathcal{J}=\{1,2,\cdots ,6\}$, is substituted into each constraint of problem (11). The corresponding values of the constraint functions are computed as follows:

$$\begin{array}{cc}\hfill & g_1\left(x^{*}\right)=1.869>1.8,g_2\left(x^{*}\right)=2.159>0.6,g_3\left(x^{*}\right)=2.000=2.0,\hfill \\ \hfill & \mathrm{and}{g}_4\left(x^{*}\right)=2.106>1.8.\hfill \end{array}$$

4. Solving the Minimal-Optimal Solution for Problem (3)

As mentioned above, the bisection method can be used to solve the min-max programming problem with a general addition-overlap function, including the problem (3), to obtain the uniform-optimal solution $x^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}$. However, no efficient method is currently available for directly computing a minimal-optimal solution to problem (3).

Although the uniform-optimal solution can be obtained for problem (3), it is not necessarily a “minimal solution” in terms of constraint satisfaction. Nevertheless, it serves as an upper bound among all optimal solutions. Therefore, identifying a minimal-optimal solution to the problem (3) involves determining which components of the uniform-optimal solution can be reduced without violating feasibility or compromising optimality. In other words, we need to distinguish which components are fixed and unchangeable, and which ones can be adjusted.

4.1. The Critical Constraints

Definition 5.

Let $x^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}$ with $x_j^{*}=y^{*}$ for all $j\in \mathcal{J}$ be the uniform-optimal solution of problem (3). Define the following:

(i).

The critical set is defined as $I\left(x^{*}\right)=\{i\in \mathcal{I}\mid g_i\left(x^{*}\right)=b_i\}$.

(ii).

For $i\in I\left(x^{*}\right)$, the constraint $g_i\left(x^{*}\right)=b_i$ is called a critical constraint.

(iii).

For $i\in I\left(x^{*}\right)$, define the binding set as $J_i\left(x^{*}\right)=J_i^{*1}\cup J_i^{*2}\cup J_i^{*3}$, and a variable $x_j$ is called a binding variable if $j\in J_i\left(x^{*}\right)$, where

$$\begin{array}{cc}\hfill J_i^{*1}& =\{j\in \mathcal{J}\mid 0\le a_{ij}<0.5 \mathrm{and} 0\le x_j^{*}\le a_{ij}\},\hfill \\ \hfill J_i^{*2}& =\{j\in \mathcal{J}\mid 0\le a_{ij}<0.5 \mathrm{and} 1-a_{ij}\le x_j^{*}\le 1\}.\hfill \\ \hfill J_i^{*3}& =\{j\in \mathcal{J}\mid 0.5\le a_{ij}\le 1 \mathrm{and} 0\le x_j^{*}\le 1\}.\hfill \end{array}$$

Lemma 3.

Let $x^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}$, with $x_j^{*}=y^{*}$ for all $j\in \mathcal{J}$, be the uniform-optimal solution of problem (3). Then, the critical set is non-empty, that is, $I\left(x^{*}\right)=\{i\in \mathcal{I}\mid g_i\left(x^{*}\right)=b_i\}\ne \varnothing$.

Proof. 

By Theorem 3, the uniform solution $x^{*}=(y^{*},\cdots ,y^{*})$ is optimal for problem (3). Suppose, for contradiction, that $I\left(x^{*}\right)=\varnothing$. Then, for every $i\in \mathcal{I}$, we have

$$\sum _{j=1}^{n}O(a_{ij},y^{*})>b_i.$$

Since the overlap function $O(a,x)$ is continuous and non-decreasing in x, we can slightly decrease $y^{*}$ to a value $y^{\prime }<y^{*}$ such that

$$\sum _{j=1}^{n}O(a_{ij},y^{\prime })\ge b_i,\forall i\in \mathcal{I}.$$

This implies that $y^{\prime }$ is still feasible for (3) but strictly smaller than $y^{*}$, which contradicts the optimality of $y^{*}$. Therefore, $I\left(x^{*}\right)\ne \varnothing$ must hold. □

Lemma 3 shows that when the optimal value $y^{*}$ of problem (3) is determined, there must exist at least one critical constraint as follows:

$$\begin{array}{c}\hfill g_i\left(x^{*}\right)=\sum _{j=1}^{n}O(a_{ij},x_j^{*})=\sum _{j=1}^{n}O(a_{ij},y^{*})=b_i,\mathrm{for}i\in I\left(x^{*}\right).\end{array}$$

(13)

Such behavior can be explicitly observed in Example 1 through the equality $g_3\left(x^{*}\right)=b_3$. Moreover, the critical constraints $g_i\left(x^{*}\right)=b_i$ for $i\in I\left(x^{*}\right)$ in (13) are essential for characterizing the minimal-optimal solution to problem (3). The theoretical foundation established in Theorems 1 and 2 rigorously supports this relationship. In particular:

• Theorem 1:(i) shows that for $0\le a\le 0.5$, the overlap function $O(a,x)$ is strictly increasing on the interval $[0,a]$.
• Theorem 1:(iii) ensures that $O(a,x)$ is strict monotonicity over the interval $[1-a,1]$ if $0\le a\le 0.5$.
• Theorem 2 guarantees that $O(a,x)$ is strictly increasing over the entire interval $[0,1]$ when $0.5\le a\le 1$.

Lemma 4

(Binding variables). Let $x^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}$, with $x_j^{*}=y^{*}$ for all $j\in \mathcal{J}$, be the uniform-optimal solution to problem (3). Let $x^{\prime }={\left(x_j^{\prime }\right)}_{j\in \mathcal{J}}$ be any other optimal solution of the same problem. Then

(i). 

For $i\in I\left(x^{*}\right)$ and $j\in J_i^{*1}$ such that $0\le x_j^{*}\le a_{ij}$, it must hold that $x_j^{\prime }=x_j^{*}$;

(ii). 

For $i\in I\left(x^{*}\right)$ and $j\in J_i^{*2}$ such that $1-a_{ij}\le x_j^{*}\le 1$, it also holds that $x_j^{\prime }=x_j^{*}$;

(iii). 

For $i\in I\left(x^{*}\right)$ and $j\in J_i^{*3}$ such that $0\le x_j^{*}\le 1$, it holds that $x_j^{\prime }=x_j^{*}$.

Proof. 

(i).

Suppose, for contradiction, that $x^{\prime }={\left(x_j^{\prime }\right)}_{j\in \mathcal{J}}\ne x^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}$ for some $j\in J_i^{*1}$. Without loss of generality, assume $x_k^{\prime }=x_k^{*}$ for all $k\in \mathcal{J}$, $k\ne r$, and $x_r^{\prime }<x_r^{*}$ for some $r\in J_i^{*1}$.

Since $0\le a_{ir}<0.5$ and $0\le x_r^{*}\le a_{ir}$, by Theorem 1-(i), the overlap function $O(a_{ir},x)$ is strictly increasing over the interval $[0,a_{ir}]$. Therefore,

$$O(a_{ir},x_r^{\prime })<O(a_{ir},x_r^{*}).$$

For the critical constraint corresponding to $i\in I\left(x^{*}\right)$, we have

$$g_i\left(x^{\prime }\right)=\sum _{j\in \mathcal{J},j\ne r}O(a_{ij},x_j^{\prime })+O(a_{ir},x_r^{\prime })<\sum _{j\in \mathcal{J},j\ne r}O(a_{ij},x_j^{*})+O(a_{ir},x_r^{*})=b_i,$$

which contradicts the feasibility of $x^{\prime }$, as the i-th critical constraint is violated.

Alternatively, suppose $x_j^{\prime }\ge x_j^{*}$ for all $j\in \mathcal{J}$, with $x_k^{\prime }=x_k^{*}=y^{*}$ for all $k\in \mathcal{J}$, $k\ne r$, and $x_r^{\prime }>x_r^{*}=y^{*}$. Then the objective value of $x^{\prime }$ is

$$Z\left(x^{\prime }\right)=\underset{j\in \mathcal{J}}{max}\left\{x_j^{\prime }\right\}=x_r^{\prime }>Z\left(x^{*}\right)=\underset{j\in \mathcal{J}}{max}\left\{x_j^{*}\right\}=y^{*},$$

which contradicts the optimality of $x^{\prime }$.

Hence, in either case, for $i\in I\left(x^{*}\right)$, we conclude that $x_j^{\prime }=x_j^{*}$ for all $j\in J_i^{*1}$.

(ii)

The proof follows a similar argument. Since $j\in J_i^{*2}$ and $1-a_{ij}\le x_j^{*}\le 1$, the overlap function $O(a_{ij},x_j)$ is strictly increasing on the interval $[1-a_{ij},1]$ by Theorem 1-(iii). For the critical constraint $g_i\left(x^{*}\right)=b_i,i\in I\left(x^{*}\right)$, reducing $x_j^{\prime }$ would decrease $O(a_{ij},x_j^{\prime })$, thereby reducing $g_i\left(x^{\prime }\right)$ below $b_i$, violating feasibility. Increasing $x_j^{\prime }$ would lead to $x_j^{\prime }>y^{*}$, which contradicts the optimality of $x^{\prime }$. Thus, it must be that $x_j^{\prime }=x_j^{*}$ for $j\in J_i^{*2}$.

(iii)

For any $j\in J_i^{*3}$. Theorem 2 ensures that $O(a_{ij},x_j)$ is strictly increasing over the entire interval $[0,1]$. Therefore, for the critical constraint $g_i\left(x^{*}\right)=b_i,i\in I\left(x^{*}\right)$, reducing $x_j^{\prime }$ would decrease $O(a_{ij},x_j^{\prime })$, and consequently $g_i\left(x^{\prime }\right)<b_i$, violating feasibility. Increasing $x_j^{\prime }$ would result in $x_j^{\prime }>x_j^{*}=y^{*}$, again contradicting the optimality of $x^{\prime }$. Hence, it must be that $x_j^{\prime }=x_j^{*}$ for $j\in J_i^{*3}$.

□

The results established in Lemma 4 reveal an essential structural property of the minimal-optimal solution to problem (3): Certain variables, especially those identified as binding variables $x_j$, for $j\in J_i\left(x^{*}\right)$ with respect to the critical constraints $g_i\left(x^{*}\right)=b_i$, where $i\in I\left(x^{*}\right)$, must remain fixed at the uniform-optimal value $y^{*}$ in any optimal solution.

Although the uniform-optimal solution $x^{*}=(y^{*},\cdots ,y^{*})$ is usually not minimal-optimal, it serves as an upper bound for each component of any minimal-optimal solution. In particular, Lemma 4 confirms that the binding variables $x_j=x_j^{*}=y^{*}$, for all $j\in J_i\left(x^{*}\right)=J_i^{*1}\cup J_i^{*2}\cup J_i^{*3}$ and $i\in I\left(x^{*}\right)$, are fixed and cannot be decreased without violating feasibility or optimality. In contrast, the remaining variables $x_j=x_j^{*}$, where $j\in \mathcal{J}\setminus J_i\left(x^{*}\right)$ for $i\in I\left(x^{*}\right)$, may be further reduced while maintaining feasibility. This observation provides a solid foundation for constructing a minimal-optimal solution of problem (3).

Example 2.

Apply the optimal value $y^{*}$ obtained in Example 1 to identify the critical set, critical constraint, and binding variables, according to Lemma 4.

From Example 1, we have the optimal value $y^{*}=0.643875$ and the uniform-optimal solution $x^{*}={\left(x_j^{*}\right)}_{1\times 6}$, where $x_j^{*}=y^{*}$ for all $j\in \mathcal{J}=\{1,\dots ,6\}$. Substituting $x^{*}$ into each constraint of problem (11) yields the following values:

$$\begin{array}{cc}\hfill & g_1\left(x^{*}\right)=1.869>1.8,g_2\left(x^{*}\right)=2.159>0.6,g_3\left(x^{*}\right)=2.000=2.0,\hfill \\ \hfill & \mathrm{and}{g}_4\left(x^{*}\right)=2.106>1.8.\hfill \end{array}$$

By Definition 5, the critical set is

$$I\left(x^{*}\right)=\left\{3\right\},\mathrm{and}\mathrm{the}\mathrm{critical}\mathrm{constraint}\mathrm{is}{g}_3\left(x^{*}\right)=b_3.$$

In particular, we have

$$\begin{array}{cc}\hfill g_3\left(x^{*}\right)& =O(0.25,x_1^{*})+O(0.4,x_2^{*})+O(0.32,x_3^{*})+O(0.3,x_4^{*})+O(0.7,x_5^{*})+O(0.8,x_6^{*})\hfill \\ \hfill & =2.0=b_3.\hfill \end{array}$$

Analyzing the overlap function components of the critical constraint:

• $0\le a_{31}=0.25,a_{33}=0.32,a_{34}=0.3\le 0.5$, but $x_j^{*}\notin [0,a_{3j}]$ for $j=1,3,4$$\Rightarrow J_3^{*1}=\varnothing$,
• $0\le a_{32}=0.4\le 0.5$ and $0.6\le x_2^{*}\le 1\Rightarrow J_3^{*2}=\left\{2\right\}$,
• $0.5\le a_{35}=0.7,a_{36}=0.8\le 1\Rightarrow J_3^{*3}=\{5,6\}$.

Combining the three subsets, the binding set is

$$J_3\left(x^{*}\right)=J_3^{*1}\cup J_3^{*2}\cup J_3^{*3}=\{2,5,6\}.$$

Therefore, the binding variables $x_2=x_5=x_6=y^{*}$ must remain fixed and cannot be reduced, while the remaining variables $x_1,x_3$, and $x_4$ may be adjusted in the process of identifying a minimal-optimal solution.

4.2. Alternative Optimal Solutions of Problem (3)

Lemma 4 identifies the binding and adjustable variables that determine the structure of a minimal-optimal solution to problem (3). The remaining challenge is to reduce the values of the adjustable variables while preserving optimality. Fortunately, since the uniform-optimal solution provides an upper bound for all optimal solutions, reducing the value of any one adjustable variable may still yield an alternative optimal solution.

Let $x^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}$ be the uniform-optimal solution to problem (3), where $x_j^{*}=y^{*}$ for all $j\in \mathcal{J}$. Define

$$x_{\left(0\right)}^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}=(y^{*},y^{*},\cdots ,y^{*}) \mathrm{and} {\underline{x}}_{\left(j\right)}=(y^{*},\cdots ,y^{*},{\underline{x}}_j^{*},y^{*},\cdots ,y^{*}),j\in \mathcal{J}$$

(14)

and

$${\underline{x}}_j^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_j\left(i\right)\right\},$$

$$\begin{array}{c}\hfill x_j\left(i\right)=\left\{\begin{array}{cc}min\left\{s_{ij}\right|O(a_{ij},s_{ij})=b_i-▵b_i\},\hfill & \mathrm{if}{b}_i-▵b_i>0,\hfill \\ 0,\hfill & \mathrm{if}{b}_i-▵b_i\le 0,\hfill \end{array}\right.\end{array}$$

(15)

with

$$▵b_i=\sum _{k\in \mathcal{J},k\ne j}O(a_{ik},y^{*})=g_i\left(x_{\left(0\right)}^{*}\right)-O(a_{ij},y^{*}).$$

By the definition in (14), the vector $x_{\left(0\right)}^{*}$ is equivalent to the uniform-optimal solution of problem (3). In the vector ${\underline{x}}_{\left(j\right)}$, all components are equal to $y^{*}$ except the j-th component, which is ${\underline{x}}_j^{*}$. The following theorem demonstrates that ${\underline{x}}_{\left(j\right)}$ is also an optimal solution.

Theorem 4.

Let the vectors $x_{\left(0\right)}^{*}$ and ${\underline{x}}_{\left(j\right)}$ be denoted as in (14). Then

(i). 

$y^{*}\ge {\underline{x}}_j^{*}$ holds;

(ii). 

${\underline{x}}_{\left(j\right)}$ is an optimal solution of problem (3).

Proof. 

(i).

From (14) and (15), we know that $g_i\left(x_{\left(0\right)}^{*}\right)\ge b_i$ for all $i\in \mathcal{I}$. Consider two cases:

• Case 1: If $b_i-▵b_i\le 0$ for all $i\in \mathcal{I}$, then $x_j\left(i\right)=0$ such that ${\underline{x}}_j^{*}=0$, hence $y^{*}\ge {\underline{x}}_j^{*}$.
• Case 2: If $b_i-▵b_i>0$ for some $i\in \mathcal{I}$, then it implies that

  $$\begin{array}{ccc}& & g_i\left(x_{\left(0\right)}^{*}\right)=▵b_i+O(a_{ij},y^{*})\ge b_i\hfill \\ & & \Rightarrow O(a_{ij},y^{*})\ge b_i-▵b_i=O(a_{ij},x_j\left(i\right)),\hfill \end{array}$$

  where $x_j\left(i\right)$ is defined as the smallest value such that $O(a_{ij},x_j\left(i\right))=b_i-▵b_i$. Since $O(a_{ij},x)$ is non-decreasing in x, it follows that $y^{*}\ge x_j\left(i\right)$. Thus,

  $$y^{*}\ge {\underline{x}}_j^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_j\left(i\right)\right\}.$$

Combining both cases, we conclude that $y^{*}\ge {\underline{x}}_j^{*}$ holds.

(ii).

For the vector ${\underline{x}}_{\left(j\right)}$, from (14) and (15), we have

$$g_i\left({\underline{x}}_{\left(j\right)}\right)=▵b_i+O(a_{ij},{\underline{x}}_j^{*}).$$

To show that ${\underline{x}}_{\left(j\right)}$ is an optimal solution to problem (3), we check the feasibility and optimality:

• Feasibility:
  Case 1: If ${\underline{x}}_j^{*}=0$, then it follows that $b_i-▵b_i\le 0$, i.e., $▵b_i\ge b_i$, for all $i\in \mathcal{I}$ and $O(a_{ij},{\underline{x}}_j^{*})=0$. Therefore,

  $$g_i\left({\underline{x}}_{\left(j\right)}\right)=▵b_i+O(a_{ij},{\underline{x}}_j^{*})=▵b_i+0=▵b_i\ge b_i.$$
  Case 2: If $b_i-▵b_i>0$ for some $i\in \mathcal{I}$, by the definition of $x_j\left(i\right)=min\left\{s_{ij}\right|O(a_{ij},s_{ij})=b_i-▵b_i\}$ and ${\underline{x}}_j^{*}={max}_{i\in \mathcal{I}}\left\{x_j\left(i\right)\right\}$, we have

  $$\begin{array}{ccc}\hfill g_i\left({\underline{x}}_{\left(j\right)}\right)& =& ▵b_i+O(a_{ij},{\underline{x}}_j^{*})\hfill \\ & \ge & ▵b_i+O(a_{ij},x_j\left(i\right))\hfill \\ & =& ▵b_i+(b_i-▵b_i)\hfill \\ & =& b_i.\hfill \end{array}$$

  In both cases, $g_i\left({\underline{x}}_{\left(j\right)}\right)\ge b_i$ for all $i\in \mathcal{I}$; therefore, ${\underline{x}}_{\left(j\right)}$ is feasible to problem (3).
• Optimality: From part (i), we know that $y^{*}\ge {\underline{x}}_j^{*}$, so

  $$Z\left({\underline{x}}_{\left(j\right)}\right)=max\{y^{*},\cdots ,y^{*},{\underline{x}}_j^{*},y^{*},\cdots ,y^{*}\}=y^{*}=Z\left(x^{*}\right).$$

  Since ${\underline{x}}_{\left(j\right)}$ is feasible and achieves the same objective value, it is an optimal solution to problem (3).

□

Theorem 4 provides valuable insight: for each $j\in \mathcal{J}=\{1,2,\cdots ,n\}$, the vector ${\underline{x}}_{\left(j\right)}$ is an optimal solution to problem (3). These alternative optimal solutions offer flexibility and can be utilized to identify a minimal-optimal solution. Furthermore, by using different combinations of such optimal solutions, it is possible to yield different minimal-optimal solutions to problem (3).

Theorem 5.

Let the vectors $x_{\left(0\right)}^{*}$ and $x_{\left(j\right)}$ be denoted as in (14). Define the index set

$$I_{\left(j\right)}^{\#}=\{i\in \mathcal{I}|\underset{i\in \mathcal{I}}{max}\left\{x_j\left(i\right)\right\}\}.$$

If $b_i-▵b_i>0$ holds for some $i\in \mathcal{I}$, then for $i\in I_{\left(j\right)}^{\#}$, it follows that

$$O(a_{ij},{\underline{x}}_j^{*})=b_i-▵b_i \mathrm{and} g_i\left(x_{\left(j\right)}\right)=b_i.$$

Proof. 

Since $b_i-▵b_i>0$ holds for some $i\in \mathcal{I}$, it follows that $I_{\left(j\right)}^{\#}=\{i\in \mathcal{I}|{max}_{i\in \mathcal{I}}\left\{x_j\left(i\right)\right\}\}\ne \varnothing$. By the definition of ${\underline{x}}_j^{*}$, we have

$$\begin{array}{c}\hfill {\underline{x}}_j^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_j\left(i\right)\right\}=x_j\left(i\right),i\in I_{\left(j\right)}^{\#}.\end{array}$$

(16)

Moreover, from Theorem 4, we know that $x_{\left(j\right)}\in X(A,b)$, i.e., it is a feasible solution to problem (3). Therefore, for all $i\in \mathcal{I}$, it holds that

$$g_i\left(x_{\left(j\right)}\right)=O(a_{ij},{\underline{x}}_j^{*})+▵b_i\ge b_i,$$

which implies

$$O(a_{ij},{\underline{x}}_j^{*})\ge b_i-▵b_i,\mathrm{for}\mathrm{all}i\in \mathcal{I}.$$

Now, using (16), for $i\in I_{\left(j\right)}^{\#}$, we have

$$\begin{array}{c}\hfill O(a_{ij},{\underline{x}}_j^{*})=O(a_{ij},\underset{i\in \mathcal{I}}{max}\left\{x_j\left(i\right)\right\})=O(a_{ij},x_j\left(i\right))=b_i-▵b_i.\end{array}$$

Therefore,

$$g_i\left(x_{\left(j\right)}\right)=O(a_{ij},{\underline{x}}_j^{*})+▵b_i=(b_i-▵b_i)+▵b_i=b_i,i\in I_{\left(j\right)}^{\#}.$$

□

4.3. Iterative Approach for Finding the Minimal-Optimal Solution

Based on the optimal value $y^{*}$ and the uniform-optimal solution $x_{\left(0\right)}^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}$, where $x_j^{*}=y^{*}$ for all $j\in \mathcal{J}$, together with the properties established in the previous sections, we propose the following iterative approach to find a minimal-optimal solution to problem (3).

• The iterative approach:

• Step 1: Perform the following process for iterations $k=1,\cdots ,n$:
  At the k-th iteration, compute the vector

  $$x_{\left(k\right)}^{*}=({\underline{x}}_1^{*},{\underline{x}}_2^{*},\cdots ,{\underline{x}}_k^{*},x_{k+1}^{\left(0\right)},\cdots ,x_n^{\left(0\right)}),$$

  where

  $$x_{k+1}^{\left(0\right)}=\cdots =x_n^{\left(0\right)}=y^{*}, \mathrm{and} {\underline{x}}_k^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_k\left(i\right)\right\}.$$
  For each component, $x_k\left(i\right)$ is defined as

  $$\begin{array}{c}\hfill x_k\left(i\right)=\left\{\begin{array}{cc}min\left\{s_{ik}\right|O(a_{ik},s_{ik})=b_i-▵b_i^{\left(k\right)}\},\hfill & \mathrm{if}{b}_i-▵b_i^{\left(k\right)}>0,\hfill \\ 0,\hfill & \mathrm{if}{b}_i-▵b_i^{\left(k\right)}\le 0,\hfill \end{array}\right.\end{array}$$

  (17)

  and

  $$\begin{array}{c}\hfill ▵b_i^{\left(k\right)}=g_i\left(x_{(k-1)}^{*}\right)-O(a_{ik},y^{*}).\end{array}$$

  (18)
• Step 2: After the n-th iteration, the vector

  $$x_{\left(n\right)}^{*}=({\underline{x}}_1^{*},{\underline{x}}_2^{*},\cdots ,{\underline{x}}_n^{*})$$

  is produced as the output. This vector is the candidate minimal-optimal solution.

To prove that the vector $x_{\left(n\right)}^{*}$ obtained through this iterative procedure is indeed a minimal-optimal solution to problem (3), we first establish the following properties.

Theorem 6.

Let the vector $x_{\left(k\right)}^{*}=({\underline{x}}_1^{*},{\underline{x}}_2^{*},\cdots ,{\underline{x}}_k^{*},x_{k+1}^{\left(0\right)},\cdots ,x_n^{\left(0\right)})$, where $k=1,2,\cdots ,n$, be obtained by the iterative approach described above. Then, the following properties hold:

(i). 

For every $k\in \mathcal{J}$, the vector $x_{\left(k\right)}^{*}$ is a feasible solution to problem (3).

(ii). 

Each component satisfies ${\underline{x}}_k^{*}\le x_k^{\left(0\right)}=y^{*}$ for all $k\in \mathcal{J}$.

(iii). 

For every $k\in \mathcal{J}$, the vector $x_{\left(k\right)}^{*}$ is an optimal solution to problem (3).

(iv). 

The inequality $g_i\left(x_{(k-1)}^{*}\right)-g_i\left(x_{\left(k\right)}^{*}\right)\ge 0$ holds for all $i\in \mathcal{I}$ and $k=1,2,\cdots ,n$.

Proof. 

(i).

According to Theorem 4 and the definition of

$${\underline{x}}_{\left(j\right)}=(y^{*},\cdots ,y^{*},{\underline{x}}_j^{*},y^{*},\cdots ,y^{*}),j\in \mathcal{J},$$

we know that the vector

$$x_{\left(1\right)}^{*}={\underline{x}}_{\left(1\right)}=({\underline{x}}_1^{*},x_2^{\left(0\right)},\cdots ,x_n^{\left(0\right)}), \mathrm{where} {\underline{x}}_1^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_1\left(i\right)\right\}$$

is an optimal solution of problem (3). Therefore, for $k=1$, we have

$$g_i\left(x_{\left(1\right)}^{*}\right)=O(a_{i1},{\underline{x}}_1^{*})+\sum _{j=2}^{n}O(a_{ij},x_j^{\left(0\right)})=O(a_{i1},{\underline{x}}_1^{*})+▵b_i^{\left(1\right)}\ge b_i,\forall i\in \mathcal{I}.$$

For $k=2$, consider the vector

$$x_{\left(2\right)}^{*}=({\underline{x}}_1^{*},{\underline{x}}_2^{*},x_3^{\left(0\right)},\cdots ,x_n^{\left(0\right)}),$$

and observe that

$$\begin{array}{ccc}\hfill g_i\left(x_{\left(2\right)}^{*}\right)& =& O(a_{i1},{\underline{x}}_1^{*})+O(a_{i2},{\underline{x}}_2^{*})+\sum _{j=3}^{n}O(a_{ij},x_j^{\left(0\right)})\hfill \\ & =& g_i\left(x_{\left(1\right)}^{*}\right)+O(a_{i2},{\underline{x}}_2^{*})-O(a_{i2},x_2^{\left(0\right)}).\hfill \end{array}$$

(19)

We consider two cases to verify the feasibility of $x_{\left(2\right)}^{*}$.

• Case 1: If $b_i-▵b_i^{\left(2\right)}\le 0$ for all $i\in \mathcal{I}$, i.e., $▵b_i^{\left(2\right)}\ge b_i$, then $x_2\left(i\right)=0$ and ${\underline{x}}_2^{*}=0$. Substituting into (19), we get

  $$\begin{array}{ccc}\hfill g_i\left(x_{\left(2\right)}^{*}\right)& =& g_i\left(x_{\left(1\right)}^{*}\right)+O(a_{i2},{\underline{x}}_2^{*})-O(a_{i2},x_2^{\left(0\right)})\hfill \\ & =& g_i\left(x_{\left(1\right)}^{*}\right)+0-O(a_{i2},y^{*})\hfill \\ & =& ▵b_i^{\left(2\right)}\hfill \\ & \ge & b_i.\hfill \end{array}$$
• Case 2: If $b_i-▵b_i^{\left(2\right)}>0$ for some $i\in \mathcal{I}$, then by construction, $x_2\left(i\right)=min\left\{s_{i2}\right|O(a_{i2},s_{i2})=b_i-▵b_i^{\left(2\right)}\}$ and ${\underline{x}}_2^{*}={max}_{i\in \mathcal{I}}\left\{x_2\left(i\right)\right\}$, it implies that

  $$\begin{array}{ccc}\hfill g_i\left(x_{\left(2\right)}^{*}\right)& =& g_i\left(x_{\left(1\right)}^{*}\right)+O(a_{i2},{\underline{x}}_2^{*})-O(a_{i2},x_2^{\left(0\right)})\hfill \\ & \ge & g_i\left(x_{\left(1\right)}^{*}\right)+O(a_{i2},x_2\left(i\right))-O(a_{i2},y^{*})\hfill \\ & =& g_i\left(x_{\left(1\right)}^{*}\right)+[b_i-▵b_i^{\left(2\right)}]-O(a_{i2},y^{*})\hfill \\ & =& g_i\left(x_{\left(1\right)}^{*}\right)+[b_i-(g_i\left(x_{\left(1\right)}^{*}\right)-O(a_{i2},y^{*}))]-O(a_{i2},y^{*})\hfill \\ & =& b_i.\hfill \end{array}$$

• Combining both cases, we conclude that $x_{\left(2\right)}^{*}$ is feasible to problem (3), i.e.,

$$\begin{array}{c}\hfill g_i\left(x_{\left(2\right)}^{*}\right)=O(a_{i1},{\underline{x}}_1^{*})+O(a_{i2},{\underline{x}}_2^{*})+\sum _{j=3}^{n}O(a_{ij},x_j^{\left(0\right)})\ge b_i,\forall i\in \mathcal{I}.\end{array}$$

The argument extends similarly to $k=3,\cdots ,n$, and in particular,

$$g_i\left(x_{\left(k\right)}^{*}\right)=\sum _{j=1}^{k}O(a_{ij},{\underline{x}}_j^{*})+\sum _{j=k+1}^{n}O(a_{ij},x_j^{\left(0\right)})\ge b_i,\forall i\in \mathcal{I}.$$

For $k=n$,

$$g_i\left(x_{\left(n\right)}^{*}\right)=\sum _{j=1}^{n}O(a_{ij},{\underline{x}}_j^{*})\ge b_i,\forall i\in \mathcal{I}.$$

(ii).

Since both $x_{\left(0\right)}^{*}$ and $x_{\left(k\right)}^{*}\in X(A,b)$ for all $k\in \mathcal{J}$, then from part (i), we know that

$$g_i\left(x_{(k-1)}^{*}\right)\ge b_i,\forall i\in \mathcal{I}.$$

Moreover, according to (17) and (18), we have

$$\begin{array}{c}\hfill x_k^{\left(0\right)}=y^{*},{\underline{x}}_k^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_k\left(i\right)\right\}, \mathrm{and} ▵b_i^{\left(k\right)}=g_i\left(x_{(k-1)}^{*}\right)-O(a_{ik},x_k^{\left(0\right)}).\end{array}$$

• If $b_i-▵b_i^{\left(k\right)}\le 0$ for all $i\in \mathcal{I}$, then $x_k\left(i\right)=0$ and ${\underline{x}}_k^{*}=0$, so ${\underline{x}}_k^{*}=0\le x_k^{\left(0\right)}=y^{*}$.
• If $b_i-▵b_i^{\left(k\right)}>0$ for some $i\in \mathcal{I}$, then it implies that

  $$\begin{array}{ccc}& & g_i\left(x_{(k-1)}^{*}\right)=▵b_i^{\left(k\right)}+O(a_{ik},x_k^{\left(0\right)})\ge b_i\hfill \\ & & \Rightarrow O(a_{ik},x_k^{\left(0\right)})\ge b_i-▵b_i^{\left(k\right)}=O(a_{ik},x_k\left(i\right)),\hfill \end{array}$$

  where $x_k\left(i\right)$ is defined as the smallest value such that $O(a_{ik},x_k\left(i\right))=b_i-▵b_i^{\left(k\right)}$. Since $O(a_{ij},x)$ is non-decreasing in x, it follows that $x_k^{\left(0\right)}\ge x_k\left(i\right)$. Thus,

  $$x_k^{\left(0\right)}\ge {\underline{x}}_k^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_k\left(i\right)\right\}.$$

Thus, ${\underline{x}}_k^{*}\le x_k^{\left(0\right)}=y^{*}$ holds for all $k\in \mathcal{J}$.

(iii).

By (i) and (ii) above, for all $k\in \mathcal{J}$, there are $x_{\left(k\right)}^{*}\in X(A,b)$ and ${\underline{x}}_k^{*}\le x_k^{\left(0\right)}=y^{*}$.

For $k=1,2,\cdots ,n-1$, we have

$$x_{\left(k\right)}^{*}=({\underline{x}}_1^{*},{\underline{x}}_2^{*},\cdots ,{\underline{x}}_k^{*},x_{k+1}^{\left(0\right)},\cdots ,x_n^{\left(0\right)})=({\underline{x}}_1^{*},{\underline{x}}_2^{*},\cdots ,{\underline{x}}_k^{*},y^{*},\cdots ,y^{*}).$$

Thus, $Z\left(x_{\left(k\right)}^{*}\right)=max\{{\underline{x}}_1^{*},{\underline{x}}_2^{*},\cdots ,{\underline{x}}_k^{*},y^{*},\cdots ,y^{*}\}=y^{*}$ for all $k<n$.

Now, assume ${\underline{x}}_k^{*}<y^{*}$ for all $k\in \mathcal{J}$. Then

$$Z\left(x_{\left(n\right)}^{*}\right)=max\{{\underline{x}}_1^{*},{\underline{x}}_2^{*},\cdots ,{\underline{x}}_n^{*}\}<y^{*},$$

which contradicts the fact that $y^{*}$ is the optimal value of problem (3). Therefore, $Z\left(x_{\left(n\right)}^{*}\right)=y^{*}$, and all $x_{\left(k\right)}^{*}$ are optimal.

(iv).

From (ii), we have $x_k^{\left(0\right)}\ge {\underline{x}}_k^{*}$; hence,

$$O(a_{ik},x_k^{\left(0\right)})\ge O(a_{ik},{\underline{x}}_k^{*}),\forall i\in \mathcal{I}.$$

It follows that

$g_i\left(x_{(k-1)}^{*}\right)-g_i\left(x_{\left(k\right)}^{*}\right)=O(a_{ik},x_k^{\left(0\right)})-O(a_{ik},{\underline{x}}_k^{*})\ge 0,\forall i\in \mathcal{I},k=1,2,\cdots ,n.$

□

Theorem 6 shows that, for all $k\in \mathcal{J}$, the vector $x_{\left(k\right)}^{*}$ produced at each step of the iterative procedure remains an optimal solution to problem (3). In particular, this implies that the final vector $x_{\left(n\right)}^{*}$, computed at the last iteration, is also optimal. Furthermore, by Definition 4 and the property of Theorem 6:(ii), that ${\underline{x}}_k^{*}\le x_k^{\left(0\right)}=y^{*}$ for all $k\in \mathcal{J}$, the sequence of iterates satisfies the following component-wise inequality:

$$x_{\left(n\right)}^{*}\le x_{(n-1)}^{*}\le \cdots \le x_{\left(1\right)}^{*}\le x_{\left(0\right)}^{*}.$$

These properties are crucial in establishing that the final output $x_{\left(n\right)}^{*}$ is a minimal-optimal solution of problem (3).

Theorem 7.

Let the vector $x_{\left(k\right)}^{*}$, for $k\in \mathcal{J}$, be obtained from the iterative approach, and $I\left(x^{*}\right)=\{i\in \mathcal{I}|g_i\left(x^{*}\right)=b_i\}$ denote the critical set. Define the index set

$$I_{\left(k\right)}^{*}=\{i\in \mathcal{I}|\underset{i\in \mathcal{I}}{max}\left\{x_k\left(i\right)\right\}\},\forall k\in \mathcal{J}.$$

If $b_i-▵b_i^{\left(k\right)}>0$ for some $i\in \mathcal{I}$ and $k\in \mathcal{J}$, then

(i). 

$I\left(x_{\left(0\right)}^{*}\right)\subseteq I\left(x_{\left(1\right)}^{*}\right)$ and $I\left(x_{\left(k\right)}^{*}\right)\subseteq I\left(x_{(k+1)}^{*}\right)$ for all $k\in \mathcal{J}\setminus \left\{n\right\}$;

(ii). 

$g_i\left(x_{\left(k\right)}^{*}\right)=b_i$, for all $i\in I_{\left(k\right)}^{*}$.

Proof. 

(i).

By Lemma 3, $I\left(x_{\left(0\right)}^{*}\right)=\{i\in \mathcal{I}|g_i\left(x_{\left(0\right)}^{*}\right)=b_i\}\ne \varnothing$. Since $b_i-▵b_i^{\left(1\right)}=b_i-▵b_i>0$ for some $i\in \mathcal{I}$, Theorem 6 provides that $g_i\left(x_{\left(1\right)}^{*}\right)=b_i,i\in I_{\left(1\right)}^{*}=I_{\left(1\right)}^{\#}$.

Assume by contradiction that there exists $i\in I\left(x_{\left(0\right)}^{*}\right)$ such that $i\notin I\left(x_{\left(1\right)}^{*}\right)$. Then,

$$g_i\left(x_{\left(0\right)}^{*}\right)=b_i,\mathrm{but}{g}_i\left(x_{\left(1\right)}^{*}\right)>b_i,$$

which implies $g_i\left(x_{\left(0\right)}^{*}\right)-g_i\left(x_{\left(1\right)}^{*}\right)<0$, contradicting Theorem 6:(iv), which states that $g_i\left(x_{\left(0\right)}^{*}\right)-g_i\left(x_{\left(1\right)}^{*}\right)\ge 0$ for all $i\in \mathcal{I}$. Hence, we have

$$I\left(x_{\left(0\right)}^{*}\right)\subseteq I\left(x_{\left(1\right)}^{*}\right).$$

The same argument applies inductively to show

$$I\left(x_{\left(k\right)}^{*}\right)\subseteq I\left(x_{(k+1)}^{*}\right),\mathrm{for}\mathrm{all}k\in \mathcal{J}\setminus \left\{n\right\}.$$

(ii).

Since $b_i-▵b_i^{\left(k\right)}>0$ for some $i\in \mathcal{I}$, it follows that $I_{\left(k\right)}^{*}=\{i\in \mathcal{I}|{max}_{i\in \mathcal{I}}\left\{x_k\left(i\right)\right\}\}\ne \varnothing$. By the definition of ${\underline{x}}_k^{*}$, we have

$$\begin{array}{c}\hfill {\underline{x}}_k^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_k\left(i\right)\right\}=x_k\left(i\right),i\in I_{\left(k\right)}^{*}.\end{array}$$

(20)

From Theorem 6:(i), we know that $x_{\left(k\right)}^{*}\in X(A,b)$. This follows that

$$g_i\left(x_{\left(k\right)}^{*}\right)=O(a_{ik},{\underline{x}}_k^{*})+▵b_i^{\left(k\right)}\ge b_i,$$

which implies

$$O(a_{ik},{\underline{x}}_k^{*})\ge b_i-▵b_i^{\left(k\right)},\mathrm{for}\mathrm{all}i\in \mathcal{I}.$$

Now, using (20), for $i\in I_{\left(k\right)}^{*}$, we have

$$\begin{array}{c}\hfill O(a_{ik},{\underline{x}}_k^{*})=O(a_{ik},\underset{i\in \mathcal{I}}{max}\left\{x_k\left(i\right)\right\})=O(a_{ik},x_k\left(i\right))=b_i-▵b_i^{\left(k\right)},\end{array}$$

so that

$$g_i\left(x_{\left(k\right)}^{*}\right)=O(a_{ik},{\underline{x}}_k^{*})+▵b_i^{\left(k\right)}=(b_i-▵b_i^{\left(k\right)})+▵b_i^{\left(k\right)}=b_i,i\in I_{\left(k\right)}^{*}.$$

□

Theorem 7 identifies that for every $i\in I_{\left(k\right)}^{*}$, the function value $g_i\left(x_{\left(k\right)}^{*}\right)=b_i$, and the corresponding component ${\underline{x}}_k^{*}$ satisfies $O(a_{ik},{\underline{x}}_k^{*})=b_i-▵b_i^{\left(k\right)}$. This confirms that such constraints are tightly satisfied by $x_{\left(k\right)}^{*}$ and, importantly, that any further decrease in the component ${\underline{x}}_k^{*}$ would cause violation of feasibility for some critical constraints. Hence, Theorem 7 provides the foundational structure and contradiction mechanism required to prove the minimal-optimality of $x_{\left(n\right)}^{*}$.

Theorem 8.

The vector $x_{\left(n\right)}^{*}=({\underline{x}}_1^{*},{\underline{x}}_2^{*},\cdots ,{\underline{x}}_n^{*})$ obtained from the iterative approach is a minimal-optimal solution to problem (3).

Proof. 

By Theorem 6:(iii), $x_{\left(n\right)}^{*}$ is an optimal solution to problem (3), i.e.,

$$\begin{array}{c}\hfill g_i\left(x_{\left(n\right)}^{*}\right)=O(a_{i1},{\underline{x}}_1^{*})+\cdots +O(a_{in},{\underline{x}}_n^{*})\ge b_i,\forall i\in \mathcal{I}.\end{array}$$

Suppose, for contradiction, that there exists another minimal-optimal solution $\widehat{x}={\left({\widehat{x}}_j\right)}_{j\in \mathcal{J}}\in X(A,b)$ such that $\widehat{x}\le x_{\left(n\right)}^{*}$, where ${\widehat{x}}_j={\underline{x}}_j^{*},j\in \mathcal{J},j\ne k$ and ${\widehat{x}}_k<{\underline{x}}_k^{*}$.

From Theorem 7, we know

$$I\left(x_{\left(k\right)}^{*}\right)\subseteq I\left(x_{\left(n\right)}^{*}\right),\mathrm{and}{g}_i\left(x_{\left(k\right)}^{*}\right)=b_i,\mathrm{for}i\in I_{\left(k\right)}^{*}.$$

Hence,

$$\begin{array}{c}\hfill g_i\left(x_{\left(k\right)}^{*}\right)=\sum _{j=1}^{k-1}O(a_{ij},{\underline{x}}_j^{*})+O(a_{ik},{\underline{x}}_k^{*})+\sum _{j=k+1}^{n}O(a_{ij},x_j^{\left(0\right)})=b_i,i\in I_{\left(k\right)}^{*},\end{array}$$

and

$$\begin{array}{c}\hfill g_i\left(x_{\left(n\right)}^{*}\right)=\sum _{j=1}^{k-1}O(a_{ij},{\underline{x}}_j^{*})+O(a_{ik},{\underline{x}}_k^{*})+\sum _{j=k+1}^{n}O(a_{ij},{\underline{x}}_j^{*})=b_i,i\in I_{\left(k\right)}^{*}.\end{array}$$

Furthermore, from the definition of $x_k\left(i\right)$ in (17), we have

$${\underline{x}}_k^{*}=x_k\left(i\right)=min\left\{s_{ik}\right|O(a_{ik},s_{ik})=b_i-▵b_i^{\left(k\right)}\},\mathrm{for}i\in I_{\left(k\right)}^{*}.$$

Since ${\widehat{x}}_k<{\underline{x}}_k^{*}$ and $O(a_{ik},x)$ is strictly increasing in x (by Theorems 1 and 2), we have

$$O(a_{ik},{\widehat{x}}_k)<O(a_{ik},{\underline{x}}_k^{*}),$$

which implies

$$\begin{array}{ccc}\hfill g_i\left(\widehat{x}\right)& =& \sum _{j=1}^{k-1}O(a_{ij},{\underline{x}}_j^{*})+O(a_{ik},{\widehat{x}}_k)+\sum _{j=k+1}^{n}O(a_{ij},{\underline{x}}_j^{*})\hfill \\ \\ & <& \sum _{j=1}^{k-1}O(a_{ij},{\underline{x}}_j^{*})+O(a_{ik},{\underline{x}}_k^{*})+\sum _{j=k+1}^{n}O(a_{ij},{\underline{x}}_j^{*})=g_i\left(x_{\left(n\right)}^{*}\right)=b_i,i\in I_{\left(k\right)}^{*}.\hfill \end{array}$$

This contradicts the assumption that $\widehat{x}\in X(A,b)$. Therefore, such $\widehat{x}$ cannot exist, and $x_{\left(n\right)}^{*}$ is indeed a minimal-optimal solution to problem (3). □

5. Solution Procedure and a Numerical Example

Based on Theorem 8, starting from the uniform-optimal solution $x_{\left(0\right)}^{*}={\left(x_j^{\left(0\right)}\right)}_{j\in \mathcal{J}}$ with $x_j^{\left(0\right)}=y^{*}$ for all $j\in \mathcal{J}$, the proposed iterative approach can be used to obtain a minimal-optimal solution $x_{\left(n\right)}^{*}$ to problem (3). Furthermore, according to Lemma 4, for the initial optimal solution $x_{\left(0\right)}^{*}$, the binding variables $x_j=x_j^{\left(0\right)}=y^{*}$, for all $j\in J_i\left(x_{\left(0\right)}^{*}\right)$ and $i\in I\left(x_{\left(0\right)}^{*}\right)$, must remain fixed and cannot be reduced. In contrast, the remaining variables $x_j$, for $j\in \mathcal{J}\setminus J_i\left(x_{\left(0\right)}^{*}\right)$ and $i\in I\left(x_{\left(0\right)}^{*}\right)$, may potentially be reduced.

By incorporating these properties, we propose a systematic solution procedure for identifying a minimal-optimal solution to the min-max programming problem involving addition-overlap function composition.

Step 1.

Check the consistency of problem (3) by verifying whether the inequality ${\sum }_{j=1}^n{a}_{ij}\ge b_i$ holds for all $i\in \mathcal{I}$, according to Proposition 3. Terminate the procedure if the problem is inconsistent.

Step 2.

Transform problem (3) into the single-variable optimization problem (10), and solve it using the method proposed in [30] or the bisection method to obtain the optimal value $y^{*}$. The corresponding uniform-optimal solution is given by $x^{*}={\left(x_j^{*}\right)}_{j\in \mathcal{J}}=(y^{*},\cdots ,y^{*})$.

Step 3.

Determine the critical set $I\left(x^{*}\right)=\{i\in \mathcal{I}|g_i\left(x^{*}\right)=b_i\}$ and, for each $i\in I\left(x^{*}\right)$, compute the corresponding binding set $J_i\left(x^{*}\right)=J_i^{*1}\cup J_i^{*2}\cup J_i^{*3}$ according to Definition 5.

Step 4.

Iteratively construct the sequence of vectors $x_{\left(k\right)}^{*}=({\underline{x}}_1^{*},{\underline{x}}_2^{*},\cdots ,{\underline{x}}_k^{*},x_{k+1}^{\left(0\right)},\cdots ,x_n^{\left(0\right)})$ for $k=1,2,\cdots ,n$, where $x_j^{\left(0\right)}=y^{*}$ for $j=k+1,\cdots ,n$.

• If $k\in J_i\left(x^{*}\right)$ for any $i\in I\left(x^{*}\right)$, set ${\underline{x}}_k^{*}=y^{*}$ by Lemma 4.
• Otherwise, compute

  $${\underline{x}}_k^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_k\left(i\right)\right\},$$

  where

  $$\begin{array}{c}\hfill x_k\left(i\right)=\left\{\begin{array}{cc}min\left\{s_{ik}\right|O(a_{ik},s_{ik})=b_i-▵b_i^{\left(k\right)}\},\hfill & \mathrm{if}{b}_i-▵b_i^{\left(k\right)}>0,\hfill \\ 0,\hfill & \mathrm{if}{b}_i-▵b_i^{\left(k\right)}\le 0,\hfill \end{array}\right.\end{array}$$

  and

  $$\begin{array}{c}\hfill ▵b_i^{\left(k\right)}=g_i\left(x_{(k-1)}^{*}\right)-O(a_{ik},y^{*}).\end{array}$$

Step 5.

Return the final vector ${\underline{\mathit{x}}}^{**}=x_{\left(n\right)}^{*}=({\underline{x}}_1^{*},{\underline{x}}_2^{*},\cdots ,{\underline{x}}_n^{*})$, which is a minimal-optimal solution to problem (3).

• Computational Complexity and Convergence: Problem (3) involves m constraints, each containing n variables. The overall computational complexity and convergence behavior of the proposed solution procedure are primarily determined by Steps 2 and 4.

In Step 2, the optimal value $y^{*}$ is obtained by solving a single-variable optimization problem using the method proposed in [30], which requires $O\left(mn\right)$ computational complexity. The convergence of this method has been formally established in [30].

In Step 4, each of the n variables is processed once. For each variable, evaluating all constraints involves computing up to $(8n+13)m+(m-1)$ operations. Thus, the total computational complexity for Step 4 is $O\left(m{n}^2\right)$.

Overall, the total computational complexity of the entire solution procedure is $O\left(m{n}^2\right)$.

Moreover, since each variable is examined exactly once, and each update either retains or reduces its value while preserving feasibility and optimality, the algorithm completes in exactly n iterations. Finally, by Theorems 6 and 8, the final solution is guaranteed to be both optimal and minimal in the sense of component-wise ordering among feasible solutions. Therefore, the proposed algorithm is guaranteed to converge to a minimal-optimal solution in a finite number of steps.

The proposed procedure provides a systematic method for constructing a minimal-optimal solution to problem (3). To demonstrate its effectiveness and practical applicability, we now apply it step-by-step to the specific instance described in Example 1.

Example 3.

Apply the proposed solution procedure to determine a minimal-optimal solution to Example 1.

Based on the data given in Example 1, we carry out the solution procedure step-by-step as follows:

• Step 1. Check the consistency of problem by Proposition 3:

$$\sum _{j=1}^6{a}_{1j}=2.52>1.8=b_1,\sum _{j=1}^6{a}_{2j}=2.98>0.6=b_2,$$

$$\sum _{j=1}^6{a}_{3j}=2.77>2.0=b_3,\mathrm{and}\sum _{j=1}^6{a}_{4j}=2.93>1.8=b_4.$$

Since the condition ${\sum }_{j=1}^6{a}_{ij}\ge b_i$ holds for all $i\in \mathcal{I}=\{1,2,3,4\}$, the problem (11) in Example 1 is consistent.

• Step 2. Solve the optimal value $y^{*}$, yielding the uniform-optimal solution $x^{*}$.

From Example 1, we have

$$\begin{array}{c}\hfill y^{*}=0.643875, \mathrm{and} x^{*}=(x_1^{*},\cdots ,x_6^{*})=(0.643875,\cdots ,0.643875).\end{array}$$

• Step 3. Determine the critical set $I\left(x^{*}\right)$ and the binding set $J_i\left(x^{*}\right)$ for each $i\in I\left(x^{*}\right)$, as defined in Definition 5.

From Example 2, we have

$$I\left(x^{*}\right)=\left\{3\right\}, \mathrm{and} J_3\left(x^{*}\right)=\{2,5,6\}.$$

• Step 4. Iteratively construct the sequence of vectors $x_{\left(k\right)}^{*}=({\underline{x}}_1^{*},\cdots ,{\underline{x}}_k^{*},x_{k+1}^{\left(0\right)},\cdots ,x_n^{\left(0\right)})$ for $k=1,2,\cdots ,6$, where $x_j^{\left(0\right)}=y^{*}$ for $j=k+1,\cdots ,6$.

• For $k=1$, since $1\notin J_3\left(x^{*}\right)=\{2,5,6\}$, compute

$${\underline{x}}_1^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_1\left(i\right)\right\},$$

where

$$\begin{array}{c}\hfill x_1\left(i\right)=\left\{\begin{array}{cc}min\left\{s_{i1}\right|O(a_{i1},s_{i1})=b_i-▵b_i^{\left(1\right)}\},\hfill & \mathrm{if}{b}_i-▵b_i^{\left(1\right)}>0,\hfill \\ 0,\hfill & \mathrm{if}{b}_i-▵b_i^{\left(1\right)}\le 0,\hfill \end{array}\right.\end{array}$$

with

$$▵b_i^{\left(1\right)}=g_i\left(x_{\left(0\right)}^{*}\right)-O(a_{i1},y^{*}),\mathrm{for}i\in \mathcal{I}=\{1,2,3,4\}.$$

Calculations then yield

$$\begin{array}{c}\hfill ▵b_1^{\left(1\right)}=g_1\left(x_{\left(0\right)}^{*}\right)-O(a_{11},y^{*})=1.86896-0.25926=1.60970,\\ \hfill ▵b_2^{\left(1\right)}=g_2\left(x_{\left(0\right)}^{*}\right)-O(a_{21},y^{*})=2.15918-0.16667=1.99251,\\ \hfill ▵b_3^{\left(1\right)}=g_3\left(x_{\left(0\right)}^{*}\right)-O(a_{31},y^{*})=2.00000-0.20000=1.80000,\\ \hfill ▵b_4^{\left(1\right)}=g_4\left(x_{\left(0\right)}^{*}\right)-O(a_{41},y^{*})=2.10643-0.20635=1.90008,\end{array}$$

$$\begin{array}{c}\hfill b_1-▵b_1^{\left(1\right)}=1.8-1.60970=0.19030,b_2-▵b_2^{\left(1\right)}=0.6-1.99251=-1.39251,\\ \hfill b_3-▵b_3^{\left(1\right)}=2.0-1.80000=0.20000,b_4-▵b_4^{\left(1\right)}=1.8-1.90008=-0.10008.\end{array}$$

Using the inverse function method specified in (8) and (9), we compute

$$x_1\left(1\right)=min\left\{s_{11}\right|O(0.35,s_{11})=0.19030\}=0.23503,x_1\left(2\right)=0,$$

$$x_1\left(3\right)=min\left\{s_{31}\right|O(0.25,s_{31})=0.20000\}=0.25,x_1\left(4\right)=0.$$

Obtain

$${\underline{x}}_1^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_1\left(i\right)\right\}=\{0.23503,0,0.25,0\}=0.25,$$

and

$$x_{\left(1\right)}^{*}=(0.25,0.643875,0.643875,0.643875,0.643875,0.643875).$$

• For $k=2$, since $2\in J_3\left(x^{*}\right)=\{2,5,6\}$, set

$${\underline{x}}_{\left(2\right)}^{*}=y^{*}=0.643875.$$

Obtain the vector

$$x_{\left(2\right)}^{*}=(0.25,0.643875,0.643875,0.643875,0.643875,0.643875).$$

• For $k=3$, since $3\notin J_3\left(x^{*}\right)=\{2,5,6\}$, compute

$${\underline{x}}_3^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_3\left(i\right)\right\},$$

$$▵b_i^{\left(3\right)}=g_i\left(x_{\left(2\right)}^{*}\right)-O(a_{i3},y^{*}), \mathrm{and} b_i-▵b_i^{\left(3\right)},\mathrm{for}i\in \mathcal{I}=\{1,2,3,4\}.$$

Calculations then yield

$$\begin{array}{cc}& b_1-▵b_1^{\left(3\right)}=1.8-1.57893=0.22107,b_2-▵b_2^{\left(3\right)}=0.6-1.67139=-1.07139,\\ & b_3-▵b_3^{\left(3\right)}=2.0-1.75758=0.24242,b_4-▵b_4^{\left(3\right)}=1.8-1.76825=0.03175,\end{array}$$

$$x_3\left(1\right)=0.28381,x_3\left(2\right)=0,x_3\left(3\right)=0.32,x_3\left(4\right)=0.03279,$$

Obtain

$${\underline{x}}_3^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_3\left(i\right)\right\}=\{0.28381,0,0.32,0.03279\}=0.32,$$

and

$$x_{\left(3\right)}^{*}=(0.25,0.643875,0.32,0.643875,0.643875,0.643875).$$

• For $k=4$, since $4\notin J_3\left(x^{*}\right)=\{2,5,6\}$, compute

$${\underline{x}}_4^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_4\left(i\right)\right\},$$

$$▵b_i^{\left(4\right)}=g_i\left(x_{\left(3\right)}^{*}\right)-O(a_{i4},y^{*}), \mathrm{and} b_i-▵b_i^{\left(4\right)},\mathrm{for}i\in \mathcal{I}=\{1,2,3,4\}.$$

Calculations then yield

$$\begin{array}{cc}& b_1-▵b_1^{\left(4\right)}=1.8-1.51474=0.28526,b_2-▵b_2^{\left(4\right)}=0.6-1.61886=-1.01886,\\ & b_3-▵b_3^{\left(4\right)}=2.0-1.76923=0.23077,b_4-▵b_4^{\left(4\right)}=1.8-1.56824=0.23176,\end{array}$$

$$x_4\left(1\right)=0.39911,x_4\left(2\right)=0,x_4\left(3\right)=0.3,x_4\left(4\right)=0.30168.$$

Obtain

$${\underline{x}}_4^{*}=\underset{i\in \mathcal{I}}{max}\left\{x_4\left(i\right)\right\}=\{0.39911,0,0.3,0.30168\}=0.39911,$$

and

$$x_{\left(4\right)}^{*}=(0.25,0.643875,0.32,0.39911,0.643875,0.643875).$$

• For $k=5$ and $k=6$, since both $k\in J_3\left(x^{*}\right)=\{2,5,6\}$, set

$${\underline{x}}_{\left(5\right)}^{*}={\underline{x}}_{\left(6\right)}^{*}=y^{*}=0.643875,$$

and obtain the final vector

$$x_{\left(6\right)}^{*}=(0.25,0.643875,0.32,0.39911,0.643875,0.643875).$$

• Step 5. Return the final vector:

$${\underline{\mathit{x}}}^{**}=x_{\left(6\right)}^{*}=(0.25,0.643875,0.32,0.39911,0.643875,0.643875),$$

which is a minimal-optimal solution to Example 1.

It is worth noting that the proposed solution procedure can be applied to obtain other minimal-optimal solutions. Theoretically, the six variables in Example 3 can be permuted in 6! = 720 different sequences. However, since the critical set $I\left(x^{*}\right)=\left\{3\right\}$ and the corresponding binding set $J_3\left(x^{*}\right)=\{2,5,6\}$, the values of variables ${\underline{x}}_2^{*}={\underline{x}}_5^{*}={\underline{x}}_6^{*}=y^{*}=0.643875$ must remain unchanged, in accordance with Lemma 4. As a result, only the remaining three variables $x_1,x_3$, and $x_4$ can be adjusted, yielding 3!=6 possible permutations. Besides the original sequence $x_1,x_2,\cdots ,x_6$ used in Example 3, the following five sequences can be considered to generate other minimal-optimal solutions:

$$\begin{array}{cc}& \mathrm{Seq}1:x_1,x_2,x_4,x_3,x_5,x_6;\mathrm{Seq}2:x_3,x_2,x_1,x_4,x_5,x_6;\\ & \mathrm{Seq}3:x_3,x_2,x_4,x_1,x_5,x_6;\mathrm{Seq}4:x_4,x_2,x_1,x_3,x_5,x_6; \mathrm{and}\mathrm{Seq}5:x_4,x_2,x_3,x_1,x_5,x_6.\end{array}$$

Accordingly, only one distinct minimal-optimal solution ${\underline{\mathit{x}}}^{**2}$ to Example 3 can be obtained using our solution procedure based on these sequences, as follows:

$${\underline{\mathit{x}}}^{**2}=(0.341365,0.643875,0.32,0.3,0.643875,0.643875).$$

6. Conclusions

In this study, we investigated a min-max optimization problem constrained by a system of addition-overlap functions. Classical methods such as the bisection approach are effective in finding a uniform-optimal solution for such a problem, where all decision variables share the same optimal value. However, these methods are insufficient for identifying minimal-optimal solutions, which are often more informative in practical applications.

To address this gap, we developed an iterative procedure that gradually reduces adjustable variables based on overlap function properties while maintaining feasibility and optimality. This approach relies on a careful identification of critical constraints and binding variables, which must remain fixed, allowing non-binding components to be selectively minimized. We formally proved that the resulting solution satisfies the condition of minimal-optimality. Through illustrative examples, we further demonstrated that the proposed method can yield multiple distinct minimal-optimal solutions, depending on the order in which variables are processed.

Our results contribute both theoretically and algorithmically: the framework enhances the understanding of solution structure in addition-overlap constrained problems and offers a practical tool for constructing minimal-optimal solutions. Future work may involve the pursuit of sufficient conditions, the development of numerical subroutines, and necessary error analyses for broader classes of overlap functions or exploring its applications in practical optimization scenarios.