A Hybrid Model of Elephant and Moran Random Walks: Exact Distribution and Symmetry Properties
Abstract
1. Introduction
- In Quantum physics [7], the recurrence relations and exact distributions obtained here provide tools to study quantum walks with memory, relevant for quantum computation and the simulation of complex quantum systems.
- In biology, the stop-or-move mechanism of our model naturally represents the foraging strategies of animals: individuals may either continue in the same direction, invert their movement, or remain stationary to exploit resources, as observed in empirical mobility data.
2. Definitions and Presentation of the Model
3. Main Results
4. Simulations
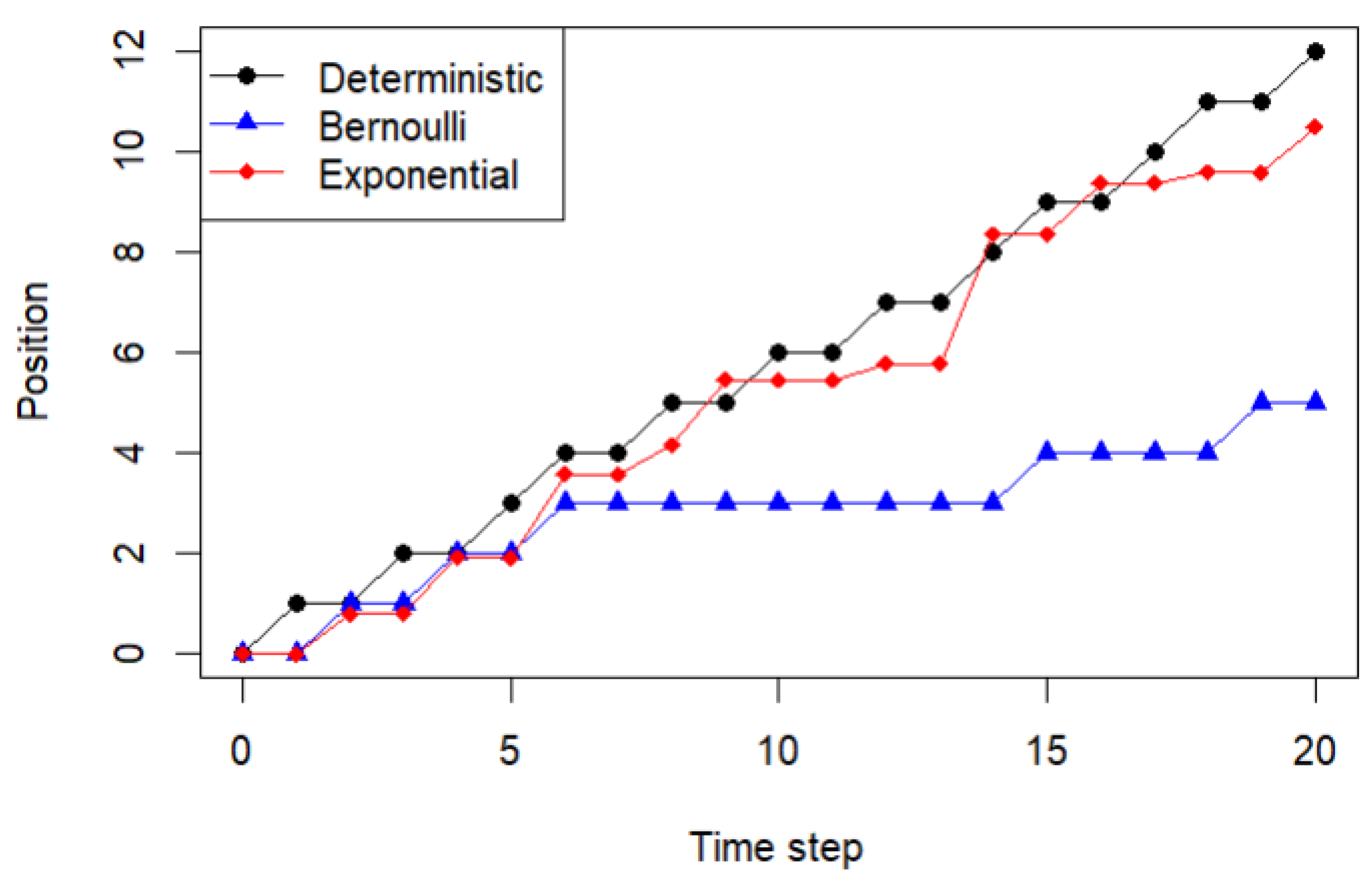
4.1. Curve of the Sequence
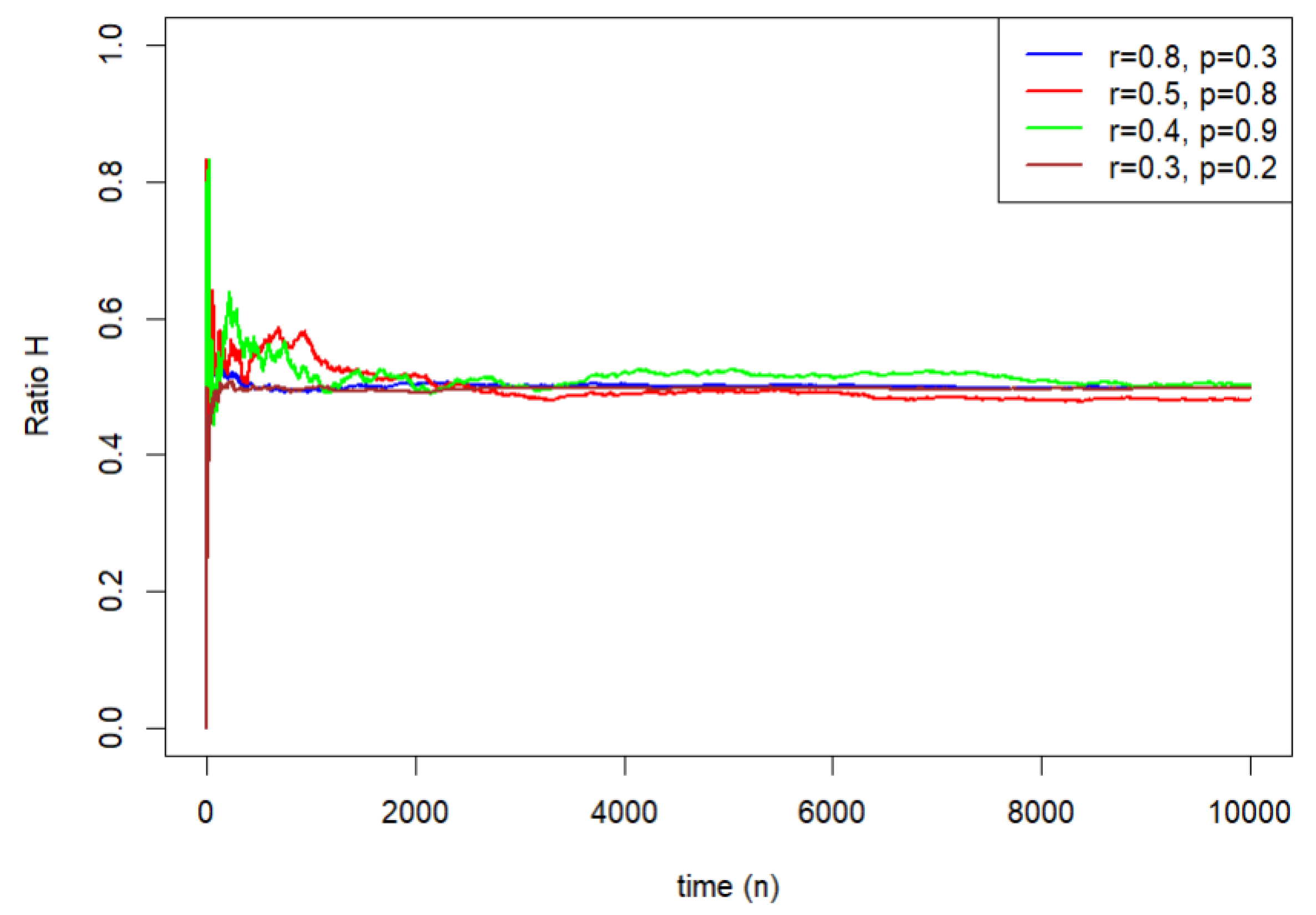
4.2. Simulations of
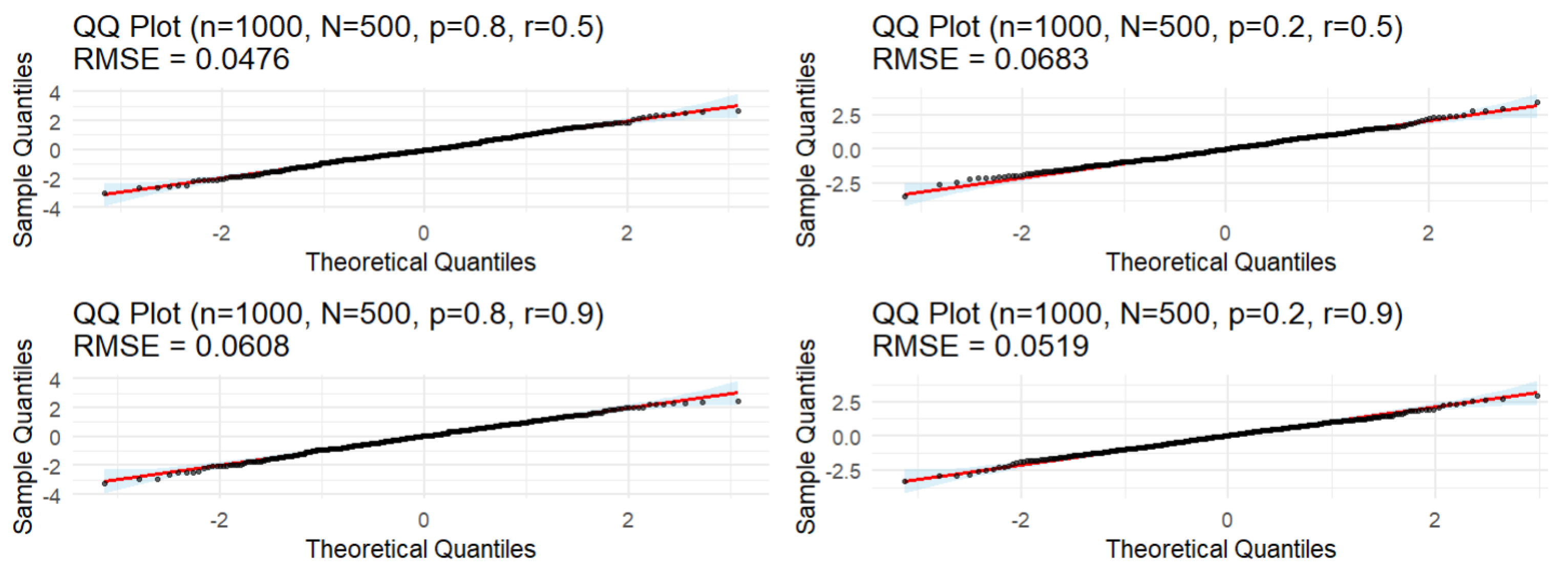
4.3. Simulations of the CLT with Respect to
- 1.
- Effect of Sample Size per Sample (n)
- (a)
- As n increases, the data generally becomes more normal.
- (b)
- This is most clearly seen in the RMSE (QQ) column, which consistently decreases as n increases for fixed N, p, r.
- (c)
- Example: For , , , RMSE drops from 0.1289 () to 0.0564 () to 0.0385 ().
- (d)
- The p-values from the normality tests also tend to become larger (less significant) as n increases, further supporting this trend.
- 2.
- Effect of Number of Samples/Replications (N)
- (a)
- As N increases, the data also becomes more normal.
- (b)
- This pattern is also very clear in the RMSE (QQ) column.
- (c)
- Example: For , , , RMSE drops from 0.0688 () to 0.0530 () to 0.0163 ().
- (d)
- This suggests that the data generation process itself may produce a perfectly normal distribution only in the limit as the number of replications grows large.
- 3.
- Effect of Parameters p and r
- (a)
- The effects of p and r are more subtle and interact with n and N.
- (b)
- There is no single, dominant pattern. For instance:
- Sometimes a combination like , produces excellent normality (e.g., row 3, row 15).
- Other combinations like , can show weaker normality for smaller n and N (e.g., row 4, row 8) but become perfectly normal with larger n and N (e.g., row 20, row 32).
- (c)
- This indicates that the impact of the data generation parameters (p, r) is complex and depends on the sample size.
- 4.
- Agreement Between Tests
- (a)
- The four normality tests generally agree on the broad conclusion (normal vs. not normal) but often disagree on the specific p-value.
- (b)
- For very large n and N (e.g., , ), the Shapiro-Wilk test returns NA. This is a known computational limitation; the test becomes too computationally expensive or unstable with very large sample sizes.
- 5.
- Overall Normality
- (a)
- Despite some low p-values for smaller n and N, the Skewness and Kurtosis values are almost always very close to 0.
- (b)
- The RMSE values are consistently low, especially for larger n and N.
- (c)
- Conclusion: The data generation process produces distributions that are very close to normal, especially when the sample size (n) and the number of replications (N) are large. The deviations from normality detected by the tests in some scenarios are minor in a practical sense.
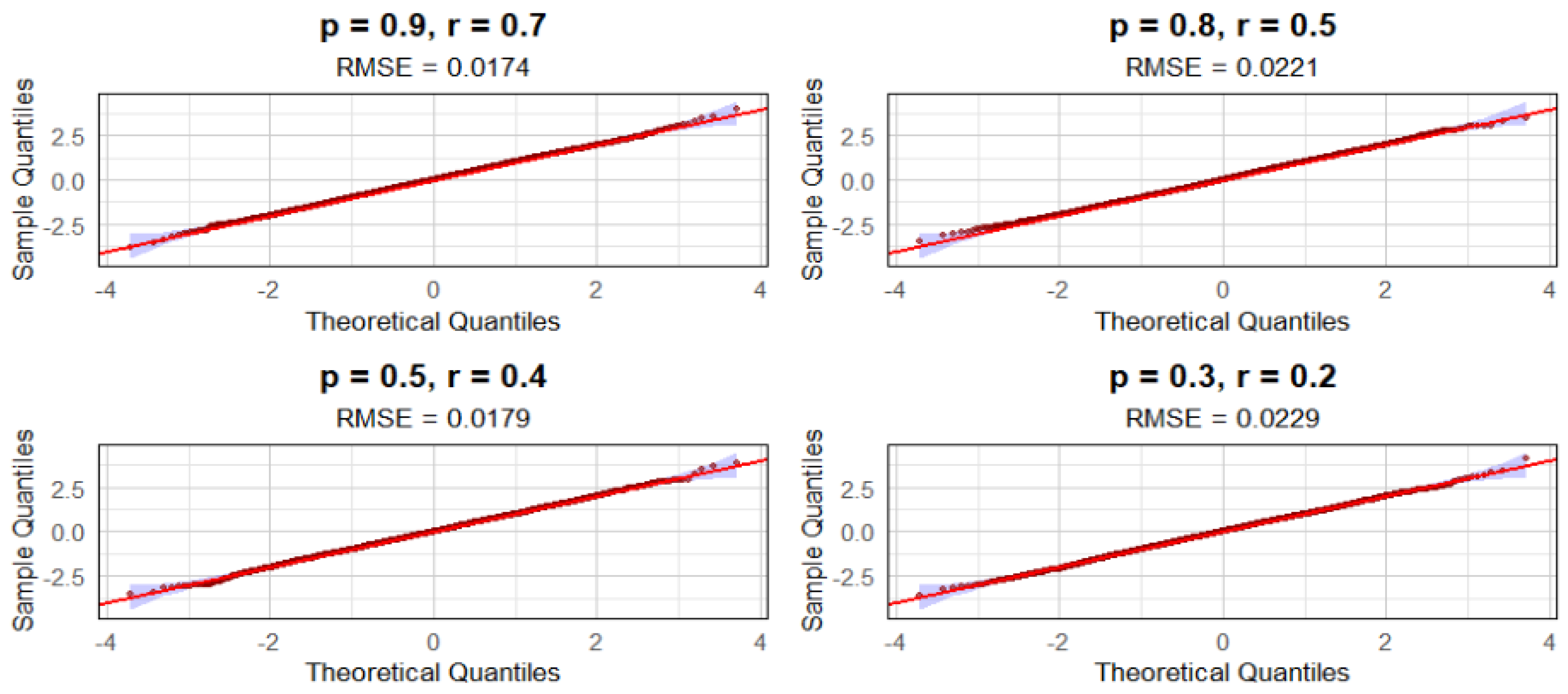
4.4. Simulations of the CLT with Respect to
5. Some Characteristics of the Distribution of the Process
6. Number of Stops of the Process
6.1. Proof of Theorem 1
6.2. Proof of Theorem 2
7. Distribution of
7.1. Proof of Theorem 4
7.2. Proof of Theorem 5
7.3. Proof of Theorem 6
8. Conclusions and Perspectives
- With probability , it takes the step , where is a scaling or transformation factor that may depend on a parameter p.
- With probability , it takes a new independent step , which could represent noise or a random perturbation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdelkader, M.; Aguech, R. Moran random walk with reset and short memory. Aims Math. 2024, 9, 19888–19910. [Google Scholar] [CrossRef]
- Laulin, L. New Insights on the Reinforced Elephant Random Walk Using a Martingale Approach. J. Stat. Phys. 2022, 186, 9. [Google Scholar] [CrossRef]
- Roy, R.; Takei, M.; Tanemura, H. Moran random walk with short memory. Electron. Commun. Probab. 2024, 29, 78. [Google Scholar]
- Bercu, B. A martingale approach for the elephant random walk. J. Phys. A Math. Theor. 2018, 51, 015201. [Google Scholar] [CrossRef]
- Gut, A.; Stadtmuller, U. Elephant random walks; A review. Ann. Univ. Sci. Budapest. Sect. Comp. 2023, 54, 171–198. [Google Scholar] [CrossRef]
- Gut, A.; Stadtmuller, U. The number of zeros in Elephant random walks with delays. Stat. Probab. Lett. 2021, 174, 109–112. [Google Scholar] [CrossRef]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Durrett, R. Probability, Theory and Examples, 4th ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Flajolet, P.; Sedgewick, R. Analytic Combinatorics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kiss, J.; Vető, B. Moments of the superdiffusive elephant random walk with general step distribution. Electron. Commun. Probab. 2022, 27, 1–12. [Google Scholar] [CrossRef]



| n | N | p | r | Shapiro p | AD p | D’Agostino p | Jarque-Bera p | Skew | Kurtosis | RMSE (QQ) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 100 | 0.8 | 0.5 | 0.0734 | 0.0553 | 0.3744 | 0.3984 | 0.2062 | −0.5213 | 0.1289 |
| 1000 | 100 | 0.9 | 0.4 | 0.7503 | 0.7294 | 0.9854 | 0.9656 | 0.0042 | −0.1294 | 0.1459 |
| 1000 | 100 | 0.7 | 0.8 | 0.6884 | 0.4449 | 0.3716 | 0.4133 | −0.2074 | 0.5020 | 0.0767 |
| 1000 | 100 | 0.6 | 0.2 | 0.1068 | 0.0777 | 0.1476 | 0.2449 | −0.3408 | −0.4590 | 0.0796 |
| 1000 | 500 | 0.8 | 0.5 | 0.3050 | 0.6493 | 0.8899 | 0.6237 | −0.0149 | −0.2108 | 0.0564 |
| 1000 | 500 | 0.9 | 0.4 | 0.3009 | 0.2340 | 0.4574 | 0.7217 | −0.0804 | −0.0740 | 0.0908 |
| 1000 | 500 | 0.7 | 0.8 | 0.0771 | 0.0300 | 0.9377 | 0.0962 | −0.0084 | −0.4738 | 0.0576 |
| 1000 | 500 | 0.6 | 0.2 | 0.2121 | 0.1353 | 0.1646 | 0.3287 | −0.1509 | −0.1255 | 0.0370 |
| 1000 | 1000 | 0.8 | 0.5 | 0.4920 | 0.9301 | 0.2997 | 0.5859 | −0.0799 | −0.0121 | 0.0385 |
| 1000 | 1000 | 0.9 | 0.4 | 0.6107 | 0.7053 | 0.2406 | 0.4919 | 0.0904 | −0.0368 | 0.0522 |
| 1000 | 1000 | 0.7 | 0.8 | 0.4501 | 0.6176 | 0.3050 | 0.4085 | −0.0790 | −0.1342 | 0.0297 |
| 1000 | 1000 | 0.6 | 0.2 | 0.1838 | 0.1821 | 0.0691 | 0.1229 | 0.1405 | 0.1473 | 0.0281 |
| 5000 | 500 | 0.8 | 0.5 | 0.1475 | 0.1519 | 0.1459 | 0.3530 | −0.1579 | 0.0135 | 0.0688 |
| 5000 | 500 | 0.9 | 0.4 | 0.8283 | 0.9572 | 0.6109 | 0.4931 | 0.0550 | −0.2362 | 0.0577 |
| 5000 | 500 | 0.7 | 0.8 | 0.9353 | 0.8440 | 0.9381 | 0.9241 | −0.0084 | 0.0854 | 0.0299 |
| 5000 | 500 | 0.6 | 0.2 | 0.8334 | 0.6808 | 0.5682 | 0.7689 | −0.0617 | −0.1001 | 0.0246 |
| 5000 | 1000 | 0.8 | 0.5 | 0.0572 | 0.0771 | 0.6327 | 0.8048 | −0.0368 | −0.0708 | 0.0530 |
| 5000 | 1000 | 0.9 | 0.4 | 0.5190 | 0.4786 | 0.2747 | 0.5219 | −0.0841 | −0.0538 | 0.0570 |
| 5000 | 1000 | 0.7 | 0.8 | 0.8795 | 0.7643 | 0.2864 | 0.5282 | 0.0821 | 0.0607 | 0.0238 |
| 5000 | 1000 | 0.6 | 0.2 | 0.7667 | 0.5681 | 0.2618 | 0.3759 | 0.0864 | 0.1307 | 0.0208 |
| 5000 | 5000 | 0.8 | 0.5 | 0.7309 | 0.8995 | 0.4333 | 0.4972 | 0.0271 | −0.0614 | 0.0163 |
| 5000 | 5000 | 0.9 | 0.4 | 0.2042 | 0.1210 | 0.1990 | 0.2875 | 0.0444 | 0.0638 | 0.0323 |
| 5000 | 5000 | 0.7 | 0.8 | 0.3480 | 0.2778 | 0.2267 | 0.3971 | −0.0418 | 0.0432 | 0.0150 |
| 5000 | 5000 | 0.6 | 0.2 | 0.3415 | 0.2645 | 0.4834 | 0.1517 | 0.0242 | −0.1255 | 0.0125 |
| 10,000 | 1000 | 0.8 | 0.5 | 0.0844 | 0.4323 | 0.0308 | 0.0931 | −0.1672 | −0.0469 | 0.0500 |
| 10,000 | 1000 | 0.9 | 0.4 | 0.7007 | 0.8221 | 0.8965 | 0.7072 | −0.0100 | 0.1274 | 0.0513 |
| 10,000 | 1000 | 0.7 | 0.8 | 0.4050 | 0.1315 | 0.1614 | 0.3744 | −0.1080 | 0.0228 | 0.0309 |
| 10,000 | 1000 | 0.6 | 0.2 | 0.7549 | 0.7786 | 0.3642 | 0.6191 | −0.0699 | −0.0591 | 0.0210 |
| 10,000 | 5000 | 0.8 | 0.5 | 0.2430 | 0.4538 | 0.0737 | 0.0859 | 0.0619 | 0.0907 | 0.0221 |
| 10,000 | 5000 | 0.9 | 0.4 | 0.8403 | 0.6826 | 0.3134 | 0.5722 | −0.0349 | −0.0222 | 0.0229 |
| 10,000 | 5000 | 0.7 | 0.8 | 0.3847 | 0.2229 | 0.7748 | 0.2187 | −0.0099 | 0.1192 | 0.0158 |
| 10,000 | 5000 | 0.6 | 0.2 | 0.3686 | 0.5618 | 0.5868 | 0.8148 | −0.0188 | 0.0235 | 0.0120 |
| 10,000 | 10,000 | 0.8 | 0.5 | - | 0.2019 | 0.4898 | 0.7856 | 0.0169 | −0.0039 | 0.0171 |
| 10,000 | 10,000 | 0.9 | 0.4 | - | 0.1200 | 0.7006 | 0.0878 | −0.0094 | −0.1064 | 0.0240 |
| 10,000 | 10,000 | 0.7 | 0.8 | - | 0.1464 | 0.2441 | 0.1870 | −0.0285 | 0.0692 | 0.0126 |
| 10,000 | 10,000 | 0.6 | 0.2 | - | 0.1863 | 0.4941 | 0.7915 | −0.0167 | 0.0013 | 0.0078 |
| n | N | p | r | Shapiro_p | AD_p | DAgostino_p | JarqueBera_p | Skew | Kurtosis | QQ_RMSE |
|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 100 | 0.9 | 0.7 | 0.0463 | 0.1680 | 0.0177 | 0.0210 | −0.579 | 3.715 | 0.1632 |
| 1000 | 100 | 0.5 | 0.4 | 0.3249 | 0.5554 | 0.4319 | 0.5485 | 0.182 | 2.605 | 0.1081 |
| 1000 | 100 | 0.3 | 0.2 | 0.5188 | 0.3811 | 0.5454 | 0.8483 | −0.140 | 3.031 | 0.1068 |
| 1000 | 500 | 0.9 | 0.7 | 0.6002 | 0.5992 | 0.7017 | 0.6046 | −0.041 | 2.796 | 0.0471 |
| 1000 | 500 | 0.5 | 0.4 | 0.4369 | 0.1138 | 0.9447 | 0.7695 | −0.007 | 2.842 | 0.0571 |
| 1000 | 500 | 0.3 | 0.2 | 0.4542 | 0.5782 | 0.4844 | 0.4689 | 0.076 | 2.777 | 0.0525 |
| 1000 | 1000 | 0.9 | 0.7 | 0.7486 | 0.9600 | 0.7452 | 0.9323 | 0.025 | 3.029 | 0.0339 |
| 1000 | 1000 | 0.5 | 0.4 | 0.6739 | 0.6254 | 0.5693 | 0.8480 | −0.044 | 2.984 | 0.0347 |
| 1000 | 1000 | 0.3 | 0.2 | 0.8592 | 0.9293 | 0.2925 | 0.5771 | −0.081 | 3.010 | 0.0323 |
| 5000 | 500 | 0.9 | 0.7 | 0.4709 | 0.6903 | 0.2177 | 0.4189 | −0.134 | 3.110 | 0.0535 |
| 5000 | 500 | 0.5 | 0.4 | 0.1679 | 0.3629 | 0.1323 | 0.2175 | 0.164 | 2.801 | 0.0646 |
| 5000 | 500 | 0.3 | 0.2 | 0.0405 | 0.1880 | 0.0405 | 0.1114 | −0.224 | 2.898 | 0.0763 |
| 5000 | 1000 | 0.9 | 0.7 | 0.5634 | 0.2362 | 0.3444 | 0.5558 | −0.073 | 2.916 | 0.0360 |
| 5000 | 1000 | 0.5 | 0.4 | 0.7521 | 0.5165 | 0.5408 | 0.8205 | 0.047 | 2.975 | 0.0325 |
| 5000 | 1000 | 0.3 | 0.2 | 0.9102 | 0.8762 | 0.9787 | 0.8108 | 0.002 | 2.900 | 0.0291 |
| 5000 | 5000 | 0.9 | 0.7 | 0.4359 | 0.1218 | 0.7831 | 0.6190 | 0.010 | 2.935 | 0.0191 |
| 5000 | 5000 | 0.5 | 0.4 | 0.2589 | 0.2820 | 0.4984 | 0.1607 | 0.023 | 3.124 | 0.0225 |
| 5000 | 5000 | 0.3 | 0.2 | 0.4999 | 0.4140 | 0.5879 | 0.5095 | −0.019 | 3.071 | 0.0183 |
| 10,000 | 1000 | 0.9 | 0.7 | 0.1261 | 0.0238 | 0.5905 | 0.7085 | −0.041 | 2.902 | 0.0489 |
| 10,000 | 1000 | 0.5 | 0.4 | 0.5546 | 0.2731 | 0.7248 | 0.5426 | 0.027 | 3.163 | 0.0387 |
| 10,000 | 1000 | 0.3 | 0.2 | 0.1446 | 0.0520 | 0.6166 | 0.3184 | 0.039 | 2.779 | 0.0461 |
| 10,000 | 3000 | 0.9 | 0.7 | 0.6385 | 0.1898 | 0.3814 | 0.4425 | −0.039 | 2.917 | 0.0213 |
| 10,000 | 3000 | 0.5 | 0.4 | 0.6471 | 0.7873 | 0.7175 | 0.4873 | 0.016 | 3.102 | 0.0247 |
| 10,000 | 3000 | 0.3 | 0.2 | 0.0193 | 0.1318 | 0.3624 | 0.0395 | 0.041 | 3.212 | 0.0355 |
| 10,000 | 5000 | 0.9 | 0.7 | 0.8361 | 0.8834 | 0.8570 | 0.9717 | 0.006 | 2.989 | 0.0147 |
| 10,000 | 5000 | 0.5 | 0.4 | 0.0709 | 0.3440 | 0.0295 | 0.0640 | −0.075 | 3.060 | 0.0255 |
| 10,000 | 5000 | 0.3 | 0.2 | 0.1867 | 0.4124 | 0.3670 | 0.4591 | −0.031 | 3.060 | 0.0217 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguech, R.; Abdelkader, M. A Hybrid Model of Elephant and Moran Random Walks: Exact Distribution and Symmetry Properties. Symmetry 2025, 17, 1709. https://doi.org/10.3390/sym17101709
Aguech R, Abdelkader M. A Hybrid Model of Elephant and Moran Random Walks: Exact Distribution and Symmetry Properties. Symmetry. 2025; 17(10):1709. https://doi.org/10.3390/sym17101709
Chicago/Turabian StyleAguech, Rafik, and Mohamed Abdelkader. 2025. "A Hybrid Model of Elephant and Moran Random Walks: Exact Distribution and Symmetry Properties" Symmetry 17, no. 10: 1709. https://doi.org/10.3390/sym17101709
APA StyleAguech, R., & Abdelkader, M. (2025). A Hybrid Model of Elephant and Moran Random Walks: Exact Distribution and Symmetry Properties. Symmetry, 17(10), 1709. https://doi.org/10.3390/sym17101709





