Homomorphic Cryptographic Scheme Based on Nilpotent Lie Algebras for Post-Quantum Security
Abstract
1. Introduction
- (i)
- The formalization of the conjugation scheme with an explicit CPA (chosen-plaintext attack) security model NCIP (Nilpotent Conjugacy/Log-Inversion Problem) and a scope of validity;
- (ii)
- A fully parameterized and publicly reproducible implementation with quantitative measurements (latency, throughput, memory, expansion, depth);
- (iii)
- A path to integration into a DBMS with integrity verification and key rotation.
2. Objective and Research Methodology
2.1. Goal
2.2. Specific Objectives
- We wish to
- Formalize the mathematical basis of Lie algebras and corresponding Lie groups relevant to cryptography (nilpotency, BCH truncation);
- Define message encoding in the algebra g (not in a group) and encryption/decryption via and conjugation in the group G;
- Construct a scheme with homomorphic addition in the cipher domain (cipher multiplication ↔ BCH-sum in g);
- Specify the security model (IND-CPA in symmetric key), constraints (malleability, no CCA), and integrity mechanisms (encrypt-then-MAC);
- Implement a prototype in Python and conduct reproducible measurements (latency/throughput, memory, cipher extension, achievable depth).
2.3. Methodology
- Encoding: with the norm constraint;
- Encryption: , where is the central randomizer.
- Addition homomorphism: (BCH terminates at depth c).
- Decryption: , and then
3. Related Works
4. Theoretical Basis: Lie Groups and Lie Algebras in Cryptography
- 1.
- General Linear Group
- i.
- An open submanifold of ;
- ii.
- Dimension: .
- i.
- Closure: ;
- ii.
- Associativity: ;
- iii.
- Identity: ;
- iv.
- Inverses:
- 2.
- Special Linear Group
- i.
- A smooth submanifold of GL(n, ℝ);
- ii.
- Dimension: .
- i.
- Closure: ;
- ii.
- Associativity: Inherited from ;
- iii.
- Identity: ;
- iv.
- Inverses:
- 1.
- Antisymmetry: ;
- 2.
- Jacobi Identity:
- 1.
- Endomorphism Lie Algebra: For a vector space , (linear maps ) is a Lie algebra under the commutator bracket ;
- 2.
- General Linear Lie Algebra: The general linear Lie algebra consists of all n × n matrices over F with the bracket ;
- 3.
- with Cross Product: is a Lie algebra under the cross product (antisymmetric and satisfied Jacobi identity);
- 4.
- Heisenberg Algebra: Basic matrices:with brackets
- i.
- All iterated commutators vanish beyond step n, enabling finite computations.
- ii.
- Converts algebraic operations into group actions;
- iii.
- Computable in polynomial time for nilpotent algebras.
- Correctness: Series completion guarantees the return of the encoding/decoding without approximations;
- Homomorphism: The product induces addition into the algebra;
- Computability: The operations are polynomial in n for a fixed c.
- Complexity of operations: Matrix operations within Lie groups are mathematically complex, which provides high security;
- Replacement of classical problems: Problems of inversion of exponential and commutator operations can replace classical problems such as the discrete logarithm;
- Potential resistance to quantum attacks: Quantum algorithms currently lack efficient solutions to problems based on Lie algebras and commutators in nilpotent structures.
- Homomorphism: Operations in algebras can be directly transferred to group operations, which allows for the processing of encrypted data.
5. Design of a Homomorphic Encryption Scheme Based on Lie Groups and Algebras
5.1. Threat Model and Security Goal
- Setup: A random key is sampled, and is given public parameters
- Query phase: adaptively submits messages and receives ciphertexts , with a fresh per query.
- Challenge: outputs two challenge messages . A random bit is chosen, and receives , with fresh .
- Guess: outputs . It wins if .
- IND-CPA confidentiality: For challenge messages of the same format/length, the attacker does not distinguish which ciphertext was obtained, except to a negligible extent;
- Key protection: Recovering or from pairs is infeasible under the NCIP (Nilpotent Conjugacy/Log Inversion Problem) assumption;
- Randomization robustness: U has high min-entropy, is chosen independently of , and belongs to the center , so it does not violate the addition homomorphism.
- CCA security: We do not claim resistance to chosen-ciphertext attacks;
- Non-malleability: Malleability is intentional for the sake of homomorphism (e.g., the product of ciphertexts corresponds to the addition of codes);
- Side channels (timing/cache/power) are handled implementation-wise (constant-time arithmetic, avoiding branching on secret bits, affinity pinning).
- Randomization : Sampled from the center with sufficient entropy (CSPRNG) and independent of ; distribution and support are chosen so as not to compromise correctness and minimize cipher extension.
- Nonce ν: Unique per encryption (e.g., monotonic counter or 96-bit random), stored publicly and fed into MAC.
- Key rotation: Periodic rotation with versioning; compromise of does not compromise the sessions under .
- Multi-tenant: Independent keys per tenant; avoids cross-tenant domain mixing via .
- Correctness: Parameters constrain the norms and BCH members so that the log is well-defined; on exiting the allowed region, abort and re-encode/parameter correction (see Section 2.3 Methodology for formal parameter specification).
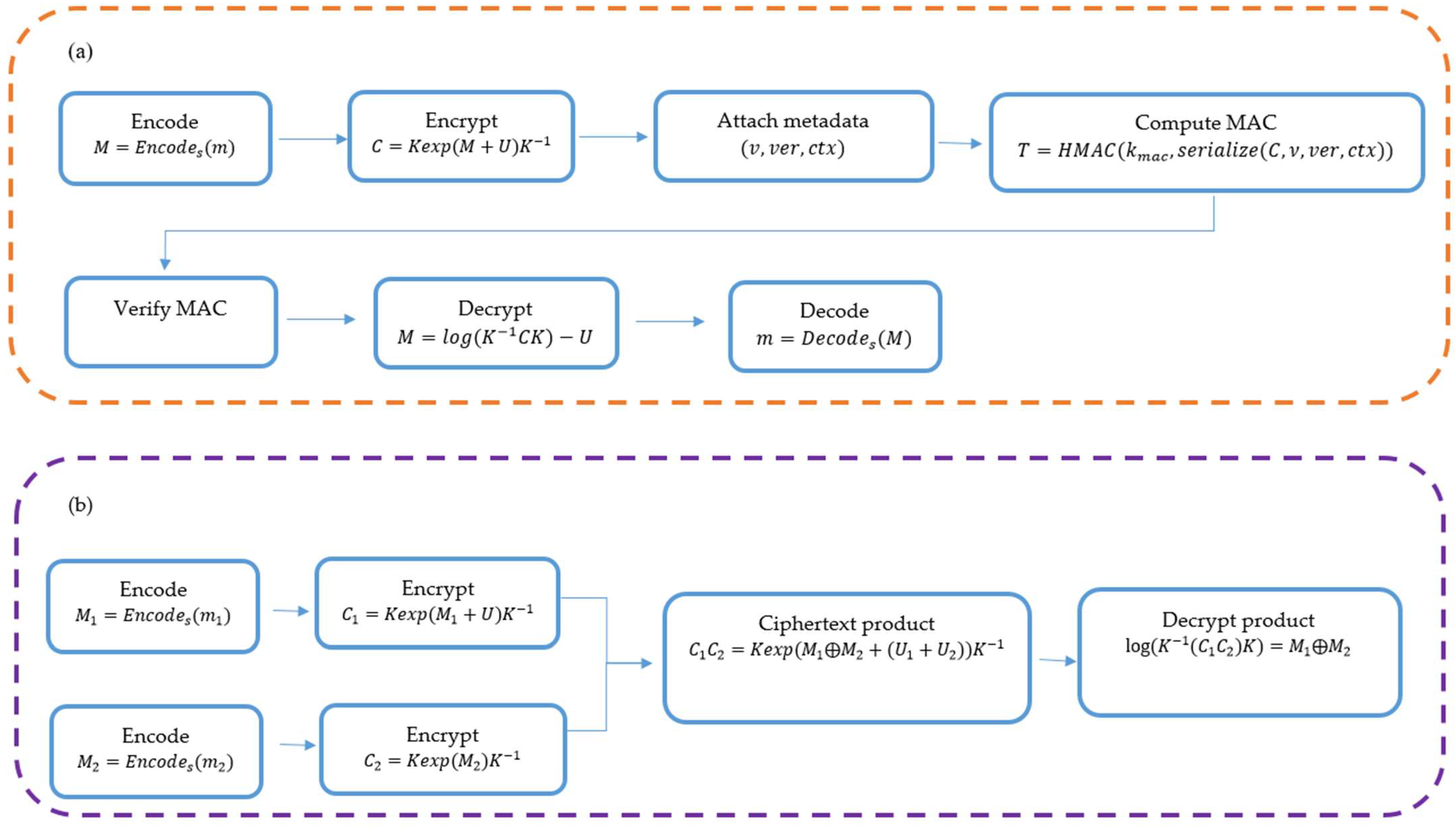
5.2. Definition of Scheme
5.3. Homomorphic Properties (Addition)
5.4. Integrity and Key Rotation
5.5. Integrating the Model with a Data Management System
- Building the database: First, let us create a simple database to store the encrypted data;
- Developing a model for data storage: The model will contain the encrypted values and their metadata;
- Implementing encryption functionality when entering the database: When entering data, the data will be encrypted before being stored in the database;
- Implementing decryption functionality when reading from the database: When the user accesses the data, it will be decrypted.
- Flask Back-End: We add HMAC generation logic and data integrity checks;
- Front-End React: We add the support to take the input of the secret key, calculate the HMAC, and post data to the server for verification.
5.6. Flask Back-End—Implementing HMAC
- HMAC: The HMAC is used for data integrity verification. First, we generate an HMAC for the encrypted data (using the secret key) and send it along with the encrypted data. Further optimization strategies and performance results are discussed in Appendix A.
- Encryption and Decryption: We use Lie group mode to encrypt and decrypt the data.
- HMAC Verification: Before decrypting the data, we check whether the HMAC we received matches the one we generated on the server. If it does not match, we return an error.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Optimization | Description | Impact on Performance | Notes |
|---|---|---|---|
| Parallelization | Using multiple processors for parallel execution of the HMAC for a large number of messages. | Can significantly reduce the execution time for large workloads. | Effective in multi-core environments (e.g., servers). |
| Caching | Caching previously computed HMAC values using an LRU (Least Recently Used) cache. | Reduces redundant computations for the same messages. Speeds up repeated requests. | Most effective when messages are repeated. Not ideal for highly variable data. |
| Using Efficient Cryptographic Algorithms | Replacing current cryptographic algorithms with faster ones like SHA-3 instead of SHA-256. | May increase the speed of HMAC generation. | Requires testing with real data to assess the impact of switching algorithms on performance. |
| Using Faster Libraries | Implementing the HMAC using specialized libraries (e.g., OpenSSL or Libsodium) instead of standard Python libraries. | Increases the operation speed due to optimizations for high performance. | OpenSSL and Libsodium are optimized for fast encryption and can significantly speed up the algorithm. |
| Parallel Caching | Combining caching and parallelization to distribute requests across multiple CPU cores with caching. | Significantly improves performance with a high request frequency. | Useful in environments with high request rates, such as web applications. |
| Memory Usage Optimization | Using efficient data structures for the temporary storage of values to reduce memory usage. | Reduces the data access time, speeding up the entire process. | Optimized data types can reduce memory usage and improve speed, especially for large datasets. |
| Lazy Loading | Loading only necessary data to perform the HMAC and delaying processing until the last possible moment. | Increases the initial speed by reducing unnecessary operations. | Useful in systems where the initial load speed is important. |
| Reducing Key Size | Using smaller, optimized keys as long as it does not compromise security. | Can reduce the HMAC computation time. | Smaller keys usually process faster, but security should not be compromised. |
| Message Length Reduction | Reducing the message length via compression or encoding before HMAC generation. | Shortening the message can reduce the number of operations required for HMAC generation. | Effective for applications processing large amounts of data with similar patterns. |
References
- Stallings, W. Cryptography and Network Security: Principles and Practice, 8th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2022. [Google Scholar]
- Schneier, B. Applied Cryptography: Protocols, Algorithms, and Source Code in C, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Goldwasser, S.; Bellare, M. Lecture notes on cryptography. In Summer Course on Cryptography; Santa Barbara, CA, USA, 2008. Available online: https://cseweb.ucsd.edu/~mihir/papers/gb.pdf (accessed on 19 June 2025).
- Wang, Y. Public Key Cryptography Standards: PKCS. arXiv 2012, arXiv:1207.5446. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. In Proceedings of the 35th Annual Symposium on Foundation of Computer Science, Washington, DC, USA, 20–22 November 1994; pp. 124–134. [Google Scholar] [CrossRef]
- Bernstein, J. Introduction to post-quantum cryptography. In Post-Quantum Cryptography; Bernstein, D.J., Buchmann, J., Dahmen, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–14. [Google Scholar] [CrossRef]
- Kulynych, B.; Lueks, W.; Isaakidis, M.; Danezis, G.; Troncoso, C. ClaimChain: Improving the security and privacy of in-band key distribution for messaging. In Proceedings of the 2018 Workshop on Privacy in the Electronic Society, Alexandria, VA, USA, 15–19 October 2018; pp. 86–103. [Google Scholar]
- Myasnikov, A.; Shpilrain, V.; Ushakov, A. Group-based cryptography. J. Math. Sci. 2011, 175, 472–516. [Google Scholar]
- Lee, J.M. Introduction to Smooth Manifolds, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Anshel, I.; Anshel, M.; Goldfeld, D. An algebraic method for public-key cryptography. Math. Res. Lett. 1999, 6, 287–291. [Google Scholar] [CrossRef]
- Paillier, P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. In Advances in Cryptology—EU-ROCRYPT ’99; Stern, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1592, pp. 223–238. [Google Scholar] [CrossRef]
- Humphreys, J. Introduction to Lie Algebras and Representation Theory, 3rd ed.; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Michael, B. Applications of Lie Theory in Cryptographic Systems. J. Gen. Lie Theory App 2024, 18, 482. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing. SIAM J. Comput. 2003, 32, 586–615. [Google Scholar] [CrossRef]
- Fujisaki, E.; Okamoto, T. Secure Integration of Asymmetric and Symmetric Encryption Schemes. In Advances in Cryptology—CRYPTO’ 99. CRYPTO 1999; Wiener, M., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1666. [Google Scholar] [CrossRef]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM 2009, 56, 6. [Google Scholar] [CrossRef]
- Bootland, C.; Castryck, W.; Szepieniec, A.; Vercauteren, F. A framework for cryptographic problems from linear algebra. J. Math. Cryptol. 2019, 14, 202–217. [Google Scholar] [CrossRef]
- Serre, J.-P. Lie Algebras and Lie Groups: 1964 Lectures; Springer: New York, NY, USA, 2006. [Google Scholar]
- Brakerski, Z. Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP. In Advances in Cryptology—CRYPTO 2012; Safavi-Naini, R., Canetti, R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7417, pp. 868–886. [Google Scholar] [CrossRef]
- Fan, J.; Vercauteren, F. Somewhat Practical Fully Homomorphic Encryption. IACR Cryptol. Eprint Arch. 2012, 2012, 144. Available online: https://eprint.iacr.org/2012/144 (accessed on 19 June 2025).
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (Leveled) Fully Homomorphic Encryption without Bootstrapping. ACM Trans. Comput. Theory 2014, 6, 1–36. [Google Scholar] [CrossRef]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic Encryption for Arithmetic of Approximate Numbers. In Advances in Cryptology—ASIACRYPT 2017; Takagi, T., Peyrin, T., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10624, pp. 409–437. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST). FIPS 203: Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM). Gaithersburg, MD, USA, 2024. Available online: https://csrc.nist.gov/pubs/fips/203/final (accessed on 19 June 2025).
- National Institute of Standards and Technology (NIST). FIPS 204: Module-Lattice-Based Digital Signature Standard (ML-DSA). Gaithersburg, MD, USA, 2024. Available online: https://csrc.nist.gov/pubs/fips/204/final (accessed on 19 June 2025).
- National Institute of Standards and Technology (NIST). FIPS 205: Stateless Hash-Based Digital Signature Standard (SLH-DSA). Gaithersburg, MD, USA, 2024. Available online: https://csrc.nist.gov/pubs/fips/205/final (accessed on 19 June 2025).
- Hofheinz, D.; Kiltz, E.; Shoup, V. Practical Chosen Ciphertext Secure Encryption from Factoring. J. Cryptol. 2013, 26, 102–118. [Google Scholar] [CrossRef]
- Khatami, L. The poset of the nilpotent commutator of a nilpotent matrix. Linear Algebra Its Appl. 2013, 439, 3763–3776. [Google Scholar] [CrossRef]
- Kreuzer, M.; Robbiano, L. Computational Commutative Algebra; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Abdollahi, A.; Akbari, S.; Maimani, H.R. Non-commuting graph of a group. J. Algebra 2006, 298, 468–492. [Google Scholar] [CrossRef]
- Khamseh, E. Bilinear cryptography using Lie algebras from p-groups. Math. Comput. Sci. 2021, 2, 71–77. [Google Scholar] [CrossRef]
- Roman’kov, V. Discrete logarithm for nilpotent groups and cryptanalysis of polylinear cryptographic system. Prikl. Diskretn. matematika. Prilozhenie 2019, 12, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Samiullah, F.; Gan, M.-L.; Akleylek, S.; Aun, Y. Quantum Resistance Group Key Management for IoTs. In Proceedings of the 2023 2nd International Conference on Emerging Trends in Electrical, Control, and Telecommunication Engineering (ETECTE), Lahore, Pakistan, 27–29 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Duong, M.T.; Moldovyan, D.N.; Do, B.V.; Nguyen, M.H. Post-quantum signature algorithms on noncommutative algebras, using difficulty of solving systems of quadratic equations. Comput. Stand. Interfaces 2023, 86, 103740. [Google Scholar] [CrossRef]
- Hong, H.; Shao, J.; Wang, L.; Xie, M.; Wei, G.; Yang, Y.; Han, S.; Lin, J. A CCA secure public key encryption scheme based on finite groups of Lie type. Sci. China Inf. Sci. 2021, 65, 119102. [Google Scholar] [CrossRef]
- Wang, N.; Liu, F. Application of the Adaptive Mixed-Order Cubature Particle Filter Algorithm Based on Matrix Lie Group Representation for the Initial Alignment of SINS. Information 2025, 16, 416. [Google Scholar] [CrossRef]
- Zeng, H.; Zou, S.; Yao, C.; Xu, C. LGNet: A Symmetric Dual-Branch Lightweight Model for Remote Sensing Scene Classification Based on Lie Group Feature Extraction and Cross-Attention Mechanism. Symmetry 2025, 17, 780. [Google Scholar] [CrossRef]
- Sophocleous, C.; Tracinà, R. Lie Group Classification for a Reduced Burgers System. Symmetry 2025, 17, 763. [Google Scholar] [CrossRef]
- Xu, C.; Shu, J.; Wang, Z.; Wang, J. Lie Group Intrinsic Mean Feature Detectors for Real-Time Industrial Surface Defect Detection. Symmetry 2025, 17, 612. [Google Scholar] [CrossRef]
- Li, Y.; Cherif, A.M.; Xie, Y. Characterization of Ricci Solitons and Harmonic Vector Fields on the Lie Group Nil4. Mathematics 2025, 13, 1155. [Google Scholar] [CrossRef]
- Fiori, S. Discrete-Time Dynamical Systems on Structured State Spaces: State-Transition Laws in Finite-Dimensional Lie Algebras. Symmetry 2025, 17, 463. [Google Scholar] [CrossRef]
- Bildirici, M.; Ucan, Y.; Tekercioglu, R. Stochastic SO(2) Lie Group Method for Approximating Correlation Matrices. Mathematics 2025, 13, 1496. [Google Scholar] [CrossRef]
- Ayala, V.; Torreblanca, M.; Valdivia, W. Conjectures on the Stability of Linear Control Systems on Matrix Lie Groups. Symmetry 2025, 17, 593. [Google Scholar] [CrossRef]
- Bauspieß, P.V. Post-Quantum Secure Biometric Systems; NTNU: Trondheim, Norway, 2024. [Google Scholar]
- Emerencia, C. A Mathematical Approach to Post-Quantum Cryptography. Ph.D. Thesis, Vrije Universiteit Brussel, Ixelles, Brussel, 2024. [Google Scholar]
- Hasić, A.; Azizović, M.; Azizović, E.; Saračević, M. Solvability and Nilpotency of Lie Algebras in Cryptography and Steganography. Mathematics 2025, 13, 1824. [Google Scholar] [CrossRef]
- Akmese, Ö.F.; Erdogan, M. Biblio-metric Analysis of Studies on Cyber Crimes Between 2000–2023. ADBA Comput. Sci. 2025, 2, 19–29. [Google Scholar] [CrossRef]
- Alaca, Y.; Celık, Y.; Goel, S. Anomaly Detection in Cyber Security with Graph-Based LSTM in Log Analysis. Chaos Theory Appl. 2023, 5, 188–197. [Google Scholar] [CrossRef]
- Seyyarer, E.; Ayata, F.; Özdem, S. The Role of Technological Approaches in Cyber Security of Autonomous Vehicles. ADBA Comput. Sci. 2025, 2, 1–6. [Google Scholar] [CrossRef]
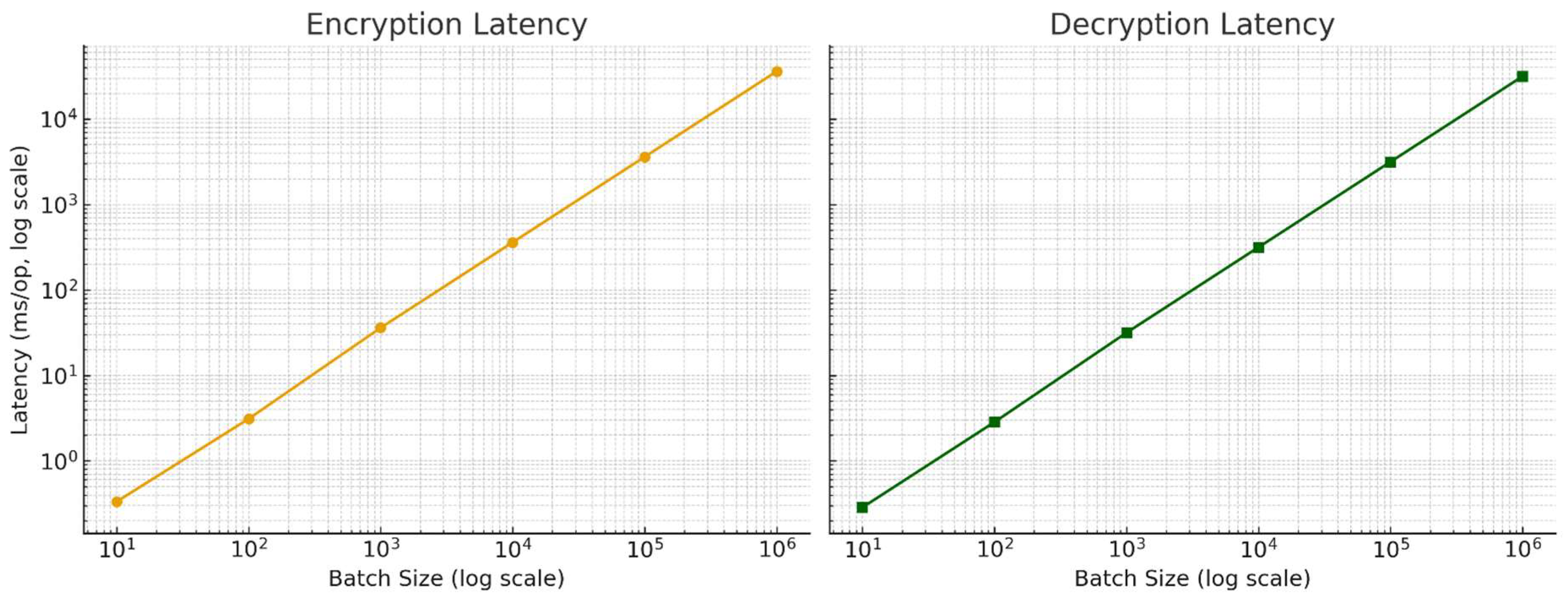


| Number of Messages | Encryption Time (s) | Homomorphic Addition Time (s) | Decryption Time (s) |
|---|---|---|---|
| 10 | 0.000334 | 0.000013 | 0.000286 |
| 100 | 0.003111 | 0.000133 | 0.002848 |
| 1000 | 0.036144 | 0.001258 | 0.031633 |
| 10,000 | 0.361436 | 0.012579 | 0.316331 |
| 100,000 | 3.614358 | 0.125793 | 3.163310 |
| 1,000,000 | 36.143582 | 1.257931 | 31.633097 |
| n | c | Ciphertext Size (|C|) | Expansion Ratio (|C|/|M|) | Depth (Median) | Depth CI95 Low | Depth CI95 High |
|---|---|---|---|---|---|---|
| 3 | 2 | 3.4 × 10−5 | 3.0 | 1.0 | 1.0 | 3.0 |
| 6 | 2 | 0.000137 | 2.4 | 0.0 | 0.0 | 1.0 |
| 9 | 3 | 0.000309 | 2.25 | 0.0 | 0.0 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selim, A.; Saračević, M.; Ćatović, A. Homomorphic Cryptographic Scheme Based on Nilpotent Lie Algebras for Post-Quantum Security. Symmetry 2025, 17, 1666. https://doi.org/10.3390/sym17101666
Selim A, Saračević M, Ćatović A. Homomorphic Cryptographic Scheme Based on Nilpotent Lie Algebras for Post-Quantum Security. Symmetry. 2025; 17(10):1666. https://doi.org/10.3390/sym17101666
Chicago/Turabian StyleSelim, Aybeyan, Muzafer Saračević, and Azra Ćatović. 2025. "Homomorphic Cryptographic Scheme Based on Nilpotent Lie Algebras for Post-Quantum Security" Symmetry 17, no. 10: 1666. https://doi.org/10.3390/sym17101666
APA StyleSelim, A., Saračević, M., & Ćatović, A. (2025). Homomorphic Cryptographic Scheme Based on Nilpotent Lie Algebras for Post-Quantum Security. Symmetry, 17(10), 1666. https://doi.org/10.3390/sym17101666








