EP-REx: Evidence-Preserving Receptive-Field Expansion for Efficient Crack Segmentation
Abstract
1. Introduction
- We propose EP-REx, a compact architecture that efficiently enlarges the receptive field to capture global context while simultaneously preserving the critical pixel-level evidence essential for crack segmentation, making it suitable for resource-constrained applications.
- We introduce a multi-scale block featuring parallel dilated depthwise convolutions. Our ablation studies validate that this design, which captures both broad context and fine details, is more effective than standard convolutional blocks for improving segmentation accuracy in a lightweight setting.
- We present IG-Gate, a parameter-free module that leverages raw input intensity and gradient cues to modulate feature responses. We demonstrate through ablation studies that this mechanism effectively enhances performance and works synergistically with our multi-scale block to better preserve critical pixel-level cues.
2. Related Work
3. Proposed Method
3.1. Preliminaries
3.2. Proposed Architecture: Encoder Path
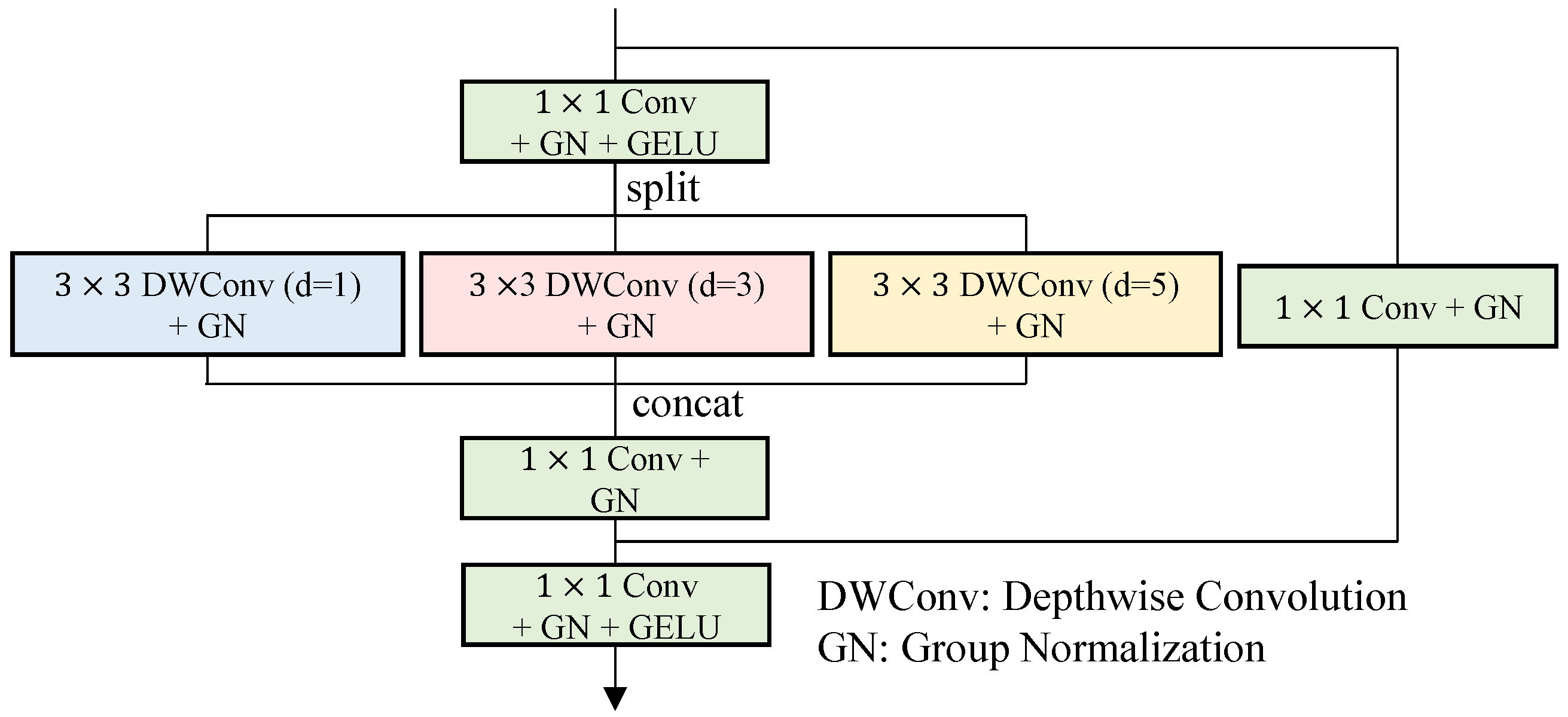
3.3. Multi-Scale Dilated Block (MSDB)
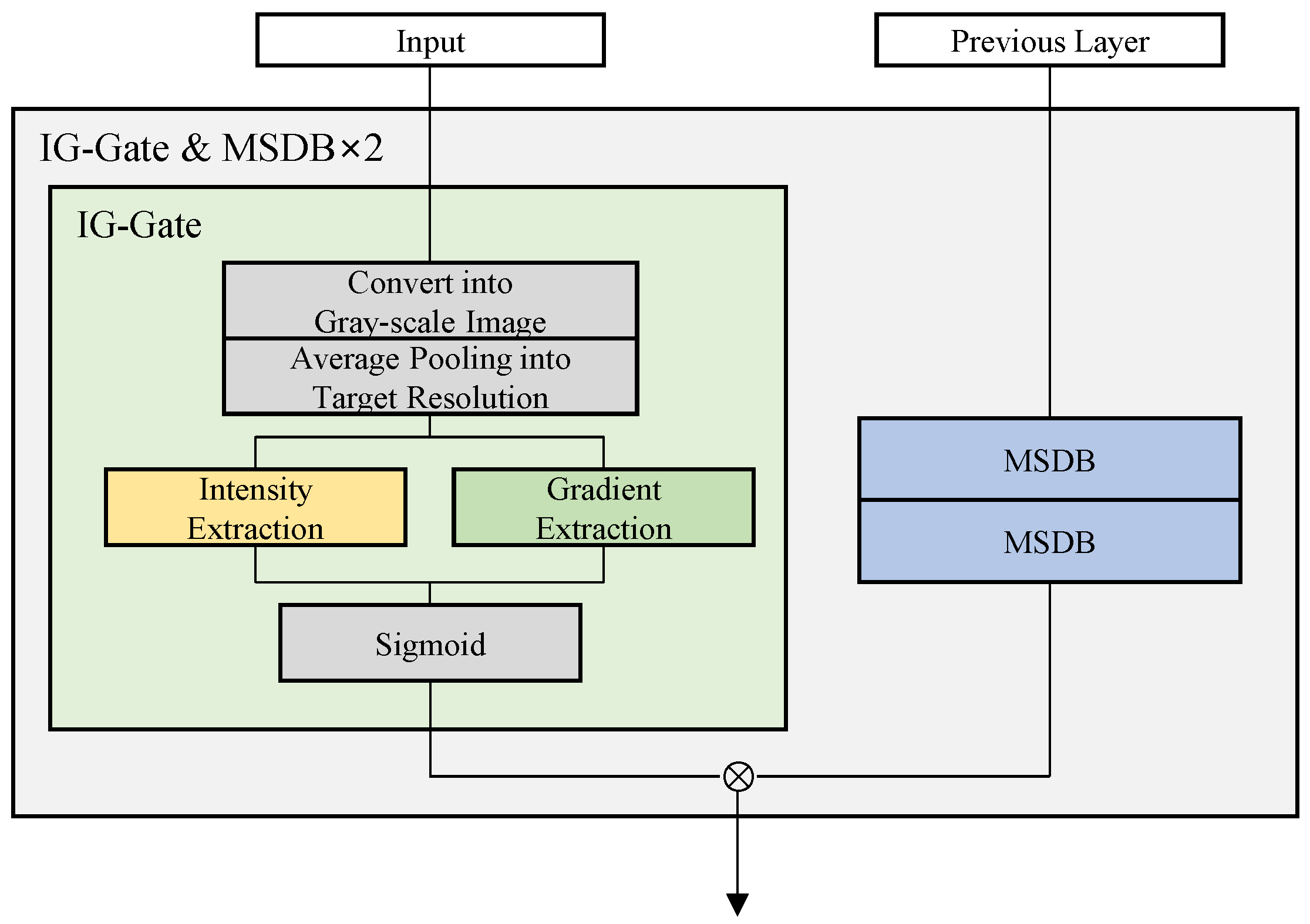
3.4. Input-Guided Gate (IG-Gate)
3.5. Decoder Path and Final Prediction
4. Experiments
4.1. Experimental Settings
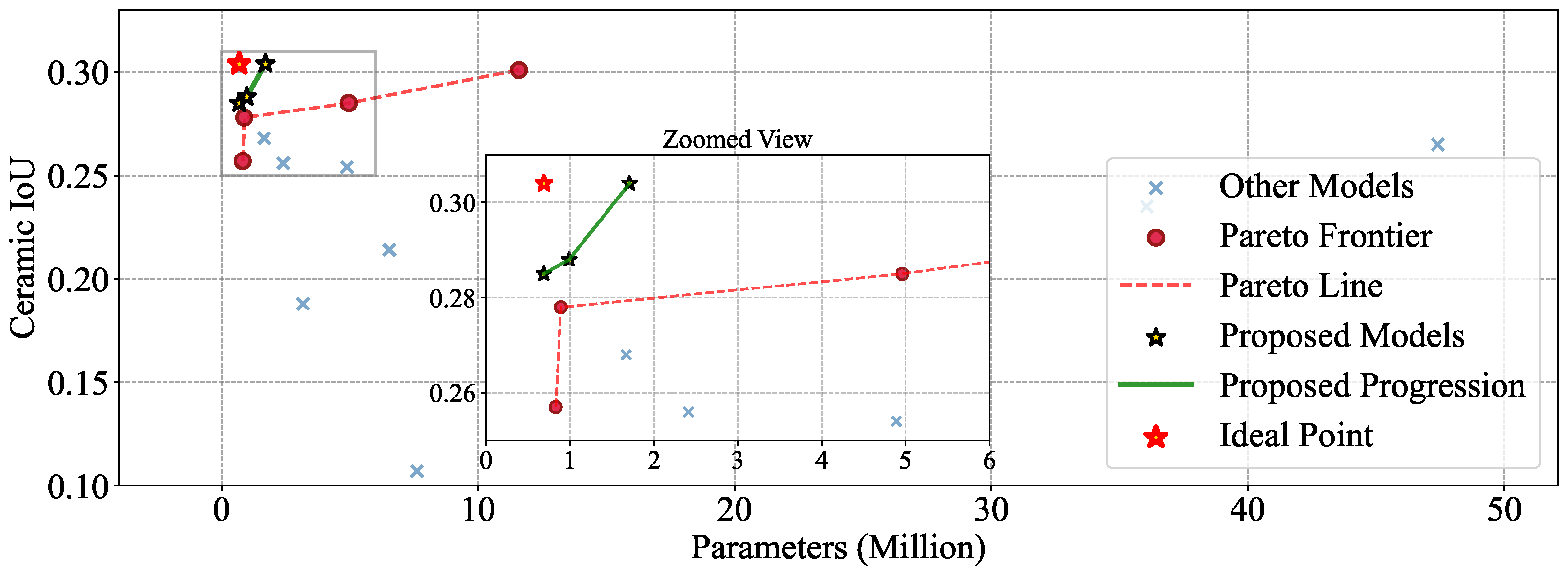
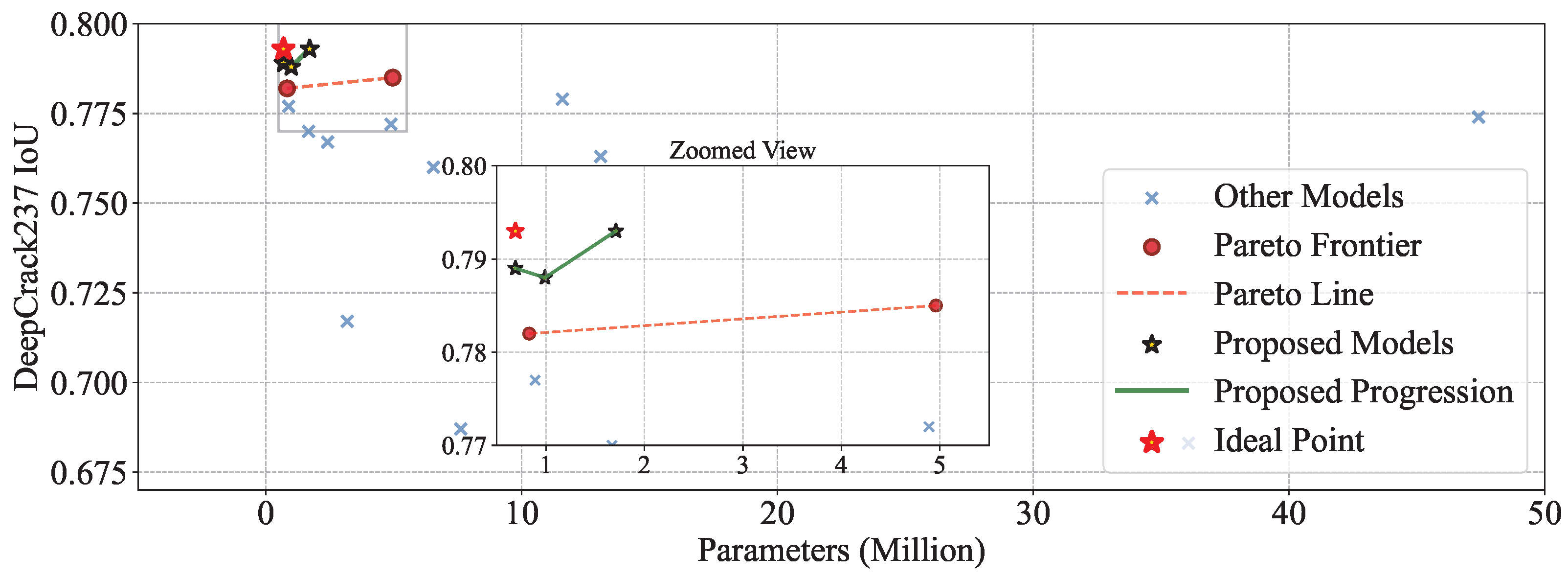
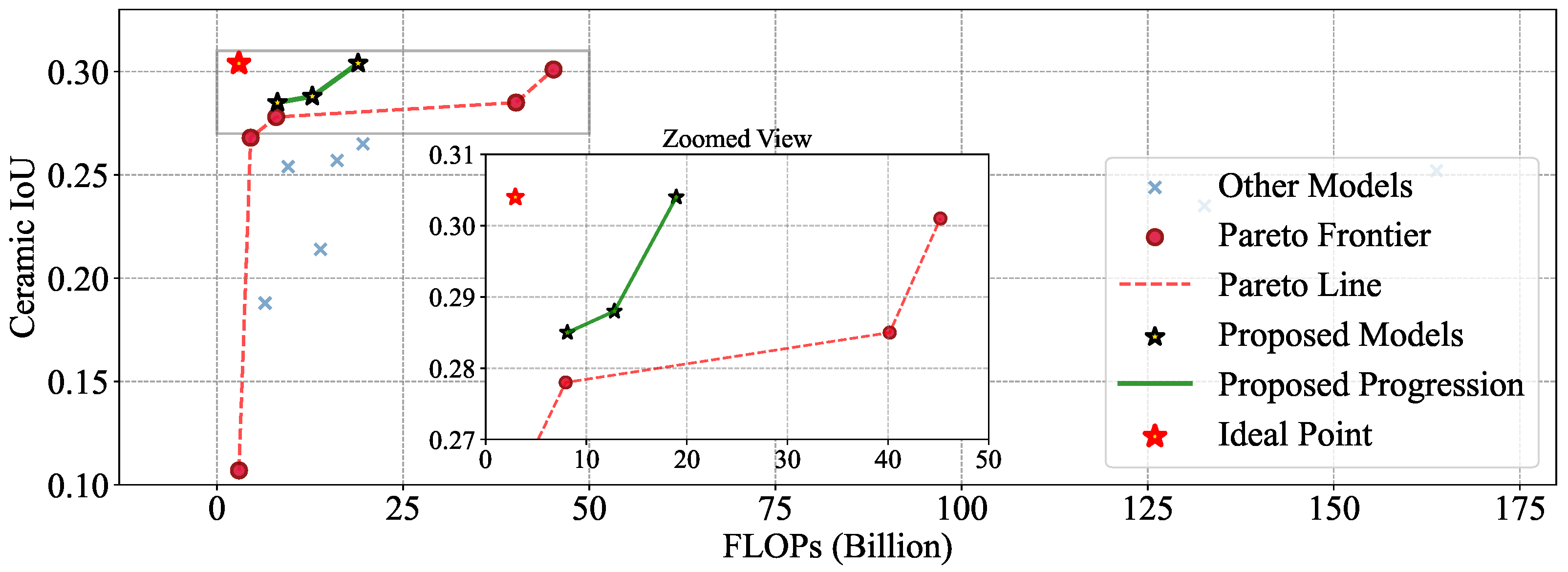
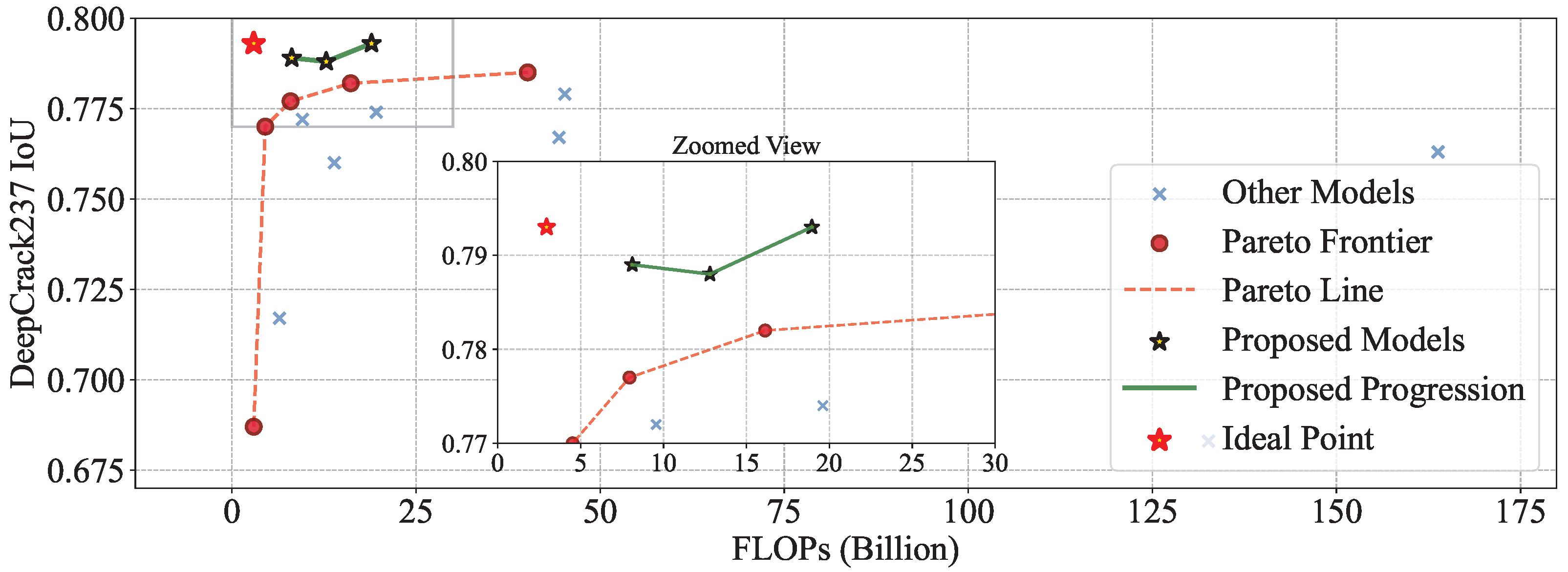
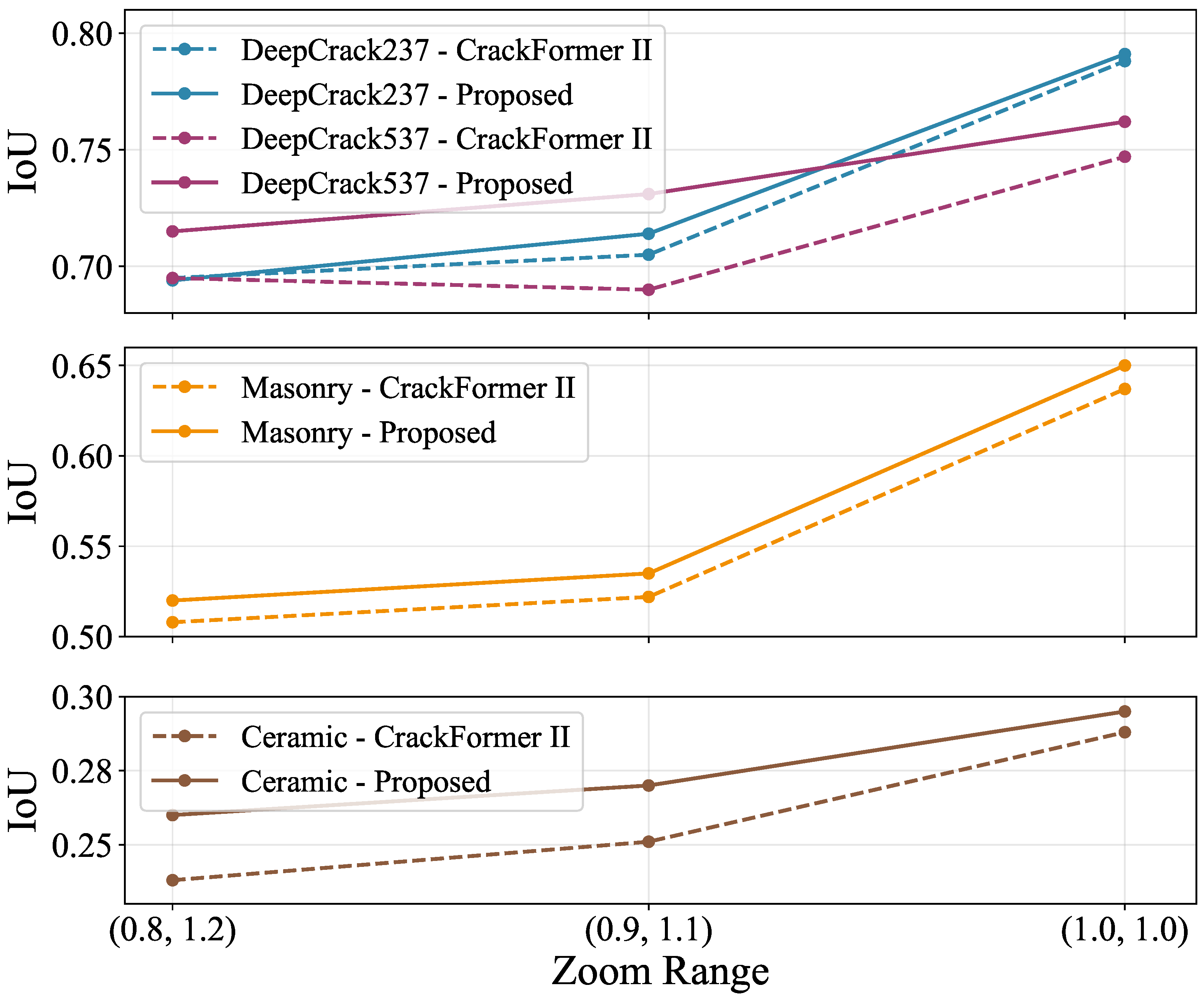
4.2. Experimental Results
4.3. Efficiency Analysis
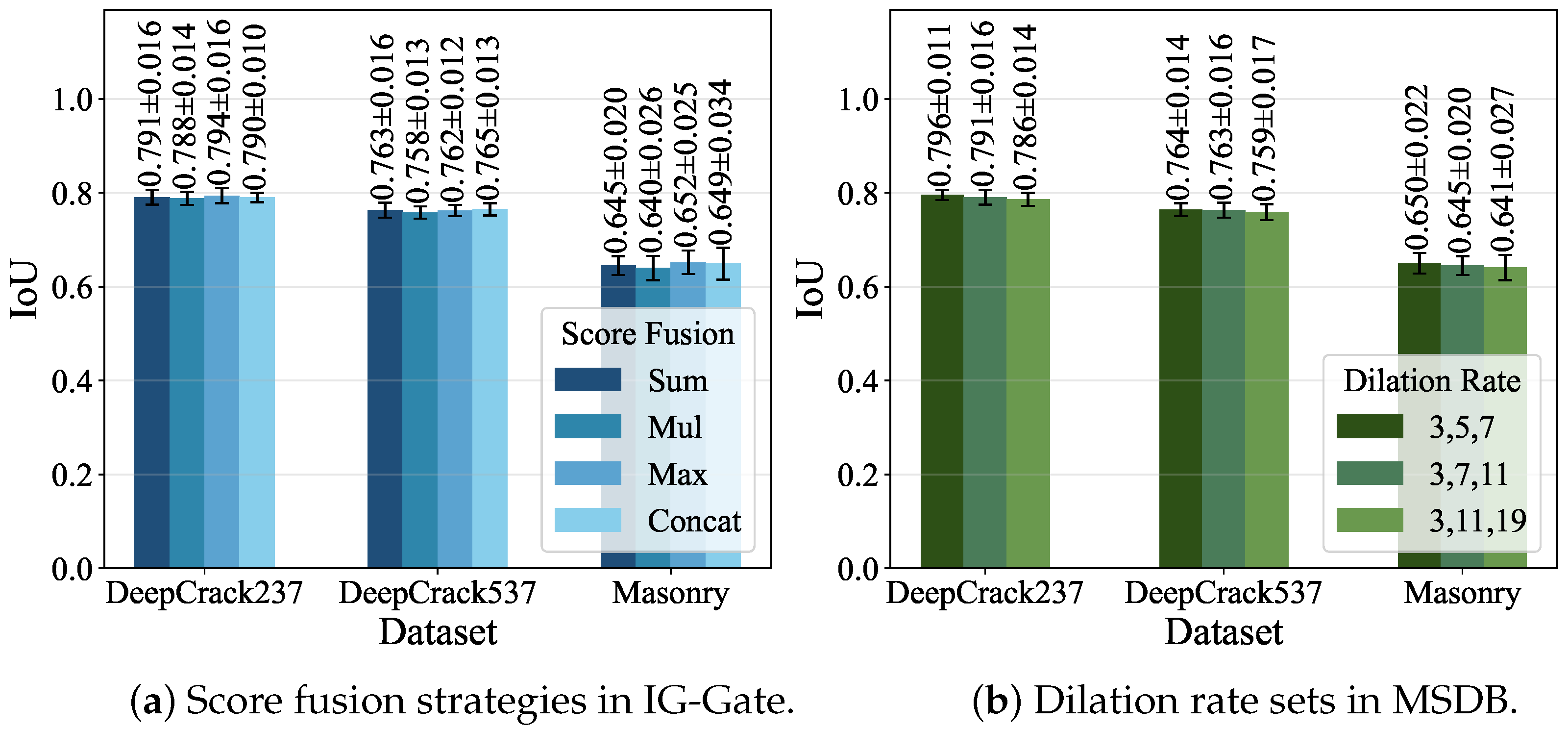
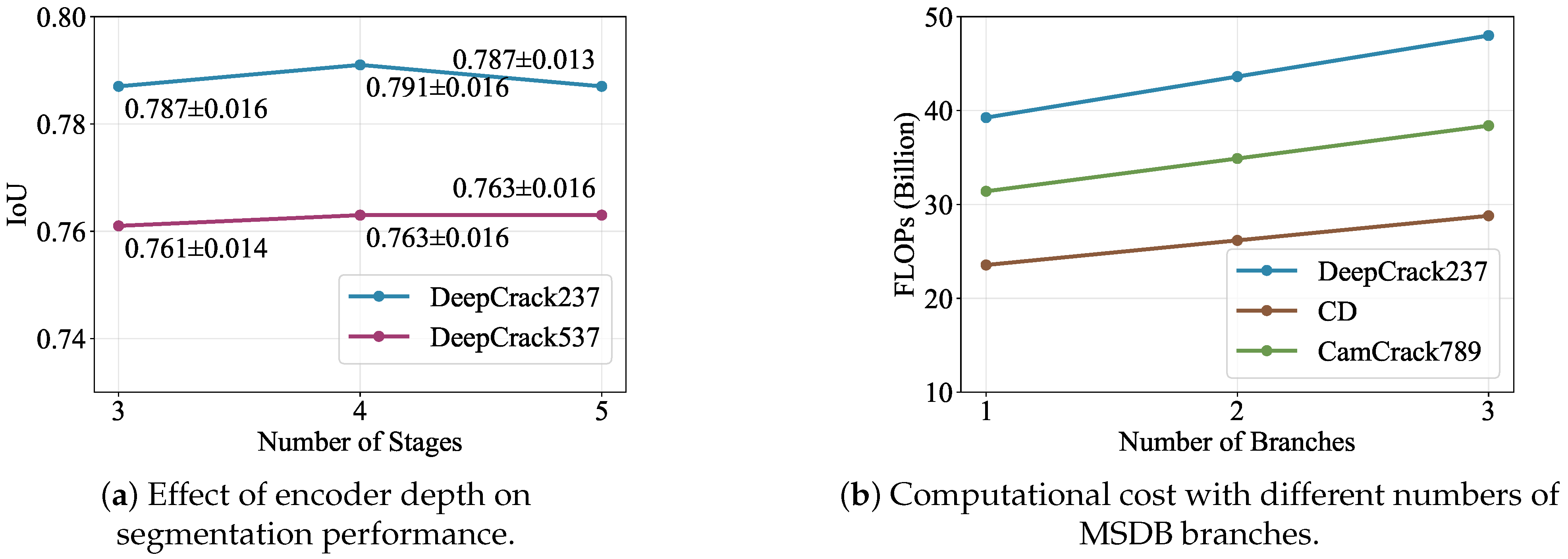
4.4. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, Q.; Cao, Y.; Li, Q.; Mao, Q.; Wang, S. CrackTree: Automatic crack detection from pavement images. Pattern Recognit. Lett. 2012, 33, 227–238. [Google Scholar] [CrossRef]
- Zou, Q.; Zhang, Z.; Li, Q.; Qi, X.; Wang, Q.; Wang, S. Deepcrack: Learning hieraarchical convolutional features for crack detection. IEEE Trans. Image Process. 2018, 28, 1498–1512. [Google Scholar] [CrossRef]
- Dong, C.Z.; Catbas, F.N. A review of computer vision–based structural health monitoring at local and global levels. Struct. Health Monit. 2021, 20, 692–743. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Y.; Yu, J.; Yue, J. Lightweight decoder U-net crack segmentation network based on depthwise separable convolution. Multimedia Syst. 2024, 30, 295. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Wu, X.; Wu, D.; Hu, H.; Liu, X.; Zhou, Y. E2S: A UAV-Based Levee Crack Segmentation Framework Using the Unsupervised Deblurring Technique. Remote Sens. 2025, 17, 935. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Martinez-Rau, L.S.; Vu, Q.N.P.; Oelmann, B.; Bader, S. On-Device Crack Segmentation for Edge Structural Health Monitoring. arXiv 2025, arXiv:2505.07915. [Google Scholar] [CrossRef]
- Kim, Y.; Yi, S.; Ahn, H.; Hong, C.H. Accurate Crack Detection Based on Distributed Deep Learning for IoT Environment. Sensors 2023, 2, 858. [Google Scholar] [CrossRef] [PubMed]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for MobileNetV3. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Ali, L.; AlJassmi, H.; Swavaf, M.; Khan, W.; Alnajjar, F. RS-Net: Residual Sharp U-Net architecture for pavement crack segmentation and severity assessment. J. Big Data 2024, 11, 116. [Google Scholar] [CrossRef]
- Zhu, G.; Liu, J.; Fan, Z.; Yuan, D.; Ma, P.; Wang, M.; Sheng, W.; Wang, K.C. A lightweight encoder–decoder network for automatic pavement crack detection. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 1743–1765. [Google Scholar] [CrossRef]
- Liang, J. CNN-based network with multi-scale context feature and attention mechanism for automatic pavement crack segmentation. Autom. Constr. 2024, 164, 105482. [Google Scholar] [CrossRef]
- Li, K.; Yang, J.; Ma, S.; Wang, B.; Wang, S.; Tian, Y.; Qi, Z.; Tian, Y. Rethinking Lightweight Convolutional Neural Networks for Efficient and High-Quality Pavement Crack Detection. IEEE Trans. Intell. Transp. Syst. 2024, 25, 237–250. [Google Scholar] [CrossRef]
- Wang, Z.; Ji, S. Smoothed Dilated Convolutions for Improved Dense Prediction. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’18), London, UK, 19–23 August 2018; pp. 2486–2495. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Duarte, K.T.; Gobbi, D.G.; Sidhu, A.S.; McCreary, C.R.; Saad, F.; Camicioli, R.; Smith, E.E.; Frayne, R. Segmenting white matter hyperintensities in brain magnetic resonance images using convolution neural networks. Pattern Recognit. Lett. 2023, 175, 90–94. [Google Scholar] [CrossRef]
- Morita, D.; Kawarazaki, A.; Koimizu, J.; Tsujiko, S.; Soufi, M.; Otake, Y.; Sato, Y.; Numajiri, T. Automatic orbital segmentation using deep learning-based 2D U-net and accuracy evaluation: A retrospective study. J. Cranio Maxillofac. Surg. 2023, 51, 609–613. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV 2018), Munich, Germany, 8–14 September 2018; pp. 833–851. [Google Scholar]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and efficient design for semantic segmentation with transformers. In Proceedings of the Advances in Neural Information Processing Systems 34, Virtual, 6–14 December 2021. [Google Scholar]
- Li, T.; Cui, Z.; Zhang, H. Semantic segmentation feature fusion network based on transformer. Sci. Rep. 2025, 15, 6110. [Google Scholar] [CrossRef]
- Fu, B.; Peng, Y.; He, J.; Tian, C.; Sun, X.; Wang, R. HmsU-Net: A hybrid multi-scale U-net based on a CNN and transformer for medical image segmentation. Comput. Biol. Med. 2024, 170, 108013. [Google Scholar] [CrossRef]
- Heidari, M.; Kazerouni, A.; Soltany, M.; Azad, R.; Aghdam, E.K.; Cohen-Adad, J.; Merhof, D. HiFormer: Hierarchical Multi-Scale Representations Using Transformers for Medical Image Segmentation. In Proceedings of the 2023 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 2–7 January 2023; pp. 6202–6212. [Google Scholar]
- Sze, V.; Chen, Y.H.; Yang, T.J.; Emer, J.S. Efficient Processing of Deep Neural Networks: A Tutorial and Survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. In Proceedings of the European Conference on Computer Vision (ECCV 2018), Munich, Germany, 8–14 September2018; pp. 122–138. [Google Scholar]
- Tan, M.; Le, Q. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning (ICML-19), Long Beach, CA, USA, 9–15 June 2019; Chaudhuri, K., Salakhutdinov, R., Eds.; Volume 97, pp. 6105–6114. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 6848–6856. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both Weights and Connections for Efficient Neural Networks. Adv. Neural. Inf. Process Syst. 2015, 28, 1135–1143. [Google Scholar]
- Yang, C.; Zhao, P.; Li, Y.; Niu, W.; Guan, J.; Tang, H.; Qin, M.; Ren, B.; Lin, X.; Wang, Y.; et al. Pruning parameterization with bi-level optimization for efficient semantic segmentation on the edge. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 15402–15412. [Google Scholar]
- Liu, Y.; Chen, K.; Liu, C.; Qin, Z.; Luo, Z.; Wang, J. Structured Knowledge Distillation for Semantic Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Dung, D.V.; Anh, L.D. Autonomous concrete crack detection using deep fully convolutional neural network. Autom. Constr. 2019, 99, 52–58. [Google Scholar] [CrossRef]
- Yang, X.; Li, H.; Yu, Y.; Luo, X.; Huang, T.; Yang, X. Automatic Pixel-Level Crack Detection and Measurement Using Fully Convolutional Network. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 1090–1109. [Google Scholar] [CrossRef]
- Li, G.; Ma, B.; He, S.; Ren, X.; Liu, Q. Automatic Tunnel Crack Detection Based on U-Net and a Convolutional Neural Network with Alternately Updated Clique. Sensors 2020, 20, 717. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Cui, L.; Qi, Z.; Meng, F.; Chen, Z. Automatic road crack detection using random structured forests. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3434–3445. [Google Scholar] [CrossRef]
- Liu, H.; Miao, X.; Mertz, C.; Xu, C.; Kong, H. CrackFormer: Transformer Network for Fine-Grained Crack Detection. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Virtual, 11–17 October 2021; pp. 3783–3792. [Google Scholar]
- Al-maqtari, O.; Peng, B.; Al-Huda, Z.; Al-Malahi, A.; Maqtary, N. Lightweight Yet Effective: A Modular Approach to Crack Segmentation. IEEE Trans. Intell. Veh. 2024, 9, 7961–7972. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, J.; Lu, X.; Xie, R.; Li, L. DeepCrack: A deep hierarchical feature learning architecture for crack segmentation. Neurocomputing 2019, 338, 139–153. [Google Scholar] [CrossRef]
- Yang, L.; Bai, S.; Liu, Y.; Yu, H. Multi-scale triple-attention network for pixelwise crack segmentation. Autom. Constr. 2023, 150, 104853. [Google Scholar] [CrossRef]
- Xiang, C.; Guo, J.; Cao, R.; Deng, L. A crack-segmentation algorithm fusing transformers and convolutional neural networks for complex detection scenarios. Autom. Constr. 2023, 152, 104894. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, Z.; Sharma, P.K.; Alfarraj, O.; Tolba, A.; Wang, J. A dual encoder crack segmentation network with Haar wavelet-based high–low frequency attention. Expert Syst. Appl. 2024, 256, 124950. [Google Scholar] [CrossRef]
- Wang, J.; Zeng, Z.; Sharma, P.K.; Alfarraj, O.; Tolba, O.; Zhang, J.; Wang, A. Dual-path network combining CNN and transformer for pavement crack segmentation. Autom. Constr. 2024, 158, 105217. [Google Scholar] [CrossRef]
- Xiang, Z.; He, X.; Zou, Y.; Jing, H. An active learning method for crack detection based on subset searching and weighted sampling. Struct. Health Monit. 2024, 23, 1184–1200. [Google Scholar] [CrossRef]
- Xu, Y.; Wei, S.; Bao, Y.; Li, H. Automatic seismic damage identification of reinforced concrete columns from images by a region-based deep convolutional neural network. Struct. Control Health Monit. 2019, 26, e2313. [Google Scholar] [CrossRef]
- Lin, C.; Zhang, Z.; Peng, J.; Li, F.; Pan, Y.; Zhang, Y. A lightweight contour detection network inspired by biology. Complex Intell. Syst. 2024, 10, 4275–4291. [Google Scholar] [CrossRef]
- Liu, H.; Yang, J.; Miao, X.; Mertz, C.; Kong, H. CrackFormer Network for Pavement Crack Segmentation. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9240–9252. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Tian, X.; Luo, C.; Tan, J. Visual inspection system for crack defects in metal pipes. Multimedia Tools Appl. 2024, 83, 81877–81894. [Google Scholar] [CrossRef]
- Xu, J.; Xiong, Z.; Bhattacharyya, S.P. PIDNet: A Real-Time Semantic Segmentation Network Inspired by PID Controllers. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 19529–19539. [Google Scholar]
- Guo, Z.; Bian, L.; Wei, H.; Li, J.; Ni, H.; Huang, X. DSNet: A Novel Way to Use Atrous Convolutions in Semantic Segmentation. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 3679–3692. [Google Scholar] [CrossRef]
- Pang, X.; Lin, C.; Li, F.; Pan, Y. Bio-inspired XYW parallel pathway edge detection network. Expert Syst. Appl. 2024, 237, 121649. [Google Scholar] [CrossRef]
- Junior, G.S.; Ferreira, J.; Millán-Arias, C.; Daniel, R.; Junior, A.C.; Fernandes, B.J.T. Ceramic Cracks Segmentation with Deep Learning. Appl. Sci. Switz. 2021, 11, 6017. [Google Scholar] [CrossRef]
- Dais, D.; Bal, İ.E.; Smyrou, E.; Sarhosis, V. Automatic crack classification and segmentation on masonry surfaces using convolutional neural networks and transfer learning. Autom. Constr. 2021, 125, 103606. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature Pyramid and Hierarchical Boosting Network for Pavement Crack Detection. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1525–1535. [Google Scholar] [CrossRef]



| Dataset | Original Resolution | Input Resolution | # Images | Train/Val/Test |
|---|---|---|---|---|
| Ceramic [50] | 100 | 60/20/20 | ||
| DeepCrack237 [37] | 237 | 142/47/48 | ||
| Masonry [51] | 240 | 144/48/48 | ||
| DeepCrack537 [37] | 537 | 316/105/106 | ||
| CD [32] | 236–– | 776 | 466/155/155 | |
| CamCrack789 [52] | 789 | 473/158/158 |
| Model Name | Ceramic | DeepCrack237 | Masonry | DeepCrack537 | CD | CamCrack789 |
|---|---|---|---|---|---|---|
| Proposed (Base) | 0.304 ± 0.024 | 0.793 ± 0.015 | 0.650 ± 0.017 | 0.768 ± 0.012 | 0.762 ± 0.006 | 0.726 ± 0.004 |
| BLCDNet | 0.256 ± 0.027⯆ | 0.767 ± 0.016⯆ | 0.579 ± 0.023⯆ | 0.742 ± 0.015⯆ | 0.727 ± 0.011⯆ | 0.710 ± 0.005⯆ |
| CSNet | 0.188 ± 0.027⯆ | 0.717 ± 0.013⯆ | 0.537 ± 0.008⯆ | 0.693 ± 0.015⯆ | 0.621 ± 0.004⯆ | 0.663 ± 0.005⯆ |
| CarNet | 0.254 ± 0.015⯆ | 0.772 ± 0.012⯆ | 0.595 ± 0.029⯆ | 0.740 ± 0.015⯆ | 0.708 ± 0.005⯆ | 0.712 ± 0.006⯆ |
| CrackFormer II | 0.285 ± 0.025 | 0.785 ± 0.017 | 0.632 ± 0.022 | 0.754 ± 0.015⯆ | 0.740 ± 0.004⯆ | 0.720 ± 0.008 |
| DSNet | 0.214 ± 0.018⯆ | 0.760 ± 0.019⯆ | 0.611 ± 0.023⯆ | 0.739 ± 0.016⯆ | 0.696 ± 0.003⯆ | 0.700 ± 0.003⯆ |
| PIDNet | 0.107 ± 0.015⯆ | 0.687 ± 0.052⯆ | 0.552 ± 0.049⯆ | 0.689 ± 0.017⯆ | 0.630 ± 0.007⯆ | 0.642 ± 0.011⯆ |
| DSUNet | 0.301 ± 0.037 | 0.779 ± 0.010 | 0.633 ± 0.023 | 0.751 ± 0.014⯆ | 0.749 ± 0.008⯆ | 0.716 ± 0.005⯆ |
| RSNet | 0.252 ± 0.013⯆ | 0.763 ± 0.018⯆ | 0.578 ± 0.011⯆ | 0.725 ± 0.013⯆ | 0.721 ± 0.011⯆ | 0.704 ± 0.002⯆ |
| U-MPSC | 0.235 ± 0.017⯆ | 0.683 ± 0.030⯆ | 0.529 ± 0.033⯆ | 0.617 ± 0.029⯆ | 0.682 ± 0.008⯆ | 0.499 ± 0.079⯆ |
| DECSNet | 0.265 ± 0.019 | 0.774 ± 0.013⯆ | 0.629 ± 0.015⯆ | 0.741 ± 0.017⯆ | 0.712 ± 0.006⯆ | 0.706 ± 0.005⯆ |
| Model Name | Ceramic | DeepCrack237 | Masonry | DeepCrack537 | CD | CamCrack789 |
|---|---|---|---|---|---|---|
| Proposed (Small) | 0.288 ± 0.026 | 0.788 ± 0.013 | 0.644 ± 0.016 | 0.766 ± 0.016 | 0.754 ± 0.003 | 0.725 ± 0.005 |
| RHACrackNet | 0.268 ± 0.023 | 0.770 ± 0.022⯆ | 0.626 ± 0.017⯆ | 0.746 ± 0.014⯆ | 0.734 ± 0.010⯆ | 0.722 ± 0.004 |
| Model Name | Ceramic | DeepCrack237 | Masonry | DeepCrack537 | CD | CamCrack789 |
|---|---|---|---|---|---|---|
| Proposed (Tiny) | 0.285 ± 0.041 | 0.789 ± 0.014 | 0.643 ± 0.022 | 0.763 ± 0.015 | 0.755 ± 0.005 | 0.719 ± 0.006 |
| LMNet | 0.257 ± 0.026 | 0.782 ± 0.017 | 0.632 ± 0.023 | 0.753 ± 0.015⯆ | 0.739 ± 0.005⯆ | 0.715 ± 0.007 |
| XYWNet | 0.278 ± 0.020 | 0.777 ± 0.017⯆ | 0.625 ± 0.028⯆ | 0.754 ± 0.018⯆ | 0.737 ± 0.004⯆ | 0.716 ± 0.005 |
| Model | #Params (M) | FLOPs (B) | |||||
|---|---|---|---|---|---|---|---|
| Ceramic | DeepCrack237 | Masonry | DeepCrack537 | CD | CamCrack789 | ||
| Proposed (Base) | 1.71 | 18.95 | 71.07 | 18.95 | 71.07 | 42.64 | 56.85 |
| BLCDNet | 2.41 | 44.43 | 166.62 | 44.43 | 166.62 | 99.97 | 133.30 |
| CSNet | 3.18 | 6.46 | 24.24 | 6.46 | 24.24 | 14.54 | 19.39 |
| CarNet | 4.89 | 9.56 | 35.86 | 9.56 | 35.86 | 21.52 | 28.69 |
| CrackFormer II | 4.96 | 40.16 | 150.60 | 40.16 | 150.60 | 90.36 | 120.48 |
| DSNet | 6.55 | 13.91 | 52.12 | 13.91 | 52.12 | 31.28 | 41.70 |
| PIDNet | 7.62 | 2.95 | 11.04 | 2.95 | 11.04 | 6.63 | 8.83 |
| DSUNet | 11.59 | 45.20 | 169.26 | 45.20 | 169.26 | 101.60 | 135.43 |
| RSNet | 13.09 | 163.80 | 614.26 | 163.80 | 614.26 | 368.56 | 491.41 |
| U-MPSC | 36.07 | 132.63 | 497.37 | 132.63 | 497.37 | 298.42 | 397.90 |
| DECSNet | 47.41 | 19.61 | 73.54 | 19.61 | 73.54 | 44.12 | 58.83 |
| Model | #Params (M) | FLOPs (B) | |||||
|---|---|---|---|---|---|---|---|
| Ceramic | DeepCrack237 | Masonry | DeepCrack537 | CD | CamCrack789 | ||
| Proposed (Small) | 0.99 | 12.80 | 47.99 | 12.80 | 47.99 | 28.79 | 38.39 |
| RHACrackNet | 1.67 | 4.52 | 16.94 | 4.52 | 16.94 | 10.16 | 13.55 |
| Model | #Params (M) | FLOPs (B) | |||||
|---|---|---|---|---|---|---|---|
| Ceramic | DeepCrack237 | Masonry | DeepCrack537 | CD | CamCrack789 | ||
| Proposed (Tiny) | 0.69 | 8.12 | 30.45 | 8.12 | 30.45 | 18.27 | 24.36 |
| LMNet | 0.83 | 16.13 | 60.50 | 16.13 | 60.50 | 36.30 | 48.40 |
| XYWNet | 0.89 | 7.95 | 29.79 | 7.95 | 29.79 | 17.88 | 23.84 |
| Modules | IoU | ||||
|---|---|---|---|---|---|
| MSDB | IG-Gate | Ceramic | DeepCrack237 | Masonry | DeepCrack537 |
| ✓ | ✓ | 0.295 ± 0.023 | 0.791 ± 0.014 | 0.650 ± 0.022 | 0.762 ± 0.011 |
| ✓ | × | 0.286 ± 0.007 | 0.786 ± 0.015 | 0.646 ± 0.016 | 0.762 ± 0.013 |
| × | ✓ | 0.291 ± 0.007 | 0.779 ± 0.009 | 0.617 ± 0.036 | 0.750 ± 0.022 |
| × | × | 0.266 ± 0.032 | 0.775 ± 0.015 | 0.632 ± 0.033 | 0.755 ± 0.017 |
| Model | #Params (M) | FLOPs (B) | |||
|---|---|---|---|---|---|
| Ceramic | DeepCrack237 | Masonry | DeepCrack537 | ||
| Proposed | 1.71 | 18.95 | 71.07 | 18.95 | 71.07 |
| MSDB Only | 1.71 | 18.95 | 71.07 | 18.95 | 71.07 |
| IG-Gate Only | 2.62 | 23.74 | 89.02 | 23.74 | 89.02 |
| Baseline | 2.62 | 23.74 | 89.02 | 23.74 | 89.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Lee, J.; Khairulov, T.; Kim, D.; Lee, J. EP-REx: Evidence-Preserving Receptive-Field Expansion for Efficient Crack Segmentation. Symmetry 2025, 17, 1653. https://doi.org/10.3390/sym17101653
Lee S, Lee J, Khairulov T, Kim D, Lee J. EP-REx: Evidence-Preserving Receptive-Field Expansion for Efficient Crack Segmentation. Symmetry. 2025; 17(10):1653. https://doi.org/10.3390/sym17101653
Chicago/Turabian StyleLee, Sanghyuck, Jeongwon Lee, Timur Khairulov, Daehyeon Kim, and Jaesung Lee. 2025. "EP-REx: Evidence-Preserving Receptive-Field Expansion for Efficient Crack Segmentation" Symmetry 17, no. 10: 1653. https://doi.org/10.3390/sym17101653
APA StyleLee, S., Lee, J., Khairulov, T., Kim, D., & Lee, J. (2025). EP-REx: Evidence-Preserving Receptive-Field Expansion for Efficient Crack Segmentation. Symmetry, 17(10), 1653. https://doi.org/10.3390/sym17101653







