On ps-Supplement Submodules

Abstract

In this work, we introduce $ps$-supplement submodules as a kind of supplements. Specifically, a submodule V of a module M is referred to as a $ps$-supplement if there exists another submodule $U\subseteq M$ such that $M=U+V$ and the intersection $U\cap V$ is projective semisimple. We demonstrate that, over an arbitrary ring, the collection $\mathcal{PS}$ of short exact sequences of the form $0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0,$ where $\mathrm{Im}\left(\psi \right)$ is a $ps$-supplement in N, constitutes a proper class. In addition, we explore several homological aspects of this class, including the symmetry of the relations between the modules. Finally, we provide that a ring R is a left SI-ring with essential socle if and only if every left R-module is $ps$-supplemented.

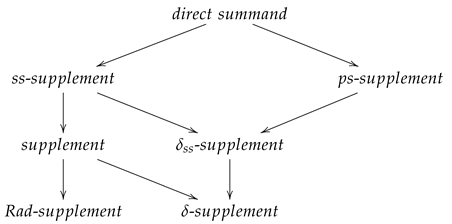
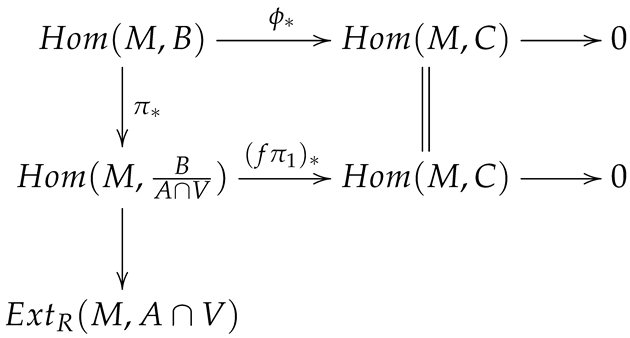1. Introduction

In recent years, various types of supplement submodules have become a prominent topic of investigation within module theory. Several authors have contributed significantly to the development of this area through a sequence of studies (see [1,2,3,4,5,6,7,8,9]), providing detailed results concerning both supplement submodules and associated ring-theoretic properties.

Buchsbaum, in [10], introduced the notion of proper classes to axiomatize scenarios where certain collections of short exact sequences give rise to Ext groups via a form of relative homological algebra. Examples include the class $\mathcal{S}plit$ of all split short exact sequences of left R-modules and the class $\mathcal{A}bs$ of all short exact sequences. Furthermore, as established in [11], the collection $\mathcal{S}upp$ consisting of exact sequences

$$0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0,$$

in which $Im\left(\psi \right)$ is a supplement in N, forms a proper class. Here, a submodule B of a module M is called a supplement to another submodule A if $M=A+B$ and $A\cap B\ll B$, meaning B is minimal with respect to this sum. Supplements generalize direct summands and play a central role in module and ring theory. Since small submodules are always $\delta$-small, the extension to $\delta$-supplements is quite natural.

These proper classes enable ring-theoretic characterizations using homological conditions. A ring R is semisimple precisely when $\mathcal{S}plit=\mathcal{A}bs$, which also implies $\mathcal{S}upp=\mathcal{A}bs$ and $\mathcal{C}o$-$\mathcal{N}eat=\mathcal{A}bs$. The ring R is (semi)perfect if and only if each (finitely generated) left R-module is supplemented [12]. Likewise, R is $\delta$-(semi)perfect exactly when every (finitely generated) left R-module is $\delta$-supplemented [13]. Moreover, ${\displaystyle \frac{R}{P\left(R\right)}}$ is perfect, where $P\left(R\right)$ denotes the sum of all radical left ideals, if and only if every left R-module is Rad-supplemented, that is, each submodule possesses such a Rad-supplement [3].

Another important generalization of direct summands is that of $ss$-supplement submodules. As described in [14], for a module M, define

$$So{c}_s\left(M\right)=\sum \{N\ll M\mid N\mathrm{is}\mathrm{simple}\}.$$

Given that $So{c}_s\left(N\right)\subseteq Rad\left(N\right)$ for any module N, a natural question arises: can we develop a similar concept by replacing $Rad\left(N\right)$ with $So{c}_s\left(N\right)$?

Following [15], we say that a submodule V of a module M is an $ss$-supplement of a submodule U if $M=U+V$ and $U\cap V\subseteq So{c}_s\left(V\right)$. It is proven in [15] that V is an $ss$-supplement of U if and only if V is a supplement and $U\cap V$ is semisimple. A module M is termed $ss$-supplemented when every submodule has an $ss$-supplement within M. The class of $ss$-supplemented modules lies strictly between that of semisimple modules and supplemented modules. According to ([15], Theorem 41), a ring R is semiperfect with semisimple Jacobson radical precisely when every left R-module is $ss$-supplemented.

In a similar spirit, ref. [16] introduced the concept of a ${\delta }_{ss}$-supplement. A submodule V of M is a ${\delta }_{ss}$-supplement of a submodule U if V is a $\delta$-supplement and the intersection $U\cap V$ is semisimple. If every submodule of a module M admits a ${\delta }_{ss}$-supplement, we call M a ${\delta }_{ss}$-supplemented module. As shown in [16], this condition characterizes those rings R for which ${\displaystyle \frac{R}{Soc{(}_{R}R)}}$ is semisimple and idempotents lift to $Soc{(}_{R}R)$.

The rest of the article is structured as follows.

In the next section, we recall preliminary concepts and foundational definitions necessary for our further discussion of $ps$-supplement submodules. This includes a review of supporting notions from the general theory of supplements.

Section 3 concentrates on the study of the class of short exact sequences defined via $ps$-supplements and investigates the associated class of $PS$-coinjective modules. We establish that this class forms a proper class over arbitrary rings. In particular, we prove that all $PS$-coinjective modules are injective if and only if every projective semisimple module is injective.

Section 4 explores several basic properties of $ps$-supplemented modules, including a new characterization of $SI$-rings and $GV$-rings.

2. Preliminaries

Throughout this paper, all rings R are assumed to be associative and possess a multiplicative identity. Unless stated otherwise, all modules considered will be unitary left R-modules. For any such module M, we adopt the standard notation: $Z\left(M\right)$ denotes the singular submodule of M.

We write $N\subseteq M$ (respectively, $N\subset M$) to indicate that N is a submodule (respectively, a proper submodule) of M.

Definition 1

([12]). Let M be an R-module. A submodule L is said to be essential in M, denoted by $L⊴M$, if every nonzero submodule of M has a nontrivial intersection with L, i.e., $L\cap K\ne 0$ for all $K\ne 0$ in M. Furthermore, a submodule N of M is called small in M, denoted by $N\ll M$, if $M\ne N+K$ for any proper submodule K of M.

Definition 2

([12]). Let M be an R-module. The socle of M, denoted by $Soc\left(M\right)$, is defined as the sum of all simple submodules contained in M.

If M has no simple submodules, we set $Soc\left(M\right)=0$. The socle is always a semisimple submodule of M.

Definition 3

([12]). For an R-module M, the radical of M, denoted by $Rad\left(M\right)$, is the intersection of all maximal submodules of M, or equivalently, the sum of all small submodules of M. In the case where M lacks maximal submodules, we define $Rad\left(M\right)=M$.

Zhou introduced a broader version of the notion of small submodules, termed $\delta$-small submodules, as given below [17].

Definition 4

([17]). Let M be an R-module and $N\subseteq M$ a submodule. We say that N is $\delta$-small in M, written as $N{\ll }_{\delta }M$, if for every proper submodule K of M with ${\displaystyle \frac{M}{K}}$ singular, the equality $M=N+K$ does not hold. The notation $\delta \left(M\right)$ refers to the sum of all δ-small submodules of M.

Lemma 1

([17], Lemma 1.9). Let P be a projective module. Then, the δ-radical of P satisfies $\delta \left(P\right)=\delta \left(R\right)P$, and it coincides with the intersection of all essential maximal submodules of P.

Definition 5

([12]). Let M be a module over a ring R, and let I be an injective R-module. If there exists an essential monomorphism $f:M⟶I$, then the pair $(I,f)$ is referred to as an injective hull of M. The injective hull is commonly denoted by $E\left(M\right)$.

Definition 6

([18]). Consider two R-modules A and C. An extension of A by C is a short exact sequence:

$$\mathbb{E}:0⟶A\stackrel{f}{⟶}B\stackrel{g}{⟶}C⟶0,$$

where B is an R-module and f and g are R-module homomorphisms. The group ${Ext}_R(C,A)$ consists of the equivalence classes of such extensions under the usual Baer sum construction.

Definition 7

([18]). Let R be a ring and let $\mathcal{P}$ be a proper class of short exact sequences of left R-modules. An R-module M is called $\mathcal{P}$-coinjective if for every left R-module K, we have

$${Ext}_{\mathcal{P}}(K,M)={Ext}_R(K,M),$$

which means that all short exact sequences of the form

$$0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$$

starting at M belong to the class $\mathcal{P}$.

The next result is attributed to R. J. Nunke.

Theorem 1

([19]). Let $\mathcal{P}$ be a collection of short exact sequences of left R-modules. If the functor ${Ext}_{\mathcal{P}}(C,A)$ is a subfunctor of the usual ${Ext}_R(C,A)$, then ${Ext}_{\mathcal{P}}(C,A)$ forms a subgroup of ${Ext}_R(C,A)$ for all R-modules A and C. Furthermore, if the composition of two $\mathcal{P}$-monomorphisms (respectively, $\mathcal{P}$-epimorphisms) is again a $\mathcal{P}$-monomorphism (respectively, a $\mathcal{P}$-epimorphism), then $\mathcal{P}$ satisfies the axioms of a proper class.

Applying Theorem 1, we aim to show that for any ring R, the class $\mathcal{PS}$—consisting of all short exact sequences of the form

$$0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$$

in which the image of $\psi$ is a $ps$-supplement in N—constitutes a proper class. To establish this, we begin by presenting some foundational observations.

Definition 8

([11]). A hereditary torsion theory τ consists of a pair $(\mathbb{T},\mathbb{F})$, where

(1) 

For all $M\in \mathbb{T}$ and $N\in \mathbb{F}$, we have $Hom(M,N)=0$;

(2) 

The class $\mathbb{T}$ is closed when taking submodules, factor modules, direct sums, and extensions;

(3) 

The class $\mathbb{F}$ is closed under submodules, extensions, and direct products.

Here, $\mathbb{T}$ and $\mathbb{F}$ are referred to as the torsion class and the torsion-free class , respectively. Such a torsion theory uniquely determines a left exact radical τ on the category of left R-modules, with $\mathbb{T}=\{M\in R\text{-}\mathrm{Mod}:\tau (M)=M\}$ and $\mathbb{F}=\{N\in R\text{-}\mathrm{Mod}:\tau (N)=0\}$. The pair $\tau :=(\mathbb{T},\mathbb{F})$ is thus identified as a hereditary torsion theory.

Definition 9

([12]). An R-module M is called flat if for every short exact sequence,

$$0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0,$$

the sequence remains exact after tensoring with any right R-module, or equivalently, if $\psi \left(M\right)$ is a pure submodule of N. Notably, all projective modules are flat.

Lemma 2

([20]). Let R be a commutative ring and S be a simple R-module. Then, S is flat if and only if it is injective.

Definition 10

([21]). A ring R is said to be an $SSI$-ring if every semisimple left R-module is injective. It is known that R is a Noetherian V-ring precisely when it satisfies the $SSI$-ring condition.

Definition 11

([13]). Let M be an R-module, and let U be a submodule of M. A submodule $V\subseteq M$ is called a $\delta$-supplement of U in M if $M=U+V$ and the intersection $U\cap V$ is δ-small in V, i.e., $U\cap V{\ll }_{\delta }V$. The module M is said to be supplemented (respectively, $\delta$-supplemented) if every submodule has a supplement (respectively, a δ-supplement) in M.

Let $1<n\in \mathbb{Z}$. Consider these left $\mathbb{Z}$-modules ${\mathbb{Z}}_n$ and $\mathbb{Q}$. It is well known that the $\mathbb{Z}$-module ${\mathbb{Z}}_n$ is artinian and so it is supplemented; that is, each submodule has a supplement in ${\mathbb{Z}}_n$. However, the $\mathbb{Z}$-module $\mathbb{Q}$ is not supplemented because it is not torsion.

Since the radical $Rad\left(M\right)$ of an R-module M is the sum of all its small submodules, this led to the following refinement.

Definition 12

([3,11,22]). A submodule V of M is said to be a Rad-supplement (also known as co-neat) of a submodule U if $M=U+V$ and $U\cap V\subseteq Rad\left(V\right)$. According to [23], the class $\mathcal{C}o$-$\mathcal{N}eat$ consisting of all short exact sequences

$$0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$$

where $Im\left(\psi \right)$ is a Rad-supplement in N, is another example of a proper class.

These various classes of short exact sequences satisfy the following chain of inclusions:

$$\mathcal{S}plit\subseteq \mathcal{S}upp\subseteq \mathcal{C}o\text{-}\mathcal{N}eat\subseteq \mathcal{A}bs.$$

Lemma 3

([17]). Let N be a submodule of an R-module M. The following statements are equivalent:

(i) 

$N{\ll }_{\delta }M$;

(ii) 

For every submodule X with $X+N=M$, there exists a projective semisimple submodule $Y\subseteq N$ such that $M=X\oplus Y$;

(iii) 

If $X+N=M$ and the quotient $M/X$ is a Goldie torsion module, then $X=M$.

The next result is an immediate consequence of Lemma 3.

Lemma 4.

Let M be an R-module. A submodule $N\subseteq M$ is δ-small in M if and only if, for every submodule $X\subseteq M$ satisfying $X+N=M$, there exists a projective semisimple submodule $N^{\prime }\subseteq N$ such that $M=X\oplus N^{\prime }$.

As a direct consequence of Lemma 4, we observe that any projective semisimple submodule of a module M is necessarily $\delta$-small in M. Inspired by this characterization, we propose a new notion of supplement submodules by generalizing the role of $\delta$-small and projective semisimple submodules.

The aim of this paper is to introduce and study the notion of $ps$-supplement submodules. Let M be a module and $V\subseteq M$ a submodule. We say that V is a $ps$-supplement in M if there exists a submodule $U\subseteq M$ such that $M=U+V$ and the intersection $U\cap V$ is a projective semisimple submodule.

This leads to the following relationships among submodule conditions:

Let $\mathcal{PS}$ denote the class of all short exact sequences of the form

$$0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0,$$

where the image of the map $\psi$ is a $ps$-supplement submodule in N. In this paper, we demonstrate that the class $\mathcal{PS}$, consisting of all such short exact sequences, is a proper class that is injectively generated by singular socle modules. We investigate certain homological properties of this proper class $\mathcal{PS}$ and provide new characterizations for left $SI$-rings and left $GV$-rings. Specifically, we define a module M to be $\mathcal{PS}$-coinjective if every short exact sequence of left R-modules of the form

$$0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$$

with M as the first module belongs to the class $\mathcal{PS}$. This property is equivalent to M being a $ps$-supplement in its injective hull $E\left(M\right)$.

For any ring R, we show that an R-module M is $\mathcal{PS}$-coinjective if and only if M is injective whenever every projective semisimple R-module is injective. Additionally, we prove that a ring R is a left $SI$-ring if and only if every singular left R-module is $\mathcal{PS}$-coinjective, and a ring R is a left $GV$-ring if and only if every simple singular left R-module is $\mathcal{PS}$-coinjective.

Furthermore, we introduce the notion of $ps$-supplemented modules and derive several properties associated with these modules. Notably, we establish that the class of $ps$-supplemented modules is closed under submodules, direct sums, and factor modules. These classes are recognized in the literature as Wisbauer classes. Finally, we prove that a ring R is a left $SI$-ring with essential socle if and only if every left R-module is $\mathcal{PS}$-coinjective, which is further equivalent to every left R-module being $ps$-supplemented.

3. The Proper Class of $\mathit{ps}$-Supplements

Definition 13

([10]). Let $\mathcal{P}$ be a class of short exact sequences of left R-modules and their associated R-module homomorphisms. If a short exact sequence

$$\mathbb{E}:0⟶K\stackrel{f}{⟶}L\stackrel{g}{⟶}M⟶0$$

belongs to $\mathcal{P}$, we say that f is a $\mathcal{P}$-monomorphismand g is a $\mathcal{P}$-epimorphism.

The class $\mathcal{P}$ is called a proper class (in the sense of Buchsbaum) if it satisfies the following conditions:

(P1)

If the short exact sequence $\mathbb{E}:0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$ is an element of $\mathcal{P}$, then $\mathcal{P}$ must also contain any short exact sequence that is isomorphic to $\mathbb{E}$.

(P2)

$\mathcal{S}plit\subseteq \mathcal{P}$.

(P3)

If two $\mathcal{P}$-monomorphisms are composed, their composition is also a $\mathcal{P}$-monomorphism, provided the composition is well defined.

(P3’)

If two $\mathcal{P}$-epimorphisms are composed, their composition is a $\mathcal{P}$-epimorphism, provided the composition is well defined.

(P4)

If ${\psi }_1$ and ${\psi }_2$ are monomorphisms, and the composition ${\psi }_2{\psi }_1$ is a $\mathcal{P}$-monomorphism, then ${\psi }_1$ is also a $\mathcal{P}$-monomorphism.

(P4’)

If ${\varphi }_1$ and ${\varphi }_2$ are epimorphisms, and the composition ${\varphi }_2{\varphi }_1$ is a $\mathcal{P}$-epimorphism, then ${\varphi }_2$ is also a $\mathcal{P}$-epimorphism.

For a module M, we denote by $So{c}_P\left(M\right)$ the sum of all projective simple submodules of M, that is,

$$So{c}_P\left(M\right)=\sum \{S\subseteq M\mid S\mathrm{is}\mathrm{simple}\mathrm{and}\mathrm{projective}\}.$$

It follows that $So{c}_P\left(M\right)\subseteq Soc\left(M\right)$, and $So{c}_P\left(M\right)$ is the largest projective semisimple submodule of M.

Based on Definition 8 and the previous observation, we can establish the following lemma:

Lemma 5.

Let R be a ring. Define $\mathbb{T}$ as the class of all projective semisimple R-modules and $\mathbb{F}$ as the class of all R-modules that do not contain any nonzero projective semisimple submodule. Then the pair $\tau :=(\mathbb{T},\mathbb{F})$ forms a cohereditary torsion theory.

Proof. 

Let ${\displaystyle \frac{X}{So{c}_P\left(M\right)}}$ be a projective simple submodule of ${\displaystyle \frac{M}{So{c}_P\left(M\right)}}$. Since ${\displaystyle \frac{X}{So{c}_P\left(M\right)}}$ is projective, the short exact sequence $0⟶So{c}_P\left(M\right)\stackrel{i}{⟶}X\stackrel{\pi }{⟶}{\displaystyle \frac{X}{So{c}_P\left(M\right)}}⟶0$ splits. Therefore, $X\cong So{c}_P\left(M\right)\oplus {\displaystyle \frac{X}{So{c}_P\left(M\right)}}$; and so, there exists a submodule Y of X such that ${\displaystyle \frac{X}{So{c}_P\left(M\right)}}\cong Y$. Then, we can write the decomposition $X=So{c}_P\left(M\right)\oplus Y$. Therefore, Y is simple and projective. Hence, $Y\subseteq So{c}_P\left(X\right)\subseteq So{c}_P\left(M\right)$—a contradiction—and thus, $So{c}_P({\displaystyle \frac{M}{So{c}_P\left(M\right)}})=0$. □

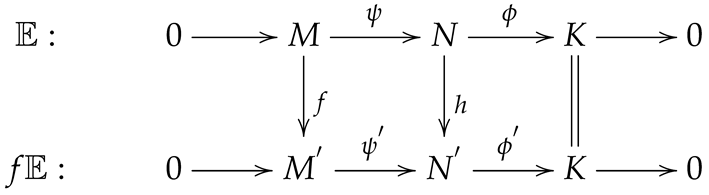
Proposition 1.

Let $g:M^{\prime }⟶M$ be a homomorphism. Then, $g^{*}:Ext(M,K)⟶Ext(M^{\prime },K)$ preserves the elements from the class $\mathcal{PS}$.

Proof. 

Let $\mathbb{E}:0⟶K⟶L\stackrel{h}{⟶}M⟶0$ be a short exact sequence in $\mathcal{PS}$ and let $g:M^{\prime }⟶M$ be a homomorphism. Then, the following diagram is obtained, where the second square is a pullback commutative with exact sequences

where $g_1\left(\mathbb{E}\right)={\mathbb{E}}_1$. Let V be a $ps$-supplement of $Ker\left(h\right)$ in L. Then, $Ker\left(h\right)+V=L$, and $Ker\left(h\right)\cap V$ is a projective semisimple module. Then $g_1^{-1}\left(V\right)+Ker\left(h^{\prime }\right)=L^{\prime }$ by the pullback diagram. Since $g_1$ induces an isomorphism between $g_1^{-1}\left(V\right)\cap Ker\left(h^{\prime }\right)$ and $V\cap Ker\left(h\right)$, $g_1^{-1}\left(V\right)\cap Ker\left(h^{\prime }\right)$ is a projective semisimple module by Corollary 5.3.3(b), [24], and Corollary 8.1.5(2), [24]. Therefore, ${\mathbb{E}}_1\in \mathcal{PS}$. □

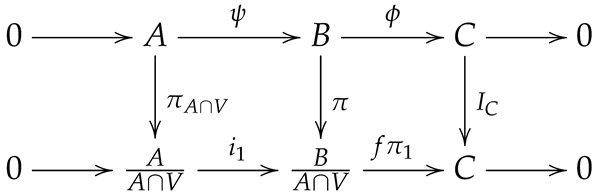
Proposition 2.

Let $f:M⟶M^{\prime }$ be a homomorphism. Then, the map $f_{*}:Ex{t}_R(K,M)⟶Ex{t}_R(K,M^{\prime })$ preserves the elements of the class $\mathcal{PS}$.

Proof. 

Let $\mathbb{E}:0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$ be a short exact sequence in $\mathcal{PS}$. Consider the left R-module $N^{\prime }={\displaystyle \frac{M^{\prime }\oplus N}{H}}$, where $H=\{(-f\left(m\right),\psi \left(m\right))\in M^{\prime }\oplus N\mid m\in M\}$ is a submodule of $M^{\prime }\oplus N$. Define the homomorphisms of left R-modules as follows:

• ${\psi }^{\prime }:M^{\prime }⟶N^{\prime }$ given by ${\psi }^{\prime }\left(m^{\prime }\right)=(m^{\prime },0)+H$;
• ${\varphi }^{\prime }:N^{\prime }⟶K$ given by ${\varphi }^{\prime }\left((m^{\prime },n)\right)=\varphi \left(n\right)$;
• $h:N⟶N^{\prime }$ given by $h\left(n\right)=(0,n)+H$.

This results in the exact sequence $f_{*}\left(\mathbb{E}\right)=f\mathbb{E}:0⟶M^{\prime }\stackrel{{\psi }^{\prime }}{⟶}{N}^{\prime }\stackrel{{\varphi }^{\prime }}{⟶}K⟶0\in Ex{t}_R(K,M^{\prime })$, and the following commutative diagram with exact rows:

This diagram shows that ${\psi }^{\prime }f=h\psi$ and ${\varphi }^{\prime }h=\varphi$. Since the extension $\mathbb{E}:0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$ belongs to the class $\mathcal{PS}$, there exists a submodule $V\subseteq N$ such that $N=\mathrm{Im}\left(\psi \right)+V$ and $\mathrm{Im}\left(\psi \right)\cap V$ is projective semisimple. Using the commutative diagram, we observe that $N^{\prime }=\mathrm{Im}\left({\psi }^{\prime }\right)+\mathrm{Im}\left(h\right)$ and $\mathrm{Im}\left({\psi }^{\prime }\right)\cap \mathrm{Im}\left(h\right)=h(\mathrm{Im}\left(\psi \right)\cap V)$. Since $\mathrm{Im}\left(\psi \right)\cap V$ is projective semisimple, it follows from Lemma 5 that $\mathrm{Im}\left({\psi }^{\prime }\right)\cap \mathrm{Im}\left(h\right)$ is projective semisimple as well, being the homomorphic image of a projective semisimple module. Therefore, $\mathrm{Im}\left(h\right)$ is a $ps$-supplement of $\mathrm{Im}\left({\psi }^{\prime }\right)$ in $N^{\prime }$, and hence, $f\mathbb{E}=f_{*}\left(\mathbb{E}\right)\in \mathcal{PS}$. □

Proposition 3.

If ${\mathbb{E}}_1,{\mathbb{E}}_2\in Ex{t}_{\mathbb{PS}}(K,M)$, then ${\mathbb{E}}_1\oplus {\mathbb{E}}_2\in Ex{t}_{\mathcal{PS}}(K\oplus K,M\oplus M)$.

Proof. 

Let ${\mathbb{E}}_1:0⟶M\stackrel{f_1}{⟶}{N}_1\stackrel{g_1}{⟶}K⟶0$ and ${\mathbb{E}}_2:0⟶M\stackrel{f_2}{⟶}{N}_2\stackrel{g_2}{⟶}K⟶0$ be two elements of $Ex{t}_{\mathcal{PS}}(K,M)$. Then, $N_1=M+V_1$, and $M\cap V_1$ is projective semisimple; $N_2=M+V_2$ and $M\cap V_2$ is projective semisimple. Since $(M\oplus M)+(V_1\oplus V_2)=N_1\oplus N_2$ and $(M\oplus M)\cap (V_1\oplus V_2)=(M\cap V_1)\oplus (M\cap V_2)$, it follows from Lemma 5 that the short exact sequence ${\mathbb{E}}_1\oplus {\mathbb{E}}_2:0⟶M\oplus M\stackrel{f}{⟶}{N}_1\oplus N_2\stackrel{g}{⟶}K\oplus K⟶0$ belongs to $Ex{t}_{\mathcal{PS}}(K\oplus K,M\oplus M)$, where $f=f_1\oplus f_2$ and $g=g_1\oplus g_2$. □

Corollary 1.

For both R-modules N and M, the following statements hold:

(1) 

$Ex{t}_{\mathcal{PS}}(N,M)$ is a subgroup of the extension $Ex{t}_R(N,M)$;

(2) 

$Ex{t}_{\mathcal{PS}}(N,M)$ is a subfunctor of the functor $Ex{t}_R(N,M)$.

Proof. 

(1) Let ${\mathbb{E}}_1$ and ${\mathbb{E}}_2$ be any elements of $Ex{t}_{\mathcal{PS}}(N,M)$. It follows from Proposition 3 that the sum ${\mathbb{E}}_1+{\mathbb{E}}_2$ of these extensions ${\mathbb{E}}_1$ and ${\mathbb{E}}_2$ is in $Ex{t}_{\mathcal{PS}}(N,M)$. Hence, $Ex{t}_{\mathcal{PS}}(N,M)$ is a subgroup of $Ex{t}_R(N,M)$.

(2) By Propositions 1 and 2, (1) $Ex{t}_{\mathcal{PS}}(N,M)$ is a subfunctor of $Ex{t}_R(N,M)$. □

Theorem 2.

Let R be an arbitrary ring. Then $\mathcal{PS}$ is a proper class.

Proof. 

According to Theorem 1 and Corollary 1, it is sufficient to verify that the composition of two $\mathcal{PS}$-epimorphisms remains a $\mathcal{PS}$-epimorphism. Suppose that $f:N⟶N^{\prime }$ and $g:N^{\prime }⟶K$ are $\mathcal{PS}$-epimorphisms. Then we consider the following commutative diagram in which all rows and columns are exact:

where $i_{\mathrm{Ker}\left(f\right)}$ and $i_{\mathrm{Ker}\left(g\right)}$ denote the canonical inclusion maps.

By assumption, there exists a submodule $V\subseteq N$ such that $N=\mathrm{Ker}\left(f\right)+V$ and $\mathrm{Ker}\left(f\right)\cap V$ is projective semisimple. Furthermore, since $\mathrm{Ker}\left(g\right)\cong {\displaystyle \frac{M}{\mathrm{Ker}\left(f\right)}}$, it follows that $\mathrm{Ker}\left(g\right)$ embeds into $N^{\prime }\cong {\displaystyle \frac{N}{\mathrm{Ker}\left(f\right)}}$.

Given that ${\displaystyle \frac{M}{\mathrm{Ker}\left(f\right)}}+{\displaystyle \frac{L}{\mathrm{Ker}\left(f\right)}}={\displaystyle \frac{N}{\mathrm{Ker}\left(f\right)}}$, it follows that ${\displaystyle \frac{M\cap L}{\mathrm{Ker}\left(f\right)}}$ is projective semisimple. Hence, we deduce that

$$M=M\cap N=M\cap \left(\mathrm{Ker}\right(f)+V)=\mathrm{Ker}\left(f\right)+M\cap V,$$

$$M\cap L=\mathrm{Ker}\left(f\right)+M\cap V\cap L,\mathrm{and}L=\mathrm{Ker}\left(f\right)+L\cap V.$$

Thus, we deduce that $N=M+(V\cap L)$. Hence,

$${\displaystyle \frac{M\cap L}{\mathrm{Ker}\left(f\right)}}\cong {\displaystyle \frac{M\cap V\cap L}{\mathrm{Ker}\left(f\right)\cap (M\cap V\cap L)}}={\displaystyle \frac{M\cap V\cap L}{\mathrm{Ker}\left(f\right)\cap V}}.$$

Since ${\displaystyle \frac{M\cap L}{\mathrm{Ker}\left(f\right)}}$, $\mathrm{Ker}\left(f\right)\cap V$, and ${\displaystyle \frac{M\cap V\cap L}{\mathrm{Ker}\left(f\right)\cap V}}$ are projective semisimple modules, it follows from Lemma 5 that $M\cap V\cap L$ is a projective semisimple module.

Therefore, $gf$ is a $\mathcal{PS}$-epimorphism, and this completes the proof. □

Definition 14.

Let R be a ring. An R-module M is said to be $\mathcal{PS}$-coinjectiveif every short exact sequence of left R-modules $0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$ starting with the module M is in the proper class $\mathcal{PS}$. It follows that a module M is $\mathcal{PS}$-coinjective if and only if it is a $ps$-supplement in every extension. Injective modules and projective semisimple modules are examples of $\mathcal{PS}$-coinjective modules.

Theorem 3.

Let R be a ring. The following statements are equivalent:

(1) 

Every $\mathcal{PS}$-coinjective R-module is injective;

(2) 

Every projective semisimple R-module is injective.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$ Since projective semisimple modules are $\mathcal{PS}$-coinjective, this direction is clear.

$\left(2\right)\Rightarrow \left(1\right)$ Let M be a $\mathcal{PS}$-coinjective module and $M\subseteq N$. Then, there exists a submodule K of N such that $N=M+K$ and $M\cap K$ is a projective semisimple module. By $\left(2\right)$, $M\cap K$ is injective, and so, we can write $K=M\cap K\oplus L$ for some submodule $L\subseteq K$. Therefore, the sum $M+K$ is direct. Hence, M is injective. □

Recall that a module M is flat if every exact sequence $0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$ is pure exact, that is, $\psi \left(M\right)$ is a pure submodule of N. Every projective module is flat. It is shown in ([20], Lemma 2.6) that a simple module over a commutative ring is flat if and only if it is injective. Using this fact, we give the next result.

Corollary 2.

Let R be a commutative Noetherian ring. Then every $\mathcal{PS}$-coinjective R-module is injective.

Proof. 

By Theorem 3, it is enough to prove that every projective semisimple left R-module is injective. Let M be any projective semisimple R-module. If $M=0$, then it is injective. Assume that $M\ne 0$. Therefore, there exists a collection ${\left\{S_i\right\}}_{i\in I}$ of projective simple submodules of M such that $M={⨁}_{i\in I}{S}_i$. Since projective modules are flat, for each $i\in I$, $S_i$ is flat and so, by Lemma 2, $S_i$ is injective. It follows from ([12], 27.3) that M is injective. □

Recall that for a ring R, every projective R-module is injective if and only if R is a quasi-Frobenius ring. On the other hand, when every $\mathcal{PS}$-coinjective R-module is injective, the ring R need not be quasi-Frobenius. According to Corollary 2, over the ring $\mathbb{Z}$, every $\mathcal{PS}$-coinjective module is injective, but $\mathbb{Z}$ is not quasi-Frobenius.

It is well known that a ring R is semisimple if and only if every cyclic left R-module is injective, which is furthermore equivalent to every simple left R-module being projective. A ring R is called a $PCI$-ring if every proper cyclic left R-module is injective, and it is called a left V-ring if every simple left R-module is injective. As a generalization of left V-rings, a ring R is called left weakly V-ring(for short $WV$-ring) if every simple left R-module is ${\displaystyle \frac{R}{I}}$-injective for every left ideal, such that ${\displaystyle \frac{R}{I}}$ is proper. For detailed information about left $WV$-rings, we refer to [21]. The next result is crucial.

Proposition 4.

Let R be a left $WV$-ring which is not a left V-ring. Then every $\mathcal{PS}$-coinjective R-module is injective.

Proof. 

Let M be a $\mathcal{PS}$-coinjective R-module. Since R is a left $WV$-ring, which is not a left V-ring, it follows from Theorem 6.6 and Lemma 6.12 in [21] that $Soc{(}_{R}R)$ is simple and essential in _RR. Therefore, R does not have a projective simple module. Now, if P is a projective semisimple R-module, we obtain that $P=0$, and so, it is clearly injective. Hence, M is injective by Theorem 3. □

Now, we give the following result. Note that this result is a consequence of Theorem 2.16 and Corollary 2.15 from [25].

Corollary 3.

Let R be a ring. Assume that every $\mathcal{PS}$-coinjective R-module is injective. Then, $R=S\times T$, where S is a semisimple ring and T is a ring with a singular socle.

Proof. 

By assumption and Theorem 3, the projective semisimple left ideal $So{c}_P{(}_{R}R)$ of R is injective, and so, we can write $R=S\oplus T$, where $S=So{c}_P\left(M\right)$ and T is a left ideal of R. It is clear that $Soc\left(T\right)$ is singular. It follows that the decomposition $R=S\oplus T$ is a decomposition of rings. □

The following proposition shows that the class of $\mathcal{PS}$-coinjective R-modules is injectively generated by all singular socle modules.

Proposition 5.

Let

$$\mathbb{E}:0⟶M⟶N⟶K⟶0$$

be a short exact sequence of modules. Then $\mathbb{E}\in \mathcal{PS}$ if and only if the sequence

$$Hom(N,X)⟶Hom(M,X)⟶0$$

is exact for each singular socle module X.

Proof. 

$(\Rightarrow )$ Let $f:M⟶X$ be a homomorphism with singular $Soc\left(X\right)$. It suffices to show that the $f_{*}\left(\mathbb{E}\right):0⟶X\stackrel{g}{⟶}T⟶K⟶0$ splits. Since $\mathcal{PS}$ is a proper class, we obtain that $f_{*}\left(\mathbb{E}\right)\in \mathcal{PS}$. Then, $g\left(X\right)+S=T$ and $g\left(X\right)\cap S$ are projective semisimple. Since $Soc\left(g\right(X\left)\right)$ is singular, $g\left(X\right)\cap S=0$, and so $f_{*}\left(\mathbb{E}\right)$ splits.

$(\Leftarrow )$ Given $X={\displaystyle \frac{M}{So{c}_P\left(M\right)}}$, by Lemma 5, ${\displaystyle \frac{M}{So{c}_P\left(M\right)}}$ has a singular socle. By assumption, there exists a submodule ${\displaystyle \frac{K}{So{c}_P\left(M\right)}}$ of ${\displaystyle \frac{N}{So{c}_P\left(M\right)}}$ such that ${\displaystyle \frac{M}{So{c}_P\left(M\right)}}\oplus {\displaystyle \frac{K}{So{c}_P\left(M\right)}}={\displaystyle \frac{N}{So{c}_P\left(M\right)}}$. Therefore, $M+K=N$ and $M\cap K\subseteq So{c}_P\left(M\right)$. □

Proposition 6.

Let M be a $\mathcal{PS}$-coinjective module and N be a $ps$-supplement in M. Then N is $\mathcal{PS}$-coinjective.

Proof. 

Let N be a $ps$-supplement in M. Then the short exact sequence

$$\mathbb{E}:0⟶N⟶M⟶{\displaystyle \frac{M}{N}}⟶0$$

is in $\mathcal{PS}$, since $N+V=M$, and $N\cap V$ is projective semisimple for some submodule V of M. Therefore, by Proposition 1.8 from [26], N is $\mathcal{PS}$-coinjective. □

The following result is a direct consequence of Proposition 6.

Corollary 4.

Every direct summand of a $\mathcal{PS}$-coinjective module is $\mathcal{PS}$-coinjective.

Proposition 7.

Let $\mathbb{E}:0⟶M⟶N⟶K⟶0$ be a short exact sequence of modules. If M and K are $\mathcal{PS}$-coinjective, then N is $\mathcal{PS}$-coinjective.

Proof. 

The result follows from Propositions 1.9 and 1.14 in [26]. □

Using Proposition 7, we see by induction that every finite direct sum of $\mathcal{PS}$-coinjective modules is $\mathcal{PS}$-coinjective.

Lemma 6.

Let $M\subseteq N\subseteq K$ be modules. Suppose that N is a direct summand of K. Then the following statements are equivalent:

(1) 

M is a $ps$-supplement in K;

(2) 

M is a $ps$-supplement in N.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$ By $\left(1\right)$, there exists a submodule L of K such that $M+L=K$, and $M\cap L$ is projective semisimple. By the modularity, we can write $N=N\cap K=N\cap (M+L)=M+N\cap L$. Now, $M\cap (N\cap L)=M\cap L$ is projective semisimple. It means that M is a $ps$-supplement in N.

$\left(2\right)\Rightarrow \left(1\right)$ Let $N\oplus V=K$ for some $V\subseteq K$. It follows from $\left(2\right)$ that we can write $N=M+X$, and $M\cap X$ is projective semisimple for some $X\subseteq N$. Then, $K=N\oplus V=(M+X)\oplus V=M+(X\oplus V)$ and $M\cap (X\oplus V)=M\cap X$. This completes the proof. □

The following theorem completely determines the structure of a $\mathcal{PS}$-coinjective module in terms of its injective hull.

Theorem 4.

An R-module M is $\mathcal{PS}$-coinjective if and only if M is a $ps$-supplement in $E\left(M\right)$.

Proof. 

$(\Rightarrow )$ It is clear.

$(\Leftarrow )$ Let M be a $ps$-supplement in $E\left(M\right)$ and let N be any extension of M. Since $E\left(M\right)\subseteq E\left(N\right)$, there exists a submodule $U\subseteq E\left(N\right)$ such that $E\left(N\right)=E\left(M\right)\oplus U$. Since M is a $ps$-supplement in $E\left(M\right)$, it follows that M is a $ps$-supplement in $E\left(N\right)$ by Lemma 6. Hence, there exists a submodule V of $E\left(N\right)$ such that $E\left(N\right)=M+V$ and $M\cap V$ is projective semisimple. By modularity, we can write $N=N\cap E\left(N\right)=N\cap (M+V)=M+N\cap V$, and $M\cap (N\cap V)=(M\cap N)\cap V=M\cap V$ is projective semisimple. This shows that M is $\mathcal{PS}$-coinjective. □

Corollary 5.

An R-module M is $\mathcal{PS}$-coinjective if and only if ${\displaystyle \frac{M}{So{c}_P\left(M\right)}}$ is a direct summand of ${\displaystyle \frac{E\left(M\right)}{So{c}_P\left(M\right)}}$.

Proof. 

It follows from Theorem 4 and Proposition 5. □

A ring R is called left hereditary if every factor module of an injective module over R is injective. Now, we characterize $\mathcal{PS}$-coinjective modules over left hereditary rings. Firstly, the following two facts need to be true.

Proposition 8.

The class of $\mathcal{PS}$-coinjective modules is closed under factor modules if and only if factor modules of injective modules are $\mathcal{PS}$-coinjective.

Proof. 

$(\Rightarrow )$ It is clear.

$(\Leftarrow )$ Let M be a $PS$-coinjective module and let $N\subseteq M$. Since M is a $\mathcal{PS}$-coinjective module, it is $ps$-supplement in $E\left(M\right)$. Then, by properties of proper classes, ${\displaystyle \frac{M}{N}}$ is also $ps$-supplement in ${\displaystyle \frac{E\left(M\right)}{N}}$. By our hypothesis, ${\displaystyle \frac{E\left(M\right)}{N}}$ is $\mathcal{PS}$-coinjective. Therefore, by Proposition 6, ${\displaystyle \frac{M}{N}}$ is a $\mathcal{PS}$-coinjective module as desired. □

Proposition 9.

Let M be a module with singular socle. If M is $\mathcal{PS}$-coinjective, then it is injective.

Proof. 

Let N be any extension of M. Since M is a $\mathcal{PS}$-coinjective module, M is a $ps$-supplement in N. Then, there exists a submodule K of N such that $M+K=N$ and $M\cap K$ is a projective semisimple module. Since $Soc\left(M\right)\subseteq Z\left(M\right)$, we can determine that $M\cap K=0$, and so, N is a direct sum of M and K. It means that M is an injective module. □

Theorem 5.

Let R be a left hereditary ring and M be an R-module. Then, the following statements are equivalent:

(1) 

M is $\mathcal{PS}$-coinjective;

(2) 

Every factor module of M is $\mathcal{PS}$-coinjective;

(3) 

Whenever $So{c}_P\left(M\right)\subseteq U\subseteq M$, ${\displaystyle \frac{M}{U}}$ is injective;

(4) 

${\displaystyle \frac{M}{So{c}_P\left(M\right)}}$ is injective.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$ Since R is a left hereditary ring, it follows from Proposition 8;

$\left(2\right)\Rightarrow \left(3\right)$ By Proposition 9;

$\left(3\right)\Rightarrow \left(4\right)$ Clear;

$\left(4\right)\Rightarrow \left(1\right)$ By Corollary 5. □

Since a simple module over any ring is projective or singular, one considers rings whose singular simple modules are injective. A ring R is called a $GV$-ring if every simple singular left R-module is injective. Clearly, every V-ring is a $GV$-ring. In [27], a ring R is called a SI-ring if every singular left R-module is injective. A domain R is a $PCI$-ring if and only if it is a $SI$-ring. $PCI$-rings and $SI$-rings are examples of V-rings. These classes of rings have been studied extensively. Now, we give a characterization of $SI$-rings and $GV$-rings.

Proposition 10.

Let R be a ring. Then, R is a $SI$-ring if and only if every singular R-module is $\mathcal{PS}$-coinjective.

Proof. 

$(\Rightarrow )$ It is obvious.

$(\Leftarrow )$ Let M be any singular R-module. By the assumption, M is $\mathcal{PS}$-coinjective. It follows from Proposition 9 that it is injective. Hence R is a $SI$-ring □

Proposition 11.

Let R be a ring. Then, R is a $GV$-ring if and only if every simple R-module is $\mathcal{PS}$-coinjective.

Proof. 

$(\Rightarrow )$ Let S be a simple R-module. If S is projective, the proof is clear. Assume that S is singular. Therefore, S is injective since R is a $GV$-ring. Thus, S is $PS$-coinjective.

$(\Leftarrow )$ Let S be a singular simple module. It follows from the hypothesis that S is $\mathcal{PS}$-coinjective. Hence, S is injective by Proposition 9. It means that R is a $GV$-ring. □

The smallest proper class for which every module from the class of modules $\mathcal{M}$ is coinjective is denoted by $\underline{k}\left(\mathcal{M}\right)$. Classes of this kind are called coinjectively generated by $\mathcal{M}$.

Proposition 12.

Let R be a ring. The proper class $\mathcal{PS}$ of R-modules is coinjectively generated by projective semisimple R-modules.

Proof. 

Let $\mathcal{X}$ be the class of all short exact sequences $0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$ such that $M\subseteq So{c}_P\left(N\right)$. We now show that $\mathcal{PS}=\underline{k}\left(\mathcal{X}\right)$. Every projective semisimple R-module is $\mathcal{PS}$-coinjective and, therefore, $\underline{k}\left(\mathcal{X}\right)\subseteq \mathcal{PS}$. By Proposition 6, we obtain $\mathcal{PS}\subseteq \underline{k}\left(\mathcal{X}\right)$. Hence, we conclude that $\mathcal{PS}=\underline{k}\left(\mathcal{X}\right)$. □

Let $\mathcal{P}$ be a proper class. A module M is said to be $\mathcal{P}$-projective (respectively, $\mathcal{P}$-coprojective) if the subgroup $Ex{t}_{\mathcal{P}}(M,K)=0$ (respectively, $Ex{t}_{\mathcal{P}}(M,K)=Ex{t}_R(M,K)$) for all left R-modules K.

Theorem 6.

Let M be an R-module. Then, the following statements are equivalent:

(1) 

M is $\mathcal{PS}$-coprojective;

(2) 

$Ex{t}_R(M,K)=0$ for every projective semisimple module K.

Proof. 

$\left(1\right)⟹\left(2\right)$ is clear.

$\left(2\right)⟹\left(1\right)$ Let $0⟶A\stackrel{\psi }{⟶}B\stackrel{\varphi }{⟶}C⟶0$ be any element of $\mathcal{PS}$. Hence, $B=A+V$ and $A\cap V$ is projective semisimple for some submodule V of B. Then, the short exact sequence

$$0⟶{\displaystyle \frac{A}{A\cap V}}\stackrel{i_1}{⟶}{\displaystyle \frac{B}{A\cap V}}\stackrel{{\pi }_1}{⟶}{\displaystyle \frac{V}{A\cap V}}⟶0$$

splits, where $i_1$ is the canonical injection and ${\pi }_1$ is the canonical projection. We can now write the following commutative diagram:

where ${\pi }_{A\cap V}$ and $\pi$ are canonical projections. Applying the functor $Hom(M,.)$, we get

Then, ${\left(f{\pi }_1\right)}_{*}$ is an epimorphism. It follows from $\left(2\right)$ that $Ex{t}_R(M,A\cap V)=0$. So, ${\pi }_{*}$ is an epimorphism. This means that ${\varphi }_{*}$ is an epimorphism. Consequently, M is $\mathcal{PS}$-coprojective. □

For an arbitrary ring R, let $\delta \left(R\right)=\delta {(}_{R}R)$.

Proposition 13.

Let R be a ring and assume $\delta \left(R\right)=0$. Then, $\mathcal{PS}$-coprojective R-modules are necessarily projective modules.

Proof. 

Let M be a $\mathcal{PS}$-coprojective R-module. Since every module is a quotient of a free module, there exists a free R-module F and an epimorphism $\psi :F⟶M$. Let $U=ker\left(\psi \right)$. Consider the short exact sequence:

$$0⟶U\stackrel{\iota }{⟶}F\stackrel{\psi }{⟶}M⟶0,$$

where $\iota$ is the canonical injection. By the hypothesis, there exists a submodule $V\subseteq F$ such that $F=U+V$ and $U\cap V$ is projective semisimple.

Since $\delta \left(R\right)=0$, we apply Lemma 1 to deduce that $\delta \left(F\right)=\delta \left(R\right)F=0$. Then, by Lemma 4, we conclude that $U\cap V{\ll }_{\delta }F$, which implies $U\cap V\subseteq \delta \left(F\right)=0$. Therefore, the short exact sequence splits, and M is projective. □

Now, we characterize the rings whose semisimple modules are $\mathcal{PS}$-coinjective.

Theorem 7.

The following statements are equivalent for a ring R:

(1) 

R is a $GV$-ring with ascending chain condition on essential right ideals;

(2) 

Every singular semisimple R-module is $\mathcal{PS}$-coinjective;

(3) 

Every semisimple R-module is $\mathcal{PS}$-coinjective.

Proof. 

$\left(1\right)\iff \left(2\right)$ By Proposition 9 and Proposition 3.13 from [28].

$\left(2\right)\iff \left(3\right)$ This follows from the fact that projective semisimple R-modules are $\mathcal{PS}$-coinjective. □

4. $\mathit{ps}$-Supplemented Modules

Let R be a ring and M be an R-module. We call Mps-supplemented if every submodule of M has (is) a $ps$-supplement in M. In this section, we obtain the various properties of $ps$-supplemented modules. Let us begin with the following proposition.

Proposition 14.

The following statements are equivalent for a module M:

(1) 

M is $ps$-supplemented;

(2) 

${\displaystyle \frac{M}{So{c}_P\left(M\right)}}$ is semisimple.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$ Let ${\displaystyle \frac{U}{So{c}_P\left(M\right)}}$ be a submodule of ${\displaystyle \frac{M}{So{c}_P\left(M\right)}}$. Then, by $\left(1\right)$, there exists $V\subseteq M$ such that $U+V=M$ and $U\cap V\subseteq So{c}_P\left(M\right)$. Hence, ${\displaystyle \frac{M}{So{c}_P\left(M\right)}}={\displaystyle \frac{U}{So{c}_P\left(M\right)}}\oplus {\displaystyle \frac{V+So{c}_P\left(M\right)}{So{c}_P\left(M\right)}}$, and so, ${\displaystyle \frac{M}{So{c}_P\left(M\right)}}$ is semisimple.

$\left(2\right)\Rightarrow \left(1\right)$ For any U submodule of M, we can write ${\displaystyle \frac{M}{So{c}_P\left(M\right)}}={\displaystyle \frac{V}{So{c}_P\left(M\right)}}\oplus {\displaystyle \frac{U+So{c}_P\left(M\right)}{So{c}_P\left(M\right)}}$, where V is submodule of M. Hence, $M=U+V$ and $U\cap V\subseteq So{c}_P\left(M\right)$. It means that M is $ps$-supplemented. □

Theorem 8.

The class of $ps$-supplemented modules is closed under direct sums.

Proof. 

Let ${\left\{M_i\right\}}_{i\in I}$ be the collection of $ps$-supplemented R-modules, where I is any index set. Put $M={⨁}_{i\in I}{M}_i$. By Proposition 14, ${\displaystyle \frac{M_i}{So{c}_P\left(M_i\right)}}$ is semisimple for all $i\in I$. Since $So{c}_P$ is radical of $R-Mod$ and ${\displaystyle \frac{M}{So{c}_P\left(M\right)}}\cong {\displaystyle \frac{{⨁}_{i\in I}{M}_i}{{⨁}_{i\in I}So{c}_P\left(M_i\right)}}\cong {⨁}_{i\in I}\left[{\displaystyle \frac{M_i}{So{c}_P\left(M_i\right)}}\right]$, we deduce that M is $ps$-supplemented by Proposition 14. □

It is well known that the relation between radical and socle of a module M is not determined. For a $ps$-supplemented module M, we prove that $Rad\left(M\right)\subseteq So{c}_P\left(M\right)$ in the following.

Proposition 15.

Let M be a $ps$-supplemented module. Then $Rad\left(M\right)\subseteq So{c}_P\left(M\right)$.

Proof. 

Let $m\in Rad\left(M\right)$. Therefore, $Rm$ is a small submodule of M. It follows from the assumption that $M=Rm+M$ and $Rm\cap M=Rm$ are projective semisimple. Hence, $Rm\subseteq So{c}_P\left(M\right)$, and so, $m\in So{c}_P\left(M\right)$. □

Proposition 16.

Let M be a $ps$-supplemented module. Then submodules and factor modules of M are $ps$-supplemented.

Proof. 

Let L be any submodule of M and let $U\subseteq L$. Since M is $ps$-supplemented, we can write $M=U+V$ and $U\cap V$ is projective semisimple for some submodule V of M. Using the modular law, we have $L=L\cap M=N\cap (U+V)=U+(L\cap V)$, and $U\cap (L\cap V)=(U\cap L)\cap V=U\cap V$ is projective semisimple. Hence, L is $ps$-supplemented.

Let $L\subseteq U\subseteq M$ be submodules. Then there exists a submodule V of M such that $M=U+V$, and $U\cap V$ is projective semisimple. Therefore, ${\displaystyle \frac{M}{L}}={\displaystyle \frac{U}{L}}+{\displaystyle \frac{V+L}{L}}$. Using the canonical epimorphism $\pi :M⟶{\displaystyle \frac{M}{L}}$, we obtain that $\pi (U\cap V)={\displaystyle \frac{(U\cap V)+L}{L}}={\displaystyle \frac{U\cap (V+L)}{L}}={\displaystyle \frac{U}{L}}\cap {\displaystyle \frac{V+L}{L}}$ is projective semisimple by Lemma 5. Hence, the factor module ${\displaystyle \frac{M}{L}}$ is $ps$-supplemented. □

Corollary 6.

Let M be a module and let ${\left\{M_i\right\}}_{i\in I}$ be a collection of $ps$-supplemented submodules of M. Then ${\sum }_{i\in I}{M}_i$ is $ps$-supplemented.

Proof. 

Put $A={⨁}_{i\in I}{M}_i$. By Theorem 8, A is $ps$-supplemented. Then we can write the epimorphism $\psi :A⟶{\sum }_{i\in I}{M}_i$ via $\psi \left({\left(a_i\right)}_{i\in I}\right)={\sum }_{i\in I_0}{a}_i$, where $I_0$ is the finite subset of the index set I. By Theorem 8, the external direct sum ${⨁}_{i\in I}{M}_i$ is a $ps$-supplemented module. It follows from Proposition 16 that the submodule ${\sum }_{i\in I}{M}_i$ of M is $ps$-supplemented. □

Theorem 9.

The following are equivalent for a ring R:

(1) 

Every left R-module is $ps$-supplemented;

(2) 

${\displaystyle \frac{R}{So{c}_P\left(R\right)}}$ is semisimple.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$ By Proposition 14.

$\left(2\right)\Rightarrow \left(1\right)$ Let M be any R-module and $\Psi :F⟶M$ be epimorphism, where F is a free left R-module. Now, ${\displaystyle \frac{F}{So{c}_{P}F}}\cong {\oplus }_{i\in I}\left[{\displaystyle \frac{R}{So{c}_P\left(R\right)}}\right]$ is semisimple as a direct sum of semisimple modules. Again, applying Proposition 14, we obtain that F is $ps$-supplemented, and so, M is $ps$-supplemented as a factor module of F according to Proposition 16. □

In [29], the class of left $SI$-rings with an essential socle was studied. Now, we give a characterization of these rings in terms of $ps$-supplement submodules.

Theorem 10.

Let R be a ring. Then, the following statements are equivalent:

(1) 

Every left R-module is $\mathcal{PS}$-coinjective;

(2) 

Every left R-module is $ps$-supplemented;

(3) 

R is a left $SI$-ring with essential socle.

Proof. 

$\left(1\right)\iff \left(2\right)$ This is obvious.

$\left(1\right)\Rightarrow \left(3\right)$ By Proposition 10, R is a left $SI$-ring and _RR is $ps$-supplemented. It follows from Proposition 14 that ${\displaystyle \frac{R}{So{c}_P\left(R\right)}}$ is injective semisimple. Since R is a left $SI$-ring, it is a left hereditary ring and so $Soc{(}_{R}R)$ is projective. Thus, by ([29], Lemma 2.6), we can determine that $Soc\left(R\right)⊴R$.

$\left(3\right)\Rightarrow \left(2\right)$ Let F be $R^{\left(I\right)}$ for any index set I. Since R is left hereditary, it follows from ([12], 39.7-(1)) that F is hereditary. Therefore $Soc\left(F\right)$ is projective. Since ${\displaystyle \frac{R}{Soc\left(R\right)}}$ is semisimple, it follows that ${\displaystyle \frac{F}{Soc\left(F\right)}}$ is semisimple. Applying Proposition 14, F is $ps$-supplemented. Hence, every left R-module is $ps$-supplemented by Proposition 16. □

Lemma 7.

A singular $ps$-supplemented module is semisimple.

Proof. 

Let M be $ps$-supplemented and a singular module. Let U be any submodule of M. By the assumption, we can write $U+V=M$, and $U\cap V$ is a projective semisimple for some submodule V of M. Since M is singular, we can determine that $U\cap V=0$, and so, $U\oplus V=M$. It means that M is semisimple. □

Theorem 11.

Let M be a module. Then, M is $ps$-supplemented if and only if $M=Z\left(M\right)\oplus N$, where $Z\left(M\right)$ is semisimple and N is $ps$-supplemented.

Proof. 

$(\Rightarrow )$ By the assumption, we can write $M=Z\left(M\right)+N$, and $Z\left(M\right)\cap N$ is projective semisimple for some submodule N of M. Since $Z\left(M\right)$ is singular, $Z\left(M\right)\cap N=0$, and so, $M=Z\left(M\right)\oplus N$. It follows from Proposition 16 that $Z\left(M\right)$ and N are $ps$-supplemented modules. By Lemma 7, $Z\left(M\right)$ is semisimple.

$(\Leftarrow )$ By Corollary 6. □

Example 1. 

(1) 

Let M be the local $\mathbb{Z}$-module ${\mathbb{Z}}_{p^2}$, where p is any prime positive integer. It follows that M is singular which is not semisimple. By Lemma 7, M is not $ps$-supplemented.

(2) 

Ref. [30] (Example 3.1). Let $T=\left(\begin{array}{cc}\mathbb{R}& \mathbb{C}\\ 0& \mathbb{C}\end{array}\right)$, where $\mathbb{R}$ and $\mathbb{C}$ are the fields of real and complex numbers, respectively. Then T is right and left artinian, right and left hereditary, right and left $SI$. It follows from Theorem 10 the left module _TT is $ps$-supplemented which is not semisimple.

A module M is called locally projective if whenever $g:N⟶K$ is an epimorphism and $f:M⟶K$ is a homomorphism, then for every finitely generated submodule $M_0$ of M, there exists a homomorphism $h:M⟶N$ such that ${gh|}_{M_0}{=f|}_{M_0}$. Every projective module is locally projective. Also, a finitely generated locally projective module is projective.

Corollary 7.

A locally projective $ps$-supplemented module is non-singular.

Proof. 

Let M be a locally projective $ps$-supplemented module. By Theorem 11, there exists a decomposition $M=Z\left(M\right)\oplus N$ such that $Z\left(M\right)$ is semisimple and N is a $ps$-supplemented submodule of M. Assume that $Z\left(M\right)\ne 0$. Therefore, we can write $Z\left(M\right)={⨁}_{i\in I}{S}_i$, where each $S_i$ is simple. Since M is locally projective, it follows that $Z\left(M\right)$ is locally projective, and so, each $S_i$ is locally projective. It means that each $S_i$ is projective, which is a contradiction. Hence, M is non-singular. □

Remark 1.

Let R be a domain and M be an R-module. Since all simple R-modules are singular, it follows from Theorem 11 that M is $ps$-supplemented if and only if it is semisimple.

5. Conclusions and Recommendation

In this paper, we studied the proper class $\mathcal{PS}$ of all short exact sequences of the form $0⟶M\stackrel{\psi }{⟶}N\stackrel{\varphi }{⟶}K⟶0$, where $\mathrm{Im}\left(\psi \right)$ is a $ps$-supplement in N, and characterized some of the rings. In particular, we proved that a ring R is a left $SI$-ring with an essential socle if and only if all modules are $ps$-supplemented and if and only if all modules are $PS$-coinjective.

Since the proper class $PS$ is injectively generated by modules with a singular socle, the relationships between the subinjectivity domains of different module classes can be studied. In addition, depending on this proper class $PS$, copurity theory can be investigated in detail.