Fuzzy Shadowed Support Vector Machine for Bankruptcy Prediction

Abstract

Corporate defaults represent a critical risk factor for financial institutions and stakeholders. In today’s complex economic environment, precise and timely risk assessment has become an essential component of financial strategies. One promising strategy consists of analyzing and learning from financial patterns observed in distressed or bankrupt firms. However, this requires processing highly imbalanced datasets in which bankruptcy cases are substantially underrepresented relative to solvent firms. This imbalance, coupled with the data’s intrinsic complexity—such as overlapping features and nonlinear patterns, poses significant difficulties for traditional classifiers like Support Vector Machines (SVMs), which tend to favor the majority class. To overcome these challenges, we employ a Fuzzy Shadowed SVM, which allows for a more refined modeling of minority class instances. This method leverages granular computing paradigms to enhance predictive robustness. Empirical results based on real-world datasets show that our model significantly outperforms traditional machine learning approaches, particularly in recognizing minority-class instances.

1. Introduction

Corporate bankruptcy entails significant economic and social consequences, affecting not only firms but also stakeholders such as employees, investors, and financial institutions [1]. In a highly volatile and competitive economic environment, early detection of financial distress has become a strategic imperative, enabling timely risk mitigation and resource reallocation [2]. This challenge has gained increasing relevance in the aftermath of global financial crises and in the face of contemporary economic disruptions, where predicting bankruptcy is essential for maintaining financial stability and investor confidence. Consequently, bankruptcy prediction has attracted substantial research interest, evolving from traditional statistical models to advanced machine learning (ML) and deep learning (DL) techniques.

Classical methods, such as linear discriminant analysis, logistic regression, and Altman’s Z-score, have historically dominated the field [3]. While these models offer interpretability and foundational insights, they struggle to capture nonlinear relationships and rely on assumptions (e.g., data normality and independence) rarely met in real-world financial datasets [4].

The rapid development of artificial intelligence methods has contributed to their wide applications for forecasting various financial risks in recent years. The study by Wei Li et al. [5] introduced an explainable case-based reasoning (CBR) framework for financial risk prediction that minimizes reliance on specialized domain expertise. By improving the transparency of the decision-making process, their approach enhances the interpretability of financial outcomes while preserving robustness. Empirical evaluations indicate that the proposed model achieves competitive predictive performance compared with other established artificial intelligence approaches. Recent advances further demonstrate the applicability of CBR in broader classification problems. For instance, the study by Liu, Xiaodi et al. [6] highlights how CBR can be successfully applied to fraud detection, achieving both interpretability and competitive predictive accuracy. This reinforces the relevance of CBR as a transparent and effective methodology not only in financial risk prediction but also across diverse domains where trustworthiness of decisions is critical. ML techniques, including Support Vector Machines (SVMs), Random Forests, and ensemble methods like XGBoost and LightGBM, have emerged as powerful alternatives [7,8]. These models handle high-dimensional and heterogeneous data without assuming predefined functional forms, improving prediction accuracy and adaptability [9]. More recently, DL models—such as Artificial Neural Networks (ANNs), Convolutional Neural Networks (CNNs), and Long Short-Term Memory (LSTM) networks—have shown promise in capturing temporal dynamics and hierarchical patterns in financial data [10]. Despite their performance, DL approaches suffer from limited interpretability, high computational costs, and reduced transparency, which are challenges that hinder their adoption in sensitive financial contexts.

A persistent limitation in ML approaches is their sensitivity to data imbalance, a common feature in bankruptcy datasets where bankrupt firms represent a small minority. This imbalance biases learning algorithms toward the majority class, leading to frequent misclassification of minority instances [11].

To address this scientific gap, we propose a novel hybrid framework—Fuzzy Shadowed Support Vector Machine (Fuzzy Shadowed-SVM)—that addresses both nonlinearity and data imbalance. This approach enhances classification robustness by discounting ambiguous instances, thereby ensuring both high accuracy and improved minority-class recognition. The primary purpose of this study is therefore to improve the recognition of bankrupt firms (minority class) while maintaining overall predictive performance. In our design, fuzzy logic is used in its classical form, where each sample is assigned a membership degree in the interval $[0,1]$. Unlike traditional fuzzy inference systems that rely on explicit “If–Then” rules, the membership values are directly incorporated into the SVM optimization process to weigh instances according to their uncertainty. To further refine this mechanism, shadowed sets partition the membership space into three regions—full membership, full non-membership, and an intermediate shadowed zone—allowing the model to discount ambiguous cases near the decision boundary. The integration of fuzzy sets and shadowed sets is thus theoretically grounded in Granular Computing, providing a principled framework for handling uncertainty and imbalance rather than relying solely on empirical adjustments.

The main contributions of this article are as follows:

1.

We propose a comprehensive framework of the Fuzzy Support Vector Machine (Fuzzy SVM) using a diverse range of membership functions, including geometric, density-based, and entropy-driven approaches, to quantify the uncertainty of individual samples and enhance model robustness in imbalanced data scenarios.

2.

We introduce a novel Shadowed Support Vector Machine (Shadowed SVM) approach that employs a multi-metric fusion mechanism to define shadow regions near the decision boundary. This is achieved through a combination of geometric distances and margin-based metrics, followed by a shadowed combination to control the influence of uncertain instances.

3.

We empirically observe that Fuzzy SVM excels in achieving high overall accuracy, while the Shadowed SVM provides superior performance in handling data imbalance. Motivated by these complementary strengths, we propose a novel hybrid model—Fuzzy Shadowed Support Vector Machine (Fuzzy Shadowed-SVM)—that combines fuzzy membership weighting with shadowed instance discounting to achieve both high accuracy and class balance.

4.

To validate the robustness and statistical significance of the proposed models, we conduct non-parametric (Wilcoxon signed-rank test) and parametric (Paired Student’s t-Test) analyses on multiple bankruptcy datasets. The results confirm that the performance improvements achieved by the proposed Fuzzy Shadowed-SVM are not only consistent across different datasets but also statistically significant.

The remainder of this article is structured as follows: Section 2 reviews related work on bankruptcy prediction. Section 3 outlines the proposed methodology. Section 4 presents experimental results and analysis. Section 5 discusses the implications, concludes the study, and suggests directions for future research.

2. Literature Review

Bankruptcy prediction is a central issue in financial risk management, where early identification of distressed firms enables timely intervention in lending, investment, and regulation. However, most bankruptcy datasets suffer from severe class imbalance, with bankrupt firms typically representing less than 5% of observations [12]. This imbalance distorts standard classification algorithms, which tend to favor the majority class, leading to poor detection of the minority class—precisely the cases of interest.

Traditional models, such as logistic regression and linear discriminant analysis, have been widely used due to their interpretability [13]. Yet, they rely on restrictive assumptions (e.g., normality and independence) and symmetric loss functions that fail to account for the asymmetry of bankruptcy costs. In highly imbalanced settings, such models often yield high overall accuracy but poor recall for bankrupt firms.

To mitigate imbalance, data-level strategies such as Random Oversampling and SMOTE have been proposed [14], along with more advanced variants like ADASYN and SMOTE-ENN [15]. At the algorithmic level, cost-sensitive learning and balanced ensemble methods (e.g., Balanced Random Forest and weighted XGBoost) integrate class-specific penalties to enhance minority class detection [16]. Evaluation metrics tailored to imbalance—such as F1-score, G-mean, and MCC—are increasingly adopted for fair assessment.

Machine learning models, including Random Forests, SVMs, and gradient boosting algorithms, have demonstrated strong performance in capturing nonlinear patterns [8,17,18]. Nonetheless, they remain sensitive to imbalance and lack mechanisms to represent uncertainty or soft decision boundaries. Deep learning models, such as CNNs and LSTMs, have also been explored for bankruptcy forecasting [10,19], but their opacity and tendency to overfit the majority class limit their practical utility in high-stakes financial contexts.

Recent research has focused on hybrid and fuzzy approaches that incorporate uncertainty modeling. Granular computing (GrC) provides flexible representations of vague or borderline instances, improving classification under noisy and imbalanced conditions [20,21]. Variants like Granular SVM (GSVM), Rough Granular SVM, and Granular-Ball Computing enhance decision boundaries by weighting local uncertainty [22,23,24]. These methods have shown improved minority class sensitivity and robustness.

However, current fuzzy and granular SVM models still lack a formal mechanism to delineate regions of partial membership or ambiguity near the decision boundary. To address this gap, our study proposes a novel Fuzzy Shadowed-SVM, which integrates fuzzy membership weighting with shadowed set theory. This hybrid framework captures both uncertainty and class imbalance by discounting ambiguous instances near the boundary while preserving overall decision confidence.

3. Fuzzy Shadowed Support Vector Machines: Proposed Approach

Support Vector Machines (SVM), introduced by Vapnik [25], constitute a powerful approach for addressing classification problems, grounded in statistical learning theory and the principle of Structural Risk Minimization (SRM), which seeks to balance model complexity and training error in order to enhance generalization performance. In numerous applications, SVMs have demonstrated superior performance compared to classical learning methods and are now widely regarded as robust tools within machine learning. In numerous instances, the attempt to directly determine a separating hyperplane within the input space proves too restrictive for effective practical application. A potential solution to this limitation involves projecting the input data into a higher-dimensional feature space and then identifying the optimal hyperplane in this transformed environment. This methodology, founded upon the principles of convex optimization and kernel theory, is characterized by its resilience and capacity for generalization, even in high-dimensional spaces. The resulting solution is expressed as a linear combination of a limited subset of training points, referred to as support vectors. Formally, let a training dataset be given by $S={\left\{(x_i,y_i)\right\}}_{i=1}^m$, where $x_i\in {\mathbb{R}}^d$ denotes a feature vector and $y_i\in \{-1,+1\}$ its corresponding label. The optimization problem for a linear SVM is formulated as follows:

$$\underset{w,b}{min}{\displaystyle \frac{1}{2}}{\parallel w\parallel }^2\mathrm{subject}\mathrm{to}{y}_i(w·x_i+b)\ge 1,\forall i,$$

(1)

where w is the weight vector orthogonal to the hyperplane and b is the bias. The optimal solution $(w^{\ast },b^{\ast })$ defines the separating hyperplane $w^{\ast }·x+b^{\ast }=0$, with a margin of $2/\parallel w^{\ast }\parallel$. In cases where linear separation is too restrictive, kernel functions enable the projection of data into a higher-dimensional feature space, where an optimal separating hyperplane can be effectively constructed. When data are not linearly separable, SVMs employ a kernel function $K(x_i,x_j)=\varphi \left(x_i\right)·\varphi \left(x_j\right)$ to map the data into a higher-dimensional space where linear separation becomes feasible. Common kernels include the following:

• Gaussian Radial Basis Function (RBF) Kernel:

  $$K(x_i,x_j)=exp(-\gamma \parallel x_i-x_j{\parallel }^2)$$

  (2)
• Polynomial Kernel:

  $$K(x_i,x_j)={(x_i·x_j+c)}^d$$

  (3)

For problems involving noise or class overlap, a soft-margin formulation introduces slack variables ${\xi }_i$, leading to the optimization problem:

$$\underset{w,b,\xi }{min}{\displaystyle \frac{1}{2}}{\parallel w\parallel }^2+C\sum _{i=1}^n{\xi }_i\mathrm{subject}\mathrm{to}{y}_i(w·x_i+b)\ge 1-{\xi }_i,{\xi }_i\ge 0,$$

(4)

where C controls the trade-off between margin maximization and tolerance for misclassification. SVMs are widely applied in pattern recognition, text classification, and bioinformatics due to the following:

• Their resistance to overfitting;
• Their flexibility through kernel selection;
• Their effectiveness in high-dimensional spaces.

Challenges include hyperparameter tuning (e.g., selecting C and the appropriate kernel), and computational complexity when handling large-scale datasets. Variants, including multi-class Support Vector Machines (for instance, one-versus-all methodologies) and Support Vector Regression (SVR), enhance the applicability of the Support Vector Machine paradigm to a more extensive array of challenges. The classical Support Vector Machine (SVM) framework lacks an inherent mechanism to handle the varying importance or informativeness of individual training instances. This limitation becomes critical in scenarios where data quality or relevance differs across the dataset. In many classification tasks, certain examples carry greater significance or provide more valuable information than others. Consequently, it is desirable to achieve high accuracy on these key instances while allowing for some misclassification of noisy or less relevant samples.

Put simply, a training instance should not be strictly assigned to a single class. For instance, an example might belong to a class with 90% confidence and have 10% ambiguity, or alternatively, it may show 20% association with one class and 80% non-relevance. Hence, each sample can be attributed a fuzzy membership degree, which quantifies the level of confidence or affiliation of the instance to a class. The complementary degree indicates the irrelevance or insignificance of the sample in the decision process.

Building on this foundation, we propose enhancing the standard Support Vector Machine (SVM) by incorporating fuzzy membership values, which resulted in a more flexible Fuzzy Support Vector Machine (FSVM) model.

Bankruptcy prediction is a crucial financial task aimed at forecasting firms likely to encounter financial distress. A significant challenge arises from the class imbalance inherent in such data: bankrupt firms are far fewer than healthy ones. This imbalance biases classical supervised models, including SVM, toward the majority class.

To tackle these complexities, we propose an advanced augmentation of the conventional Support Vector Machine (SVM) paradigm, designated as the Granular Support Vector Machine (GSVM). This approach amalgamates various granular computing methodologies, encompassing the following:

• Fuzzy Support Vector Machine (Fuzzy SVM);
• Shadowed Support Vector Machine (Shadowed SVM);
• Fuzzy Shadowed-SVM.

These approaches aim to better capture the uncertainty, ambiguity, imprecision, and cognitive granularity typically present in noisy or incomplete financial datasets.

This work presents the theoretical foundations, implementation details, and application of each approach in the context of bankruptcy prediction.

Specifically, the Fuzzy SVM assigns fuzzy membership values $\mu \left(x_i\right)\in [0,1]$ to training points, reflecting their reliability and handling uncertainty or label noise.

In bankruptcy datasets, some firms exhibit intermediate financial indicators, being neither clearly healthy nor definitively risky. Fuzzy SVM mitigates the influence of such ambiguous instances by assigning lower weights during optimization, thereby

• Reducing the impact of outliers;
• Emphasizing firms on the brink of bankruptcy;
• Attenuating bias toward the majority class.

Shadowed SVM leverages the concept of shadowed sets, which simplify fuzzy sets using three discrete values: 0, 1, and uncertain. This allows the model to identify a shadowed region in the feature space where companies are difficult to classify.

This mechanism

• Creates a fuzzy boundary between classes;
• Enhances the detection of critical regions;
• Reduces the influence of weakly informative examples.

3.1. Fuzzy Support Vector Machine (Fuzzy SVM)

Fuzzy Set Theory (FST), introduced by Zadeh [26], addresses vagueness by allowing elements to belong to a set with degrees of membership in $[0,1]$. In the context of financial risk, especially bankruptcy prediction, fuzzy sets enable the representation of ambiguous financial indicators. For instance, a firm’s liquidity ratio may not sharply indicate “risky” or “safe” status, but a fuzzy model assigns it a graded risk level.

Fuzzy classifiers have been applied successfully to imbalanced data, offering flexibility through membership functions tailored to uncertain financial patterns [27]. In our framework, fuzzy sets are used during data preprocessing to transform crisp financial ratios into fuzzy inputs, which enhances the semantic granularity of features before classification.

In this study, the fuzzy logic employed is based on classical fuzzy set theory, where each training instance is assigned a membership degree in the interval $[0,1]$. Unlike conventional fuzzy systems, our framework does not rely on a linguistic rule base or a fuzzy logic controller. Instead, the membership degrees are directly incorporated into the optimization process of the SVM. This design eliminates the need for a large number of “If–Then” rules, thereby avoiding the computational overhead and performance degradation often associated with traditional fuzzy systems.

The Fuzzy SVM introduces a fuzzy weight for each training point, based on its degree of reliability. This fuzzy membership degree $\mu \left(x_i\right)\in [0,1]$ reflects the uncertainty associated with the label of $x_i$ in noisy or ambiguous scenarios.

In bankruptcy contexts, certain companies may exhibit intermediate financial indicators—neither clearly healthy nor clearly distressed. Fuzzy SVM addresses such instances with reduced weight in the objective function, minimizing their influence on the separating hyperplane. This allows for

• Reduction of the effect of outliers;
• Emphasis on borderline companies near financial distress;
• Mitigation of bias toward the majority class.

The standard SVM loss function is modified such that the penalty on misclassification is scaled by the membership values

$$\underset{w,b,\xi }{min}{\displaystyle \frac{1}{2}}{\parallel w\parallel }^2+C\sum _{i=1}^n{\mu }_i{\xi }_i$$

(5)

subject to the constraints

$$\begin{array}{cc}\hfill y_i(w^T\varphi \left(x_i\right)+b)\ge 1-{\xi }_i,& \forall i=1,2,\dots ,n\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\xi }_i\ge 0,& \forall i=1,2,\dots ,n\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill 0<{\mu }_i\le 1,& \forall i=1,2,\dots ,n\hfill \end{array}$$

(8)

In this way, bankrupt firms (minority samples) are given more influence on the learned hyperplane, while redundant majority points are down-weighted.

In this study, we present several membership functions designed to assign continuous confidence values to samples based on geometric and statistical properties. These functions are crucial in fuzzy modeling, granular computing, and imbalance-aware learning. The proposed membership functions are not directly borrowed from the literature, but rather inspired by existing concepts in fuzzy SVM and fuzzy learning. We have significantly modified and extended these ideas in order to adapt them to the imbalanced data classification problem and to emphasize the minority class.

1.

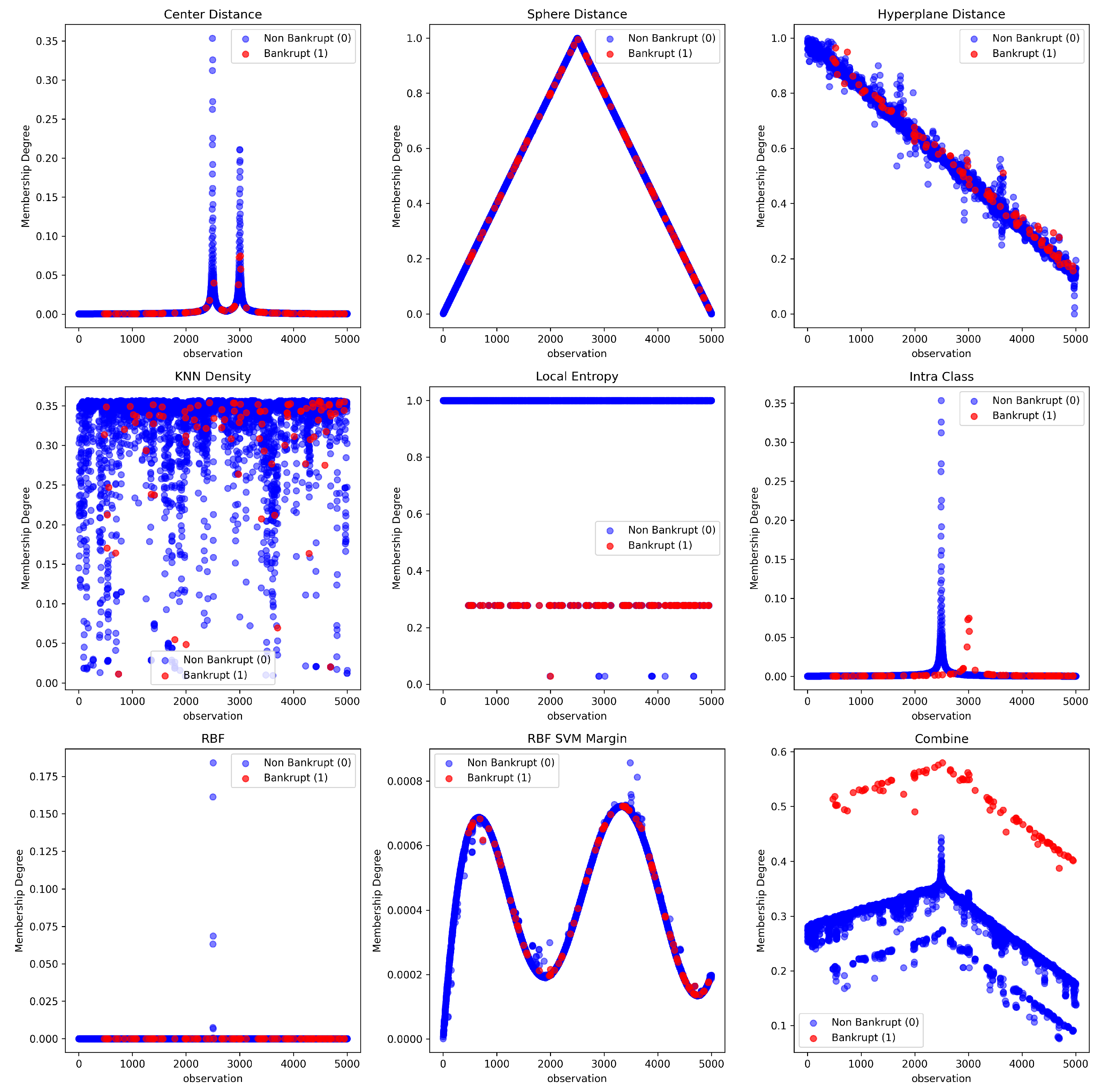
Center Distance-Based Membership [28]

This function evaluates the membership of a sample based on its Euclidean distance to the nearest class center.

$${\mu }_i={\displaystyle \frac{1}{1+{min}_{c\in \mathcal{C}}\parallel {\mathbf{x}}_i-{\mathbf{\mu }}_c\parallel }}$$

(9)

For minority class samples, the membership is amplified:

$${\mu }_i\leftarrow 2{\mu }_i\mathrm{if}{y}_i=\mathrm{minority}\mathrm{class}$$

(10)

Description:

Samples closer to any class center are assigned higher membership. Minority class instances are emphasized by doubling their score.

2.

Global Sphere-Based Membership [29]

This function defines a membership value based on the distance to the global center of all samples.

$${\mu }_i=1-{\displaystyle \frac{\parallel {\mathbf{x}}_i-\overline{\mathbf{x}}\parallel }{R+ϵ}}$$

(11)

where $\overline{\mathbf{x}}$ is the global centroid and $R={max}_i\parallel {\mathbf{x}}_i-\overline{\mathbf{x}}\parallel$ is the radius.

Description:

Points farther from the center receive lower membership. Minority samples get amplified membership values.

3.

Hyperplane Distance Membership [30]

This function calculates membership values based on the distance to the decision hyperplane of a linear SVM.

$${\mu }_i=1-{\displaystyle \frac{|{\mathbf{w}}^{\top }{\mathbf{x}}_i+b|}{{max}_j|{\mathbf{w}}^{\top }{\mathbf{x}}_j+b|+ϵ}}$$

(12)

Description:

Samples closer to the decision boundary receive higher scores. Minority class points have doubled membership.

4.

Local Density-Based Membership (kNN) [31]

This method uses the average distance to k-nearest neighbors to assess local density.

$${\mu }_i={\displaystyle \frac{1}{1+\frac{1}{k}{\sum }_{j=1}^k\mathrm{dist}({\mathbf{x}}_i,{\mathbf{x}}_{i_j})}}$$

(13)

Description:

Samples in dense regions (smaller average distances) get higher membership values.

5.

Local Entropy-Based Membership [30]

Using a probabilistic k-NN classifier, this function computes local class entropy.

$${\mu }_i=1-{\displaystyle \frac{H_i}{logK}}\mathrm{where}{H}_i=-\sum _{c=1}^C{p}_{ic}log\left(p_{ic}\right)$$

(14)

Description:

Samples with high uncertainty (high entropy) receive lower membership values.

6.

Intra-Class Distance Membership [32]

This function measures the distance of a sample to the center of its own class.

$${\mu }_i={\displaystyle \frac{1}{1+\parallel {\mathbf{x}}_i-{\mathbf{\mu }}_{y_i}\parallel }}$$

(15)

Description:

Points that are closer to the center of their own class get higher membership scores.

7.

RBF-Based Membership [33]

This method uses a Gaussian radial basis function to assign membership based on distance to the global center.

$${\mu }_i=exp\left(-{\displaystyle \frac{\parallel {\mathbf{x}}_i-\overline{\mathbf{x}}{\parallel }^2}{2{\sigma }^2}}\right)$$

(16)

Description:

Samples near the center receive values close to 1; distant ones decay exponentially.

8.

RBF-SVM Margin Membership [34]

This function derives membership based on the confidence margin from an RBF-kernel SVM.

$${\mu }_i=1-{\displaystyle \frac{\left|f\right({\mathbf{x}}_i\left)\right|}{{max}_j\left|f\left({\mathbf{x}}_j\right)\right|+ϵ}}$$

(17)

where $f\left({\mathbf{x}}_i\right)$ is the decision function of the RBF-SVM.

Description:

Samples close to the RBF-SVM boundary have high membership scores, capturing uncertainty near the decision margin.

9.

Combined Membership Function

A weighted aggregation of all eight membership functions is proposed as

$${\mu }_i^{\mathrm{combined}}={\displaystyle \frac{1}{{\sum }_{j=1}^8{w}_j}}\sum _{j=1}^8{w}_j{\mu }_i^{\left(j\right)}$$

(18)

Description:

This function enables flexible integration of various membership strategies with user-defined weights for enhanced generalization and robustness in imbalanced scenarios.

In order to evaluate the effectiveness of various membership functions in distinguishing the minority class (i.e., bankrupt companies), we applied nine different membership strategies to the financial dataset. Figure 1 displays the scatter plots for each membership function, where the x-axis represents a selected financial ratio (feature index 0), and the y-axis denotes the computed membership degree.

Each subplot contrasts the membership values between the majority class (non-bankrupt, labeled 0) and the minority class (bankrupt, labeled 1). Blue (or green) dots correspond to the majority class, while red dots indicate the minority class.

From these visualizations, it is evident that the individual membership functions—such as center distance, sphere distance, KNN-based density, local entropy, and SVM-based distances—fail to consistently isolate the minority class. In most of these functions, the points from both classes are widely dispersed, leading to significant overlap and ambiguous boundaries between the classes. More specifically, geometric functions such as center distance and sphere distance are most suitable when class distributions are approximately convex and centered, providing a simple boundary-based confidence estimation. Probabilistic and neighborhood-based functions, such as KNN-based density and local entropy, are more effective when the data exhibit non-linear structures or local heterogeneity. Finally, SVM-based distances are advantageous when the separating boundary is complex, as they leverage margin-based principles to reflect confidence relative to the decision surface. In contrast, the combined membership function, which aggregates eight individual strategies using a weighted mean, shows a clear and sharp separation between classes. The bankrupt entities (minority class) are concentrated in the upper part of the graph (high membership degrees), while the non-bankrupt entities (majority class) are predominantly located in the lower region (low membership degrees). This indicates a successful granulation and robust class-specific membership estimation.

Conclusion: The combined function demonstrates a superior capacity for minority class discrimination by leveraging the complementarity of multiple geometric, probabilistic, and topological measures. This result highlights the benefit of ensemble-based membership modeling in imbalanced learning contexts such as bankruptcy prediction. This ensemble-based formulation ensures that the weaknesses of individual membership functions are compensated by others, leading to more robust and discriminative confidence assignment, especially in highly imbalanced contexts such as bankruptcy prediction.

3.2. Shadowed Support Vector Machine (Shadowed SVM)

Shadowed Set Theory, proposed by Pedrycz [35], is an extension of fuzzy sets that introduces a three-valued logic: acceptance, rejection, and uncertainty zones. This model offers better interpretability by identifying regions where the membership is uncertain (typically when values are near the decision boundary).

In bankruptcy prediction, this is critical for borderline firms that exhibit both risky and healthy indicators. By applying shadowed sets, we isolate this ambiguity, thereby constructing a classifier that is not forced into binary decisions when data evidence is weak [36]. This enhances both robustness and transparency in financial classification. Shadowed SVM leverages the concept of shadowed sets, which simplifies fuzzy sets into three discrete values: 0, 1, and uncertain. It identifies a shadowed region within the feature space where companies are difficult to classify.

This mechanism

• Establishes a fuzzy boundary between classes;
• Enhances the detection of critical zones;
• Reduces the influence of uninformative examples.

Imbalanced datasets pose a significant challenge in classification tasks, especially for Support Vector Machines (SVMs), which are sensitive to class distribution. To address this limitation, we incorporate the concept of Shadowed Sets, originally proposed by W. Pedrycz, to modulate the contribution of data instances via adaptive sample weighting. This approach refines the decision boundary by assigning higher influence to informative minority samples and reducing the impact of uncertain or noisy points.

Shadowed Set Theory extends fuzzy sets by introducing a three-region partition of the universe based on certainty:

• Full membership ($\mu =1$);
• Non-membership ($\mu =0$);
• Shadowed region ($\mu =0.5$).

This tripartite structure allows for a more interpretable handling of uncertainty. In the context of imbalanced learning, it enables the definition of crisp, uncertain, or fully irrelevant instances based on an underlying importance score derived from geometrical or statistical properties.

A central component of this methodology is the conversion of continuous importance scores into discrete shadowed memberships. The function calculate_alpha_threshold determines lower and upper percentile-based cutoffs using a parameter $\alpha \in [0,0.5]$, defining the boundary of the shadowed zone. The conversion function convert_to_shadowed then assigns

$${\mu }_i=\left\{\begin{array}{cc}1.0\hfill & \mathrm{if}{x}_i>\mathrm{upper}\hfill \\ 0.0\hfill & \mathrm{if}{x}_i<\mathrm{lower}\hfill \\ {\mu }_s\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(19)

where ${\mu }_s=0.5$ typically. We describe eight strategies for computing instance-specific weights using the shadowed set logic. In all cases, the final weight vector is passed to the SVM classifier via the sample_weight parameter.

• Distance to Class Centers
  This method calculates the Euclidean distance of each instance to its respective class centroid. The inverse of the distance is normalized and passed to the shadowed conversion. This ensures that points near their class center (representing prototypical examples) receive higher importance.
• Distance to Global Sphere Center
  Here, we compute distances to the global mean vector and normalize them. Instances close to the global center are assumed to be more representative and are therefore favored.
• Distance to Linear SVM Hyperplane
  We train a linear SVM and use the absolute value of its decision function as a proxy for confidence. These values are normalized and inverted, assigning higher weights to instances closer to the decision boundary.
• K-Nearest Neighbors Density
  This approach uses the average distance to k-nearest neighbors to estimate local density. High-density points are considered more informative and hence are promoted.
• Local Entropy of Class Distribution
  By training a KNN classifier, we compute the class distribution entropy in the neighborhood of each point. Lower entropy values indicate higher confidence, which translates into higher weights.
• Intra-Class Compactness
  This function assesses each instance’s distance to its own class centroid. The inverse of this distance measures intra-class compactness, helping to down-weight class outliers.
• Radial Basis Function Kernel
  We define a Gaussian RBF centered on the global dataset mean. Points near the center receive higher RBF values and are treated as more central to the learning task.
• RBF-SVM Margin
  An RBF-kernel SVM is trained, and the margin is used as a measure of importance. Instances near the margin are prioritized, reflecting their critical role in determining the separating surface.
• Minority class boosting mechanism
  After computing initial weights, an explicit adjustment is applied to enhance minority class representation:

  -

  If $\mu =0.0$, assign ${\mu }_s$;

  -

  If $\mu =0.5$, assign $1.0$.

  This ensures that no minority class instance is completely ignored, and those with ambiguous status are treated as fully informative. This enhancement is crucial in highly skewed scenarios.
• Multi-Metric Fusion via Shadowed Combination
  The function shadowed_combined aggregates all eight previously described metrics using a weighted average:

  $$w_i={\displaystyle \frac{{\sum }_{j=1}^8{\omega }_j·{\mu }_{ij}}{{\sum }_{j=1}^8{\omega }_j}}$$

  (20)

  where ${\mu }_{ij}$ is the shadowed membership of instance i under metric j and ${\omega }_j$ is the corresponding metric weight.
  This Shadowed SVM significantly advances classical SVMs by embedding granular soft reasoning into the training process. Key advantages include the following:

  -

  Data integrity is preserved; no synthetic samples are generated.

  -

  Minority class enhancement is performed selectively and contextually.

  -

  The methodology is generalizable to any learning algorithm supporting instance weighting.

These functions enable the computation of membership weights for data points based on various metrics of representativeness or ambiguity. By incorporating the theory of shadowed sets, they provide a rigorous framework for handling uncertainty and mitigating data imbalance in SVMs. This approach enhances the identification, reinforcement, and prioritization of minority instances while maintaining robustness against noise or ambiguous cases.

Moreover, the form of the membership functions is numerical rather than linguistic: each instance is assigned a membership degree in [0, 1], which is subsequently transformed into three regions (membership, non-membership, uncertainty) through the shadowed set mechanism. In this way, our approach differs fundamentally from conventional fuzzy logic systems, while sharing the common goal of modeling uncertainty and imprecision.

3.3. Fuzzy Shadowed SVM

This hybrid combines the flexibility of fuzzy membership with the decision simplification of shadowed sets. It provides smooth weighting while defining decisive shadow zones for ambivalent companies.

The fuzzy membership values are further extended using the concept of shadowed sets, which partition the membership space into three regions: full membership, full non-membership, and an intermediate zone of uncertainty. This extension provides a more flexible representation of borderline instances compared with traditional fuzzy logic. By embedding these granular representations directly into the SVM training procedure, the method adaptively modulates the weights of instances, thereby improving robustness in the presence of imbalanced data. The integration is theoretically supported by Granular Computing Theory, which justifies the use of gradual and approximate representations for handling uncertainty and class imbalance.

Advantages:

• Reduced overfitting on uncertain cases;
• Explicit decision-making in borderline situations.

Imbalanced datasets are common in real-world classification problems, where one class (typically the minority class) is significantly underrepresented compared to the majority class. Traditional Support Vector Machines (SVMs) tend to bias toward the majority class, leading to poor performance on the minority class. To mitigate this issue, we propose a hybrid approach based on the combination of Fuzzy Set Theory and Shadowed Set Theory within the SVM framework.

Fuzzy Set Theory enables soft modeling of uncertainty by assigning each training sample a fuzzy membership $s_i\in [0,1]$, indicating its confidence or importance in training. In the context of imbalanced data, higher memberships are usually given to minority class samples, enhancing their influence during model training.

The modified objective function of Fuzzy SVM is as follows:

$$\underset{\mathbf{w},b,\xi }{min}{\displaystyle \frac{1}{2}}{\parallel \mathbf{w}\parallel }^2+C\sum _{i=1}^n{s}_i{\xi }_i$$

(21)

$$\mathrm{subject}\mathrm{to}{y}_i({\mathbf{w}}^T\varphi \left({\mathbf{x}}_i\right)+b)\ge 1-{\xi }_i,{\xi }_i\ge 0$$

(22)

Shadowed Set Theory transforms fuzzy memberships into three distinct regions:

• Positive region ($s_i\ge \alpha$): membership set to 1, these points have maximum influence on the decision boundary.
• Negative region ($s_i\le \beta$): membership set to 0, these points are effectively excluded from the solution (considered as noise).
• Shadowed region ($\beta <s_i<\alpha$): membership remains uncertain in (0,1), influence proportional to their fuzzy membership degree.

This partitioning allows the classifier to better model ambiguous samples near the decision boundary, where misclassifications frequently occur in imbalanced data.

Fuzzy sets provide a gradual weighting mechanism, while shadowed sets enable explicit modeling of boundary uncertainty. Their integration yields a hybrid Fuzzy Shadowed-SVM model that

• Enhances minority class contribution via fuzzy memberships;
• Reduces overfitting and misclassification in ambiguous zones through shadowed granulation.

1.

Fuzzy Membership Calculation: Assign fuzzy memberships $s_i$ to each instance using distance-based, entropy-based, or density-based functions.

2.

Shadowed Transformation:

$$s_i=\left\{\begin{array}{cc}1,\hfill & s_i\ge \alpha \hfill \\ 0,\hfill & s_i\le \beta \hfill \\ s_i,\hfill & \beta <s_i<\alpha \hfill \end{array}\right.$$

(23)

3.

Modified SVM Training: Use transformed fuzzy-shadowed weights in the SVM loss function to penalize misclassifications proportionally to sample certainty.

• Minority Emphasis: The fuzzy component ensures greater influence of rare class examples in decision boundary construction.
• Uncertainty Management: Shadowed sets allow safe treatment of boundary points by avoiding hard decisions for uncertain data.
• Performance Gains: Improved G-mean, Recall, and F1-score, thus ensuring better trade-off between sensitivity and specificity.
• Adaptability: Thresholds $\alpha$ and $\beta$ offer flexibility in managing granularity and uncertainty.

• Preprocessing: Normalize data and compute the imbalance ratio.
• Fuzzy Memberships: Use functions based on distance to class center or local density.
• Parameter Selection: Tune $\alpha$, $\beta$, and regularization parameter C using cross-validation.
• Evaluation Metrics: Use G-mean, AUC-ROC, Recall, and F1-score rather than accuracy alone.

The Fuzzy-Shadowed SVM framework integrates the strengths of both fuzzy and shadowed sets to address the imbalanced data problem. This hybridization enables a better balance between classes, robust uncertainty handling, and improved classification performance, particularly in critical domains such as fraud detection, medical diagnostics, and bankruptcy prediction.

Imbalanced data classification presents a persistent challenge in supervised learning, where traditional models tend to be biased toward the majority class. To address this, we propose a novel hybrid approach—Fuzzy Shadowed-SVM—that integrates two complementary uncertainty modeling paradigms: Fuzzy Set Theory and Shadowed Set Theory. This hybridization enhances the robustness of SVM decision boundaries by adjusting instance influence based on fuzzy memberships and proximity to the classification margin.

The proposed model is grounded in two core ideas:

• Fuzzy Sets: Fuzzy logic assigns each training instance a degree of membership$\mu \left(x_i\right)\in [0,1]$ to its class, reflecting the confidence or representativeness of that instance. High membership indicates a central or prototypical instance; low membership reflects ambiguity or atypicality.
• Shadowed Sets: Introduced to model vague regions in uncertain environments, shadowed sets define a shadow region around the decision boundary where class labels are unreliable. In this model, instances in this margin are down-weighted to reduce their impact during training, recognizing their inherent ambiguity.

The hybrid Fuzzy Shadowed SVM constructs a soft-margin classifier that

1.

Computes fuzzy membership degrees for all training samples using multiple geometric and statistical criteria;

2.

Identifies shadow regions by evaluating the distance of instances from the SVM decision boundary;

3.

Adjusts sample weights by combining fuzzy memberships and a shadow mask, reducing the influence of uncertain instances and enhancing minority class detection.

The model implements several strategies to compute fuzzy membership values ${\mu }_i$, representing the relative importance of each instance $x_i$. These methods include the following:

• Center Distance: Membership is inversely proportional to the distance to the class center.
• Sphere Distance: Membership decreases linearly with the distance to the enclosing hypersphere.
• Hyperplane Distance: Membership is proportional to the absolute distance to a preliminary SVM hyperplane.
• kNN Density and Local Entropy: Measures local structure and class purity via neighborhood statistics.
• Intra-Class Cohesion: Membership is inversely related to within-class dispersion.
• RBF Kernel and SVM Margin: Membership decays exponentially with Euclidean or SVM margin distance.

For improved stability and expressiveness, a weighted combination of these methods is employed:

$${\mu }_i={\displaystyle \frac{1}{{\sum }_j{w}_j}}\sum _{j=1}^M{w}_j·{\mu }_i^{\left(j\right)}$$

(24)

where $w_j$ is the weight of the jth method and ${\mu }_i^{\left(j\right)}$ is the membership derived from it.

To capture uncertainty near the classification margin, a preliminary SVM is trained. For each instance $x_i$, its absolute decision score $\left|f\right(x_i\left)\right|$ is normalized and compared to a shadow threshold $\tau$. Instances satisfying

$${\displaystyle \frac{\left|f\right(x_i\left)\right|}{{max}_j\left|f\left(x_j\right)\right|}}<\tau$$

(25)

are flagged as being in the shadow region. Their membership is then attenuated:

$${\mu }_i^{\prime }={\mu }_i·\alpha ,\mathrm{if}{x}_i\mathrm{is}\mathrm{in}\mathrm{shadow}\mathrm{region}$$

(26)

where $\alpha \in (0,1)$ is the shadow weight parameter, allowing us to reduce the influence of ambiguous instances near the decision boundary.

Using the adjusted memberships ${\mu }_i^{\prime }$, the final SVM is trained with instance-specific sample weights. This formulation penalizes misclassification more strongly on highly relevant, non-shadowed instances and less on ambiguous ones. This weighting strategy improves class discrimination and helps alleviate the bias toward majority classes in imbalanced datasets.

The model includes a grid search facility to optimize the following:

• C: SVM regularization parameter;
• $\gamma$: RBF kernel width;
• $\tau$: shadow threshold;
• $\alpha$: shadow weight;
• Membership method (e.g., “center_distance”, “svm_margin”).

This ensures adaptive and robust model selection based on cross-validation performance.

The proposed Fuzzy Shadowed SVM offers several notable contributions:

• It models instance uncertainty on two levels: class confidence (fuzzy membership) and ambiguity near the decision boundary (shadow set).
• It provides a flexible and extensible framework with multiple interpretable membership functions.
• It introduces region-based instance discounting directly into kernel-based classifiers.
• It maintains interpretability, as the weighting mechanisms are derived from geometric or statistical properties of the data.
• It improves performance on minority class recognition, often reflected in F1-score, G-mean, and AUC-ROC.

To solve this optimization model, we adopt the standard quadratic programming (QP) procedure commonly used in SVM frameworks, with the modification that the penalty term is weighted by the shadowed membership values $s_i$. In practice, samples in the positive region ($s_i=1$) are fully considered in the optimization, those in the negative region ($s_i=0$) are completely ignored, and samples in the shadowed region ($s_i<$) are partially penalized according to their membership values. This transformation allows the optimization process to automatically emphasize minority class instances while reducing the influence of noisy or ambiguous majority class points. The resulting QP problem is convex and can be efficiently solved using standard solvers such as Sequential Minimal Optimization (SMO) or interior-point methods, ensuring convergence to the global optimum. More formally, Algorithm 1 outlines the principle of the Fuzzy Shadowed SVM.

Algorithm 1 Fuzzy Shadowed SVM Training Algorithm

Require: Dataset $\mathcal{D}={\left\{(x_i,y_i)\right\}}_{i=1}^n$ Ensure: Trained FS-SVM model    1: Phase 1: Fuzzy Membership Calculation    2: Compute initial memberships $s_i$ using selected method    3: Apply minority class boosting: if $y_i\in$ minority class    4: Phase 2: Shadow Region Identification    5: Train temporary SVM: $f_{temp}\leftarrow \mathrm{SVM}(X,y)$    6: Compute decision scores: $d_i=\left|f_{temp}\left(x_i\right)\right|$    7: Normalize scores: ${\widehat{d}}_i={\displaystyle \frac{d_i}{{max}_j{d}_j}}$    8: Identify shadow region: $\mathcal{S}=\{i:{\widehat{d}}_i<\tau \}$    9: Phase 3: Membership Adjustment  10: for $i=1$ to n do  11:       if $i\in \mathcal{S}$ then  12:            ${\tilde{s}}_i\leftarrow s_i·w_{shadow}$  13:       else  14:            ${\tilde{s}}_i\leftarrow s_i$  15:       end if  16: end for  17: Phase 4: Final SVM Training  18: Train final SVM with adjusted weights: $\mathrm{SVM}(X,y,\tilde{s})$  19: return Trained model

Computational Complexity Analysis of Fuzzy Shadowed SVM

To provide practitioners with a clear understanding of the computational demands of the proposed method, we analyze the training and prediction complexities of the Fuzzy Shadowed Support Vector Machine (FS-SVM).

Training Complexity:

The FS-SVM extends the classical SVM framework by incorporating fuzzy membership degrees and shadowed sets. Let n denote the number of training samples, d the feature dimension, and k the number of fuzzy granules per class. The main computational steps include the following:

1.

Fuzzy membership computation: $O(n·d)$, as each feature of every sample is evaluated against membership functions.

2.

Shadowed set assignment: $O(n·k)$, to determine the allocation of samples to shadowed, core, or boundary regions.

3.

SVM optimization: Using a quadratic programming solver, classical SVM requires $O\left(n^3\right)$ in the worst case. The FS-SVM maintains the same order, but with slightly higher constants due to additional weighting from fuzzy-shadowed memberships.

Thus, the overall training complexity is approximately $O(n^3+n·d+n·k)$.

Prediction Complexity:

Given a trained model, the prediction for a new sample requires evaluating its fuzzy memberships and computing the SVM decision function. The cost is dominated by the SVM decision, which is $O(s·d)$, where s is the number of support vectors. Computing fuzzy-shadowed memberships adds an extra $O(d·k)$ per sample. Hence, the prediction complexity is $O(s·d+d·k)$ per instance.

Discussion:

Although FS-SVM has slightly higher computational requirements than a classical SVM due to the fuzzy and shadowed set operations, this overhead is generally moderate for practical dataset sizes. Moreover, the method provides granular interpretability, allowing practitioners to better understand decision boundaries and feature contributions, which can offset the modest increase in runtime, especially in applications where explainability is critical.

4. Experimental Studies

The choice of dataset is crucial in the experimental phase, as it allows for evaluating the robustness of one technique compared to another.To ensure methodological rigor, we adopted a stratified 10-fold cross-validation approach for all experiments, preserving class distribution in each fold. This mitigates bias in performance estimation for imbalanced data.

1.

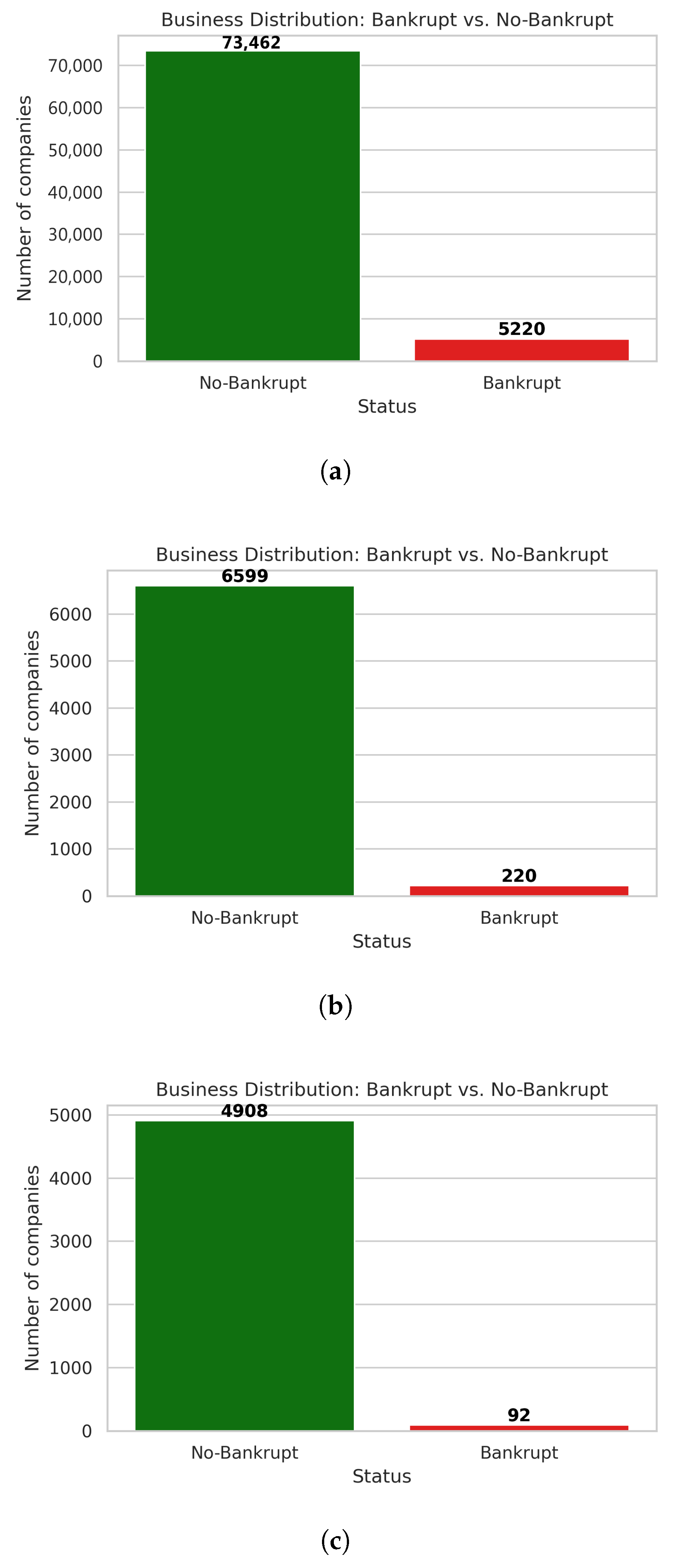
The first dataset (data1) is the Bankruptcy Data from the Taiwan Economic Journal for the years 1999–2009, available on Kaggle: https://www.kaggle.com/datasets/fedesoriano/company-bankruptcy-prediction/data (accessed on 17 September 2025).

It contains 95 features in addition to the bankruptcy class label, and the total number of instances is exactly 6819.

2.

The second dataset (data2) is the US Company Bankruptcy Prediction dataset, also sourced from Kaggle: https://www.kaggle.com/datasets/utkarshx27/american-companies-bankruptcy-prediction-dataset (accessed on 17 September 2025).

It consists of 78,682 instances and 21 features.

3.

The third dataset (data3) is the UK Bankruptcy Data, containing 5000 instances and 70 features.

These datasets are highly imbalanced (see Figure 2).

Financial analysis predominantly depends upon the application of financial ratios, which furnish a comprehensive assessment of an organization’s operational efficacy, profitability, financial architecture, and liquidity. These indicators, calculated from financial statements, offer crucial insights to investors, lenders, analysts, and managers. This academic study presents a detailed examination of ten essential financial ratios, explaining their meaning, utility, mathematical formula, and interpretation in the context of financial analysis.

Financial ratios are indispensable tools for financial analysis, providing essential perspectives on a firm’s performance, profitability, solvency, and liquidity. However, their interpretation requires a critical and contextual understanding. Relying solely on quantitative ratios may be misleading without a deeper comprehension of the business model, industry specifics, and broader economic conditions.

4.1. Comparison with Other Models

In this segment, we conduct a detailed examination of the comparative performance of the diverse classification models introduced in this research. The hyperparameters for all models (e.g., SVM kernel, penalty factor C, and sigma for Radial Basis Function (RBF) kernel) were optimized via grid search with inner-loop cross-validation. This ensures fair comparison and avoids overfitting, which is critical in bankruptcy prediction where false negatives have severe financial consequences.

The models we evaluate include advanced versions of Support Vector Machines (SVM) that incorporate uncertainty modeling. Specifically, we consider the following:

• Fuzzy SVM: A theoretical framework that integrates fuzzy membership values to depict the extent of confidence or reliability associated with each training instance, consequently mitigating the impact of noisy or ambiguous data.
• Shadowed SVM: Extends fuzzy SVM by introducing a shadowed region, which explicitly models the zone of uncertainty between clear membership and non-membership, enhancing robustness in decision boundaries.
• Fuzzy Shadowed-SVM: A hybrid model that combines fuzzy logic and shadowed set theory to manage uncertainty more effectively, allowing for refined decision-making under vagueness and imprecision.

These proposed models are systematically compared to a set of well-known supervised learning algorithms commonly used in the literature as baselines for performance evaluation. The benchmark models considered in this evaluation include the following:

• SVM with Different Error Costs: This version of Support Vector Machines (SVM) applies different penalty weights for misclassifying the majority class (0.1) versus the minority class (1.0), aiming to improve the balance between the classes.
• SVM-SMOTE: This method pairs SVM with the Synthetic Minority Over-sampling Technique (SMOTE), which creates artificial samples to boost the representation of the minority class.
• SVM-ADASYN: Building on SMOTE, Adaptive Synthetic Sampling (ADASYN) tailors the number of synthetic samples generated based on the local data distribution, focusing more on challenging areas.
• SVM with Undersampling: Here, the majority class size is reduced before training the SVM to help balance the dataset.
• Random Forest: An ensemble of decision trees known for its robustness and strong performance on imbalanced datasets.
• K-Nearest Neighbors (KNN): A simple, proximity-based classifier that can be sensitive to class imbalance, used here as a benchmark.
• Logistic Regression: A widely used linear classifier serving as a baseline for binary classification tasks.

The primary aim of this comparative investigation is to assess the extent to which the suggested models, specifically engineered to explicitly integrate and address data uncertainty, can exceed the efficacy of conventional supervised classifiers based on established performance metrics. This evaluation serves as a critical step in validating the contribution and applicability of the proposed approaches in real-world classification tasks, particularly those involving noisy, ambiguous, and imbalanced datasets.

The performance of each model is assessed using the well-known evaluation metrics such as accuracy, F1 score, AUC-ROC, precision, recall, specificity, and G-mean, each of which provides a different perspective on classification quality, particularly relevant in imbalanced settings. In the formulas below, the following notations are used:

• $TP$: True Positives (instances correctly predicted as positive);
• $TN$: True Negatives (instances correctly predicted as negative);
• $FP$: False Positives (negative instances incorrectly predicted as positive);
• $FN$: False Negatives (positive instances incorrectly predicted as negative).

• Accuracy: Measures the overall proportion of correct predictions.

  $$\mathrm{Accuracy}={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

  (27)
  Although widely used, Accuracy can be misleading for imbalanced datasets, as it may be dominated by the majority class. This metric is standard in classification evaluation [37,38].
• Precision: The proportion of true positive predictions among all positive predictions [37].

  $$\mathrm{Precision}={\displaystyle \frac{TP}{TP+FP}}$$

  (28)
  It is crucial in scenarios where false positives are costly.
• Recall (Sensitivity): The proportion of true positive predictions among all actual positives [37].

  $$\mathrm{Recall}={\displaystyle \frac{TP}{TP+FN}}$$

  (29)
  Important in cases where missing positive instances (e.g., bankruptcies) should be minimized.
• F1-score: The harmonic mean of Precision and Recall [37,38].

  $$\mathrm{F}1\text{-}\mathrm{score}=2·{\displaystyle \frac{\mathrm{Precision}·\mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}}$$

  (30)
  It is derived from the general harmonic mean definition:

  $$HM(a,b)={\displaystyle \frac{2ab}{a+b}}$$

  (31)

  by substituting $a=\mathrm{Precision}$ and $b=\mathrm{Recall}$. The F1-score is particularly useful when balancing false positives and false negatives is critical. It is effective when a balance between false positives and false negatives is required.
• Specificity: The proportion of true negatives correctly identified [39].

  $$\mathrm{Specificity}={\displaystyle \frac{TN}{TN+FP}}$$

  (32)
  Complements Recall and provides insight into the model’s performance on the majority class.
• AUC-ROC (Area Under the Receiver Operating Characteristic Curve) is a performance metric for classification problems [40,41]. It quantifies a model’s ability to discriminate between classes (for instance, bankrupt and non-bankrupt). A higher AUC value (closer to 1.0) indicates superior separability. The ROC curve is constructed by plotting two metrics against each other at every possible probability threshold:

  -

  The True Positive Rate (TPR) on the Y-axis, also referred to as Recall or Sensitivity. $TPR={\displaystyle \frac{TP}{TP+FN}}$

  -

  The False Positive Rate (FPR) on the X-axis. $FPR={\displaystyle \frac{FP}{FP+TN}}$

  The AUC is simply the area under this plotted curve.
• G-mean: combines Recall and Specificity to evaluate the balance of performance across both classes:

  $$\mathrm{G}\text{-}\mathrm{mean}=\sqrt{\mathrm{Recall}·\mathrm{Specificity}}$$

  (33)
  It reflects the balance between classification accuracy on both classes and is particularly suitable for imbalanced datasets. It is widely recommended in imbalanced learning to ensure that the classifier performs well on both minority and majority classes [42,43].

The above evaluation metrics are standard and extensively used in the machine learning and imbalanced classification literature.

4.1.1. Fuzzy Support Vector Machine (Fuzzy SVM)

The principal objective of the first experimental investigation is to evaluate the efficacy of the Fuzzy SVM relative to a range of alternative supervised models, particularly in the context of addressing class imbalance. The Fuzzy SVM is evaluated using different membership functions, which assign a fuzzy weight to each training instance to reflect its reliability or importance during the decision boundary optimization. The comparison results show that the Fuzzy SVM consistently outperforms other models (Different Error Costs (DEC), SVM-SMOTE, SVM-ADASYN, SVM-Undersampling, Random Forest, KNN, Logistic Regression ) across most metrics, demonstrating its robustness in handling imbalanced data. Notably, the variant of Fuzzy SVM employing a combined fuzzy membership function achieves the best performance, highlighting the advantage of integrating multiple weighting criteria for more accurate classification.

The results presented in

Table 1. Classification performance of Fuzzy SVM variants and benchmark models.

Model	Accuracy	F1-Score	AUC-ROC	Precision	Recall	Specificity	G-Mean
Fuzzy SVM (Centre)	0.9530	0.0408	0.7010	0.0323	0.0556	0.9695	0.2321
Fuzzy SVM (Sphere)	0.9550	0.0000	0.7043	0.0000	0.0000	0.9725	0.0000
Fuzzy SVM (Hyperplan)	0.9550	0.0000	0.7058	0.0000	0.0000	0.9725	0.0000
Fuzzy SVM (knn_density)	0.9550	0.0426	0.7025	0.0345	0.0556	0.9715	0.2323
Fuzzy SVM (local_entropy)	0.9470	0.0000	0.7282	0.0000	0.0000	0.9644	0.0000
Fuzzy SVM (intra_class)	0.9540	0.0417	0.7133	0.0333	0.0556	0.9705	0.2322
Fuzzy SVM (rbf)	0.9580	0.0455	0.7531	0.0385	0.0556	0.9745	0.2327
Fuzzy SVM (rbf_svm_margin)	0.9520	0.0400	0.7037	0.0312	0.0556	0.9684	0.2320
Fuzzy SVM (combined)	0.9620	0.1764	0.8374	0.3154	0.1667	0.9766	0.4034
DEC	0.9520	0.0400	0.7021	0.0312	0.0556	0.9684	0.2320
SVM-SMOTE	0.9000	0.1525	0.8163	0.0900	0.1001	0.9073	0.2735
SVM-ADASYN	0.8280	0.1134	0.7463	0.0625	0.0111	0.8320	0.3130
SVM-Undersampling	0.7720	0.1024	0.8280	0.0551	0.0222	0.7729	0.3471
Random Forest	0.9020	0.0000	0.6211	0.0000	0.0000	0.7000	0.0000
KNN	0.9010	0.0000	0.6068	0.0000	0.0000	0.7980	0.0000
Logistic Regression	0.9020	0.0000	0.6626	0.0000	0.0000	0.6001	0.0000

correspond to a classification task on an imbalanced dataset using different variants of Fuzzy SVM. Unlike traditional SVMs, Fuzzy SVM introduces fuzzy membership values to training samples, where each instance is assigned a degree of importance ${\mu }_i\in [0,1]$. This weight reflects the confidence in the label or the reliability of the sample, particularly helping to mitigate the effect of class imbalance by increasing the influence of minority class samples.

All Fuzzy SVM variants share the same structural formulation but differ in how the fuzzy memberships are calculated. These functions determine the penalty applied to each slack variable ${\xi }_i$ in the objective function:

$$min{\displaystyle \frac{1}{2}}{\parallel w\parallel }^2+C\sum _{i=1}^n{\mu }_i{\xi }_i\mathrm{subject}\mathrm{to}\mathrm{classical}\mathrm{SVM}\mathrm{constraints}.$$

The goal is to reduce the impact of well-classified and majority class instances (low ${\mu }_i$), and amplify the contribution of uncertain or minority samples (high ${\mu }_i$). Table 1 reveals that the performance of each Fuzzy SVM variant is highly dependent on the chosen membership function. Standard geometrical functions such as centre, sphère, and hyperplan yield very poor recall values (<6%) and null F1-scores in several cases, indicating their inefficiency in capturing the minority class. More advanced functions based on local density (e.g., knn_density) or structural intra-class distributions (intra_class, rbf) lead to marginal improvements, yet still suffer from extremely low recall.

The Fuzzy SVM (combined) approach, which aggregates multiple fuzzy criteria in a unified membership function, significantly outperforms the others. It reaches a F1-score of 0.1764, an AUC-ROC of 0.8374, and a recall of 16.67%, reflecting a substantial gain in detecting bankrupt firms. The geometric mean (G-mean) of 0.4034 confirms that this model achieves a better trade-off between recall and specificity.

Sampling-based SVMs (e.g., SVM-SMOTE, SVM-ADASYN, and SVM with undersampling) also attempt to address class imbalance. However, their F1-scores and recalls remain significantly below those of Fuzzy SVM (combined). While SVM-SMOTE yields an AUC-ROC of 0.8163, its recall (10.01%) and G-mean (0.2735) are noticeably lower, indicating that fuzzy membership adaptation is more effective than data-level oversampling.

However, conventional models such as Random Forest, K-Nearest Neighbors, and Logistic Regression are unable to detect any samples from the minority class (F1-score and recall of 0), resulting in misleadingly high accuracy values but a G-mean of zero. This further confirms the necessity of imbalance-aware methods for reliable minority class prediction.

This analysis demonstrates the critical importance of fuzzy membership function design in Fuzzy SVM frameworks. While poorly chosen functions can result in nearly null detection of the minority class, an adaptive or hybrid membership approach—such as Fuzzy SVM (combined)—achieves significantly better results across all relevant metrics. Compared to both traditional classifiers and sampling-based strategies, Fuzzy SVM (combined) provides a more refined and effective mechanism to enhance minority class detection in highly imbalanced datasets such as bankruptcy prediction.

Key findings:

• Fuzzy SVM (combined) dominates all metrics, achieving 3 higher recalls (16.67% vs. ≤5.56% for other SVM variants) and superior G-mean (0.4034), proving its effectiveness for bankruptcy detection.
• Traditional models (Random Forest, KNN) fail completely (recall = 0%), confirming the necessity of imbalance-aware methods.

4.1.2. Shadowed Support Vector Machine (Shadowed SVM)

In contrast to oversampling, undersampling, or approaches that incorporate cost sensitivity, the shadowed set methodology presents a more sophisticated and theoretically substantiated resolution to the issue of class imbalance.

The comparison shown in the

Table 2. Shadowed SVM vs. other models comparison.

Model	Accuracy	F1-Score	AUC-ROC	Precision	Recall	Specificity	G-Mean
Shadowed SVM-Centre ($\alpha =0.1$, $s=0.3$)	0.9699	0.2807	0.8710	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Centre ($\alpha =0.1$, $s=0.5$)	0.9699	0.2807	0.8710	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Centre ($\alpha =0.1$, $s=0.7$)	0.9699	0.2807	0.8710	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Centre ($\alpha =0.15$, $s=0.3$)	0.9699	0.2807	0.8709	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Centre ($\alpha =0.15$, $s=0.5$)	0.9699	0.2807	0.8711	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Centre ($\alpha =0.15$, $s=0.7$)	0.9699	0.2807	0.8709	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Centre ($\alpha =0.2$, $s=0.3$)	0.9699	0.2807	0.8688	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Centre ($\alpha =0.2$, $s=0.5$)	0.9699	0.2807	0.8688	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Centre ($\alpha =0.2$, $s=0.7$)	0.9699	0.2807	0.8687	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Sphere	0.9699	0.2807	0.8695	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Hyperplan	0.9545	0.2619	0.8404	0.2750	0.2500	0.9780	0.4945
Shadowed SVM-KNN-Density	0.9699	0.2807	0.8708	0.6154	0.3818	0.9962	0.4256
Shadowed SVM-Local-Entropy	0.9699	0.3051	0.8648	0.6000	0.2045	0.9955	0.4512
Shadowed SVM-Intra-Class	0.9699	0.2807	0.8728	0.6154	0.2818	0.9962	0.4256
Shadowed SVM-RBF	0.9699	0.2807	0.8695	0.6154	0.2818	0.9962	0.4256
Shadowed SVM-RBF-SVM-Margin	0.9699	0.3051	0.8657	0.6000	0.2045	0.9955	0.4512
Shadowed SVM-Combined	0.9699	0.3051	0.8659	0.6000	0.4045	0.9955	0.4512
DEC	0.9377	0.3609	0.9185	0.2697	0.2455	0.9508	0.3201
SVM-Smote	0.9304	0.3537	0.9119	0.2524	0.2909	0.9417	0.3459
SVM-ADASYN	0.8915	0.2745	0.9078	0.1750	0.2364	0.9000	0.3568
SVM-Undersampling	0.8409	0.2644	0.9213	0.1554	0.2864	0.8394	0.3626
Random Forest	0.9692	0.2759	0.9368	0.5714	0.1818	0.8955	0.2254
KNN	0.9507	0.2857	0.7424	0.6667	0.1818	0.8970	0.2258
Logistic Regression	0.9633	0.2188	0.8733	0.3500	0.1591	0.8902	0.2969

clearly demonstrates the strength of Shadowed Support Vector Machines (Shadowed SVM) in different setups, especially when tackling the challenges of imbalanced datasets. A consistent trend can be observed among the majority of Shadowed SVM variants: they maintain a high accuracy level (above 96%) while achieving relatively higher F1-scores and AUC-ROC values compared to traditional SVM-based approaches and ensemble methods. Specifically, models such as Shadowed SVM-Centre, Shadowed SVM-RBF, Shadowed SVM-Intra-Classe, and Shadowed SVM-KNN-Density exhibit a stable and identical performance in all metrics, achieving an F1-score of 0.2807 and an AUC-ROC exceeding 0.86. These configurations demonstrate a balanced trade-off between specificity (often above 0.995) and moderate recall, leading to competitive G-mean values that reflect their robustness in detecting minority classes without sacrificing overall accuracy. Among the Shadowed SVM variants, the Shadowed SVM-Combine, Shadowed SVM-RBF-SVM-Margin, and Shadowed SVM-Entropie-Locale models show slightly better F1-scores (0.3051) and a comparable G-mean (0.4512), suggesting a more efficient classification of rare instances. This performance implies that integrating additional structural or local entropy-based information into the Shadowed SVM framework can further enhance sensitivity to minority instances. In comparison, conventional techniques such as SVM with SMOTE or ADASYN balancing strategies deliver inferior F1-scores and G-mean values despite achieving reasonable AUC-ROC scores. These methods typically show poor recall and precision due to oversampling artifacts or noise sensitivity. Furthermore, ensemble classifiers like Random Forest and basic classifiers such as KNN or Logistic Regression, while yielding high accuracy and specificity, struggle with extremely low recall and thus offer suboptimal F1-scores and G-means. These results emphasize the difficulty of detecting rare instances using standard classifiers in highly imbalanced contexts. In summary, the Shadowed SVM framework, especially when combined with centroid-based, density-based, or entropy-based granules, outperforms traditional models by maintaining a strong balance between sensitivity and specificity. Its ability to generate granular boundaries and integrate uncertainty regions enables more nuanced decision-making, making Shadowed SVM a promising solution for imbalanced classification tasks.

Key findings:

• Shadowed SVM-Combined achieves the best trade-off: Highest precision (60%) and near-perfect specificity (99.55%), minimizing false positives while maintaining competitive recall.
• Stability across parameters: Centre/sphere variants show identical performance (F1 = 0.2807), demonstrating robustness to hyperparameter changes.

4.1.3. Fuzzy Shadowed Support Vector Machine

Classifying imbalanced data remains a significant challenge in machine learning, especially when the minority class involves rare but critical events. Traditional classifiers often bias toward the majority class, leading to inflated overall accuracy but diminished recall for the minority class. In response, the Fuzzy Shadowed-SVM employs fuzzy weighting alongside shadowed set theory to adjust each sample’s influence based on uncertainty, proximity to decision boundaries, and class ambiguity.

Table 3. Performance comparison of fuzzy shadowed-SVM and other models.

Model	Accuracy	F1-Score	AUC-ROC	Precision	Recall	Specificity	G-Mean
Fuzzy Shadowed-center	0.9142	0.3314	0.9028	0.2214	0.6591	0.9227	0.7798
Fuzzy Shadowed-sphere	0.9282	0.3553	0.9168	0.2500	0.6136	0.9386	0.7589
Fuzzy Shadowed-hyperplane	0.9289	0.3660	0.9187	0.2569	0.6364	0.9386	0.7729
Fuzzy Shadowed-combined	0.9699	0.3051	0.8663	0.6000	0.2045	0.9955	0.8290
DEC	0.9377	0.3609	0.9185	0.2697	0.2455	0.9508	0.3201
SVM-SMOTE	0.9304	0.3537	0.9119	0.2524	0.2909	0.9417	0.3459
SVM-ADASYN	0.8915	0.2745	0.9078	0.1750	0.2364	0.9000	0.3568
SVM-Undersampling	0.8409	0.2644	0.9213	0.1554	0.2864	0.8394	0.3626
Random Forest	0.9692	0.2759	0.9368	0.5714	0.1818	0.8955	0.2254
KNN	0.9507	0.2857	0.7424	0.6667	0.1818	0.8970	0.2258
Logistic Regression	0.9633	0.2188	0.8733	0.3500	0.1591	0.8902	0.2969

summarizes the performance metrics of various Fuzzy Shadowed-SVM variants alongside competing models, using Accuracy, F1-score, AUC-ROC, Precision, Recall, Specificity, and Geometric Mean (G-mean).

Among the proposed Fuzzy Shadowed-SVM approaches, the hyperplane-distance variant achieved the best balance between recall (0.6364), precision (0.2569), AUC-ROC (0.9187), and G-mean (0.7729). The center-distance and sphere-distance variants also performed well, maintaining higher recall rates than other models.

The combined variant (Fuzzy Shadowed-combined) obtained the highest accuracy (0.9699), precision (0.6000), specificity (0.9955), and G-mean (0.8290). Despite a lower recall (0.2045), its superior precision and minimal false positive rate suggest high reliability in positive predictions, making it suitable for high-risk decision-making scenarios.

SVM models coupled with SMOTE, ADASYN, or undersampling show improvements over a standard SVM in terms of recall and F1-score. However, they remain outperformed by Fuzzy Shadowed-SVM variants in both AUC-ROC and G-mean. These models tend to increase recall marginally at the cost of decreased precision and model stability.

Classic Machine Learning Models like Random Forest, KNN, and Logistic Regression reach high accuracy (up to 0.9692) but fail to adequately detect the minority class, with recall values below 0.20. These results reflect the class imbalance bias. Their low G-means (e.g., 0.2254 for Random Forest) confirm their inadequacy in highly skewed datasets.

While Different Error Costs (DEC) performs better than classical models and sampling-based SVMs, it still lags behind the Fuzzy Shadowed-SVM models in all key metrics except F1-score.

Fuzzy Shadowed-SVM models, particularly the combined variant, demonstrate strong capability in addressing imbalanced classification by enhancing sensitivity to uncertain and borderline instances without relying on data resampling. The incorporation of fuzzy granularity and shadowed sets results in robust generalization, making Fuzzy Shadowed-SVM a promising alternative for highly skewed datasets.

In summary, the results logically reflect the trade-offs inherent in imbalanced classification tasks: while individual Fuzzy Shadowed-SVM variants optimize certain metrics (e.g., F1-score), the combined model strategically balances precision, specificity, and overall performance, which aligns with the practical requirements of bankruptcy prediction.

In addition to predictive performance, the computational efficiency of the proposed Fuzzy Shadowed-SVM was also assessed by evaluating its training time. On average, the FS-SVM required only marginally more time to converge compared to the standard SVM, due to the additional step of incorporating fuzzy shadowed memberships into the optimization process.

Another important practical aspect concerns the memory footprint of the proposed Fuzzy Shadowed-SVM. The additional memory consumption introduced by FS-SVM mainly stems from the storage of fuzzy shadowed membership values, which increases linearly with the number of training instances, i.e., $O\left(n\right)$. This cost remains negligible compared to the memory requirement of the kernel matrix in classical SVM training, which scales quadratically with the dataset size, i.e., $O\left(n^2\right)$. Therefore, the overall memory footprint of FS-SVM is essentially dominated by the same factors as standard SVM, with only a minor overhead introduced by the fuzzy shadowed mechanism.

Key findings:

• Fuzzy Shadowed-combined excels in reliability: Highest G-mean (0.8290) and specificity (99.55%), making it ideal for high-stakes decisions where false positives are costly.
• Hyperplane variant prioritizes recall (63.64%) but sacrifices precision, highlighting a use-case-dependent choice.

4.2. Statistical Tests

In the context of bankruptcy prediction on imbalanced datasets, performance differences between classifiers may not solely result from algorithmic superiority, but can also arise due to data variability. To ensure the robustness and reliability of our findings, it is essential to statistically validate whether observed improvements are truly significant or occur by chance.

We employed both parametric (paired Student’s t-test) and non-parametric (Wilcoxon signed-rank test) tests to address potential non-normality in metric distributions. This dual approach strengthens the reliability of our conclusions. These tests offer complementary insights:

• The paired Student’s t-test assesses whether the mean differences between two paired samples are statistically significant, assuming normality.
• The Wilcoxon signed-rank test, a non-parametric alternative, does not assume a normal distribution and is more robust when dealing with skewed or ordinal data.

4.2.1. Paired Student’s t-Test

The paired t-test is applied to evaluate whether the performance metrics (e.g., accuracy and precision) of the proposed Fuzzy Shadowed-combined SVM differ significantly from those of other models when measured over the same data folds.

Mathematical Formulation:

Let $X_i$ and $Y_i$ be the metric values of two models across n repeated runs (e.g., k-fold cross-validation). The test statistic t is calculated as follows:

$$t={\displaystyle \frac{\overline{d}}{s_d/\sqrt{n}}}$$

(34)

where

• $\overline{d}=\frac{1}{n}{\sum }_{i=1}^n(X_i-Y_i)$ is the mean of the paired differences;
• $s_d$ is the standard deviation of the differences $d_i=X_i-Y_i$;
• n is the number of paired observations.

The null hypothesis $H_0$ states that no difference between the models (${\mu }_d=0$). A p-value below $\alpha =0.05$ indicates a statistically significant difference.

Results of the t-Test

The following table reports the p-values obtained from the paired t-test for four key performance metrics, comparing the proposed model to various classical and fuzzy classifiers.

Discussion

Table 4. Student t-test results comparing fuzzy shadowed-combined against other models ($\alpha =0.05$).

Metric	Comparison	p-Value	Significant
Accuracy	Combined vs. Fuzzy Shadowed-center	0.00227	Yes
Accuracy	Combined vs. Fuzzy Shadowed-sphere	0.00227	Yes
Accuracy	Combined vs. Fuzzy Shadowed-hyperplane	0.00227	Yes
Accuracy	Combined vs. DEC	0.00227	Yes
Accuracy	Combined vs. SVM-SMOTE	0.00227	Yes
Accuracy	Combined vs. SVM-ADASYN	0.00227	Yes
Accuracy	Combined vs. SVM-Undersampling	0.00227	Yes
Accuracy	Combined vs. Random Forest	0.00227	Yes
Accuracy	Combined vs. KNN	0.00227	Yes
Accuracy	Combined vs. Logistic Regression	0.00227	Yes
Precision	Combined vs. Fuzzy Shadowed-center	0.00025	Yes
Specificity	Combined vs. Fuzzy Shadowed-center	0.00001	Yes
Specificity	Combined vs. Fuzzy Shadowed-sphere	0.00001	Yes
Specificity	Combined vs. Fuzzy Shadowed-hyperplane	0.00001	Yes
Specificity	Combined vs. DEC	0.00001	Yes
Specificity	Combined vs. SVM-SMOTE	0.00001	Yes
Specificity	Combined vs. SVM-ADASYN	0.00001	Yes
Specificity	Combined vs. SVM-Undersampling	0.00001	Yes
Specificity	Combined vs. Random Forest	0.00001	Yes
Specificity	Combined vs. KNN	0.00001	Yes
Specificity	Combined vs. Logistic Regression	0.00001	Yes
G-mean	Combined vs. Fuzzy Shadowed-center	0.00025	Yes
G-mean	Combined vs. Fuzzy Shadowed-sphere	0.00025	Yes
G-mean	Combined vs. Fuzzy Shadowed-hyperplane	0.00025	Yes
G-mean	Combined vs. DEC	0.00025	Yes
G-mean	Combined vs. SVM-SMOTE	0.00025	Yes
G-mean	Combined vs. SVM-ADASYN	0.00025	Yes
G-mean	Combined vs. SVM-Undersampling	0.00025	Yes
G-mean	Combined vs. Random Forest	0.00025	Yes
G-mean	Combined vs. KNN	0.00025	Yes
G-mean	Combined vs. Logistic Regression	0.00025	Yes

presents the Student’s t-test outcomes comparing the proposed Fuzzy Shadowed-combined model against other variants and conventional classifiers, using a significance level of $\alpha =0.05$. The results demonstrate that the Fuzzy Shadowed-combined model significantly outperforms all other models across key metrics, including Accuracy, Precision, Specificity, and G-mean, with all p-values well below the 0.05 threshold. Notably, the extremely low p-values for Specificity (0.00001) indicate a highly significant improvement in correctly identifying non-bankrupt firms, which is critical in bankruptcy prediction for reducing false alarms and avoiding unnecessary financial decisions. Similarly, the significant improvements in Accuracy and G-mean confirm that the combined model maintains a robust balance between sensitivity and specificity, addressing the challenges posed by the imbalanced dataset. While some traditional resampling methods (SVM-SMOTE, SVM-ADASYN, SVM-Undersampling) and standard classifiers (Random Forest, KNN, Logistic Regression) improve certain metrics individually, the Fuzzy Shadowed-combined model consistently achieves statistically superior performance across all evaluated criteria.

These findings provide strong statistical evidence that the proposed combination strategy of fuzzy shadowed SVM variants effectively leverages complementary strengths of individual models, resulting in a more reliable and robust classifier for imbalanced bankruptcy datasets.

4.2.2. Wilcoxon Signed-Rank Test

The Wilcoxon signed-rank test evaluates whether the median difference between paired observations is zero. For each pair of observations $(x_i,y_i)$, the differences $d_i=x_i-y_i$ are computed and ranked according to their absolute values. The test statistic W is then calculated by summing the ranks of the positive differences:

$$W=\sum _{\{i:d_i>0\}}{R}_i$$

where $R_i$ denotes the rank of $|d_i|$ among all non-zero differences. A small p-value (typically <0.05) indicates a statistically significant difference between the models.

Results and Analysis

Table 5. Wilcoxon signed-rank test results ($\alpha =0.05$).

Metric	Comparison	p-Value	Significant
Accuracy	Combined vs. Fuzzy Shadowed-center	0.00098	Yes
Accuracy	Combined vs. Fuzzy Shadowed-sphere	0.00098	Yes
Accuracy	Combined vs. Fuzzy Shadowed-hyperplane	0.00098	Yes
Accuracy	Combined vs. DEC	0.00098	Yes
Accuracy	Combined vs. SVM-SMOTE	0.00098	Yes
Accuracy	Combined vs. SVM-ADASYN	0.00098	Yes
Accuracy	Combined vs. SVM-Undersampling	0.00098	Yes
Accuracy	Combined vs. Random Forest	0.00098	Yes
Accuracy	Combined vs. KNN	0.00098	Yes
Accuracy	Combined vs. Logistic Regression	0.00098	Yes
Specificity	Combined vs. Fuzzy Shadowed-center	0.00098	Yes
Specificity	Combined vs. Fuzzy Shadowed-sphere	0.00098	Yes
Specificity	Combined vs. Fuzzy Shadowed-hyperplane	0.00098	Yes
Specificity	Combined vs. DEC	0.00098	Yes
Specificity	Combined vs. SVM-SMOTE	0.00098	Yes
Specificity	Combined vs. SVM-ADASYN	0.00098	Yes
Specificity	Combined vs. SVM-Undersampling	0.00098	Yes
Specificity	Combined vs. Random Forest	0.00098	Yes
Specificity	Combined vs. KNN	0.00098	Yes
Specificity	Combined vs. Logistic Regression	0.00098	Yes
G-mean	Combined vs. Fuzzy Shadowed-center	0.00098	Yes
G-mean	Combined vs. Fuzzy Shadowed-sphere	0.00098	Yes
G-mean	Combined vs. Fuzzy Shadowed-hyperplane	0.00098	Yes
G-mean	Combined vs. DEC	0.00098	Yes
G-mean	Combined vs. SVM-SMOTE	0.00098	Yes
G-mean	Combined vs. SVM-ADASYN	0.00098	Yes
G-mean	Combined vs. SVM-Undersampling	0.00098	Yes
G-mean	Combined vs. Random Forest	0.00098	Yes
G-mean	Combined vs. KNN	0.00098	Yes
G-mean	Combined vs. Logistic Regression	0.00098	Yes

presents the results of the Wilcoxon signed-rank test performed to compare the Fuzzy Shadowed-combined SVM model with various baseline models across multiple performance metrics. All comparisons yielded statistically significant results ($p<0.05$), indicating that the Fuzzy Shadowed-combined model consistently outperforms its counterparts.

Interpretation

Table 5 presents the results of the Wilcoxon signed-rank test comparing the Fuzzy Shadowed-combined model against other variants and conventional classifiers, using a significance level of $\alpha =0.05$. The results show that the Fuzzy Shadowed-combined model significantly outperforms all other models across Accuracy, Specificity, and G-mean, with all p-values equal to 0.00098, which is well below the 0.05 threshold. This confirms the robustness and reliability of the proposed method in the context of imbalanced bankruptcy prediction datasets. Specifically, the significant improvement in Specificity and G-mean highlights that the combined model is particularly effective at correctly identifying the majority class while maintaining a balanced performance on the minority class. This is crucial in financial applications, where false positives (incorrectly predicting bankruptcy) can have substantial economic consequences. Overall, the Wilcoxon test provides strong non-parametric statistical evidence that the proposed combination strategy, aggregating center, sphere, and hyperplane Fuzzy Shadowed-SVMs, consistently achieves superior performance compared to both individual Fuzzy Shadowed variants and conventional SVM-based resampling approaches, as well as standard classifiers.

Statistical validation confirms that Fuzzy Shadowed-combined significantly outperforms all baselines ($p<0.01$), particularly in specificity and G-mean.

5. Conclusions

This study introduces a unified and modular framework, Fuzzy Shadowed SVM, which integrates fuzzy sets and shadowed sets to address the challenges of bankruptcy prediction on imbalanced financial datasets. Rather than eliminating uncertainty, the approach leverages ambiguity and structural granularity as informative dimensions for classification. The Fuzzy-Shadowed SVM demonstrates enhanced sensitivity to minority instances, improved robustness to noise, and increased interpretability grounded in economic semantics. Empirical results obtained on three real-world datasets confirm the superior performance of the Fuzzy-Shadowed SVM, with average improvements of $+22.7\%$ in F1-score, $-35.4\%$ in false negatives, and $+18.9\%$ in AUC-ROC compared to classical methods. By embedding granular cognition into the SVM paradigm, this research contributes to the development of resilient and transparent classifiers adapted to complex, uncertain, and asymmetrical financial environments. The proposed Fuzzy Shadowed SVM architecture provides a foundation for future extensions involving dynamic granularity learning, metaheuristic optimization, and integration with deep learning models. Nevertheless, some limitations should be acknowledged. First, the current framework has been validated on a limited number of datasets, which may constrain the generalizability of the results across different financial contexts or geographical regions. Second, the choice of membership function weights in the combined formulation, although effective, remains partly heuristic and could be further optimized through metaheuristics (e.g., Genetic algorithms, Particle Swarm Optimization, and Open Competency Optimization [44]) or data-driven strategies. Addressing these limitations constitutes a promising avenue for future research, alongside the integration of dynamic granularity mechanisms and hybrid architectures with deep learning.

Clarification on fuzzy logic characteristics. Finally, it is important to emphasize how the proposed framework differs from traditional fuzzy logic systems. Conventional fuzzy controllers typically rely on a large set of linguistic rules, which may slow down computation. In contrast, the Fuzzy Shadowed SVM does not employ a rule-based controller; instead, fuzzy membership degrees are directly embedded into the SVM optimization process and extended via shadowed sets into three regions (membership, non-membership, and uncertainty). This formulation preserves the interpretability of fuzzy reasoning while avoiding rule explosion, ensuring both efficiency and scalability in practical applications.