Sharp Front Approach Solutions to Some Doubly Degenerate Reaction-Diffusion Models

Abstract

Approximate analytical solutions to doubly degenerate reaction-diffusion models pertinent to population dynamics and chemical kinetics have been developed. The double integral-balance method applied to preliminary transformed models and by a direct integration approach has provided physically reasonable results. The model equation scaling has revealed the time and length scales, as well as the characteristic velocity of the process and the Fourier number as the controlling dimensionless group.

1. Introduction

1.1. Fisher–Kolmogorov–Petrovsky–Piskunov Models with Doubly Degenerate Diffusivities

This work addresses an approximate solution to a degenerate reaction–diffusion equation expressed in a general form as

$${\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{\partial u}{\partial x}}\left(D\left(u\right){\displaystyle \frac{\partial u}{\partial x}}\right)+f\left(u\right)$$

(1)

where the source term $f\left(u\right)$ relies on a general version of the Fisher–Kolmogorov–Petrovsky–Piskunov (Fisher-KPP) equation [1,2].

The functional relationship $D\left(u\right)$ could be a power-law $D\left(u\right)=D_0{u}^m$ [3,4] or a sum (or products) such as that considered here: $D\left(u\right)=\left(1-u\right)u^m$ [5] or $D\left(u\right)=\left(u+\epsilon u^2\right)$ [6]. Irrespective of the functional form of $D\left(u\right)$, the model (1) is a degenerate parabolic equation because $D\left(u\right)$ becomes zero at any point where $u=0$. This feature results in solutions propagating with finite speeds and sharp fronts [3,6,7], a fact used in the development of the solutions presented in this work.

For example, with $D\left(u\right)=\left(1-u\right)u^m$, the model (1) [5] (mentioned as Model 1) becomes

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{\partial u}{\partial x}}\left(\left(1-u\right)u^m{\displaystyle \frac{\partial u}{\partial x}}\right)+u\left(1-u\right)\Rightarrow \\ \hfill \Rightarrow {\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{\partial u}{\partial x}}\left(u^m{\displaystyle \frac{\partial u}{\partial x}}\right)-{\displaystyle \frac{\partial u}{\partial x}}\left(u^{m+1}{\displaystyle \frac{\partial u}{\partial x}}\right)+u-u^2\end{array}$$

(2)

and can be presented in an extended (decomposed) form with two degenerate diffusion terms that explain the terminology used.

Further, with $D\left(u\right)=\left(u+\epsilon u^2\right)$ [6], we also have an extended version with two degenerate diffusion terms (mentioned as Model 2), namely

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{\partial u}{\partial x}}\left[\left(u+\epsilon u^2\right){\displaystyle \frac{\partial u}{\partial x}}\right]+u\left(1-u\right)\Rightarrow \\ \hfill \Rightarrow {\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{\partial u}{\partial x}}\left(u{\displaystyle \frac{\partial u}{\partial x}}\right)+{\displaystyle \frac{\partial u}{\partial x}}\left(\epsilon u^2{\displaystyle \frac{\partial u}{\partial x}}\right)+u-u^2\end{array}$$

(3)

with $0\le \epsilon \ll 1$, $0\le u\left(x,t\right)\le 1$ and $0\le u_0\left(x\right)\le 1$

Note: In these two models, the original formulations are with $D_0=1$. We will comment on this problem further when $D_0$ is not neglected.

The extended versions, with decomposed diffusion terms and growth functions, will be very useful in the approximate solutions developed in this work.

The model (1) (precisely with the power-law diffusivity) has been used in numerous studies on reaction-diffusion problems related to population dynamics [8,9], combustion flame dynamics [9], thermal shock waves [10], and non-linear concentration-dependent diffusion mass transfer with absorption or reactions [11,12]). Its linear case, with $D=const$, was first published in Fisher’s seminal article [1] and by Kolmogorov et al. [2], also known as the Fisher–KPP equation. We especially mention the power-law diffusivity model because, as (2) and (3) demonstrate, this simple form of the diffusion function appears in their decomposed versions and affects the behavior of the entire solution, as we shall explain in the following.

We limit ourselves to references to a few fundamental research works mentioned above to provide an adequate basis for the findings developed in this article, as there is an extensive amount of literature devoted to many facets of this kind of model and its solutions that cannot be covered here.

Beginning with Fisher’s work [1] and continuing in numerous subsequent works [3,5,6,7,8,9,13,14,15] (commented on in the sequel of this article), the traveling wave approach is the standard method for solving the model (1) as a Cauchy problem. All these studies, and other studies copying their style, provide solutions that can be considered as a sum of two components: a traveling wave analysis where the variable is changed to $z=x-ct$, where $c>0$ is the traveling wave speed and a numerical solution. In the case of the linear Fisher–KPP equation, that is with $D\left(u\right)=D_0=1$ (this is a common approach in all articles mentioned above and a characteristic feature of all studies where pure mathematics without any physical analysis is applied), the solution, in terms of the variable $U\left(z\right)$ that should be solved, is

$${\displaystyle \frac{{\partial }^{2}U}{\partial z^2}}+c{\displaystyle \frac{\partial U}{\partial z}}+f\left(U\right),\infty <U\left(z\right)<\infty$$

(4)

satisfying the conditions: $U\left(z\right)<,1$ with $U(-\infty )=1$ and $U(+\infty )=0$. As it is well-known, this equation has only one exact solution [16] $c=5/\sqrt{6}\approx 2.04$

For example, in the case of Model 1, the traveling wave transform yields [5]

$$-c{\displaystyle \frac{dU}{dz}}={\displaystyle \frac{d}{dz}}\left((1-U)U^m{\displaystyle \frac{d}{dz}}\right)+U(1-U)$$

(5)

with boundary conditions $U(-\infty )=1$ and $U(+\infty )=0$. The standard approach to analyze (5) is to write it in the phase plane system, using

$$v=(1-U)U^{m-1}{\displaystyle \frac{dU}{dz}}$$

(6)

to obtain [5]

$${\displaystyle \frac{dU}{dz}}={\displaystyle \frac{v}{(1-U)U^{m-1}}}$$

(7)

$${\displaystyle \frac{dv}{dz}}=-{\displaystyle \frac{(c+v)v+U^m{(1-U)}^2}{U^m(1-U)}}$$

(8)

which a singular ordinary differential equation system. As a final step, the solution profile was obtained by the fourth-order Runge–Kutta method for increasing z, with step size control.

This is only an example of the main stream in solutions to the Fisher–KPP type equations, linear or degenerate. For problems where solutions to the equations do not have analytical solutions (exact or approximate), different solution techniques such as the method of monotone e solutions [17], Haar wavelets [18], the Sinc collocation method [19], series solutions [20], and self-similar solutions [21] have been applied.

Moreover, the solutions mentioned highlight two issues: the absence of scaling analysis and the physical interpretations of the results. The former problem comes from formulations such as (2) and (3), where the diffusion coefficients are missing (actually assumed as $D_0=1$ or avoided, which makes the model dimensionally inconsistent). These are the main deficiencies of the solutions mentioned above (and many others not cited here), resulting in, to a greater extent, hardly interpretable final results from a physical point of view.

This is the author’s standpoint, and the solutions developed in this article clarify it by applying scaling and definitions of characteristic time and length scales (Section 2) and approximate solutions (Section 3) where all these scales appear, allowing us to physically analyze the solution behaviors. The solutions developed use the concept of the sharp front approach that appears in the traveling wave solutions but apply an integral method utilizing the Barenblatt profile (the solution of the degenerate diffusion equation) since the requirements of a sharp front are automatically reached. Detailed remarks are particularly summed up in Section 3.2 and will be revealed as the solutions are developed. We will, however, discuss certain touching points with well-known traveling wave studies, whatever is allowed.

1.2. The Main Idea to Solve the Model at Issue

Using the idea of a finite penetration depth that evolves in time, and could be thought of as solutions with sharp fronts moving in time, in this study we depart from the traditional approach and explore approximate integral-balance solutions. These solutions’ fronts divide the medium in which the processes occur into two zones: an active (populated) zone and an inactive (unpopulated) zone (assuming, for simplicity’s sake, a one-dimensional semi-infinite space). For the sake of exposition clarity, the method—specifically, the approaches employed for its application—is explained in the Appendix (see Appendix A.1) and demonstrated through the solutions developed.

1.3. Aim

The main direction in this study is the development of approximate sharp front integral-balance solutions of the doubly degenerate Fisher–KPP models mentioned at the beginning. A primary step allowing this approach is the decomposition, down to a sum of power laws, of both the diffusivities and growth functions. Special attention is paid to the model scaling and the determination of the proper time and length characteristic scales and, consequently, the controlling dimensionless groups.

1.4. Further Text Organization

This study’s continuation is organized as follows: The full scaling of the models of interest is discussed in Section 2, which determines the characteristic time and length scales and the Fourier number as the governing dimensionless group. The integral-balance solutions are developed step-by-step in Section 3: Model 1 is covered in Section 3.1, while Model 2’s solution is developed in Section 3.3. Next, a generalized version of Model 2 is solved in Section 3.4. Section 3.2 is a crucial section wherein unique remarks are used to fine-tune the answers appearing through the solution development. This enables us to observe what they touch at certain points and moments using the traveling wave concept.

2. Completing the Scaling of the Incomplete Scaled Model

Before continuing toward solutions, we stress the importance of the complete scaling of the model equation. The general model (1)) as well as (2) and (3) are scaled only concerning $u\left(x,t\right)$, that is $0<u\left(x,t\right)=U\left(x,t\right)/U_{ref}<1$, while the spatial coordinate x and the time t are not scaled. The incomplete scaling versions appearing in many studies require a serious scale analysis (see Section 2) before further solutions are developed.

Let us rewrite (1) as

$${\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{\partial u}{\partial x}}\left(D_0\phi \left(u\right){\displaystyle \frac{\partial u}{\partial x}}\right)+G\varphi \left(u\right),D\left(u\right)=D_0\phi \left(u\right),f\left(u\right)=G\varphi \left(u\right)$$

(9)

We need complete scaling concerning the time and the spatial coordinates.

We especially introduced the diffusivity $D_0$ and the coefficient G, which in the model (9) have dimensions of m²s⁻¹ and s⁻¹, respectively, because the model should be dimensionally homogeneous. Very often, these two coefficients are accepted as equal to unity (or suppressed through rescaling) [3,5,6,8,9,13,14], as in (2) and (3), which certainly facilitates the calculations; however, this step does not mean that they lose their dimensions and physical meanings. We especially stress the importance of this because the solutions developed in the sequel need clear definitions of the time and length scales, a problem that we will resolve now and use its results further in the solution analysis.

Consider that the process has time and length scales $t_0$ and L, respectively. Introducing $\overline{t}=t/t_0$ and $\overline{x}=x/L$, we can transform (9) as

$${\displaystyle \frac{\partial u}{\partial \overline{t}}}=t_0{\displaystyle \frac{D_0}{L^2}}{\displaystyle \frac{\partial u}{\partial \overline{x}}}\left(\phi \left(u\right){\displaystyle \frac{\partial u}{\partial \overline{x}}}\right)+t_{0}Gu\left(1-u\right),m>0$$

(10)

Now, the model is dimensionless, and the term of the growth function immediately reveals that the factor G defines the time scale, namely $t_0=1/G$. Thus, the dimensionless time ratio $t/t_0$, defining the Fourier number, in terms of the model, is $Fo=Gt$. This allows us to define the length scale L as

$$t_0{\displaystyle \frac{D_0}{L^2}}={\displaystyle \frac{1}{G}}{\displaystyle \frac{D_0}{L^2}}\Rightarrow {\displaystyle \frac{1}{G}}{\displaystyle \frac{D_0}{L^2}}=1\Rightarrow L=\sqrt{{\displaystyle \frac{D_0}{G}}}$$

(11)

Further, we may rewrite a completely dimensionless model resembling, to some extent, (2) and (3), as

$${\displaystyle \frac{\partial u}{\partial Fo}}={\displaystyle \frac{\partial u}{\partial x}}\left(\phi \left(u\right){\displaystyle \frac{\partial u}{\partial x}}\right)+\varphi \left(u\right),m>0$$

(12)

and only in this case, the diffusivity and the factor of the growth function are equal to unity. Consequently, the two models considered here can be rewritten in dimensionless forms as

$${\displaystyle \frac{\partial u}{\partial Fo}}={\displaystyle \frac{\partial u}{\partial x}}\left(\left(1-u\right)u^m{\displaystyle \frac{\partial u}{\partial x}}\right)+u\left(1-u\right),m>0$$

(13)

and

$${\displaystyle \frac{\partial u}{\partial Fo}}={\displaystyle \frac{\partial u}{\partial x}}\left[u\left(1+\epsilon u^{m-1}\right){\displaystyle \frac{\partial u}{\partial x}}\right]+u\left(1-u\right),m>1$$

(14)

Last but not least, the product $DG$ (the linear case) has a dimension of m²s⁻², leading to a characteristic velocity of $V_0=\sqrt{DG}$. This is also valid in the nonlinear case, where the velocity scale is defined by $\sqrt{D_{0}G}$. This is significant for the following examination of the results developed.

Remark 1 

(The task is for the model to be completely scaled). The above scaling analysis has only one task: the correct evaluation of the dimensionless groups controlling the diffusion process. Even though what follows will deal with the semi-scaled models (2) and (3), since this is imposed by the applied solution method, these dimensionless groups will appear in the final solutions, and we should be able to interpret them correctly.

Commonly, in the studies referred to above, starting from seminal works [1,2], there are initial changes of variables such as $\tau =Gt$, i.e., $\tau =t/\left(1/G\right)$ and $\overline{x}=x/\left(\sqrt{(D/G}\right)$, that finally lead to an equation without dimensional coefficients. It is strange to see that in all those referred studies, the problem concerning the definition of a characteristic velocity is not discussed; this is a common result when physical interpretations go astray due to focusing only on mathematical issues. It raises a question about the backward question: how to interpret the model solution physically?

3. Solutions

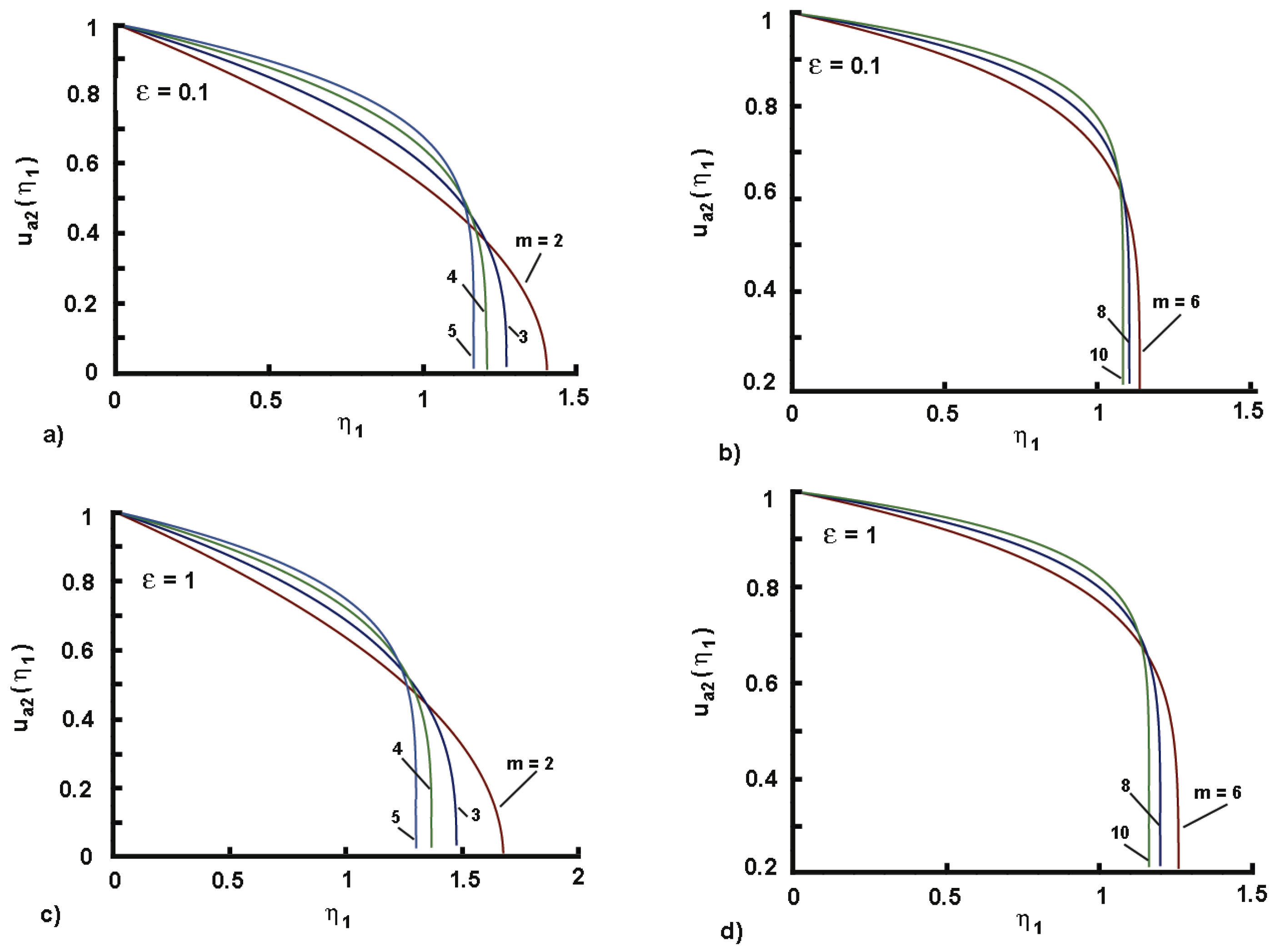
3.1. Model 1

Consider the semi-scaled and extended version of (2)

$${\displaystyle \frac{\partial u}{\partial t}}=D_0{\displaystyle \frac{\partial u}{\partial x}}\left(u^m{\displaystyle \frac{\partial u}{\partial x}}\right)-D_0{\displaystyle \frac{\partial u}{\partial x}}\left(u^{m+1}{\displaystyle \frac{\partial u}{\partial x}}\right)+G\left(u-u^2\right)$$

(15)

And as the first step, we need to transform the diffusion terms as

$${\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{D_0}{m+1}}{\displaystyle \frac{{\partial }^2{u}^{m+1}}{\partial x^2}}-{\displaystyle \frac{D_0}{m+2}}{\displaystyle \frac{{\partial }^2{u}^{m+2}}{\partial x^2}}+G\left(u-u^2\right)$$

(16)

Applying the double-integration technique to (16), the integral relation is

$$\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{\displaystyle \frac{\partial u}{\partial t}}dxdx=\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{\displaystyle \frac{D_0}{m+1}}{\displaystyle \frac{{\partial }^2{u}^{m+1}}{\partial x^2}}dxdx-\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{\displaystyle \frac{D_0}{m+2}}{\displaystyle \frac{{\partial }^2{u}^{m+2}}{\partial x^2}}dxdx+G\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}\left(u-u^2\right)dxdx$$

(17)

Then, with the Leibniz rule applied to the left side and integrating the diffusion terms on the right side, as well as taking into account the Goodman conditions (A4), we get

$${\displaystyle \frac{d}{dt}}\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}u\left(x,t\right)dxdx=D_0\left({\displaystyle \frac{{\left(u_s\right)}^{n\left(m+1\right)}}{m+1}}-{\displaystyle \frac{{\left(u_s\right)}^{n\left(m+2\right)}}{m+2}}\right)+G\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}\left(u-u^2\right)dxdx$$

(18)

The integral relation (18) physically means that the time variation of the density (concentration) in the domain is balanced by the input at the boundary ($x=0$ ) and the total (integral) generation of the local growth function. At this step, we assume $u_0=u\left(x,0\right)=0$; that is, we have an initially virgin medium. The sharp front separates the medium into two zones: $u\left(x,t\right)>0$ for $0\le x\le \delta \left(t\right)$, an undisturbed (still virgin) area, and $u\left(x,t\right)=0$ for $x\ge \delta \left(t\right)$.

The assumed Barenblatt profile (A5) [22,23] is

$$u_a=u_s{\left(1-x/\delta \right)}^n$$

(19)

where, for the Dirichlet boundary condition, we have $u_s=1$.

Replacing $u\left(x,t\right)$ by $u_a\left(x,\delta \right)$ in (18 and performing the integration, taking into account the Goodman conditions (A4) at the front $\delta$ ), the result is

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{\left(n+1\right)\left(n+2\right)}}{\displaystyle \frac{d{\delta }^2}{dt}}={\displaystyle \frac{D_0}{m+1}}{\left(u_s\right)}^{n\left(m+1\right)}-{\displaystyle \frac{D_0}{m+2}}{\left(u_s\right)}^{n\left(m+2\right)}+\\ \hfill +G\left[{\displaystyle \frac{{\delta }^2}{\left(n+1\right)\left(n+2\right)}}-{\displaystyle \frac{{\delta }^2}{\left(2n+1\right)\left(2n+2\right)}}\right]\end{array}$$

(20)

Rearranging (20), we get

$${\displaystyle \frac{d{\delta }^2}{dt}}=D_0{\displaystyle \frac{\left(n+1\right)\left(n+2\right)}{\left(m+1\right)\left(m+2\right)}}+G{\delta }^2\left[{\displaystyle \frac{3n}{4n+2}}\right]\Rightarrow {\displaystyle \frac{d{\delta }^2}{dt}}=A+B{\delta }^2$$

(21)

where

$$A=D_0\left({\displaystyle \frac{\left(n+1\right)\left(n+2\right)}{\left(m+1\right)\left(m+2\right)}}\right)=D_{0}N\left(n,m\right),B=G\left[{\displaystyle \frac{3n}{4n+2}}\right]=GM\left(n\right)$$

(22)

or as $A=D_{0}N(n,m)$ and $B=GM\left(n\right)$

Equation (22) is separable with a solution.

$${\delta }^2=C_1{e}^{Bt}-{\displaystyle \frac{A}{B}}$$

(23)

The initial condition $\delta \left(t=0\right)=0$ yields $C_1=A/B\equiv A/G\equiv D_0/G$ having a dimension m². Then, the penetration depth is

$$\begin{array}{c}\hfill \delta =\sqrt{{\displaystyle \frac{A}{B}}}\sqrt{e^{Bt}-1}\Rightarrow \delta =\sqrt{{\displaystyle \frac{D_0}{G}}}\sqrt{{\displaystyle \frac{N\left(n,m\right)}{M\left(n\right)}}}\sqrt{e^{MFo}-1}=\\ \hfill =\sqrt{{\displaystyle \frac{D_0}{G}}}\sqrt{K\left(n,m\right)}\sqrt{e^{MFo}-1},K\left(n,m\right)={\displaystyle \frac{N\left(n,m\right)}{M\left(n\right)}}\end{array}$$

(24)

, taking into account that the Fourier number is defined as $Fo=Gt$.

For $t\to 0_{+}$, we have $e^{MGt}\approx 1+MGt$. Taking into account that $A\equiv D_0$, $\delta \approx \sqrt{At}\equiv \sqrt{D_{0}t}$; we have a Gaussian diffusion with a front moving with the square-root law.

For a long time, when $e^{MGt}\gg 1$, the front dynamics follow an exponential law, namely

$$\delta \left(t\right)\approx \sqrt{{\displaystyle \frac{D_0}{G}}}\sqrt{K\left(n,m\right)}\sqrt{e^{MGt}}\equiv \sqrt{{\displaystyle \frac{D_0}{G}}}\sqrt{e^{MGt}}\equiv \sqrt{{\displaystyle \frac{D_0}{G}}}{e}^{\left(MG/2\right)t}$$

(25)

Bearing in mind that the factor $A\equiv D_0$ has a dimension of m²s⁻¹, the rate constant of the growing penetration depth is $G/2$. The ratio $A/G\equiv D_0/G$ with a dimension of m² defines a factor $\sqrt{A/G}$ with a dimension of length; that confirms the physical adequacy of the relationship (25).

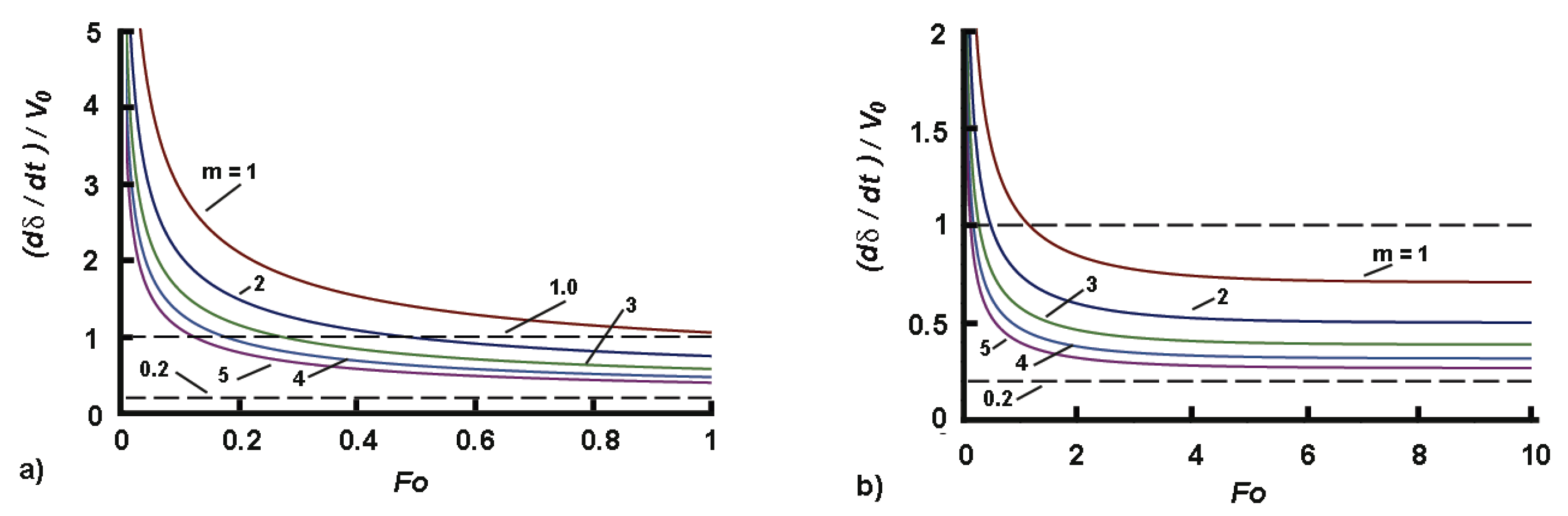
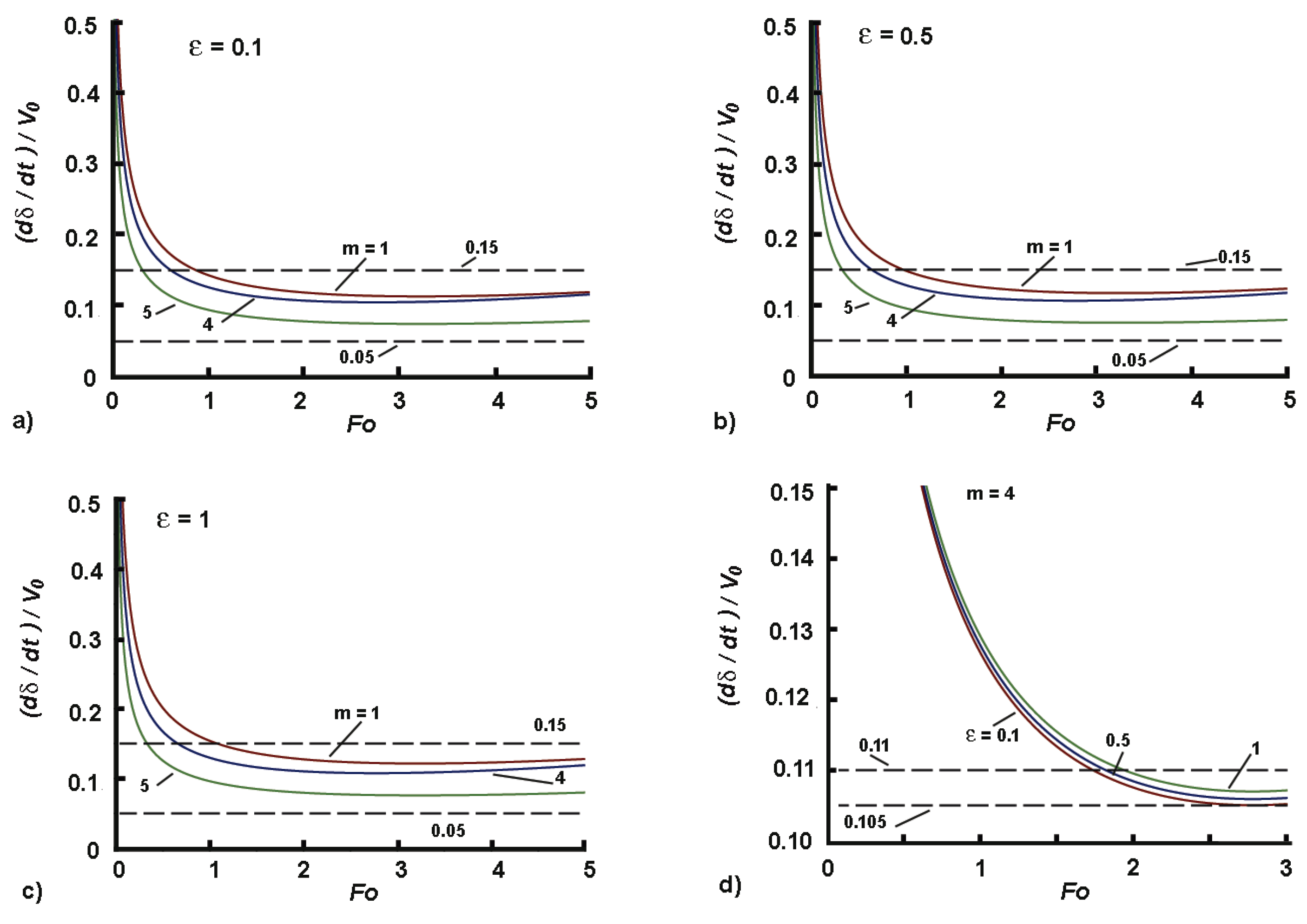
3.1.1. The Front Speed

The speed of the front $d\delta \left(t\right)/dt$ is

$${\displaystyle \frac{d\delta \left(t\right)}{dt}}={\displaystyle \frac{d}{dt}}\left(\sqrt{{\displaystyle \frac{A}{B}}}\sqrt{e^{Bt}-1}\right)=\sqrt{AB}{\displaystyle \frac{e^{Bt}}{2\sqrt{e^{Bt}-1}}}$$

(26)

Hence, for $t_{0+}$, we have ${\displaystyle \frac{d\delta \left(t\right)}{dt}}\to \infty$, a fact well known from the integral-balance solutions of diffusion models [22]. Further, for $e^{Bt}\gg 1$, from (26), the speed can be approximated as ${\displaystyle \frac{d\delta \left(t\right)}{dt}}\approx \sqrt{AB}\sqrt{e^{Bt}}$, and we have an exponential growth of the front.

In detail, because $A\equiv D_0$ and $B\equiv G$ we get from (26), paraphrasing the above relationships, that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d\delta \left(t\right)}{dt}}=\sqrt{AB}{\displaystyle \frac{e^{Bt}}{2\sqrt{e^{Bt}-1}}}={\displaystyle \frac{\sqrt{D_{0}G}}{2}}M\left(n\right)\sqrt{K(n,m)}{\displaystyle \frac{e^{MFo}}{\sqrt{e^{MFo}-1}}}=\hfill \\ \hfill & ={\displaystyle \frac{V_0}{2}}\sqrt{N(n,m)M\left(n\right)}{\displaystyle \frac{e^{MFo}}{\sqrt{e^{MFo}-1}}}\hfill \end{array}$$

(27)

Thus, the characteristic velocity $V_0$ naturally appears in the expression of the front speed. The scaled front speed is shown in Figure 1.

Moreover, from the solution above, we have $A=D_0{\displaystyle \frac{\left(n+1\right)\left(n+2\right)}{\left(m+1\right)\left(m+2\right)}}\equiv {\displaystyle \frac{D_0}{\left(m+1\right)\left(m+2\right)}}$ and then $\sqrt{D_{0}G}\equiv {\displaystyle \frac{V_0}{2}}{\displaystyle \frac{1}{\sqrt{\left(m+1\right)\left(m+2\right)}}}$. Thus, the increase in m (the increase in the model degeneracy) not only reduces the penetration depth (the distance from the boundary to the front) but also reduces the front speed. This behavior is shown in Figure 1.

Remark 2 

(The profile exponent). In all numerical simulations in the sequel of this study, the exponent of the assumed parabolic profile was taken as $n=1/m$. This comes from the solutions in [10,23,24], and more details are available in Section 3.2.

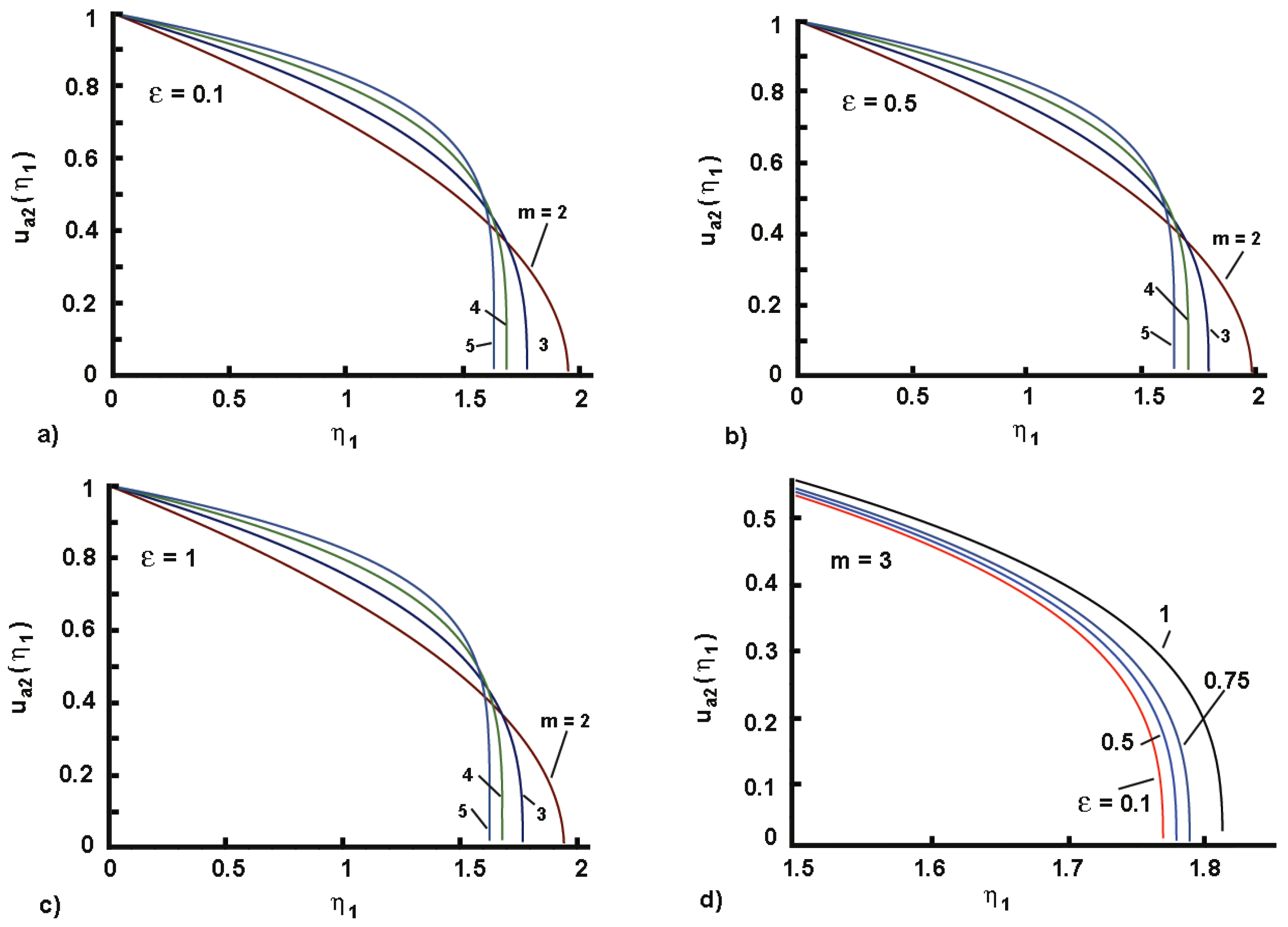
3.1.2. The Approximate Profile

Now, the approximate solution can be expressed as

$$u_{a-1}={\left(1-{\displaystyle \frac{x}{\sqrt{\frac{D_0}{G}}\sqrt{K\left(n,m\right)}\sqrt{e^{MGt}-1}}}\right)}^n$$

(28)

In (28), we can define a dimensionless variable $z=x/\sqrt{D_0/G}$ because $\sqrt{D_0/G}$ is the characteristic length scale. Moreover, the product $Gt=Fo$ defines the Fourier number. This allows the profile to be simply written as

$$u_{a-1}={\left(1-{\displaystyle \frac{z}{\sqrt{K\left(n,m\right)}\sqrt{e^{MFo}-1}}}\right)}^n$$

(29)

For $z=\sqrt{K\left(n,m\right)}\sqrt{e^{MFo}-1}$, we define the front of the penetration depth where $u_a=0$. The approximate profile expressed through the dimensionless spatial variable z at various time intervals (represented by the Fourier number $Fo$) is shown in Figure 2. Furthermore, since the ratio $z/\left(K\left(n,m\right)\sqrt{e^{MFo}-1}\right)$ is dimensionless, the profile can be simply expressed as

$$\begin{array}{cc}\hfill & u_a={\left(1-X\right)}^n,X={\displaystyle \frac{x}{\delta }}={\displaystyle \frac{x}{\sqrt{\frac{D_0}{G}}\sqrt{K\left(n,m\right)}\sqrt{e^{MFo}-1}}}=\hfill \\ \hfill & ={\displaystyle \frac{z}{\sqrt{K\left(n,m\right)}\sqrt{e^{MFo}-1}}},0\le X\le 1\hfill \end{array}$$

(30)

It is also possible to define an alternative similarity variable ${\eta }_1$ as

$${\eta }_1={\displaystyle \frac{x}{\sqrt{\frac{D_0}{G}}\sqrt{e^{MGFo}-1}}}$$

(31)

Then, the approximate solution can be presented as

$$u_{a1}={\left(1-{\displaystyle \frac{{\eta }_1}{\sqrt{K\left(n,m\right)}}}\right)}^n$$

(32)

From (32), the front is defined by ${{\eta }_1}_{\left(front\right)}=\sqrt{K\left(n,m\right)}$. The solution (32 ) as a function of the similarity variable ${\eta }_1$ is shown in Figure 3 and we can see the effect of the degeneracy exponent m on the front length and profile evolution.

Remark 3. 

Concerning the result (26), we have to mention that it differs from the concept of the traveling wave solution, where the change of variable $z=x-ct$ stipulates the wave velocity c as a constant. However, if we suggest that $c=c\left(t\right)$ is time-dependent, then we would have $z=x-c\left(t\right)$, and the result of the change of variables in the governing diffusion-reaction equation would be quite different from that commonly solved. This is beyond the scope of this work, and this remark only clarifies the difference in the used solution concepts. But some comments concerning the present solution and the traveling wave approach are summarized in the next Section 3.2; see the note:The boundary conditions applied.

3.2. Some Important Notes Concerning the Used Barenblatt Profile

Before continuing to the other models of interest, we have to stress some important points forming the solution background, namely

• Barenblatt-Profile: The profile (19) [23] originates from the similarity solution of Zel’dovich and Kompanetz [24] (see also [10] ) and is sometimes called the Barenblat–Pattle profile (as used in the point source solution of Pattle [25]. It was extensively explored in solutions of high-order non-linear diffusions [26,27] with exponent $n=1/m$ (this was confirmed independently in [22] applying optimization of the solution concerning the value of n because the boundary conditions are not enough to define it at the solution beginning [28].
• Barenblatt-Profile (additional comments): To some extent, the sharp front solution with the Barenblatt profile (19) could be related to the so-called type I sharp front traveling waves [4]. In this specific case, the traveling wave variable $z=x-ct$ tends to some finite value $z_{maz}\le \infty$ as $u=0$, and the asymptotic solution is $u\left(z\right)\propto {\left(kc\right)}^{1/m}{(z_{maz}-z)}^{1/m}$ that can simply be presented as $u\left(z\right)\equiv {(1-z/z_{maz})}^{1/m}$, i.e., a construction resembling the Barenblatt profile, where $z_{maz}$ defines the penetration front.
  Furthermore, there is a traveling wave solution local to the moving front [21], precisely to the left side where $x\to \delta$, in the form $u(x,t)\propto {(x-l\left(t\right))}^{\alpha }$ (in terms of [21]) that can be presented as $u\propto {(x-l\left(t\right))}^{1/m}$ and can simply be presented, following the style of this work, as $u\propto {(1-x/l\left(t\right))}^{1/m}$ or, in terms of [21]), as $u\propto {(1-\mu )}^{1/m}$, such that $\mu =x/l\left(t\right)\in [0,1]$ and $u\in [0,1]$; this is a wave driven mainly by the diffusion process with a little effect from the growth term. For a detailed analysis with many possible situations concerning the model 1, and touching on some points of the results developed here, see [29,30].
  To clarify some elements of the present solutions, we have to mention that traveling waves in population dynamics and combustion theory appear as invasion fronts and combustion fronts, respectively [31], corresponding to the propagation of the penetration depth $\delta \left(t\right)$ in the integral-balance method.
• The boundary conditions applied: Boundary-like conditions, $u\left(z\right)\to 1$ for $z\to -\infty$ and $u\left(z\right)\to 0$ for $z\to +\infty$, are used in the traveling wave solutions. To a certain degree, the former condition simplifies the solution mathematically, allowing a Dirichlet condition at $x=0$; that is, only the positive axis is taken into consideration. The Goodman sharp front conditions [32,33] logically replace the second condition when using the integral-balance approach, i.e., $du(x=\delta )/dx=u(x=\delta )=0$ (see Equation (A4)).
  To clarify the above standpoint, if an exact solution $u_e\left(x,t\right)$ coming from the traveling wave approach exists, with boundary conditions ${u_e}_{\left(x\to -\infty \right)}=1$, ${u_e}_{\left(x\to +\infty \right)}=0$, then we may construct the function $V_e\left(x,t\right)=1-u_e\left(x,t\right)$; we consequently get ${V_e}_{\left(x\to -\infty \right)}=0$ and ${V_e}_{\left(x\to +\infty \right)}=1$. Similarly, with the function $V_a\left(x,t\right)=1-u_a\left(x,t\right)$, we have ${V_a}_{\left(x\to -\infty \right)}=0.$ and ${V_a}_{\left(x\to +\infty \right)}=1$. However, in the assumed Barenblatt profile, we have $u_a\left(x=0\right)=1$, while $u_a\left(x=\delta \right)\approx u_a\left(x\to \infty \right)$.
  With the Barenblatt parabolic profile, the condition ${u_e}_{\left(x\to -\infty \right)}=1\Rightarrow {V_e}_{\left(x\to -\infty \right)}=0$ is replaced by ${u_a}_{\left(x=0\right)}=1$, as well as ${u_e}_{\left(x\to +\infty \right)}=0\Rightarrow {V_e}_{\left(x\to +\infty \right)}=1$, which is replaced by ${u_a}_{\left(x=\delta \right)}=0\Rightarrow {V_a}_{\left(x=\delta \right)}=1$. In this context, we must emphasize that the range of the approximate solution based on the parabolic profile is $0\le X\le 1$, that is, $0\le x\le \delta$ instead of $-\infty \le x\le +\infty$. At the end of this comment, $u_a$ models the density (concentration) profile, while $V_a$, to some extent, corresponds to a traveling pulse attaining unity at $x=\delta$, instead of $x=+\infty$.
• The sharp front conditions: In [7], it was shown that a traveling wave with a sharp front should be distinct. This indicates that there is a discontinuous derivative at the front (since $du/dz=du/dx$, we will use $du/dx$ in light of the Barenblatt profile): the left derivative, $du/dx\left({\delta }^{-}\right)eq0$, while the right derivative tends to zero, i.e., $du/dx\left({\delta }^{+}\right)=0$ (refer to the analysis of the wave shapes about Figure 2.1 in [7]). It is simple to verify that the Barenblatt profile ${\left(1-x/\delta \right)}^n$ complies with these criteria at the front; in fact, the Goodman boundary requirements (A4) implicitly provide the second criterion regarding the right derivative.

3.3. Model 2

The model of Sanches-Garduno and Maini [6] (3) for the sake of the coherency of the developed solutions can be represented in a more general form as

$${\displaystyle \frac{\partial u}{\partial t}}=D_0{\displaystyle \frac{\partial u}{\partial x}}\left[u\left(1+\epsilon u^{m-1}\right){\displaystyle \frac{\partial u}{\partial x}}\right]+Gu\left(1-u\right),m\ge 2$$

(33)

with $0\le \epsilon \ll 1$, $0\le u\left(x,t\right)\le 1$, and $u_0\left(x,0\right)=0$. As it follows (3), we have $m=2$ such that $u\left(1+\epsilon u\right)=u+\epsilon u^2$.

Now, performing scaling of (33), which is similar to what was carried out earlier, we get a time scale $t_0=1/G$ and a length scale $L=\sqrt{D_0/G}$ because both equations (3) and (33), (respectively (2 ) ) generally have equal structures.

As the first step, let us rearrange (33 ) as

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial u}{\partial t}}=D_0{\displaystyle \frac{\partial u}{\partial x}}\left(u{\displaystyle \frac{\partial u}{\partial x}}\right)+D_0{\displaystyle \frac{\partial u}{\partial x}}\left(\epsilon u^{m-1}{\displaystyle \frac{\partial u}{\partial x}}\right)+Gu\left(1-u\right)\Rightarrow \hfill \\ \hfill & \Rightarrow {\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{D_0}{2}}{\displaystyle \frac{{\partial }^2{u}^2}{\partial x^2}}+\epsilon {\displaystyle \frac{D_0}{m}}{\displaystyle \frac{{\partial }^2{u}^m}{\partial x^2}}+Gu\left(1-u\right)\hfill \end{array}$$

(34)

Now, applying the double integration to the second form of (34),

$$\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{\displaystyle \frac{\partial u}{\partial t}}dxdx=\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{\displaystyle \frac{D_0}{2}}{\displaystyle \frac{{\partial }^2{u}^2}{\partial x^2}}dxdx+\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}\epsilon {\displaystyle \frac{D_0}{m}}{\displaystyle \frac{{\partial }^2{u}^m}{\partial x^2}}dxdx+\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}Gu\left(1-u\right)dxdx$$

(35)

With the Leibniz rule in the left-hand side and integrating the diffusion terms, applying the Goodman conditions, we get (denoting $u\left(x,0\right)=u_s=1$) ( i.e., a Dirichlet boundary condition)as well as with the assumed profile $u_a={\left(1-x/\delta \right)}^n$ replacing $u\left(x,t\right)$ in (35). The equation concerning $\delta \left(t\right)$ is

$${\displaystyle \frac{d{\delta }^2}{dt}}=D_0\left[(n+1)\left(n+2\right)+{\displaystyle \frac{\epsilon }{m}}{\displaystyle \frac{(n+1)\left(n+2\right)}{\left(mn+1\right)\left(mm+2\right)}}\right]+G{\delta }^2\left[1-{\displaystyle \frac{(n+1)\left(n+2\right)}{\left(2n+1\right)\left(2n+2\right)}}\right]$$

(36)

For $\epsilon =0$, the first term in (36) is the same in the linear Fisher model when the double integration is applied.

Rearrangement of (36) yields

$${\displaystyle \frac{d{\delta }^2}{dt}}=D_e(n+1)\left(n+2\right)+G{\delta }^2{\displaystyle \frac{3n}{4n+2}}b,D_e=D_0\left(1+{\displaystyle \frac{\epsilon }{m}}{\displaystyle \frac{1}{\left(mn+1\right)\left(mn+2\right)}}\right)=D_{0}F\left(\epsilon ,m\right)$$

(37)

, where $D_e$ is an effective diffusivity having the same dimension as $D_0$ because the term in the brackets is dimensionless.

In a more compact form, we have

$${\displaystyle \frac{d{\delta }^2}{dt}}=A+B{\delta }^2,A=D_e\left(n+1\right)\left(n+2\right)=D_{e}N\left(n\right),B=G\left({\displaystyle \frac{3n}{4n+2}}\right)=GM\left(n\right)$$

(38)

with $N\left(n\right)=\left(n+1\right)\left(n+1\right)$ and $M\left(n\right)={\displaystyle \frac{3n}{4n+2}}$

This is the same equation as (21) with a solution

$$\begin{array}{cc}\hfill & \delta \left(t\right)=\sqrt{{\displaystyle \frac{A}{B}}}\sqrt{e^{Bt}-1}\Rightarrow \sqrt{{\displaystyle \frac{D_e}{G}}}\sqrt{\left(n+1\right)\left(n+2\right)}\sqrt{e^{M\left(n\right)Gt}-1}=\sqrt{{\displaystyle \frac{D_e}{G}}}\sqrt{N\left(n\right)}\sqrt{e^{M\left(n\right)Fo}-1},\hfill \\ \hfill & N\left(n\right)=\left(n+1\right)\left(n+2\right),M\left(n\right)={\displaystyle \frac{\left(4n+2\right)}{3n}}\hfill \end{array}$$

(39)

Shifting from $D_e$ to $D_0$, we have

$$\delta \left(t\right)=\sqrt{{\displaystyle \frac{D_0}{G}}}\sqrt{F\left(\epsilon ,m\right)}\sqrt{N\left(n\right)}\sqrt{e^{M\left(n\right)Fo}-1}$$

(40)

As mentioned in (33), the model of Sanchez-Garduno and Maini corresponds to the case $m=2$, and then $F\left(\epsilon ,m\right)=\left(1+{\displaystyle \frac{\epsilon }{2}}{\displaystyle \frac{1}{\left(2n+1\right)\left(2n+2\right)}}\right)$. With $n=1/m=1/2$, as mentioned in (33), the model of Sanchez-Garduno and Maini corresponds to the case $m=2$, and then $F\left(\epsilon ,m\right)=\left(1+{\displaystyle \frac{\epsilon }{2}}{\displaystyle \frac{1}{\left(2n+1\right)\left(2n+2\right)}}\right)$. With $n=1/m=1/2$, for instance, we have $F\left(\epsilon ,m\right)=1+ϵ/24$.

3.3.1. The Speed of the Profile

From (40), we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d\delta \left(t\right)}{dt}}=\sqrt{{\displaystyle \frac{D_0}{G}}}\sqrt{F(\epsilon ,m)}\sqrt{N\left(n\right)}{\displaystyle \frac{B{e}^{Bt}}{2\sqrt{e^{Bt}-1}}}={\displaystyle \frac{\sqrt{D_{0}G}}{2}}M\left(n\right)\sqrt{F(\epsilon ,m)}\sqrt{N\left(n\right)}{\displaystyle \frac{e^{M\left(n\right)Fo}}{\sqrt{e^{M\left(n\right)Fo}-1}}}=\hfill \\ \hfill & ={\displaystyle \frac{V_0}{2}}M\left(n\right)\sqrt{F(\epsilon ,m)}\sqrt{N\left(n\right)}{\displaystyle \frac{e^{M\left(n\right)Fo}}{\sqrt{e^{M\left(n\right)Fo}-1}}}\hfill \end{array}$$

(41)

For $e^{M\left(n\right)Fo}$ approximated as $e^{M\left(n\right)Fo}\approx 1+M\left(n\right)Fo$, in the denominator of (41), i.e., when $e^{M\left(n\right)Fo}\ll 1$, we have

$${\displaystyle \frac{d\delta \left(t\right)}{dt}}\approx {\displaystyle \frac{V_0}{2}}\sqrt{M\left(n\right)}\sqrt{F(\epsilon ,m)}\sqrt{N\left(n\right)}{\displaystyle \frac{e^{M\left(n\right)Fo}}{\sqrt{Fo}}}$$

(42)

From (41) (as well as from (42)), we see that there is an infinite speed for $t_{0^{+}}$. For $e^{M\left(n\right)Fo}\gg 1$, mainly for a long time, we have

$${\displaystyle \frac{d\delta \left(t\right)}{dt}}\approx {\displaystyle \frac{V_0}{2}}\sqrt{F\left(\epsilon ,m\right)}\sqrt{N\left(n\right)}M\left(n\right)e^{M\left(n\right)Fo/2}\equiv {\displaystyle \frac{V_0}{2}}\sqrt{F\left(\epsilon ,m\right)}{e}^{M\left(n\right)Fo/2}$$

(43)

For $t\to \infty$, practically for $Fo\ge 10$, the front asymptotically attains its final speed. The scaled (dimensionless) front speed is

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d\delta \left(t\right)}{dt}}/V_0={\displaystyle \frac{M\left(n\right)\sqrt{F(\epsilon ,m)}\sqrt{N\left(n\right)}}{2}}{\displaystyle \frac{e^{M\left(n\right)Fo}}{\sqrt{e^{M\left(n\right)Fo}-1}}}\Rightarrow Fo\to \infty \hfill \\ \hfill & \Rightarrow {\displaystyle \frac{d\delta \left(t\right)}{dt}}/V_0={\displaystyle \frac{M\left(n\right)\sqrt{F(\epsilon ,m)}\sqrt{N\left(n\right)}}{2}}\hfill \end{array}$$

(44)

because the limit of the time-dependent term of (44) for $t\to \infty$ is unity.

We can see from the plots in Figure 4 that there are no visually distinguishable effects of $ϵ$ on the final front speed (see panels a), b), and c)). This standpoint is in agreement with plots (panel d). Moreover, the $3D$ plot of $F(ϵ,m)$ in Figure 5 reveals that the range of variations of this term is too narrow to have a serious effect on the penetration depth, the front speed, and its final (asymptotic) value.

3.3.2. Approximate Solution

Moreover, because $B=D_{0}F(\epsilon ,m)N\left(n\right)$ and $Bt=M\left(n\right)Gt=M\left(n\right)Fo$, the approximate solution is

$$u_{a2}={\left(1-{\displaystyle \frac{x}{\sqrt{\frac{D_0}{G}}\sqrt{F\left(\epsilon ,m\right)}\sqrt{N\left(n\right)}\sqrt{e^{MFo}-1}}}\right)}^n$$

(45)

Defining the dimensionless distance $z={\displaystyle \frac{x}{\sqrt{D_0/G}}}$, as well as $X=x/\delta \left(t\right)$ we have

$$\begin{array}{cc}\hfill & u_{a2}={\left(1-{\displaystyle \frac{z}{\sqrt{F\left(\epsilon ,m\right)}\sqrt{N\left(n\right)}\sqrt{e^{M\left(n\right)Fo}-1}}}\right)}^n={\left(1-X\right)}^n,\hfill \\ \hfill & X={\displaystyle \frac{z}{\sqrt{F\left(\epsilon ,m\right)}\sqrt{N\left(n\right)}\sqrt{e^{M\left(n\right)Fo}-1}}}\hfill \end{array}$$

(46)

Furthermore, as in the case of Model 1, we may extract from the solution the similarity variable ${\eta }_1={\displaystyle \frac{x}{\sqrt{\frac{D_0}{G}}\sqrt{e^{MFo}-1}}}$ and express the approximate solution as

$$u_{a2}=1-{\displaystyle \frac{{\eta }_1}{\sqrt{F(\epsilon ,m)N\left(n\right)}}}$$

(47)

with front defined by ${{\eta }_1}_{\left(front\right)}=\sqrt{F\left(\epsilon ,m\right)}\sqrt{N\left(n\right)}$.

The plots of the approximate solution with simultaneous effects of $\epsilon$ and m are shown in Figure 6. It is hard to see a strong effect of $\epsilon$ in all panels. Looking especially at panel d), we can see a weak effect of $\epsilon$ on the profiles near the front.

3.4. A More General Version of Model 2

Consider a general version of Model 2, i.e., Equation (3), expressed as

$${\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{\partial u}{\partial x}}\left[D_{0}u\left(1+\epsilon u^m\right){\displaystyle \frac{\partial u}{\partial x}}\right]+Gu\left(1-u\right),m\ge 1$$

(48)

and its extended form (regarding the decomposed and then transformed diffusion term) as

$${\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{D_0}{2}}{\displaystyle \frac{{\partial }^2{u}^2}{\partial x^2}}+\epsilon {\displaystyle \frac{D_0}{m+2}}{\displaystyle \frac{{\partial }^2{u}^{m+2}}{\partial x^2}}+Gu\left(1-u\right)$$

(49)

Applying the double integration and mutadis mutandis, we get

$$\begin{array}{c}\hfill {\displaystyle \frac{d{\delta }^2}{dt}}=D_0\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{\epsilon }{m+2}}\right)\left(n+1\right)\left(n+2\right)+G{\delta }^2\left({\displaystyle \frac{3n}{4n+2}}\right)=\\ \hfill =D_e\left(n+1\right)\left(n+2\right)+G{\delta }^2\left({\displaystyle \frac{3n}{4n+2}}\right)A+B{\delta }^2\end{array}$$

(50)

$$\begin{array}{cc}\hfill & A=D_0\left({\displaystyle \frac{m+2\left(1+\epsilon \right)}{2\left(m+2\right)}}\right)\left(n+1\right)\left(n+2\right)=D_e\left(n+1\right)\left(n+2\right),\hfill \\ \hfill & B={\displaystyle \frac{3n}{4n+2}},D_e=D_0{F}_1(\epsilon ,m),F_1(\epsilon ,m)=\left({\displaystyle \frac{m+2\left(1+\epsilon \right)}{2\left(m+2\right)}}\right)\hfill \end{array}$$

(51)

Because $\epsilon \ll 1$, as defined in [6], we may easily see that $A\to \left(D_0/2\right)\left(n+1\right)\left(n+2\right)$. That is, for small $\epsilon$, we may expect a little effect of m. The same behavior can be observed for high values of m when we can accept that $m\gg 2\left(1+\epsilon \right)$ (see, as examples, the plots of the solution profiles in Figure 7.

Equation (50) is the same as (39), with a solution

$$\begin{array}{cc}\hfill & \delta \left(t\right)=\sqrt{{\displaystyle \frac{A}{B}}}\sqrt{e^{Bt}-1}\Rightarrow =\sqrt{{\displaystyle \frac{D_0}{G}}}\sqrt{N\left(n\right)}\sqrt{F_1(\epsilon ,m)}\sqrt{e^{M\left(n\right)t}-1},\hfill \\ \hfill & N\left(n\right)=(n+1)(n+2),M\left(n\right)={\displaystyle \frac{3n}{4n+2}}\hfill \end{array}$$

(52)

Thus, all relations about the front speed established earlier are valid here too, taking into account only the differences in the numerical terms.

Therefore, the approximate solution is

$$\begin{array}{cc}\hfill & u_a={\left(1-{\displaystyle \frac{x}{\sqrt{\frac{D_0}{G}}\sqrt{F_1(\epsilon ,m)}\sqrt{N\left(n\right)}\sqrt{e^{Bt}-1}}}\right)}^n={\left(1-{\displaystyle \frac{z}{\sqrt{N\left(n\right)}\sqrt{e^{MGt}-1}}}\right)}^n=\hfill \\ \hfill & ={\left(1-{\displaystyle \frac{z}{\sqrt{N\left(n\right)}\sqrt{F_1(\epsilon ,m)}\sqrt{e^{M\left(n\right)Fo}-1}}}\right)}^n={\left(1-X\right)}^n\hfill \end{array}$$

(53)

with

$$z={\displaystyle \frac{x}{\sqrt{\frac{D_e}{G}}}}={\displaystyle \frac{x}{\sqrt{\frac{D_0}{G}}\sqrt{\left(\frac{m+2\left(1+\epsilon \right)}{2\left(m+2\right)}\right)}}},X={\displaystyle \frac{x}{\sqrt{\frac{D_0}{G}}\sqrt{\left(\frac{m+2\left(1+\epsilon \right)}{2\left(m+2\right)}\right)}\sqrt{N\left(n\right)}\sqrt{e^{MFo}-1}}}$$

(54)

For $m=2$, we recover (45).

We can also extract the similarity variable ${\eta }_1={\displaystyle \frac{x}{\sqrt{\frac{D_0}{G}}\sqrt{e^{MFo}-1}}}$, thus expressing the solution as

$$u_a={\left(1-{\displaystyle \frac{{\eta }_1}{\sqrt{\left(\frac{m+2\left(1+\epsilon \right)}{2\left(m+2\right)}\right)}\sqrt{N\left(n\right)}}}\right)}^n$$

(55)

with a front defined by ${\eta }_{1\left(front\right)}=\sqrt{\left({\displaystyle \frac{m+2\left(1+\epsilon \right)}{2\left(m+2\right)}}\right)}\sqrt{N\left(n\right)}$.

We can see that at high values of the exponent m, the effect of $\epsilon$ is negligible if we are in the range $0<\epsilon <1$. The situation when $\epsilon$ could be considered outside this restrictive range envisages problems to be resolved, but it is beyond the scope of this work.

3.5. Additional Notes Concerning More Complex Growth Functions

Here we only stress the attention to some cases when the growth function is more complex than the classical Fisher formulation $u(1-u)$ and that the results of the double-integration technique do not change the main equation concerning the penetration front $\delta \left(t\right)$. To demonstrate the result of the integral solution, we consider some cases, among them:

3.5.1. A Modified Fisher’s (Newell–Whitehead–Segel) Growth Function

This is a slight modification of Fisher’s growth function [34,35], known from the Newell–Whitehead–Segel equation [36], namely

$$f_{NWS}\left(u\right)=Gu\left(1-u^k\right)=G\left(u-u^{k+1}\right)$$

(56)

The double integration, with an assumption of Dirichlet boundary condition at $x=0$ and a sharp front at $x=\delta$, yields

$$G\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{f}_{NWS}\left(u\right)=G{\delta }^2\left[{\displaystyle \frac{1}{\left(n+1\right)\left(n+2\right)}}-{\displaystyle \frac{1}{\left(n\left(k+1\right)+1\right)\left(n\left(k+1\right)+2\right)}}\right]=G{\delta }^2{\Phi }_{NWS}\left(n,k\right)$$

(57)

3.5.2. Zeldovich’s Growth Function

The Zeldovich growth function, in a general case, is defined as

$$f_Z\left(u\right)=G{u}^p\left(1-u^q\right)$$

(58)

and appears in [37,38] with $p=2$ and $q=1$, that is $f_Z{\left(u\right)}_{1,2}=u^2\left(1-u\right)$.

For this subsection, we will use (58), and then the double-integration provides

$$\begin{array}{cc}\hfill & G\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{f}_Z\left(u\right)dxdx=G\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}\left(u^p-u^{p+q}\right)dxdx=\hfill \\ \hfill & =G{\delta }^2\left({\displaystyle \frac{1}{\left(np+1\right)\left(np+2\right)}}-{\displaystyle \frac{1}{\left(n\left(p+q\right)+1\right)\left(n\left(p+q\right)+2\right)}}\right)=G{\delta }^2{\Phi }_Z\left(n,p,q\right)\hfill \end{array}$$

(59)

In the specific case with $p=2$ and $q=1$, we have

$${\Phi }_Z\left(n,2,1\right)=\left({\displaystyle \frac{1}{\left(2n+1\right)\left(2n+2\right)}}-{\displaystyle \frac{1}{\left(3n+1\right)\left(3n+2\right)}}\right)$$

(60)

3.5.3. Nagumo’s Growth Function-Version 1

In a general formulation, this growth function is [39,40]

$$f_{N1}\left(u\right)=Gu\left(1-u^k\right)\left(u^m-\alpha \right)=G\left(u^{m+1}-u^{m+k+1}-\alpha u+\alpha u^{k+1}\right)$$

(61)

The double integration, with an assumption of Dirichlet boundary condition at $x=0$ and a sharp front at $x=\delta$, yields

$$\begin{array}{cc}\hfill & G\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{f}_{N1}\left(u\right)=G{\delta }^2\left[\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\left(n\left(m+1\right)+1\right)\left(n\left(m+1\right)+2\right)}}-\hfill \\ \hfill & \\ \hfill & {\displaystyle \frac{1}{\left(n\left(m+k+1\right)+1\right)\left(n\left(m+k+1\right)+2\right)}}+\hfill \\ \hfill & \\ \hfill & +\alpha \left({\displaystyle \frac{1}{\left(n\left(k+1\right)+1\right)\left(n\left(k+1\right)+2\right)}}-{\displaystyle \frac{1}{\left(n+1\right)\left(n+2\right)}}\right)\hfill \end{array}\right]=\hfill \\ \hfill & =G{\delta }^2{\Phi }_{N1}\left(k,m,\alpha \right)\hfill \end{array}$$

(62)

Then, similarly to the previous calculations, we have

$${\displaystyle \frac{d{\delta }^2}{dt}}=A+B{\delta }^2$$

(63)

Thus, we have the same equation where the term A is a result of the integration of the diffusivity, while $B=G$ controls the rate of time evolution of $\delta \left(t\right)$, and there are no strong differences with the preceding examples. With all exponents (i.e., k and m stipulated), the parameter $\alpha$ allows controlling the rate factor of the front because $\delta \left(t\right)\equiv \sqrt{e^{Bt}}\equiv \sqrt{e^{{\Phi }_{N1}Gt}}\equiv \sqrt{e^{{\Phi }_{N1}\left(k,m,\alpha \right)Fo}}$.

3.5.4. Nagumo’s Growth Function-Version 2

Let us consider the simplest version of Nagumo’s growth function [39] with $k=m=1$ (a cubic polynomial) [41] and its extended (decomposed version)

$$f_{N2}\left(u\right)=Gu\left(1-u\right)\left(u-\alpha \right)=G\left(u^2-u^3-\alpha u+\alpha u^2\right),0<\alpha <1$$

(64)

The double integration, with an assumption of Dirichlet boundary condition at $x=0$ and a sharp front at $x=\delta$, yields

$$\begin{array}{cc}\hfill & G\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{f}_{N1}\left(u\right)dxdx=\hfill \\ \hfill & =G{\delta }^2\left[{\displaystyle \frac{1}{\left(2n+1\right)\left(2n+2\right)}}-{\displaystyle \frac{1}{\left(3n+1\right)\left(3n+2\right)}}-{\displaystyle \frac{\alpha }{\left(n+1\right)\left(n+2\right)}}+{\displaystyle \frac{\alpha }{\left(2n+1\right)\left(2n+2\right)}}\right]=\hfill \\ \hfill & =G{\delta }^2{\Phi }_{N2}\left(n,\alpha \right)\hfill \end{array}$$

(65)

or as in a more compact version

$$\begin{array}{cc}\hfill & \underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{f}_{N1}\left(u\right)dxdx=G{\delta }^2{\Phi }_{N2}\left(n,\alpha \right),\hfill \\ \hfill & {\Phi }_{N2}\left(n,\alpha \right)={\displaystyle \frac{\left(3n+1\right)\left(3n+2\right)-\left(2n+1\right)\left(2n+2\right)}{\left(2n+1\right)\left(2n+2\right)\left(3n+1\right)\left(3n+2\right)}}-\alpha {\displaystyle \frac{3n}{\left(n+2\right)\left(2n+1\right)\left(2n+2\right)}}\hfill \end{array}$$

(66)

Then, similarly to the previous calculations, we have a separable differential equation concerning $\delta \left(t\right)$, where the term A is a result of the integration of the diffusivity, while $B=G{\Phi }_{N2}\left(n,\alpha \right)$, and there are no strong differences from the preceding examples. We can see that the parameter $\alpha$ can control the magnitude of ${\Phi }_{N2}\left(n,\alpha \right)$ because $0<\alpha <1$. Consequently, taking into account that $Bt=Gt{\Phi }_{N2}\left(n,\alpha \right)=Fo{\Phi }_{N2}\left(n,\alpha \right)$, this will affect the rate constant of the growing in time front.

3.5.5. Nagumo’s Growth Function-Version 3

With $m=2$, the generalized version (61) becomes

$$f_{N3}\left(u\right)=u\left(1-u^2\right)\left(1-u^k\right)=u-u^{k+1}-u^2+u^{k+2}$$

(67)

The double integration results in

$$\begin{array}{cc}\hfill & G\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{f}_{N3}\left(u\right)dxdx=G{\delta }^2{\Phi }_{N3}\left(n,\alpha \right)\hfill \\ \hfill & {\Phi }_{N3}\left(n,\alpha \right)={\displaystyle \frac{1}{\left(n+1\right)\left(n+2\right)}}-{\displaystyle \frac{1}{\left(n\left(k+1\right)+1\right)\left(n\left(k+1\right)+2\right)}}-\hfill \\ \hfill & -{\displaystyle \frac{1}{\left(2n+1\right)\left(2n+2\right)}}+{\displaystyle \frac{1}{\left(n\left(k+2\right)+1\right)\left(n\left(k+2\right)+2\right)}}\hfill \end{array}$$

(68)

All consequent calculations are the same as those already demonstrated in the other examples.

Remark 4 

(On the complex growth functions). As we demonstrated with direct examples, the presentation (decomposition) of the complex growth functions as polynomials allows direct integrations to be easily performed. This result is a special feature of the Barenblatt profile, simply presented as $u={(1-z)}^n$, $0<z<1$. In case we have $u^k$, then k only multiplies the exponent n, namely $u^k={(1-z)}^{kn}$, without changes in the profile structure. The final result is a numerical factor controlling the rate of the front.

3.6. A Multi-Term Diffusivity: A Point View

The diffusivity functions in the solved and investigated models consist of two terms. Still, the solution performed and the preceding point concerning complex growth functions provoked the development of this section.

Let us suggest that the diffusivity, as a concentration (density) dependent function, can be expressed as

$$D\left(u\right)=D_{0}f\left(u\right)=D_0\sum _{i=1}^N{a}_1{u}^{m1}+a_2{u}^{m2}+a_3{u}^{m3}+\dots a_N{u}^{mN}$$

(69)

where the coefficients $a_i$ and the exponents $m_i>0$ can be obtained by data fitting of real data (there are such examples in [42].

Now, we will test the double-integration technique on the functional relationship (69). For the sake of simplicity, we take $N=3$. Thus, we get

$$\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}D\left(u\right)dxdx=\underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}{D}_0\left(a_1{u}^{m1}+a_2{u}^{m2}+a_3{u}^{m3}\right)dxdx$$

(70)

With the Barenblatt profile and taking into account the preceding results, we get

$$\begin{array}{cc}\hfill & \underset{0}{\overset{\delta }{\int }}\underset{x}{\overset{\delta }{\int }}D\left(u\right)dxdx=\hfill \\ \hfill & D_0\left[a_1{\displaystyle \frac{1}{\left(n{m}_1+1\right)\left(n{m}_1+2\right)}}+a_2{\displaystyle \frac{1}{\left(n{m}_2+1\right)\left(n{m}_2+2\right)}}+a_3{\displaystyle \frac{1}{\left(n{m}_3+1\right)\left(n{m}_3+2\right)}}\right]\hfill \end{array}$$

(71)

Then, getting the term $\left(n+1\right)\left(n+2\right)$ from the integration of the time-dependent term, we have

$$A_3=D_0\sum _{i=1}^3{a}_i{\displaystyle \frac{\left(n+1\right)\left(n+2\right)}{\left(n{m}_i+1\right)\left(n{m}_i+2\right)}}$$

(72)

and the equation about ${\delta }^3$ is (with a well-known solution)

$${\displaystyle \frac{d{\delta }^2}{dt}}=A_3+B{\delta }^2$$

(73)

where the term B depends on the type of growth function.

Therefore, the double-integration technique of the integral-balance method involving the Barenblatt profile applies to multi-term power-law functions modeling the diffusivity.

4. Outlines of the Main Results

• The work demonstrated the applicability of the integral-balance method (not using the traveling wave concept) to doubly degenerate diffusion-reaction equations where both the diffusivity and growth function contain terms of power-law type.
• With the Barenblatt parabolic profile, we have an adequate approach coming from well-known solutions of degenerate diffusion models, but it has never applied to the reaction-diffusion models considered here.
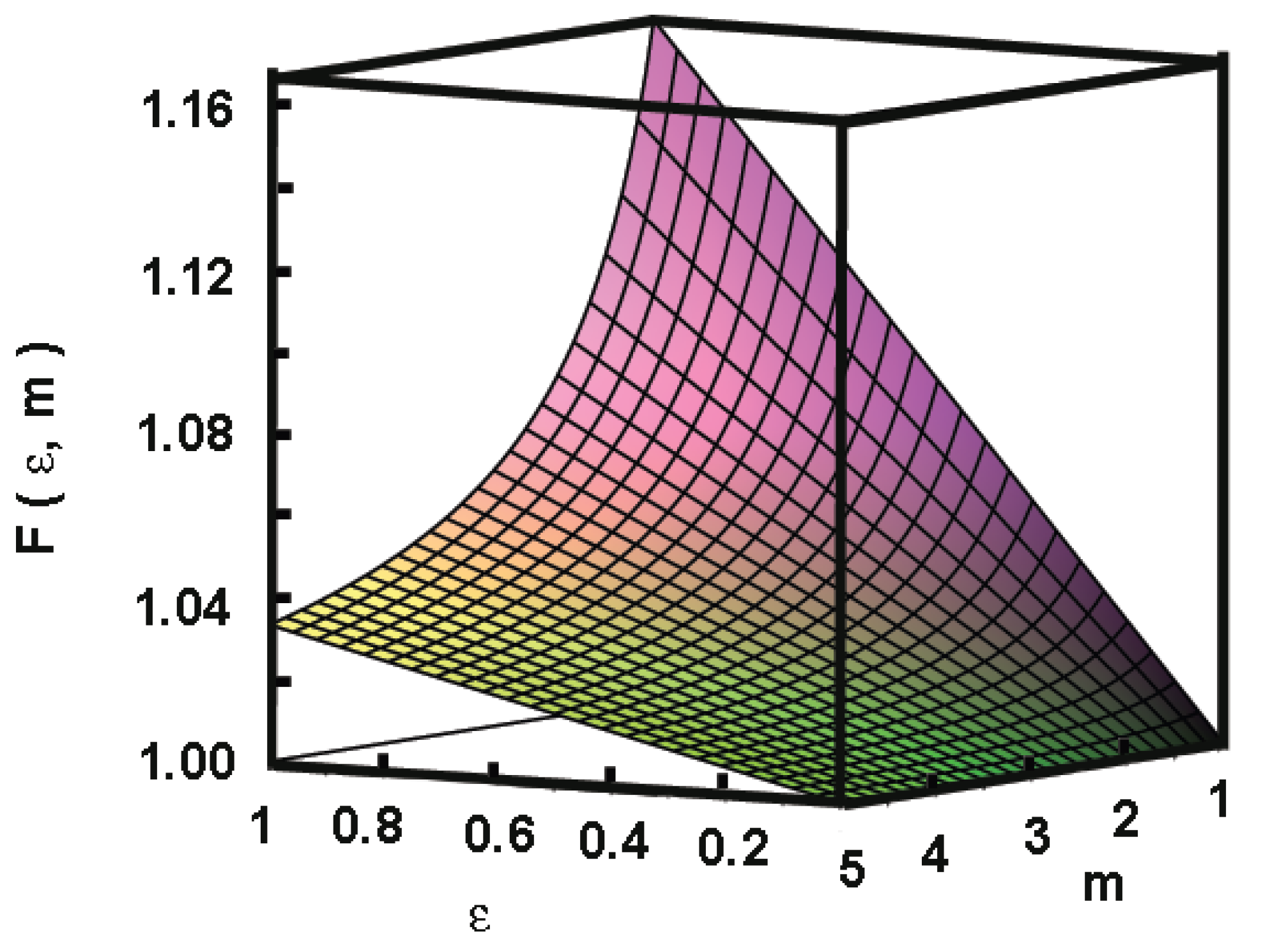
• The direct integration solutions show that the only dimensionless group governing the diffusion process is the prefactor A, which specifies the model’s time scale and, in turn, the Fourier number $Fo=At$. It is important to note that all of the papers cited in this work lack the scaling analysis performed here. According to Gurtin and MacCamy [13], the transformation $\tau =\left(e^{At}-1\right)/A$ appears naturally as a pseudo-time scale in the approximate solution created by the direct integration approach. It can also be used to formulate an effective similarity variable that mimics the Boltzmann one.
• The significance of the prefactor A in the diffusion process control is once again demonstrated by the approximate solution developed through the direct integration, which explicitly specifies the length scale $\sqrt{D_0/A}$ and a dimensionless spatial variable $X=x/\sqrt{D_0/A}$. The initial scaling of the model and the physical interpretation of the results enable all these estimates.

5. Conclusions

The double-integration techniques of the integral-balance method and the implementation of the Barenblatt parabolic profile allowed approximate sharp front solutions of doubly-degenerate diffusion-reaction equations to be developed, clearly defining the role of the exponents in the degenerate terms in the control of front propagation and its speed. In both models solved, the growth function is of Fisher’s type. However, additional tests with growth functions taken from other diffusion-reaction models reveal that the structure of the equation defining sharp front evolution in time does not change; the only effect is on the prefactor of the Fourier number. Last but not least, the complete scaling analysis of the models allows us to define the characteristic length and time scales, as well as the characteristic velocity scale. The approximate solution, intrinsically, by virtue of its construction using the ratio $x/\delta$, defines a new similarity variable that, for a short time, approaches the Boltzmann definition in the case of Gaussian diffusion.