Numerical Study of Carreau Fluid Flow in Symmetrically Branched Tubes

Abstract

The non-Newtonian Carreau fluid model is a suitable model for pseudoplastic fluids and can be used to characterize fluids not so different from biological fluids, such as the blood, and fluids involved in geological processes, such as lava and magma. These fluids are frequently conveyed by complex flow structures, which consist of a network of channels that allow the fluid to flow from one place (source or sink) to a variety of locations or vice versa. These flow networks are not randomly arranged but show self-similarity at different spatial scales. Our work focuses on the design of self-similar branched flow networks that look the same on any scale. The flow is incompressible and stationary with a viscosity following the Carreau model, which is important for the study of complex flow systems. The flow division ratios, the flow resistances at different scales, and the geometric size ratios for maximum flow access are studied, based on Computational Fluid Dynamics (CFD). A special emphasis is placed on investigating the possible incidence of flow asymmetry in these symmetric networks. Our results show that asymmetries may occur for both Newtonian and non-Newtonian fluids and shear-thinning fluids most affect performance results. The lowest flow resistance occurs when the diameters of the parent and daughter ducts are equal, and the more uniform distribution of flow resistance occurs for a ratio between the diameters of the parent and daughter ducts equal to 0.75. Resistances for non-Newtonian fluids are 4.8 to 5.6 times greater than for Newtonian fluids at Reynolds numbers of 100 and 250, respectively. For the design of engineering systems and the assessment of biological systems, it is recommended that the findings presented are taken into account.

1. Introduction

Complex flow systems are an important object of investigation due to the central importance of understanding natural systems and the development of the design of engineering systems such as aero-space gadgets, thermal devices, and lab-on-chip systems [1,2]. This work investigates flow in dendritic networks [3,4,5], characterized by self-symmetry at different scales, and carrying a non-Newtonian fluid that is described by a Carreau model [6,7]. The possibility of flow asymmetries arising in these symmetric networks is highlighted [3,4,5,8,9].

Dendritic networks with symmetric branches designed based on the principle of structural isomers were studied for the flow of Newtonian fluid. Asymmetric splitting effects of the flow in these symmetric-branched networks are attributed to consecutive alignments between tubes of different branching levels [3].

Asymmetric branching structures in real systems are common in natural and biological systems [7,10]. The tracheobronchial tree is a nice example, exhibiting dichotomous branching with a systematic reduction in size, which must be asymmetric to function properly. Efficient gas transport is associated with the degree of asymmetry exhibited by the tracheobronchial tree, which ensures a uniform supply to the terminal acinar units and a shorter average transport time compared to symmetrical trees [5].

Carreau fluids are a class of non-Newtonian fluids, and describe many fluids that occur in physiological, geological, and engineering processes [10,11,12,13]. The studies in these areas are, for example, those that examined the fluid transport in complex flow structures, dynamic dispersion of solutes within tubes, the flow driven by wavy cilia within a micro-channel, the blood flow in a stenosed coronary bypass, melting during the flow of fluid induced by a stretching cylinder, and hydraulic fracture propagating in an elastic material [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19].

For fluid transport, systems that connect a point-to-area or volume and vice versa are not only ubiquitous in natural systems but also in manufactured systems [1,20]. The dendritic pattern of these systems is characterized by a self-similar property. This property is scale-independent; it is exhibited at all levels of observation and is characterized by a power law [21]. Understanding the flow structure is critical for accurately designing flow systems. So, the implications of the existence of self-similarity in the characteristics inherent to the fluid flows must be analyzed.

For the vascular system, assuming Hagen–Poiseuille flow, Hess [22] and Murray [23] state that volumetric flow must be proportional to the cube of diameter in a vessel optimized to require minimum work to drive and maintain fluid. Therefore, optimal branching designs require that the cube of the diameter of a parent vessel is equal to the sum of the cubes of the diameters of the daughter vessels. For symmetrical vessels, the ratio of daughter to parent diameters is 2^−1/3 (Hess–Murray Law). This homothetic law only applies to vessels with rigid and impermeable walls, and laminar flows of Newtonian fluid [22,23].

This study aims to investigate the potential for asymmetric flows of Carreau fluid within dendritic networks with symmetrical branching that are characterized by the property of self-similarity. The effect of the network size constraints on the design is also addressed. The following questions are intended to be addressed by this study: will asymmetries resemble Newtonian fluid flows if they arise? Do asymmetric effects benefit from the structure’s svelteness? Are there significant resistance variations when the homothetic laws for tube diameters differ from the Hess–Murray law? Will the flow distribution patterns be different when compared to Newtonian fluids? To answer these questions, a 3D-Computational Fluid Dynamics (CFD) study [24] is used to simulate Carreau fluid flows through a dendritic dichotomic network of tubes with three branching levels. Understanding how flow occurs in complex networks helps in the design of distribution networks in industry, agriculture, etc., but also helps in the understanding of flow features in natural systems, such as river formation and maintenance, lava transport, etc.

2. Methods

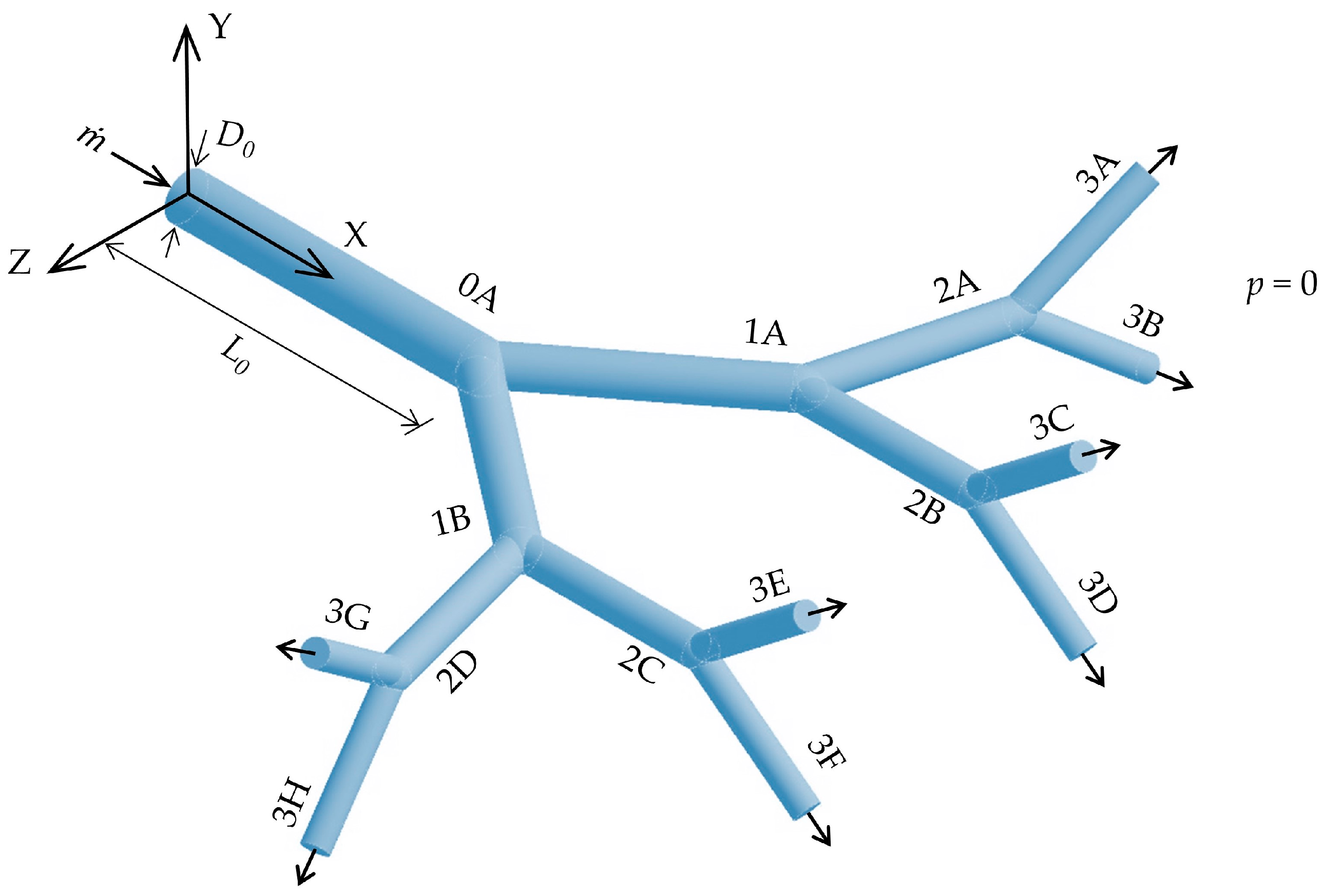
2.1. Geometrical Modeling

Figure 1 depicts a self-similar network of symmetrical branching ducts. This dendritic flow network consists of three branching levels of cylindrical tubes and eight outlets that transport a non-Newtonian fluid described by the Carreau fluid model.

According to the constructal design method [20], constraints, degrees of freedom, and purpose must be clearly defined. As a design constraint, the network has a constant total volume of tubes at each branching level (V_i) equal to 7.0685 × 10⁻⁵ m³, which is kept fixed throughout the study. The angle between the daughter tubes is also kept fixed and equal to 75°. This angle is associated with lower pressure drops in bifurcated systems for fluid flows under a laminar regime [23,25]. In addition, the ratio between the length and diameter of the tube at level zero is kept fixed and equal to 6.77, based on the fact that this ratio varies between 6.3 and 7.0 [22,23] for natural systems. The system’s degree of freedom is the ratio between the diameter of the daughter and parent ducts (a_D). Thus, the dendritic fluidic structures are built according to the following equations:

$${\mathrm{V}}_{\mathrm{i}}={\displaystyle \frac{\mathsf{\pi }}{4}}{2}^{\mathrm{i}}\left({{\mathrm{D}}_{\mathrm{i}}}^2{\mathrm{L}}_{\mathrm{i}}\right)$$

(1)

$${\mathrm{V}}_{\mathrm{T}}={\sum }_{\mathrm{i}=0}^3{\mathrm{V}}_{\mathrm{i}}=4\mathrm{V}$$

(2)

$${\mathrm{a}}_{\mathrm{D}}={\mathrm{D}}_{\mathrm{i}+1}/{\mathrm{D}}_{\mathrm{i}}$$

(3)

$$\mathsf{\theta }=75°, {\mathrm{L}}_0/{\mathrm{D}}_0=6.77$$

(4)

where V_i is the branch level volume, θ is the angle between daughter tubes, D is the diameter, L is the length, a_D is the ratio between diameters of the parent and daughter ducts, and the indices i and i + 1 represent parent and daughter ducts, respectively. The values between 0 and 3 can be applied to index i. A small index means a smaller branching level (i.e., fewer tubes, fewer outlets, closer to the inlet). The notice level’s volume is constant and the length ratio is a non-constant parameter; this allows one degree of freedom for the system.

Another key trait is the network’s svelteness. The non-dimensional svelteness index characterizes the bulk of tubes in the dendritic network design and is defined as the ratio of global to local length scales. A higher svelteness in a network indicates easier flow access and a more efficient method of fluid transport.

Figure 1 shows the fluid flow system, the notice has tubes in the same plane in branch levels 0 to 2 and tubes that are rotated by 90 degrees compared to the tubes at lower levels in branch level 3. This change in the plane is justified because, for a diameter ratio of less than 0.7, there is a structural overlap of the ducts of the third branching level. Symmetry is not altered, since the angles, diameters, and lengths remain identical in size for each flow plane. For additional details about symmetrical structures with rotated levels, see [3,4].

2.2. Mathematical Modeling

Consider a 3D laminar flow regime (Re_D < 2100) through a network of tubes. Navier–Stokes equations for a steady of an isothermal and incompressible Newtonian fluid are expressed in Cartesian coordinates as

$$\nabla ·\mathbf{u}=0$$

(5)

$$\mathsf{\rho }\mathbf{u}\nabla ·\mathbf{u}=-\nabla \mathrm{p}+\nabla ·\mathsf{\tau }$$

(6)

where u is the velocity vector field, p is the pressure, and τ is the stress tensor. The constitutive equation of the stress tensor can be expressed by

$$\mathsf{\tau }=2\mathsf{\eta }(\dot{\mathsf{\gamma }})\mathbf{D}$$

(7)

$$\dot{\mathsf{\gamma }}={\left(0.5 \mathrm{t}\mathrm{r} \mathbf{D}\right)}^{\mathbf{1}/\mathbf{2}}$$

(8)

$$\mathbf{D}=\nabla \mathbf{u}+{\nabla \mathbf{u}}^{\mathbf{T}}$$

(9)

where $\mathsf{\eta }(\dot{\mathsf{\gamma }})$ is the viscosity, $\dot{\mathsf{\gamma }}$ the strain rate tensor magnitude, D is the strain rate tensor, and tr is the trace operator.

For the flow of non-Newtonian fluids, it is necessary to define a viscosity function to accurately describe the fluid behavior. The two-parameter power law expresses the simplest fluid model.

$$\mathsf{\eta }(\dot{\mathsf{\gamma }})={\mathrm{k}(\dot{\mathsf{\gamma }})}^{\mathrm{n}-1}$$

(10)

where k is the fluid consistency index, and n is the fluid behavior index. Pseudoplastic or shear-thinning behavior is characterized by an index n less than 1, and dilatant or shear-thickening behavior by n greater than 1 [26]. If n = 1, the Newtonian behavior is recovered.

Certain fluids require four parameters to accurately characterize them, rather than simply two (Equation (10)). The four-parameter Carreau rheological model [27] is defined as

$$\mathsf{\eta }(\dot{\mathsf{\gamma }})={\mathsf{\eta }}_{\mathrm{\infty }}+\left({\mathsf{\eta }}_0-{\mathsf{\eta }}_{\mathrm{\infty }}\right){\left[1+{\left(\mathsf{\lambda }\dot{\mathsf{\gamma }}\right)}^2\right]}^{\left(\mathrm{n}-1\right)/2}$$

(11)

where η₀ is the viscosity at zero shear rate, η_∞ is the viscosity at infinite shear rate, λ is the time constant, and n is the fluid behavior index. The dimensionless form of this model is

$$\tilde{\mathsf{\eta }}={\displaystyle \frac{\mathsf{\eta }(\dot{\mathsf{\gamma }})}{{\mathsf{\eta }}_{\mathrm{\infty }}}}$$

(12)

$$\mathsf{\eta }\mathrm{*}={\displaystyle \frac{{\mathsf{\eta }}_0}{{\mathsf{\eta }}_{\mathrm{\infty }}}}$$

(13)

and for pseudoplastic fluid flows, the dimensionless groups for dynamic similarity are the Reynolds number with η_c = η₀ and the Carreau number

$${\mathrm{R}\mathrm{e}}_{\mathrm{D}}={\displaystyle \frac{\mathsf{\rho }{\mathrm{u}}_0{\mathrm{D}}_0}{{\mathsf{\eta }}_{\mathrm{C}}}}$$

(14)

$$\tilde{\lambda }={\displaystyle \frac{\mathsf{\lambda }{\mathrm{u}}_0}{{\mathrm{D}}_0}}$$

(15)

where $\mathsf{\rho }$ is the density, u₀ is the velocity in the inlet tube, D₀ is the inlet tube diameter, Re_D is Reynolds number, and $\tilde{\lambda }$ is the Carreau number.

2.3. Numerical Modeling

The Navier–Stokes equations were solved using the Computational Fluid Dynamics (CFD) code ANSYS^® FLUENT. The coupled solution, the pressure-based formulation applied to low-velocity incompressible fluid flows, and the laminar viscosity model were chosen as solution parameterizations.

The pressure–velocity coupling used the coupled method with a pseudo-transient iterative algorithm with the time step set to automatic. The sub-relaxation parameterized were 0.5 for pressure, 1.0 for density, 1.0 for forces, and 0.5 for momentum. The least square cell-based method was used for the gradients, the second order scheme was used for the pressure discretization, and the second order upwind scheme was used for the advective term in the spatial discretization of the transport equations. The residual criteria for the continuity and momentum equations are set to 10⁻⁶.

The parameterization of the materials for the non-Newtonian fluid was selected with the Carreau model and the shear rate-dependent method. The variables used in the parameterization of the Carreau fluid model are depicted in

Table 1. Applied rheological parameters of the Carreau model.

ReD	$\tilde{\mathit{\lambda }}$	λ	η*	n	Case
100	175	3	15	0.35	C1
	175	3	15	0.60	C2
	2917	50	15	0.35	C3
	2917	50	15	0.60	C4
250	438	3	15	0.35	C5
	438	3	15	0.60	C6
	7292	50	15	0.35	C7
	7292	50	15	0.60	C8

.

The boundary conditions for the dendritic flow network are as follows: the mass flow rate is prescribed ($\dot{\mathrm{m}}$) at the inlet tube and is equal to 0.1639 kg/s and 0.4097 kg/s for non-Newtonian fluid with Re_D = 100 and 250, respectively.

The fluid chosen for this study is blood ($\mathsf{\rho }$ = 1060 kg/m³), which has a viscosity of 1.789 × 10⁻⁵ Pa∙s when seen as a Newtonian fluid and a Carreau fluid when η₀ = 0.1391 Pa∙s, η_∞ = 0.009275 Pa∙s, values for time constant (λ), and flow index (n) are depicted in Table 1. The atmosphere pressure was specified for the tube outlet (i.e., p = 0) and the no-slip and no-penetration boundary conditions were applied for tube walls.

To verify the mesh uncertainty, the Grid Convergence Index (GCI) method [28,29] is applied.

Table 2. Grid convergence index for different configurations at Re_D = 100 and $\tilde{\lambda }$ = 175.

	1.00	0.85	0.80	0.75	0.70	0.65	0.60
EuN1	0.357	0.502	0.811	2.291	5.051	14.066	56.916
EuN2	0.351	0.498	0.805	2.281	4.980	13.780	55.920
EuN3	0.346	0.488	0.789	2.261	4.966	13.746	55.584
N1	4,673,233	4,647,629	4,940,460	4,931,950	5,207,548	5,468,679	6,134,257
N2	2,788,063	3,873,024	4,117,050	4,109,958	4,691,485	4,926,738	5,526,358
N3	531,438	762,199	837,684	859,554	973,490	1,093,821	1,303,078
GCI	1.57%	1.40%	1.16%	1.13%	1.20%	1.19%	2.18%

shows the grid study for a non-Newtonian fluid a Carreau fluid model for Reynolds number equal to 100 and Carreau number equal to 175. In Table 2, N represents the number of cells, and indices 1, 2, and 3 represent the grid’s refinement. A higher index indicates a greater spacing between the cells. According to a Richardson extrapolation, the value of the parameter Eu (dimensionless pressure head loss) checks whether the mesh result is in an asymptotic region. For this method, a maximum GCI value of 5% is considered to be acceptable [28].

For the structure with a_D = 0.6, Re_D = 100, and $\tilde{\lambda }$ = 175, we obtained a GCI of 2.18%. A necessary parameterization for a quality network is to maintain proportionality between cell sizes and tube diameters. For convergence of the numerical model, the geometry with the smallest diameter ratio and the largest Re_D requires sufficiently small and well-distributed cells. The grid configuration has ten hexahedral cell layers in the tube wall (i.e., the layers needed to create an accurate computational domain) with a total of 2.7 × 10⁶ to 5.5 × 10⁶ hexahedral cells.

Comparing the flow models in the CFD branched structures, the numerical and mathematical models were validated, and the flow was in bifurcated structures. n < 1 (pseudo-plastic or shear-thinning fluid) is used a structure with one generation (i.e., two outputs) [30], and n = 1 (Newtonian fluid flow) is used a structure with two generations (i.e., four outputs) [31,32]. So, an adequate geometric modification of the network shown in Figure 1 was required to achieve equivalence with the verification geometries under consideration, resulting in the reduction in branching levels without modifying the mesh parameterization or dimensions used in the model of this study. The relative error for each author, with their respective performance markers, is 8% [30], 9% [31] to 3% [32].

Table 3. Comparison of geometric relationships for validation of the computational model.

Flow structure	Pellejero (2020) [30]	Present CFD study with one branching level
Number of branching levels	1	1
aD	1.00	1.00
aL	1.00	1.00
$\mathsf{\theta }$	135°	75°
${\mathrm{V}}_{\mathrm{T}}$	1	1
${\mathrm{V}}_{\mathrm{D}}/{\mathrm{V}}_{\mathrm{T}}$	0.1	0.1
$\mathsf{\rho }$ (kg/m3)	1000	1000
η0 (Pa∙s)	0.0015	0.0015
η∞ (Pa∙s)	0.0001	0.0001
λ (s)	333,333.33	333,333.33
n	0.35	0.35
ReD	300	300
$\tilde{\lambda }$	150	150
Hexahedral cells	4,588,271	4,288,949
RT (Pa∙s/kg)	0.019752721	0.021560961
$\mathsf{\epsilon }=\left|{\displaystyle \frac{{\mathrm{R}}_{\mathrm{r}\mathrm{e}\mathrm{f}\left[30\right]}-{\mathrm{R}}_{\mathrm{T}}}{{\mathrm{R}}_{\mathrm{T}}}}\right|$	-----	0.083

shows all the parameters used to validate the numerical model for the flows of a Carreau fluid. It should be noted that the fluid properties, diameter ratio a_D, and other geometrical relationships are identical to the reference study [30]. The sole difference between the studies is the angle between the daughter tubes.

The robustness and validity of the proposed model are verified since both results present the same order of magnitude.

2.4. Network Flow Performance

To investigate the effect of Carreau fluid through the dendritic flow network, the following quantities are defined, for a better understanding of the results and ease in comparing the results

$${\mathrm{R}}_{\mathrm{T}}=∆\mathrm{p}/\dot{\mathrm{m}}$$

(16)

where R_T is the total flow resistance, Δp is the pressure drop, and ṁ is the mass flow rate.

The pressure head loss can be obtained by using the Euler number according to

$$\mathrm{E}\mathrm{u}=\mathsf{\rho }{\mathrm{A}}_{\mathrm{t}\mathrm{u}\mathrm{b}\mathrm{e}}^2∆\mathrm{p}/{\dot{\mathrm{m}}}^2$$

(17)

where Eu is the Euler number and can be thought of as a measure of the pressure forces to inertial forces ratio (dimensionless pressure head loss), and A_tube is the cross-sectional area of the inlet tube. The ratio between the total resistance of the network and the resistance of a network designed based on the Hess–Murray law is

$$\mathrm{H}\mathrm{R}\mathrm{M}={\mathrm{R}}_{\mathrm{T}}/{\mathrm{R}}_{\mathrm{H}\mathrm{M}}$$

(18)

where HMR can be thought of as a measure of the comparison between the resistance of the system and the resistance of the branched system that presents the minimum pumping work according to the premises of the Hess–Murray law (dimensionless resistance ratio), and R_HM is the total flow resistance of a network designed according to the power law a_D = 2^−1/3 (Hess–Murray law) [20]. The ratio of network flow resistance of a Carreau fluid to a Newtonian fluid is

$$\mathrm{C}\mathrm{N}\mathrm{R}={\mathrm{R}}_{\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{u}}/{\mathrm{R}}_{\mathrm{n}\mathrm{e}\mathrm{w}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{a}\mathrm{n}}$$

(19)

where CNR is the dimensionless resistance ratio between the Carreau and Newtonian fluid models, which characterizes the proportional magnitude of these two quantities, R_Carreau is the total flow resistance according to the rheological parameters of the Carreau fluid model (Table 1), and R_newtonian is the total flow resistance of the Newtonian fluid model (μ = 0.0035 Pa∙s), with both resistances defined according to Equation (16).

To investigate the asymmetry in the flow between tubes and quantify the possible differences in the distribution of mass flow in each of the tubes of the dendritic network, the following parameter is defined:

$$\mathrm{F}\mathrm{R}\mathrm{P}={\dot{\mathrm{m}}}_{\mathrm{t}\mathrm{u}\mathrm{b}\mathrm{e},\mathrm{m}}/{\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}$$

(20)

where FRP is the flow partitioning ratio, means the fraction of the mass flow rate flowing through each pipe relative to the system supply mass flow rate, ${\dot{\mathrm{m}}}_{\mathrm{t}\mathrm{u}\mathrm{b}\mathrm{e},\mathrm{m}}$ is the mass flow rate at the outlet of tubes in a specific branching level m, and ${\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}$ is the mass flow rate at the inlet of the network.

3. Results and Discussion

Velocity and pressure fields were obtained by CFD numerical simulations to determine how rheological fluid characteristics and other design parameters affect fluid transport across the dendritic network. Our study should cover a range of diameter ratio a_D (including Hess–Murray’s law) to include the values that characterize the optimal performance geometry or reduced flow resistance. The selection of this range was based on the homothetic laws cited in [22,23,25] and the works cited in the references [3,4,5,8,9]. The diameter ratio a_D used here is between 0.6 and 1.0. Our investigation was carried out in a flow laminar regime, and the Reynolds numbers and Carreau model parameters that were selected are those that describe blood flow in larger veins and arteries. The range of the Reynolds number is 100 ≤ Re_D ≤ 250, and the parameters of the Carreau model are depicted in Table 1. The conservative choice of these parameters is convenient given the number of branches in our geometry (Figure 1), but it also allows us to obtain data in the literature for validating the numerical model and may later our results serve as a benchmark for future research.

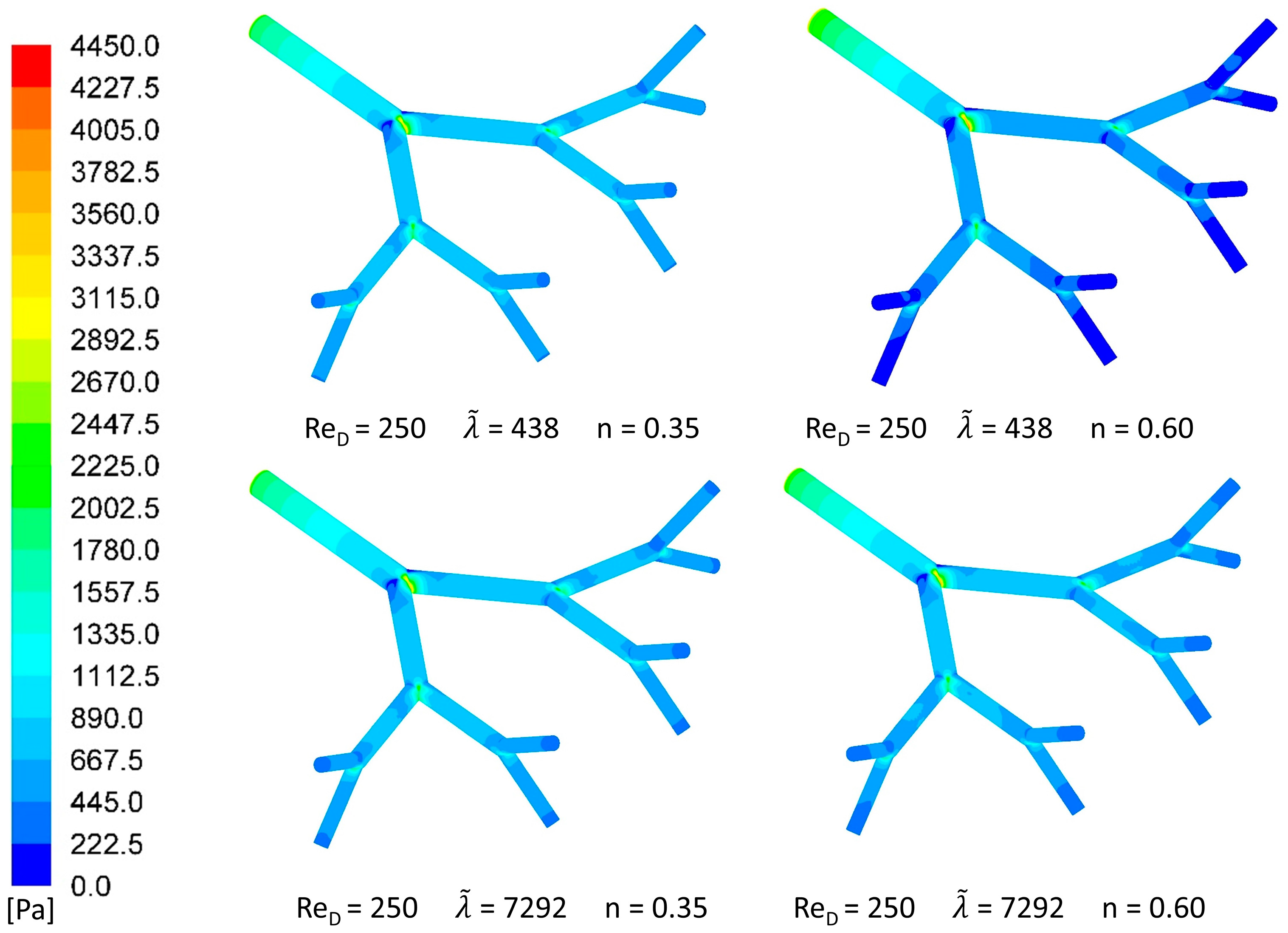
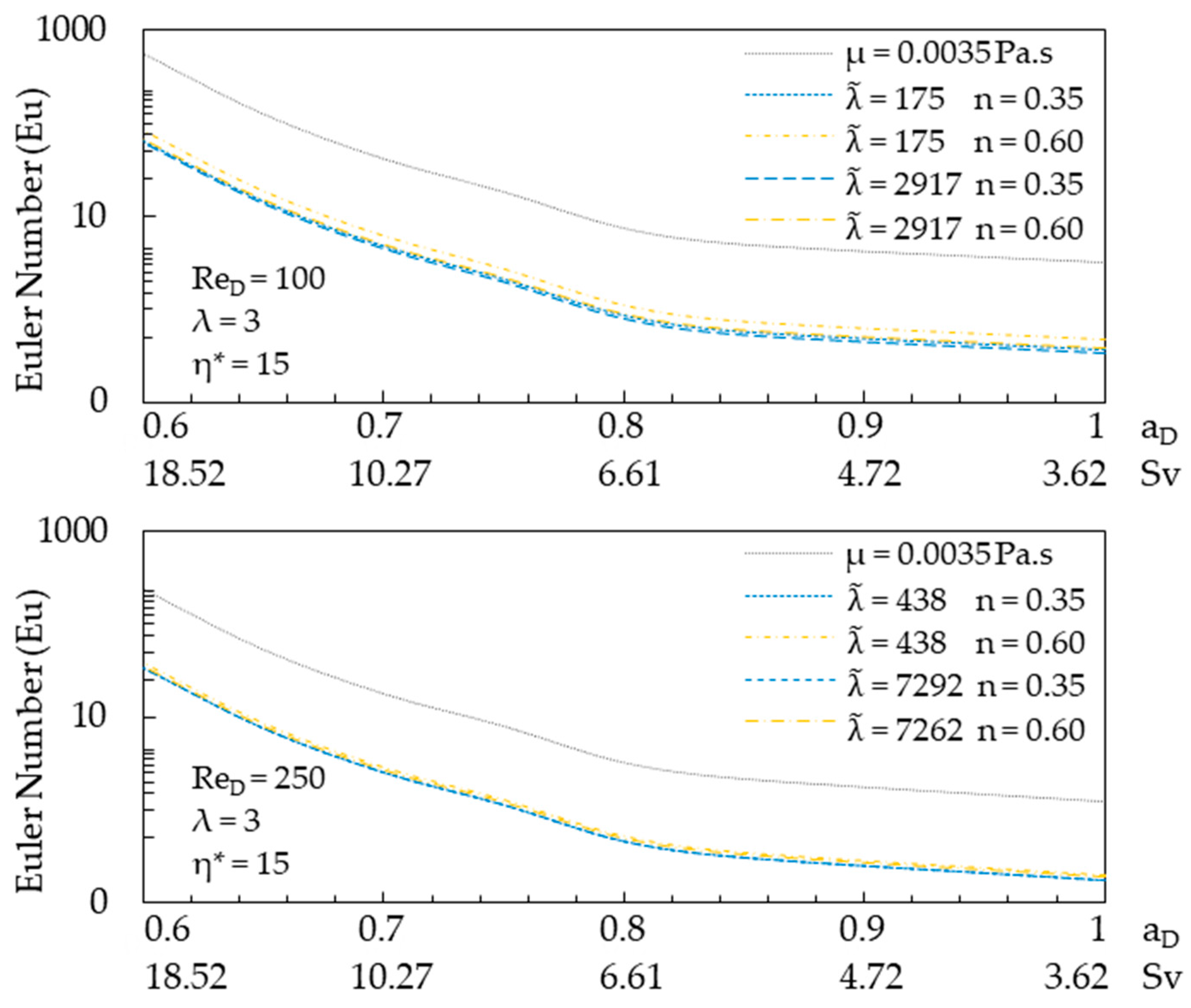
3.1. Pressure Drop Characteristics

Figure 2 shows the static pressure distribution along the dendritic flow network with three branching levels. Equal scales were adopted for all the structures with the same Reynolds number to compare fields and static pressure [22,23,25], the criterion was to adopt the maximum pressure that occurs on the entry surface of the model.

Comparing the influence of rheological parameters on the variation in the Euler number, the fluid behavior index n gave a ratio of 1.103 to 1.429 times between similar cases and the Carreau number gave a ratio of 1.030 to 1.311 times. Thus, pressure gradients were more sensitive to the variation in the n and had a greater influence on the fluid flow than the other parameters (i.e., viscosity at zero shear rates, viscosity at infinite shear rate, and time constant). Notice that the fluid behavior index n measured the degree of non-Newtonian behavior and n ≠ 1 distinguished fluid shear-thinning/shear-thickening behavior.

The static pressure profile has the highest pressures in the lowest branch level of tubes and decreases as they approach the outlet as branch levels increase.

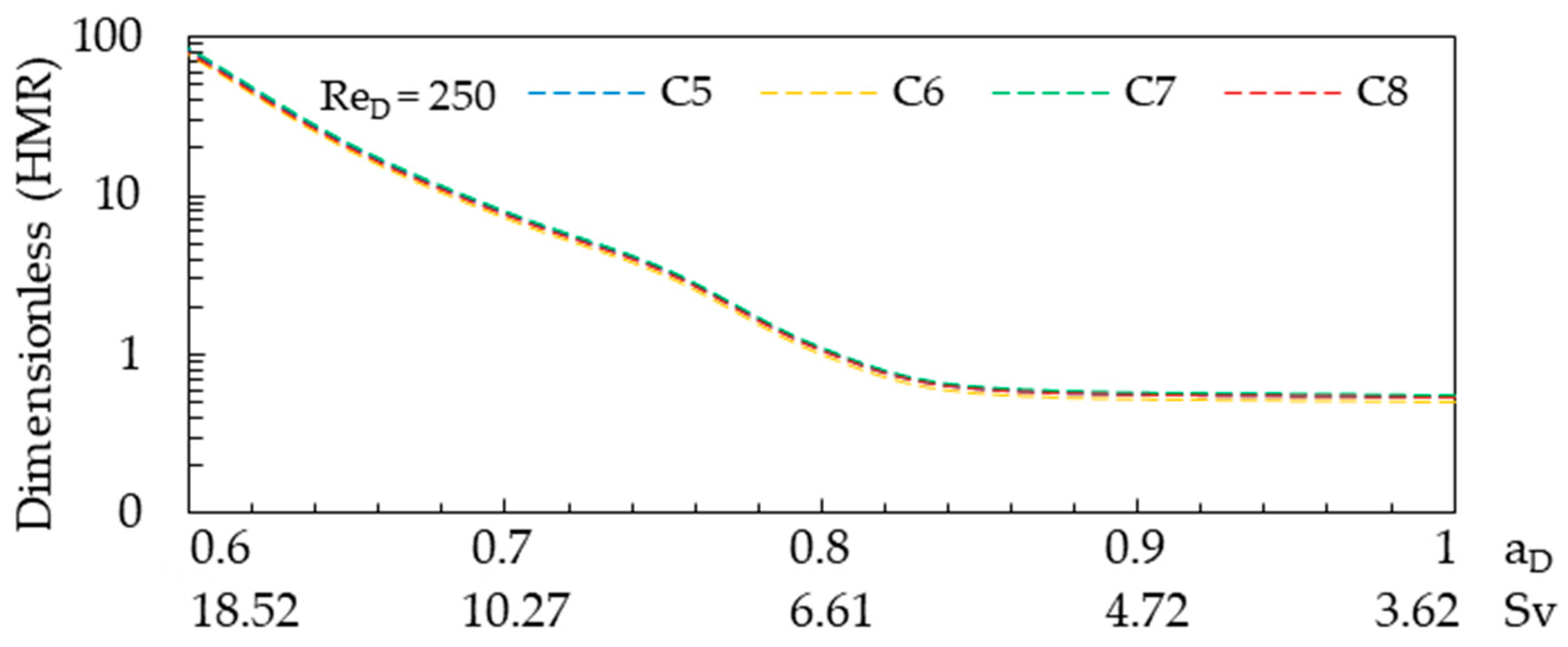
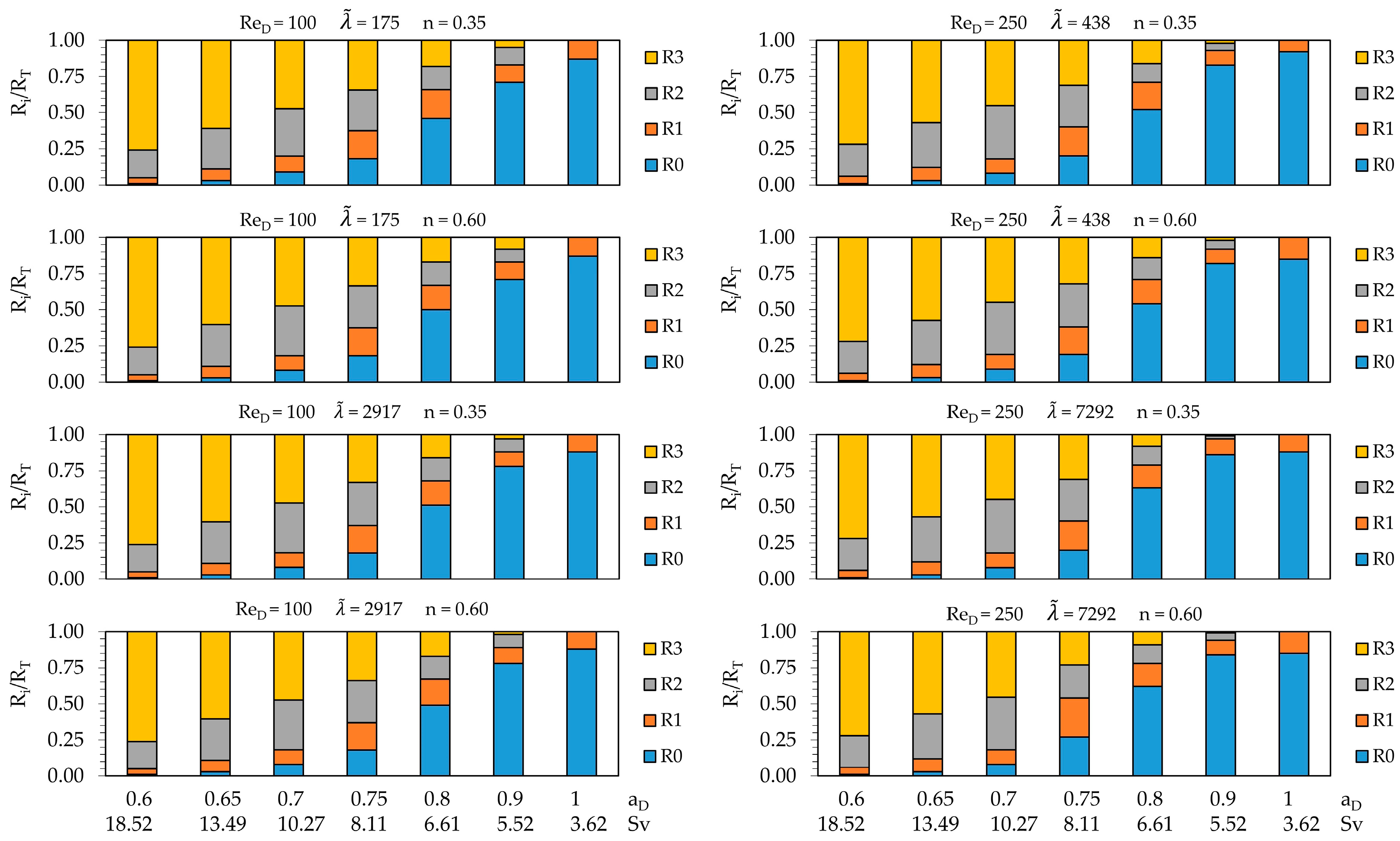
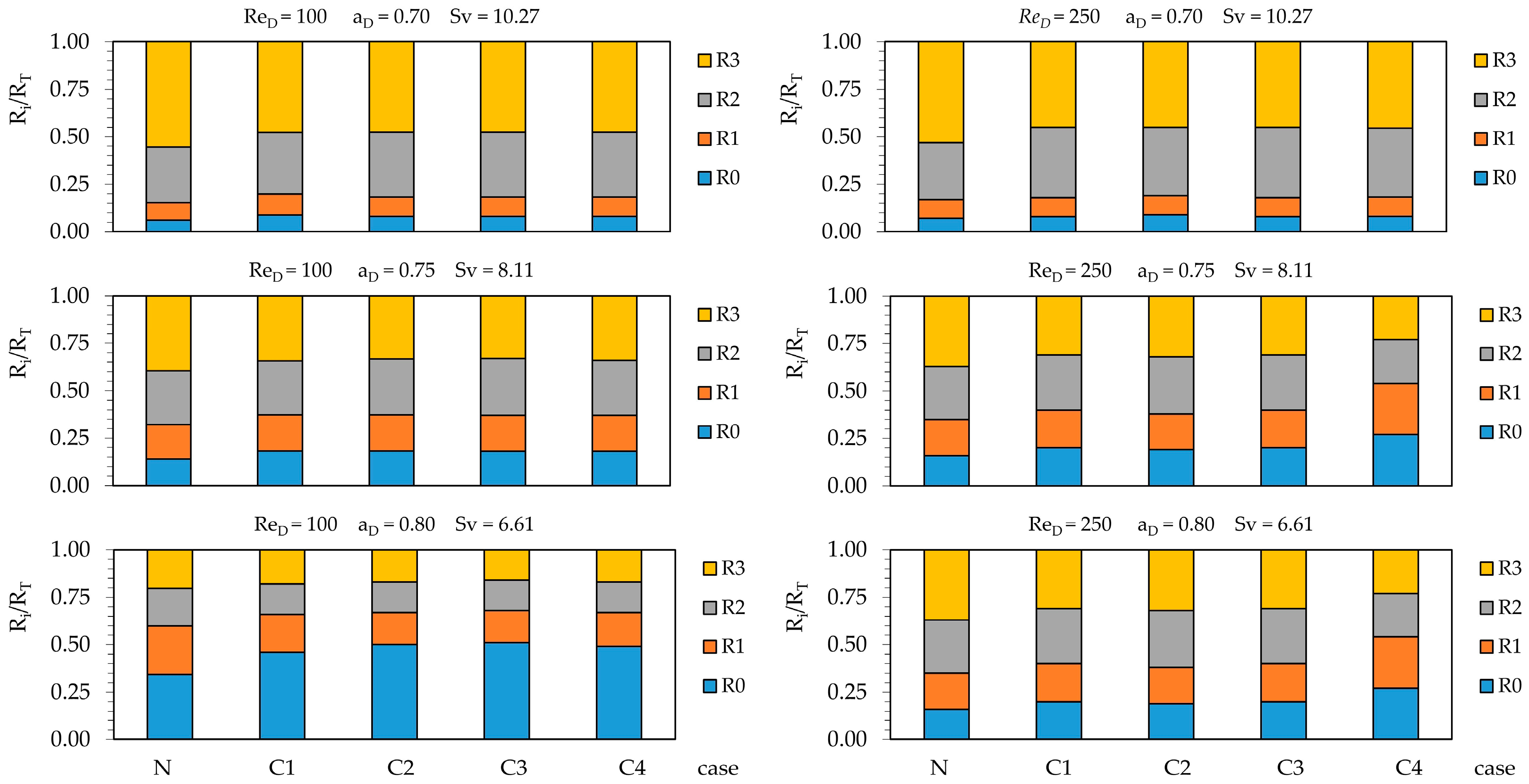
3.2. Hess–Murray Law

The dimensionless flow resistance of the dendritic networks (Equation (18)) is shown in Figure 3. The response of the flow is parameterized according to the Carreau fluid model as a function of the Reynolds number, Carreau number, and diameters ratio. The rheological parameters of each case are shown in Table 1.

The lowest dimensionless resistance HRM occurs for a_D = 1. In general, for a_D < 2^−1/3 then HMR > 1, and for a_D > 2^−1/3 HMR < 1. A similar trend was found for the Newtonian fluid flow through a network of tubes [3,4].

According to Figure 3, the general trend is that the lower fluid behavior indexes, the higher the resistance ratio, which increases as the Reynolds number (Re_D) and the Carreau number ($\tilde{\lambda }$) increase. This means that for a_D > 0.8, the HRM network resistance is a little less than that of a network built based on a_D = 0.8 (Hess–Murray law). It is important to note that the value of dimensionless resistance remains quite close to 1 for a_D ≥ 0.8. This can be explained by the geometric constraint related to constant volume (Equation (1)), which caused a decrease in the length of the tubes when a_D increased.

For the diameter ratios a_D less than 0.80 (Hess–Murray Law), the slope of the dimensionless resistance curve increased significantly. Friction losses began to be significant, as a_D was smaller and the tubes were longer. The influence of different parameters on the HMR resistance ratio can be obtained. For a Reynolds number of 100, HRM was 57.5 to 64.9 times greater for the network with a svelteness ratio of 18.52. In addition, for a Reynolds number of 250, a ratio of 76.3 to 85.5 times greater was obtained for the same slenderness ratio.

For all cases, the lower the value of n is, the greater the pressure loss was for the cases with the same Carreau and Reynolds numbers. This is explained because the fluid behavior index n controls the rate of reduction in viscosity as the flow deformation rate increases. Therefore, the pressure loss along the pipes suffered the effects of this rheological parameter as the fluid became more pseudoplastic. The calculated average increment was 0.99%, 6.14%, 7.41%, and 5.36% for couples C1&C2, C3&C4, C5&C6, C7&C8, respectively.

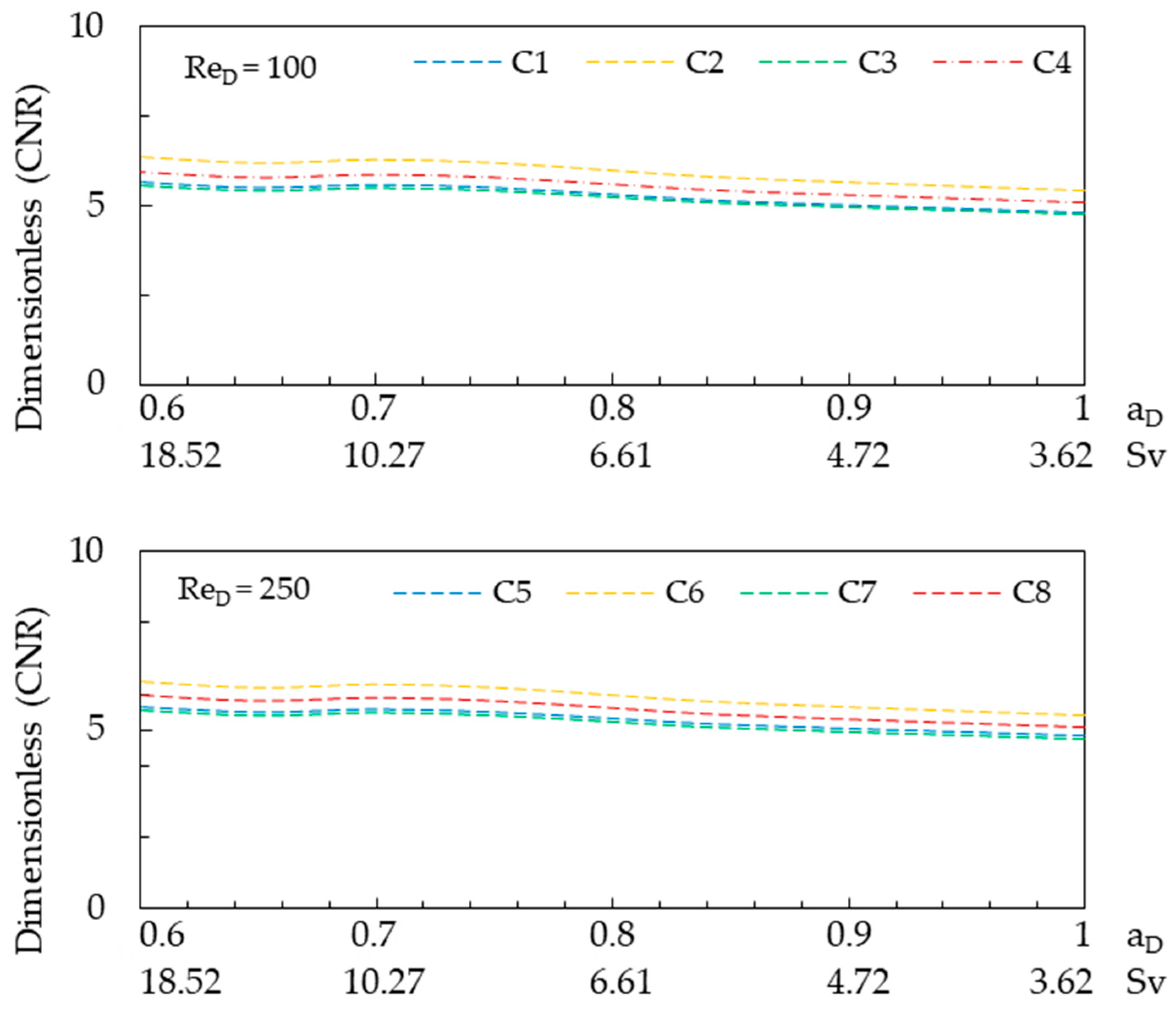
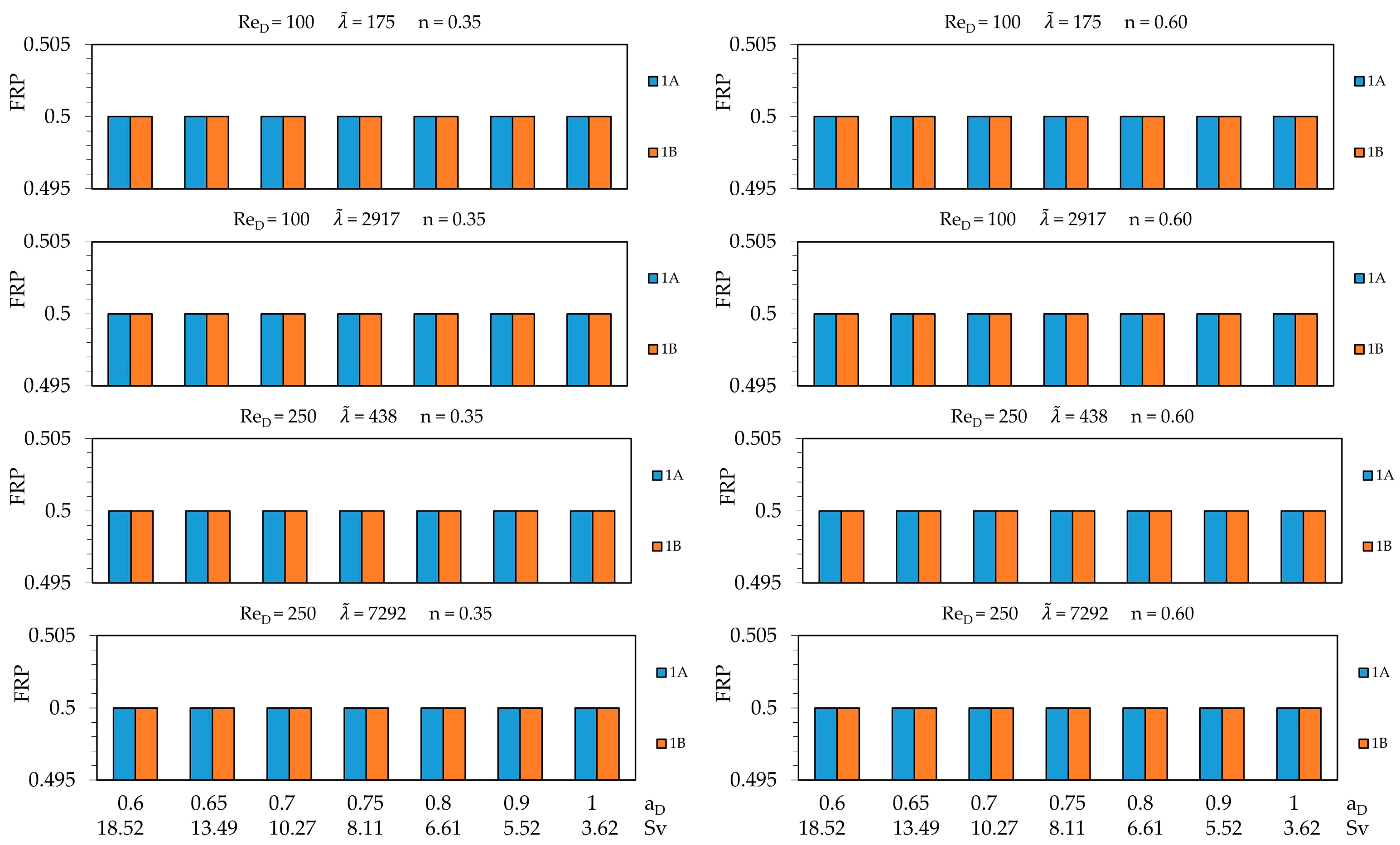
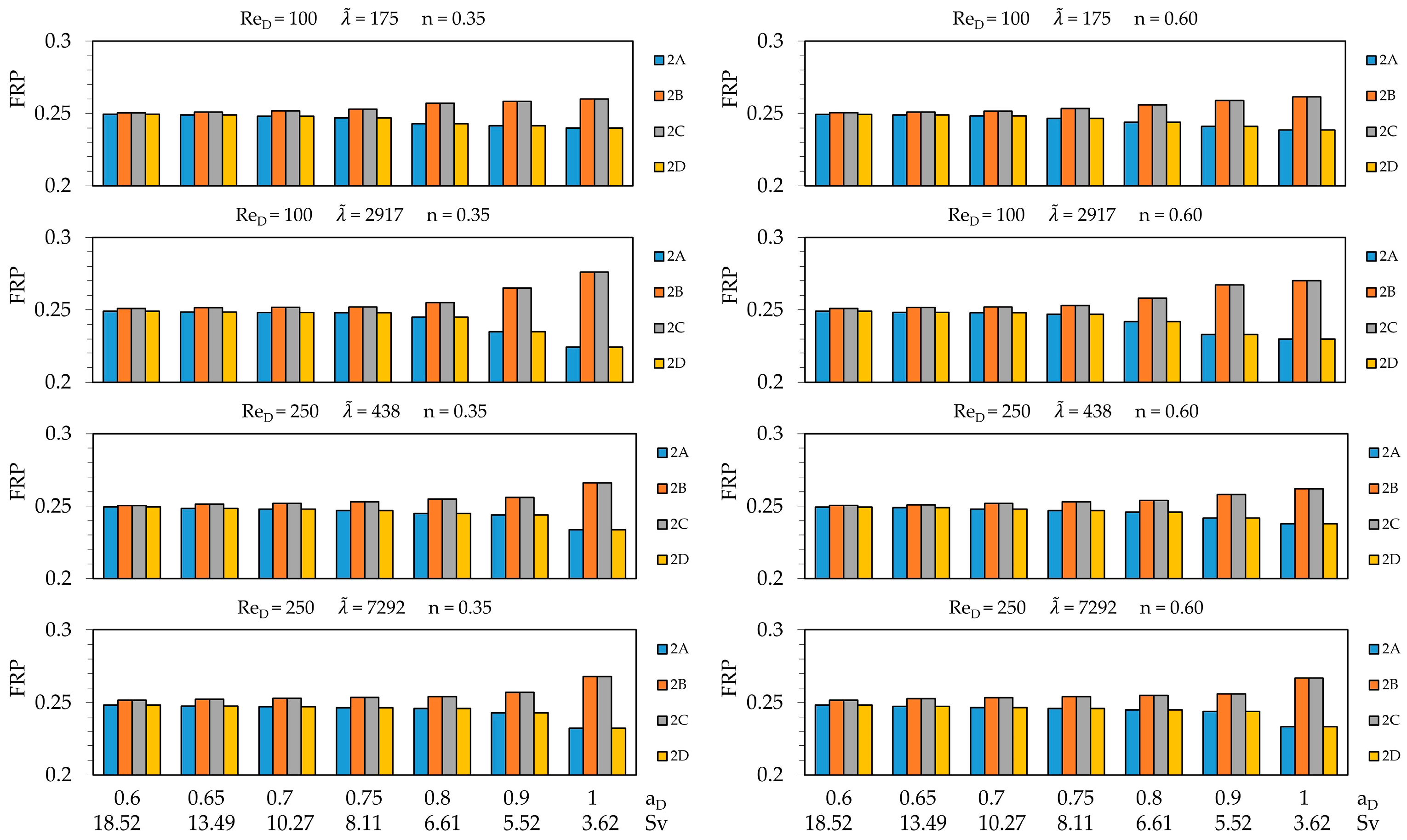
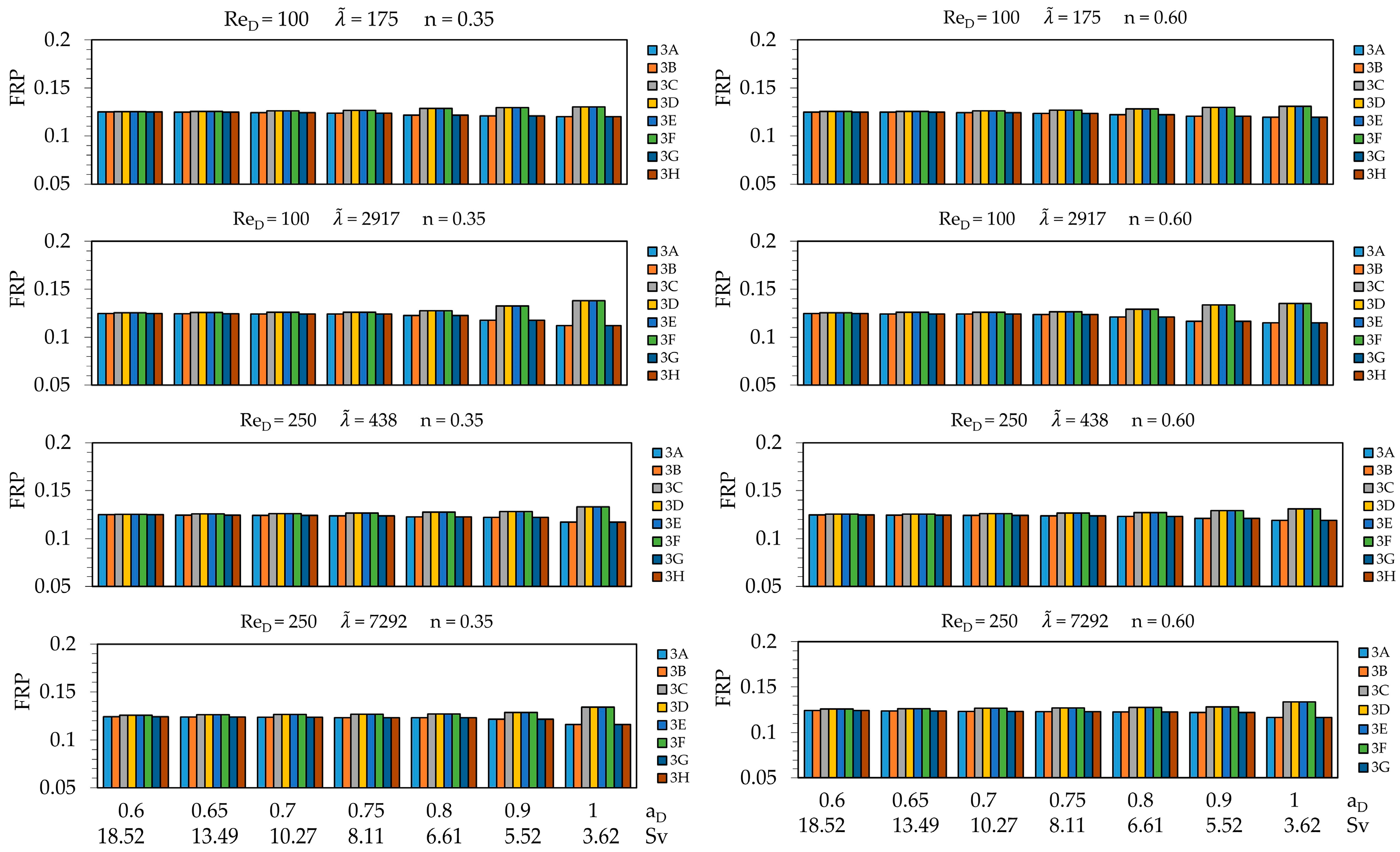
3.3. Network Flow Performance Evaluation

Figure 4 shows the relationship between the dimensionless resistance ratio and the svelteness index. For a network of tubes under volume constraint, the external and the internal scales can be defined as the square root of the area occupied by the flow configuration and the cubic root of the volume of the flow configuration [20,33].

$$\mathrm{S}\mathrm{v}={\mathrm{A}}^{1/2}/{{\mathrm{V}}_{\mathrm{T}}}^{1/3}$$

(21)

where Sv is the svelteness index, A is the total area occupied by the system, and V_T is the total volume of tubes in the dendritic network according to Equation (2).

A large Sv indicates a configuration with lower resistance losses, whereas a small Sv indicates the opposite. Reducing svelteness means reducing system performance, as explained by [20]. Svelteness is also a marker of the impact of localized losses for Sv < 10; local losses are significant in comparison to the friction loss [33].

According to Figure 4, the CNR resistance ratio increased as the svelteness of the dendritic network increased or the diameter ratio decreased. The resistance ratio was also influenced by the Reynolds number and Carreau number. In summary, the flow resistance of the Carreau fluid was higher than the flow resistance of the Newtonian fluid. For Reynolds numbers 100 and 250, the flow of the Carreau fluid was approximately 4.8 and 5.6 times higher, respectively. For Sv < 10, a greater slope of the curve was observed meaning that the flow in these networks experienced greater resistance variations in the flow of the Carreau fluids than in the flows of the Newtonian fluids. For Sv > 10, the values of CNR were nearly constant meaning, that neither the Newtonian nor Carreau fluid flows exhibited appreciable resistance changes at higher svelteness indices. This observation converges and highlights the impact of localized losses compared to friction losses; the more svelte the structure is, the slenderer the network is, and fewer total losses occur [33].

In general, the variation in the CNR with the fluid behavior index was more significant than with the Carreau number, which supports the findings shown in Figure 2. It should be noted that as the Reynolds number increased, so did the CNR.

Figure 5 shows the variation in the Euler number with the ratio between the diameters of the daughter and parent tubes, the Reynolds number, the Carreau number, and the rheological parameters. The Euler number increased as the Reynolds number decreased, and also decreased as the diameter ratio increased or the svelteness index decreased. The svelteness can be correlated on the abscissa axis; the higher the value of a_D, the less slender the structure is, and vice versa. Although the Euler number had a significant decrease with a_D and increased with the Reynolds number, variations in the parameters that defined the Carreau fluid had a negligible effect on the Euler number.

Note that for a svelteness index greater than 10, the slope of the dimensionless pressure head loss curve increased significantly. This means that the forces of pressure were greater than the inertial forces, which justifies the lower performance of a svelte network [33].

3.4. Flow Asymmetry Evaluation

The flow resistance distribution in the dendritic network of the tubes is represented in Figure 6. This figure shows that for the ratio between the diameters from 0.70 to 0.80, the distribution of the flow resistance between the branching levels was more homogenous. Notice also that the branching level 0 had the highest flow resistance for a_D > 0.8 and branching level 3 for a_D < 0.8. For branching levels 0 and 1, the flow resistance increased with a_D, whereas for branching levels 2 and 3, it decreased with a_D. Similar results were found with Newtonian fluid flow [3,4], where the flow resistances for branching levels 0 to 3 were not dependent on the Reynolds number. Regarding the variation in rheological parameters for a given diameter ratio, only small variations were observed in the flow resistance.

Figure 7 shows the flow resistance distribution for branching levels 0 to 3 as a function of rheological parameters. Notably, there was a near-equality in the R_i/R_T ratios between the branching levels for non-Newtonian fluid flow with the same Reynolds number and Carreau number. The smaller the diameter ratio or the higher the slenderness ratio, the more similar the R_i/R_T ratios were and the smaller the influences of the rheological parameters.

Comparing the non-Newtonian and the Newtonian fluid flows, there was an increase in the R_i/R_T ratios at all the branching levels. It was also found that branching level 0 had the highest flow resistance for a_D > 0.8 and branching level 3 for a_D < 0.8, a similar trend presented by Newtonian fluid flows.

The most homogeneous distribution of resistances depended on the Reynolds number, so as the inertia forces increased, the networks with higher uniform resistance distributions occurred for a_D < 0.80, a result known for the flow of Newtonian fluids [3,4],. This same trend was observed for flows of Carreau fluids, where the diameter ratio a_D = 0.75 supported the most homogeneous distribution of the flow resistances among all the branching levels.

Figure 8, Figure 9 and Figure 10 show the dimensionless flow partitioning ratio that is transported by each tube. A dissimilar flow distribution in the tubes at the system outlet was observed, which means asymmetry in the flow of the Carreau fluids in the self-similar symmetric networks of tubes. Notice that flow asymmetry also occurred in the networks transporting Newtonian fluids [3,4].

Notice that these figures also show that “the tube at level j tube that is aligned with tube level i − 2 carries more fluid than the tube at level i tube that is not aligned with a tube at level i − 2”. As a result, the value of FPR at the level 3 results for tubes A to H were as follows: FPR_3A < FPR_3B, FPR_3C > FPR_3D, FPR_3E < FPR_3F and FPR_3G > FPR_3H. It is also worth noting that this simple rule also explains and justifies the findings of another research [3,8,9]. It is also important to note that the differences between FRP were more significant for Carreau fluids than for Newtonian fluids. The flow with a higher Carreau number ($\tilde{\lambda }$) and lower flow index n tends to transport less fluid at the peripheral tubes.

Regarding the homogeneity of the FRP, the flow of Carreau fluids similar to Newtonian fluid [3,4] shows that as the svelteness index increased or the diameter ratio decreased the runoff distribution tended to be more homogeneous.

4. Conclusions

This study is about the flow of Carreau fluids in self-similar dendritic networks. It is considered to be the main constraint that the volume at each branching level remains constant. It specifically analyzes how rheological parameters and geometric constraints affect the performance of the flow network. The key findings of this study are stated below.

As expected, the performance of a self-similar network conducting Newtonian and Carreau fluids is dissimilar. The fluid behavior where the shear-thinning is the rheological parameter that most impacts performance results. Our work also assesses the flow asymmetry across the network, in addition to focusing on the performance of dendritic networks based on flow resistance. Asymmetric effects on fluid transport depend not only on the Reynolds number and Carreau number but on the daughters-to-parent diameter ratio, the alignment of tubes at different levels of branching, and also the svelteness index of the network. Asymmetric effects on fluid transport are more significant for Carreau fluids than Newtonian fluids.

In a complex structure with a constant volume constraint at each branching level, the performance must be evaluated from different perspectives:

• The network with the least resistance has the lowest svelteness ratio and the largest diameter ratio (i.e., Sv = 3.62 and a_D = 1.0);
• Svelte structures tend to better distribute fluid flow, within the studied range, the geometry with Sv = 18.52 and a_D = 0.60 presented the most homogeneous FRP between the model outputs, at the cost of increasing the yield strength by approximately 100 times;
• According to the construction law, the most homogeneous flow distribution with the lowest possible energy cost is also facilitating access. Thus, the structure that best distributes resistances R_i/R_T along the branch levels is the one that eases the flows, and a_D = 0.75 and Sv = 8.11 characterize the network that best achieves this objective.

In addition to the Reynolds number and the daughter-to-parent diameter ratio, asymmetric effects on fluid transport are also influenced by the alignment of tubes at different levels of branching. The latter is a major cause of flow asymmetry. Our results also show that asymmetric effects on fluid flow and losses in the connection between different pipes are influenced by the svelteness index.

Our findings indicate that within the geometric constraint used in our investigation, the network design with superior performance deviates slightly from Hess–Murray’s law. However, this law remains a good starting point for studies in self-similar flow networks.

Upcoming Studies

We are working hard on the studies of asymmetric effects on symmetric structures; our next steps are as follows:

• Study of the effects of Carreau fluid flow on isomeric structures;
• Expansion and validation of other non-Newtonian fluid flow models;
• Explore and evaluate tree-shaped networks with more than three levels of branching;
• Examine how homothetic relationships affect structures with asymmetrical bifurcations and their requirements for symmetric flows.