Abstract
In the present article, the method which was obtained from a combination of the conformable fractional double Laplace transform method (CFDLTM) and the homotopy perturbation method (HPM) was successfully applied to solve linear and nonlinear conformable fractional partial differential equations (CFPDEs). We included three examples to help our presented technique. Moreover, the results show that the proposed method is efficient, dependable, and easy to use for certain problems in PDEs compared with existing methods. The solution graphs show close contact between the exact and CFDLTM solutions. The outcome obtained by the conformable fractional double Laplace transform method is symmetrical to the gain using the double Laplace transform.
Keywords:
conformable partial derivative; conformable double Laplace decomposition method; homotopy perturbation method MSC:
35A44; 65M44; 35A22
1. Introduction
Several applications in advanced science are modeled by linear and nonlinear fractional partial differential equations (FPDEs), for instance, in mathematics, fluids mechanics, physics, biology, chemistry, economics, electromagnetic theory, signal processing, etc. The authors in [1] utilized the homotopy perturbation method (HPM) to handle nonlinear ordinary differential equations and partial differential equations. Through this, solving FPDEs lured the concern of many authors (see [2,3,4,5,6]). Various researchers assisted with fractional derivatives of FPDEs, for example, Caputo [7], Liouville [8], and Ross [9]. The homotopy perturbation method has been extended and used to acquire approximate and exact solutions of fractional-order linear and nonlinear PDEs [10,11,12]. Recently, in [13], the authors extend the familiar limit definition of the derivative of the function and offer the so-called conformable fractional derivative (CFD). Many scientists have been applying the CFD in numerous employments (see [14,15]). The Laplace transform method (LTM) in [16,17] is one of the famous methods for gaining the approximate and exact solutions of FDEs. The researcher in [18] constructed the single conformable Laplace transform method (SCLTM) to solve FPDEs in the conformable fractional derivative sense. The authors in [19] solved time fractional diffusion-wave (TFDW) equations by employing the meshless generalized finite difference method. Series of time-independent integer-order boundary value problems were obtained by transforming the time-fractional diffusion-wave initial-boundary value problem, and the linear algebraic systems were built by the application of the GFDM [20]. The researchers in [21] found the numerical solution of fractional-time-space differential equations with the spectral fractional Laplacian by using the generalized exponential time-differentiating method. In [22], the authors presented a new method of the double Laplace transform called the conformable double Laplace transform (CDLT) and implemented it to solve the conformable fractional partial differential equation. Many strong methods have been improved and developed to gain numerical and exact solutions of fractional linear and nonlinear partial differential equations, for example, the (CLTM) [18,23], the modified Laplace transform for certain generalized fractional operators [24], fractional double Laplace transform method (FDLTM), and its properties [25]. This study aims to implement the conformable double Laplace transform method (CDLTM) to obtain the exact and approximate solutions of a class of CFPDEs. The remainder of this article is organized as follows: In Section 2, we introduce essential definitions and address some properties of the conformable double Laplace transform method (DLTM), as well as the single Laplace transform method (SLTM) and properties of conformable derivatives (CDs). In Section 3, we introduce the basic idea of a CDL and (CALM) for solving (PDEs). In Section 4, some applications of the offered method are used to gain the exact and approximate solutions of conformable fractional linear and nonlinear partial differential equations. Lastly, Section 5 contains the conclusion.
2. Conformable Double Laplace Transform Method (CDLTM) and Properties of Conformable Derivatives (CDs)
In this section, we present some definitions and the basic properties of the conformable double Laplace transform method (CDLTM), conformable single Laplace transform method (CSLTM), and the properties of conformable derivatives (CDs).
Definition 1
([6,26]). Let ; thus, the conformable fractional derivatives (CFDs) of the function and of order β and α are defined by
where .
Definition 2
([6,26]). The conformable fractional partial derivatives (CFPDs) of order β of the functions are defined as follows:
where ,
The following theorem represents the relationship between the conformable partial derivatives (CPDs) and the first partial derivative.
Theorem 1
([6,22]). Let and be α- and β-differentiable at a point and . Thus,
and
Proof.
By taking Definitions 1 and 2, and using in Equation (1), we obtain
To prove Equation (3), take in Equation (4); thus,
□
In the following example, we introduce some properties of the (CFDs) of certain functions.
Example 1.
Let and and thus,
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- .
Conformable Double Laplace Transform Method (CDLTM)
Definition 3
([6]). Let f be a real valued function. The conformable single Laplace transform method (CSLTM) is defined by
where p and s are complex variables of the conformable fractional Laplace transform method.
Definition 4
([6]). The CSLTM of a function with two variables with respect to μ and η of is denoted by
Definition 5
([26]). The CDLTM is defined by
where refers to the CDLTM, and of the conformable integral with respect to μ and respectively.
Theorem 2
([22]). Let and be two functions which use the CDLTM. Then,
- 1.
- where .
- 2.
- 3.
Proof.
(1) By employing the definition of the CDLTM, we get
(2) By taking the definition of the conformable double Laplace transform method (CDLTM), we obtain
Now, using the definition of the CALM to integrate inside the bracket in the above equation, we get
By substituting Equation (9) into Equation (8), one can get
Similarly, we can prove (3). □
Definition 6
([5]). The CDLTM of the conformable partial derivatives of orders α-th and β-th and is given by
and the CDLTM for the first- and second-order fractional derivatives is given by
where and represent the α-th- and β-th-order conformable fractional partial derivatives.
In the next theorem, we generalize the conformable fractional double Laplace transform method (CFDLTM) for -time conformable fractional derivatives.
Theorem 3
([22,26]). Let and such that . Also, let the CFLTM of the functions and exist. Then,
and
where and denote the -time conformable fractional derivatives of function with order α and β, respectively.
In the following example, we calculate the CFDLTM for certain functions:
Example 2.
Let and and thus,
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- where
- 7.
- .
3. Analysis of the Method (CDLTM)
This part illustrates the suggested approach (CFDLTM) and (CSLTM). We consider the general form of linear and nonlinear CFPDEs in the following form:
with initial conditions
where denote the time is an order of a conformable fractional derivative of function and the linear operator is defined as , the symbol denotes the nonlinear operator, and is a known analytical function, and are given functions. To solve Equation (15), the following steps are needed:
First step: Using the CDLTM for Equation (15) and CSLTM for Equation (16), respectively, we will gain
and
By substituting Equation (18) into Equation (17), we gain
Second step: By operating the inverse CDLTM for Equation (19), one can get
The nonlinear term is expressed as
The few terms of the Adomian polynomials for are denoted by
Third step: Now, we apply the homotopy perturbation method (HPM), as follows:
and we get
Fourth step: Matching the coefficient of the power of q, the following approximation is obtained:
The subsequent terms are
Therefore, the exact solution of Equation (15) is given by
4. Application
This part of this paper offers some well-known partial differential equations in the sense of conformable fractional derivatives.
Example 3.
Consider a singular conformable fractional Boussinesq’s equation in one dimension [6] as follows:
with the initial conditions
By utilizing the CDLTM for Equation (26) and CSLTM for Equation (27), respectively, we yield
After an assessment, Equation (28) can be simplified to
By substituting Equation (27) into Equation (29), we have
By applying the inverse CDLTM to Equation (30), we obtain
Now, we apply the homotopy perturbation method (HPM), , and we get
The nonlinear terms are defined by
The Adomian polynomials of and are defined by
and
Moreover, the few components of the Adomian polynomials of Equation (26) are given as follows:
and
By matching the coefficient of the same power of the following approximation is given:
and
Then, we have
The first iteration is given by
At we have
Similarly, in the case of we have
In the same way, at , we have
and so on. The solution of this series is denoted by
Therefore,
Therefore, the solution of Equation (26) can be written in the form
Additionally, to obtain the exact solution, assume ; thus, we have
Figure 1 shows the exact solution at and the approximate solution for different values of and . Refer to Example 3.
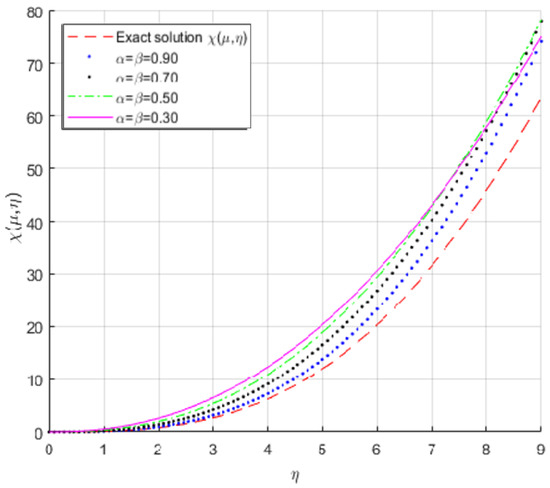
Figure 1.
The exact and approximation solutions of .
Table 1 shows the numerical solution for different values of and for the function .

Table 1.
Numerical solution for different values of and for the function .
Example 4.
Consider a singular conformable fractional thermo-elasticity-coupled system in one dimension [27], as follows:
Subject the initial condition as follows:
By using the CDLTM for Equation (42) and CSLTM for Equation (43), respectively, one can get
and
By substituting Equation (43) into Equations (44) and (45), we have
and
By using the inverse CDLTR to Equations (46) and (47), we get
and
Now, we apply the homotopy perturbation method (HPM) and get
and
By matching the coefficients of the same powers of q, we have
The first iteration is given by
and
and
and
In a similar way, we obtain
and
Therefore, the series of solutions is denoted by
Hence,
and
By simplifying Equations (54) and (55), we gain the solution of Equation (42), as follows:
By taking , the exact solution becomes
Figure 2 shows that the exact solution at and the approximate solution for a different value of and as and . Refer to Example 4.
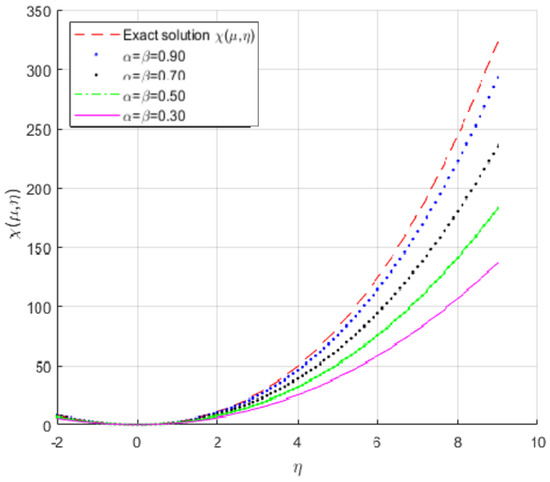
Figure 2.
The exact and approximation solutions of .
Figure 3 shows the exact and approximate solutions of for Example 4 for different values of and .
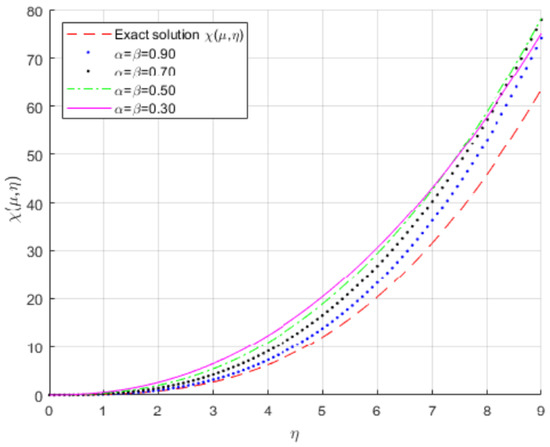
Figure 3.
The exact and approximation solutions of .
Table 2 shows the numerical solution for different values of and for the function . Table 3 shows the numerical solution for different values of and for the function .

Table 2.
Numerical solution for different values of and for function .

Table 3.
Numerical solution for different values of and for the function .
Example 5.
Consider a conformable fractional of a partial differential equation in one dimension [28], as follows:
The initial condition is
In order to implement our method for Equations (57) and (58), we must have
and
The nonlinear terms and are defined by
We have a few terms of the Adomian polynomials for and that are denoted by
and
and
The few components of the Adomian polynomials of Equation (57) are given as follows:
and
where and the first iteration is given by
Hence,
Similarly,
The approximate solution of Equation (57) is given by
Hence, the conformable solution becomes
By taking , the exact solution of Equation (57) is given by
Figure 4 shows the exact solution at and the approximate solution for different values of and is as follows: and . Refer to Example 5.
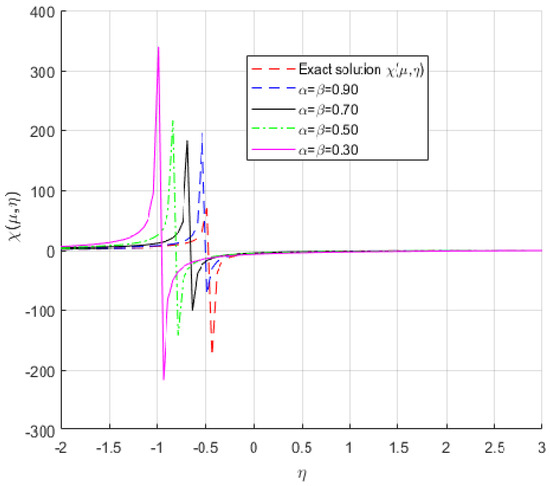
Figure 4.
The exact and approximation solutions of .
Table 4 shows the numerical solution for different values of and for the function .

Table 4.
The numerical solution for different values of and for the function .
5. Conclusions
In the current study, we have successfully applied the method that combined the conformable double Laplace transform method (CDLTM) and the homotopy perturbation method (HPM) to obtain the exact solutions of conformable fractional partial differential equations (FPDEs). The results show that the CDLTM is suitable, effective, useful, reliable, and sufficient for acquiring the exact solutions of CFPDEs. Moreover, three examples were discussed to confirm our method. In the future, we will apply this method to solve some mathematical problems related to physics and engineering that involve singularity.
Author Contributions
Methodology, H.E.G.; formal analysis, H.E.G.; investigation, M.R.G.; data curation, M.R.G.; writing—original draft preparation, M.R.G. and H.E.G.; writing—review and editing, H.E.G. All authors have read and agreed to the published version of the manuscript.
Funding
The author would like to extend his sincere appreciation to Researchers Supporting Project number (RSPD 2024R948), King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chakraverty, S.; Mahato, N.; Karunakar, P.; Rao, T.D. Advanced Numerical and Semi-Analytical Methods for Differential Equations, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019; pp. 131–139. [Google Scholar]
- Debtnath, L. Nonlinear Partial Dierential Equations for Scientist and Engineers; Birkhauser: Boston, MA, USA, 1997. [Google Scholar]
- Podlubny, I. Fractional differential equations: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Math. Sci. Eng. 1999, 198, 41–119. [Google Scholar]
- Aslan, E.C.; Mustafa Inc.; Al Qurashi, M.M.; Baleanu, D. On numerical solutions of time-fraction generalized Hirota Satsuma coupled KdV equation. J. Nonlinear Sci. Appl. 2017, 2, 724–733. [Google Scholar] [CrossRef]
- Ozkan, O.; Kurt, A. Conformable Fractional Double Laplace Transform and its Applications to Fractional Partial Integro-Differential Equations. J. Fract. Calc. Appl. 2020, 11, 70–81. [Google Scholar]
- Eltayeb, H.; Mesloub, S.; Abdalla, Y.T.; Kılıçman, A. A Note on Double Conformable Laplace Transform Method and Singular One Dimensional Conformable Pseudohyperbolic Equations. Mathematics 2019, 7, 949. [Google Scholar] [CrossRef]
- Caputo, M. Linear Models of Dissipation Whose Q Is almost Frequency Independent. Ann. Geophys. 1966, 19, 383–393. [Google Scholar] [CrossRef]
- Liouville, J. Memory on a few questions of geometry and mechanics, and on a new kind of calculation to solve these questions. J. l’École Polytech. 1832, 13, 131–169. (In French) [Google Scholar]
- Ross, B. The development of fractional calculus 1695–1900. Hist. Math. 1974, 4, 75–89. [Google Scholar] [CrossRef]
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals 2005, 26, 695–700. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Homotopy perturbation method for nonlinear partial differential equation of fractional order. Phys. Lett. A 2007, 365, 345–350. [Google Scholar] [CrossRef]
- Wang, Q. Homotopy perturbation method for fractional Kdv-Burgers Equation. Chaos Solitons Fractals 2008, 35, 843–850. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Thabet, H.; Kendre, S. Analytical solutions for conformable space time fractional partial diferential equations via fractional di erential transform. Chaos Solitons Fractals 2018, 109, 238–245. [Google Scholar] [CrossRef]
- Yaslan, H.C. New analytic solutions of the conformable spacetime fractional Kawahara equation. Opt. Int. J. Light Electron Opt. 2017, 140, 123–126. [Google Scholar] [CrossRef]
- Alfaqeih, S.; Kayijuka, I. Solving System of Conformable Fractional Differential Equations by Conformable Double Laplace Decomposition Method. J. Partial. Differ. Equ. 2020, 33, 275–290. [Google Scholar]
- Kilicman, A.; Gadain, H.E. An application of double Laplace transform and Sumudu transform. Lobachevskii J. Math. 2009, 30, 214–223. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Qing, L.; Li, X. Meshless analysis of fractional diffusion-wave equations by generalized finite difference method. Appl. Math. Lett. 2024, 157, 109204. [Google Scholar] [CrossRef]
- Qing, L.; Li, X. Analysis of a meshless generalized finite difference method for the time-fractional diffusion-wave equation. Comput. Math. Appl. 2024, 172, 134–151. [Google Scholar] [CrossRef]
- Difonzo, F.V.; Garrappa, R. A Numerical Procedure for Fractional-Time-Space Differential Equations with the Spectral Fractional Laplacian. In Fractional Differential Equations. INDAM 2021; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Özkan, O.; Kurt, A. On conformable double Laplace transform. Opt. Quantum Electron. 2018, 50, 103. [Google Scholar] [CrossRef]
- Hashemi, M.S. Invariant subspaces admitted by fractional differential equations with conformable derivatives. Chaos Solitons Fractals 2018, 107, 161–169. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. A modified Laplace transform for certain generalized fractional operators. Results Nonlinear Anal. 2018, 1, 88–98. [Google Scholar]
- Kiliciman, A.; Omran, M. On fractional double Laplace transform and its applications. J. Nonlinear Sci. Appl. 2017, 10, 1744–1754. [Google Scholar] [CrossRef]
- Eltayeb, H.; Bachar, I.; Gad-Allah, M. Solution of singular one-dimensional Boussinesq equation by using double conformable Laplace decomposition method. Adv. Differ. Equ. 2019, 2019, 293. [Google Scholar] [CrossRef]
- Gadain, H.E. Application of double natural decomposition method for solving singular one dimensional boussinesq equation. Filomat 2018, 32, 4389–4401. [Google Scholar] [CrossRef]
- Javeed, S.; Baleanu, D.; Waheed, A.; Shaukat Khan, M.; Affan, H. Analysis of homotopy perturbation method for solving fractional order differential equations. Mathematics 2019, 7, 40. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).