Expressions for Stress Concentration Factors for T-Joints of Hollow and Concrete-Filled Square Cross-Sections for In-Plane Axial and Bending Loads
Abstract
1. Introduction
2. Hot Spot Stress
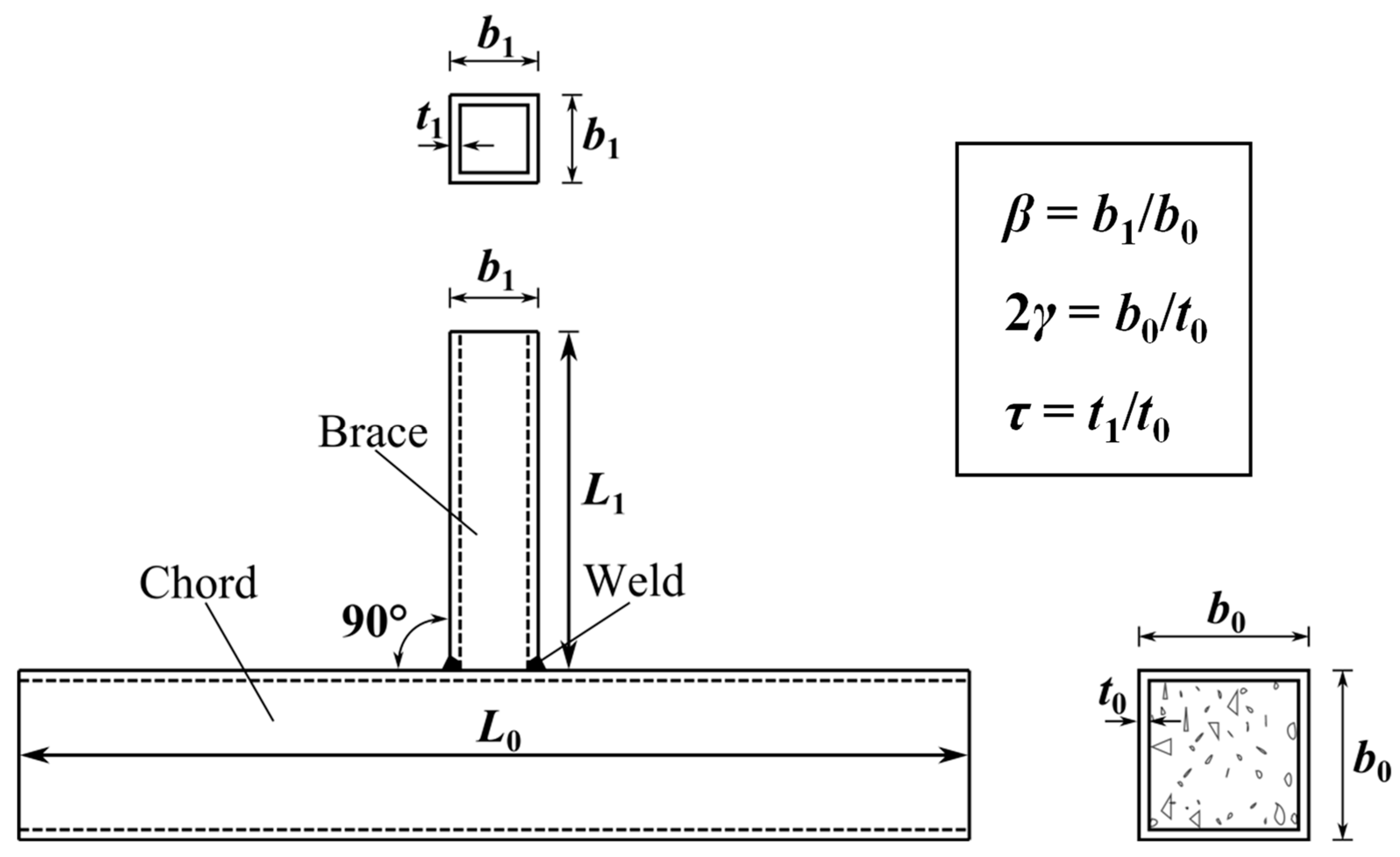
2.1. Geometrical Details of T-Joints
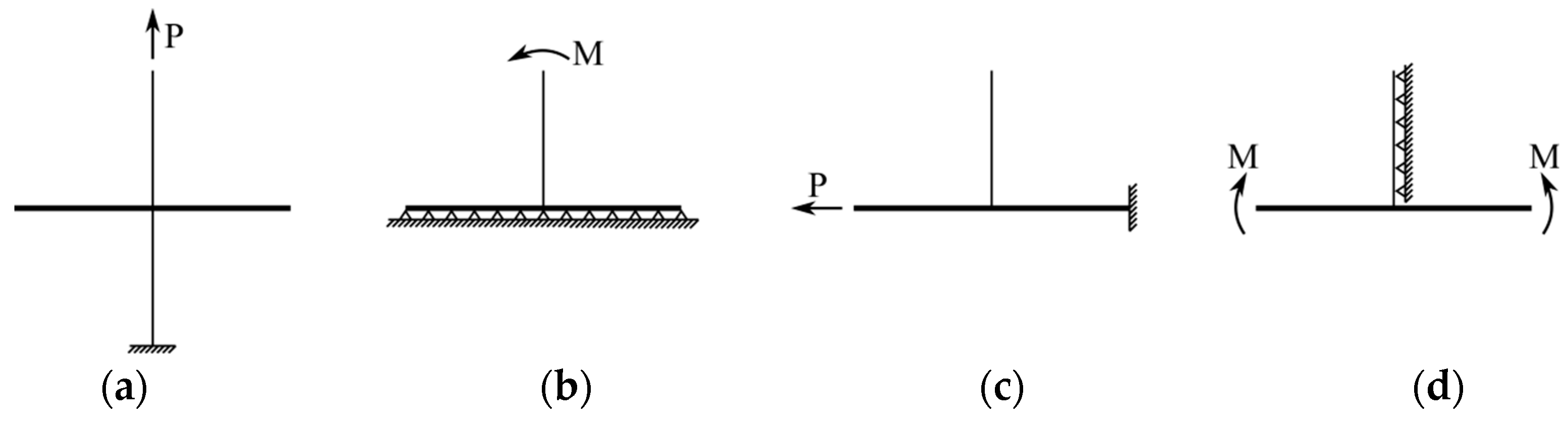
2.2. Load Cases
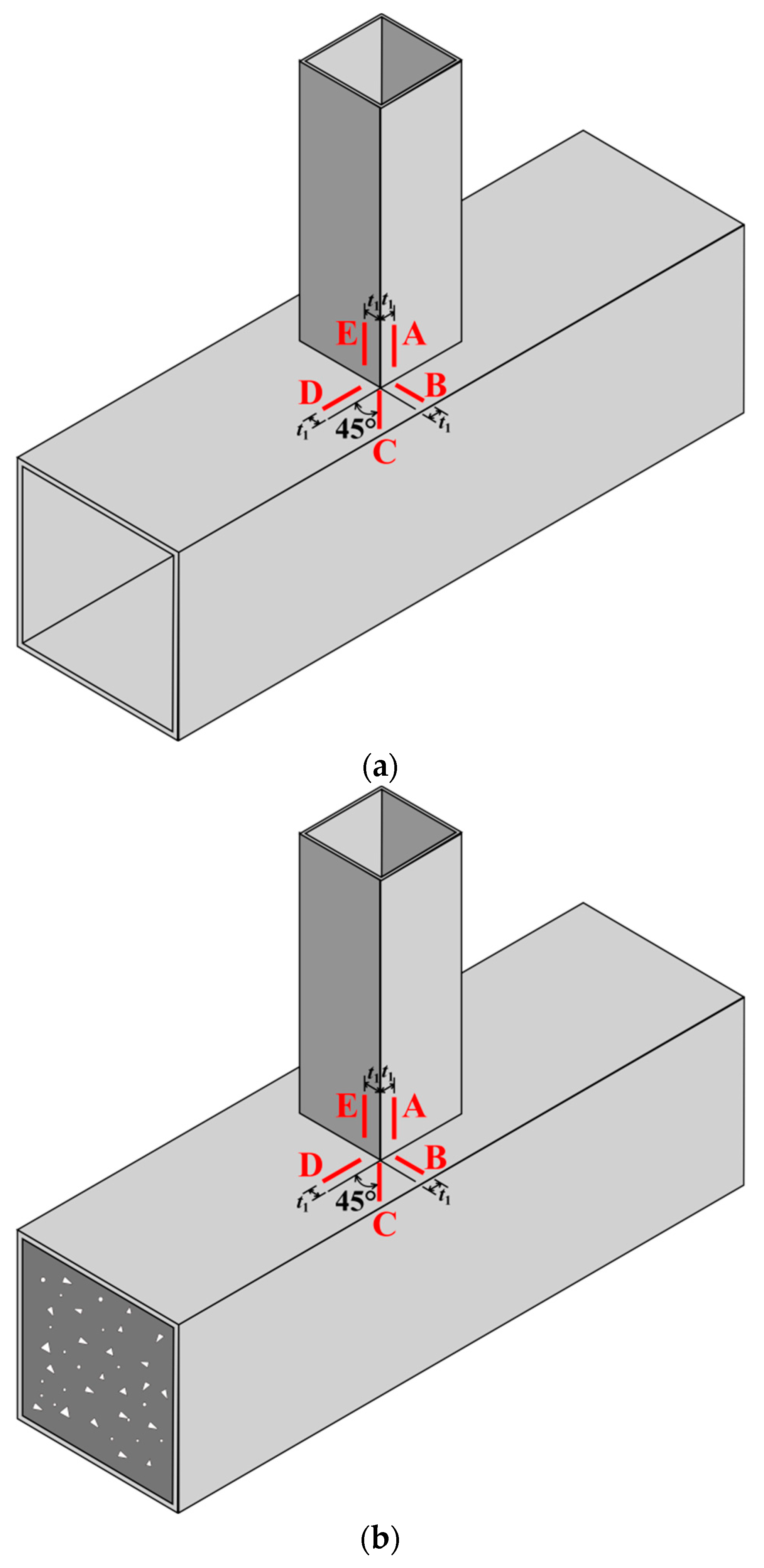
2.3. Hot Spot Locations
2.4. Brief Introduction about SCFs in SHS-CFSHS Joints Subjected to Axial Force in the Brace
3. Finite Element Model and Validation
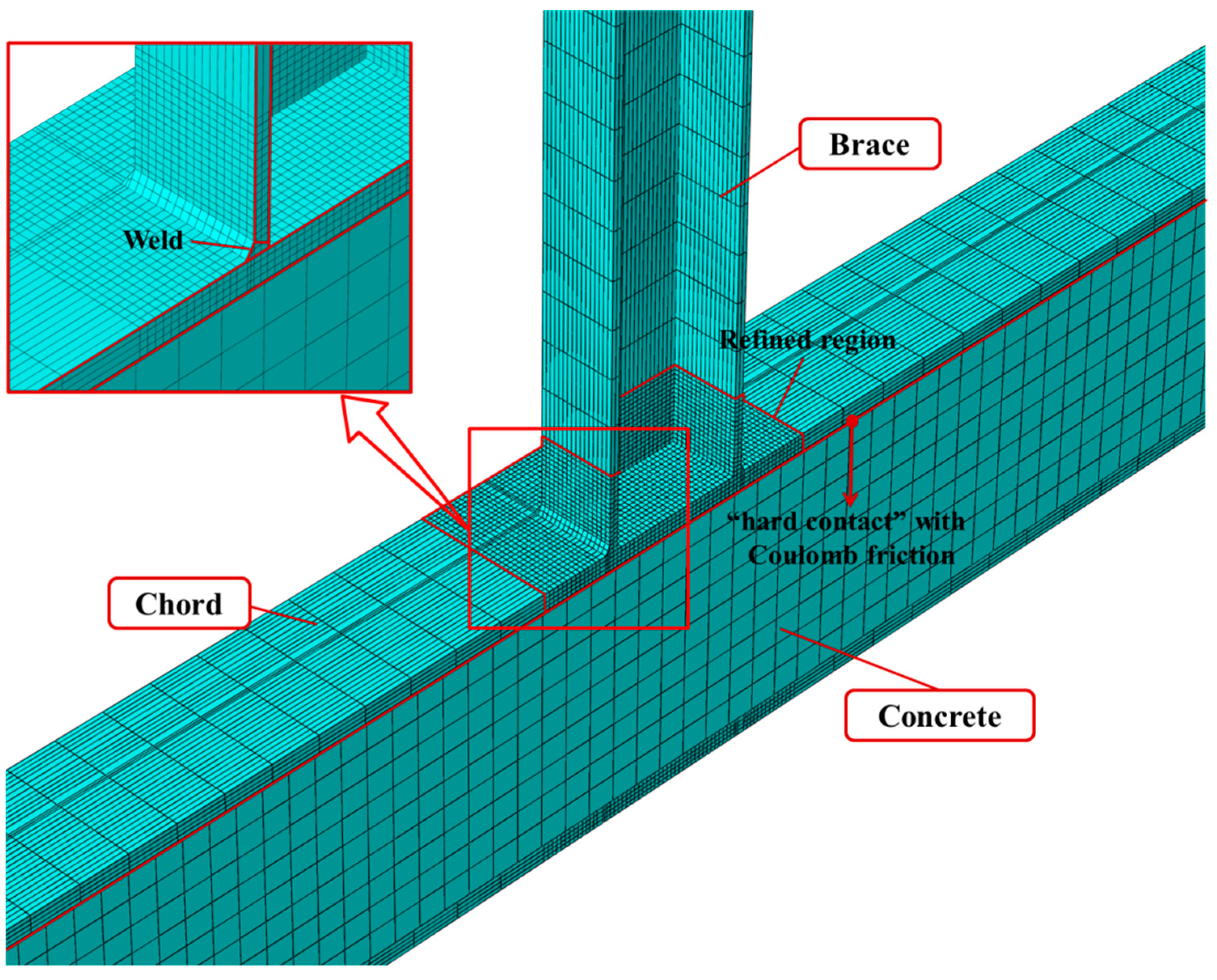
3.1. Establishment of Finite Element Models
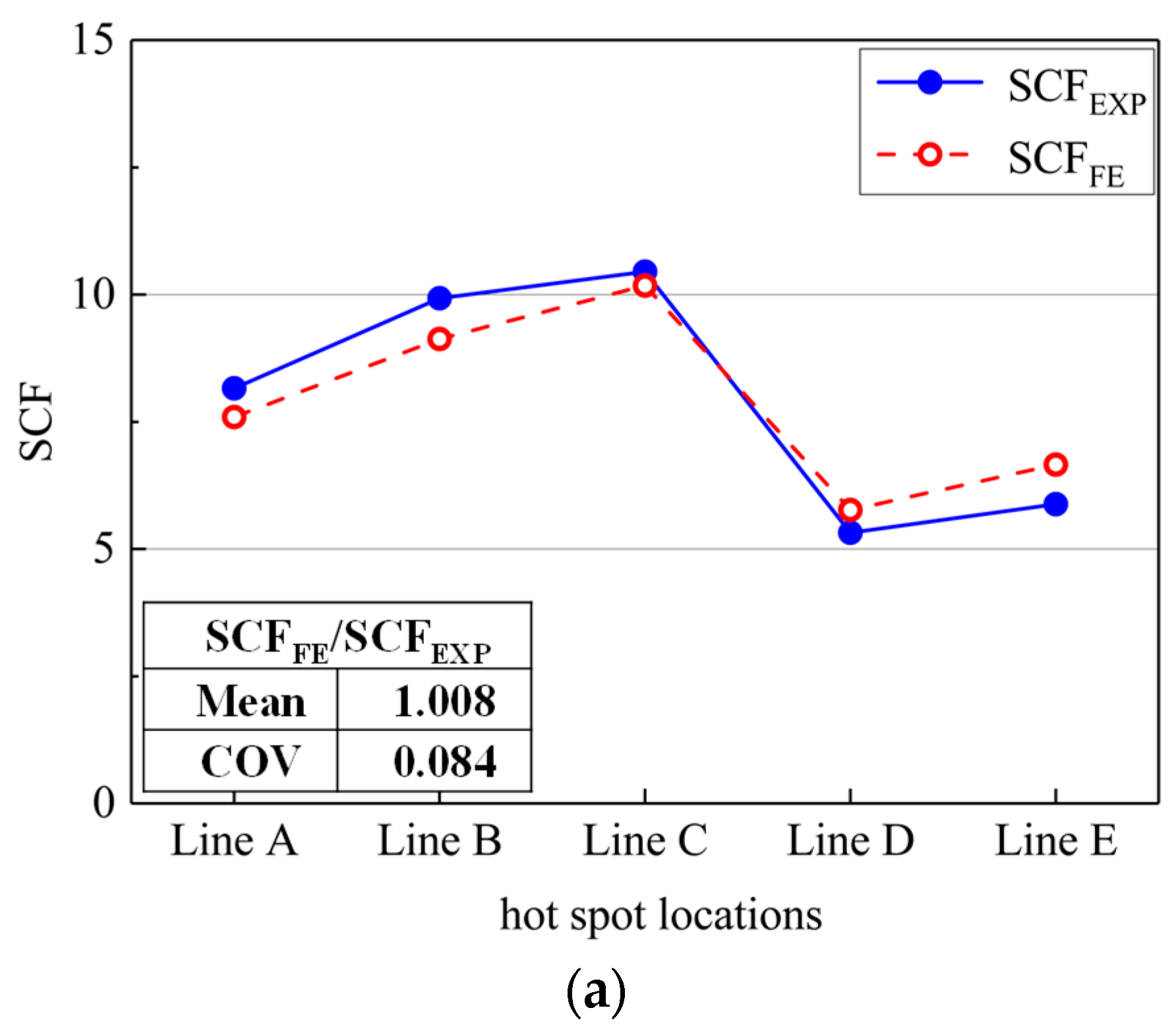
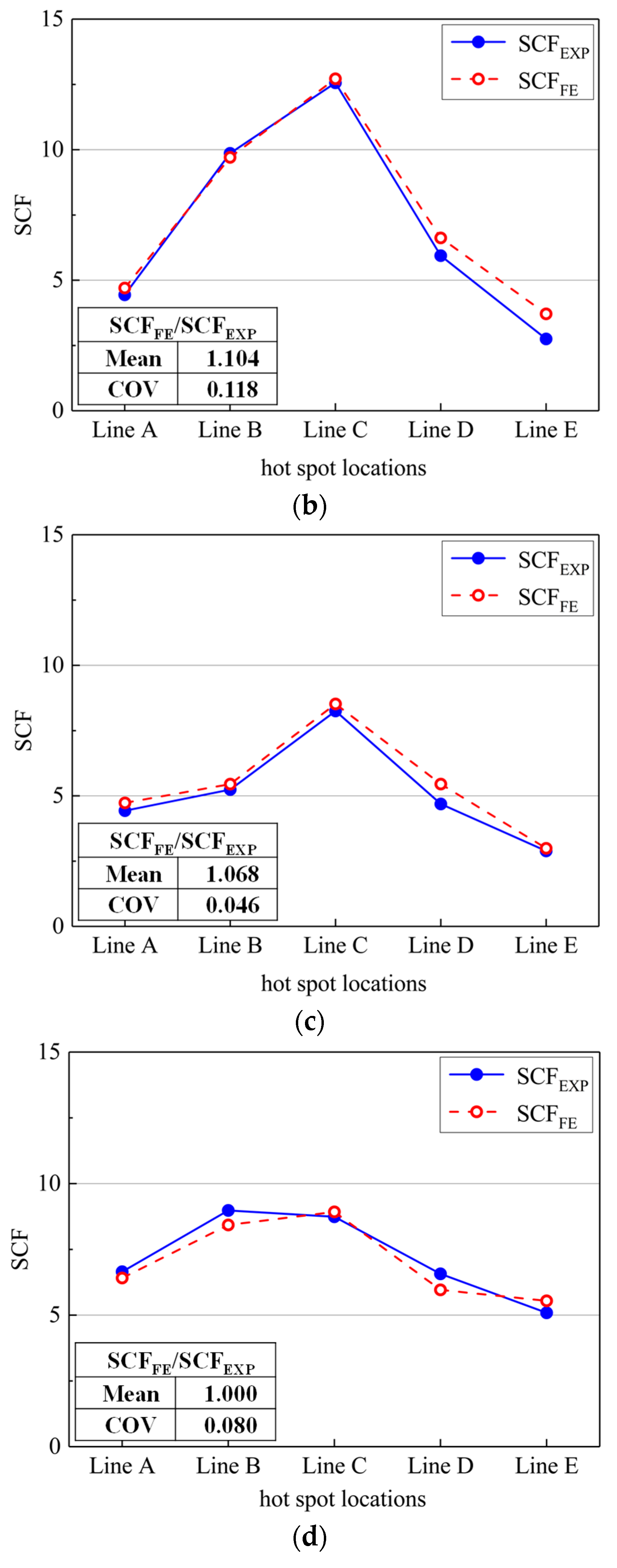
3.2. Validation of Finite Element Models
4. Parametric Study and Proposed Design Equations
4.1. Parameter Selection
4.2. General Parametric Formulae for SCFs
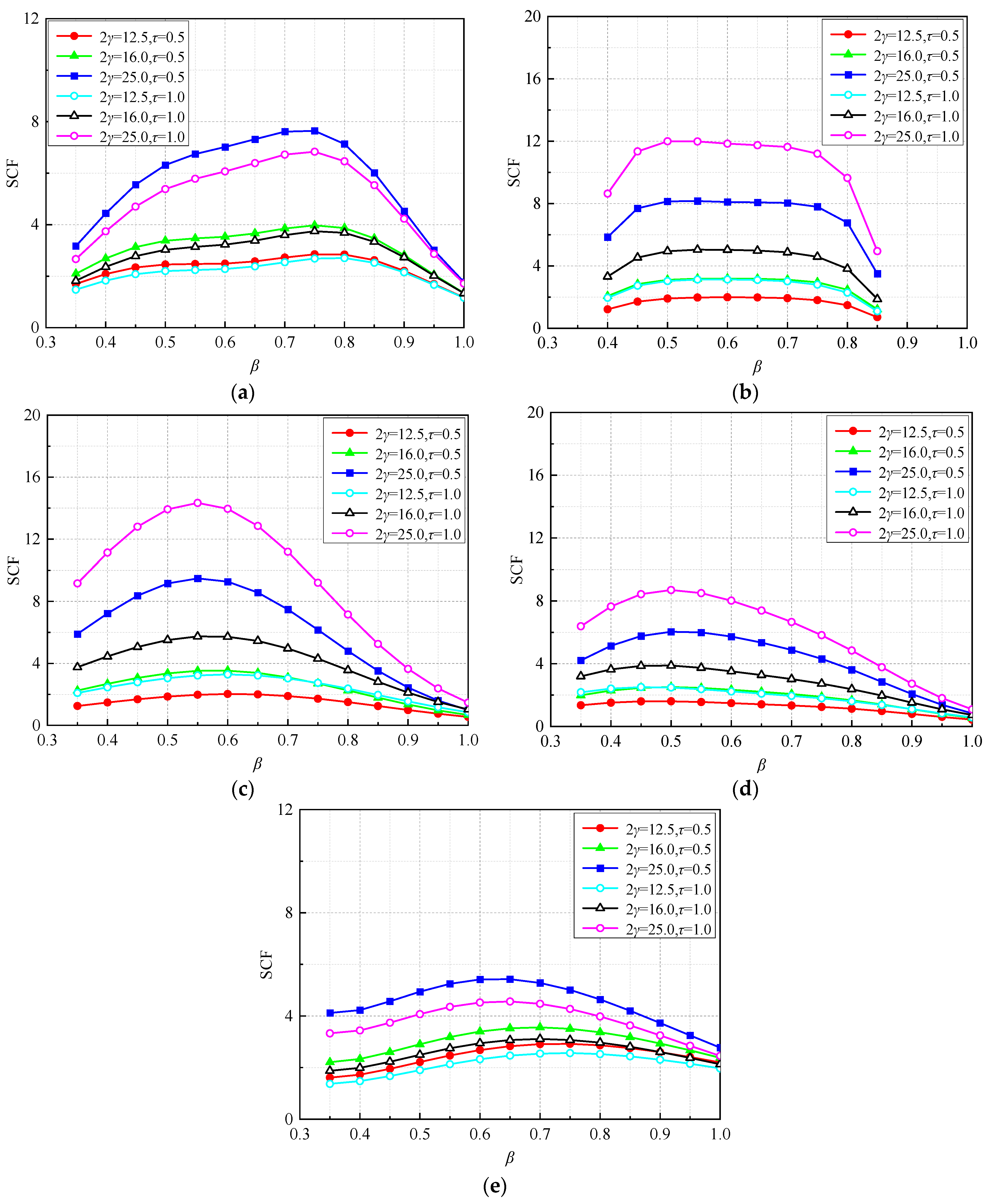
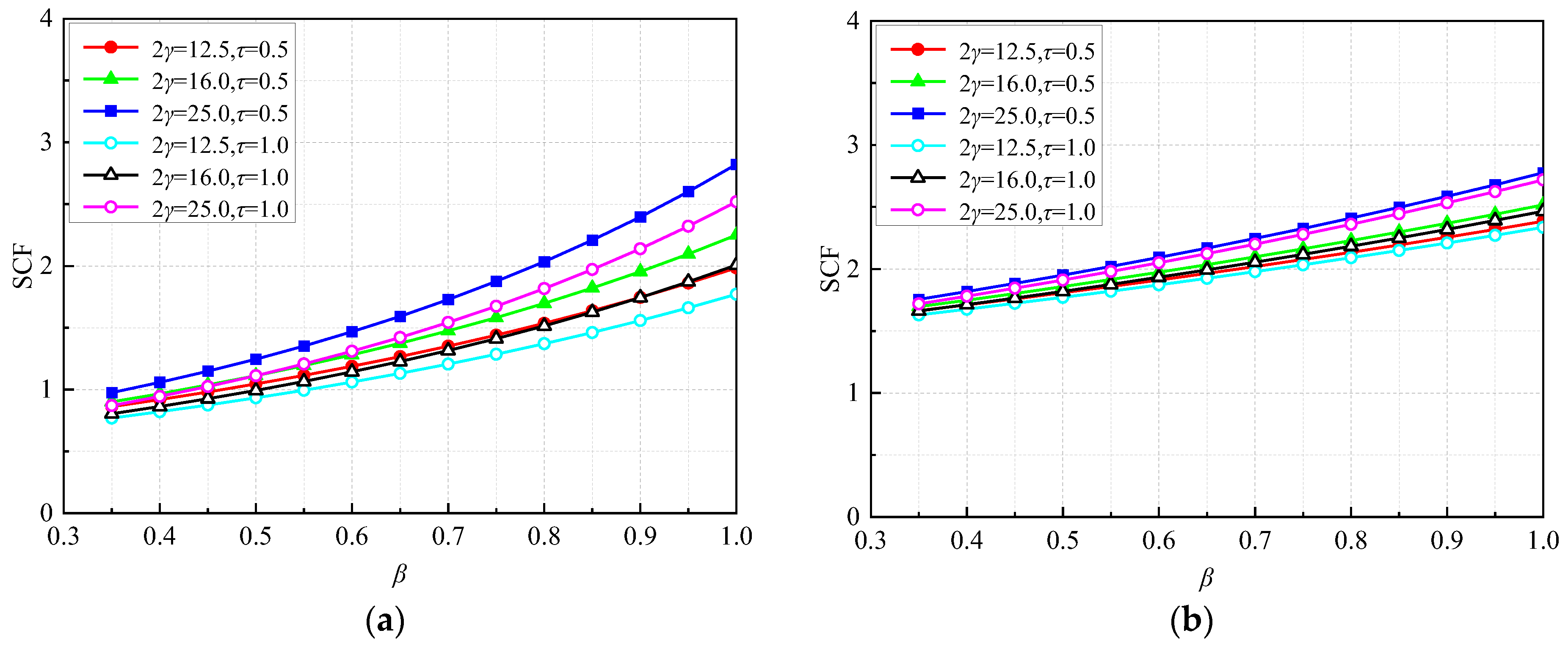
4.3. SCF Formulae and Graphs for In-Plane Bending in the Brace
- (1)
- While keeping 2γ and τ constant, the parabola-like curves of SCFs can be found with the increase of β. The maximum SCFs are found for the medium β values.
- (2)
- While keeping β and τ constant, the higher the 2γ value, the higher the SCF, due to the higher bending deformation. For the higher 2γ value (2γ = 25.0), the maximum SCFs generally occur in the chord at lines B and C. For the lower 2γ value (2γ ≤ 16.0), comparable SCFs can be found in the chord and brace, thereby the SCFs at all the lines need to be checked.
- (3)
- While keeping β and 2γ constant, different influences of τ on the SCFs can be found. The higher the τ value, the lower the SCF in the brace, whereas it has opposite trend in the chord. Moreover, τ has less influence on the brace.
4.4. SCF Formulae and Graphs for Axial Force in the Chord
- (1)
- While keeping 2γ and τ constant, the SCFs increase with the increase of β values, which approximately keeps a linear relationship.
- (2)
- While keeping β constant, the higher the 2γ value and τ value, the higher the SCF at lines C and D.
- (3)
- All the non-dimensional parameters have less influence on the SCFs in the chord.
4.5. SCF Formulae and Graphs for In-Plane Bending in the Chord
- (1)
- The SCFs increase as the values of β and 2γ increase separately, similar to the conclusions of axial force in the chord. However, the SCFs are negatively correlated with τ, contrary to the axial force in the chord.
- (2)
- All the non-dimensional parameters have a much larger influence at line C compared with line D.
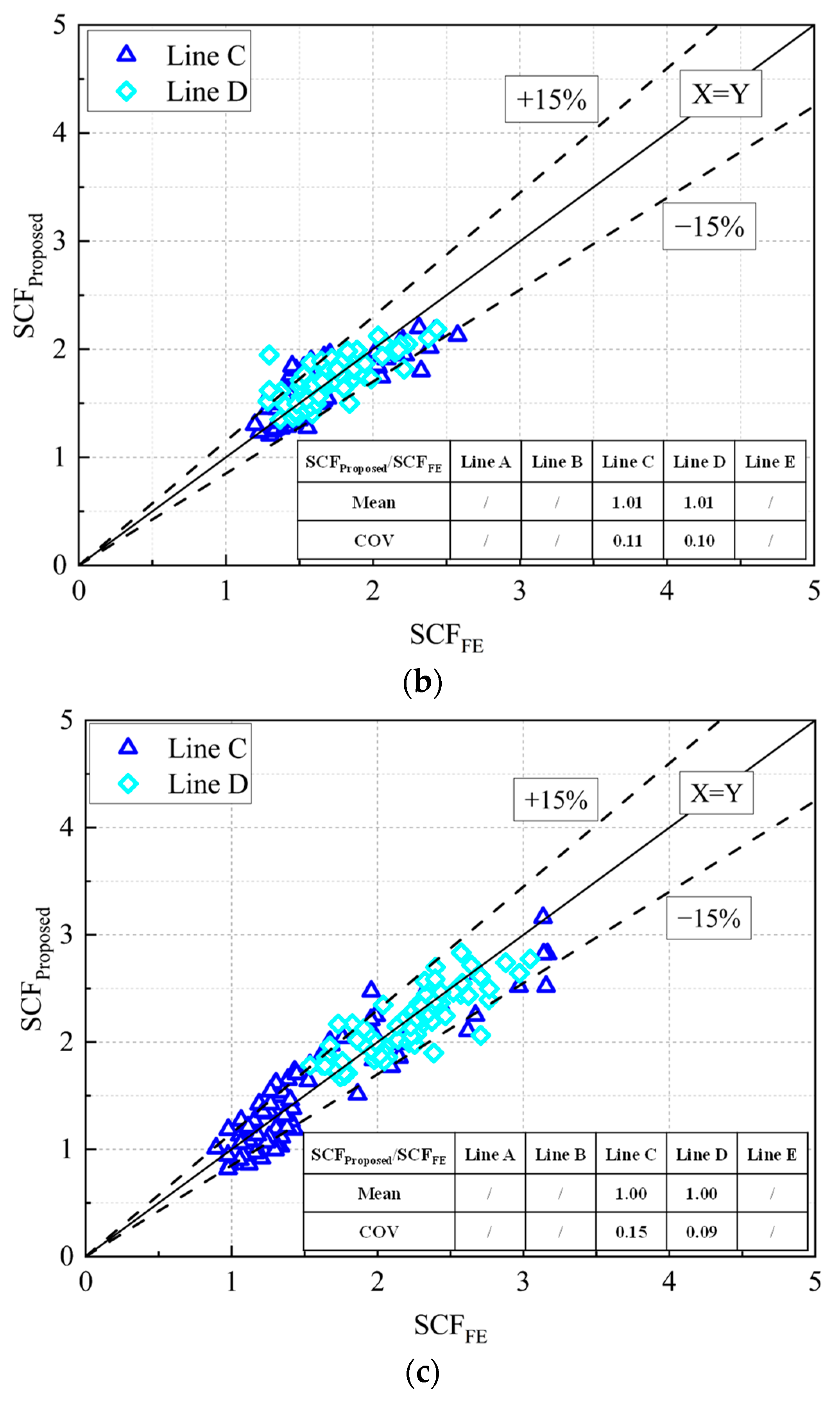
5. Comparisons of SCFs Derived from Formulae and FE Analysis
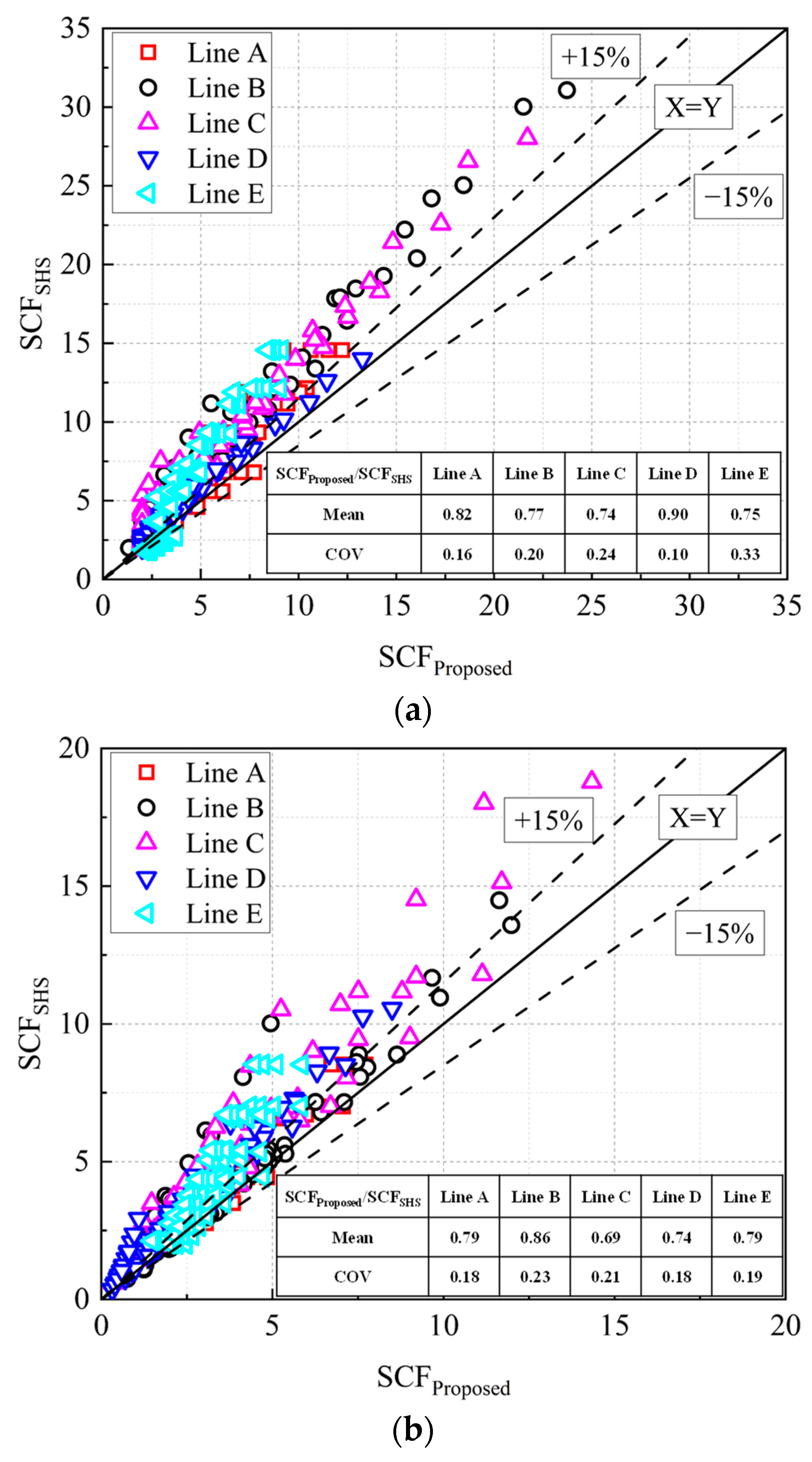
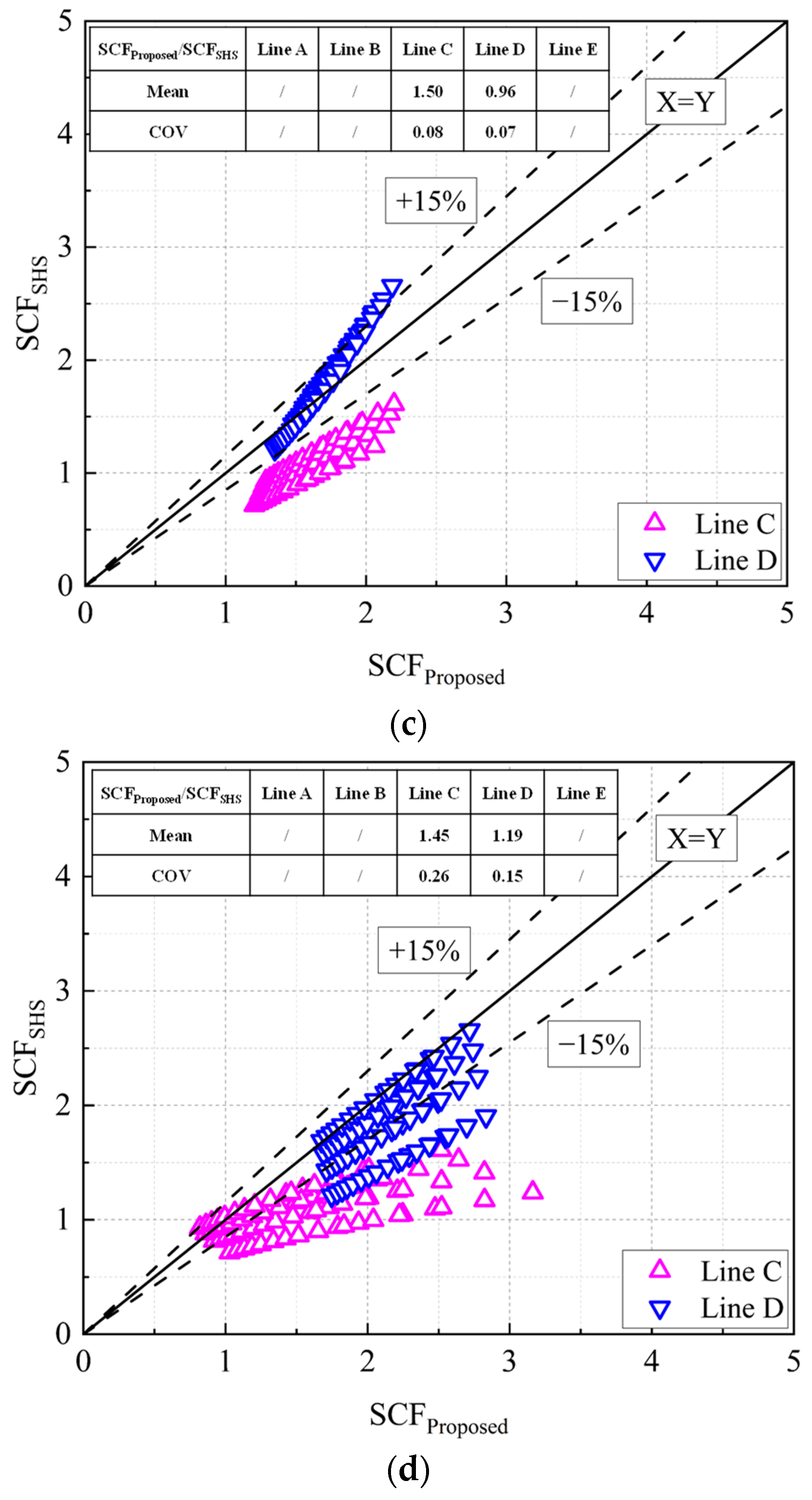
6. Comparisons of SCF Formulae between SHS-CFSHS T-Joints and Empty SHS T-Joints
7. Conclusions
- (1)
- A good agreement with the experimental results indicated that three-dimensional FE models developed by ABAQUS were accurate to capture the SCFs at all hot spot locations.
- (2)
- For in-plane bending in the brace, the maximum SCFs were found to occur at lines B and C for the tick-walled chord (2γ = 25.0). Meanwhile, for the thin-walled (2γ ≤ 16.0) chord, the SCFs at all the lines needed to be checked.
- (3)
- Under axial force in the chord and in-plane bending in the chord, only SCFs at lines C and D needed to be considered. There was a similar trend for SCFs which were positive which correlated with β and 2γ for both load cases. However, for in-plane bending in the chord, the SCFs were negatively correlated with τ, contrary to the axial force in the chord.
- (4)
- The comparisons of the SCFs derived from proposed formulae and the FE analysis indicated a good accuracy of multiple regression analysis. The proposed equations are applicable to the following range of parameters: 0.35 ≤ β ≤ 1.0; 12.5 ≤ 2γ ≤ 25.0 and 0.25 ≤ τ ≤ 1.0.
- (5)
- The comparisons of SCFs between SHS-CFSHS joints based on proposed formulae and empty SHS joints using CIDECT formulae were carried out. There were reductions of 10~26% and 14~31% in the SCFs in SHS-CFSHS joints compared to empty SHS joints for axial force in the brace and in-plane bending in the brace, respectively. In addition, a general increase was found for the loads in the chord. It should be noted that the SCFs caused by loads in the chord were much lower than those caused by loads in the brace.
- (6)
- This investigation focused on the SCF of SHS-CFSHS joints under the in-plane bending moment in the brace, axial force in the chord and the in-plane bending moment in the chord, and proposed corresponding design equations. The debonding between the concrete infill and steel tube should be considered in future work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- van Wingerde, A.M. The fatigue behaviour of T- and X-joint made of square hollow sections. HERON 1992, 37, 1–182. [Google Scholar]
- van Wingerde, A.M.; Packer, J.A.; Wardenier, J. New guidelines for fatigue design of HSS connections. J. Struct. Eng. 1996, 122, 125–132. [Google Scholar]
- van Wingerde, A.M.; Packer, J.A.; Wardenier, J. Criteria for the fatigue assessment of hollow structural section connections. J. Constr. Steel Res. 1995, 35, 71–115. [Google Scholar]
- van Wingerde, A.M.; Packer, J.A.; Wardenier, J. SCF formulae for fatigue design of K-connections between square hollow sections. J. Constr. Steel Res. 1997, 43, 87–118. [Google Scholar]
- Packer, J.A.; Wardenier, J. Stress connectration facors for non-90° X-connections made of square hollow sections. Can. J. Civ. Eng. 1998, 25, 370–375. [Google Scholar]
- Mashiri, F.R.; Zhao, X.L.; Grundy, P. Fatigue tests and design of welded T connections in thin cold-formed square hollow sections under in-plane bending. J. Struct. Eng. 2002, 128, 1413–1422. [Google Scholar]
- Chiew, S.P.; Lee, C.K.; Lie, S.T.; Ji, H.L. Fatigue behaviors of square-to-square hollow section T-joint with corner crack. I: Experimental studies. Eng. Fract. Mech. 2007, 74, 703–720. [Google Scholar]
- Lee, C.K.; Chiew, S.P.; Lie, S.T.; Ji, H.L. Fatigue behaviors of square-to-square hollow section T-joint with corner crack. II: Numerical modeling. Eng. Fract. Mech. 2007, 74, 721–738. [Google Scholar]
- Morgan, M.R.; Lee, M.M.K. Stress concentration factors in tubular K-joints under in-plane moment loading. J. Struct. Eng. 1998, 124, 382–390. [Google Scholar]
- Morgan, M.R.; Lee, M.M.K. Parametric equations for distributions of stress concentration factors in tubular K-joints under out-of-plane moment loading. Int. J. Fatigue 1998, 20, 449–461. [Google Scholar]
- Matti, F.N.; Mashiri, F.R. Experimental and numerical studies on SCFs of SHS T-joints subjected to static out-of-plane bending. Thin Walled Struct. 2020, 146, 106453. [Google Scholar]
- Shao, Y.B. Geometrical effect on the stress distribution along weld toe for tubular T- and K-joints under axial loading. J. Constr. Steel Res. 2007, 63, 1351–1360. [Google Scholar]
- Zhao, X.L.; Packer, J.A. (Eds.) Recommended Fatigue Design Procedure for Welded Hollow Section Joints; IIW doc. XV-1035-99; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- EN 1993-1-9; Eurocode 3(EC3). Design of Steel Structures—Part 1–9: Fatigue. European Committee for Standardization: Brussels, Belgium, 2005.
- Zhao, X.L.; Herion, S.; Packer, J.A.; Puthli, R.S.; Sedlacek, G.; Wardenier, J.; Weynand, K.; Van Wingerde, A.M.; Yeomans, N.F. Design Guide for Circular and Rectangular Hollow Section Welded Joints under Fatigue Loading; CIDECT Design Guide No.8; TÜV-Verlag: Cologne, Germany, 2000. [Google Scholar]
- Liu, Y.; Xiong, Z.; Luo, Y.; Cheng, G.; Liu, G.; Yang, J. Double-composite rectangular truss bridge and its joint analysis. J. Traffic Transp. Eng. 2015, 2, 249–257. [Google Scholar]
- Chen, J.; Chen, J.; Jin, W.L. Experiment investigation of stress concentration factor of concrete-filled tubular T joints. J. Constr. Steel Res. 2010, 66, 1510–1515. [Google Scholar]
- Xu, F.; Chen, J.; Jin, W.L. Experimental investigation of SCF distribution for thin-walled concrete-filled CHS joints under axial tension loading. Thin Walled Struct. 2015, 93, 149–157. [Google Scholar]
- Wang, K.; Tong, L.W.; Zhu, J.; Zhao, X.L.; Mashiri, F.R. Fatigue behavior of welded T-joints with a CHS brace and CFCHS chord under axial loading in the brace. J. Bridge Eng. 2013, 18, 142–152. [Google Scholar]
- Udomworarat, P.; Miki, C.; Ichikawa, A.; Sasaki, E.; Sakamoto, T.; Mitsuki, K.; Hosaka, T. Fatigue and ultimate strengths of concrete filled tubular K-joints on truss girder. J. Struct. Eng. 2000, 46A, 1627–1635. [Google Scholar]
- Udomworarat, P.; Miki, C.; Ichikawa, A.; Komechi, M.; Mitsuki, K.; Hosaka, T. Fatigue performance of composite tubular K-joints for truss type bridge. Struct. Eng. Earthq. Eng. 2002, 19, 65s–79s. [Google Scholar]
- Kim, I.G.; Chung, C.H.; Shim, C.S.; Kim, Y.J. Stress concentration factors of N-joints of concrete-filled tubes subjected to axial loads. Int. Steel Struct. 2014, 14, 1–11. [Google Scholar]
- Tong, L.W.; Xu, G.W.; Yang, D.L.; Mashiri, F.R.; Zhao, X.L. Stress concentration factors in CHS-CFSHS T-joints: Experiments, FE analysis and formulae. Eng. Struct. 2017, 151, 406–421. [Google Scholar]
- Tong, L.W.; Xu, G.W.; Yang, D.L.; Mashiri, F.R.; Zhao, X.L. Fatigue behavior and design of welded tubular T-joints with CHS brace and concrete-filled chord. Thin Walled Struct. 2017, 120, 180–190. [Google Scholar]
- Chen, K.; Huang, H.; Zheng, Q.; Wu, Q.; Nakamura, S. Experimental Research on the Calculating Method of Stress Concentration Factor for CFST K-Joint. J. Struct. Eng. 2023, 149, 04023006. [Google Scholar]
- Matti, F.; Mashiri, F. Stress concentration factors of concrete-filled T-joints under in-plane bending: Experiments, FE analysis and formulae. Materials 2022, 15, 6421. [Google Scholar] [CrossRef]
- Zhao, J.; Xiao, L.; Wei, X.; Li, X. Parametric study and neural network-based prediction for stress concentration factor of concrete-filled steel tubular T-joint. Ocean Eng. 2024, 305, 117972. [Google Scholar]
- Xiao, L.; Wei, X.; Zhao, J.; Wu, C. Hot spot stress concentration factor of CFST T/Y joints based on modified equivalent thickness. Structures 2023, 51, 910–925. [Google Scholar]
- Jiang, L.; Liu, Y.; Fam, A.; Liu, J.; Liu, B. Stress concentration factor parametric formulae for concrete-filled rectangular hollow section K-joints with perfobond ribs. J. Constr. Steel Res. 2019, 160, 579–597. [Google Scholar]
- Jiang, L.; Liu, Y.; Fam, A.; Liu, B.; Pu, B.; Zhao, R. Experimental and numerical analyses on stress concentration factors of concrete-filled welded integral K-joints in steel truss bridges. Thin Walled Struct. 2023, 183, 110347. [Google Scholar]
- Matti, F.N.; Mashiri, F.R. Design formulae for predicting the stress concentration factors of concrete-filled T-joints under out-of-plane bending. Structures 2020, 28, 2073–2095. [Google Scholar]
- Lan, X.; Chan, T.M.; Young, B. Experimental and numerical studies on stress concentration factors of high strength steel fabricated box X-joints. Thin Walled Struct. 2021, 164, 107858. [Google Scholar]
- Jiang, L.; Liu, Y.J.; Fam, A. Stress concentration factors in joints of square hollow section (SHS) brace and concrete-filled SHS chord under axial tension in brace. Thin Walled Struct. 2018, 132, 79–92. [Google Scholar]
- GB50010-2010; Chinese Standard: Code for Design of Concrete Structures. China Standards Press: Beijing, China, 2010. (In Chinese)
- GB50661-2011; Chinese Standard: Code for Welding of Steel Structures. China Architecture & Building Press: Beijing, China, 2011. (In Chinese)
- Feng, R.; Young, B. Design of cold-formed stainless steel tubular T- and X-joints. J. Constr. Steel Res. 2011, 67, 421–436. [Google Scholar]
- Choo, Y.S.; Qian, X.D.; Liew, J.Y.R.; Wardenier, J. Static strength of thick-walled CHS X-joints—Part I. New approach in strength definition. J. Constr. Steel Res. 2003, 59, 1201–1228. [Google Scholar]
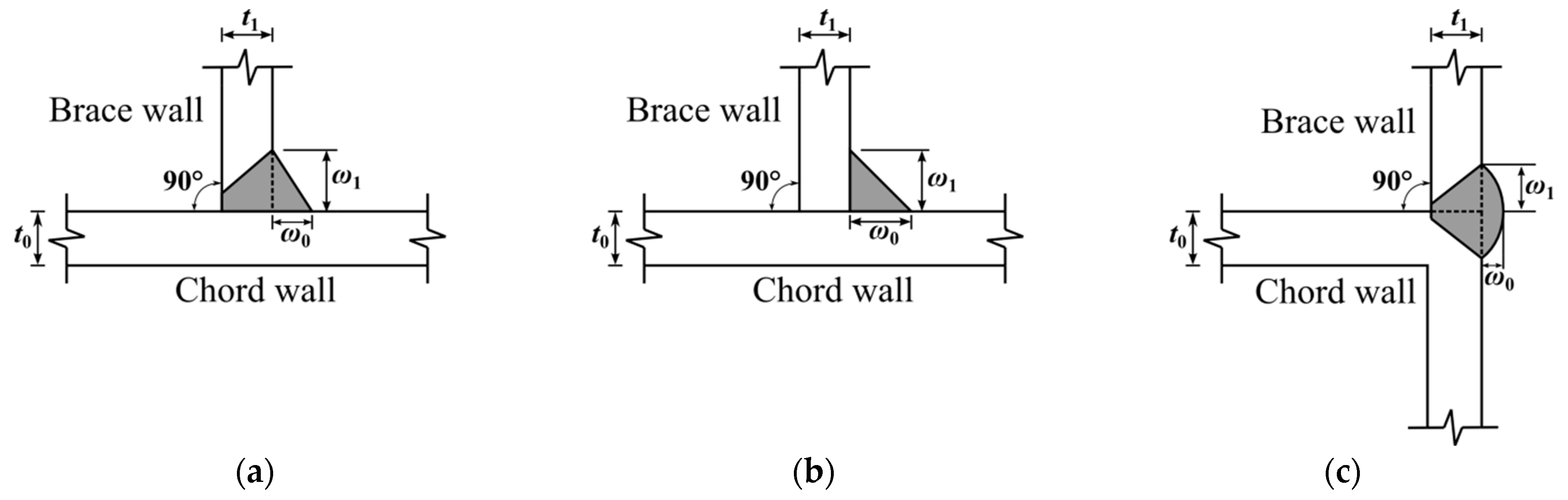


| Types | Application Conditions | ω0 | ω1 |
|---|---|---|---|
| Butt weld | t1 > 8 mm | t1/2 | t1 |
| Fillet weld | t1 ≤ 8 mm | ||
| Weld for full width joints | full width joints | ≥3 mm | t1 |
| Specimen No. | Chord Dimensions (mm) | Brace Dimensions (mm) | SCFEXP | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| b0 | h0 | t0 | L0 | b1 | h1 | t1 | L1 | A | B | C | D | E | |
| 1 | 350 | 350 | 16 | 4130 | 250 | 250 | 16 | 2165 | 12.48 | 15.25 | 17.52 | 15.26 | 6.26 |
| 2 | 350 | 350 | 16 | 4130 | 200 | 200 | 16 | 2165 | 9.39 | 21.84 | 21.74 | 12.06 | 2.00 |
| 3 | 350 | 350 | 16 | 4130 | 200 | 200 | 12 | 2165 | 10.48 | 13.06 | 15.40 | 10.52 | 2.94 |
| 4 | 350 | 350 | 16 | 4130 | 200 | 200 | 10 | 2165 | 11.85 | 14.06 | 13.31 | 11.64 | 5.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Jiang, L.; Wang, X.; Gao, S.; Cui, H.; Liu, J.; Zhou, H. Expressions for Stress Concentration Factors for T-Joints of Hollow and Concrete-Filled Square Cross-Sections for In-Plane Axial and Bending Loads. Symmetry 2024, 16, 1082. https://doi.org/10.3390/sym16081082
Gao L, Jiang L, Wang X, Gao S, Cui H, Liu J, Zhou H. Expressions for Stress Concentration Factors for T-Joints of Hollow and Concrete-Filled Square Cross-Sections for In-Plane Axial and Bending Loads. Symmetry. 2024; 16(8):1082. https://doi.org/10.3390/sym16081082
Chicago/Turabian StyleGao, Liyong, Lei Jiang, Xingzheng Wang, Sheng Gao, Hongxu Cui, Jun Liu, and Hekuan Zhou. 2024. "Expressions for Stress Concentration Factors for T-Joints of Hollow and Concrete-Filled Square Cross-Sections for In-Plane Axial and Bending Loads" Symmetry 16, no. 8: 1082. https://doi.org/10.3390/sym16081082
APA StyleGao, L., Jiang, L., Wang, X., Gao, S., Cui, H., Liu, J., & Zhou, H. (2024). Expressions for Stress Concentration Factors for T-Joints of Hollow and Concrete-Filled Square Cross-Sections for In-Plane Axial and Bending Loads. Symmetry, 16(8), 1082. https://doi.org/10.3390/sym16081082






