On the Spanning Cyclability of k-ary n-cube Networks †
Abstract
1. Introduction
2. Preliminaries
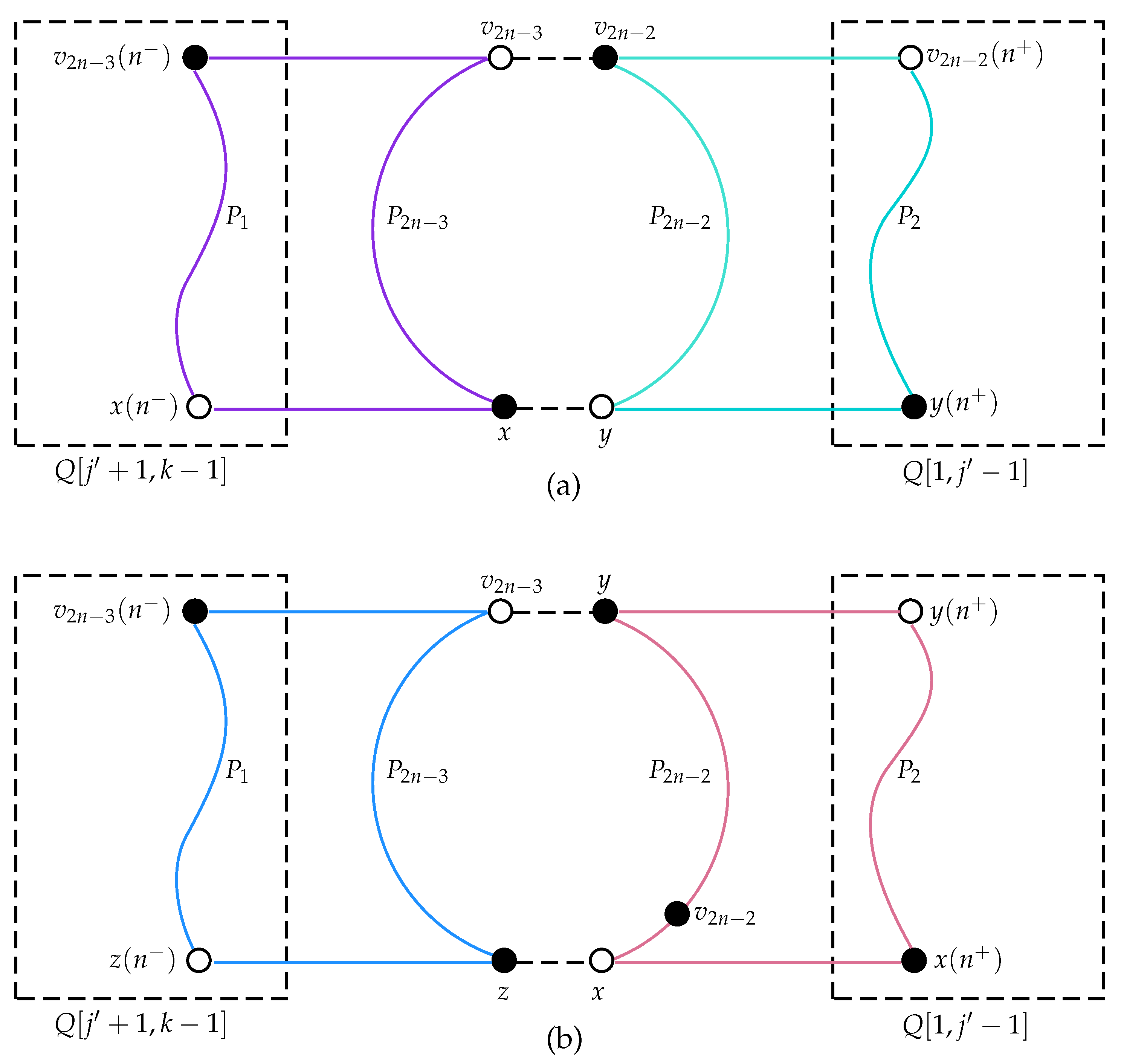
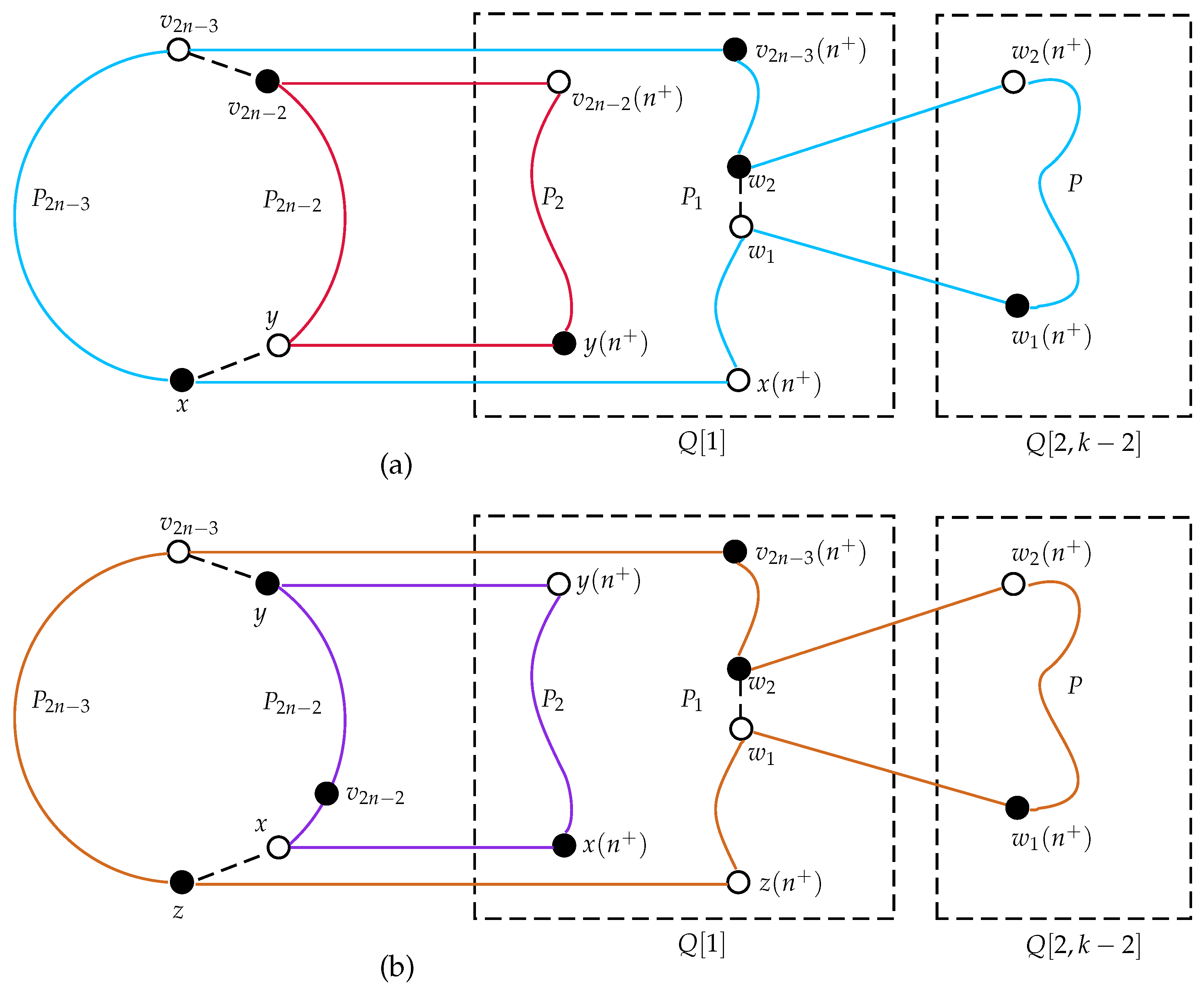
3. Spanning Cyclability of Bipartite -ary -cubes
4. Experimental Results and Analysis
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leighton, F.T. Introduction to Parallel Algorithms and Architecture: Arrays, Trees, Hypercubes; Morgan Kaufmann: San Mateo, CA, USA, 1992. [Google Scholar]
- Saad, Y.; Schultz, M.H. Topological properties of hypercubes. IEEE Trans. Comput. 1988, 37, 867–872. [Google Scholar] [CrossRef]
- Bose, B.; Broeg, B.; Kwon, Y.; Ashir, Y.A. Lee distance and topological propertices of k-ary n-cubes. IEEE Trans. Comput. 1995, 44, 1021–1030. [Google Scholar] [CrossRef]
- Dally, W.J. Performance analysis of k-ary n-cube interconnection networks. IEEE Trans. Comput. 1990, 19, 775–785. [Google Scholar] [CrossRef]
- Xu, J.-M. Topological Structure and Analysis of Interconnection Networks; Kluwer Academic Publishers: Boston, MA, USA, 2001. [Google Scholar]
- Xu, J.-M.; Ma, M. A survey on cycle and path embedding in some networks. Front. Math. China 2009, 4, 217–252. [Google Scholar] [CrossRef]
- Hsieh, S.-Y.; Chen, G.H.; Ho, C.W. Fault-free Hamiltonian cycles in faulty arrangement graphs. IEEE Trans. Parallel Distrib. Syst. 1999, 10, 223–237. [Google Scholar] [CrossRef]
- Lin, T.; Hsieh, S.-Y.; Juan, J.S. Embedding cycles and paths in product networks and their applications to multiprocessor systems. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1081–1089. [Google Scholar]
- Wang, S.; Feng, K.; Zhang, S.; Li, J. Embedding long cycles in faulty k-ary 2-cubes. Appl. Math. Comput. 2012, 218, 5409–5413. [Google Scholar] [CrossRef]
- Xu, M.; Hu, X.D.; Xu, J.-M. Edge-pancyclicity and Hamiltonian laceability of the balanced hypercubes. Appl. Math. Comput. 2007, 189, 1393–1401. [Google Scholar] [CrossRef]
- Sabir, E.; Fan, J.; Meng, J.; Cheng, B. Structure fault-tolerant Hamiltonian cycle and path embeddings in bipartite k-ary n-cube networks. IEEE Trans. Rel. 2024, 73, 257–269. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, S. Embedding hamiltonian paths in k-ary n-cubes with conditional edge faults. Theor. Comput. Sci. 2011, 412, 6570–6584. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, S.; Yang, Y. Hamiltonian path embeddings in conditional faulty k-ary n-cubes. Inf. Sci. 2014, 268, 463–488. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, L. Hamiltonian paths of k-ary n-cubes avoiding faulty links and passing through prescribed linear forests. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 1752–1760. [Google Scholar] [CrossRef]
- Zhuang, H.; Li, X.-Y.; Chang, J.-M.; Wang, D. An efficient algorithm for Hamiltonian path embedding of k-ary n-cubes under the partitioned edge fault model. IEEE Trans. Parallel Distrib. Syst. 2023, 34, 1802–1815. [Google Scholar] [CrossRef]
- Zhuang, H.; Li, X.-Y.; Chang, J.-M.; Lin, C.-K.; Liu, X. Embedding Hamiltonian paths in k-ary n-cubes with exponentially-many faulty edges. IEEE Trans. Comput. 2023, 72, 3245–3258. [Google Scholar] [CrossRef]
- Chen, X.-B. Paired 2-disjoint path covers of multidimensional torus networks with faulty edges. Inf. Process. Lett. 2016, 116, 107–110. [Google Scholar] [CrossRef]
- Li, J.; Melekian, C.; Zuo, S.; Cheng, E. Unpaired many-to-many disjoint path covers on bipartite k-ary n-cube networks with faulty elements. Int. J. Found. Comput. Sci. 2020, 31, 371–383. [Google Scholar] [CrossRef]
- Shih, Y.-K.; Kao, S.-S. One-to-one disjoint path covers on k-ary n-cubes. Theor. Comput. Sci. 2011, 412, 4513–4530. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, S. Many-to-many disjoint path covers in k-ary n-cubes. Theor. Comput. Sci. 2013, 491, 103–118. [Google Scholar] [CrossRef]
- Hao, R.-X.; Zhang, R.; Feng, Y.-Q.; Zhou, J.-X. Hamiltonian cycle embedding for fault tolerance in balanced hypercubes. Appl. Math. Comput. 2014, 244, 447–456. [Google Scholar] [CrossRef]
- Lin, C.-K.; Tan, J.-M.; Hsu, L.-H.; Kung, T.-L. Disjoint cycles in hypercubes with prescribed vertices in each cycle. Discrete Appl. Math. 2013, 161, 2992–3004. [Google Scholar] [CrossRef]
- Yang, M.-C.; Hsu, L.-H.; Hung, C.-N.; Cheng, E. 2-spanning cyclability problems of some generalized Petersen graphs. Discuss. Math. Graph Theory 2020, 40, 713–731. [Google Scholar]
- Qiao, H.; Meng, J.; Sabir, E. Embedding spanning disjoint cycles in enhanced hypercube networks with prescribed vertices in each cycle. Appl. Math. Comput. 2022, 435, 127481. [Google Scholar] [CrossRef]
- Qiao, H.; Sabir, E.; Meng, J. The spanning cyclability of Cayley graphs generated by transposition trees. Discrete Appl. Math. 2023, 328, 60–69. [Google Scholar] [CrossRef]
- Wu, W.; Sabir, E.; Qiao, H. Embedding spanning disjoint cycles in augmented cube networks with prescribed vertices in each cycle. Int. J. Parall. Eme. Distr. Sys. 2023, 38, 342–361. [Google Scholar] [CrossRef]
- Wu, W.; Sabir, E. Embedding spanning disjoint cycles in hypercube networks with prescribed edges in each cycle. Axioms 2023, 12, 861. [Google Scholar] [CrossRef]
- Hsu, L.-H.; Lin, C.-K. Graph Theory and Interconnection Networks; CRC Press: New York, NY, USA, 2008. [Google Scholar]
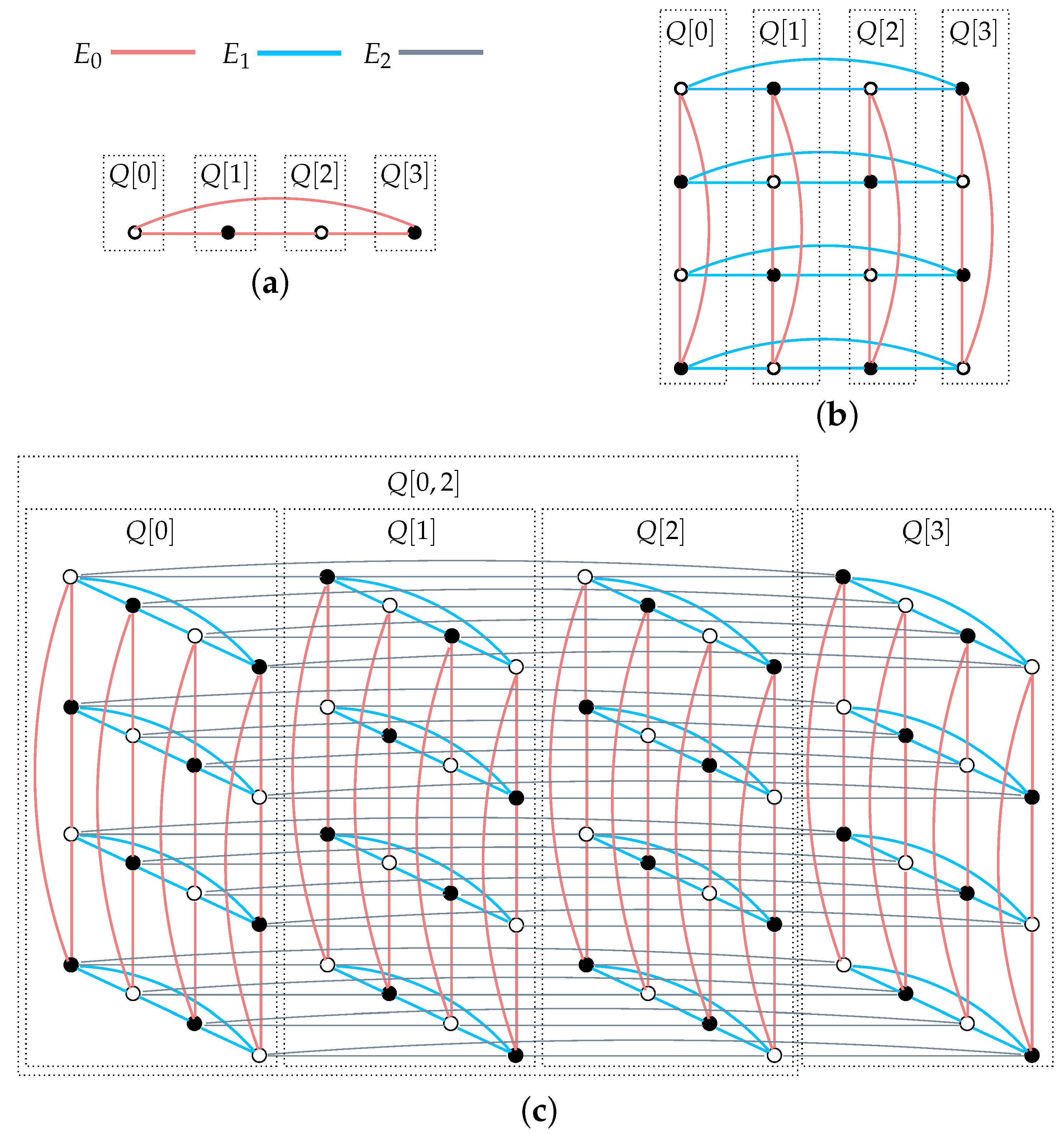
| Prescribed Vertices | Spanning Disjoint Cycles |
|---|---|
| {000, 111, 222, 333} | |
| {000, 010, 102, 212, 322} | |
| {000, 001, 010, 113, 202} | |
| {000, 020, 022, 100, 110} | |
| {000, 010, 001, 011} | |
| {000, 003, 030, 033, 133} | |
| {000, 010, 012, 022, 021} | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, H.; Zhang, W. On the Spanning Cyclability of k-ary n-cube Networks. Symmetry 2024, 16, 1063. https://doi.org/10.3390/sym16081063
Qiao H, Zhang W. On the Spanning Cyclability of k-ary n-cube Networks. Symmetry. 2024; 16(8):1063. https://doi.org/10.3390/sym16081063
Chicago/Turabian StyleQiao, Hongwei, and Wanping Zhang. 2024. "On the Spanning Cyclability of k-ary n-cube Networks" Symmetry 16, no. 8: 1063. https://doi.org/10.3390/sym16081063
APA StyleQiao, H., & Zhang, W. (2024). On the Spanning Cyclability of k-ary n-cube Networks. Symmetry, 16(8), 1063. https://doi.org/10.3390/sym16081063





