Dynamics of Symmetrical Discontinuous Hopfield Neural Networks with Poisson Stable Rates, Synaptic Connections and Unpredictable Inputs

Abstract

The purpose of this paper is to study the dynamics of Hopfield neural networks with impulsive effects, focusing on Poisson stable rates, synaptic connections, and unpredictable external inputs. Through the symmetry of impulsive and differential compartments of the model, we follow and extend the principal dynamical ideas of the founder. Specifically, the research delves into the phenomena of unpredictability and Poisson stability, which have been examined in previous studies relating to models of continuous and discontinuous neural networks with constant components. We extend the analysis to discontinuous models characterized by variable impulsive actions and structural ingredients. The method of included intervals based on the B-topology is employed to investigate the networks. It is a novel approach that addresses the unique challenges posed by the sophisticated recurrence.

1. Introduction

Neuroscience is a rapidly developing field, and researchers are constantly studying various aspects of brain activity and neural networks. Understanding the oscillatory and recurrent behaviors in neural networks is critical for advancements in various fields such as neuroscience, artificial intelligence, and complex system modeling.

John J. Hopfield, in papers [1,2], presented a model,

$$\begin{array}{c}\hfill {\displaystyle y_i^{\prime }\left(t\right)=a_i{y}_i\left(t\right)+\sum _{j=1}^p{b}_{ij}{f}_j\left(y_j\left(t\right)\right)+c_i\left(t\right),}\end{array}$$

(1)

where $t,y_i,i=1,\dots p,$ are from the real axis, $y_i\left(t\right)$ and $y_i^{\prime }\left(t\right)$, $i=1,\dots p$, denote the membrane potentials of neuron i and their rates of change; and p is the total number of neurons in the network. Moreover, $a_i,i=1,\dots ,p$ are rates of self-regulation or reset potentials for neurons $i=1,\dots ,p$ when they are isolated; $f_j$, $j=1,2,\dots ,p$, are the activation functions for neurons $j,j=1,\dots ,p$, which determine how the membrane potential influences other neurons; $b_{ij}$, $i,j=1,2,\dots ,p$ are the weights of the connection between neurons $j,$ and $i,$ $i,j=1,2,\dots ,p$; $c_i\left(t\right)$, $i=1,2,\dots ,p$, are input functions representing external stimuli or inputs to neurons $i,$ $i=1,2,\dots ,p$.

Impulsive neural networks are specifically designed to handle sudden input data or changes in system dynamics. They are inspired by how biological neurons respond to stimuli, such as pain or temperature changes, by transmitting corresponding signals to the brain. Just as biological neurons can undergo sudden changes in their state, impulsive artificial neural networks are engineered to mimic this behavior and adapt to sudden changes or disturbances in the input. This unique design makes them particularly useful in scenarios where the input data are prone to sudden changes, such as in applied mathematics.

Recent studies have emphasized the exploration of chaotic and recurrent signals within neural networks [3,4,5]. Recurrence types, such as periodicity, quasi-periodicity, and Poisson stable motions, originate in the theory of celestial dynamics and have been applied to various areas of applied mathematics. Currently, the theory of oscillations is widely developed in a chaotic sense, and more than the classical functions are needed to describe complex systems’ dynamics. Therefore, new models and solutions of models and new functions are required. This is why the unpredictable functions were introduced [6].

The proof of the stability of unpredictable functions is based on the method of included intervals, which is a new and efficient instrument for verifying convergence. This method, which is a significant contribution to the field, extends to spaces of discontinuous functions based on the B-topology, further enhancing its applicability and relevance in the field of applied mathematics. It plays a crucial role in our understanding of the behavior of impulsive neural networks.

In numerous real-world scenarios, continuous processes within neural network systems are often subject to abrupt interruptions caused by impulsive events or impacts [7,8,9,10,11]. This study investigates the dynamics of such discontinuous Hopfield neural networks, emphasizing the symmetrical nature of the model. By treating impact actions as the limits of continuous processes of short duration, we establish that the functional structure of impulsive equations mirrors that of the differential ones. The symmetrical property of the model facilitates a detailed examination of network states during sharp jumps, enabling the exploration of complex models of processes with impulses. The symmetry ensures that the mathematical model accurately captures the behavior of these processes, and the research follows the dynamical ideas of J. Hopfield [1,2]. This is why we maintain a structural symmetry between the impulsive and differential parts of the models [5,12].

In this article, we delve into the unpredictability and Poisson stability of impulsive Hopfield-type neural networks with variable coefficients, which is a novel area of study. We also explore sequences that characterize Poisson stability and unpredictability synchronized for external input and output solutions. This research adds to the existing body of knowledge and provides new insights into the behavior of impulsive neural networks.

Throughout the paper, $\mathbb{N}$, $\mathbb{Z}$ and $\mathbb{R}$ denote the sets of natural numbers, integers, and real numbers, respectively. Introduce the norm

${\displaystyle ∥\psi ∥=\underset{i}{max}\left|{\psi }_i\right|,i=1,2,\dots ,p,}$ where $\left|·\right|$—is the absolute value and p is a fixed natural number; $\psi =({\psi }_1,\dots ,{\psi }_p)$ is a vector, such that ${\psi }_i\in \mathbb{R},i=1,2,\dots ,p$. Consequently, ${\displaystyle ∥D∥=\underset{i}{max}\sum _{j=1}^p\left|d_{ij}\right|,i=1,2,\dots ,p}$, means the norm for the $n\times n$ matrix $D=\left\{d_{ij}\right\}$, $i,j=1,$ $2,\dots ,p$.

We investigate, in this paper, the existence and stability of unpredictable solutions of symmetrical impulsive discontinuous Hopfield-type neural networks of the form

$$\begin{array}{c}{\displaystyle y_i^{\prime }\left(t\right)=a_i\left(t\right)y_i\left(t\right)+\sum _{j=1}^p{b}_{ij}\left(t\right)f_j\left(y_j\left(t\right)\right)+c_i\left(t\right),t\ne {\theta }_k,}\\ {\displaystyle \mathsf{\Delta }{y}_i{|}_{t={\theta }_k}={\alpha }_{ik}{y}_i\left({\theta }_k\right)+\sum _{j=1}^p{\beta }_{ijk}{g}_j\left(y_j\left({\theta }_k\right)\right)+{\gamma }_{ik},}\end{array}$$

(2)

where $t,y_i\in \mathbb{R}$, $i=1,\dots p$, $y_i\left(t\right)$ correspond to the membrane potential of the unit i, $i=1,\dots p$, and p is the number of neurons in the network. The sequence ${\theta }_k,k\in \mathbb{Z}$ of discontinuity moments is increasing, such that $|{\theta }_k|\to \infty$ as $k\to \infty .$

Similarly to the differential part of the model, the coefficients ${\alpha }_{ik},i=1,2,\dots ,p$, and $k\in \mathbb{Z}$ in the impulsive equation are constants of self-regulation for the units or reset of potentials. When the units are isolating, the constants ${\beta }_{ijk}$, $i,j=1,2,\dots ,p$, $k\in \mathbb{Z}$, denote the weights for connection between units j and i, while $g_j$ and $j=1,2,\dots ,p$ are activation vectors, and the sequences ${\gamma }_{ik}$, $i=1,2,\dots ,p,k\in \mathbb{Z}$, are external impulses for the network. One can see that the impulsive part of the model possesses the same structure as the differential part. This is why we refer to the model as symmetrical one.

Suppose impact actions are considered as limits of continuous ones. In that case, the jump presentations must admit the functional structure of the differential equation. Hence, considering neural networks with impulses mimicking the structure of continuous rates is of great interest. In our research, we have proposed a neural network with newly structured impacts, completely imitating the rates. Our proposal makes excellent sense for applications, as impacts are limitations of their rate counterparts. Consequently, the issues which motivated J. Hopfield are now valid for the model under investigation in all of its parts. Since the impulsive actions are compatible with the differential equation in this study, it covers all similar neural networks considered previously.

The symmetry is completely or partially ignored in the literature [7,8,9,10,11,13,14,15,16,17], but the arguments above prove that it must be considered if one wants to conduct effective research on this topic. It has to be mentioned that ignorance on this topic is either due to the theoretical difficulties of impulsive systems or the absence of biological and engineering arguments for novelty. We are applying the experience accumulated in the books [18,19] for discontinuous dynamics. Moreover, we are the first to introduce the symmetry in [12], where mathematical and biological arguments have been formulated. The first types are based on the limiting processes, which are standardized to obtain discrete analogs of continuous models, and the second one appeals to the founders’ original ideas, such as those presented by J. Hopfield [1,2]. We provide the initial explanation for the model in the hope that neuroscience specialists will accept and adapt our suggestions further. The symmetry will open up new possibilities for productive application of the methods introduced and developed within the last few years for various types of impulsive systems [20,21,22] and networks [23,24,25]. Another interesting opportunity involves combining methods for discontinuous dynamics with those for synchronization [26,27].

We assume that $a_i\left(t\right)$, $b_{ij}\left(t\right)$, $c_i\left(t\right)$, $f_j,g_j:\mathbb{R}\to {\mathbb{R}}^p$ are continuous functions and the coefficients ${\alpha }_{ik}$, ${\beta }_{ijk}$, and ${\gamma }_{ik}$ are real numbers.

The present paper continues what was initiated in the article [12], where impulsive neural networks of the following form were studied:

$$\begin{array}{c}{\displaystyle x_i^{\prime }\left(t\right)=a_i{x}_i\left(t\right)+\sum _{j=1}^p{b}_{ij}{f}_j\left(x_j\left(t\right)\right)+c_i\left(t\right),t\ne {\theta }_k,}\\ {\displaystyle \mathsf{\Delta }{x}_i{|}_{t={\theta }_k}={\alpha }_i{x}_i\left({\theta }_k\right)+\sum _{j=1}^p{\beta }_{ij}{g}_j\left(x_j\left({\theta }_k\right)\right)+{\gamma }_{ik}.}\end{array}$$

(3)

It deserves to be emphasized that constancy dominates in coefficients of the model. Precisely, rates of self-regulation $a_i,{\alpha }_i,i=1,\dots ,p$, activation functions $f_i,g_i$, $i=1,2,\dots ,p$, connection weights $b_{ij},{\beta }_{ij}$, and $i,j=1,2,\dots ,p$ are real constants. This is not surprising, since traditionally, the networks have fixed connection weights or coefficients. However, there are extensions and variations of the Hopfield model that introduce variable coefficients. These modifications can allow for more flexible and adaptive behavior [28,29,30,31,32,33,34,35,36]. The dynamics of networks will still involve updating neuron states iteratively until the network reaches a stable state or settles into a limit cycle. It is clear that with variable coefficients, the convergence properties and stability of network states may change dynamically as the coefficients are adjusted. Networks with variable components can be applied to tasks where the underlying relationships or patterns are not fixed and may change over time, for example, in pattern recognition tasks where the importance of features varies depending on context, or in adaptive control systems where the network needs to learn and adjust to changing environments.

Another reason for the study of the system (2) besides the model (3) is the theoretical challenges connected to sophisticated dynamics of unpredictability, which now is more saturated in the model’s interiors. We must analyze the role of unpredictable components and consider sufficiency of the unpredictability combined with Poisson stability. That is, we must not simply involve variable coefficients to make the research align more closely with the applications and increase its mathematical merits; we must also create more wide-reaching structural possibilities.

2. Preliminaries

In what follows, we will use the vector form of the model because of its effectiveness in representing mathematical concepts and the proof of the main statements. For this purpose, throughout the paper we shall denote $\mathcal{A}\left(t\right)$, $\mathcal{B}\left(t\right)$ as $p\times p$ matrix functions, as follows,

$$\begin{array}{c}\hfill \mathcal{A}\left(t\right)=\left(\begin{array}{cccc}{a}_1\left(t\right)& 0& \dots & 0\\ 0& a_2\left(t\right)& \dots & 0\\ ⋮& ⋮& \dots & ⋮\\ 0& 0& \dots & a_p\left(t\right)\end{array}\right),\mathcal{B}\left(t\right)=\left(\begin{array}{cccc}{b}_{11}\left(t\right)& b_{12}\left(t\right)& \dots & b_{1p}\left(t\right)\\ b_{21}\left(t\right)& b_{22}\left(t\right)& \dots & b_{2p}\left(t\right)\\ ⋮& ⋮& \dots & ⋮\\ b_{p1}\left(t\right)& b_{p2}\left(t\right)& \dots & b_{pp}\left(t\right)\end{array}\right),t\in \mathbb{R}.\end{array}$$

Moreover, $A_k$ and $B_k$ as $p\times p$ matrix-sequences

$$\begin{array}{c}\hfill A_k=\left(\begin{array}{cccc}{\alpha }_{1k}& 0& \dots & 0\\ 0& {\alpha }_{2k}& \dots & 0\\ ⋮& ⋮& \dots & ⋮\\ 0& 0& \dots & {\alpha }_{pk}\end{array}\right),B_k=\left(\begin{array}{cccc}{\beta }_{11k}& {\beta }_{12k}& \dots & {\beta }_{1pk}\\ {\beta }_{21k}& {\beta }_{22k}& \dots & {\beta }_{2pk}\\ ⋮& ⋮& \dots & ⋮\\ {\beta }_{p1k}& {\beta }_{p2k}& \dots & {\beta }_{ppk}\end{array}\right),k\in \mathbb{Z},\end{array}$$

and, $F\left(y\right)$, $\mathcal{C}\left(t\right)$, $G\left(y\right)$ are $p\times 1$ vector functions and ${\mathsf{\Gamma }}_k$ is $p\times 1$ vector sequence, of the following vector form:

$$\begin{array}{c}\hfill F\left(y\right)=\left(\begin{array}{c}{f}_1\left(y_1\right)\\ f_2\left(y_2\right)\\ ⋮\\ f_p\left(y_p\right)\end{array}\right),\mathcal{C}\left(t\right)=\left(\begin{array}{c}{c}_1\left(t\right)\\ c_2\left(t\right)\\ ⋮\\ c_p\left(t\right)\end{array}\right),G\left(y\right)=\left(\begin{array}{c}{g}_1\left(y_1\right)\\ g_2\left(y_2\right)\\ ⋮\\ g_p\left(y_p\right)\end{array}\right),{\mathsf{\Gamma }}_k=\left(\begin{array}{c}{\gamma }_{1k}\\ {\gamma }_{2k}\\ ⋮\\ {\gamma }_{pk}\end{array}\right),t\in \mathbb{R},k\in \mathbb{Z}.\end{array}$$

Thus, using the suggested notations, the symmetric discontinuous Hopfield-type neural networks (2) can be written as follows:

$$\begin{array}{ccc}\hfill & & y^{\prime }=\mathcal{A}\left(t\right)y+\mathcal{B}\left(t\right)F\left(y\right)+\mathcal{C}\left(t\right),t\ne {\theta }_k,\hfill \\ & & \mathsf{\Delta }y{|}_{t={\theta }_k}=A_{k}y+B_{k}G\left(y\right)+{\mathsf{\Gamma }}_k,\hfill \end{array}$$

(4)

where $y=colon(y_1,\dots ,y_p)\in {\mathbb{R}}^p$, $t\in \mathbb{R}$, $k\in \mathbb{Z}$.

2.1. Poisson Stable and Unpredictable Continuous and Discontinuous Functions

Let us provide the basic definitions and useful lemmas.

Definition 1 

([37]). A sequence ${\kappa }_i,i\in \mathbb{Z}$ in $\mathbb{R}$ is called Poisson stable, provided that it is bounded and there exists a sequence $l_n\to \infty$ and $n\in \mathbb{N}$ of positive integers which satisfies ${\kappa }_{i+l_n}\to {\kappa }_i$ as $n\to \infty$ on bounded intervals of integers.

Definition 2 

([37]). A uniformly continuous and bounded function $u:\mathbb{R}\to {\mathbb{R}}^p$ is Poisson stable if there exists a sequence $t_n$ which diverges to infinity, such that $u(t+t_n)\to u\left(t\right)$ as $n\to \infty$ uniformly on compact subsets of $\mathbb{R}$.

Consider sequences of real numbers $t_n,{\theta }_k$, with indices $n\in \mathbb{N},k\in \mathbb{Z}$. They are assumed to strictly increase with regard to the indices. Sequence ${\theta }_k,k\in \mathbb{Z}$ is unbounded in both directions. Moreover, it satisfies $\underline{\theta }\le {\theta }_{k+1}-{\theta }_k\le \overline{\theta }$ with positive numbers $\underline{\theta }$, $\overline{\theta }$. We provide the description of a Poisson couple in the following definition.

Definition 3 

([12]). A couple $(t_n,{\theta }_k)$ of sequences $t_n,{\theta }_k$, $n\in \mathbb{N},k\in \mathbb{Z}$, is called a Poisson couple if there exists a sequence $l_n$, $n\in \mathbb{N}$, which diverges to infinity, such that

$${\theta }_{k+l_n}-t_n-{\theta }_k\to 0asn\to \infty ,$$

(5)

uniformly on each bounded interval of integers k.

Definition 4 

([18]). A sequence ${\tau }_k$, $k\in \mathbb{Z}$ is said to be part of the $(w,p)-$ property if there exists a positive real number w and integer p which satisfy ${\tau }_{k+p}-{\tau }_k=w$ for all $k\in \mathbb{Z}$.

Lemma 1 

([12]). Assume that sequences $t_n,{\theta }_k$, $n\in \mathbb{N},k\in \mathbb{Z}$, satisfy the following conditions

(i) 

sequence ${\theta }_k$ admits the $(w,p) -$ property;

(ii) 

$t_n=nw$, where $n\in \mathbb{N}$;

then $(t_n,{\theta }_k)$ is a Poisson couple.

Definition 5 

([18]). Two piecewise continuous functions $F\left(t\right)$ and $G\left(t\right)$ from $\mathcal{D}$ are said to be $ϵ$—equivalent on a bounded interval J if the points of discontinuity of the functions $F\left(t\right)$ and $G\left(t\right)$ in J can be respectively numerated ${\theta }_i^F$ and ${\theta }_i^G$, $i=1,2,\dots ,k$, such that $|{\theta }_i^F-{\theta }_i^G|<ϵ$ for each $i=1,2,\dots ,k$, and $\left|\right|F\left(t\right)-G\left(t\right)\left|\right|<ϵ$ for each $t\in J$, except those between ${\theta }_i^F$ and ${\theta }_i^G$ for each i.

In the case that F and G are $ϵ$—equivalent on J, we also say that the functions are in $ϵ$—neighborhoods of each other. The topology defined with the aid of such neighborhoods is called the B-topology [18].

Let us consider the set $\mathcal{D}$ of conditional uniform continuous vector functions $v\left(t\right)=(v_1\left(t\right),v_2\left(t\right),\dots ,v_p\left(t\right))$, $v_i\left(t\right):\mathbb{R}\to \mathbb{R}$, $i=1,2,\dots ,p$. The functions are continuous except at a countable set of moments where they exhibit left continuity. The sets of discontinuity points are unbounded from both sides and do not have finite accumulation points. There is no requirement for the discontinuity moments to be common across functions in $\mathcal{D}.$

We will use the following concepts, such as conditional uniform continuity and $B$−topology from [18], which create a framework for understanding the Poisson stable behavior of discontinuous functions.

Definition 6 

([12]). An element $v\left(t\right)$ of $\mathcal{D}$ with discontinuity moments ${\theta }_k,k\in \mathbb{Z}$, is said to be a discontinuous Poisson stable function, if there exists a sequence $t_n\to \infty$ of real numbers such that $(t_n,{\theta }_k)$, $n\in \mathbb{N},k\in \mathbb{Z}$ is a Poisson couple and $v(t+t_n)\to v\left(t\right)$ as $n\to \infty$ on each bounded interval of real numbers in B topology.

The sequence $t_n$ in the last definition is called the Poisson or convergence sequence.

As one can see from the Definition 6 for discontinuous Poisson stability, we need a convergence sequence $t_n$, which is common for both the function convergence and discontinuity points ${\theta }_k,k\in \mathbb{Z}$, which are connected as Poisson couple $(t_n,{\theta }_k)$.

Then, we write $\widehat{\left[\xi ,\zeta \right]},\xi ,\zeta \in \mathbb{R}$ to denote the interval $[\xi ,\zeta ]$, if $\xi \le \zeta$ and interval $[\zeta ,\xi ]$, if $\zeta <\xi$.

Definition 7 

([12]). A discontinuous Poisson stable function $v\left(t\right)$ of $\mathcal{D}$ with discontinuity moments ${\theta }_k,k\in \mathbb{Z}$ and convergence sequence $t_n$ is said to be discontinuous unpredictable, provided that $(t_n,{\theta }_k)$, $n\in \mathbb{N},k\in \mathbb{Z}$, is a Poisson couple, and there exist positive numbers ${ϵ}_0,\delta$ and sequences $s_n$ of real numbers and $m_n$ of integers, both of which diverges to infinity such that interval $[s_n-\delta ,s_n+\delta ]\subseteq [\widehat{{\theta }_{m_n},({\theta }_{m_n+l_n}}-t_n)]$ does not contain discontinuity points of $v\left(t\right)$ and $v(t+t_n)$, and $\parallel v(t+t_n)-v\left(t\right)\parallel \ge {ϵ}_0$ on the interval.

The divergence estimated by ${ϵ}_0$ is said to be separation property, and $s_n$ is the divergence sequence.

In what follows, we shall say that $v\left(t\right)$ is a discontinuous unpredictable function with Poisson couple $(t_n,{\theta }_k)$ and divergence sequence $s_n$.

2.2. The “Diagonal” Poisson Stability of the Linear Homogenous Impulsive System

Let us denote by $Y(t,s)$ the transition matrix, [18], of the system associated with (4),

$$\begin{array}{c}{y}^{\prime }\left(t\right)=\mathcal{A}\left(t\right)y\left(t\right),t\ne {\theta }_k,\\ {\mathsf{\Delta }y|}_{t={\theta }_k}=A_{k}y\left({\theta }_k\right),\end{array}$$

(6)

where $t\in \mathbb{R}$.

It is assumed, in the paper, that

(C1)

$∥Y(t,s)∥\le K{e}^{\lambda (t-s)}$ with constants $K\ge 1$ and $\lambda <0$.

Also, the following assertion is needed for the proof of the Poisson stability in the paper.

Lemma 2. 

Assume that the following conditions are valid

• The entries of matrix $\mathcal{A}\left(t\right)$ are continuously Poisson stable with the sequence of convergence $t_n$, $n\in \mathbb{N};$
• The sequence $A_k,k\in \mathbb{Z},$ is Poisson stable with a convergence sequence $l_n$, $n\to \infty$;
• The convergence sequence $t_n,n\in \mathbb{N},$ and discontinuity moments ${\theta }_k,k\in \mathbb{Z},$ make a Poisson couple $(t_n,{\theta }_k)$;
• The condition $\left(C1\right)$ is fulfilled.

Then, for arbitrary interval $[c,d]$ and positive number ε, there exists a natural k, such that for all $t\in [c,d],|t-{\theta }_i| > \epsilon ,$ and $n>k$, the following inequality holds

$$\begin{array}{c}\hfill \parallel Y(t+t_n,s+t_n)-Y(t,s)\parallel \le \epsilon \frac{K}{\lambda }(1+\frac{1}{\underline{\theta }})e^{\frac{\lambda }{2}(t-s)}.\end{array}$$

(7)

Proof. 

Due to these conditions, there exists a number k, such that for $n>k$ it is true that $\parallel \mathcal{A}(t+t_n)-\mathcal{A}\left(t\right)\parallel <\epsilon ,\parallel A_{i+l_n}-A_i\parallel <\epsilon$ and $|t-{\eta }_i|<\epsilon$ implies that ${\eta }_{i+l_n}<t+t_n<{\eta }_{i+l_n+1},$ where ${\eta }_i={\theta }_i-t_n,$ for all $i\in \mathbb{Z}.$

Moreover, it is true that

$$\begin{array}{c}\frac{\partial Y(t+t_n,s+t_n)}{\partial t}=\mathcal{A}\left(t\right)Y(t+t_n,s+t_n)+[\mathcal{A}(t+t_n)-\mathcal{A}\left(t\right)]Y(t+t_n,s+t_n),t\ne {\eta }_k,\\ \mathsf{\Delta }Y(t+t_n,s+t_n){|}_{t={\eta }_k}=A_{k}Y({\eta }_k+t_n,s+t_n)+[A_{k+l_n}-A_k]Y({\eta }_k+t_n,s+t_n).\end{array}$$

(8)

Consequently, if $i(s,t)$ denotes the number of points ${\theta }_i$ in the interval $(s,t),$

$$Y(t+t_n,s+t_n)=Y(t,s)+{\int }_s^{t}Y(t,u)[\mathcal{A}(u+t_n)-\mathcal{A}\left(u\right)]Y(u+t_n,s+t_n)du+$$

$$\sum _{s\le {\eta }_i<t}Y(t,{\eta }_i)[A_{i+l_n}-A_i]Y({\eta }_i+t_n,s+t_n),$$

and

$$\parallel Y(t+t_n,s+t_n)-Y(t,s)\parallel \le {\int }_s^t\parallel Y(t,u)\parallel \parallel \mathcal{A}(u+t_n)-\mathcal{A}\left(u\right)\parallel \parallel Y(u+t_n,s+t_n\parallel du+$$

$$\sum _{s\le {\theta }_i<t}\parallel Y(t,{\eta }_i)\parallel \parallel A_{i+l_n}-A_i\parallel \parallel Y({\eta }_i+t_n,s+t_n)\parallel \le {\int }_s^t\epsilon K{e}^{\lambda (t-s)}du+\sum _{s\le {\theta }_i<t}\epsilon K{e}^{\lambda (t-s)}=$$

$$\frac{\epsilon K}{\lambda }{e}^{\lambda (t-s)}(t-s)+i(s,t)\epsilon K{e}^{\lambda (t-s)}\le \epsilon \frac{K}{\lambda }(1+\frac{1}{\underline{\theta }})e^{\frac{\lambda }{2}(t-s)}.$$

□

3. Main Results

We will study the problem of the existence and uniqueness of discontinuous unpredictable oscillations for system (4).

In this article, the following symbols will be employed:

${\displaystyle m_{\mathcal{B}}=\underset{t\in \mathbb{R}}{sup}\parallel \mathcal{B}\left(t\right)\parallel ,}$	${\displaystyle m_F=\underset{\parallel u\parallel <H}{sup}\parallel F\left(u\right)\parallel ,}$	${\displaystyle m_{\mathcal{C}}=\underset{t\in \mathbb{R}}{sup}\parallel \mathcal{C}\left(t\right)\parallel ,}$
${\displaystyle m_B=\underset{k\in \mathbb{Z}}{sup}\parallel B_k\parallel ,}$	${\displaystyle m_G=\underset{\parallel u\parallel <H}{sup}\parallel G\left(u\right)\parallel ,}$	${\displaystyle m_{\mathsf{\Gamma }}=\underset{k\in \mathbb{Z}}{sup}\parallel {\mathsf{\Gamma }}_k\parallel }$

Lemma 3. 

A bounded vector function $y\left(t\right)=(y_1\left(t\right),\dots ,y_p\left(t\right))$ is a solution of system (4) if and only if it is a solution of the following integral equations:

$$\begin{array}{c}\hfill {\displaystyle y\left(t\right)=\underset{-\infty }{\overset{t}{\int }}Y(t,s)[\mathcal{B}\left(s\right)F\left(y\left(s\right)\right)+\mathcal{C}\left(s\right)]ds+\sum _{{\theta }_k<t}Y(t,{\theta }_k+)[B_{k}G\left(y\left({\theta }_k\right)\right)+{\mathsf{\Gamma }}_k]}\end{array}$$

(9)

for all $k\in \mathbb{Z}$.

Consider the subset $\mathcal{Q}\subset \mathcal{D}$ of $p$—dimensional discontinuous Poisson stable functions $\psi :\mathbb{R}\to {\mathbb{R}}^p$, $\psi =({\psi }_1,{\psi }_2,\dots ,{\psi }_p)$ with the set of discontinuity moments ${\theta }_k$, $k\in \mathbb{Z}$, and the common convergence sequence $t_n$, $n=1,2,\dots$. In the set, $\mathcal{Q}$ determines the norm ${\displaystyle {∥\psi ∥}_1=\underset{t\in \mathbb{R}}{sup}\parallel \psi \left(t\right)\parallel }$. Moreover, ${\parallel \psi \parallel }_1<H$ for all $\psi \left(t\right)\in \mathcal{Q}$, where H is a positive fixed number, and the convergence sequence $t_n$ and discontinuity moments ${\theta }_k$, $k=0,1,2,\dots$ make a Poisson couple $(t_n,{\theta }_k)$.

The following conditions are needed:

(C2)

the coefficients of matrices $\mathcal{A}\left(t\right),\mathcal{B}\left(t\right)$, and the input $\mathcal{C}\left(t\right)$, are continuous Poisson stable and the sequence of convergence $t_n$, $n\in \mathbb{N},$ is common for all their coordinates;

(C3)

the sequences $\left\{A_k\right\}$, $\left\{B_k\right\}$, $\left\{{\mathsf{\Gamma }}_k\right\}$, $k\in \mathbb{Z}$ are Poisson stable with a common convergence sequence $l_n$, $n\to \infty$;

(C4)

there exist positive numbers $l_F$ and $l_G$, such that $\parallel F\left(x\right)-F\left(y\right)\parallel \le l_F\parallel x-y\parallel$, $\parallel G\left(x\right)-G\left(y\right)\parallel \le l_G\parallel x-y\parallel$, for all $x,y\in {\mathbb{R}}^p$;

(C5)

$K\left({\displaystyle \frac{1}{-\lambda }\left(m_{\mathcal{B}}{m}_F+m_{\mathcal{C}}\right)+\frac{1}{1-e^{\lambda \underline{\theta }}}\left(m_B{m}_G+m_{\mathsf{\Gamma }}\right)}\right)<H;$

(C6)

$K\left({\displaystyle \frac{l_F{m}_{\mathcal{B}}}{-\lambda }+\frac{l_G{m}_B}{1-e^{\lambda \underline{\theta }}}}\right)<1$;

(C7)

$K{l}_F{m}_{\mathcal{B}}+\frac{1}{\underline{\theta }}ln(1+K{l}_G{m}_B)<-\lambda$.

Let us introduce the following integral operator $\mathsf{\Pi }\psi \left(t\right)$ in the space $\mathcal{Q}$, such that

$$\begin{array}{c}\hfill {\displaystyle \mathsf{\Pi }\psi \left(t\right)=\underset{-\infty }{\overset{t}{\int }}Y(t,s)[\mathcal{B}\left(s\right)F\left(\psi \left(s\right)\right)+\mathcal{C}\left(s\right)]ds+\sum _{{\theta }_k<t}Y(t,{\theta }_k+)[B_{k}G\left(\psi \left({\theta }_k\right)\right)+{\mathsf{\Gamma }}_k]}\end{array}$$

for all $k\in \mathbb{Z}$.

Lemma 4. 

If $\psi \left(t\right)\in \mathcal{Q}$, then $\mathsf{\Pi }\psi \left(t\right)\in \mathcal{Q}$.

Proof. 

For a function $\psi \left(t\right)\in \mathcal{Q}$ and we have found that

$$\begin{array}{ccc}\hfill \parallel \mathsf{\Pi }\psi \left(t\right)\parallel & =& {\displaystyle \parallel \underset{-\infty }{\overset{t}{\int }}Y(t,s)[\mathcal{B}\left(s\right)F\left(\psi \left(s\right)\right)+\mathcal{C}\left(s\right)]ds+\sum _{{\theta }_k<t}Y(t,{\theta }_k+)[B_{k}G\left(\psi \left({\theta }_k\right)\right)+{\mathsf{\Gamma }}_k]\parallel }\hfill \\ & \le & \underset{-\infty }{\overset{t}{\int }}\parallel Y(t,s)\parallel [\parallel \mathcal{B}\left(s\right)\parallel \parallel F\left(\psi \left(s\right)\right)\parallel +\parallel \mathcal{C}\left(s\right)\parallel ]ds\hfill \\ & +& {\displaystyle \sum _{{\theta }_k<t}\parallel Y(t,{\theta }_k+)\parallel [\parallel B_k\parallel \parallel G\left(\psi \left({\theta }_k\right)\right)\parallel +\parallel {\mathsf{\Gamma }}_k\parallel ]}\hfill \\ & \le & {\displaystyle \underset{-\infty }{\overset{t}{\int }}K{e}^{\lambda (t-s)}\left(m_{\mathcal{B}}{m}_F+m_{\mathcal{C}}\right)ds+\sum _{{\theta }_k<t}K{e}^{\lambda (t-{\theta }_k)}\left(m_B{m}_G+m_{\mathsf{\Gamma }}\right)}\hfill \\ & \le & \frac{K}{-\lambda }\left(m_{\mathcal{B}}{m}_F+m_{\mathcal{C}}\right)+\frac{K}{1-e^{\lambda \underline{\theta }}}\left(m_B{m}_G+m_{\mathsf{\Gamma }}\right).\hfill \end{array}$$

So, based on condition $\left(C5\right)$, it is true that ${∥\mathsf{\Pi }\psi ∥}_1<H$.

Let us check that the Poisson stability of $\mathsf{\Pi }\psi \left(t\right)$ is valid.

According to the method of included intervals introduced in [38], we fix a positive number $ϵ$ and $[a,b],-\infty <a<b<\infty$ and will prove that $\parallel \mathsf{\Pi }\psi (t+t_n)-\mathsf{\Pi }\psi \left(t\right)\parallel <ϵ$ on $[a,b]$ for sufficiently large n. Then, we choose real numbers $c<a$, $b<d$ and $\zeta >0$ to satisfy the inequalities

$$\begin{array}{c}\hfill 2K\left(\frac{m_{\mathcal{B}}{m}_F+m_{\mathcal{C}}}{-\lambda }+\frac{m_B{m}_G+m_{\mathsf{\Gamma }}}{1-e^{\lambda \underline{\theta }}}\right)e^{\lambda (a-c)}<\frac{ϵ}{2},\end{array}$$

(10)

$$\begin{array}{c}\hfill {\displaystyle (1+\frac{1}{\underline{\theta }})\frac{K\epsilon (m_{\mathcal{B}}{m}_F+m_{\mathcal{C}})}{-{\lambda }^2(1-e^{\lambda \underline{\theta }})}(e^{-\lambda \zeta }-1)<\frac{ϵ}{8},}\end{array}$$

(11)

$$\begin{array}{c}\hfill \frac{K\zeta }{\lambda }(m_F+l_F{m}_{\mathcal{B}}+1)<\frac{ϵ}{8},\end{array}$$

(12)

$$\begin{array}{c}\hfill \frac{2K(m_{\mathcal{B}}{m}_F+l_F{m}_{\mathcal{B}}H+m_{\mathcal{C}})}{-\lambda \left(1-e^{\lambda \underline{\theta }}\right)}\left(e^{-\lambda \zeta }-1\right)<\frac{ϵ}{8},\end{array}$$

(13)

and

$$\begin{array}{c}\hfill \frac{K\zeta }{1-e^{\lambda \underline{\theta }}}(m_B{m}_G+m_B{l}_G+m_G+m_{\mathsf{\Gamma }}+1)<\frac{ϵ}{8}.\end{array}$$

(14)

To prove convergence, we first introduce the following difference

$$\begin{array}{ccc}& & \mathsf{\Pi }\psi (t+t_n)-\mathsf{\Pi }\psi \left(t\right)\hfill \\ & & {\displaystyle =\underset{-\infty }{\overset{t+t_n}{\int }}Y(t+t_n,s)[\mathcal{B}\left(s\right)F\left(\psi \left(s\right)\right)+\mathcal{C}\left(s\right)]ds+\sum _{{\theta }_k<t+t_n}Y(t+t_n,{\theta }_k+)[B_{k}G\left(\psi \left({\theta }_k\right)\right)+{\mathsf{\Gamma }}_k]}\hfill \\ & & {\displaystyle -\underset{-\infty }{\overset{t}{\int }}Y(t,s)[\mathcal{B}\left(s\right)F\left(\psi \left(s\right)\right)+\mathcal{C}\left(s\right)]ds-\sum _{{\theta }_k<t}Y(t,{\theta }_k+)[B_{k}G\left(\psi \left({\theta }_k\right)\right)+{\mathsf{\Gamma }}_k]}\hfill \\ & & =\underset{-\infty }{\overset{t}{\int }}Y(t+t_n,s+t_n)[\mathcal{B}(s+t_n)F\left(\psi (s+t_n)\right)+\mathcal{C}(s+t_n)]ds\hfill \\ & & {\displaystyle +\sum _{{\theta }_k<t}Y(t+t_n,{\theta }_{k+l_n}+)[B_{k+l_n}G\left(\psi \left({\theta }_{k+l_n}\right)\right)+{\mathsf{\Gamma }}_{k+l_n}]}\hfill \\ & & {\displaystyle -\underset{-\infty }{\overset{t}{\int }}Y(t,s)[\mathcal{B}\left(s\right)F\left(\psi \left(s\right)\right)+\mathcal{C}\left(s\right)]ds-\sum _{{\theta }_k<t}Y(t,{\theta }_k+)[B_{k}G\left(\psi \left({\theta }_k\right)\right)+{\mathsf{\Gamma }}_k].}\hfill \end{array}$$

For $t\in [a,b]$ we find that

$$\begin{array}{ccc}\parallel \mathsf{\Pi }\psi (t+t_n)-\mathsf{\Pi }\psi \left(t\right)\parallel \hfill & =& {\displaystyle \parallel \underset{-\infty }{\overset{t}{\int }}Y(t+t_n,s+t_n)\mathsf{\Phi }(s+t_n)ds+\sum _{{\theta }_k<t}Y(t+t_n,{\theta }_{k+l_n}+){\mathsf{\Psi }}_{k+l_n}}\hfill \\ \hfill & & {\displaystyle -\underset{-\infty }{\overset{t}{\int }}Y(t,s)\mathsf{\Phi }\left(s\right)ds-\sum _{{\theta }_k<t}Y(t,{\theta }_k+){\mathsf{\Psi }}_k\parallel ,}\hfill \end{array}$$

(15)

where $\mathsf{\Phi }\left(u\right)=\mathcal{B}\left(u\right)F\left(\psi \right(u\left)\right)+\mathcal{C}\left(u\right)$ and ${\mathsf{\Psi }}_j=B_{j}G\left(\psi \left({\theta }_j\right)\right)+{\mathsf{\Gamma }}_j$, with ${\displaystyle \underset{u}{sup}\parallel \mathsf{\Phi }\left(\psi \left(u\right)\right)\parallel =\underset{u}{sup}\parallel \mathcal{B}\left(u\right)F\left(\psi \left(u\right)\right)+\mathcal{C}\left(u\right)\parallel \le m_{\mathcal{B}}{m}_F+m_{\mathcal{C}}}$ and ${\displaystyle \underset{j}{sup}\parallel {\mathsf{\Psi }}_j\parallel =\underset{j}{sup}\parallel B_{j}G\left(\psi \left({\theta }_j\right)\right)+{\mathsf{\Gamma }}_j\parallel \le m_B{m}_G+m_{\mathsf{\Gamma }}}$, respectively.

Taking into account the Poisson sequence $t_n,n\in \mathbb{N},$ and discontinuity moments ${\theta }_k,k\in \mathbb{Z}$, we make use of the Poisson couple $(t_n,{\theta }_k)$, as well as applying conditions (C2) and (C3), one can make the number n sufficiently large, such that $\left|{\theta }_{k+l_n}-t_n-{\theta }_k\right|<\zeta$, $\parallel \psi \left({\theta }_{k+l_n}\right)-\psi \left({\theta }_k\right)\parallel <\zeta$, $\parallel B_{k+l_n}-B_k\parallel <\zeta$, $\parallel {\mathsf{\Gamma }}_{k+l_n}-{\mathsf{\Gamma }}_k\parallel <\zeta$, $\parallel \psi (t+t_n)-\psi \left(t\right)\parallel <\zeta$, and $\parallel \mathcal{B}(t+t_n)-\mathcal{B}\left(t\right)\parallel <\zeta$, $\parallel \mathcal{C}(t+t_n)-\mathcal{C}\left(t\right)\parallel <\zeta$ for all $t\in [c,b]$, ${\theta }_k\in [c,b],k\in \mathbb{Z}$.

So, according to the above inequalities, we have found that

$$\begin{array}{ccc}\hfill & \hfill & {\displaystyle \underset{t\in [c,b]}{sup}}\parallel \mathsf{\Phi }(t+t_n)-\mathsf{\Phi }\left(t\right)\parallel ={\displaystyle \underset{t\in [c,b]}{sup}}\parallel \mathcal{B}(t+t_n)F\left(\psi (t+t_n)\right)+\mathcal{C}(t+t_n)-\mathcal{B}\left(t\right)F\left(\psi \left(t\right)\right)-\mathcal{C}\left(t\right)\parallel \hfill \\ \hfill & \hfill & \le \underset{t\in [c,b]}{sup}[\parallel \mathcal{B}(t+t_n)-\mathcal{B}\left(t\right)\parallel \parallel F\left(\psi (t+t_n)\right)\parallel +\parallel \mathcal{B}\left(t\right)\parallel \parallel F\left(\psi (t+t_n)\right)-F\left(\psi \left(t\right)\right)\parallel \hfill \\ \hfill & \hfill & +\parallel \mathcal{C}(t+t_n)-\mathcal{C}\left(t\right)\parallel ]\le m_F\zeta +l_F{m}_{\mathcal{B}}\zeta +\zeta ;\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill & \hfill & {\displaystyle \underset{k\in \mathbf{Z}}{sup}\parallel {\mathsf{\Psi }}_{k+l_n}-{\mathsf{\Psi }}_k\parallel =\underset{k\in \mathbf{Z},{\theta }_k\in [c,b]}{sup}\parallel B_{k+l_n}G\left(\psi \left({\theta }_{k+l_n}\right)\right)+{\mathsf{\Gamma }}_{k+l_n}-B_{k}G\left(\psi \left({\theta }_k\right)\right)-{\mathsf{\Gamma }}_k\parallel }\hfill \\ \hfill & \hfill & \le \underset{k\in \mathbf{Z},{\theta }_k\in [c,b]}{sup}[\parallel B_{k+l_n}-B_k\parallel ∥G\left(\psi \left({\theta }_{k+l_n}\right)\right)∥+\parallel B_k\parallel ∥G\left(\psi \left({\theta }_{k+l_n}\right)\right)-G\left(\psi \left({\theta }_k\right)\right)∥\hfill \\ \hfill & \hfill & +∥{\mathsf{\Gamma }}_{k+l_n}-{\mathsf{\Gamma }}_k∥]\le m_G\zeta +l_G{m}_B\zeta +\zeta .\hfill \end{array}$$

(17)

Consider the difference in (15) separately for intervals $(-\infty ,c]$ and $[c,t]$ to obtain that $\parallel \mathsf{\Pi }\psi (t+t_n)-\mathsf{\Pi }\psi \left(t\right)\parallel \le J_1+J_2,$ where

$$\begin{array}{c}{\displaystyle J_1=\underset{-\infty }{\overset{c}{\int }}\parallel Y(t+t_n,s+t_n)\parallel \parallel \mathsf{\Phi }(s+t_n)\parallel ds+\sum _{{\theta }_k<c}\parallel Y(t+t_n,{\theta }_{k+l_n}+)\parallel \parallel {\mathsf{\Psi }}_{k+l_n}\parallel }\hfill \\ {\displaystyle +\underset{-\infty }{\overset{c}{\int }}\parallel Y(t,s)\parallel \parallel \mathsf{\Phi }\left(s\right)\parallel ds+\sum _{{\theta }_k<c}\parallel Y(t,{\theta }_k+)\parallel \parallel {\mathsf{\Psi }}_k\parallel }\hfill \end{array}$$

and

$$\begin{array}{c}{J}_2=\underset{c}{\overset{t}{\int }}\parallel Y(t+t_n,s+t_n)-Y(t,s)\parallel \parallel \mathsf{\Phi }(s+t_n)\parallel ds+\underset{c}{\overset{t}{\int }}\parallel Y(t,s)\parallel \parallel \mathsf{\Phi }(s+t_n)-\mathsf{\Phi }\left(s\right)\parallel ds\hfill \\ {\displaystyle +\sum _{c\le {\theta }_k<t}∥Y(t+t_n,{\theta }_{k+l_n}+)-Y(t,{\theta }_k+)∥\parallel {\mathsf{\Psi }}_{k+l_n}\parallel +\sum _{c\le {\theta }_k<t}∥Y(t,{\theta }_k+)∥\parallel {\mathsf{\Psi }}_{k+l_n}-{\mathsf{\Psi }}_k\parallel .}\hfill \end{array}$$

Let us continue with the estimation of the constants $J_1$ and $J_1.$ Firstly, we find that (10) implies

$$\begin{array}{c}{\displaystyle J_1\le 2\underset{-\infty }{\overset{c}{\int }}K{e}^{\lambda (t-s)}[m_{\mathcal{B}}{m}_F+m_{\mathcal{C}}]ds+2\sum _{{\theta }_k<c}K{e}^{\lambda (t-{\theta }_k)}\left(m_B{m}_G+m_{\mathsf{\Gamma }}\right)}\hfill \\ <\left(\frac{2K}{-\lambda }(m_{\mathcal{B}}{m}_F+m_{\mathcal{C}})+\frac{2K}{1-e^{\lambda \underline{\theta }}}\left(m_B{m}_G+m_{\mathsf{\Gamma }}\right)\right)e^{\lambda (a-c)}<\frac{ϵ}{2}.\hfill \end{array}$$

Applying Lemma 2 and estimations (11)–(14), (16) and (17), one can verify that

$$\begin{array}{ccc}& & {\displaystyle J_2\le \sum _{c\le {\theta }_k<t}\underset{{\theta }_k}{\overset{{\theta }_{k+l_n}-t_n}{\int }}\epsilon \frac{K}{\lambda }(1+\frac{1}{\underline{\theta }})e^{\frac{\lambda }{2}(t-s)}\left(m_{\mathcal{B}}{m}_F+m_{\mathcal{C}}\right)ds}\hfill \\ & & +\underset{c}{\overset{t}{\int }}K{e}^{\lambda (t-s)}(m_F\zeta +l_F{m}_{\mathcal{B}}\zeta +\zeta )ds+\hfill \\ & & {\displaystyle \sum _{c\le {\theta }_k<t}\underset{{\theta }_k}{\overset{{\theta }_{k+l_n}-t_n}{\int }}K{e}^{\lambda (t-s)}(2m_{\mathcal{B}}{m}_F+l_F{m}_{\mathcal{B}}2H+2m_{\mathcal{C}})ds}\hfill \\ & & {\displaystyle +\sum _{c\le {\theta }_k<t}K{e}^{\lambda (t-{\theta }_k)}\zeta \left(m_B{m}_G+m_{\mathsf{\Gamma }}\right)+\sum _{c\le {\theta }_k<t}K{e}^{\lambda (t-{\theta }_k)}(m_G\zeta +l_G{m}_B\zeta +\zeta )}\hfill \\ & & {\displaystyle \le \epsilon \frac{K}{\lambda }(1+\frac{1}{\underline{\theta }})\frac{e^{-\lambda \zeta }-1}{-\lambda (1-e^{\lambda \underline{\theta }})}(m_{\mathcal{B}}{m}_F+m_{\mathcal{C}})}\hfill \\ & & +\frac{K\zeta }{-\lambda }(m_F+l_F{m}_{\mathcal{B}}+1)+\frac{2K(e^{-\lambda \zeta }-1)}{-\lambda (1-e^{\lambda \underline{\theta }})}(m_{\mathcal{B}}{m}_F+l_F{m}_{\mathcal{B}}H+m_{\mathcal{C}})\hfill \\ & & +\frac{K\zeta }{1-e^{\lambda \underline{\theta }}}\left(m_B{m}_G+m_{\mathsf{\Gamma }}\right)+\frac{K\zeta }{1-e^{\lambda \underline{\theta }}}(m_G+l_G{m}_B+1)<\frac{ϵ}{2}.\hfill \end{array}$$

Thus, we have determined that $\parallel \mathsf{\Pi }\psi (t+t_n)-\mathsf{\Pi }\psi \left(t\right)\parallel \le J_1+J_2<ϵ$, for $t\in [a,b]$. Therefore, $\mathsf{\Pi }\psi (t+t_n)\to \mathsf{\Pi }\psi \left(t\right)$ uniformly in B-topology as $n\to \infty$ on each bounded interval. □

Lemma 5. 

The operator $\mathsf{\Pi }:\mathcal{Q}\to \mathcal{Q}$ is contractive.

Proof. 

For elements $\phi$ and $\psi$ of the set $\mathcal{Q}$, we have found that

$$\begin{array}{ccc}\hfill \parallel \mathsf{\Pi }\phi \left(t\right)-\mathsf{\Pi }\psi \left(t\right)\parallel & =& \underset{-\infty }{\overset{t}{\int }}∥Y(t,s)∥[\parallel \mathcal{B}\left(s\right)\parallel ∥F\left(\phi \right(s\left)\right)-F\left(\psi \right(s\left)\right)∥]ds\hfill \\ & +& {\displaystyle \sum _{{\theta }_k<t}∥Y(t,{\theta }_k+)∥[\parallel B_k\parallel ∥G\left(\phi \left({\theta }_k\right)\right)-G\left(\psi \left({\theta }_k\right)\right)∥]}\hfill \\ & \le & \underset{-\infty }{\overset{t}{\int }}K{e}^{\lambda (t-s)}{l}_F{m}_{\mathcal{B}}\parallel \phi \left(s\right)-\psi \left(s\right)\parallel ds\hfill \\ & +& {\displaystyle \sum _{{\theta }_k<t}K{e}^{\lambda (t-{\theta }_k)}{l}_G{m}_B\parallel \phi \left({\theta }_k\right)-\psi \left({\theta }_k\right)\parallel }\hfill \\ & \le & \frac{K}{-\lambda }{l}_F{m}_{\mathcal{B}}\parallel \phi \left(t\right)-\psi \left(t\right)\parallel +\frac{K}{1-e^{\lambda \underline{\theta }}}{l}_G{m}_B\parallel \phi \left(t\right)-\psi \left(t\right)\parallel \hfill \\ & \le & (\frac{K}{-\lambda }{l}_F{m}_{\mathcal{B}}+\frac{K}{1-e^{\lambda \underline{\theta }}}{l}_G{m}_B){\parallel \phi \left(t\right)-\psi \left(t\right)\parallel }_1.\hfill \end{array}$$

Therefore, the inequality ${\parallel \mathsf{\Pi }\phi \left(t\right)-\mathsf{\Pi }\psi \left(t\right)\parallel }_1\le K(\frac{1}{-\lambda }{l}_F{m}_{\mathcal{B}}+\frac{1}{1-e^{\lambda \underline{\theta }}}{l}_G{m}_B){\parallel \phi \left(t\right)-\psi \left(t\right)\parallel }_1$. Thus, the operator $\mathsf{\Pi }$ is contractive by means of condition $\left(C6\right)$. □

Theorem 1. 

If conditions (C1)–(C7) are fulfilled, then impulsive system (4) has a unique globally exponentially stable discontinuous Poisson stable solution.

Proof. 

To demonstrate the completeness of $\mathcal{Q}$, we begin by considering a Cauchy sequence ${\varphi }_r\left(t\right)$, $r\in \mathbb{N}$, contained within $\mathcal{Q}$, which converges to the limit function $\varphi \left(t\right)$ on $\mathbb{R}$. Then, we fix a closed and bounded interval $I\subset \mathbb{R}.$ We write ${\theta }_k,k=j,j+1,\dots ,j+m$ to denote the discontinuity points of both $\varphi \left(t\right)$ and ${\varphi }_r\left(t\right)$, and ${\theta }_k^n={\theta }_{k+l_n}-t_n,k=j,j+1,\dots ,j+m$, the discontinuity points of $\varphi (t+t_n)$ and ${\varphi }_r(t+t_n)$ within interval I. Then, we choose n to be sufficiently large that $|{\theta }_k^n-{\theta }_k|<ϵ,k=j,j+1,\dots ,j+m$. Due to the convergence of ${\varphi }_r\left(t\right)$, it follows that $\left|\right|\varphi (t+t_n)-{\varphi }_r(t+t_n)\left|\right|<\frac{ϵ}{3}$ and $\left|\right|{\varphi }_r\left(t\right)-\varphi \left(t\right)\left|\right|<\frac{ϵ}{3}$ for a sufficiently large r. Since the sequence ${\varphi }_r\left(t\right)\in \mathcal{Q}$, for a sufficiently large n$\left|\right|{\varphi }_r(t+t_n)-{\varphi }_r\left(t\right)\left|\right|<\frac{ϵ}{3}$ for $t\notin \left[\widehat{{\theta }_k,{\theta }_k^n}\right]$, while $|{\theta }_k^n-{\theta }_k|<ϵ$, $k=j,j+1,\dots ,j+m$. Thus, for a sufficiently large r and n, it is true that

$$\begin{array}{ccc}\left|\right|\varphi (t+t_n)-\varphi \left(t\right)\left|\right|\hfill & <\hfill & \left|\right|\varphi (t+t_n)-{\varphi }_r(t+t_n)\left|\right|+\left|\right|{\varphi }_r(t+t_n)-{\varphi }_r\left(t\right)\left|\right|\hfill \\ \hfill & +\hfill & \left|\right|{\varphi }_r\left(t\right)-\varphi \left(t\right)\left|\right|<ϵ\hfill \end{array}$$

(18)

for all $t\notin \left[\widehat{{\theta }_k,{\theta }_k^n}\right],k=j,j+1,\cdots ,j+m$. That is, $\varphi (t+t_n)\to \varphi \left(t\right)$ in B-topology as $n\to \infty$ on I. The completeness of $\mathcal{Q}$ is proved.

When we apply the contraction mapping theorem, due to Lemmas 4 and 5, there exists a unique solution $\omega \left(t\right)\in \mathcal{Q}$ of the system (4).

Finally, we will study the asymptotic stability of the oscillation $\omega \left(t\right)$. It is true that [18],

$$\begin{array}{c}\hfill {\displaystyle \omega \left(t\right)=Y(t,t_0)\omega \left(t_0\right)+\underset{t_0}{\overset{t}{\int }}Y(t,s)[\mathcal{B}\left(s\right)F\left(\omega \left(s\right)\right)+\mathcal{C}\left(s\right)]ds+\sum _{{\theta }_k<t}Y(t,{\theta }_k+)[B_{k}G\left(\omega \left({\theta }_k\right)\right)+{\mathsf{\Gamma }}_k]}\end{array}$$

for all $k\in \mathbb{Z}.$

Let $z\left(t\right)=(z_1,z_2,\dots ,z_p)$ be another solution of system (4). One can write

$$\begin{array}{c}\hfill {\displaystyle z\left(t\right)=Y(t,t_0)z\left(t_0\right)+\underset{t_0}{\overset{t}{\int }}Y(t,s)[\mathcal{B}\left(s\right)F\left(z\left(s\right)\right)+\mathcal{C}\left(s\right)]ds+\sum _{{\theta }_k<t}Y(t,{\theta }_k+)[B_{k}G\left(z\left({\theta }_k\right)\right)+{\mathsf{\Gamma }}_k]}\end{array}$$

for all $t\in \mathbb{R}.$

Making use of the relation

$$\begin{array}{ccc}\hfill \omega \left(t\right)-z\left(t\right)& =& Y(t,t_0)[\omega \left(t_0\right)-z\left(t_0\right)]\hfill \\ & +& \underset{t_0}{\overset{t}{\int }}Y(t,s)\mathcal{B}\left(s\right)\left[F\left(\omega \right(s\left)\right)-F\left(z\right(s\left)\right)\right]ds\hfill \\ & +& {\displaystyle \sum _{t_0\le {\theta }_k<t}Y(t,{\theta }_k+)B_k[G\left(\omega \left({\theta }_k\right)\right)-G\left(z\left({\theta }_k\right)\right)]}\hfill \end{array}$$

we find that

$$\begin{array}{ccc}\hfill ∥\omega \left(t\right)-z\left(t\right)∥& \le & K{e}^{\lambda (t-t_0)}∥\omega \left(t_0\right)-z\left(t_0\right)∥\hfill \\ & +& \underset{t_0}{\overset{t}{\int }}K{e}^{\lambda (t-s)}{m}_{\mathcal{B}}\parallel ∥F\left(\omega \right(s\left)\right)-F\left(z\right(s\left)\right)∥\hfill \\ & & {\displaystyle +\sum _{t_0\le {\theta }_k<t}K{e}^{\lambda (t-{\theta }_k)}{m}_B\parallel G\left(\omega \left({\theta }_k\right)\right)-G\left(z\left({\theta }_k\right)\right)\parallel }\hfill \\ & & \le K{e}^{\lambda (t-t_0)}\left|\right|\omega \left(t_0\right)-z\left(t_0\right)\left|\right|\hfill \\ & +& K{l}_F{m}_{\mathcal{B}}\underset{t_0}{\overset{t}{\int }}{e}^{\lambda (t-s)}\left|\left|\omega \right(s)-z(s)\right||ds\hfill \\ & & {\displaystyle +K{l}_G{m}_B\sum _{t_0\le {\theta }_k<t}{e}^{\lambda (t-{\theta }_k)}\left|\right|\omega \left({\theta }_k\right)-z\left({\theta }_k\right)\left|\right|.}\hfill \end{array}$$

Thus, it can be confirmed that

$$\begin{array}{ccc}\hfill ∥\omega \left(t\right)-z\left(t\right)∥& \le & K{e}^{\lambda (t-t_0)}\parallel \omega \left(t_0\right)-z\left(t_0\right)\parallel \hfill \\ & +& K{l}_F{m}_{\mathcal{B}}\underset{t_0}{\overset{t}{\int }}{e}^{\lambda (t-s)}∥\omega \left(s\right)-z\left(s\right)∥ds\hfill \\ & & {\displaystyle +K{l}_G{m}_B\sum _{t_0\le {\theta }_k<t}{e}^{\lambda (t-{\theta }_k)}\parallel \omega \left({\theta }_k\right)-z\left({\theta }_k\right)\parallel .}\hfill \end{array}$$

Now, applying the Gronwall–Bellman Lemma for discontinuous functions [18], one can determine that

$$\begin{array}{c}\hfill \parallel \omega \left(t\right)-z\left(t\right)\parallel \le K\parallel \omega \left(t_0\right)-z\left(t_0\right)\parallel e^{(\lambda +K{l}_F{m}_{\mathcal{B}})(t-t_0)}{(1+K{l}_G{m}_B)}^{k(t_0,t)}.\end{array}$$

From the last inequality, it follows that

$$\begin{array}{c}\hfill \parallel \omega \left(t\right)-z\left(t\right)\parallel \le K\parallel \omega \left(t_0\right)-z\left(t_0\right)\parallel e^{(\lambda +K{l}_F{m}_{\mathcal{B}}+\frac{1}{\underline{\theta }}ln(1+K{l}_G{m}_B))(t-t_0)}\end{array}$$

(19)

for $t\ge t_0$.

Consequently, condition $\left(C7\right)$ implies that $\omega \left(t\right)$ is an exponentially stable solution of (4). □

From now on, we shall need the following condition.

(C8)

The vector function $\mathcal{C}\left(t\right)$ in system (4) satisfies condition $C\left(2\right)$, and there exist positive numbers ${ϵ}_0,\delta$ and sequence $s_n$, which diverge to infinity, such that $\parallel \mathcal{C}(t+t_n)-\mathcal{C}\left(t\right)\parallel \ge {ϵ}_0$ for each $t\in [s_n-\delta ,s_n+\delta ]$ and $n\in \mathbb{N}$.

The unpredictability of the solution for the system (4) is established by the next theorem.

Theorem 2. 

If conditions (C1)–(C8) are valid, then system (4) has a unique exponentially stable unpredictable solution.

Proof. 

In accordance with the Theorem 1, system (4) has a unique exponentially stable Poisson stable solution $\omega \left(t\right)=({\omega }_1\left(t\right),\dots ,{\omega }_p\left(t\right))$. So, to prove this theorem, we need only to show that the solution of (4) satisfies the separation property.

Corresponding to Definition 7, the interval $[s_n-\sigma ,s_n+\sigma ]\subseteq [{\theta }_{m_n},{\widehat{{\theta }_{m_{n+l_n}}-t}}_n]$ does not admit discontinuity points of functions $\omega \left(t\right)$, $\omega (t+t_n)$. That is why studies of unpredictability ignore the presence of a discontinuity moments.

We have determined that

$$\begin{array}{c}\hfill {\displaystyle \omega \left(t\right)=\omega \left(s_n\right)+\underset{s_n}{\overset{t}{\int }}\mathcal{A}\left(s\right)\omega \left(s\right)ds+\underset{s_n}{\overset{t}{\int }}\mathcal{B}\left(s\right)F\left(\omega \left(s\right)\right)ds+\underset{s_n}{\overset{t}{\int }}\mathcal{C}\left(s\right)ds.}\end{array}$$

and

$$\begin{array}{c}\hfill {\displaystyle \omega (t+t_n)=\omega (s_n+t_n)+\underset{s_n}{\overset{t}{\int }}\mathcal{A}(s+t_n)\omega (s+t_n)ds+\underset{s_n}{\overset{t}{\int }}\mathcal{B}(s+t_n)F\left(\omega (s+t_n)\right)ds+\underset{s_n}{\overset{t}{\int }}\mathcal{C}(s+t_n)ds.}\end{array}$$

Therefore, it is true that

$$\begin{array}{ccc}\hfill & \hfill & {\displaystyle \omega (t+t_n)-\omega \left(t\right)=\omega (s_n+t_n)-\omega \left(s_n\right)+\underset{s_n}{\overset{t}{\int }}\mathcal{A}(s+t_n)\omega (s+t_n)ds}\hfill \\ \hfill & \hfill & {\displaystyle -\underset{s_n}{\overset{t}{\int }}\mathcal{A}\left(s\right)\omega \left(s\right)ds+\underset{s_n}{\overset{t}{\int }}\mathcal{B}(s+t_n)F\left(\omega (s+t_n)\right)ds-\underset{s_n}{\overset{t}{\int }}\mathcal{B}\left(s\right)F\left(\omega \left(s\right)\right)ds}\hfill \\ \hfill & \hfill & {\displaystyle +\underset{s_n}{\overset{t}{\int }}\mathcal{C}(s+t_n)ds-\underset{s_n}{\overset{t}{\int }}\mathcal{C}\left(s\right)ds.}\hfill \end{array}$$

To check the unpredictability of the solution, we choose a positive number $\eta$ and $r,k\in \mathbb{N}$, such that the following inequalities

$$\eta <\delta ,$$

(20)

$$\parallel \mathcal{A}(s+t_n)-\mathcal{A}\left(s\right)\parallel <(\frac{1}{r}+\frac{2}{k}){ϵ}_0,t\in \mathbb{R},$$

(21)

$$\parallel \mathcal{B}(s+t_n)-\mathcal{B}\left(s\right)\parallel <(\frac{1}{r}+\frac{2}{k}){ϵ}_0,t\in \mathbb{R},$$

(22)

$$\begin{array}{ccc}\hfill & & \eta [\frac{1}{2}-(\frac{1}{r}+\frac{2}{k})\left[H+\mu +m_F+l_F{m}_{\mathcal{B}}\right]\ge \frac{3}{2r},\hfill \end{array}$$

(23)

and

$$\parallel \omega (t+s)-\omega \left(t\right)\parallel <{ϵ}_{0}min\{1/k,1/4r\},\left|s\right|<\eta ,t\in \mathbb{R},$$

(24)

are satisfied.

Next, we fix the numbers $\eta ,r,k$ and $n\in \mathbb{N}$.

Then, we denote

$$\mathsf{\Delta }=\parallel \omega (s_n+t_n)-\omega \left(t_n\right)\parallel$$

and consider the two alternatives: $\left(a\right)$ $\mathsf{\Delta }\ge {ϵ}_0/r,$ $\left(b\right)$ $\mathsf{\Delta }<{ϵ}_0/r.$

$\left(a\right)$ If $\mathsf{\Delta }\ge {ϵ}_0/r$ holds, we find that

$$\begin{array}{ccc}\hfill \parallel \omega (t+s)-\omega \left(t\right)\parallel & \ge & \parallel \omega (s_n+t_n)-\omega \left(s_n\right)\parallel -\parallel \omega \left(s_n\right)-\omega \left(t\right)\parallel \hfill \\ & -& \parallel \omega (t+t_n)-\omega (s_n+t_n)\parallel >{ϵ}_0/r-{ϵ}_0/4r-{ϵ}_0/4r={ϵ}_0/2r,\hfill \end{array}$$

for $t\in [s_n-\eta ,s_n+\eta ],$ $n\in \mathbb{N}.$

$\left(b\right)$ If $\mathsf{\Delta }<{ϵ}_0/r$ is true, then from (22), it follows that

$$\begin{array}{ccc}\hfill \parallel \omega (t+t_n)-\omega \left(t\right)\parallel & \le & \parallel \omega (s_n+t_n)-\omega \left(s_n\right)\parallel +\parallel \omega \left(s_n\right)-\omega \left(t\right)\parallel \hfill \\ & +& \parallel \omega (t+t_n)-\omega (s_n+t_n)\parallel \hfill \\ & <& {ϵ}_0/r+{ϵ}_0/k+{ϵ}_0/k=(1/r+2/k){ϵ}_0,\hfill \end{array}$$

for $t\in [s_n,s_n+\eta ].$

Applying (20)–(24) and due to the condition (C8), one can find that

$$\begin{array}{l}\parallel \omega (t+t_n)-\omega \left(t\right)\parallel \ge \parallel \underset{s_n}{\overset{t}{\int }}(\mathcal{C}(s+t_n)-\mathcal{C}\left(s\right))ds\parallel -\parallel \omega (s_n+t_n)-\omega \left(s_n\right)\parallel \\ +\parallel \underset{s_n}{\overset{t}{\int }}(\mathcal{A}(s+t_n)-\mathcal{A}\left(s\right))\omega (s+t_n)\parallel +\parallel \underset{s_n}{\overset{t}{\int }}\mathcal{A}\left(s\right)(\omega (s+t_n)-\omega \left(s\right))ds\parallel \\ +\parallel \underset{s_n}{\overset{t}{\int }}(\mathcal{B}(s+t_n)-\mathcal{B}\left(s\right))F\left(\omega (s+t_n)\right)ds\parallel +\parallel \underset{s_n}{\overset{t}{\int }}\mathcal{B}\left(s\right)[F\left(\omega (s+t_n)\right)-F\left(\omega \left(s\right)\right)]ds\parallel \\ \ge {ϵ}_0\frac{\eta }{2}-\frac{{ϵ}_0}{r}+{ϵ}_0(\frac{1}{r}+\frac{2}{k})\eta \left[H+\mu \right]+{ϵ}_0(\frac{1}{r}+\frac{2}{k})\eta \left[m_F+l_F{m}_{\mathcal{B}}\right]\\ \ge -\frac{{ϵ}_0}{r}+\frac{3{ϵ}_0}{2r}\ge \frac{{ϵ}_0}{2r}\end{array}$$

(25)

for $t\in [s_n+\eta /2,s_n+\eta ]$. Thus, we determine that

$$\begin{array}{c}\hfill {\displaystyle \parallel \omega (t+t_n)-\omega \left(t\right)\parallel \ge \frac{{ϵ}_0}{2r}}\end{array}$$

for $t\in [s_n+\frac{\eta }{2},s_n+\eta ]$. In accordance with the inequalities obtained in cases $\left(a\right)$ and $\left(b\right)$, we see that the solution $\omega \left(t\right)$ is discontinuous and unpredictable with $\overline{\delta }=\frac{\eta }{4}$ and the divergence sequence ${\overline{s}}_n=s_n+\frac{3\eta }{4},n\in \mathbb{N}$.

So, we have obtained the unpredictability of the solution $\omega \left(t\right)$ of the system (4). □

4. An Example

We consider an example of a Hopfield neural network where the coefficients besides the inputs are Poisson stable functions and the inputs are unpredictable ones. Given that periodic, quasi-periodic, and almost-periodic functions fall within the class of Poisson stable functions, we opt for quasi-periodic coefficients as Poisson stable components in the example.

Construction of an unpredictable sequence as the solution of the logistic equation

$$\begin{array}{c}\hfill \begin{array}{c}{\kappa }_{k+1}=\mu {\kappa }_k(1-{\kappa }_k),k\in \mathbb{Z},\hfill \end{array}\end{array}$$

(26)

can be found in [6]. It was proved that for each $\mu \in [3+{(2/3)}^{1/2},4]$, there exists an unpredictable solution ${\tau }_k$, $k\in \mathbb{Z}$ of (26), which belongs to the interval $[0,1]$.

There is an example of an unpredictable function in [6],

$$U\left(t\right)={\int }_{-\infty }^t{e}^{-4(t-s)}\mathsf{\Omega }\left(s\right)ds,$$

where $\mathsf{\Omega }\left(t\right)$ is a piecewise constant function defined on the real axis through the equation $\mathsf{\Omega }\left(t\right)={\tau }_k$ for $t\in [k,k+1),$ $k\in \mathbb{Z}.$ It is worth noting that $U\left(t\right)$ is bounded on the whole real axis, such that ${\displaystyle \underset{t\in \mathbb{R}}{sup}\left|U\left(t\right)\right|\le \frac{1}{4}.}$

Let us consider the symmetrical impulsive Hopfield-type neural networks

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{d{y}_i\left(t\right)}{dt}=a_i\left(t\right)y_i\left(t\right)+\sum _{j=1}^p{b}_{ij}\left(t\right)f_j\left(y_j\left(t\right)\right)+c_i\left(t\right),t\ne {\theta }_k,}\hfill \\ {\displaystyle \mathsf{\Delta }{y}_i{|}_{t={\theta }_k}={\alpha }_{ik}{y}_i\left({\theta }_k\right)+\sum _{j=1}^p{\beta }_{ijk}{g}_j\left(y_j\left({\theta }_k\right)\right)+{\gamma }_{ik},}\hfill \end{array}\end{array}$$

(27)

where $p=3,$ the self regulation $a_1\left(t\right)=-0.8+0.1(sint+cos\sqrt{2}t)$, $a_2\left(t\right)=-1.6+0.1(sint+cos\sqrt{2}t)$, $a_3=0.23+0.1(sin\sqrt{2}t+cost)$, the synaptic connection weights $b_{11}=0.02(sint+cos\sqrt{3}t)$, $b_{12}=0.02(sint+cos\sqrt{2}t)$, $b_{13}=0.02(sint+cos\sqrt{5}t)$, $b_{21}=0.02(sint+cos\sqrt{2}t)$, $b_{22}=0.02(sint+cos\sqrt{3}t))$, $b_{23}=0.02(sin\sqrt{3}t+cost)$, $b_{31}=0.02(sin\sqrt{2}t+cost)$, $b_{32}=0.02(sin\sqrt{3}t+cost)$, $b_{33}=0.02(sin\sqrt{2}t+cost)$ are quasi periodic, and the external inputs $c_1\left(t\right)=0.05U^3\left(t\right)$, $c_2\left(t\right)=0.24U\left(t\right)$, and $c_3=-0.18U^3\left(t\right)$ are unpredictable functions. The set of discontinuity moments of the system ${\theta }_k$ is defined by the sequence ${\theta }_k=3k+{\tau }_k$, $k\in \mathbb{Z}$. The impulsive rates are equal to ${\alpha }_{1k}=0.5-0.1|sink+cos\sqrt{5}k|$, ${\alpha }_{2k}=0.7-0.1|sin\sqrt{2}k+cosk|$, ${\alpha }_{3k}=0.78-0.1|sink+cos\sqrt{3}k|$, and the instantaneous synaptic connection weights ${\beta }_{11k}=0.02(sink+cos\sqrt{3}k)$, ${\beta }_{12k}=0.02(sin\sqrt{5}k+cosk)$, ${\beta }_{13k}=0.02(sin\sqrt{5}k+cosk)$, ${\beta }_{21k}=0.02(sink+cos\sqrt{3}k)$, ${\beta }_{22k}=0.02(sink+cos\sqrt{2}k)$, ${\beta }_{23k}=0.02(sink+cos\sqrt{5}k)$, ${\beta }_{31k}=0.02(sink+cos\sqrt{3}k)$, ${\beta }_{32k}=0.02(sin\sqrt{2}k+cosk)$, ${\beta }_{33k}=0.02(sink+cos\sqrt{2}k)$ are also quasi-periodic sequences, and the external impulsive inputs are equal to ${\gamma }_{1k}=0.06{\tau }_k$, ${\gamma }_{2k}=-0.08{\tau }_k$, ${\gamma }_{3k}=-0.07{\tau }_k$. The activation functions are presented by $f\left(s\right)=0.08sin\left(\frac{s}{2}\right)$ and impact activations $g\left(s\right)=0.05arctan\left(\frac{s}{5}\right)$.

Moreover, the functions $F\left(y\right)$ and $G\left(y\right)$ are bounded; that is, there exist positive numbers $m_F=0.08$, $m_G=0.05,$ and Lipschitz conditions are met, i.e., $l_F=0.04$ and $l_G=0.01$. By verifying that the coefficients of the system satisfy $K=4.54$ and $\lambda =-0.152$, one can find that the condition $\left(C1\right)$ is valid. Moreover, one can check that the conditions $\left(C2\right)$–$\left(C8\right)$ are satisfied. Thus, according to the Theorem 2, there exists a unique asymptotically stable discontinuous unpredictable solution, $\omega \left(t\right)$, of the system (27).

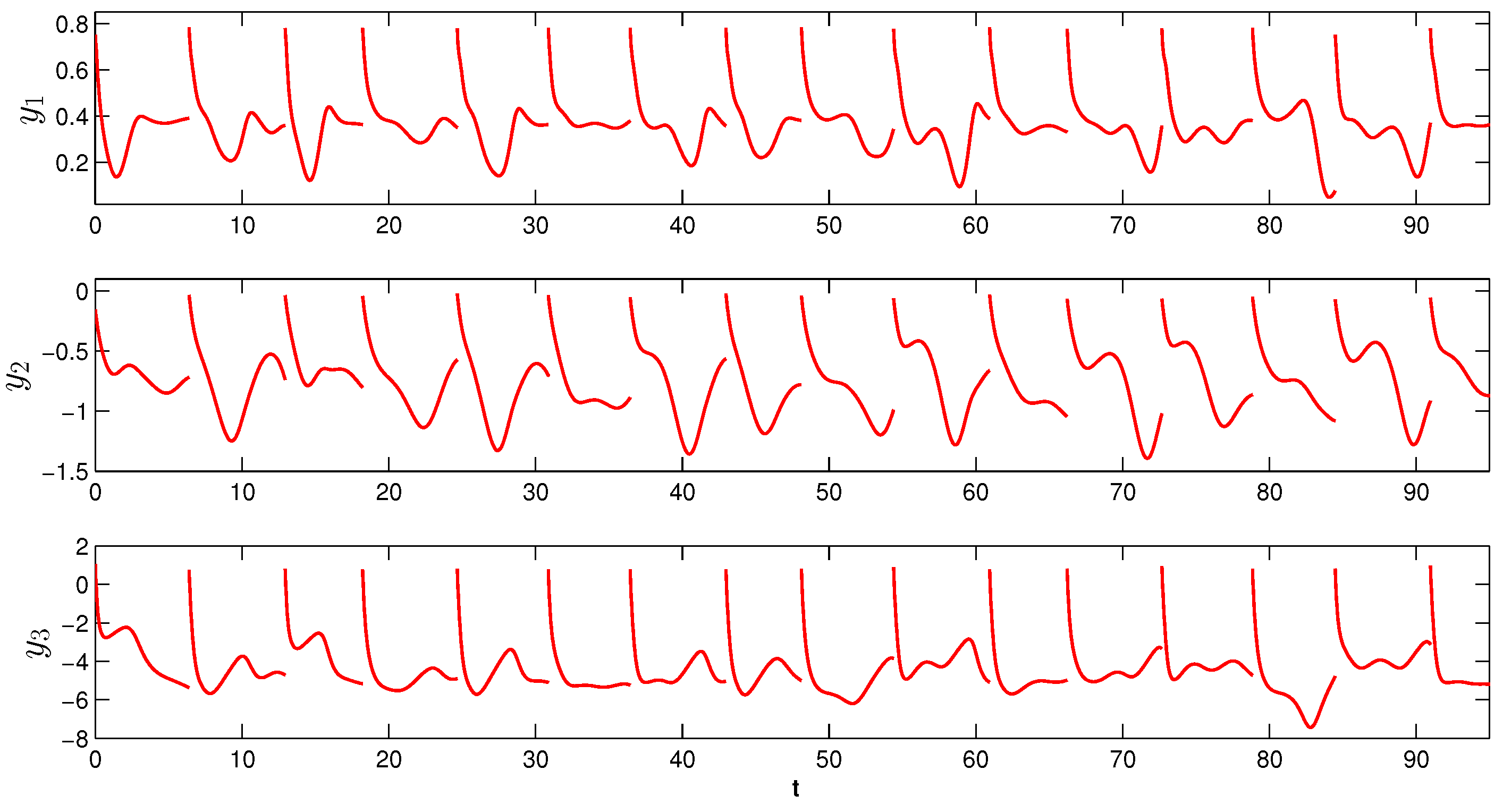
It is worth noting that the simulation of a unpredictable solution is not possible, since the initial value is unknown. That is why we will simulate a solution $y\left(t\right)$ which approaches the unpredictable solution $\omega \left(t\right)$ as time increases. Instead of the curve describing the almost periodic solution, one can take the graph of $y\left(t\right)$, as shown in Figure 1 and Figure 2. The graphs of coordinates and trajectory of the function with the initial values $(y_1\left(0\right),y_2\left(0\right),y_2\left(0\right))=(0.734,-0.455,1.065)$.