Timelike Surface Couple with Bertrand Couple as Joint Geodesic Curves in Minkowski 3-Space
Abstract
1. Introduction
2. Preliminaries
3. Main Results
- (1)
- If we setthen we can naturally indicate the sufficient condition for being geodesic curves on aswhere , , and and are not identically zero.
- (2)
- If we setthenwhere , , and and are not identically zero. As there are no constraints associated with the curves specified in Equations (16), (18) or (20), the surface bundle with as joint geodesic curve can be derived by choosing appropriate marching-scale functions. We use {, } to denote the with {, } as common geodesic curves.
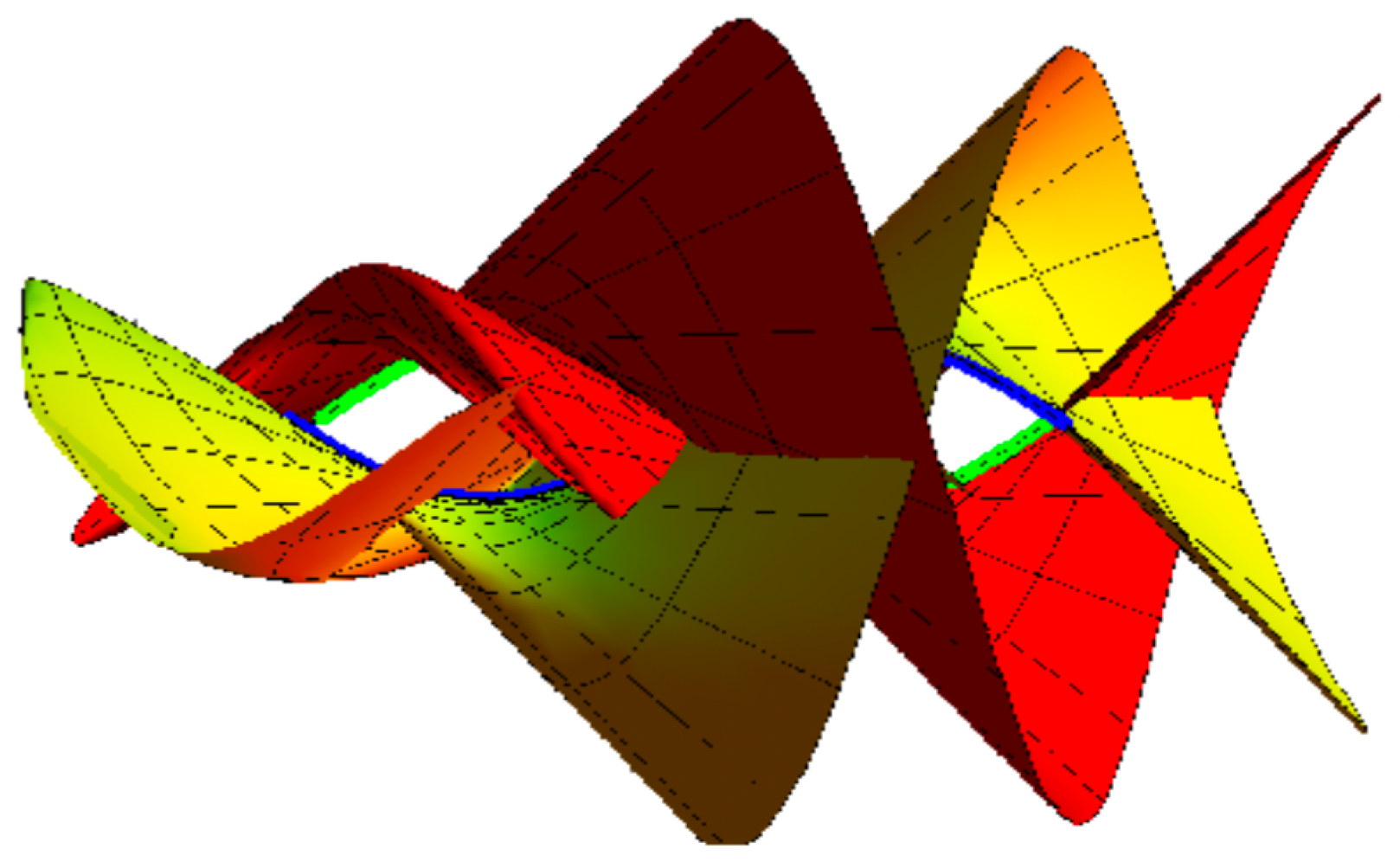
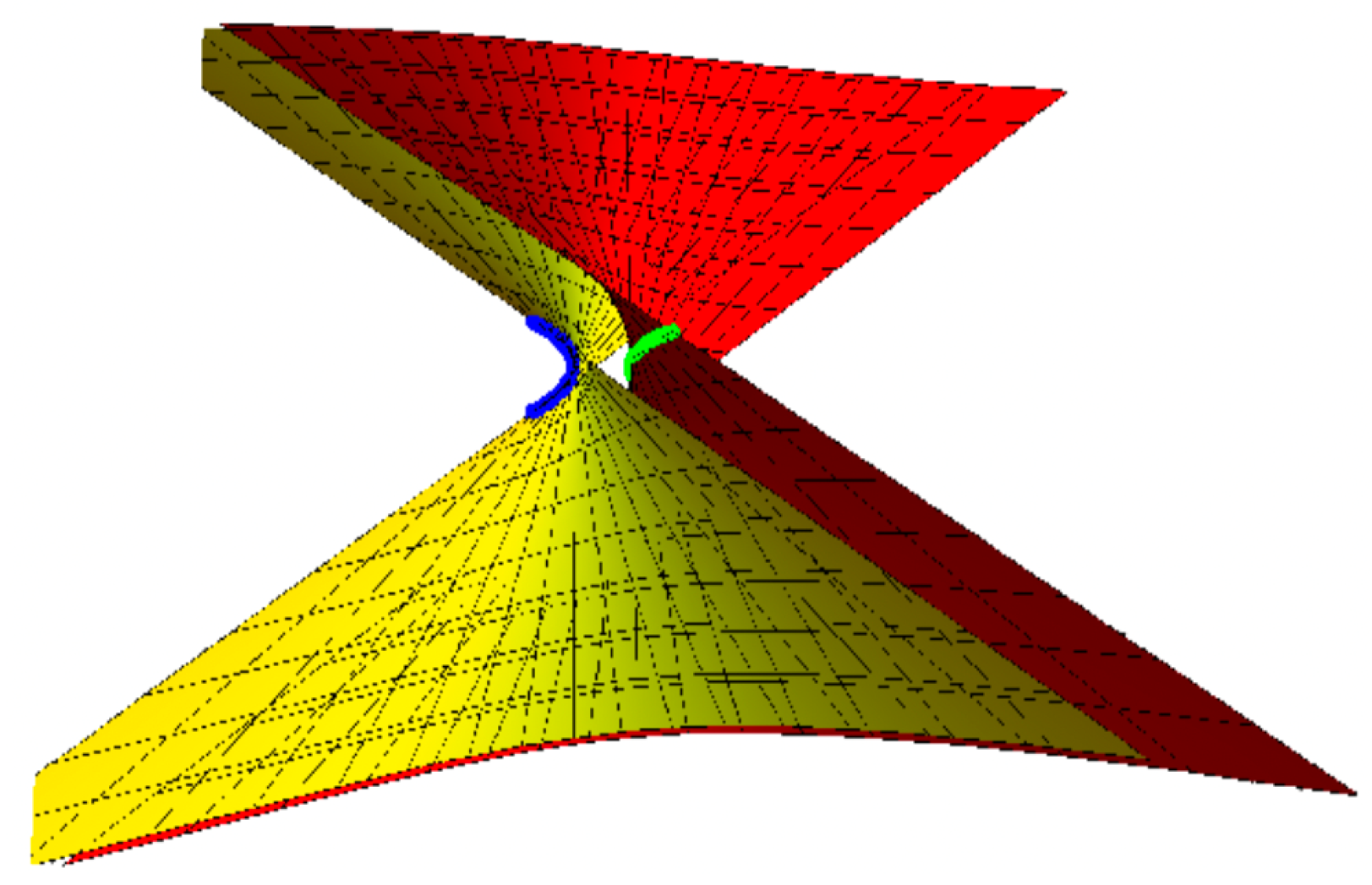
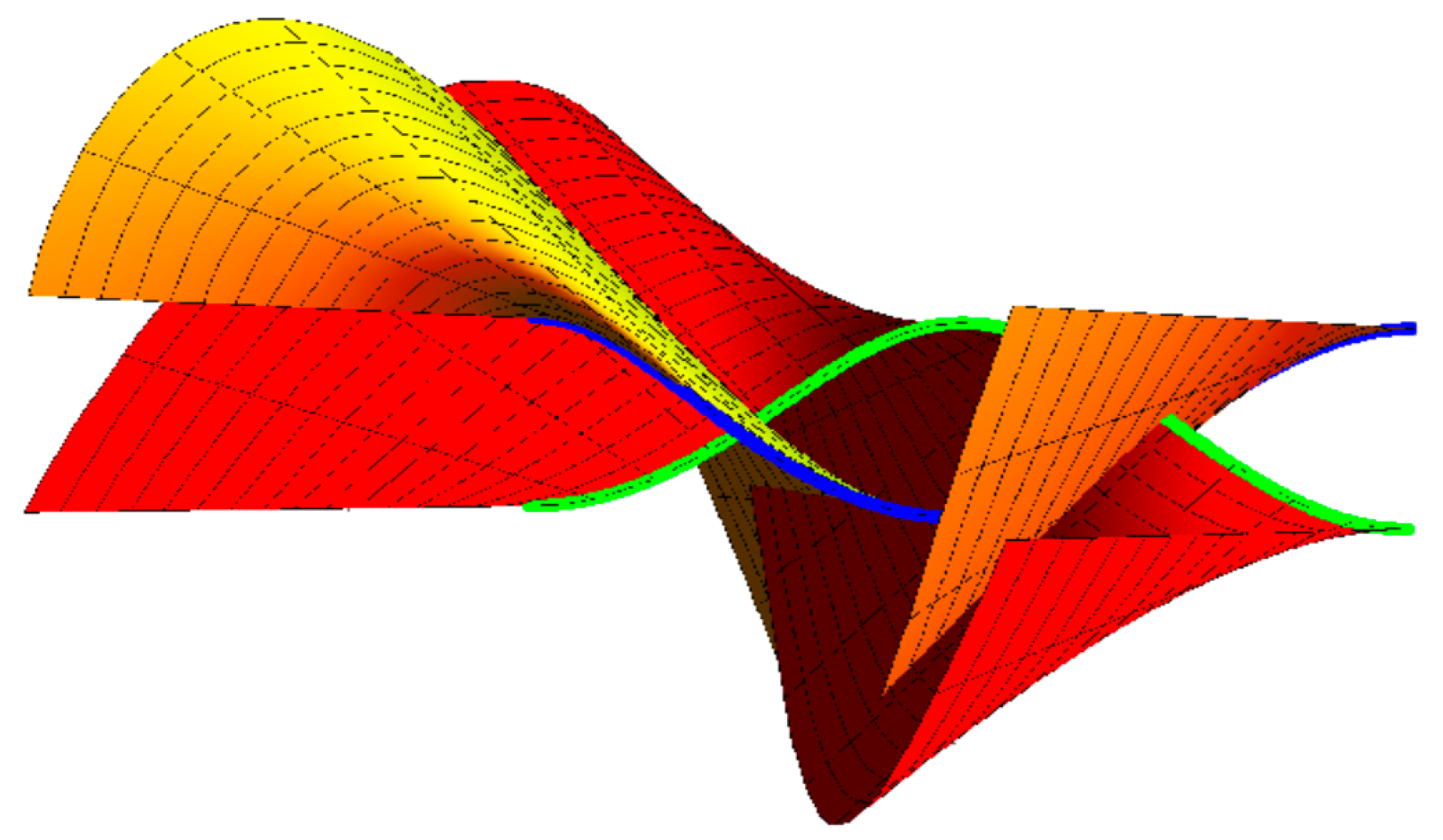
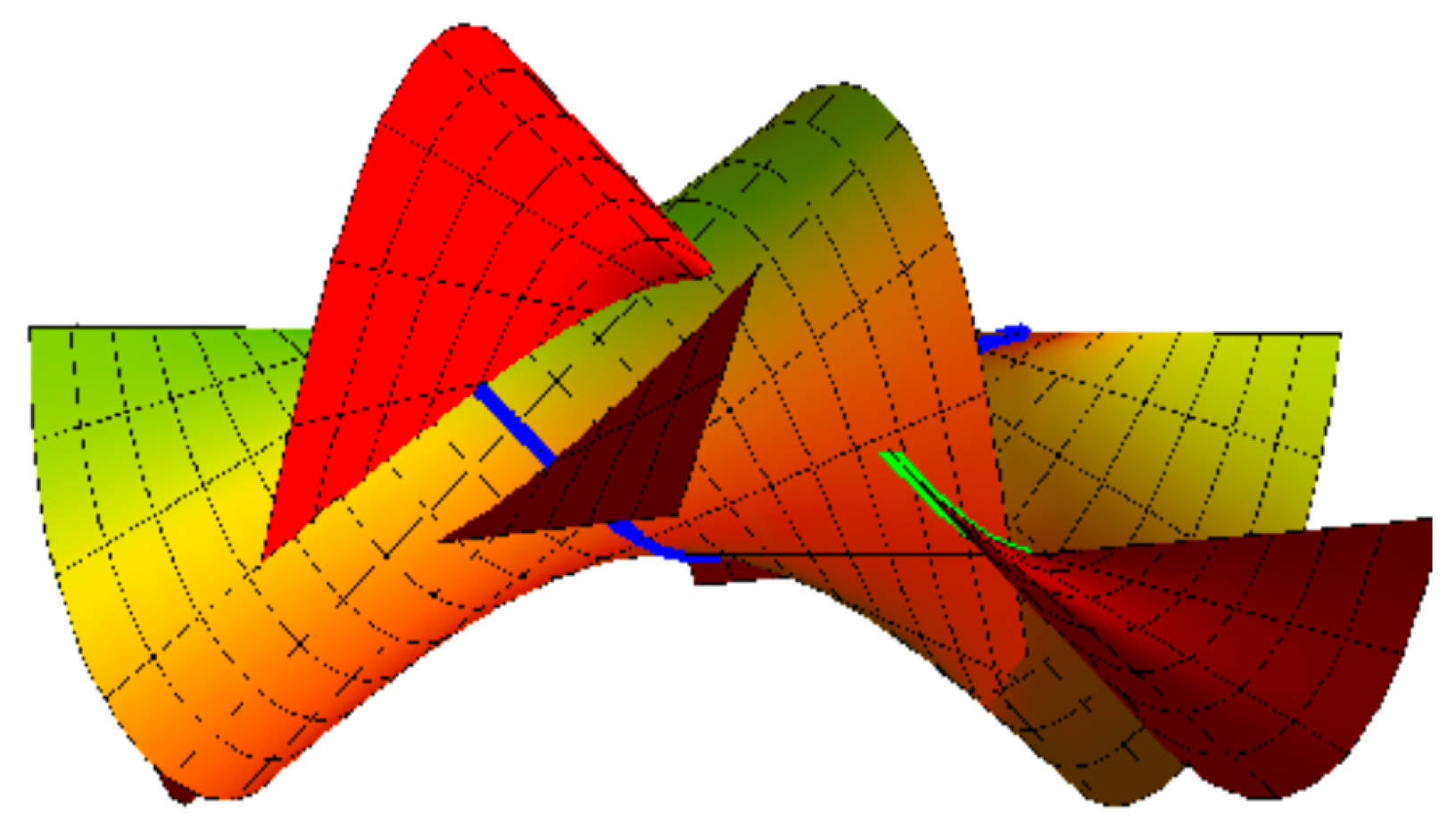
Ruled with Joint Geodesic
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spivak, M.A. Comprehensive Introduction to Differential Geometry, 2nd ed.; Publish or Perish: Houston, TX, USA, 1979. [Google Scholar]
- Do Carmo, M.P. Differential Geometry of Curves and Surfaces; Prentice-Hall: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- O’Neil, B. Semi-Riemannian Geometry, with Applications to Relativity; Academic Press: New York, NY, USA, 1983. [Google Scholar]
- Walfare, J. Curves and Surfaces in Minkowski Space. Ph.D. Thesis, Faculty of Science, K.U. Leuven, Leuven, Belgium, 1995. [Google Scholar]
- Ravani, B.; Ku, T.S. Bertrand offsets of ruled and developable surfaces. Comput.-Aided Des. 1991, 23, 145–152. [Google Scholar] [CrossRef]
- Sprott, K.S.; Ravani, B. Cylindrical milling of ruled surfaces. Int. J. Adv. Manuf. Technol. 2008, 38, 649–656. [Google Scholar] [CrossRef]
- Brond, R.; Jeulin, D.; Gateau, P.; Jarrin, J.; Serpe, G. Estimation of the transport properties of polymer composites by geodesic propagation. J. Microsc. 1994, 176, 167–177. [Google Scholar] [CrossRef]
- Bryson, S. Virtual spacetime: An environment for the visualization of curved spacetimes via geodesic flows. In Proceedings of the Proceedings Visualization ’92, Boston, MA, USA, 19–23 October 1992; pp. 291–298. [Google Scholar]
- Haw, R.J.; Munchmeyer, R.C. Geodesic curves on patched polynomial surfaces. Comput. Graph. Forum 1983, 2, 225–232. [Google Scholar] [CrossRef]
- Agarwal, K.; Har-Peled, S.; Sharir, M.; Varadarajan, K.R. Approximating shortest paths on a convex polytope in three dimensions. J. ACM 1997, 44, 567–584. [Google Scholar] [CrossRef]
- Har-Peled, S. Approximate shortest-path and geodesic diameter on convex polytopes in three dimensions. Discret. Comput. Geom. 1999, 21, 217–231. [Google Scholar] [CrossRef]
- Haw, R.J. An application of geodesic curves to sail design. Comput. Graph. Forum 1985, 4, 137–139. [Google Scholar] [CrossRef]
- Goldenberg, R.; Kimmel, R.; Rivlin, E.; Rudzsky, M. Fast geodesic active contours. IEEE Trans. Image Process 2001, 10, 1467–1475. [Google Scholar] [CrossRef] [PubMed]
- Novotni, M.; Klein, R. Computing geodesic paths on triangular meshes. In Proceedings of the 17th Brazilian Symposium on Computer Graphics and Image Processing, Curitiba, Brazil, 20 October 2004; pp. 341–347. [Google Scholar]
- Wang, G.J.; Tang, K.; Tai, C.L. Parametric representation of a surface bundle with a common spatial geodesic. Comput.-Aided Des. 2004, 36, 447–459. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Wang, G.J. A new method for designing a developable surface utilizing the surface bundle through a given curve. Prog. Nat. Sci. 2008, 18, 105–110. [Google Scholar] [CrossRef]
- Li, C.Y.; Wang, R.H.; Zhu, C.G. An approach for designing a developable surface through a given line of curvature. Comput.-Aided Des. 2013, 45, 621–627. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, G.J. Designing developable surface bundle through given curve as its common asymptotic curve. J. Zhejiang Univ. 2013, 47, 1246–1252. [Google Scholar]
- Atalay, G.S.; Kasap, E. Surfaces family with common Smarandache geodesic curve. J. Sci. Arts 2017, 4, 651–664. [Google Scholar]
- Abdel-Baky, R.A.; Alluhaib, N. Surfaces family with a common geodesic curve in Euclidean 3-Space . Int. J. Math. Anal. 2019, 13, 433–447. [Google Scholar] [CrossRef]
- Abdel-Baky, R.A. Timelike surfaces with a common asymptotic curve in Minkowski 3-Space . Riv. Mat. Univ. Parma 2017, 8, 379–395. [Google Scholar]
- Ergün, E.; Bayram, E.; Kasap, E. Surface bundle with a common line of curvature in Minkowski 3-space. Acta Math. Sin. 2014, 30, 2103–2118. [Google Scholar] [CrossRef]
- Alluhaib, N.; Abdel-Baky, R.A. A surface family with a common asymptotic null curve in Minkowski 3-space . Math. Probl. Eng. 2021, 2021, 3901527. [Google Scholar]
- Atalay, G.S.; Kasap, E. Surfaces family with common null asymptotic. Appl. Math. Comput. 2015, 260, 135–139. [Google Scholar] [CrossRef]
- Atalay, G.S. Surfaces family with a common Mannheim geodesic curve. J. Appl. Math. Comput. 2018, 2, 155–165. [Google Scholar]
- Jiang, X.; Jiang, P.; Meng, J.; Wang, K. Surface bundle couple interpolating Bertrand couple as common asymptotic curves in Galilean space . Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150114. [Google Scholar] [CrossRef]
- Almoneef, A.A.; Abdel-Baky, R.A. Surface family couple with Bertrand couple as common geodesic curves in Galilean 3-space . Mathematics 2023, 11, 2391. [Google Scholar] [CrossRef]
- Matsuda, H.; Yorozu, S. Notes on Bertrand curves. Yokohama Math. J. 2003, 50, 41–58. [Google Scholar]
- Almoneef, A.A.; Abdel-Baky, R.A. Surface family couple with Bertrand couple as mutual geodesic curves in Euclidean 3-space. AIMS Math. 2023, 8, 20546–20560. [Google Scholar] [CrossRef]
- Al-Jedani, A.; Abdel-Baky, R.A. A surface family with a mutual geodesic curve in Galilean 3-space . Mathematics 2023, 11, 2971. [Google Scholar] [CrossRef]
- Papaioannou, S.G.; Kiritsis, D. An application of Bertrand curves and surface to CAD/CAM. Comput.-Aided Des. 1985, 17, 348–352. [Google Scholar] [CrossRef]
- Görgülü, E.; Ozdamar, E. A generalizations of the Bertrand curves as general inclined curves in E n. Commun. Fac. Sci. Uni. Ankara. Ser. A1 1986, 35, 53–60. [Google Scholar] [CrossRef]
- Izumiya, S.; Takeuchi, N. Generic properties of helices and Bertrand curves. J. Geom. 2002, 74, 97–109. [Google Scholar] [CrossRef]
- Tanriöver, N. Some properties of Bertrand curves in Lorentzian n-space . Int. J. Geom. Methods Mod. Phys. 2016, 13, 1650064. [Google Scholar] [CrossRef]
- Whittemore, J.K. Bertrand curves and helices. Duke Math. J. 1940, 6, 235–245. [Google Scholar] [CrossRef]
- Kazaz, M.; Uğurlu, H.H. Bertrand Partner D-Curves in the minkowski3-space E3-1. Math. Sci. Appl. E-Notes 2014, 2, 68–82. [Google Scholar]
- Aksoyak, F.K.; Gök, I.S.M.A.I.L.; Ilarslan, K. Generalized null Bertrand curves in Minkowski space-time. Ann. Alexandru Ioan Cuza Univ. Math. 2014, 60, 489–502. [Google Scholar] [CrossRef]
- Magid, M.A. Timelike surfaces in Lorentz 3-space with prescribed mean curvature and Gauss map. Hokkaido Math. J. 1991, 20, 447–464. [Google Scholar] [CrossRef]
- Önder, M.; Uğurlu, H.H. Frenet frames and invariants of timelike ruled surfaces. Ain Shams Eng. J. 2013, 4, 507–513. [Google Scholar] [CrossRef]
- Babaarslan, M.; Munteanu, M.I. Time-like loxodromes on rotational surfaces in Minkowski 3-space. Ann. Alexandru Ioan Cuza Univ.-Math. 2015, 61, 471–484. [Google Scholar]
- Alluhaibi, N.; Abdel-Baky, R.A. Kinematic Geometry of Timelike Ruled Surfaces in Minkowski 3-Space . Symmetry 2022, 14, 749. [Google Scholar] [CrossRef]
- Babaarslan, M.; Kayacik, M. Time-like loxodromes on helicoidal surfaces in Minkowski 3-space. Filomat 2017, 31, 4405–4414. [Google Scholar] [CrossRef]
- Li, Y.; Mofarreh, F.; Abdel-Baky, R.A. Timelike Circular Surfaces and Singularities in Minkowski 3-Space. Symmetry 2022, 14, 1914. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, L.; Li, P.; Chang, Y. Singularities of Osculating Developable Surfaces of Timelike Surfaces along Curves. Symmetry 2022, 14, 2251. [Google Scholar] [CrossRef]
- Gür, M.S. Geometric properties of timelike surfaces in Lorentz-Minkowski 3-space. Filomat 2023, 37, 5735–5749. [Google Scholar] [CrossRef]
- Yapar, Z.; Sa, Y. On the geometry of closed timelike ruled surfaces in dual Lorentzian space. Int. J. Appl. Math. 2016, 29, 7–18. [Google Scholar] [CrossRef]
- Yapar, Z.; Sagiroglu, Y. On a motion of a line along two closed ruled surfaces. Int. J. Math. Anal. 2015, 9, 1877–1887. [Google Scholar] [CrossRef]
- Atalay, G.Ş.; Kasap, E. Developed Motion of Robot End-Effector of Timelike Ruled Surfaces With Spacelike Rulings (The First Case). Hagia Sophia J. Geom. 2020, 2, 9–21. [Google Scholar]
- Güler, F.; Kasap, E. A path planning method for robot end effector motion using the curvature theory of the ruled surfaces. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850048. [Google Scholar] [CrossRef]
- Li, Y.L.; Zhu, Y.S.; Sun, Q.Y. Singularities and dualities of pedal curves in pseudo-hyperbolic and de Sitter space. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150008. [Google Scholar] [CrossRef]
- Li, Y.L.; Nazra, S.; Abdel-Baky, R.A. Singularities properties of timelike sweeping surface in Minkowski 3-Space. Symmetry 2022, 14, 1996. [Google Scholar] [CrossRef]
- Li, Y.L.; Chen, Z.; Nazra, S.; Abdel-Baky, R.A. Singularities for timelike developable surfaces in Minkowski 3-Space. Symmetry 2023, 15, 277. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mofarreh, F. Timelike Surface Couple with Bertrand Couple as Joint Geodesic Curves in Minkowski 3-Space. Symmetry 2024, 16, 732. https://doi.org/10.3390/sym16060732
Mofarreh F. Timelike Surface Couple with Bertrand Couple as Joint Geodesic Curves in Minkowski 3-Space. Symmetry. 2024; 16(6):732. https://doi.org/10.3390/sym16060732
Chicago/Turabian StyleMofarreh, Fatemah. 2024. "Timelike Surface Couple with Bertrand Couple as Joint Geodesic Curves in Minkowski 3-Space" Symmetry 16, no. 6: 732. https://doi.org/10.3390/sym16060732
APA StyleMofarreh, F. (2024). Timelike Surface Couple with Bertrand Couple as Joint Geodesic Curves in Minkowski 3-Space. Symmetry, 16(6), 732. https://doi.org/10.3390/sym16060732






