A New Adaptive Levenberg–Marquardt Method for Nonlinear Equations and Its Convergence Rate under the Hölderian Local Error Bound Condition
Abstract
1. Introduction
2. The New Adaptive LM Algorithm and Its Global Convergence
| Algorithm 1 (ALLM Algorithm) |
| Step 1. Given , . Set . Step 2. If , stop. Otherwise let Step 3. Compute Step 4. Compute , and by Equations (9), (6) and (8). Set Step 5. Set Step 6. Choose as Step 7. Set and return to Step 2. |
3. Convergence Rate
4. Numerical Experiments
- NF: The number of function calculations.
- NJ: The number of Jacobian calculations.
- NT: We generally use the ‘’ to indicate the total computations.
| AELM | ALLM | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Function | |||||||||
| NF/NJ/NT | NF/NJ/NT | NF/NJ/NT | NF/NJ/NT | NF/NJ/NT | NF/NJ/NT | NF/NJ/NT | |||
| 1 | 4 | 1 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 |
| 10 | 13/13/65 | 13/13/65 | 13/13/65 | 13/13/65 | 13/13/65 | 13/13/65 | 13/13/65 | ||
| 100 | 16/16/80 | 16/16/80 | 16/16/80 | 16/16/80 | 16/16/80 | 16/16/80 | 16/16/80 | ||
| 2 | 2 | 1 | 8/8/24 | 8/8/24 | 8/8/24 | 8/8/24 | 8/8/24 | 8/8/24 | 8/8/24 |
| 10 | 11/11/33 | 11/11/33 | 11/11/33 | 11/11/33 | 11/11/33 | 11/11/33 | 11/11/33 | ||
| 100 | 15/15/45 | 15/15/45 | 15/15/45 | 15/15/45 | 15/15/45 | 15/15/45 | 15/15/45 | ||
| 3 | 4 | 1 | 8/8/40 | 8/8/40 | 8/8/40 | 8/8/40 | 8/8/40 | 8/8/40 | 8/8/40 |
| 10 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | ||
| 100 | 12/12/60 | 12/12/60 | 12/12/60 | 12/12/60 | 12/12/60 | 12/12/60 | 12/12/60 | ||
| 4 | 4 | 1 | 13/13/65 | 7/7/35 | 7/7/35 | 7/7/35 | 7/7/35 | 7/7/35 | 7/7/35 |
| 10 | 16/16/80 | 9/9/45 | 9/9/45 | 9/9/45 | 9/9/45 | 9/9/45 | 9/9/45 | ||
| 100 | 61/50/261 | 11/11/55 | 11/11/55 | 11/11/55 | 11/11/55 | 11/11/55 | 11/11/55 |
- Iter: Number of iterations.
- F: Final value of the norm of the function.
- Time: CPU time in seconds.
| AELM | ALLM | |||||
|---|---|---|---|---|---|---|
| Function | ||||||
| Iters/F/Time | Iters/F/Time | Iters/F/Time | Iters/F/Time | |||
| Extended Rosenbrock | 500 | −10 | 19/2.7631 × 10−7/0.30 | 19/2.7858 × 10−7/0.27 | 19/2.7744 × 10−7/0.29 | 19/2.7631 × 10−7/0.28 |
| −1 | 16/1.7341 × 10−7/0.23 | 14/2.5509 × 10−7/0.19 | 15/3.3852 × 10−7/0.20 | 16/1.7341 × 10−7/0.25 | ||
| 1 | 17/2.2186 × 10−7/0.24 | 17/1.9553 × 10−7/0.25 | 17/2.0901 × 10−7/0.22 | 17/2.2186 × 10−7/0.23 | ||
| 10 | 19/3.9252 × 10−7/0.29 | 19/3.8895 × 10−7/0.25 | 19/3.9066 × 10−7/0.27 | 19/3.9252 × 10−7/0.29 | ||
| 100 | 23/1.3154 × 10−7/0.42 | 23/1.3142 × 10−7/0.30 | 23/1.3150 × 10−7/0.34 | 23/1.3154 × 10−7/0.37 | ||
| 1000 | −10 | 19/3.9156 × 10−7/1.63 | 19/3.9442 × 10−7/1.52 | 19/3.9299 × 10−7/1.53 | 19/3.9156 × 10−7/1.64 | |
| −1 | 16/2.5034 × 10−7/1.43 | 14/3.8204 × 10−7/1.10 | 16/1.2047 × 10−7/1.28 | 16/2.5034 × 10−7/1.34 | ||
| 1 | 17/3.1868 × 10−7/1.46 | 17/2.8057 × 10−7/1.40 | 17/2.9943 × 10−7/1.36 | 17/3.1868 × 10−7/1.46 | ||
| 10 | 20/1.3911 × 10−7/1.67 | 20/1.3781 × 10−7/1.93 | 20/1.3866 × 10−7/1.65 | 20/1.3911 × 10−7/1.57 | ||
| 100 | 23/1.8652 × 10−7/2.06 | 23/1.8646 × 10−7/1.90 | 23/1.8638 × 10−7/1.90 | 23/1.8652 × 10−7/1.98 | ||
| Extended Helical valley | 501 | −10 | 42/1.3356 × 10−6/0.68 | 3/5.1316 × 10−7/0.03 | 13/3.7044 × 10−7/0.17 | 14/3.2573 × 10−7/0.23 |
| −1 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | ||
| 1 | 8/3.1758 × 10−7/0.13 | 8/1.4137 × 10−7/0.09 | 8/2.1648 × 10−7/0.10 | 8/3.1758 × 10−7/0.12 | ||
| 10 | 8/1.8981 × 10−9/0.12 | 8/8.0024 × 10−10/0.10 | 8/1.2568 × 10−9/0.10 | 8/1.8981 × 10−9/0.11 | ||
| 100 | 8/5.9124 × 10−10/0.12 | 8/3.9747 × 10−10/0.11 | 8/4.8399 × 10−10/0.11 | 8/5.9124 × 10−10/0.12 | ||
| 1000 | −10 | 7/2.3766 × 10−13/0.53 | 6/3.0134 × 10−13/0.45 | 6/1.5143 × 10−9/0.44 | 7/2.3766 × 10−13/0.55 | |
| −1 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | ||
| 1 | 8/1.8337 × 10−8/0.69 | 8/7.2043 × 10−9/0.68 | 8/1.1804 × 10−8/0.62 | 8/1.8337 × 10−8/0.67 | ||
| 10 | 8/1.6817 × 10−11/0.66 | 8/1.0758 × 10−11/0.61 | 8/1.4744 × 10−11/0.60 | 8/1.6817 × 10−11/0.65 | ||
| 100 | 26/9.3824 × 10−13/2.51 | 35/1.0739 × 10−7/3.29 | 26/6.6675 × 10−8/2.18 | 26/6.9835 × 10−11/2.16 | ||
| Discrete boundary value | 500 | −10 | 6/3.3487 × 10−3/0.11 | 6/3.3666 × 10−3/0.07 | 6/3.3631 × 10−3/0.09 | 6/3.3487 × 10−3/0.12 |
| −1 | 4/1.2234 × 10−3/0.06 | 4/1.2579 × 10−3/0.04 | 4/1.2417 × 10−3/0.05 | 4/1.2234 × 10−3/0.04 | ||
| 1 | 3/3.5633 × 10−4/0.04 | 3/3.6008 × 10−4/0.03 | 3/3.5823 × 10−4/0.03 | 3/3.5633 × 10−4/0.03 | ||
| 10 | 5/6.7290 × 10−3/0.08 | 5/6.7739 × 10−3/0.06 | 5/6.7614 × 10−3/0.06 | 5/6.7290 × 10−3/0.08 | ||
| 100 | 12/1.3651 × 10−4/0.23 | 13/1.3834 × 10−5/0.16 | 12/1.5752 × 10−4/0.17 | 12/1.3651 × 10−4/0.16 | ||
| 1000 | −10 | 6/3.6656 × 10−3/0.52 | 6/3.6804 × 10−3/0.50 | 6/3.6780 × 10−3/0.47 | 6/3.6656 × 10−3/0.48 | |
| −1 | 4/1.4253 × 10−3/0.30 | 4/1.4669 × 10−3/0.30 | 4/1.4474 × 10−3/0.30 | 4/1.4253 × 10−3/0.31 | ||
| 1 | 3/1.3022 × 10−4/0.22 | 3/1.3092 × 10−4/0.20 | 3/1.3058 × 10−4/0.21 | 3/1.3022 × 10−4/0.21 | ||
| 10 | 5/6.5900 × 10−3/0.40 | 5/6.6346 × 10−3/0.38 | 5/6.6209 × 10−3/0.35 | 5/6.5900 × 10−3/0.39 | ||
| 100 | 13/9.9458 × 10−5/1.09 | 13/1.0869 × 10−4/1.06 | 13/1.0505 × 10−4/1.07 | 13/9.9458 × 10−5/1.08 | ||
| Discrete integral equation | 500 | −10 | 12/1.2304 × 10−5/1.06 | 12/1.2171 × 10−5/1.03 | 12/1.2238 × 10−5/1.04 | 12/1.2304 × 10−5/1.06 |
| −1 | 9/1.5928 × 10−5/0.76 | 9/1.4153 × 10−5/0.76 | 9/1.5162 × 10−5/0.75 | 9/1.5928 × 10−5/0.76 | ||
| 1 | 7/1.3357 × 10−5/0.59 | 7/1.3770 × 10−5/0.58 | 7/1.3592 × 10−5/0.58 | 7/1.3357 × 10−5/0.58 | ||
| 10 | 10/9.3502 × 10−6/0.86 | 8/9.0151 × 10−6/0.67 | 9/1.5419 × 10−5/0.76 | 10/9.3502 × 10−6/0.86 | ||
| 100 | 10/4.5155 × 10−9/0.91 | 10/4.5463 × 10−9/0.89 | 10/4.5306 × 10−9/0.88 | 10/4.5155 × 10−9/0.91 | ||
| 1000 | −10 | 12/1.7452 × 10−5/4.50 | 12/1.7265 × 10−5/4.48 | 12/1.7358 × 10−5/4.50 | 12/1.7452 × 10−5/4.51 | |
| −1 | 10/6.0308 × 10−6/3.71 | 10/5.2005 × 10−6/3.73 | 10/5.6998 × 10−6/3.70 | 10/6.0308 × 10−6/3.67 | ||
| 1 | 8/5.1495 × 10−6/2.86 | 8/5.3838 × 10−6/2.90 | 8/5.2754 × 10−6/2.50 | 8/5.1495 × 10−6/2.86 | ||
| 10 | 10/1.4251 × 10−5/3.73 | 9/5.0675 × 10−6/3.30 | 10/5.7297 × 10−6/3.59 | 10/1.4251e × 10−5/3.66 | ||
| 100 | 10/6.3828 × 10−9/3.86 | 10/6.4261 × 10−9/3.83 | 10/6.4040 × 10−9/3.81 | 10/6.3828 × 10−9/3.83 | ||
| Broyden banded | 500 | −10 | 10/3.8446 × 10−12/0.17 | 10/3.9166 × 10−12/0.16 | 10/4.3882 × 10−12/0.14 | 10/3.8446 × 10−12/0.17 |
| −1 | 26/6.9212 × 10−6/0.52 | 31/1.2468 × 10−5/0.53 | 28/1.6756 × 10−5/0.50 | 25/1.2128 × 10−5/0.50 | ||
| 1 | 12/1.5063 × 10−5/0.20 | 12/1.5060 × 10−5/0.20 | 12/1.5061 × 10−5/0.19 | 12/1.5063 × 10−5/0.20 | ||
| 10 | 18/1.7636 × 10−5/0.33 | 18/1.7636 × 10−5/0.30 | 18/1.7636 × 10−5/0.28 | 18/1.7636 × 10−5/0.28 | ||
| 100 | 24/1.0280 × 10−5/0.44 | 24/1.0280 × 10−5/0.36 | 24/1.0280 × 10−5/0.37 | 24/1.0280 × 10−5/0.37 | ||
| 1000 | −10 | 10/3.5499 × 10−12/0.90 | 10/3.8124 × 10−12/0.91 | 10/4.6220 × 10−12/0.90 | 10/3.5499 × 10−12/0.99 | |
| −1 | 33/9.9927 × 10−6/3.35 | 27/9.6110 × 10−6/2.54 | 33/2.6949 × 10−5/3.04 | 28/9.7912 × 10−6/2.62 | ||
| 1 | 12/2.1201 × 10−5/1.22 | 12/2.1196 × 10−5/1.08 | 12/2.1199 × 10−5/1.09 | 12/2.1201 × 10−5/1.17 | ||
| 10 | 18/2.4886 × 10−5/1.82 | 18/2.4886 × 10−5/1.59 | 18/2.4886 × 10−5/1.68 | 18/2.4886 × 10−5/1.68 | ||
| 100 | 24/1.4499 × 10−5/2.80 | 24/1.4499 × 10−5/2.42 | 24/1.4499 × 10−5/2.37 | 24/1.4499 × 10−5/2.54 | ||
| AELM | ALLM | |||||
|---|---|---|---|---|---|---|
| Function | ||||||
| Iters/F/Time | Iters/F/Time | Iters/F/Time | Iters/F/Time | |||
| Extended Rosenbrock | 500 | −10 | 19/2.7631 × 10−7/0.30 | 19/2.7841 × 10−7/0.26 | 19/2.7734 × 10−7/0.26 | 19/2.7635 × 10−7/0.30 |
| −1 | 16/1.7341 × 10−7/0.23 | 14/1.7729 × 10−7/0.17 | 15/3.2343 × 10−7/0.21 | 16/1.7288 × 10−7/0.20 | ||
| 1 | 17/2.2186 × 10−7/0.24 | 17/1.8677 × 10−7/0.25 | 17/2.0435 × 10−7/0.25 | 17/2.2121 × 10−7/0.22 | ||
| 10 | 19/3.9252 × 10−7/0.29 | 19/3.8875 × 10−7/0.24 | 19/3.9061 × 10−7/0.26 | 19/3.9243 × 10−7/0.25 | ||
| 100 | 23/1.3154 × 10−7/0.42 | 23/1.3134 × 10−7/0.29 | 23/1.3145 × 10−7/0.33 | 23/1.3149 × 10−7/0.33 | ||
| 1000 | −10 | 19/3.9156 × 10−7/1.63 | 19/3.9423 × 10−7/1.50 | 19/3.9284 × 10−7/1.54 | 19/3.9140 × 10−7/1.56 | |
| −1 | 16/2.5034 × 10−7/1.43 | 14/2.3878 × 10−7/1.05 | 15/4.5237 × 10−7/1.24 | 16/2.4969 × 10−7/1.32 | ||
| 1 | 17/3.1868 × 10−7/1.46 | 17/2.7048 × 10−7/1.33 | 17/2.9369 × 10−7/1.36 | 17/3.1809 × 10−7/1.33 | ||
| 10 | 20/1.3911 × 10−7/1.67 | 20/1.3786 × 10−7/1.53 | 20/1.3857 × 10−7/1.57 | 20/1.3919e × 10−7/1.59 | ||
| 100 | 23/1.8652 × 10−7/2.06 | 23/1.8649 × 10−7/1.83 | 23/1.8655 × 10−7/1.80 | 23/1.8633 × 10−7/1.81 | ||
| Extended Helical valley | 501 | −10 | 42/1.3356 × 10−6/0.68 | 3/7.5853 × 10−13/0.04 | 13/1.7643 × 10−7/0.18 | 14/2.0341 × 10−7/0.19 |
| −1 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | ||
| 1 | 8/3.1758 × 10−7/0.13 | 8/1.0595 × 10−7/0.11 | 8/1.9230 × 10−7/0.11 | 8/3.2101 × 10−7/0.09 | ||
| 10 | 8/1.8981 × 10−9/0.12 | 8/4.7841 × 10−10/0.11 | 8/9.5278 × 10−10/0.10 | 8/1.6935 × 10−9/0.10 | ||
| 100 | 8/5.9124 × 10−10/0.12 | 8/2.0055 × 10−10/0.10 | 8/3.2729 × 10−10/0.13 | 8/4.9161 × 10−10/0.13 | ||
| 1000 | −10 | 7/2.3766 × 10−13/0.53 | 5/7.4481 × 10−10/0.36 | 6/1.7998 × 10−12/0.51 | 6/4.6416 × 10−7/0.42 | |
| −1 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | ||
| 1 | 8/1.8337 × 10−8/0.69 | 8/4.1226 × 10−9/0.59 | 8/9.1462 × 10−9/0.62 | 8/1.7753 × 10−8/0.63 | ||
| 10 | 8/1.6817 × 10−11/0.66 | 8/2.2703 × 10−11/0.59 | 8/3.2386 × 10−11/0.60 | 8/4.0803 × 10−11/0.64 | ||
| 100 | 26/9.3824 × 10−13/2.51 | 46/2.6770 × 10−11/3.70 | 26/8.5493 × 10−9/2.09 | 26/2.8466 × 10−10/2.15 | ||
| Discrete boundary value | 500 | −10 | 6/3.3487 × 10−3/0.11 | 4/3.1555 × 10−3/0.04 | 4/4.2613 × 10−3/0.04 | 4/4.7919 × 10−3/0.05 |
| −1 | 4/1.2234 × 10−3/0.06 | 3/7.2588 × 10−4/0.03 | 3/7.1034 × 10−4/0.03 | 3/6.9394 × 10−4/0.04 | ||
| 1 | 3/3.5633 × 10−4/0.04 | 3/4.1479 × 10−6/0.03 | 3/4.1402 × 10−6/0.04 | 3/4.1324 × 10−6/0.04 | ||
| 10 | 5/6.7290 × 10−3/0.08 | 4/2.4328 × 10−3/0.05 | 4/ 3.0758 × 10−3/0.05 | 4/3.4218 × 10−3/0.05 | ||
| 100 | 12/1.3651 × 10−4/0.23 | 11/4.2188 × 10−5/0.16 | 12/1.5591 × 10−5/0.18 | 12/1.3814 × 10−5/0.18 | ||
| 1000 | −10 | 6/3.6656 × 10−3/0.52 | 4/3.5180 × 10−3/0.29 | 4/4.5349 × 10−3/0.29 | 4/5.0429 × 10−3/0.28 | |
| −1 | 4/1.4253 × 10−3/0.30 | 3/9.3230 × 10−4/0.21 | 3/9.1090 × 10−4/0.21 | 3/8.8813 × 10−4/0.23 | ||
| 1 | 3/1.3022 × 10−4/0.22 | 2/2.6311 × 10−4/0.13 | 2/2.6303 × 10−4/0.13 | 2/2.6296 × 10−4/0.13 | ||
| 10 | 5/6.5900 × 10−3/0.40 | 4/2.5604 × 10−3/0.29 | 4/3.0932 × 10−3/0.30 | 4/3.4004 × 10−3/0.27 | ||
| 100 | 13/9.9458 × 10−5/1.09 | 11/1.2743 × 10−4/0.88 | 11/2.1884 × 10−4/0.93 | 11/2.1536 × 10−4/0.85 | ||
| Discrete integral equation | 500 | −10 | 12/1.2304 × 10−5/1.06 | 12/1.2047 × 10−5/1.03 | 12/1.2171 × 10−5/1.05 | 12/1.2294 × 10−5/1.04 |
| −1 | 9/1.5928 × 10−5/0.76 | 9/1.0655 × 10−5/0.75 | 9/1.2735 × 10−5/0.76 | 9/ 1.4195 × 10−5/0.76 | ||
| 1 | 7/1.3357 × 10−5/0.59 | 7/1.0869 × 10−5/0.57 | 7/1.0772 × 10−5/0.58 | 7/1.0633 × 10−5/0.57 | ||
| 10 | 10/9.3502 × 10−6/0.86 | 9/4.8669 × 10−6/0.75 | 9/1.3758 × 10−5/0.76 | 10/9.7578 × 10−6/0.84 | ||
| 100 | 10/4.5155 × 10−9/0.91 | 10/4.5453 × 10−9/0.89 | 10/4.5300 × 10−9/0.90 | 10/4.5154 × 10−9/0.88 | ||
| 1000 | −10 | 12/1.7452 × 10−5/4.50 | 12/1.7133 × 10−5/4.41 | 12/1.7285 × 10−5/4.46 | 12/1.7441 × 10−5/4.47 | |
| −1 | 10/6.0308 × 10−6/3.71 | 9/1.5092 × 10−5/3.25 | 9/1.8533 × 10−5/3.27 | 10/5.2150 × 10−6/3.66 | ||
| 1 | 8/5.1495 × 10−6/2.86 | 7/1.5749 × 10−5/2.48 | 7/1.5610 × 10−5/2.50 | 7/1.5367 × 10−5/2.62 | ||
| 10 | 10/1.4251 × 10−5/3.73 | 9/8.5398 × 10−6/3.25 | 10/5.1845 × 10−6/3.62 | 10/1.4626 × 10−5/3.71 | ||
| 100 | 10/6.3828 × 10−9/3.86 | 10/6.4246 × 10−9/3.76 | 10/6.4031 × 10−9/3.79 | 10/6.3825 × 10−9/3.77 | ||
| Broyden banded | 500 | −10 | 10/3.8446 × 10−12/0.17 | 10/3.795 × 10−12/0.16 | 10/4.3814 × 10−12/0.17 | 10/3.8105 × 10−12/0.16 |
| −1 | 26/6.9212 × 10−6/0.52 | 29/6.5177 × 10−6/0.45 | 28/1.6459 × 10−5/0.44 | 25/1.1907 × 10−5/0.42 | ||
| 1 | 12/1.5063 × 10−5/0.20 | 12/1.5059 × 10−5/0.20 | 12/1.5061 × 10−5/0.20 | 12/1.5063 × 10−5/0.18 | ||
| 10 | 18/1.7636 × 10−5/0.33 | 18/1.7636 × 10−5/0.30 | 18/1.7636 × 10−5/0.33 | 18/1.7636 × 10−5/0.31 | ||
| 100 | 24/1.0280 × 10−5/0.44 | 24/1.0280 × 10−5/0.36 | 24/1.0280 × 10−5/0.40 | 24/1.0280 × 10−5/0.36 | ||
| 1000 | −10 | 10/3.5499 × 10−12/0.90 | 10/4.5936 × 10−12/0.86 | 10/3.810 × 10−12/0.89 | 10/5.7143 × 10−12/0.93 | |
| −1 | 33/9.9927 × 10−6/3.35 | 29/1.5374 × 10−5/2.76 | 31/1.8408 × 10−5 /2.84 | 28/9.7968 × 10−6/2.61 | ||
| 1 | 12/2.1201 × 10−5/1.22 | 12/2.1194 × 10−5/1.07 | 12/2.1198 × 10−5/1.08 | 12/2.1201 × 10−5/1.13 | ||
| 10 | 18/2.4886 × 10−5/1.82 | 18/2.4886 × 10−5/1.69 | 18/2.4886 × 10−5/1.64 | 18/2.4886 × 10−5/1.65 | ||
| 100 | 24/1.4499 × 10−5/2.80 | 24/1.4499 × 10−5/2.30 | 24/1.4499 × 10−5/2.33 | 24/1.4499 × 10−5/2.51 | ||
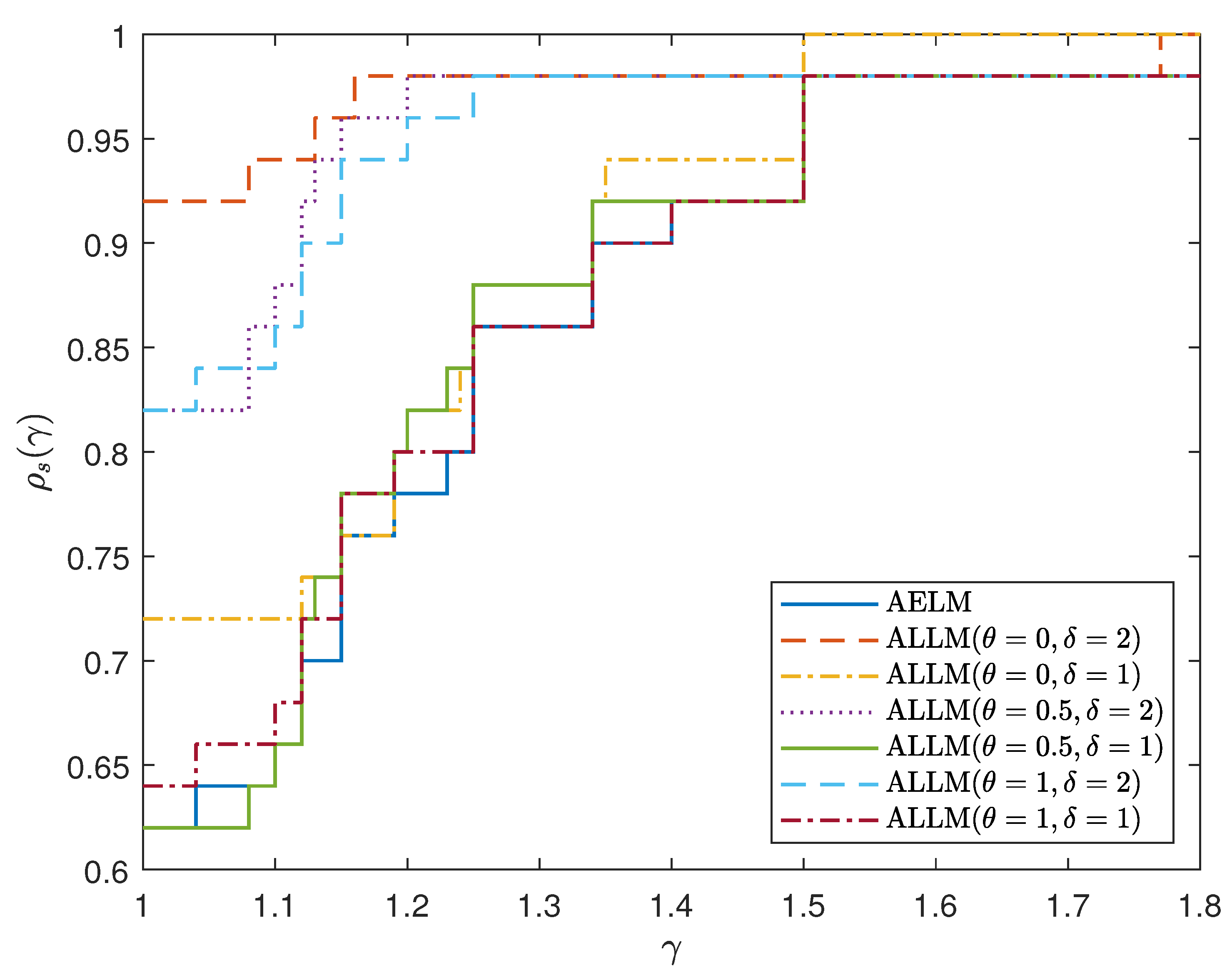
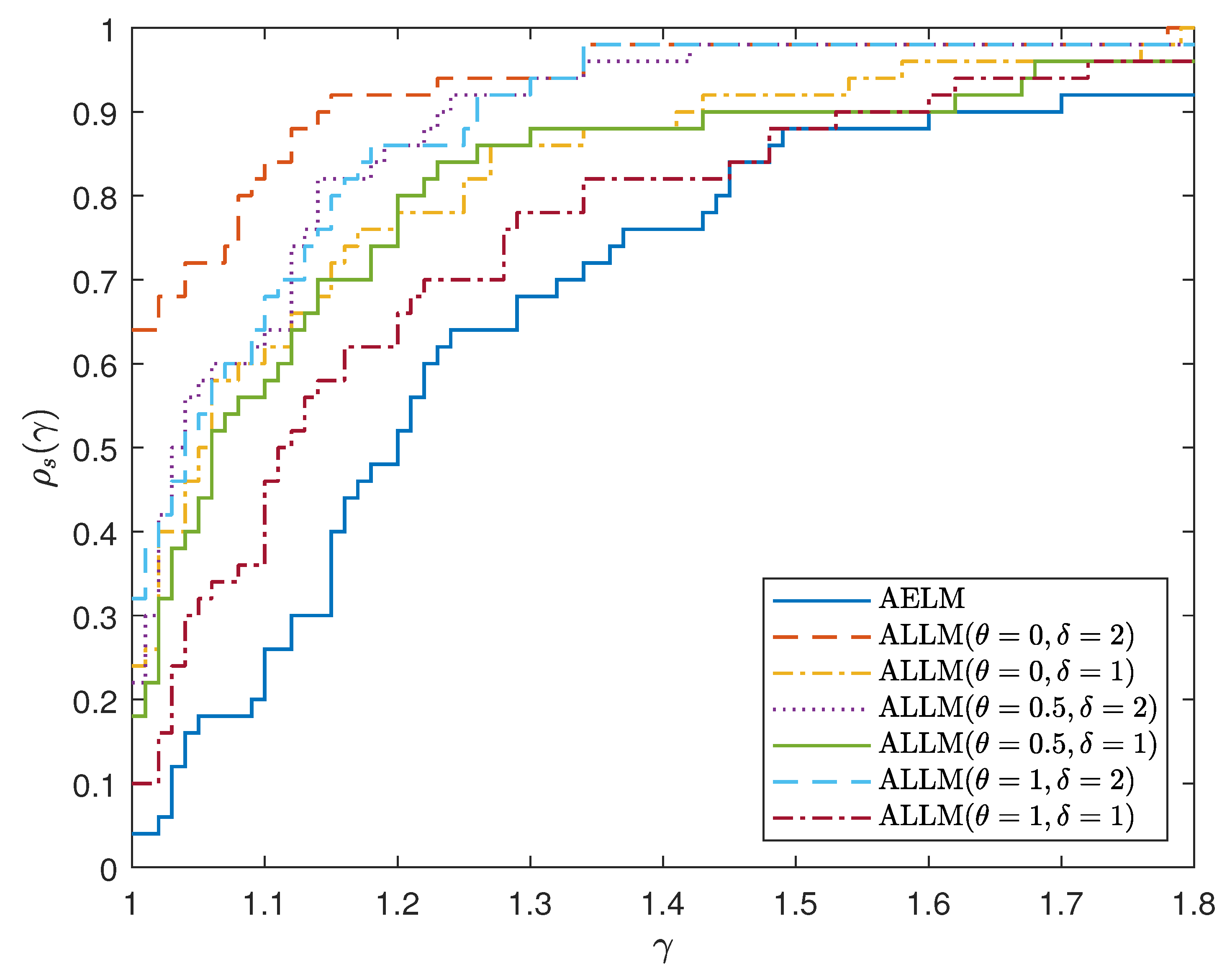
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leonov, E.; Polbin, A. Numerical Search for a Global Solution in a Two-Mode Economy Model with an Exhaustible Resource of Hydrocarbons. Math. Model. Comput. Simul. 2022, 14, 213–223. [Google Scholar] [CrossRef]
- Xu, D.; Bai, Z.; Jin, X.; Yang, X.; Chen, S.; Zhou, M. A mean-variance portfolio optimization approach for high-renewable energy hub. Appl. Energy 2022, 325, 119888. [Google Scholar] [CrossRef]
- Manzoor, Z.; Iqbal, M.S.; Hussain, S.; Ashraf, F.; Inc, M.; Tarar, M.A.; Momani, S. A study of propagation of the ultra-short femtosecond pulses in an optical fiber by using the extended generalized Riccati equation mapping method. Opt. Quantum Electron. 2023, 55, 717. [Google Scholar] [CrossRef]
- Vu, D.T.S.; Gharbia, I.B.; Haddou, M.; Tran, Q.H. A new approach for solving nonlinear algebraic systems with complementarity conditions. Application to compositional multiphase equilibrium problems. Math. Comput. Simul. 2021, 190, 1243–1274. [Google Scholar] [CrossRef]
- Maia, L.; Nornberg, G.; Pacella, F. A dynamical system approach to a class of radial weighted fully nonlinear equations. Commun. Partial Differ. Equ. 2021, 46, 573–610. [Google Scholar] [CrossRef]
- Vasin, V.V.; Skorik, G.G. Two-stage method for solving systems of nonlinear equations and its applications to the inverse atmospheric sounding problem. In Doklady Mathematics; Springer: New York, NY, USA, 2020; Volume 102, pp. 367–370. [Google Scholar]
- Luo, X.l.; Xiao, H.; Lv, J.h. Continuation Newton methods with the residual trust-region time-stepping scheme for nonlinear equations. Numer. Algorithms 2022, 89, 223–247. [Google Scholar] [CrossRef]
- Waziri, M.Y.; Ahmed, K. Two descent Dai-Yuan conjugate gradient methods for systems of monotone nonlinear equations. J. Sci. Comput. 2022, 90, 1–53. [Google Scholar] [CrossRef]
- Pes, F.; Rodriguez, G. A doubly relaxed minimal-norm Gauss–Newton method for underdetermined nonlinear least-squares problems. Appl. Numer. Math. 2022, 171, 233–248. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 1999. [Google Scholar]
- Yamashita, N.; Fukushima, M. On the rate of convergence of the Levenberg-Marquardt method. In Topics in Numerical Analysis: With Special Emphasis on Nonlinear Problems; Springer: New York, NY, USA, 2001; pp. 239–249. [Google Scholar]
- Fan, J.Y.; Yuan, Y.X. On the quadratic convergence of the Levenberg-Marquardt method without nonsingularity assumption. Computing 2005, 74, 23–39. [Google Scholar] [CrossRef]
- Fischer, A. Local behavior of an iterative framework for generalized equations with nonisolated solutions. Math. Program. 2002, 94, 91–124. [Google Scholar] [CrossRef]
- Ma, C.; Jiang, L. Some research on Levenberg–Marquardt method for the nonlinear equations. Appl. Math. Comput. 2007, 184, 1032–1040. [Google Scholar] [CrossRef]
- Fan, J.Y. A modified Levenberg-Marquardt algorithm for singular system of nonlinear equations. J. Comput. Math. 2003, 625–636. [Google Scholar]
- Amini, K.; Rostami, F.; Caristi, G. An efficient Levenberg–Marquardt method with a new LM parameter for systems of nonlinear equations. Optimization 2018, 67, 637–650. [Google Scholar] [CrossRef]
- Rezaeiparsa, Z.; Ashrafi, A. A new adaptive Levenberg–Marquardt parameter with a nonmonotone and trust region strategies for the system of nonlinear equations. Math. Sci. 2023, 1–13. [Google Scholar] [CrossRef]
- Ahookhosh, M.; Aragón Artacho, F.J.; Fleming, R.M.; Vuong, P.T. Local convergence of the Levenberg–Marquardt method under Hölder metric subregularity. Adv. Comput. Math. 2019, 45, 2771–2806. [Google Scholar] [CrossRef]
- Wang, H.Y.; Fan, J.Y. Convergence rate of the Levenberg-Marquardt method under Hölderian local error bound. Optim. Methods Softw. 2020, 35, 767–786. [Google Scholar] [CrossRef]
- Zeng, M.; Zhou, G. Improved convergence results of an efficient Levenberg–Marquardt method for nonlinear equations. J. Appl. Math. Comput. 2022, 68, 3655–3671. [Google Scholar] [CrossRef]
- Chen, L.; Ma, Y. A modified Levenberg–Marquardt method for solving system of nonlinear equations. J. Appl. Math. Comput. 2023, 69, 2019–2040. [Google Scholar] [CrossRef]
- Li, R.; Cao, M.; Zhou, G. A New Adaptive Accelerated Levenberg–Marquardt Method for Solving Nonlinear Equations and Its Applications in Supply Chain Problems. Symmetry 2023, 15, 588. [Google Scholar] [CrossRef]
- Grippo, L.; Lampariello, F.; Lucidi, S. A nonmonotone line search technique for Newton’s method. SIAM J. Numer. Anal. 1986, 23, 707–716. [Google Scholar] [CrossRef]
- Ahookhosh, M.; Amini, K. A nonmonotone trust region method with adaptive radius for unconstrained optimization problems. Comput. Math. Appl. 2010, 60, 411–422. [Google Scholar] [CrossRef][Green Version]
- Ahookhosh, M.; Amini, K. An efficient nonmonotone trust-region method for unconstrained optimization. Numer. Algorithms 2012, 59, 523–540. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, D. A derivative-free affine scaling trust region methods based on probabilistic models with new nonmonotone line search technique for linear inequality constrained minimization without strict complementarity. Int. J. Comput. Math. 2019, 96, 663–691. [Google Scholar] [CrossRef]
- Powell, M.J.D. Convergence properties of a class of minimization algorithms. In Nonlinear Programming 2; Elsevier: Amsterdam, The Netherlands, 1975; pp. 1–27. [Google Scholar]
- Behling, R.; Iusem, A. The effect of calmness on the solution set of systems of nonlinear equations. Math. Program. 2013, 137, 155–165. [Google Scholar] [CrossRef]
- Stewart, G.; Sun, J. Matrix Perturbation Theory; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]
- Schnabel, R.B.; Frank, P.D. Tensor methods for nonlinear equations. SIAM J. Numer. Anal. 1984, 21, 815–843. [Google Scholar] [CrossRef]
- Moré, J.J.; Garbow, B.S.; Hillstrom, K.E. Testing unconstrained optimization software. ACM Trans. Math. Softw. (TOMS) 1981, 7, 17–41. [Google Scholar] [CrossRef]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Rui, S. A New Adaptive Levenberg–Marquardt Method for Nonlinear Equations and Its Convergence Rate under the Hölderian Local Error Bound Condition. Symmetry 2024, 16, 674. https://doi.org/10.3390/sym16060674
Han Y, Rui S. A New Adaptive Levenberg–Marquardt Method for Nonlinear Equations and Its Convergence Rate under the Hölderian Local Error Bound Condition. Symmetry. 2024; 16(6):674. https://doi.org/10.3390/sym16060674
Chicago/Turabian StyleHan, Yang, and Shaoping Rui. 2024. "A New Adaptive Levenberg–Marquardt Method for Nonlinear Equations and Its Convergence Rate under the Hölderian Local Error Bound Condition" Symmetry 16, no. 6: 674. https://doi.org/10.3390/sym16060674
APA StyleHan, Y., & Rui, S. (2024). A New Adaptive Levenberg–Marquardt Method for Nonlinear Equations and Its Convergence Rate under the Hölderian Local Error Bound Condition. Symmetry, 16(6), 674. https://doi.org/10.3390/sym16060674




