A Blockchain-Based Privacy Preserving Intellectual Property Authentication Method

Abstract

With the continuous advancement of information technology, a growing number of works, including articles, paintings, and music, are being digitized. Digital content can be swiftly shared and disseminated via the Internet. However, it is also vulnerable to malicious plagiarism, which can seriously infringe upon the rights of creators and dampen their enthusiasm. To protect creators’ rights and interests, a sophisticated method is necessary to authenticate digital intellectual property rights. Traditional authentication methods rely on centralized, trustworthy organizations that are susceptible to single points of failure. Additionally, these methods are prone to network attacks that can lead to data loss, tampering, or leakage. Moreover, the circulation of copyright information often lacks transparency and traceability in traditional systems, which leads to information asymmetry and prevents creators from controlling the use and protection of their personal information during the authentication process. Blockchain technology, with its decentralized, tamper-proof, and traceable attributes, addresses these issues perfectly. In blockchain technology, each node is a peer, ensuring the symmetry of information. However, the transparent feature of blockchains can lead to the leakage of user privacy data. Therefore, this study designs and implements an Ethereum blockchain-based intellectual property authentication scheme with privacy protection. Firstly, we propose a method that combines elliptic curve cryptography (ECC) encryption with digital signatures to achieve selective encryption of user personal information. Subsequently, an authentication algorithm based on Zero-Knowledge Succinct Non-Interactive Argument of Knowledge (zk-SNARK) is adopted to complete the authentication of intellectual property ownership while encrypting personal privacy data. Finally, we adopt the InterPlanetary File System (IPFS) to store large files, solving the problem of blockchain storage space limitations.

1. Introduction

The development of the Internet enables people to share their digital creations, such as music, video, pictures, etc., anytime and anywhere, which usually requires a lot of time and energy from creators. However, digital content distributed on the Internet is easy to capture, easy to copy, and fast to spread [1], which means digital content can easily be maliciously copied, posing a serious threat to the protection of intellectual property rights. In order to protect the rights and interests of creators, increase their enthusiasm, and, at the same time, protect the privacy and security of users, an advanced method must be adopted to ensure the reliability and traceability of data.

Copyright protection technology of digital content must also keep up with the rapid development of digitalization. The traditional method of copyright protection requires a centralized and trustworthy organization, which has many limitations, including reliance on centralized organizations and untraceable and easily tampered-with copyright records. Specifically, centralized institutions carry the risk of a single point of failure, and once a central server fails, it can lead to system paralysis, forced suspension of copyright protection services for creators, or even data loss, causing copyright disputes. Secondly, via traditional methods, the circulation of copyright information often lacks transparency and traceability, and creators are unable to control the use and protection of their personal information during the authentication process. This opacity can create information asymmetry between users and institutions, potentially leading to the misuse of information and thus increasing the risk of privacy leakage. Finally, traditional methods are susceptible to the risk of data tampering, as network attackers can modify or forge copyright information, thereby infringing on the rights of creators, leading to copyright disputes and piracy issues. Therefore, traditional intellectual property protection methods are obviously no longer able to meet the development needs of the digital copyright industry, and there is an urgent need for new technology to solve the above problems.

In 2008, Satoshi Nakamoto published a paper titled “Bitcoin: A peer-to-peer electronic cash system” [2], which proposed a decentralized trading system with blockchain technology as the core technology. In blockchain technology, each node is a peer, ensuring the symmetry of information. Blockchain technology is a decentralized distributed ledger technology in which all nodes participate in maintaining a public ledger through a consensus mechanism. Blockchain uses cryptographic hash functions to calculate a hash value of data in a block, and the latter block stores the hash value of the previous block, forming a chain structure. Due to the characteristics of hash functions, any modification to data will cause changes in the hash value, thereby disrupting the integrity of the blockchain. This method achieves the immutability of on-chain data [3]. Due to the openness and transparency of the ledger, as well as the chain structure of storage, it is easy to trace the entire transaction chain. The decentralized, tamper-proof, and traceable features of blockchain technology perfectly solve the three problems faced by traditional intellectual property protection technologies mentioned above.

However, blockchain technology also has some shortcomings when used for intellectual property authentication. Intellectual property requires the provision of creators’ personal information, work details, and other privacy information during the authentication process. The transparent nature of blockchain technology requires all information to be stored in public ledgers, and all nodes in the blockchain can view it, which leads to the leakage of creators’ privacy information. Moreover, blockchain technology uses pseudonyms rather than complete anonymity, but with the help of big data analysis and sociological mining methods, real identities in the real world can be mapped to public key addresses [4,5]. Users all hope that their privacy and security can be protected, especially in scenarios like intellectual property authentication where personal privacy data must be submitted. Therefore, there is an urgent need for a new technology that can achieve intellectual property authentication while protecting privacy data.

In this paper, we propose a method that combines ECC encryption and digital signatures to achieve selective encryption of user personal information after analyzing the issue of personal privacy information leakage in blockchain-based intellectual property authentication processes. An authentication algorithm based on zk-SNARK is adopted to achieve the authentication of intellectual property ownership in the case of encrypting personal privacy data. The main contributions of this paper are outlined as follows:

• We propose a scheme that combines ECC encryption and digital signature to achieve selective disclosure of personal information. Then, a digital signature algorithm is adopted for the intellectual property registration information to ensure the integrity and non-falsifiability of the registration information.
• We propose an intellectual property authentication algorithm based on zk-SNARK. The user first generates a digital digest of the plaintext intellectual property registration information through a hash algorithm and then encrypts the intellectual property registration information and uploads it to the blockchain. Finally, the zero-knowledge proof algorithm is used to verify the digital abstract without exposing plaintext information.
• We utilize the IPFS distributed storage system for storing large files, while only the IPFS address of the file is recorded on the blockchain. This approach effectively addresses the issue of limited storage capacity on the blockchain, enabling the accommodation of large files without the constraints of blockchain space.

2. Related Work

2.1. Intellectual Property Protection

Blockchain-based intellectual property protection systems are currently a popular research direction in blockchain applications. Many researchers have implemented and improved some blockchain-based intellectual property protection systems. There are also many related technological studies in the academic field.

The Digital Rights Management (DRM) platform is an important management platform for current digital copyright protection, developed to address the piracy of digital content. IBM, Intel, and other companies are all involved in launching corresponding products, systems, and specifications, but these products still cannot avoid the drawbacks of centralization. Therefore, Zhang et al. [6] integrated blockchain technology with DRM technology and developed a blockchain-based DRM system. This system can record copyright transactions and authorization information on the blockchain, solving the centralized drawbacks of traditional DRM technology. Garba et al. [7] developed a blockchain DRM system to ensure the security of digital content. The system enhances the scalability of the blockchain by using overlay networks and PBFT consensus algorithms and introduces lightweight encryption technology to encrypt images with watermarks to enhance the security of the system. Liang et al. [8] proposed a blockchain copyright protection system that combines homomorphic encryption technology and smart contracts specifically designed for circuit design copyright protection. This system is capable of real-time identity verification and has the ability to expand data storage, thereby enhancing the security and scalability of the entire system. Zhu et al. [9] designed and implemented a blockchain-based tracking service framework aimed at enhancing the protection of original works. By meticulously constructing the data layer, contract layer, logic layer, and application layer of the framework and introducing an automated reward and incentive mechanism, it promotes the generation and protection of original works while achieving the recording, protection, review, and tracking of original work registration and related transactions. Xiao et al. [10] implemented a blockchain-based image copyright protection system based on the fabric consortium chain and, for the first time, adopted the national standard recommended GM algorithm to protect the system’s data security, making the system more suitable for China’s business environment. Guo et al. [11] designed a blockchain-based multimedia content copyright management scheme for the education industry, which innovatively introduces three smart contract models: copyright registration of multimedia content, secure encrypted storage of content data, and a distributed copyright verification system. This solution opens up new ideas and possibilities for applying smart contract technology to the field of digital copyright protection. Tan et al. [12] integrated blockchain technology with digital rights management by recording copyright and transaction data of digital works on the blockchain, ensuring the security of data from illegal modifications and achieving instant traceability of information.

The above research work adopted blockchain technology and its related technologies to solve the problems existing in the current digital copyright protection system. However, as a cost-effective data storage medium [13], it is impractical to directly store raw files and other data information of digital works on blockchain, which can lead to the continuous expansion of blockchain’s data capacity. To solve the storage problem of large files on the blockchain, researchers have turned their attention to emerging InterPlanetary File System (IPFS) technology [14] to find solutions. Moreover, research [15] has also validated the effectiveness of IPFS in expanding blockchain storage capabilities, so most solutions have adopted IPFS to overcome the storage limitations of blockchain technology.

Xu et al. [16] developed a high-security digital copyright protection platform that integrates blockchain, IPFS technology, and smart contracts. In this system, blockchain takes on the task of recording copyright metadata to ensure the reliability of copyright verification while the original content is stored via IPFS. Ansori et al. [17] proposed an audio detection method based on perceptual hashing to address the issue of piracy in centralized music-sharing platforms. This method is used for copyright protection in decentralized music sharing, detecting infringement by comparing audio fingerprints, and using IPFS distributed storage to store music files. In addition, refs. [18,19,20,21] also successfully constructed a digital copyright protection platform by combining blockchain technology with IPFS. The application of this fusion technology not only ensures the security of copyright data and transparency of transactions but also efficiently manages a large amount of file data.

2.2. Privacy Preservation

Due to the characteristics of blockchain technology, transaction information is widely disseminated across all nodes, which may lead to the privacy of transaction information being compromised [22]. Therefore, various cryptocurrency solutions aimed at enhancing privacy protection have emerged, e.g., Zerocash [23]. Zerocash achieves the goal of hiding both parties and their transaction details using zero-knowledge proof technology. There are also many such cryptocurrencies, such as Litecoin, Monroe [24], Zerocoin [25], and so on. Privacy protection for user identity is not only about individual users caring about the security of their private information but also about companies unwilling to expose sensitive business information to competitors. For example, in Bitcoin transactions, although the transaction address is in the form of a pseudonym and does not disclose any personal information, the security of this privacy protection method still needs to be strengthened. By analyzing information on the blockchain, attackers may still be able to trace the connection between transactions and accounts through information such as ID and IP address and thus infer personal identity information. Therefore, relevant scholars have proposed some privacy protection schemes.

In terms of research on protecting user personal identity privacy, Li et al. [26] proposed a scheme that can protect transaction privacy in blockchain-based elliptic curve ring signature technology. This scheme constructs a privacy data storage protocol to achieve privacy protection of user identity. Qiao et al. [27] designed an innovative blockchain signature mechanism that utilizes aggregate signature technology, which can maintain privacy and security, reduce the computational burden of signature and verification processes, and reduce the demand for blockchain storage space, thereby enhancing the efficiency of data transmission. Heilman et al. [28] proposed a transactional anonymous payment protocol through blind signatures and smart contracts. Wang [29] developed a transaction privacy encryption scheme based on consortium chain technology to address the potential threat to user privacy caused by power information leakage and the potential disruption of fairness in microgrid markets. The ElGamal encryption algorithm was used to encrypt the identities of both parties involved in the transaction, and certificate-free encryption technology was optimized to achieve secure encryption and verification of electricity transactions. With the help of alliance blockchain and smart contract technology, this solution implements decentralized transaction processing, which not only ensures the security of transactions but also improves the efficiency of transaction processing. Lax Gianluca et al. [30] utilized blockchain smart contract technology to introduce a decentralized privacy setting management strategy, which avoids unauthorized modification of user personal information on social platforms through the automatic verification function of smart contracts.

In terms of user data privacy protection, Bonneau et al. [31] developed an anonymous cryptocurrency payment system called Mixcoin, which can conceal the association between transaction addresses, thereby enhancing the privacy of the transaction process. Kosba et al. [32] developed a distributed smart contract framework that incorporates zero-knowledge proof technology, avoiding direct disclosure of transaction information on the blockchain and effectively maintaining transaction privacy. Wang et al. [33] proposed a new algorithm to ensure the privacy of blockchain transactions based on Pedersen’s commitment and zero-knowledge proof. The algorithm uses Pedersen’s commitment to mask transaction amounts and ensures their correctness through zero-knowledge proof. Alsuqaih et al. [34] proposed an effective access control framework to address the issue of personal information data and medical privacy data leakage in the medical field caused by the use of blockchain technology. This framework enables patients to determine the access permissions to their data.

3. Proposed Method

3.1. Problem Analysis

Data stored on the blockchain can achieve data traceability and tamper resistance. Especially in the field of intellectual property certification, using blockchain technology to record the registration information of intellectual property can ensure the immutability and traceability of intellectual property information, greatly reducing the difficulty of evidence collection in the process of intellectual property traceability. The decentralized storage mode of blockchain also avoids the potential single point of failure problem that may occur in centralized storage. The openness of blockchain allows any node to freely join the network, and through consensus mechanisms, data in the network can obtain high reliability. Therefore, blockchain-based intellectual property authentication methods can overcome many of the problems associated with traditional centralized authentication schemes. However, although the open and transparent nature of blockchain technology enables the traceability of the authentication process, it also causes many problems in terms of privacy protection. Therefore, the following issues must be considered before model design can commence:

1.

How to store intellectual property registration information on a publicly transparent blockchain without disclosing the user’s personal privacy information.

Blockchain technology, with its open, transparent, and tamper-proof features, is commonly used in applications such as identity verification and intellectual property authentication. In our scheme, the registration details of intellectual property are recorded on the blockchain, making them accessible for public viewing. However, the natural openness of blockchain technology conflicts with the need for privacy protection in the process of intellectual property registration: on the one hand, it is necessary to store intellectual property-related information and personal identity information on the chain, retaining evidence of intellectual property ownership. On the other hand, data on the blockchain are visible to all participating nodes. How to effectively conceal sensitive information of users and intellectual property in such an open and transparent system while avoiding privacy leakage has become a problem that needs to be solved. Therefore, we use ECC encryption to encrypt user and intellectual property privacy information, store it on the chain, and ensure the integrity and authenticity of the data through digital signature algorithms.

2.

How to authenticate intellectual property ownership while encrypting personal information.

In order to protect user privacy on a transparent blockchain, it is necessary to encrypt user personal information before uploading it to the blockchain for storage. However, achieving intellectual property ownership authentication while encrypting personal information is a problem that needs to be solved. Therefore, we propose an intellectual property authentication method based on non-interactive zero-knowledge proof, which achieves the protection of the user’s personal privacy information while completing the authentication of intellectual property. The entire process is as follows: the creator first performs a hash operation on the registration information containing personal information and intellectual property information in the plaintext to obtain a hash value. Then, a non-interactive zero-knowledge proof algorithm is used to generate a zero-knowledge proof regarding the hash operation. Finally, personal information is encrypted, and the encrypted registration information and generated zero-knowledge proof are uploaded to the system. Other nodes in the blockchain can verify the authenticity of the hash operation through the uploaded zero-knowledge proofs.

3.

How to save large files in capacity-limited blocks.

Blockchain is a distributed ledger that contains various transaction records and is essentially a decentralized database. However, the storage capacity of each block in the blockchain is limited, usually limited to around 1 MB. In the process of intellectual property registration, creators need to upload intellectual property works, and the size of intellectual property works usually exceeds the capacity limit of the blockchain. In addition, the size of the zero-knowledge proof file generated in question 2 also exceeds the capacity limit of the block, so it cannot be directly stored on the blockchain. To address this issue, we adopt IPFS to store all intellectual property works and zero-knowledge proofs. After storing the content in IPFS, IPFS will return a hash address for the content. In the blockchain, only the hash address needs to be stored to determine the corresponding original file in IPFS. In this way, large files are stored offline, successfully overcoming blockchain storage limitations without affecting blockchain performance.

3.2. Blockchain Platform Selection

As blockchain technology becomes more widely adopted, numerous blockchain development environments tailored to specific scenarios have emerged. Among these many options, the Ethereum and Bitcoin blockchains are the two most frequently used platforms. In addition, there are other significant platforms, including Hyperledger Fabric. A comparison of several blockchain platforms is presented in Table 1.

Table 1. Comparison of blockchain platforms.

Blockchain Platforms	Programmable Support	Supported Chain Types	Community Ecosystem
Bitcoin	No	Public chain	Resourceful
Ethereum	Yes	Public and Private chain	Resourceful
Fabric	Yes	Private and Consortium chain	Growing

Our intellectual property authentication scheme is based on smart contract technology. As a platform that supports smart contract development, the Ethereum blockchain provides the ability to implement the functions required for the scheme. In addition, Ethereum can support a wide variety of chains that can meet the needs of different application scenarios. Ethereum also has a large and vibrant community consisting of developers, researchers, and various businesses who work together to promote the growth of the Ethereum ecosystem, providing technical assistance, development tools, and educational resources, bringing abundant resources and strong support to developers. Therefore, after careful consideration, our scheme chooses Ethereum as the blockchain platform.

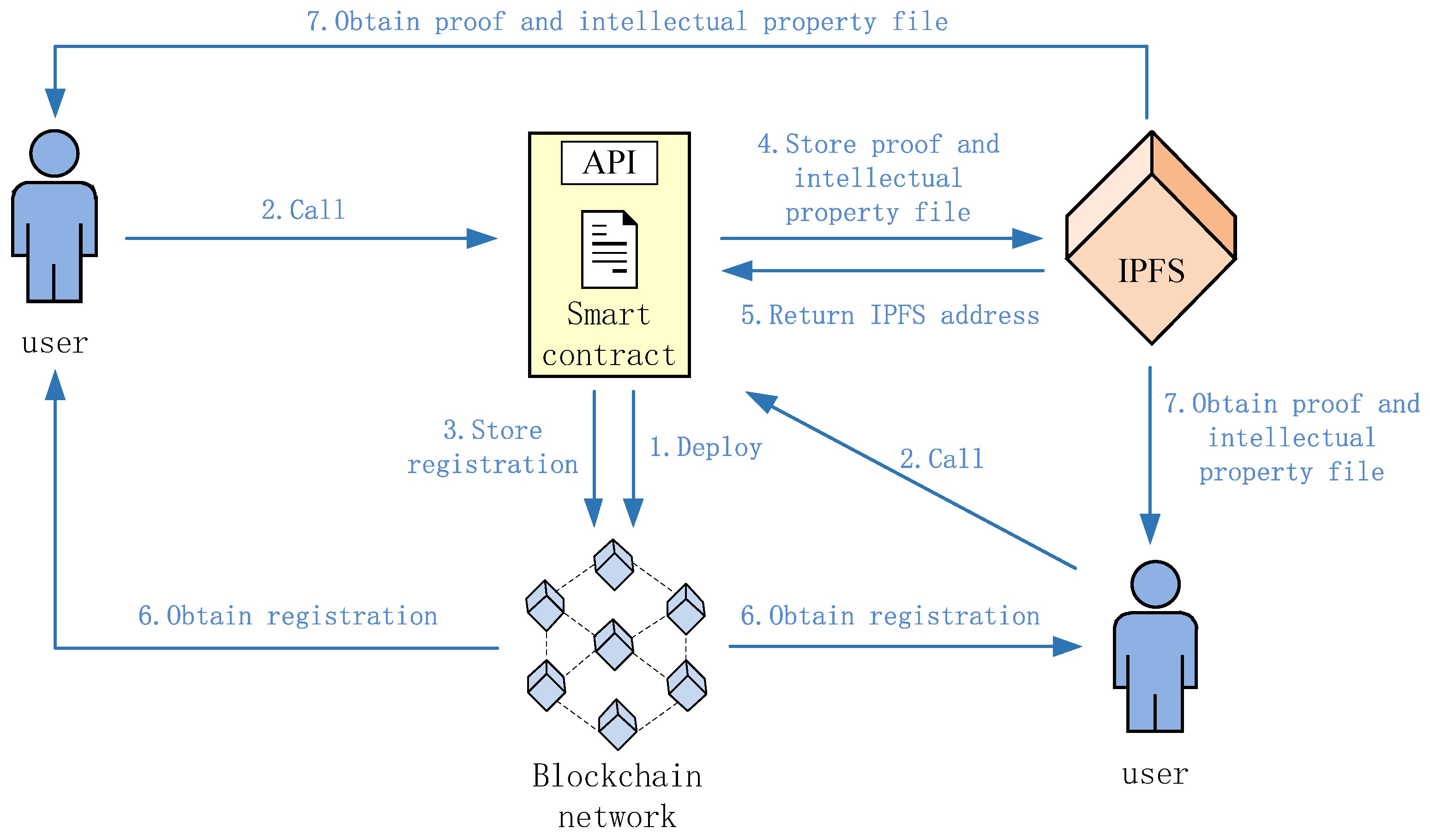
3.3. Architecture Design

The traditional authentication method requires users to provide personal information and compare it with the information stored in the database to complete authentication. However, personal information sent during the authentication process is easily intercepted, leading to privacy leakage. Despite years of effort by researchers to develop many authentication methods that do not require users’ personal information, users still need to provide at least some personal information, and they cannot independently choose which information to hide and which information to disclose. In order to solve the problems of traditional authentication methods mentioned above, we propose an intellectual property authentication scheme based on zero-knowledge proof that can selectively expose personal information or completely not expose any personal information. The architecture diagram of this scheme is shown in Figure 1.

Figure 1. The architecture diagram.

From Figure 1, it can be seen that the scheme is divided into four entities: user, blockchain, IPFS, and smart contract. Initially, the system manager deploys the smart contract to the blockchain network. Then, the user fills in the intellectual property registration information according to the parameters specified in the smart contract, generates a hash digest of the registration information through a hash function, and calls the function in the smart contract to upload the intellectual property registration information to the blockchain network. Subsequently, the user generates a zero-knowledge proof related to the hash function and calls the function in the smart contract to upload both the intellectual property file and the zero-knowledge proof file to IPFS for distributed storage. If successfully uploaded, IPFS will return a storage address. Other users can obtain the registration information from the blockchain records. Finally, they can access the zero-knowledge proof file using the storage address recorded on the registration information to authenticate the intellectual property.

The entire plan is divided into seven steps, as shown in Figure 2.

Figure 2. Overall scheme flowchart.

Step 1: Filling in information phase.

Intellectual property creators shall fill in the relevant fields according to the requirements of Table 2 for intellectual property registration in plaintext form.

Table 2. Registration information structure.

Field Name	Description	Disclosure Rules
name	Author name	optional
id	Author’s ID number	optional
institution	The author’s affiliated institution(school or workplace)	optional
file_name	Intellectual property name	optional
file_type	The type of intellectual property	optional
file_addr	The storage location of intellectual property on IPFS	optional
proof_addr	The storage location of zero-knowledge proofs on IPFS	public
eth_addr	The author’s Ethereum address	public
encrypt_pk	The public key used for encrypting information	public
hash	The hash value of the registration information	public
signature	The digital signature of the registration information	public

Step 2: Hash digest generation phase.

A hash digest of plaintext registration information is generated using the $SHA256$ hash function.

Step 3: Digital signature generation phase.

The creator uses their private key to generate a digital signature of the hash digest generated in the previous step.

Step 4: Zero-knowledge proof generation phase.

The creator generates a zero-knowledge proof concerning the hash operation in step 2 and uploads it along with the verification key to IPFS. Then, IPFS will return a storage address.

Step 5: Encryption phase.

The creator creates a selective disclosure rule for the intellectual property registration information and selects personal privacy information, such as ID number, that they do not want to be exposed. The smart contract will automatically encrypt plaintext intellectual property registration information through the creator’s public key based on the rule.

Step 6: Uploading phase.

The encrypted intellectual property registration information is uploaded to the Ethereum blockchain network. Although all nodes in the blockchain can view the registration information, since the privacy information was encrypted in step 5, personal privacy information will not be disclosed.

Step 7: Zero-knowledge proof verification phase.

All other users in the blockchain can obtain zero-knowledge proof files through the storage address in step 4 to authenticate the registered information.

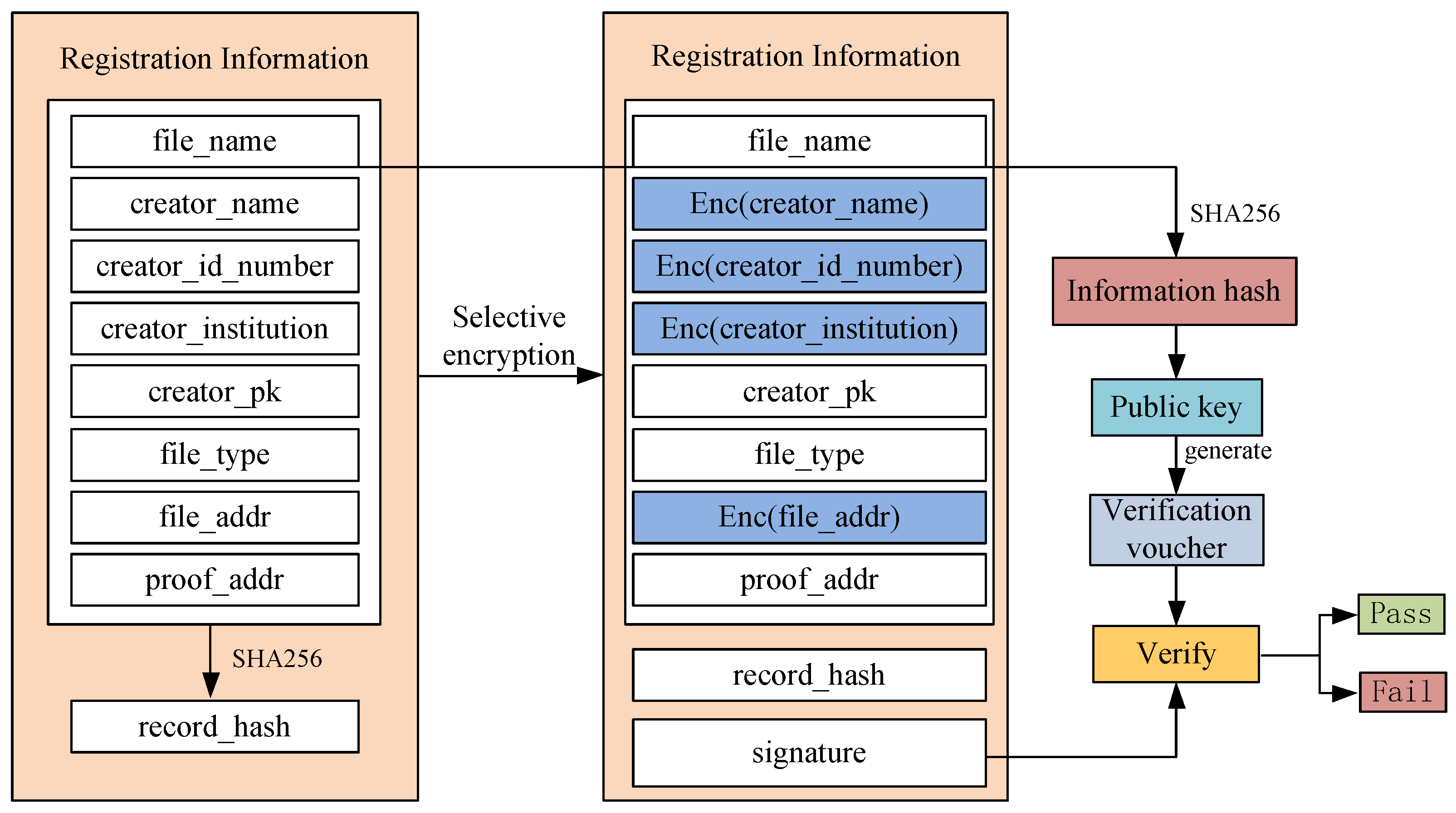
3.4. Selective Information Disclosure Scheme

When registering intellectual property rights, it is easy to disclose the user’s personal identity and confidential intellectual property information. In our proposed scheme, users can selectively disclose their identity information or encrypt the information they do not want to disclose. Creators need to upload intellectual property and author-related information as proof of intellectual property registration. The content of the intellectual property registration information structure is shown in Table 2.

Intellectual property registration information includes the intellectual property name, author’s name, author’s ID number, author’s institution, intellectual property type, intellectual property storage location on IPFS, zero-knowledge proof storage location on IPFS, author’s Ethernet address, encryption public key, registration information hash value, and a digital signature generated by the hash value. Among them, the storage location of zero-knowledge proof on IPFS must be publicly available as it is used by other nodes to obtain zero-knowledge proof files for intellectual property authentication. The public encryption key is used to encrypt personal information that needs to be hidden. Only the creator can use the corresponding private key for decryption, and this field must be public. The hash value of registration information is calculated from the plaintext of all the fields mentioned above using the $SHA256$ hash function, which serves as the digest of the entire intellectual property registration information. This field is one of the important parameters for zero-knowledge proof verification and must also be made public.

3.4.1. Digital Signature Generation

Firstly, users need to accurately fill out the required fields in the intellectual property registration information in clear text. Next, users must concatenate the contents of each field in the intellectual property registration information to obtain a string composed of concatenated field contents, which is voucher data to be signed. Then, a hash operation is performed on the concatenated string to obtain a hash value, which is also known as the digest of intellectual property registration information. Finally, the intellectual property creator uses their private key to sign the hash digest of the registration information, thereby generating a digital signature of the registration information, which is attached to the intellectual property registration information. This digital signature is mainly used to verify the authenticity and integrity of all field contents in the registration information to ensure that the certificate has not been tampered with or forged. The process of generating signatures is shown in Figure 3, and the main pseudocodes of the signature generation algorithm logic are shown in Algorithm 1.

Algorithm 1 Digital Signature Generation

1: Input:  $recordInfo,sk$ 2: Output:  $Signature$ 3: function  $signatureGenerate(recordInfo,sk)$ 4:    $h=SHA256\left(recordInfo\right)$ 5:    $P=CalcEccPoint(k,G)$           ▹P is a point on an elliptic curve 6:    $Signature=CalcSignature(h,k,P,sk)$ 7:    return $Signature$ 8: end function

Figure 3. Digital signature generation.

The specific process of the signature generation algorithm is as follows:

• The private key $sk$ is a random integer within [1, $n-1$], where n is the multipliable order of the elliptic curve parameters.

  $$sk=Rand(1,n-1).$$

  (1)
• Calculate the public key $pk$ using the $sk$ and elliptic curve base point G, as shown in Equation (2).

  $$pk=sk·G.$$

  (2)
• Calculate the hash digest h of intellectual property registration information m using the $SHA256$ hash function. The relationship between m and h is shown in Equation (3).

  $$h=SHA256\left(m\right).$$

  (3)
• Choose a random number $k\in [1,2,\dots ,n-1]$ and multiply it by the base point G of the elliptic curve to obtain a point $P=(x_1,y_1)$ on the elliptic curve. The specific calculation method of function $calcEccPoint$() in Algorithm 1 is shown in Equation (4).

  $$(x_1,y_1)=k·G.$$

  (4)
• Calculate the signature using Equations (5) and (6), where $r,s\in Z_p^{★}$.

  $$r=x_{1}modn,$$

  (5)

  $$s=[k^{-1}·(h+r·sk)]modn.$$

  (6)

3.4.2. Digital Signature Verification

Firstly, we use the digest (the hash field) of the intellectual property registration information generated in Section 3.4.1 to calculate the publicly available encryption public key (the encrypt_pk field) in the intellectual property registration information to generate a voucher for verifying the digital signature. The verification voucher is compared with the digital signature information. If the comparison results are consistent, it indicates that the intellectual property registration information is signed by the intellectual property creator himself and has not been tampered with. If the comparison results are inconsistent, it indicates that the intellectual property registration information may have been tampered with or forged. The signature verification process is shown in Figure 4, and the signature verification algorithm is shown in Algorithm 2.

Figure 4. Digital signature verification.

The specific process of the signature verification algorithm is as follows:

• Verify that both r and s in $signature=(r,s)$ are integers within the range of [1, $n-1$], otherwise verification will fail.
• Calculate the parameter w according to Equations (7), $w\in Z_p^{★}$.

  $$w=s^{-1}modn.$$

  (7)
• Calculate parameters u and v according to Equations (8) and (9), $u,v\in Z_p^{★}$.

  $$u=\left(\begin{array}{c}h·w\end{array}\right)modn,$$

  (8)

  $$v=\left(\begin{array}{c}r·w\end{array}\right)modn.$$

  (9)
• Calculate another point $Q=(x_2,y_2)$ on the elliptic curve based on parameters u and v. The specific calculation method of function $calcEccPoint$() in Algorithm 2 is shown in Equation (10).

  $$\left(\begin{array}{c}{x}_2,y_2\end{array}\right)=u·G+v·pk.$$

  (10)
• Verify the $signature=(r,s)$. If Equation (11) holds, verification is successful; otherwise, verification fails.

  $$r=x_{2}modn.$$

  (11)

Algorithm 2 Digital Signature Verification

1: Input:  $recordInfo,signature,pk,n$   2: Output: $True$ or $False$   3: function  $signatureVerify(recordInfo,signature,pk,n)$   4:    $require(1\le signature.r\le n-1)$   5:    $require(1\le signature.s\le n-1)$   6:    $(w,u,v)=calcParam(recordInfo,signature)$               ▹$u,v\in Z_p^{★}$   7:    $Q=calcEccPoint(u,v,pk)$             ▹Q is a point on an elliptic curve   8:    $if(signature.r==Q.x)$   9:       return $True$ 10:    $else$ 11:       return $False$ 12: end function

3.5. Authentication Scheme Design

Our scheme employs a special type of succinct, non-interactive zero-knowledge proof. The key features of zk-SNARK include allowing the verifier to confirm the correctness of statements without revealing any vital information, thereby protecting user privacy, a concept referred to as zero-knowledge. Additionally, the proofs are consistently small in size, meeting the succinct criterion. The verification process is non-interactive, meaning the verifier does not need to make any further inquiries to validate the proof. zk-SNARKs can prove any computational relationship, encompassing both P and NP problems, where $\omega$ represents a confidential value that must remain undisclosed. The fundamental transformation relationship of the zk-SNARK protocol is illustrated in Figure 5.

Figure 5. The core equivalent transformation relationship of zk-SNARK.

To avoid revealing secret $\omega$, it is necessary to use the R1CS constraint to describe the operational rules of algorithm $F\left(\omega \right)$ equivalently. It is important to publicly disclose the R1CS constraint, then convert $F\left(\omega \right)$ to satisfy any computational relationship $F\left(\omega \right)$ equivalently, then equivalently transform $F\left(\omega \right)$ into the polynomial coefficient vector $\overrightarrow{s}$ of the objective polynomial $z\left(x\right)$ divided by the QAP polynomial, and finally, equivalently transform it into calculating the discrete logarithm point (polynomial commitment) of the elliptic curve based on the polynomial coefficient vector $\overrightarrow{s}$, forming the discrete logarithm difficulty problem. The verifier reconstructed the integer division relationship based on elliptic curve discrete logarithmic points (polynomial commitment) and verified the correctness of the vector $\overrightarrow{s}$, but the prover did not leak the vector $\overrightarrow{s}$. The following sections provide a detailed introduction to NP problems, R1CS constraints, and QAP.

3.5.1. NP Problem and Reduction

When the solution time of a problem is polynomial proportional to its scale, we say that the problem has polynomial time complexity. Usually, such problems are divided into two categories: P problems and NP problems. P problems refer to problems that can be solved by deterministic Turing machines in polynomial time. For such problems, an algorithm exists that can quickly find the solution to the problem under the constraint of polynomial functions of input size. On the other hand, NP problems are problems where candidate solutions can be verified by deterministic Turing machines in polynomial time. Intuitively speaking, NP problems refer to problems that easily verify the correctness of a solution, but the process of finding a solution may be difficult and usually cannot be solved in polynomial time. For example, given the function value y and the hash function $SHA256$, the hash preimage x is found. The hash preimage x and function value y are required to satisfy $y=SHA256\left(x\right)$. This problem cannot be solved in polynomial time for the preimage x and requires exponential time. However, once the preimage x is given, it can be verified in polynomial time whether the preimage x and the function value y satisfy the $SHA256$ calculation relationship.

The polynomial division problem is another NP problem. Given a polynomial $z\left(x\right)$ of order n and three sets of polynomials $u_0\left(x\right),u_1\left(x\right),\dots ,u_m\left(x\right)$, $v_0\left(x\right),v_1\left(x\right),\dots ,v_m\left(x\right)$, $w_0\left(x\right),w_1\left(x\right),\dots ,w_m\left(x\right)$ of order $n-1$, find vector $\overrightarrow{s}$ and satisfy the integer division relationship of Equation (12).

$$z\left(x\right)|\left(\sum _{i=0}^m{s}_i·u_i\left(x\right)·\sum _{i=0}^m{s}_i·{\nu }_i\left(x\right)-\sum _{i=0}^m{s}_i·w_i\left(x\right)\right),$$

(12)

where vector $\overrightarrow{s}$ is the coefficient of each set of polynomials. If vector $\overrightarrow{s}$ is not known, you can only randomly select a vector $\overrightarrow{s}$ to verify whether the division relationship of Equation (12) holds. Therefore, exponential time is required to violently search for vector $\overrightarrow{s}$. However, once the vector $\overrightarrow{s}$ is given, it can be quickly verified whether the polynomial satisfies the integer division relationship.

Reduction is a proof strategy that transforms the solution of one problem into the solution of another, which is both efficient and reliable. If problem A can be reduced to problem B, it means that once the solution to problem B is found, this solution can be used to deal with problem A. Our scheme takes the user’s intellectual property registration information as the hash preimage x, calculates the hash function value y through the $SHA256$ function, and then reduces the problem of finding the hash preimage x to the polynomial division problem. This is because the polynomial division problem is more suitable as an input for zero-knowledge proof algorithm circuits.

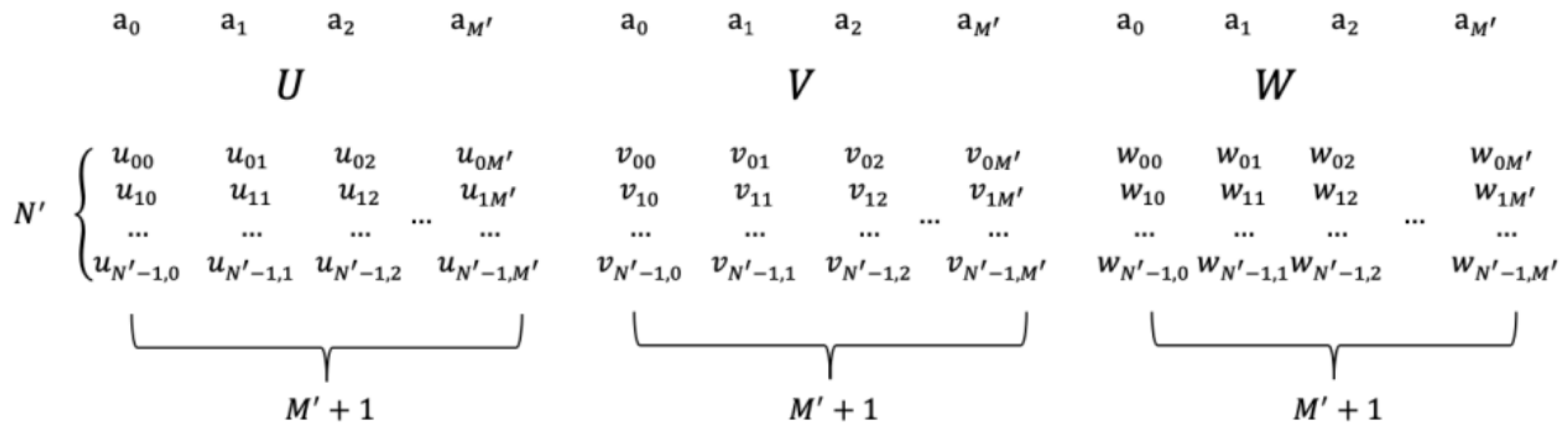
3.5.2. R1CS

A Rand-1 Constraint System (R1CS) is a sequence of three vectors $a,b,c$ whose solution is a vector $\overrightarrow{s}$ that satisfies Equation (13).

$$s·a+s·b-s·c=0.$$

(13)

Given $M^{\prime }$ variables (the first variable is always set to 1) and constraints, all R1CS descriptions can be seen in Figure 6 as follows:

$$U★V=W.$$

(14)

Figure 6. R1CS structure.

Each row is a constraint, and the constraint in the first row can be represented as follows:

$$\left(\sum _{i=0}^{M^{\prime }}{a}_i{u}_{0i}\right)★\left(\sum _{i=0}^{M^{\prime }}{a}_i{v}_{0i}\right)=\left(\sum _{i=0}^{M^{\prime }}{a}_i{w}_{0i}\right).$$

(15)

3.5.3. QAP and Arithmetic Circuits

Quadratic arithmetic programs (QAPs) can be seen as an abstract representation of a specific set of computations, expressing computational tasks in the form of polynomials and quadratic equations. Through this approach, QAP can transform complex computational tasks into problems that validate polynomials with specific relationships. This transformation enables verification of the correctness of calculations without revealing specific computational details, which is precisely the characteristic required for zero-knowledge proof. The polynomial division problem mentioned in Section 3.5.1 is an m-bit QAP.

In mathematics, when a series of correspondences between x and y are given, a polynomial can be determined through Lagrangian interpolation:

$$p\left(x\right)=y_0{l}_0\left(x\right)+y_0{l}_0\left(x\right)+\cdots +y_n{l}_n\left(x\right).$$

(16)

Among them, $l_0\left(x\right),l_1\left(x\right),\dots ,l_n\left(x\right)$ refer to the Lagrangian basis, and the calculation formula is as follows:

$$\begin{array}{cc}\hfill l_j\left(x\right)& =\prod _{i=0,i\ne j}^n\frac{x-x_i}{x_j-x_i}\hfill \\ \hfill & \hfill =\left(\frac{x-x_0}{x_j-x_0}\right)\left(\frac{x-x_0}{x_j-x_0}\right)...\left(\frac{x-x_{j-1}}{x_j-x_{j-1}}\right)\left(\frac{x-x_{j+1}}{x_j-x_{j+1}}\right)...\left(\frac{x-x_{n-1}}{x_j-x_{n-1}}\right)\left(\frac{x-x_{n+1}}{x_j-x_{n+1}}\right).\hfill \end{array}$$

(17)

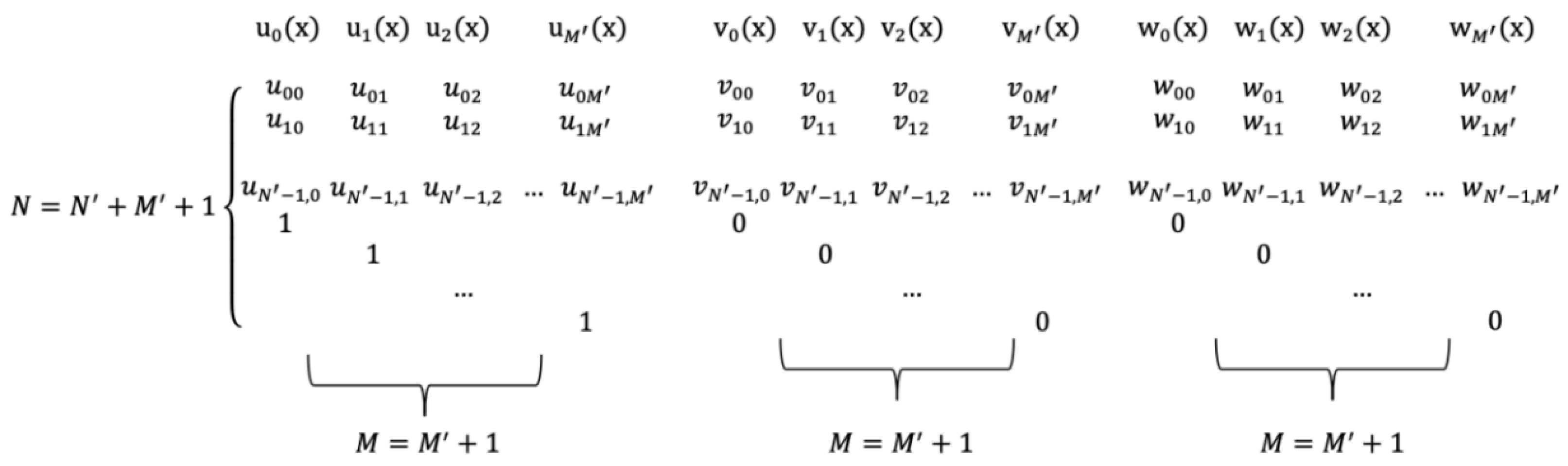
In the framework of R1CS, U, V, and W in Figure 6 represent vectors based on the Lagrangian basis rather than traditional polynomial coefficient forms. Before mapping R1CS to the QAP, in order to ensure that the polynomials obtained after mapping to QAP maintain nonlinear independence, it is necessary to first extend the existing constraint system to introduce new constraints. Mapping R1CS to the QAP is shown in Figure 7.

Figure 7. R1CS mapping to QAP.

3.5.4. Zero-Knowledge Proof Generation

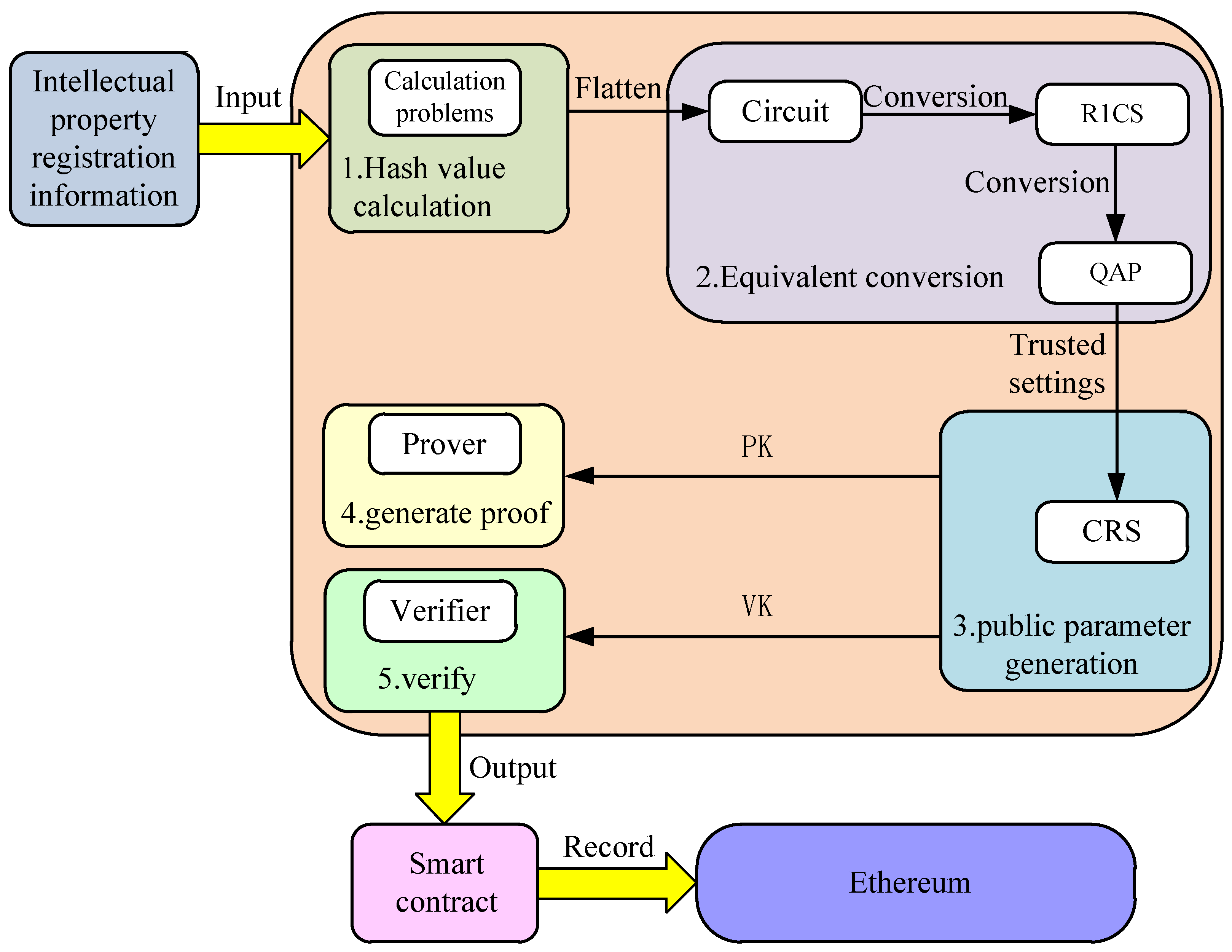
The algorithmic flow of our scheme, depicted in Figure 8, starts by flattening the hash operation on the user’s intellectual property registration information into a low-order circuit, then converting it into an R1CS structure as described in Section 3.5.2. Next, it is converted into a QAP to make it easier to use the zero-knowledge proof algorithm. To ensure the security of zero-knowledge proof, a trusted setup is required to generate a common reference string (CRS) from which the proving key (PK) and verifying key (VK) are derived. Although the proving key and the verifying key are functionally independent, they are interdependent when used. The proof generated by the proving key can only be correctly verified through the corresponding verifying key. The generation and verification process of zero-knowledge proof in our scheme has been optimized. Our scheme adopts off-chain generation proof and on-chain verification to alleviate the computational pressure on the Ethereum blockchain network and improve its efficiency. After users generate proof off-chain, they upload it to the chain and verify it through the deployed smart contract.

Figure 8. The algorithmic flow.

The verification scheme in Figure 8 refers to verifying the hash operation $y=SHA256\left(x\right)$, where x represents the intellectual property registration information and y represents the digest of the registration information. The process of flattening in the figure is to encode the hash operation into a low-order circuit, convert the low-order circuit into an R1CS structure, and then convert it to a QAP. This article uses the zorates tool to convert hash operations to QAPs. The zorates code is shown in Algorithm 3. To ensure the security of the non interactive zero-knowledge proof interaction process, it is necessary to set its trustworthiness and generate a public string for generating and verifying proofs. In order to alleviate the computational pressure on Ethereum and improve its efficiency, this article adopts a combination of on-chain and off-chain methods to optimize this method. In other words, the proof generation part that requires a large amount of computation is placed offline, and only identity verification operations are performed on the chain.

Algorithm 3 Conversion from Hash to R1CS

1: import “hashes/sha256/256bitPadded” as sha256   2: import “utils/pack/u32/unpack128” as unpack128   3: import “utils/pack/u32/pack128” as pack128   4: def main(private field[2] preimage, field h0, field h1):   5:    u32[4] a_bits = unpack128(preimage[0])   6:    u32[4] b_bits = unpack128(preimage[1])   7:    u32[8] privkey = […a_bits, …b_bits]   8:    u32[8] res = sha256(privkey)   9:    assert(h0 == pack128(res[0..4])) 10:    assert(h1 == pack128(res[4..8]))

The specific process of generating zero-knowledge proof is as follows:

Step 1: Define a relationship generator.

$$\begin{array}{c}\hfill R=(p,G_1,G_2,G_T,e,g,h,l,{\{u_i\left(X\right),v_i\left(X\right),w_i\left(X\right)\}}_{i=0}^m,t\left(X\right))\wedge \left|p\right|=\lambda .\end{array}$$

(18)

Step 2: Convert hash into an arithmetic circuit.

Convert the $SHA256$ operation for calculating personal information hash values into an arithmetic circuit. Then, convert it into R1CS constraints and QAP polynomials using the methods introduced in Section 3.5.2 and Section 3.5.3. Next, define $statement$ as $(a_1,\dots a_l)\in {\mathbb{Z}}_p^l$ and $witness$ as $(a_{1+1},\dots a_m)\in {\mathbb{Z}}_p^{m-1}$. Satisfy the following Equation (19) when $a_0=1$:

$$\begin{array}{c}\hfill \sum _{i=0}^m{a}_i{u}_i\left(X\right)·\sum _{i=0}^m{a}_i{v}_i\left(X\right)=\sum _{i=0}^m{a}_i{w}_i\left(X\right)+h\left(X\right)t\left(X\right).\end{array}$$

(19)

Step 3: Generate CRS.

Randomly select parameter $\alpha ,\beta ,\gamma ,\delta ,x\in Z_p^{★}$, let $\tau =(\alpha ,\beta ,\gamma ,\delta ,x)$, $\sigma =({\left[{\sigma }_1\right]}_1,{\left[{\sigma }_2\right]}_2)$, and calculate ${\sigma }_1$, ${\sigma }_2$ through $Setup\left(R\right)$:

$$\begin{array}{c}\hfill \left.{\sigma }_1=\left(\begin{array}{c}\alpha ,\beta ,\delta ,{\left\{x^i\right\}}_{i=0}^{n-1},{\left\{\frac{\beta u_i\left(x\right)+\alpha v_i\left(x\right)+w_i\left(x\right)}{\gamma }\right\}}_{i=0}^i\\ \\ {\left\{\frac{\beta u_i\left(x\right)+\alpha v_i\left(x\right)+w_i\left(x\right)}{\delta }\right\}}_{i=i+1}^m,{\left\{\frac{x^{i}t\left(x\right)}{\delta }\right\}}_{i=0}^{n-2}\end{array}\right.\right),\end{array}$$

(20)

$$\begin{array}{c}\hfill {\sigma }_2=\left(\beta ,\gamma ,\delta ,{\left\{x^i\right\}}_{i=0}^{n-1}\right),\end{array}$$

(21)

where ${\sigma }_1$ is a point on elliptic curve $G_1$, and ${\sigma }_2$ is a point on elliptic curve $G_2$.

Step 4: Generate the proving key and verifying key.

The proving key $Pk$ and verifying key $Vk$ can be calculated using Equations (22) and (23).

$$\begin{array}{c}\hfill Pk=\left(\begin{array}{c}{\left(\delta ,{\left\{x^i\right\}}_{i=0}^{n-1}\right)}_1,{\left({\left\{x^i\right\}}_{i=0}^{n-1}\right)}_2\\ {\left({\left\{\frac{\beta u_i\left(x\right)+\alpha {\nu }_i\left(x\right)+w_i\left(x\right)}{\delta }\right\}}_{i=i+1}^m,{\left\{\frac{x^{i}t\left(x\right)}{\delta }\right\}}_{i=0}^{n-2}\right)}_1\end{array}\right),\end{array}$$

(22)

$$\begin{array}{c}\hfill Vk=\left(\begin{array}{c}{\left(\alpha ,{\left\{\frac{\beta u_i\left(x\right)+\alpha v_i\left(x\right)+w_i\left(x\right)}{\gamma }\right\}}_{i=0}^i\right)}_1\\ {(\beta ,\gamma ,\delta )}_2\end{array}\right).\end{array}$$

(23)

It can be seen that the size of $Vk$ depends on the number of common input variables, and the size of $Pk$ is related to the overall number of variables.

Step 5: Generate the zero-knowledge proof $\pi$.

$$\begin{array}{c}\hfill \pi \leftarrow Prove(R,\sigma ,a_1,\dots ,a_m).\end{array}$$

(24)

Choose $r,s\in Z_p^{★}$ and calculate the zero-knowledge proof $\pi =({\left[A\right]}_1,{\left[C\right]}_1,{\left[B\right]}_2)$ when $u_i\left(x\right),v_i\left(x\right),w_i\left(x\right),h\left(x\right)$ are known, where

$$\begin{array}{c}\hfill A=\alpha +\sum _{i=0}^m{a}_i{u}_i\left(x\right)+r\delta ,\end{array}$$

(25)

$$\begin{array}{c}\hfill B=\beta +\sum _{i=0}^m{a}_i{\nu }_i\left(x\right)+s\delta ,\end{array}$$

(26)

$$\begin{array}{c}\hfill C=\frac{{\sum }_{i=i+1}^m{a}_i(\beta u_i\left(x\right)+\alpha v_i\left(x\right)+w_i\left(x\right))+h\left(x\right)t\left(x\right))}{\delta }+As+Br-rs\delta ,\end{array}$$

(27)

where A is a point on $G_1$, B is a point on $G_1/G_2$, and C is a point on $G_1$. The calculation formula for $h\left(x\right)t\left(x\right)/\delta$ in Equation (27) is as follows:

$$\begin{array}{c}\hfill \frac{h\left(x\right)t\left(x\right)}{\delta }=\sum _{i=0}^{N-2}\frac{h_i{x}^{i}t\left(x\right)}{\delta }.\end{array}$$

(28)

The verifier verifies whether Equation (29) holds and outputs true or false.

$$\begin{array}{c}\hfill {\left[A\right]}_1·{\left[B\right]}_2={\left[\alpha \right]}_1·{\left[\beta \right]}_2+\sum _{i=0}^l{a}_i{\left[\frac{\beta u_i\left(x\right)+\alpha v_i\left(x\right)+w_i\left(x\right)}{\gamma }\right]}_1·{\left[\gamma \right]}_2+{\left[C\right]}_1·{\left[\delta \right]}_2.\end{array}$$

(29)

3.5.5. Authentication

After the user successfully uploads and records their intellectual property registration information on the blockchain, the hash value of the certificate will be recorded on the blockchain. At the same time, the blockchain will also record the user’s blockchain address eth_addr, the user’s digital signature, the hash value of intellectual property information hash, and the zero-knowledge proof address proof_addr of the hash digest of intellectual property information stored on IPFS. Using this zero-knowledge proof document, other users can verify the registration information of intellectual property. The specific authentication process mainly includes the following steps:

Step 1: getMessage→(eth_addr, hash, proof_addr, signature).

When users apply for intellectual property verification, they need to submit the application using their own blockchain address eth_addr for the verification node to verify. The verification node will use this address to call the smart contract and retrieve user information stored on the blockchain, including eth_addr, hash, proof_addr, and signature.

Step 2: getZeroProof(proof_addr)→$\pi$.

The verification node then utilizes the proof_addr to obtain the zero-knowledge proof $\pi$ stored in IPFS.

Step 3: verifyZeroProof($\pi$,pp,vk) → accept or reject.

The verification node uses the verification key $Vk$ and the system provided public parameter $pp$ to verify the zero-knowledge proof $\pi$. If verification is successful, the result is $accept$, otherwise $reject$.

The main pseudocode algorithms for the above authentication process are presented in Algorithm 4.

Algorithm 4 Intellectual Property Authentication

1: Input:  $recordInfo,signature,pp$   2: Output: $accept$ or $reject$   3: function  $signatureVerify(recordInfo,signature,pp)$   4:    $(eth\_addr,hash,proof\_addr,signature)=getMessage\left(\right)$   5:    ($\pi ,Vk)=getZeroProof(proof\_addr)$   6:    $if\left(verifySig\right(signature)==false)$   7:       return $reject$   8:    $if\left(verifyZeroProof\right(\pi ,pp,Vk)==false)$   9:       return $reject$ 10:    return $accept$ 11: end function

4. Security Analysis

Our scheme encrypts user identity information using ECC encryption technology and verifies intellectual property using zero-knowledge proof technology. The combination of ECC and zero-knowledge proof technology provides a solid security foundation for this scheme.

(1)

Data immutability feature

This solution runs on a blockchain network, benefiting from the decentralized nature of the blockchain. The transaction data in the network are public and immutable, ensuring that user identity information and transaction data are not maliciously modified and maintaining data integrity.

(2)

Resist the risk of a single point of failure

Due to the use of distributed ledger technology, each node in the blockchain network stores all data information, effectively avoiding the possibility of a single point of failure in centralized systems. Even if some nodes fail, it will not affect the stable operation of the entire network.

(3)

Integrity assurance

The true identity information submitted by the user, which is generated through zero-knowledge proof, must pass the verification of the verification node, ensuring that the verifier can believe that they have knowledge while providing necessary knowledge.

(4)

Verification accuracy

In cases where accurate knowledge cannot be provided, the user’s information verification request will not be passed, ensuring that the verifier cannot be deceived and ruling out the possibility of identity information forgery or submission of empty information.

(5)

Protecting privacy and security

The user initially uses the $SHA256$ algorithm for hash calculation, and based on the unidirectionality of the hash function, it is impossible to deduce the user’s personal information in reverse. When using zero-knowledge proof for identity verification, it ensures that there will be no leakage of personal information during the verification process.

5. Performance Analysis

5.1. Encryption Algorithm

Our scheme uses ECC to protect the user’s personal data. In the experiment, the key length is set to the commonly used 1024 bits, 2048 bits, and 3072 bits to evaluate the performance differences of encryption algorithms under various key length conditions. Testing includes the key generation time, encryption time, and decryption time. The test results are shown in Table 3.

Table 3. ECC algorithm test result.

Key Length (bit)	1024	2048	3072
Generation time (ms)	3.2	21.5	74.6
Encryption time (ms)	17.1	109.7	382.2
Decryption time (ms)	4.3	33.1	151.7
Total time (ms)	24.6	164.3	610.3

We compare it with the Paillier encryption algorithm, which is widely used in the field of privacy protection and is known to have excellent performance. In the same experimental setup, the Paillier algorithm is tested for key generation, encryption, and decryption time using equally long data inputs to evaluate its performance when using keys of the same length. The test results of the Paillier algorithm are shown in Table 4.

Table 4. Paillier algorithm test result.

Key Length (bit)	1024	2048	3072
Generation time (ms)	30.8	191.5	1639.5
Encryption time (ms)	4.5	23.2	76.3
Decryption time (ms)	3.2	25.4	72.2
Total time (ms)	38.5	240.1	1788

Table 3 and Table 4 demonstrate that, under the same test conditions, a performance comparison of the ECC and Paillier encryption algorithms for 128-bit personal information shows that, with a 1024-bit key length, ECC’s encryption and decryption efficiency is slightly lower than that of the Paillier algorithm, but the difference is very small, only 12.6 ms. The encryption and decryption processes can be completed within milliseconds, making the gap negligible. As the key length increases to 3072 bits, the encryption and decryption efficiency gap between ECC and Paillier widens; it remains on the millisecond scale, but Paillier’s key generation time also extends to 1.64 s. Considering that in practical application development, not all scenarios require long keys, especially when uploading data on blockchain platforms like Ethereum, where gas fees and limited storage capacity are concerns, long keys are not the ideal choice. In terms of total time, the ECC algorithm used in our scheme exhibits higher efficiency compared to the Paillier algorithm.

5.2. Zero-Knowledge Proof Algorithm

Our scheme utilizes zero-knowledge proof technology to authenticate intellectual property while protecting privacy. The focus is on the efficiency of the zero-knowledge proof, particularly the proving and verification times, which are the two key performance indicators. Proving time is the time required to generate a zero-knowledge proof, during which the prover uses private data (the hash preimage in our scheme) to construct a proof that can prove a certain assertion to the verifier without exposing private data. The proving time depends on algorithm complexity and data size. Verification time is the time when the verifier checks whether the proof is valid based on the proof and the verifying key provided by the prover. It similarly depends on algorithm complexity and data size. Experimental results indicate that while the proving time increases linearly with data size, the verification time remains relatively constant, between 335 ms and 345 ms. Our scheme adopts the method of off-chain generation of proofs and on-chain verification, so as the amount of data increases, the prover’s proof time increases without any impact on the performance of the entire blockchain system. The verification time is very short and almost unaffected by the size of the data. The experimental results are shown in Figure 9 and Figure 10.

Figure 9. Proving time.

Figure 10. Verification time.

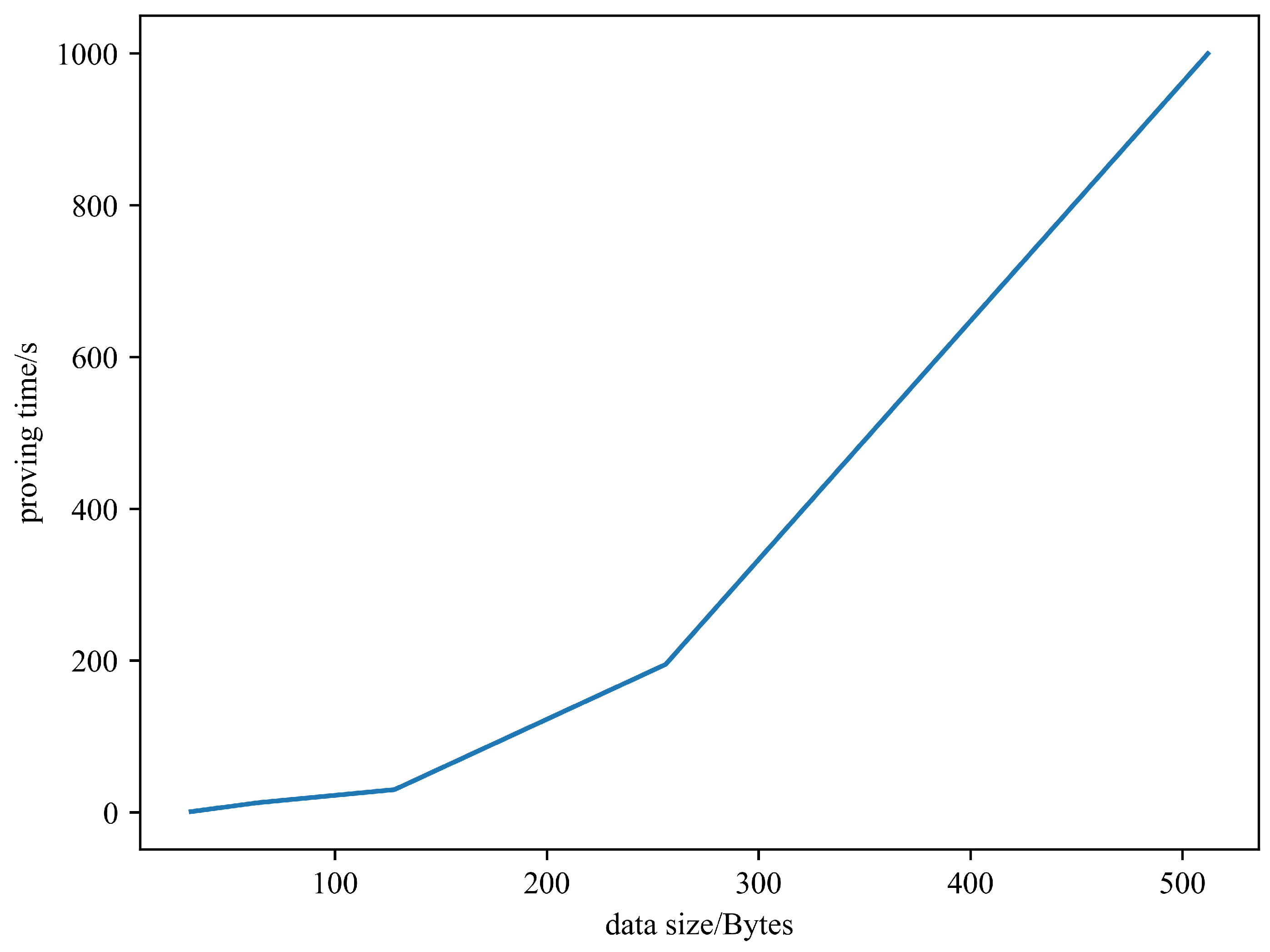
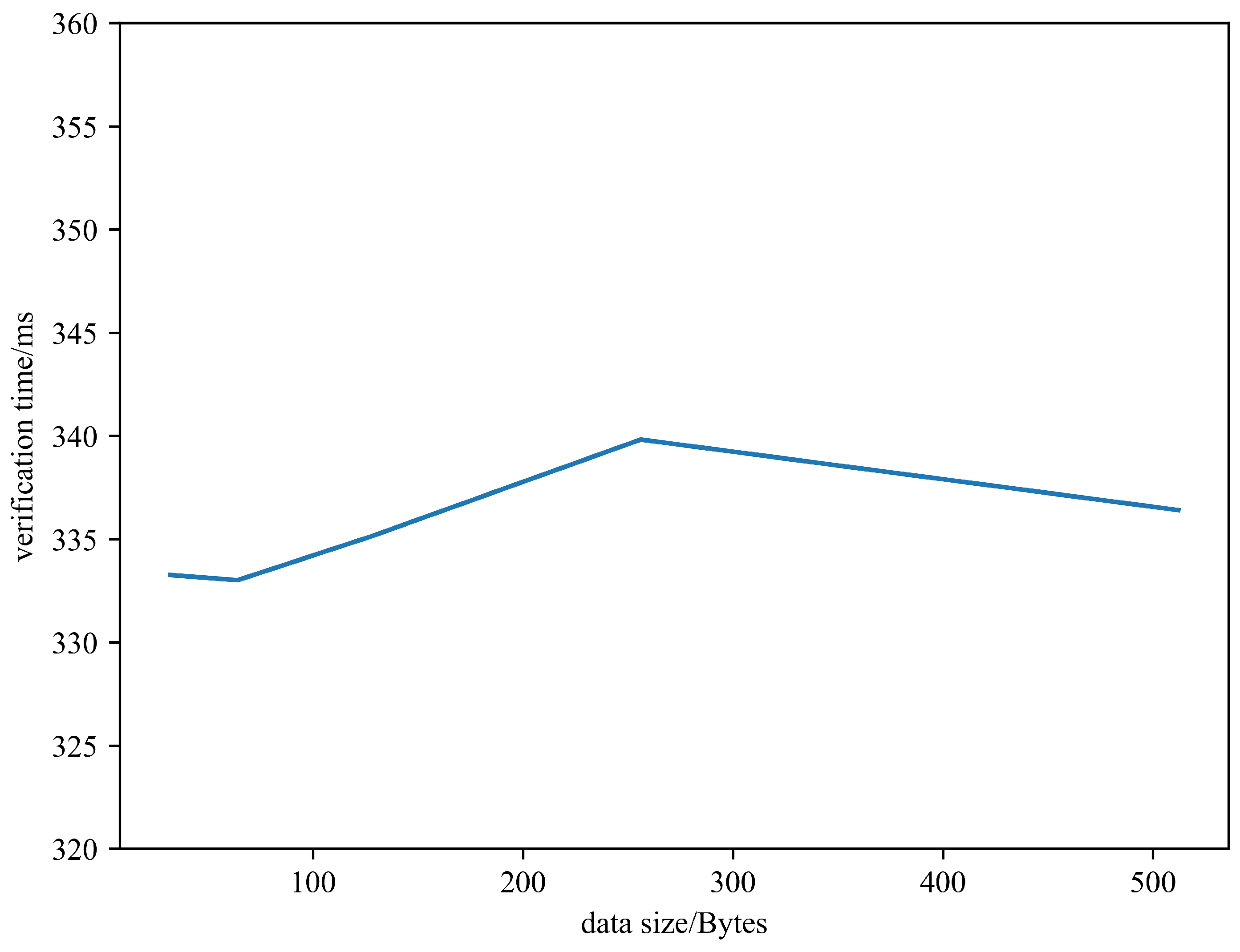
6. Conclusions

After analyzing the issue of personal privacy information leakage in the process of blockchain-based intellectual property authentication, we proposed a blockchain-based intellectual property authentication method with privacy protection. Firstly, we proposed a scheme that combines ECC encryption and digital signatures to address the issue of personal privacy information leakage during the intellectual property registration process, allowing for selective disclosure of personal information. We also adopted a digital signature algorithm to ensure the integrity and non-falsifiability of the registration authentication information. Additionally, we introduced a zk-SNARK-based algorithm to authenticate encrypted information, enabling the verification of intellectual property ownership while safeguarding personal privacy data. Finally, to address the issue of storing large intellectual property and zero-knowledge proof files, which are too voluminous for blockchain, we introduced the IPFS distributed storage system. This system accommodates all large files externally while only the corresponding storage addresses are recorded on the blockchain. To assess the performance of our algorithm comprehensively, we conducted tests on its efficiency in encryption, decryption, and the generation and verification of zero-knowledge proofs. The results show that the scheme performed well. In the future, we will explore a more efficient privacy protection scheme that simultaneously protects users’ intellectual property and their personal privacy and security.