A Deterministic and Stochastic Fractional-Order ILSR Rumor Propagation Model Incorporating Media Reports and a Nonlinear Inhibition Mechanism

Abstract

Nowadays, rumors spread more rapidly than before, leading to more panic and instability in society. Therefore, it is essential to seek out propagation law in order to prevent rumors from spreading further and avoid unnecessary harm. There is a connection between rumor models and symmetry. The consistency of a system or model is referred to as the level of symmetry under certain transformations. For this purpose, we propose a fractional-order Ignorant–Latent–Spreader–Remover (ILSR) rumor propagation model that incorporates media reports and a nonlinear inhibition mechanism. Firstly, the boundedness and non-negativeness of the solutions are derived under fractional differential equations. Secondly, the threshold is used to evaluate and illustrate the stability both locally and globally. Finally, by utilizing Pontryagin’s maximum principle, we obtain the necessary conditions for the optimal control in the fractional-order rumor propagation model, and we also obtain the associated optimal solutions. Furthermore, the numerical results indicate that media reports can decrease the spread of rumors in different dynamic regions, but they cannot completely prevent rumor dissemination. The results are also exhibited and corroborated by replicating the model with specific hypothetical parameter values. It can be inferred that fractional order yields more favorable outcomes when rumor permanence in the population is higher. The presented method facilitates the acquisition of profound insights into the dissemination dynamics and subsequent consequences of rumors within a societal network.

1. Introduction

Rumor is unverified information about news or events, which is easily generated and widely disseminated [1]. Particularly, with the development of science and technology, digital media has emerged as a primary means of providing information, leading to the large-scale spread of rumors and an uncontrollable situation. Since it is impossible to verify whether rumors are true or false, several rumors can generate unnecessary tensions and potential disruptions in individuals’ daily lives. For instance, unusual purchasing behavior concerning salt is driven by the fear stemming from the rumor related to the Fukushima nuclear accident. Numerous rumors have emerged since the outbreak of COVID-19, leading to a range of negative impacts worldwide such as panic buying and ineffective purchases [2]. This not only upset the pharmaceutical market but also generated numerous unnecessary obstacles and difficulties for epidemic prevention efforts. As a result, investigating the dynamics of rumor dissemination, controlling its progression, and reducing the harmful effects of rumors have all emerged as essential concerns.

In the study of rumor propagation, mathematical models are widely used by scholars. Daley and Kendall demonstrated the distinctions between rumors and disease propagation by categorizing individuals into ignorants, spreaders, and stiflers and created the classic DK rumor-spreading model in 1964 [3]. In 1973, Maki and Thompson modified the DK model to study the MK model [4], where interpersonal communication leads to rumor propagation. According to some scholars, the complexity of the rumor propagation process cannot be captured by DK and MK models, especially in the complex topology of social networks. Zanette designed a model framework to simulate the propagation of rumors in small-world networks [5]. To better understand the way rumors spread, more and more factors are being considered by creating more rational models, such as hesitating mechanisms [6], inhibiting strategies, and attitude adjustment [7], etc. To a certain extent, the innovations of these scholars contribute to the spread of rumors, which, in turn, further research.

To accurately capture the dynamics of rumor dissemination through mathematical models, the incidence function plays a crucial role that should not be overlooked. Capasso et al. proposed a function $f(I)=\frac{kI}{1+(I/\alpha )}$, where $I$ denoted the infective class, the parameter $k$ indicated contact rate, and $\alpha$ depicted the saturation phenomena of a large number of infectious individuals, making them more realistic [8]. Moreover, it is more reasonable to utilize the nonlinear propagation function by introducing the psychological factor, which effectively depicts the crowding effect and more complex behaviors on rumor propagation [9,10]. Many scholars employed the saturation functions to reflect the nature of certain phenomena and obtain more accurate results in related rumor propagation [11,12,13]. Thus, we incorporate a saturated incidence rate in our model. Given the various ways in which rumors can propagate, individuals can easily access information on social media platforms, which makes the control of rumor-spreading more complex. In fact, whenever rumors prevail on social media platforms, the media coverage provides rumor-dispelling information to influence individuals’ behavior, which can help to prevent social panic and maintain social harmony. Cui et al. used the form $f\left(I\right)=\mu e^{-mI}$, where the parameter $\mu$ indicated contact rate and the parameter m > 0 demonstrated that the significant influence of media coverage on the spread of contagious illnesses should not be disregarded [14]. Sahu et al. proposed the SEQIRHS model with contact transmission rate $f\left(I\right)=\tilde{\beta }{e}^{-m\frac{\tilde{I}}{\tilde{N}}}$, where the parameter $\mu$ indicated contact rate, the parameter $m>0$ demonstrated the influence of media coverage, and $N$ represented the total number of groups to mirror the impact of media reports [15]. It is apparent that the media coverage did not impact the basic reproduction number; however, it led to a reduction in the count of individuals who were contagious. The form $f\left(S\right)={\beta }_1-\frac{{\beta }_{2}S}{m+S}$ $\left({\beta }_1>{\beta }_2>0,m>0\right)$, where ${\beta }_1$ denoted contact rate, was proposed in [16,17,18], where $g\left(S\right)=\frac{{\beta }_{2}S}{m+S}$ indicated the diminished contact rate through media coverage. Cheng et al. introduced a nonlinear factor $f\left(M\right)={\beta }_1-{\beta }_2\frac{M}{\alpha +M}\left({\beta }_1>{\beta }_2>0,\alpha >0\right)$, where $M$ represented the cumulative density of media coverage to modify the contact rate by combining media coverage and time delay [19]. Pan et al. studied a SIDRW rumor model that combines media coverage and rumor refutation [20]. Later on, Guo et al. proposed two models, SEIMR and SICMR, respectively, considering media coverageand the refutation mechanism [21,22]. Various mathematical models are available to examine the influence of media coverage on rumor spreading. Therefore, the proposed model should take into account the impact of media coverage on the dissemination of rumors among individuals.

Obviously, the intervention strategies of the government and the media coverage cannot indefinitely increase due to the constraints of various limited resources. As rumors spread, managing them becomes increasingly challenging. Given that the law of rumor propagation is analogous to that of disease propagation, many researchers have employed the rumor propagation model with a nonlinear inhibition mechanism [23,24,25,26]. The objective of studying rumor propagation is to restrain rumor spreading. Due to the significant damage caused by rumors, several control measures to reduce losses have been proposed by scholars, such as optimal control strategies [25], time-dependent controllers [27], discontinuous control strategies [28], event-triggered control [29], hybrid control strategy [30], and so on. Actually, the spread of rumors is often influenced by various environmental disturbances, such as interrupted network signals, lost data packets, individual cognitive differences, and so on. These factors contribute to the increased uncertainty in the process of spreading rumors. Zhu et al. proposed a rumored model incorporating noise interference, where they discovered that the level of noise was directly related to the total number of individuals involved and inversely related to the rumor lifecycle [31]. Tong et al. established a stochastic IFCD rumor propagation model on heterogeneous networks [32]. Ghosh et al. introduced a stochastic rumor model combining counter-rumor spreaders and found that stochastic factors significantly contributed to suppressing rumor propagation [33]. Therefore, it is necessary to consider random factors when modeling the spread of rumors.

Obviously, the above-mentioned models have almost discussed the propagation mechanism of rumors in integer order. However, historical information has an impact on the dynamic nature of rumors. Zhang et al. first introduced the memory effect through traditional integer-order differential equations [34]. When rumors appear, an individual’s experience and scientific knowledge affect whether rumors are accepted. Fractional calculus offers innovative methods to characterize memory effects, serving as an extension of integral calculus. Until now, Caputo derivatives, which are extensively used in various fields such as science, biology, engineering, computer, chaos, and many others, have been undergoing significant development in recent decades [35,36,37,38,39,40,41,42,43]. Singh conducted an analysis and dynamics of rumor diffusion in a social network using fractional derivatives that incorporate the Atangana–Baleanu derivative [43]. This research appears to be an exciting new direction for the study of rumor diffusion, and it could potentially provide valuable insights into how rumors spread through social networks. Ye et al. examined a study on a rumor model in two distinct linguistic contexts that incorporate fractional-order dynamics in reaction–diffusion processes [44]. The impact of memory on rumor propagation was investigated, and it can be observed from the results that fractional calculus can be employed to more accurately describe the rumor-spreading process.

However, early memories are blurred by individual forgetting processes and have a minimal impact on the present [35]. Generally, individuals rely on their latest memory to make a judgment, which is based on the recently acquired information from government officials and media reports. On the other hand, due to the limited resources, anomalous propagation occurs, which is characterized by explosive growth in the initial stage and slow dissipation in the later stage. Considering the previous study, we establish an Ignorant–Latent–Spreader–Remover (ILSR) rumor propagation model with media reports and a nonlinear inhibition mechanism under the Caputo fractional derivative, which comprehensively considers the crowding effect, memory effect, and anomalous propagation.

The organization of the remaining sections of the paper is outlined as follows.

In Section 2, we provide a brief overview of some fundamental definitions of fractional calculus. In Section 3, we propose an improved fractional-order ILSR rumor model. In Section 4, the analysis primarily examines the stability of both local and global asymptotic equilibria. In Section 5, we focus on the optimal control problem. In Section 6, we present the ILSR rumor model incorporating fractional stochastic elements. In Section 7, the numerical simulation is examined and supplemented with comments. Finally, the conclusion is presented in Section 8.

2. Numerous Concepts Associated with the Field of Fractional Calculus

In this section, we provide explanations for fractional-order integration and discuss various characteristics of the fractional-order differential equation [45]. The definitions of the Riemann–Liouville and Caputo formulas are highly significant and extensively researched.

Definition 1.

The fractional derivative of a continuous function $f\left(t\right)$ on $\left[t_0,\infty \right)$ known as the Caputo derivative with order $\alpha >0$, is investigated as follows [46,47]:

$${}_{t_0}{}^{C}D_t^{\alpha }f\left(t\right)=\frac{1}{\Gamma \left(n-\alpha \right)}{\displaystyle {\int }_{t_0}^t\frac{f^{\left(n\right)}\left(\tau \right)}{{\left(t-\tau \right)}^{\alpha +1-n}}d\tau ,t\ge }{t}_0,$$

(1)

where $n=⌈\alpha ⌉$ contains the smallest integer greater than α, and the Caputo fractional derivative of the function $f\left(t\right)$ on $\left[t_0,\infty \right)$ is provided by $\underset{\alpha \to n}{\lim }{}_{t_0}{}^{C}D_t^{\alpha }f\left(t\right)=f^n\left(0\right)$ $+{\displaystyle {\int }_{t_0}^t{f}^{n+1}\left(\tau \right)}d\tau =f^{\left(n\right)}\left(t\right),$ $n=1,2,\dots .$ The Gamma function is represented by $\Gamma \left(s\right)={\displaystyle {\int }_0^{\infty }{t}^{s-1}{e}^{-t}dt}.$ Specially, for $0<\alpha <1$, definition can be equivalently expressed as:

$${}_{t_0}{}^{C}D_t^{\alpha }f\left(t\right)=\frac{1}{\Gamma \left(1-\alpha \right)}{\displaystyle {\int }_{t_0}^t\frac{f^{\prime }\left(\tau \right)}{{\left(t-\tau \right)}^{\alpha }}d\tau ,t\ge }{t}_0,$$

Lemma 1.

The Laplace transform of the function $f\left(t\right)=t^{j-1}{E}_{\alpha ,j}\left(\pm \omega t^{\alpha }\right)$ is defined as [46]:

$$L\left(t^{j-1}{E}_{\alpha ,j}\left(\pm \omega t^{\alpha }\right)\right)=\frac{s^{\alpha -j}}{s^{\alpha }\pm \omega },$$

(2)

where $E_{\alpha ,j}$ is a two-parameter Mittag–Leffler function.

Lemma 2.

If the function $f\left(t\right)$ satisfies the subsequent set of criteria [46,47], it obtains:

1. 

$f\left(t\right)$ and $f^{\prime }\left(t\right)$ exhibit continuity throughout $R^n,n\ge 1$.

2. 

$‖f\left(t\right)‖\le c_1+c_2‖t‖$ for all $t\in R^n$, with $c_1$ and $c_2$ consisting of a pair of positive variables.

Subsequently, a distinct solution for $R_{+}^n$ is established for System (1).

Lemma 3.

Assume that $f\left(t\right)\in C\left[a,b\right]$ and ${}_0{}^{C}D_t^{\alpha }f\left(t\right)\in C\left[a,b\right]$ for $\alpha \in \left(0,1\right]$, subsequently, we obtain the following (Generalized Mean Value Theorem [48]):

$$f\left(t\right)=f\left(a\right)+\frac{1}{\Gamma \left(\alpha \right)}{}_a{}^{C}D_t^{\alpha }f\left(\xi \right){\left(t-a\right)}^{\alpha },a<\xi <t,\forall t\in \left(a,b\right].$$

(3)

If $f\left(t\right)\in C\left[a,b\right]$ and ${}_0{}^{C}D_t^{\alpha }f\left(t\right)\ge 0,\forall t\in \left(a,b\right],$ then $\forall t\in \left(a,b\right]$, the function $f\left(t\right)$ is non-increasing.

Definition 2.

Consider the following linear fractional-order derivative [49]:

$$\begin{array}{l}{}_0{}^{C}D_t^{\alpha }\left(X\left(t\right)\right)=\Phi \left(X\right),\\ X_{t_0}={\left(x_{t_0}^1,x_{t_0}^2,\dots ,x_{t_0}^n\right)}^T,\end{array}$$

(4)

where $X_t\left(t\right)={\left(x_t^1,x_t^2,\dots ,x_t^n\right)}^T,\Phi \left(X\right):R^n\to R_{+}^n$, and $0<\alpha \le 1$. The stability of System (4) tends to be a stable state if $\left|\arg \left({\lambda }_i\right)\right|>\frac{\alpha \pi }{2},i=1,2,\dots ,n$ meets all eigenvalues ${\lambda }_i$ of $X\left(t\right)$.

Definition 3.

Provided that System (3) with $f\left(t\right)$ is a differentiable function, accordingly, the stability of the equilibrium point $x^{*}$ can be characterized as asymptotically stable when all eigenvalues ${\lambda }_i$ of the Jacobian matrix evaluated at $x^{*}$ meet certain conditions $\left|\arg \left({\lambda }_i\right)\right|>\frac{\alpha \pi }{2}$. If for some eigenvalues ${\lambda }_i$, $\left|\arg \left({\lambda }_i\right)\right|<\frac{\alpha \pi }{2}$, the equilibrium point $x^{*}$ is unstable [50].

3. Description of the Model

In this section, we present an Ignorant–Latent–Spreader–Remover (ILSR) model with fractional-order dynamics. The total population has been divided into four categories: Inorants, who have not been exposed to the rumor and are more likely to trust it, denoted by $I\left(t\right)$; Latents, who could question the rumor and remain silent in the short term after hearing the rumor, Refs. [51,52], denoted by $L\left(t\right)$; Spreaders who are aware of the rumor and actively spread it, denoted by $S\left(t\right)$; and Removers who have had contact with the Spreaders but resist and do not spread the rumor or lose interest in the rumor, denoted by $R\left(t\right)$.

The following are the propagation rules:

(i)

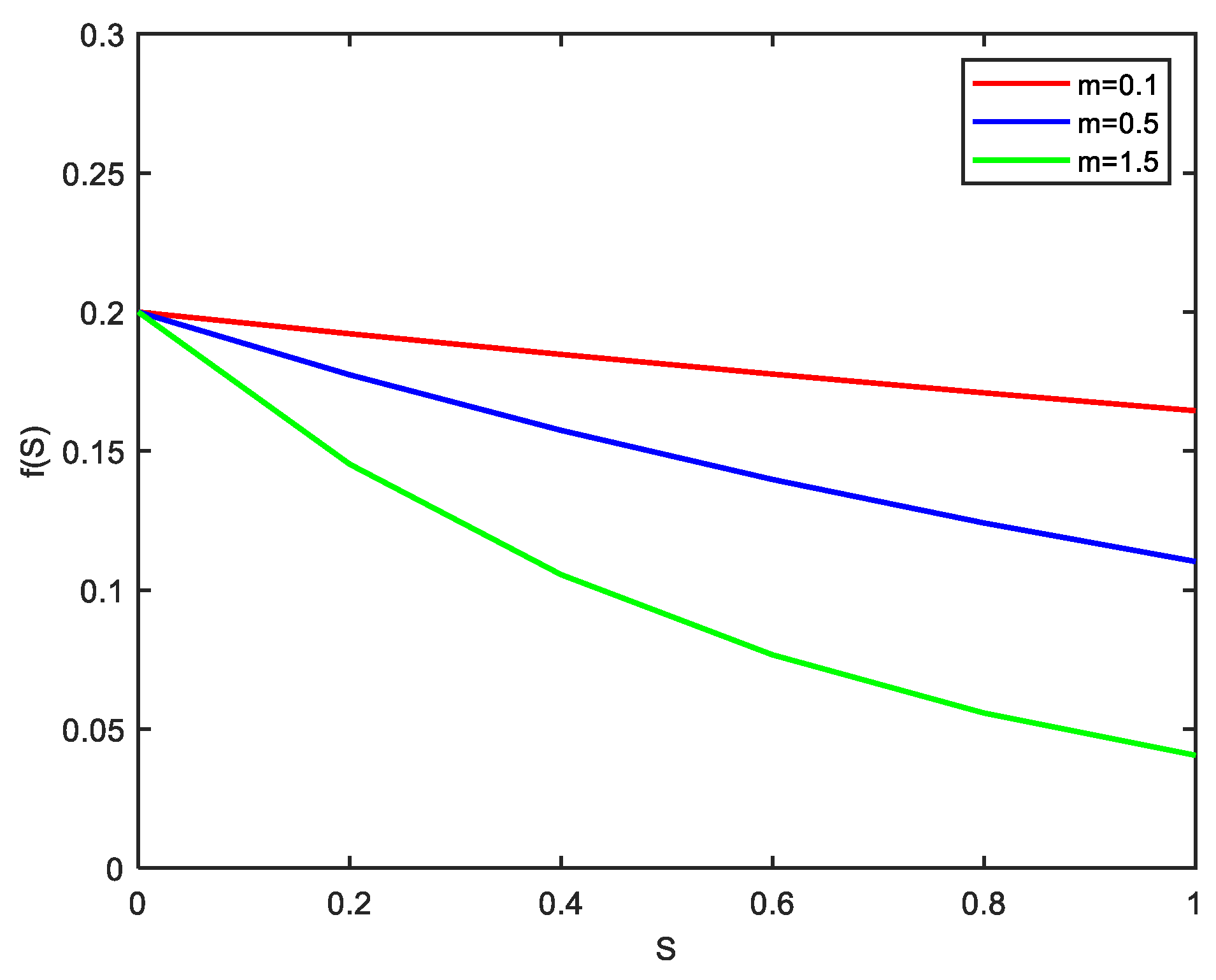
When an Ignorant has contact with a Latent, the Ignorant is affected and becomes a Latent with the possibility of $\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}$, where $\beta$ denotes the rumor contact rate, $\delta$ denotes the saturation constant, and $m$ implies the level of the media reports. Obviously, $\frac{\beta e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}\to \beta$ as $S\left(t\right)\to 0$. The timely popularization of scientific knowledge and countering rumors through media reports can help control rumors to a certain extent. The influence of media reports on communication is not inherently decisive, Ref. [15]. The transmission rate $f\left(S\right)=\frac{\beta e^{-mS}}{1+\delta S}$ is influenced by media reports in Figure 1.

(ii)

Some Latents may tend to become Spreaders with a transfer rate $\epsilon$ and the parameter $\phi$ represents the recovery rate of Spreaders when they are exposed to the impacts of the forgetting mechanism.

(iii)

$\gamma S\left(t\right)/\left(1+kS\left(t\right)\right)$ represents a saturated treatment function that represents the nonlinear inhibition mechanism, where $\gamma >1$ and $k\ge 0$. $\gamma /k$ means the highest level of inhibition measure for the Spreaders group.

(iv)

We make the assumption that the rate of immigration is $\Lambda$, while the rate of emigration is $\mu$. All the parameters of the model are assumed to possess constant and positive values.

In accordance with the previously mentioned propagation rules, Figure 2 presents a schematic diagram. Taking into account the assumptions above, the dynamic equation of the fractional-order ILSR rumor model is defined as follows:

$$\left\{\begin{array}{l}{}_0{}^{C}D_t^{\alpha }I\left(t\right)=\Lambda -\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\mu I\left(t\right),\\ {}_0{}^{C}D_t^{\alpha }L\left(t\right)=\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\epsilon L\left(t\right)-\mu L\left(t\right),\\ {}_0{}^{C}D_t^{\alpha }S\left(t\right)=\epsilon L\left(t\right)-\frac{\gamma S\left(t\right)}{1+kS\left(t\right)}-\phi S\left(t\right)-\mu S\left(t\right),\\ {}_0{}^{C}D_t^{\alpha }R\left(t\right)=\frac{\gamma S\left(t\right)}{1+kS\left(t\right)}+\phi S\left(t\right)-\mu R\left(t\right),\end{array}\right.$$

(5)

where ${}_0{}^{C}D_t^{\alpha }$ is the fractional operator in the Caputo sense with the range of $\alpha ,0<\alpha \le 1$ and the initial conditions are $I\left(0\right)=I_0\ge 0,L\left(0\right)=L_0\ge 0,S\left(0\right)=S_0\ge 0,R\left(0\right)=$ $R_0\ge 0$.

The solution of Model (5) demonstrates positivity and remains within bounds. since $\left(I\left(t\right),L\left(t\right),S\left(t\right),R\left(t\right)\right)\in R_{+}^4,$ the following theorem is acquired.

Theorem 1.

The solution of Model (5) is a bounded solution in $R_{+}^4.$

Proof. 

We note that the non-negative region $R_{+}^4$ is positively invariant. Utilizing System (5), we acquire the following expression:

$$\begin{array}{l}{\left.{}_0{}^{C}D_t^{\alpha }I\left(t\right)\right|}_{I\left(t\right)=0}=\Lambda \ge 0,\\ {\left.{}_0{}^{C}D_t^{\alpha }L\left(t\right)\right|}_{L\left(t\right)=0}=\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}\ge 0,\\ {\left.{}_0{}^{C}D_t^{\alpha }S\left(t\right)\right|}_{S\left(t\right)=0}=\epsilon L\left(t\right)\ge 0,\\ {\left.{}_0{}^{C}D_t^{\alpha }R\left(t\right)\right|}_{R\left(t\right)=0}=\frac{\gamma S\left(t\right)}{1+kS\left(t\right)}+\phi S\left(t\right)\ge 0\end{array}$$

(6)

.

If $\left(I\left(0\right),L\left(0\right),S\left(0\right),R\left(0\right)\right)\in R_{+}^4$, then according to System (6) and Lemma 3, the solution of Model (5) can only be on high hyperplanes $I\left(t\right)=0,$ $L\left(t\right)=0,S\left(t\right)=0,$ and $R\left(t\right)=0$. Thus, $R_{+}^4$ is positively invariant. □

Theorem 2.

The region $\Omega =\left\{\left(I\left(t\right),L\left(t\right),S\left(t\right),R\left(t\right)\right)\in R_{+}^4,0\le I\left(t\right)+L\left(t\right)\right.+S\left(t\right)\left.+R\left(t\right)\le \frac{\Lambda }{\mu }\right\}$ possesses a positive invariant set for Model (5).

Proof. 

Provided that $N\left(t\right)=I\left(t\right)+L\left(t\right)+S\left(t\right)+R\left(t\right)$, and adding the first four equations of Model (5), we acquire the following expression:

$${}_0{}^{C}D_t^{\alpha }N\left(t\right)=\Lambda -\mu \left(I\left(t\right)+L\left(t\right)+S\left(t\right)+R\left(t\right)\right),$$

(7)

Then, ${}_0{}^{C}D_t^{\alpha }N\left(t\right)=\Lambda -\mu N\left(t\right),$ according to Lemma 1, the Laplace transform is applied to the previous equation, and the result is:

$$N\left(t\right)\le N\left(0\right)E_{\alpha }\left(-\mu t^{\alpha }\right)+\frac{\Lambda }{\mu }\left(1-E_{\alpha }\left(-\mu t^{\alpha }\right)\right).$$

(8)

Since $0\le E_{\alpha }\left(-\mu t^{\alpha }\right)\le 1$, we obtain $N\left(t\right)\le \frac{\Lambda }{\mu }+N\left(0\right).$ This implies that $N\left(t\right)$ is bounded, thus, $I\left(t\right),L\left(t\right),S\left(t\right)$, and $R\left(t\right)$ are bounded.

Therefore, all solutions to Model (5) remain positive and bounded. Next, we will present proof that the solution is unique. □

Theorem 3.

A unique solution $X\left(t\right)\in R_{+}^4$ for each initial condition $X\left(0\right)=\left(I_0,L_0,S_0,R_0\right),\forall t\ge 0$ exists in Model (5).

Proof. 

To validate the existence and uniqueness, the approach used in [53] is adopted. Define $H\left(X\right)=\left(H_1\left(X\right),H_2\left(X\right),H_3\left(X\right),H_4\left(X\right)\right),$ as follows:

$$\begin{array}{l}{H}_1\left(X\right)=\Lambda -\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\mu I\left(t\right),\\ H_2\left(X\right)=\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\epsilon L\left(t\right)-\mu L\left(t\right),\\ H_3\left(X\right)=\epsilon L\left(t\right)-\frac{\gamma S\left(t\right)}{1+kS\left(t\right)}-\phi S\left(t\right)-\mu S\left(t\right),\\ H_4\left(X\right)=\frac{\gamma S\left(t\right)}{1+kS\left(t\right)}+\phi S\left(t\right)-\mu R\left(t\right).\end{array}$$

(9)

Furthermore, for any $X,\overline{X}\in {\Omega }_1$, construct a function as follows:

$$\begin{array}{ll}‖H\left(X\right)-H\left(\overline{X}\right)‖& =\left|H_1\left(X\right)-H_1\left(\overline{X}\right)\right|+\left|H_2\left(X\right)-H_2\left(\overline{X}\right)\right|+\left|H_3\left(X\right)-H_3\left(\overline{X}\right)\right|\\ & +\left|H_4\left(X\right)-H_4\left(\overline{X}\right)\right|\\ & =\left|\Lambda -\frac{\beta IS{e}^{-mS}}{1+\delta S}-\mu I-\Lambda +\frac{\beta \overline{I}\overline{S}{e}^{-m\overline{S}}}{1+\delta \overline{S}}+\mu \overline{I}\right|\\ & +\left|\frac{\beta IS{e}^{-mS}}{1+\delta S}-\left(\epsilon +\mu \right)L-\frac{\beta \overline{I}\overline{S}{e}^{-m\overline{S}}}{1+\delta \overline{S}}+\left(\epsilon +\mu \right)\overline{L}\right|\\ & +\left|\epsilon L-\frac{\gamma S}{1+kS}-\left(\phi +\mu \right)S-\epsilon \overline{L}+\frac{\gamma \overline{S}}{1+k\overline{S}}+\left(\phi +\mu \right)\overline{S}\right|\\ & +\left|\frac{\gamma S}{1+kS}+\phi S-\mu R-\frac{\gamma \overline{S}}{1+k\overline{S}}-\phi \overline{S}+\mu \overline{R}\right|\\ & \le l_1\left|I-\overline{I}\right|+l_2\left|L-\overline{L}\right|+l_3\left|S-\overline{S}\right|+l_4\left|R-\overline{R}\right|\\ & \le L‖\left(I,L,S,R\right)-\left(\overline{I},\overline{L},\overline{S},\overline{R}\right)‖\\ & \le L‖X-\overline{X}‖,\end{array}$$

where

$$\begin{array}{l}L=\max \left(l_1,l_2,l_3,l_4\right),\\ l_1=\frac{2\beta }{\delta }+\mu ,\\ l_2=2\epsilon +\mu ,\\ l_3=\frac{2\gamma }{k}+2\phi +\mu ,\\ l_4=\mu .\end{array}$$

Hence, $H\left(X\right)$ satisfies the Lipschitz condition with each initial condition $X\left(0\right)=\left(I_0,L_0,S_0,R_0\right),\forall t\ge 0$. The proposed fractional-order ILSR model always has a unique solution. □

The variables $R\left(t\right)$ absent among the initial three equations can be simplified by reducing Model (5) as follows:

$$\left\{\begin{array}{l}{}_0{}^{C}D_t^{\alpha }I\left(t\right)=\Lambda -\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\mu I\left(t\right),\\ {}_0{}^{C}D_t^{\alpha }L\left(t\right)=\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\epsilon L\left(t\right)-\mu L\left(t\right),\\ {}_0{}^{C}D_t^{\alpha }S\left(t\right)=\epsilon L\left(t\right)-\frac{\gamma S\left(t\right)}{1+kS\left(t\right)}-\phi S\left(t\right)-\mu S\left(t\right).\end{array}\right.$$

(10)

4. Analysis of the Model

This section presents the stability results of Model (10). Firstly, rumor-demise equilibrium $E^0$ and rumor-permanence equilibrium $E^{*}$ are considered. And then, $R_0$ is used to represent the basic reproduction number. Lastly, the local stability for both equilibria is analyzed. According to the next-generation matrix method [54], we derive the basic reproduction number $R_0$ for Model (10) using the matrices $F_1$ and $V_1$, which stand for the transmission part. If $Q={\left(I,L,S\right)}^T$, the original equation can be reformulated as follows:

$$\frac{dQ}{dt}=F_1\left(x\right)-V_1\left(x\right),$$

where

$$F_1=\left(\begin{array}{l}\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}\\ 0\\ 0\end{array}\right),$$

$$V_1=\left(\begin{array}{c}\left(\epsilon +\mu \right)L\left(t\right)\\ \left[\frac{\gamma }{1+kS\left(t\right)}+\phi +\mu \right]I\left(t\right)-\epsilon L\left(t\right)\\ \left(\frac{\beta S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}+\mu \right)I\left(t\right)-\Lambda \end{array}\right).$$

On differentiation (10), the $F_2$ and $V_2$ yield the following expression:

$$F_2=\left(\begin{array}{ccc}0& \frac{\beta I{e}^{-mS}\left[\left(1-mS\right)\left(1+\delta S\right)-\delta S\right]}{{\left(1+\delta S\right)}^2}& \frac{\beta S}{1+\delta S}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),$$

$$V_2=\left(\begin{array}{ccc}\epsilon +\mu & 0& 0\\ -\epsilon & \frac{\gamma }{{\left(1+kS\right)}^2}+\phi +\mu & 0\\ 0& \frac{\beta I{e}^{-mS}\left[\left(1-mS\right)\left(1+\delta S\right)-\delta S\right]}{{\left(1+\delta S\right)}^2}& \frac{\beta S}{1+\delta S}+\mu \end{array}\right).$$

The Jacobian matrices of $F_2$ and $V_2$ are obtained at the rumor-demise equilibrium $E^0$:

$$\begin{array}{l}{F}_2^0=F_2\left(E^0\right)=\left(\begin{array}{ccc}0& \beta I^0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),\\ V_2^0=V_2\left(E^0\right)=\left(\begin{array}{ccc}\epsilon +\mu & 0& 0\\ -\epsilon & \gamma +\phi +\mu & 0\\ 0& \beta I^0& \mu \end{array}\right).\end{array}$$

Therefore, the $R_0$ considered as the spectral radius of $F_2^0{\left(V_2^0\right)}^{-1}$ is obtained as follows:

$$R_0=\frac{\beta \epsilon \Lambda }{\mu \left(\epsilon +\mu \right)\left(\gamma +\phi +\mu \right)}.$$

It is clear that saturated incidence, media reports, and nonlinear inhibition mechanisms have no impact on the value of $R_0$.

Theorem 4.

The rumor-demise equilibrium $E^0$ is considered to be locally asymptotically stable if $R_0<1$ and $R_0>1$ becomes unstable.

Proof. 

The main purpose of the investigation is to assess the stability criterion at $E^0$. The general Jacobian matrix of Model (10) is calculated as follows:

$$E^0=\left(\begin{array}{ccc}-\frac{\beta S{e}^{-mS}}{1+\delta S}-\mu & 0& -\frac{\beta I{e}^{-mS}\left[\left(1-mS\right)\left(1+\delta S\right)-\delta S\right]}{{\left(1+\delta S\right)}^2}\\ \frac{\beta S{e}^{-mS}}{1+\delta S}& -\left(\epsilon +\mu \right)& \frac{\beta I{e}^{-mS}\left[\left(1-mS\right)\left(1+\delta S\right)-\delta S\right]}{{\left(1+\delta S\right)}^2}\\ 0& \epsilon & -\frac{\gamma }{{\left(1+kS\right)}^2}-\phi -\mu \end{array}\right),$$

After substituting the rumor-demise equilibrium point $E^0$ in the Jacobian matrix, we obtain the following expression:

$$J\left(E^0\right)=\left(\begin{array}{ccc}-\mu & 0& -\frac{\beta \Lambda }{\mu }\\ 0& -\left(\epsilon +\mu \right)& \frac{\beta \Lambda }{\mu }\\ 0& \epsilon & -\left(\gamma +\phi +\mu \right)\end{array}\right).$$

The eigenvalues can be obtained by solving the characteristic equation of the Jacobian matrix $E^0$, which is given by the following expression:

$$\det \left(J\left(E^0\right)-\lambda I\right)=0,$$

(11)

This gives the following equation:

$$\left(\lambda +\mu \right)\left({\lambda }^2+\left(2\mu +\epsilon +\gamma \right)\lambda +\left(\epsilon +\mu \right)\left(\gamma +\phi +\mu \right)\left(1-R_0\right)\right)=0.$$

(12)

For $R_0<1$, all the three eigenvalues of $J\left(E^0\right)$ have negative real parts. If $R_0>1$, two eigenvalues of $E^0$ have negative real parts, while one eigenvalue exhibits a positive real part. Therefore, by utilizing the Routh–Hurwitz criteria [55], it can be concluded that all solutions of Equation (12) possess negative real parts and meet the given condition $\left|\arg \left(\lambda \right)\right|>\frac{\alpha \pi }{2}$. Consequently, according to Definition 2, the rumor-demise equilibrium $E^0$ of the rumor exhibits local asymptotic stability. If $R_0>1$, Equation (12) has a positive real root. Therefore, in accordance with Definition 2.6, $E^0$ is unstable. □

Theorem 5.

The rumor-permanence equilibrium $E^{*}$ is locally asymptotically stable under the condition of $R_0>1$.

Proof. 

At the rumor-permanence equilibrium point $E^{*}$, the Jacobian matrix is obtained as follows:

$$J\left(E^{*}\right)=\left(\begin{array}{ccc}-\frac{\beta S^{*}{e}^{-m{S}^{*}}}{1+\delta S^{*}}-\mu & 0& -\frac{\beta I^{*}{e}^{-m{S}^{*}}\left[\left(1-m{S}^{*}\right)\left(1+\delta S^{*}\right)-\delta S^{*}\right]}{{\left(1+\delta S^{*}\right)}^2}\\ \frac{\beta S^{*}{e}^{-m{S}^{*}}}{1+\delta S^{*}}& -\left(\epsilon +\mu \right)& \frac{\beta I^{*}{e}^{-m{S}^{*}}\left[\left(1-m{S}^{*}\right)\left(1+\delta S^{*}\right)-\delta S^{*}\right]}{{\left(1+\delta S^{*}\right)}^2}\\ 0& \epsilon & -\frac{\gamma }{{\left(1+k{S}^{*}\right)}^2}-\phi -\mu \end{array}\right).$$

The characteristic equation can be expressed as follows:

$$\det \left(J\left(E^{*}\right)-\lambda I\right)=0.$$

(13)

Furthermore, it could be depicted as follows:

$${\lambda }^3+L_1{\lambda }^2+L_2\lambda +L_3=0,$$

(14)

where the coefficients $L_1,L_2,L_3$ are as follows:

$$\begin{array}{l}{L}_1=3\mu +\epsilon +\phi +\frac{\beta S^{*}{e}^{-m{S}^{*}}}{1+\delta S^{*}}+\frac{\gamma }{{\left(1+k{S}^{*}\right)}^2}>0,\\ L_2=\left(\epsilon +\mu \right)\left(\mu +\phi +\frac{\gamma }{{\left(1+k{S}^{*}\right)}^2}\right)\left(1+\frac{\beta S^{*}{e}^{-m{S}^{*}}}{1+\delta S^{*}}\right)+\frac{\beta \epsilon I^{*}{e}^{-m{S}^{*}}\left[\left(1-m{S}^{*}\right)\left(1+\delta S^{*}\right)-\delta S^{*}\right]}{{\left(1+\delta S^{*}\right)}^2},\\ L_3=\left(\mu +\frac{2\beta S^{*}{e}^{-m{S}^{*}}}{1+\delta S^{*}}\right)\frac{\beta \epsilon I^{*}{e}^{-m{S}^{*}}\left[\left(1-m{S}^{*}\right)\left(1+\delta S^{*}\right)-\delta S^{*}\right]}{{\left(1+\delta S^{*}\right)}^2}.\end{array}$$

(15)

By a direct calculation, if $L_2>0,L_3>0$ and $L_1{L}_2-L_3>0$, it adheres to the Routh–Hurwitz criterion and satisfies the condition $\left|\arg \left({\lambda }_i\right)\right|>\frac{\alpha \pi }{2},i=1,2,3$. All solutions to Equation (15) exhibit a negative real part according to Definition 3. □

Theorem 6.

If $R_0<1$ and Condition (6) is satisfied, then the rumor-demise equilibrium $E^0$ of Model (10) is globally asymptotically stable.

Proof.

From Model (10), we can derive the following conditions: $E_0=\left(\frac{\Lambda }{\mu },0,0\right).$ Now, the fractional-order Lyapunov function is considered as

$$P\left(t\right)=\left(I-I_0-I_0\ln \frac{I}{I_0}\right)+L\left(t\right)+S\left(t\right),$$

(16)

where, $I_0=\frac{\Lambda }{\mu }$.

The differentiation of Equation (16) with respect to Model (10) can be expressed as follows:

$$\begin{array}{ll}{}_0{}^{C}D_t^{\alpha }{\rm P}\left(t\right)& =\left(1-\frac{I_0}{I}\right){}_0{}^{C}D_t^{\alpha }I\left(t\right)+{}_0{}^{C}D_t^{\alpha }L\left(t\right)+{}_0{}^{C}D_t^{\alpha }S\left(t\right)\\ & \le \left(1-\frac{I_0}{I}\right)\left(\mu I_0-\frac{\beta IS{e}^{-mS}}{1+\delta S}-\mu I\right)+\frac{\beta IS{e}^{-mS}}{1+\delta S}-\epsilon L-\mu L\\ & +\epsilon L-\frac{\gamma S}{1+kS}-\phi S-\mu S\\ & \le -\mu I{\left(1-\frac{I_0}{I}\right)}^2+\frac{\beta I_{0}S{e}^{-mS}}{1+\delta S}-\mu L-\left(\frac{\gamma }{1+kS}+\phi +\mu \right)S,\end{array}$$

Now, it can be observed from above that if $\frac{\beta I_{0}S{e}^{-mS}}{1+\delta S}\le \mu L+\left(\frac{\gamma }{1+kS}+\phi +\mu \right)S,$ then ${}_0{}^{C}D_t^{\alpha }L\left(t\right)\le 0$. Therefore, according to Lassalle’s invariance principle [56], the rumor-demise equilibrium $E_0$ of Model (10) is globally asymptotically stable when $R_0<1$. □

5. Fractional Optimal Control of the Model

The objective of this section is to devise a control strategy for regulating the dissemination of fractional rumors. The primary purpose of fractional optimal control is to reduce the relative density of spreading rumors. In the meantime, it is imperative to take into account the management of expenses in the actual situation. In view of this, we present a suggested approach for effectively managing System (5.9), which can be evaluated through the application of Pontryagin’s maximum principle [57]. Hence, Model (5) represents the model that includes the control mechanism as follows:

$$\left\{\begin{array}{l}{}_0{}^{C}D_t^{\alpha }I\left(t\right)=\Lambda -\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\mu I\left(t\right),\\ {}_0{}^{C}D_t^{\alpha }L\left(t\right)=\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\left(\epsilon +\mu +u_1\left(t\right)\right)L\left(t\right),\\ {}_0{}^{C}D_t^{\alpha }S\left(t\right)=\epsilon L\left(t\right)-\left(\frac{\gamma }{1+kS\left(t\right)}+\phi +\mu +u_2\left(t\right)\right)S\left(t\right),\\ {}_0{}^{C}D_t^{\alpha }R\left(t\right)=\frac{\gamma S\left(t\right)}{1+kS\left(t\right)}+\phi S\left(t\right)-\mu R\left(t\right)+u_1\left(t\right)L\left(t\right)+u_2\left(t\right)S\left(t\right).\end{array}\right.$$

(17)

where $u_1\left(t\right)$ and $u_2\left(t\right)$ signify the influence of education or network management on the rumor propagation. The average cost of controlling and educating for $L\left(t\right)$ and $S\left(t\right)$ is employed by ${\psi }_i$ and ${\varphi }_i\left(i=1,2\right)$. The expected period is $[0,T]$. The objective function of the optimal control is established as follows:

$$J\left(u_1\left(t\right),u_2\left(t\right)\right)={\displaystyle {\int }_0^T\left[{\psi }_{1}L\left(t\right)+{\psi }_{2}S\left(t\right)+{\varphi }_1{u}_1^2\left(t\right)+{\varphi }_2{u}_2^2\left(t\right)\right]dt}.$$

(18)

The feasible region of $u_1\left(t\right)$ and $u_2\left(t\right)$ is as follows:

$$U\left\{\left.\left(u_1\left(t\right),u_2\left(t\right)\right)\right|0\le u_1\left(t\right)\le u_1^{\max },0\le u_2\left(t\right)\le u_2^{\max },t\in \left(0,T\right]\right\}$$

where $u_1^{\max }<1$ and $u_2^{\max }<1$ are the upper bound of $u_1\left(t\right)$ and $u_2\left(t\right)$, respectively. Optimal control $u_1^{*}$ and $u_2^{*}$ meet $J\left(u_1^{*},u_2^{*}\right)=\min \left\{J\left(u_1\left(t\right),u_2\left(t\right)\right):\left(u_1\left(t\right),u_2\left(t\right)\right)\in U\right\}$. The most effective measures to reduce the transmission of the rumor while minimizing expenses are obtained.

Therefore, the following Lagrangian function is defined as follows:

$$\mathcal{L}\left(L\left(t\right),S\left(t\right),u_1\left(t\right),u_2\left(t\right)\right)={\psi }_{1}L\left(t\right)+{\psi }_{2}S\left(t\right)+{\varphi }_1{u}_1^2\left(t\right)+{\varphi }_2{u}_2^2\left(t\right)$$

(19)

The definition of the Hamiltonian function is as follows:

$$\begin{array}{ll}H\left(L\left(t\right),S\left(t\right),R\left(t\right),u_i\left(t\right),{\lambda }_j\left(t\right)\right)& =\mathcal{L}\left(L\left(t\right),S\left(t\right),u_1\left(t\right),u_2\left(t\right)\right)\\ & +{\lambda }_1\left(t\right)\left\{\Lambda -\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\mu I\left(t\right)\right\}\\ & +{\lambda }_2\left(t\right)\left\{\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\left(\epsilon +\mu +u_1\left(t\right)\right)L\left(t\right)\right\}\\ & +{\lambda }_3\left(t\right)\left\{\epsilon L\left(t\right)-\left(\frac{\gamma }{1+kS\left(t\right)}+\phi +\mu +u_2\left(t\right)\right)S\left(t\right)\right\}\\ & +{\lambda }_4\left(t\right)\left\{\frac{\gamma S\left(t\right)}{1+kS\left(t\right)}+\phi S\left(t\right)-\mu R\left(t\right)+u_1\left(t\right)L\left(t\right)+u_2\left(t\right)S\left(t\right)\right\}.\end{array}$$

(20)

where $i=1,2$ and $j=1,2,3,4$. By utilizing Pontryagin’s maximum principle, we are able to establish the following theorem.

Theorem 7.

Consider $I^{*},L^{*},S^{*}$, and $R^{*}$ as the state solutions that yield optimal state solutions, along with their respective optimal controls $\left(u_1^{*},u_2^{*}\right)$ for the optimal control Problem (17). Then, there exist the adjoint variables ${\lambda }_1\left(t\right),{\lambda }_2\left(t\right),{\lambda }_3\left(t\right)$ and ${\lambda }_4\left(t\right)$ that meet the given conditions as follows:

$$\left\{\begin{array}{ll}{}_0{}^{C}D_t^{\alpha }{\lambda }_1\left(t\right)=& {\lambda }_1\left(t\right)\left(\frac{\beta S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}+\mu \right)-{\lambda }_2\left(t\right)\frac{\beta S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)},\\ {}_0{}^{C}D_t^{\alpha }{\lambda }_2\left(t\right)=& -{\psi }_1-{\lambda }_2\left(t\right)\left(\epsilon +\mu +u_1\left(t\right)\right)-{\lambda }_3\left(t\right)\epsilon -{\lambda }_4\left(t\right)u_1\left(t\right),\\ {}_0{}^{C}D_t^{\alpha }{\lambda }_3\left(t\right)=& -{\psi }_2+{\lambda }_1\left(t\right)\beta e^{-mS\left(t\right)}I\left(t\right)\left[\frac{\left(1-mS\left(t\right)\right)\left(1+\delta S\left(t\right)\right)-\delta S\left(t\right)e^{-mS\left(t\right)}}{{\left(1+\delta S\left(t\right)\right)}^2}\right]\\ & -{\lambda }_2\left(t\right)\beta e^{-mS\left(t\right)}I\left(t\right)\left[\frac{\left(1-mS\left(t\right)\right)\left(1+\delta S\left(t\right)\right)-\delta S\left(t\right)e^{-mS\left(t\right)}}{{\left(1+\delta S\left(t\right)\right)}^2}\right]\\ & +{\lambda }_3\left(t\right)\left(\frac{\gamma }{{\left(1+kS\left(t\right)\right)}^2}+\phi +\mu +u_2\left(t\right)\right)-{\lambda }_4\left(t\right)\left(\frac{\gamma }{{\left(1+kS\left(t\right)\right)}^2}+\phi +u_2\left(t\right)\right),\\ {}_0{}^{C}D_t^{\alpha }{\lambda }_4\left(t\right)=& {\lambda }_4\left(t\right)\mu .\end{array}\right.$$

(21)

with the transversality conditions ${\lambda }_j\left(t\right)$ for $j=1,2,3,4$. The optimal controls $u_1^{*}$ and $u_2^{*}$ are given by the following expression:

$$\begin{array}{l}{u}_1^{*}=\min \left\{\max \left\{\frac{\left({\lambda }_2-{\lambda }_4\right)L^{*}}{2{\varphi }_1},0\right\},u_1^{\max }\right\},\\ u_2^{*}=\min \left\{\max \left\{\frac{\left({\lambda }_3-{\lambda }_4\right)S^{*}}{2{\varphi }_2},0\right\},u_2^{\max }\right\}.\end{array}$$

(22)

Proof. 

By applying Pontryagin’s maximum principle [57] and denoting $I\left(t\right)=I^{*},$ $L\left(t\right)=L^{*},S\left(t\right)=S^{*}$ and $R\left(t\right)=R^{*}$, we derive the following adjoint equation:

$$\left\{\begin{array}{ll}{}_0{}^{C}D_t^{\alpha }{\lambda }_1\left(t\right)=-\frac{\partial H\left(t\right)}{\partial I\left(t\right)}& ={\lambda }_1\left(t\right)\left(\frac{\beta S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}+\mu \right)-{\lambda }_2\left(t\right)\frac{\beta S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)},\\ {}_0{}^{C}D_t^{\alpha }{\lambda }_2\left(t\right)=-\frac{\partial H\left(t\right)}{\partial L\left(t\right)}& =-{\psi }_1-{\lambda }_2\left(t\right)\left(\epsilon +\mu +u_1\left(t\right)\right)-{\lambda }_3\left(t\right)\epsilon -{\lambda }_4\left(t\right)u_1\left(t\right),\\ {}_0{}^{C}D_t^{\alpha }{\lambda }_3\left(t\right)=-\frac{\partial H\left(t\right)}{\partial S\left(t\right)}& =-{\psi }_2+{\lambda }_1\left(t\right)\beta e^{-mS\left(t\right)}I\left(t\right)\left[\frac{\left(1-mS\left(t\right)\right)\left(1+\delta S\left(t\right)\right)-\delta S\left(t\right)e^{-mS\left(t\right)}}{{\left(1+\delta S\left(t\right)\right)}^2}\right]\\ & -{\lambda }_2\left(t\right)\beta e^{-mS\left(t\right)}I\left(t\right)\left[\frac{\left(1-mS\left(t\right)\right)\left(1+\delta S\left(t\right)\right)-\delta S\left(t\right)e^{-mS\left(t\right)}}{{\left(1+\delta S\left(t\right)\right)}^2}\right]\\ & +{\lambda }_3\left(t\right)\left(\frac{\gamma }{{\left(1+kS\left(t\right)\right)}^2}+\phi +\mu +u_2\left(t\right)\right)-{\lambda }_4\left(t\right)\left(\frac{\gamma }{{\left(1+kS\left(t\right)\right)}^2}+\phi +u_2\left(t\right)\right),\\ {}_0{}^{C}D_t^{\alpha }{\lambda }_4\left(t\right)=-\frac{\partial H\left(t\right)}{\partial R\left(t\right)}& ={\lambda }_4\left(t\right)\mu .\end{array}\right.$$

Based on the optimality condition, the differentiation of Equation (20) in relation to $u_1\left(t\right)$ and $u_2\left(t\right)$ is obtained as follows:

$$\begin{array}{l}{\left.\frac{\partial H\left(t\right)}{\partial u_1\left(t\right)}\right|}_{u_1\left(t\right)=u_1^{*}}=2{\varphi }_1{u}_1^{*}-{\lambda }_2\left(t\right)L^{*}+{\lambda }_4\left(t\right)L^{*}=0,\\ {\left.\frac{\partial H\left(t\right)}{\partial u_2\left(t\right)}\right|}_{u_2\left(t\right)=u_2^{*}}=2{\varphi }_2{u}_2^{*}-{\lambda }_3\left(t\right)S^{*}+{\lambda }_4\left(t\right)S^{*}=0,\end{array}$$

(23)

The optimal control is then obtained as follows:

$$u_1^{*}=\frac{\left({\lambda }_2\left(t\right)-{\lambda }_4\left(t\right)\right)L^{*}}{2{\varphi }_1},u_2^{*}=\frac{\left({\lambda }_3\left(t\right)-{\lambda }_4\left(t\right)\right)S^{*}}{2{\varphi }_2}.$$

(24)

By combining the attributes of a bounded set $U$, the intervals of $u_1^{*}$ and $u_2^{*}$ are obtained as follows:

$$\begin{array}{l}{u}_1^{*}=\min \left\{\max \left\{\frac{\left({\lambda }_2-{\lambda }_4\right)L^{*}}{2{\varphi }_1},0\right\},u_1^{\max }\right\},\\ u_2^{*}=\min \left\{\max \left\{\frac{\left({\lambda }_3-{\lambda }_4\right)S^{*}}{2{\varphi }_2},0\right\},u_2^{\max }\right\}.\end{array}$$

(25)

□

6. ILSR Rumor Model with Fractional Stochastic

Due to the inherent volatility that occurs during times of crisis, rapid changes in government policies and media coverage may occur. Various noise environments unavoidably affect the propagation of rumors. A crucial component of Brownian motion is symmetry. Zhang et al. applied significant discoveries that came from using the symmetry approach to backward stochastic differential equations [58]. As far as we know, there are few mathematical models of rumor propagation considering both fractional-order operators and stochastic processes simultaneously. Now, white noise is added to the rightmost side of each equation in the Fractional-Order System (5) to transform it into a Fractional Stochastic System. We consider all of the modeling equations in Model (5) and integrate white noise terms that exhibit Wiener process features in the modified fractional-order stochastic ILSR model. These modifications can render modeling equations that describe rumor propagation with significantly more precision, as shown below:

$$\left\{\begin{array}{l}{}_0{}^{C}D_t^{\alpha }I\left(t\right)=\Lambda -\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\mu I\left(t\right)+{\sigma }_1\mu I\left(t\right)\frac{d{B}_1\left(t\right)}{dt},\\ {}_0{}^{C}D_t^{\alpha }L\left(t\right)=\frac{\beta I\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\epsilon L\left(t\right)-\mu L\left(t\right)+{\sigma }_2\mu L\left(t\right)\frac{d{B}_2\left(t\right)}{dt},\\ {}_0{}^{C}D_t^{\alpha }S\left(t\right)=\epsilon L\left(t\right)-\frac{\gamma S\left(t\right)}{1+kS\left(t\right)}-\phi S\left(t\right)-\mu S\left(t\right)+{\sigma }_3\mu S\left(t\right)\frac{d{B}_3\left(t\right)}{dt},\\ {}_0{}^{C}D_t^{\alpha }R\left(t\right)=\frac{\gamma S\left(t\right)}{1+kS\left(t\right)}+\phi S\left(t\right)-\mu R\left(t\right)+{\sigma }_4\mu R\left(t\right)\frac{d{B}_4\left(t\right)}{dt},\end{array}\right.$$

(26)

where ${\sigma }_i,i=1,2,3,4$ are the non-negative values of the intensities of Brownian motions; $B_i\left(t\right),i=1,2,3,4$ are white noise processes.

The fractional-order Lyapunov stability method can be employed to examine Model (26) for fractional stochastic stability at the rumor-demise equilibrium point $E^0$ as follows:

$$\begin{array}{l}I\left(t\right){}_0{}^{C}D_t^{\alpha }I\left(t\right)+L\left(t\right){}_0{}^{C}D_t^{\alpha }L\left(t\right)+S\left(t\right){}_0{}^{C}D_t^{\alpha }S\left(t\right)+R\left(t\right){}_0{}^{C}D_t^{\alpha }R\left(t\right)\\ =\Lambda I\left(t\right)-\frac{\beta I^2\left(t\right)S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\mu I^2\left(t\right)+{\sigma }_1\mu I^2\left(t\right)\frac{d{B}_1\left(t\right)}{dt}+\frac{\beta I\left(t\right)S\left(t\right)L\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}\\ -\epsilon L^2\left(t\right)-\mu L^2\left(t\right)+{\sigma }_2\mu L^2\left(t\right)\frac{d{B}_2\left(t\right)}{dt}+\epsilon L\left(t\right)S\left(t\right)-\phi S^2\left(t\right)-\frac{\gamma S^2\left(t\right)}{1+kS\left(t\right)}-\mu S^2\left(t\right)\\ +{\sigma }_3\mu S^2\left(t\right)\frac{d{B}_3\left(t\right)}{dt}+\phi S\left(t\right)R\left(t\right)+\frac{\gamma S\left(t\right)R\left(t\right)}{1+kS\left(t\right)}-\mu R^2\left(t\right)+{\sigma }_4\mu R^2\left(t\right)\frac{d{B}_4\left(t\right)}{dt}.\\ =\Lambda I\left(t\right)+\frac{\beta I\left(t\right)S\left(t\right)L\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}+I^2\left(t\right)\left[-\frac{\beta S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\mu +{\sigma }_1\mu \frac{d{B}_1\left(t\right)}{dt}\right]\\ +L^2\left(t\right)\left(-\epsilon -\mu +{\sigma }_2\mu \frac{d{B}_2\left(t\right)}{dt}\right)+\epsilon L\left(t\right)S\left(t\right)+S^2\left(t\right)\left(-\phi -\frac{\gamma }{1+kS\left(t\right)}-\mu +{\sigma }_3\mu \frac{d{B}_3\left(t\right)}{dt}\right)\\ +\phi S\left(t\right)R\left(t\right)++\frac{\gamma S\left(t\right)R\left(t\right)}{1+kS\left(t\right)}+R^2\left(t\right)\left(-\mu +{\sigma }_4\mu \frac{d{B}_4\left(t\right)}{dt}\right)\le 0.\end{array}$$

The fractional stochastic Model (26) is stable at $0$ under the following conditions:

$$\begin{array}{l}-\frac{\beta S\left(t\right)e^{-mS\left(t\right)}}{1+\delta S\left(t\right)}-\mu +{\sigma }_1\mu \frac{d{B}_1\left(t\right)}{dt}\le 0,\\ -\epsilon -\mu +{\sigma }_2\mu \frac{d{B}_2\left(t\right)}{dt}\le 0,\\ -\phi -\frac{\gamma }{1+kS\left(t\right)}-\mu +{\sigma }_3\mu \frac{d{B}_3\left(t\right)}{dt}\le 0,\\ -\mu +{\sigma }_4\mu \frac{d{B}_4\left(t\right)}{dt}\le 0.\end{array}$$

(27)

The main aim of this section is to demonstrate the combination of white noise and fractional-order operators and evaluate the performance of the resulting model.

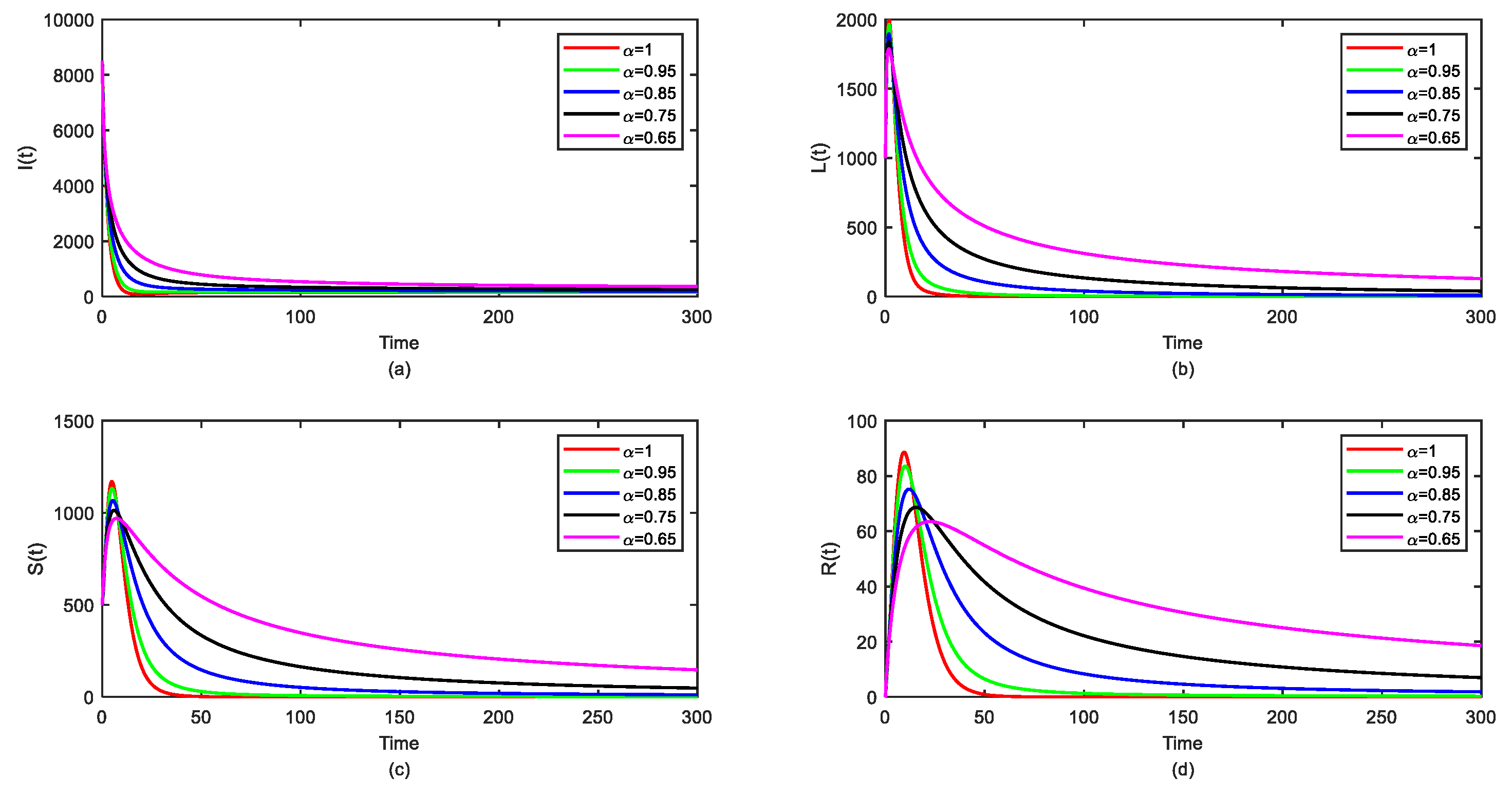
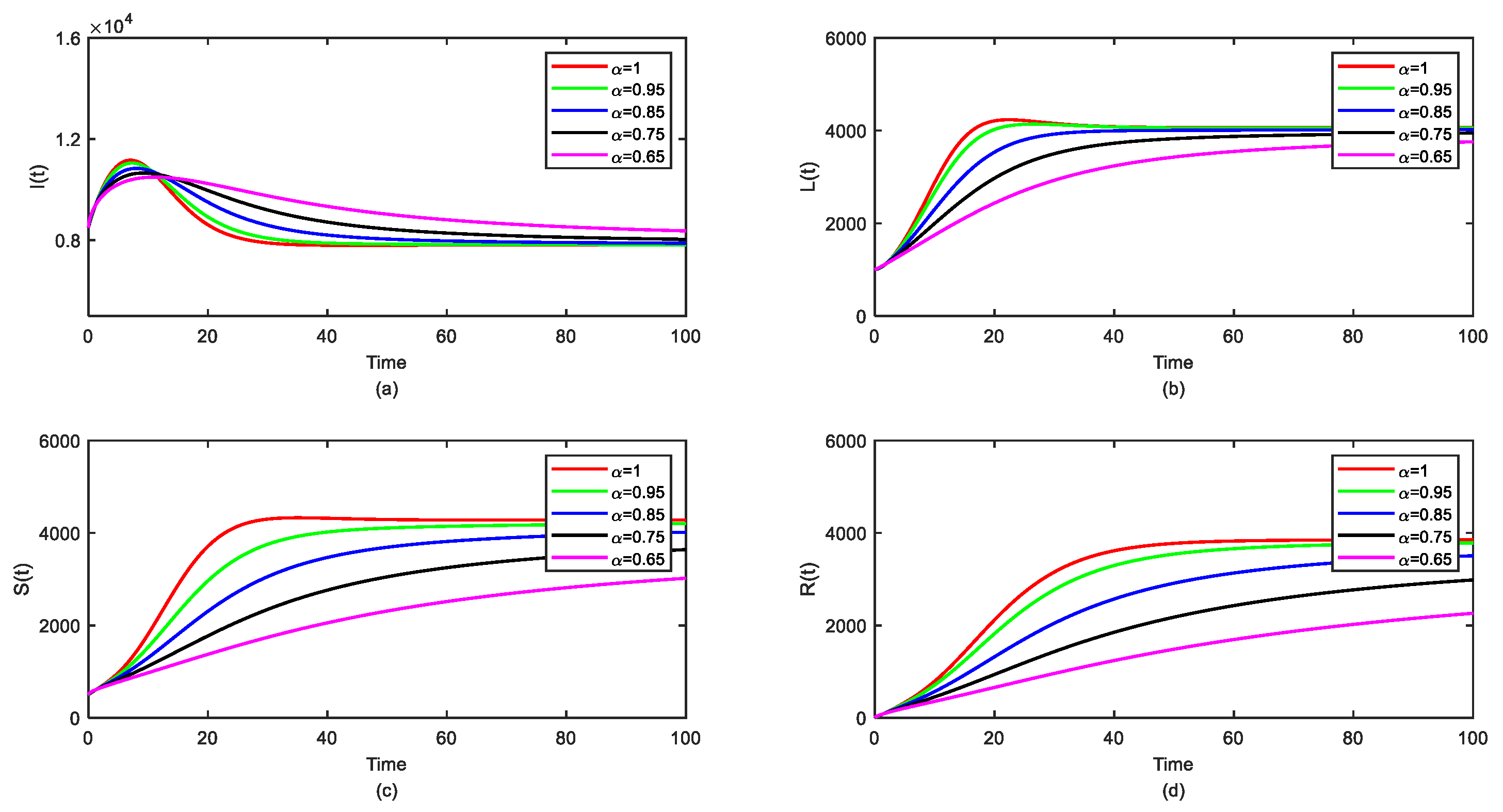
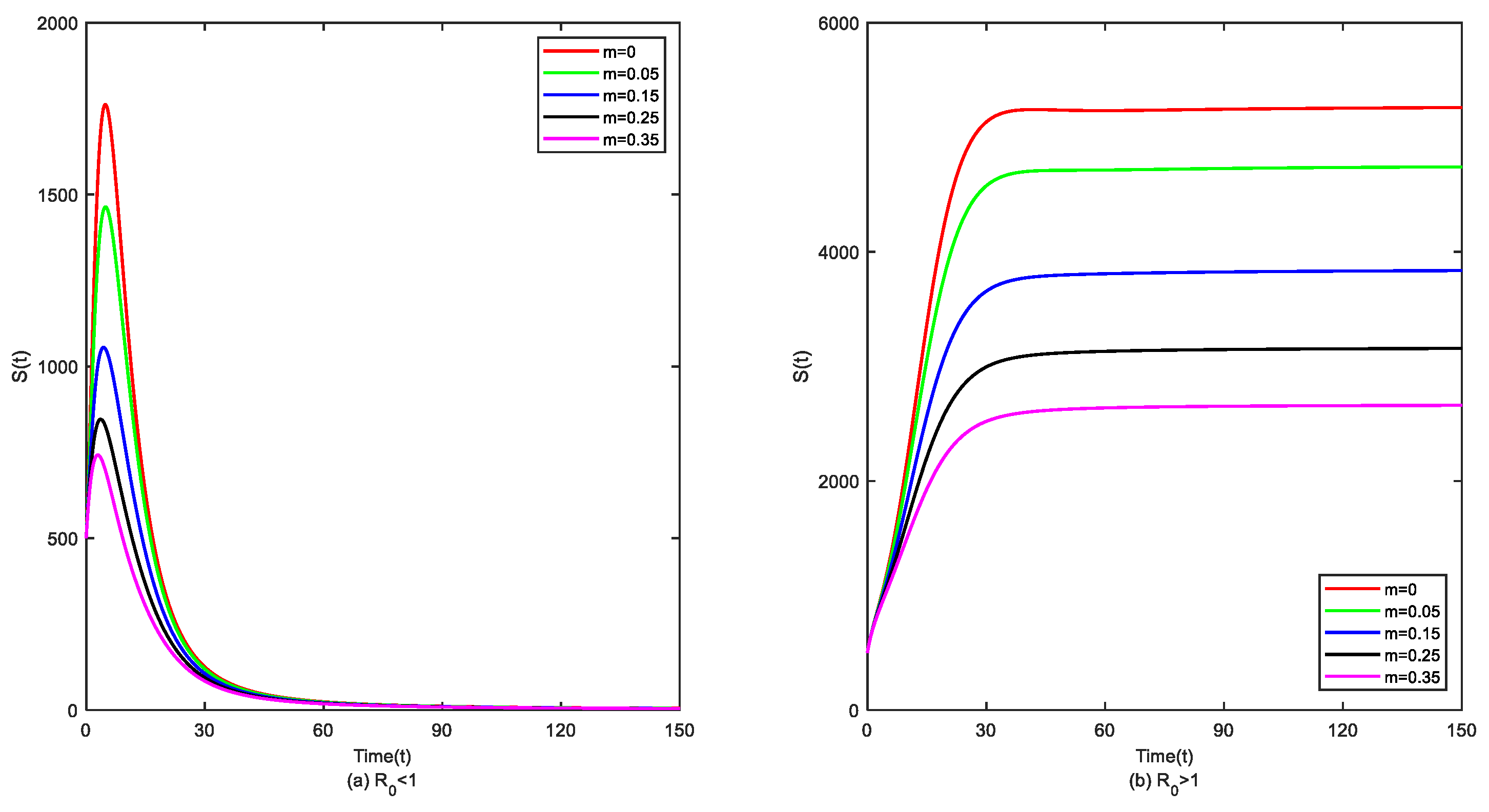
7. Sensitivity Analysis and Numerical Simulation

7.1. Sensitivity Analysis

In this section, we will analyze the sensitivity of the parameters in the fractional rumor model. The following conditions are satisfied

$$\begin{array}{l}{A}_{\beta }=\frac{\beta }{R_0}\frac{\partial R_0}{\partial \beta }=1>0,\\ A_{\epsilon }=\frac{\epsilon }{R_0}\frac{\partial R_0}{\partial \epsilon }=\frac{{\mu }^2\left(\gamma +\phi +\mu \right)}{\epsilon \left(\epsilon +\mu \right)}>0,\\ A_{\gamma }=\frac{\gamma }{R_0}\frac{\partial R_0}{\partial \gamma }=-\frac{\mu \gamma \left(\epsilon +\mu \right)}{\gamma +\phi +\mu }<0,\\ A_{\sigma }=\frac{\phi }{R_0}\frac{\partial R_0}{\partial \phi }=-\frac{\mu \phi \left(\epsilon +\mu \right)}{\gamma +\phi +\mu }<0,\end{array}$$

(28)

In conclusion, $\beta$ and $\epsilon$ are sensitive, and all the remaining parameters with the reproduction number are not sensitive. Sensitivity analysis shows that it is possible to reduce the rumor contact rate $\beta$ and transfer rate $\epsilon$, thus lowering the value of $R_0$.

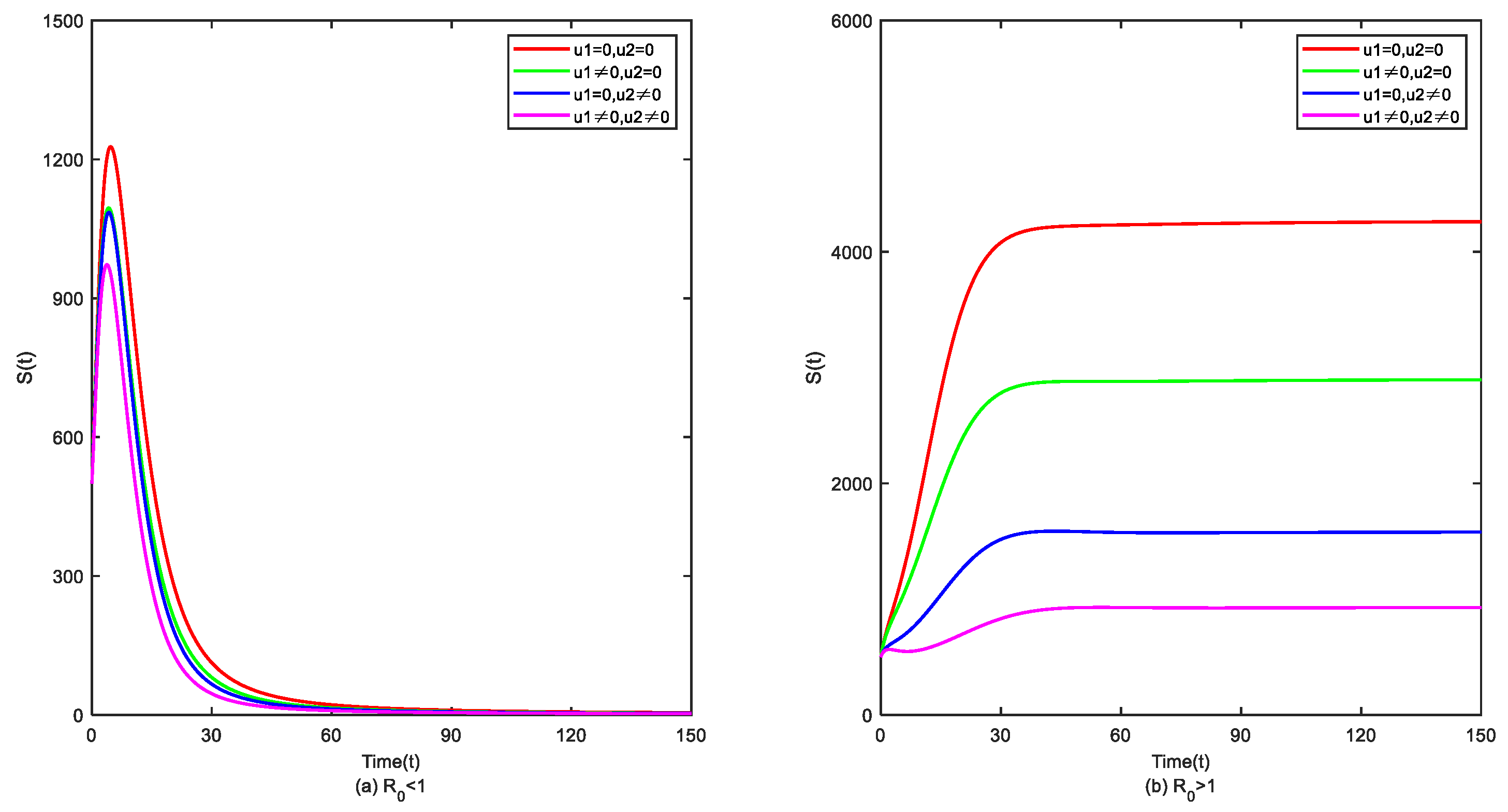
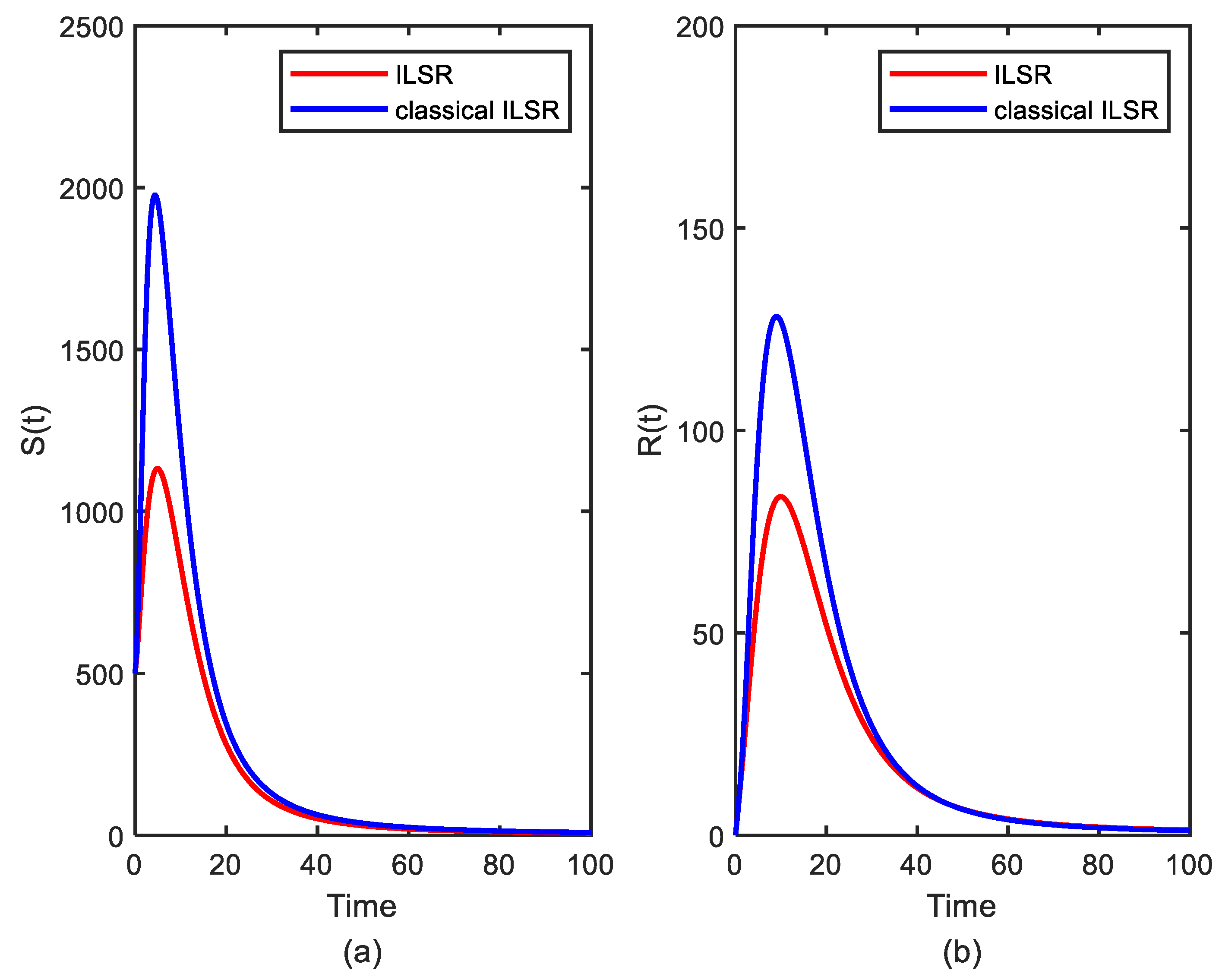
7.2. Numerical Simulation

The MATLAB program is used in this section and the fractional Euler method is applied to investigate the behavior of fractional-order differential equations. The version of MATLAB is R2021a. The fractional Euler method [59] is employed to solve fractional-order differential equations and obtain discretized equations, as described below:

$$\begin{array}{l}I\left(t_p\right)=I\left(t_0\right)+\frac{h^{\alpha }}{\Gamma \left(\alpha +1\right)}{\displaystyle \sum _{j=0}^{p-1}{c}_{j,p}\left[\Lambda -\frac{\beta I\left(t_j\right)S\left(t_j\right)}{1+bS\left(t_j\right)}-\frac{\delta I\left(t_j\right)M\left(t_j\right)}{k+M\left(t_j\right)}-\left(\eta +\mu \right)I\left(t_j\right)\right]},\\ S\left(t_p\right)=S\left(t_0\right)+\frac{h^{\alpha }}{\Gamma \left(\alpha +1\right)}{\displaystyle \sum _{j=0}^{p-1}{c}_{j,p}\left[\frac{\beta I\left(t_j\right)S\left(t_j\right)}{1+bS\left(t_j\right)}+\frac{\delta I\left(t_j\right)M\left(t_j\right)}{k+M\left(t_j\right)}-\left(\gamma +\epsilon +\mu \right)S\left(t_j\right)\right]},\\ C\left(t_p\right)=C\left(t_0\right)+\frac{h^{\alpha }}{\Gamma \left(\alpha +1\right)}{\displaystyle \sum _{j=0}^{p-1}{c}_{j,p}\left[\gamma S\left(t_j\right)-\left(\omega +\mu \right)C\left(t_j\right)\right]},\\ R\left(t_p\right)=R\left(t_0\right)+\frac{h^{\alpha }}{\Gamma \left(\alpha +1\right)}{\displaystyle \sum _{j=0}^{p-1}{c}_{j,p}\left[\eta I\left(t_j\right)+\epsilon S\left(t_j\right)+\omega C\left(t_j\right)-\mu R\left(t_j\right)\right]},\\ M\left(t_p\right)=M\left(t_0\right)+\frac{h^{\alpha }}{\Gamma \left(\alpha +1\right)}{\displaystyle \sum _{j=0}^{p-1}{c}_{j,p}\left[m_0+\rho M\left(t_j\right)-\xi M\left(t_j\right)\right]},\end{array}$$

for $p=1,2,\dots ,N$ where the $c_{j,p}={\left(p-j\right)}^{\alpha }-{\left(p-1-j\right)}^{\alpha }.$ The fractional Euler method is employed for the subsequent numerical solutions of the fractional-order differential equations.

In Refs. [6,15], the initial conditions are used to define $\Lambda =0.3,\beta =0.1,\delta =0.1,$ $m=0.1,\mu =0.2,\epsilon =0.2,\gamma =0.01,k=1,\phi =0.02$, and the different derivative order $0<\alpha \le 1$. The basic reproduction number is $R_0=0.33<1$. Figure 3 presents depictions of the evolution of (a) Ignorants, (b) Latents, (c) Spreaders, and (d) Removers in a rumor-eliminating case for Model (5). In this case, the order of the derivative is given by $\alpha =0.65,0.75,0.85,0.95,1$. The initial number of individuals is provided by $\left(I_0,L_0,S_0,R_0\right)=\left(8500,1000,500,0\right).$ The graphs provide evidence of the convergence of the solutions toward the analytical steady-state solution of the system in the rumor-demise case in Figure 3. With the decrease in the order $\alpha$, the convergence rate of the rumor propagation curve slows down and eventually tends to stabilize, which shows the memory effect. From the perspective of public opinion transmission, it suggests that such rumors tend to persist for a longer duration. Further, it exhibits abnormal propagation at a lower order $\alpha$, which is characterized by an explosively fast spread in the initial stage and a slower spread in the subsequent stage in Figure 3c. When the order is $\alpha =1$, the fractional-order differential equation is converted into an integer-order one, which leads to the absence of the memory effect.

The initial parameters are given with the parameters $\Lambda =2,\beta =0.08,\delta =0.1,$ $m=0.1,\mu =0.1,\epsilon =0.2,\gamma =0.1,k=0.1,\phi =0.02,$ and for varying degrees of derivative order $0<\alpha \le 1$. The calculation result of the basic reproduction number is $R_0=4.60>1$. The initial number of individuals are determined using the same settings as above. The results obtained from simulating the spread of rumors are shown in Figure 4. The different convergence rates of rumor propagation depend on the value of the order $\alpha$. The larger the order $\alpha$, the more rapidly the curve approaches stability in the rumor-permanence case. Therefore, continuous and timely popularization of scientific knowledge and refutation of rumors are necessary to suppress rumors.

The factor of media reports affects System (5) with different $m$ for $\alpha =0.95$ in Figure 5. Other parameters are shown as mentioned above, $R_0=0.33$ and $R_0=4.60$. Obviously, the larger the value of parameter $m$, the smaller the peak value of rumor-spreading. This implies that the higher the level of media reports, the wider the range of influence on rumor propagation. The media reports, whether in the rumor-demise case or the rumor-permanence case, can effectively suppress rumor propagation by spreading effective refutations and popularizing scientific knowledge.

The factor of the nonlinear inhibition mechanism in System (5) with different $k$ for $\alpha =0.95$ is shown in Figure 6. Other parameters are the same as mentioned above, $R_0=0.33$ and $R_0=4.60$. It can be inferred that the larger $k$ is, the higher the peak value of Spreaders $S\left(t\right)$ tends to be both in the rumor-demise case and the rumor-permanence case. Hence, we can adjust the parameter $k$ to minimize the impacts of rumor propagation, especially in the rumor-permanence case in Figure 6b.

To demonstrate the validity of optimal control, we selected the same parameters as mentioned above, $R_0=0.33$ and $R_0=4.60$. As illustrated in Figure 7, which shows the evolutions of rumor under various control strategies, we find that the evolutions of Spreaders who are under control, $u_1\ne 0,u_2\ne 0$, are significantly greater than those without control and those with single control, $u_1\ne 0$ or $u_2\ne 0$, respectively. Furthermore, while System (5) was under control, the rumor was also dispelled quickly even for $\alpha =0.95$ as shown in Figure 7a, incorporating the memory effect. This indicates that properly optimized controls can effectively restrict rumor propagation.

For the numerical simulation of the Fractional Stochastic System (26), the value of the parameter is defined in Figure 3. Rumor-demise equilibrium $E^0$ of the Model (5) exhibits both local and global asymptotic stability in the deterministic part. All parameters are denoted as mentioned above, $R_0=0.33$. It considers ${\sigma }_1={\sigma }_2={\sigma }_3=$ ${\sigma }_4=6.2$ to be the values of the white noise intensities. Figure 8a shows that the Fractional Stochastic System (26) is unstable at the rumor-demise equilibrium point. Additionally, if ${\sigma }_1={\sigma }_2={\sigma }_3={\sigma }_4=0.8$, then Figure 8b shows that the Fractional Stochastic System (26) is asymptotically mean-square stable around the rumor-demise point. The numerical simulation of the Fractional Stochastic System (26) indicates that the system will stay stable as long as the intensities of the minor fluctuations stay below a certain threshold value. In contrast, the system becomes unstable if the intensities exceed a certain threshold value, even though it is originally stable, which is consistent with Ref. [60]. Therefore, external disturbances play a significant role in rumor propagation as they might alter its stability.

The comparison model takes into account the ILSR model without considering the saturated incidence, media reports, and nonlinear inhibition mechanism while keeping other parameters unchanged. Refs. [51,52] refers to this as classical ILSR. From Figure 9, we can easily observe the evolutions of $S\left(t\right)$ and $R\left(t\right)$ over time when it satisfies $R_0=0.33<1,\alpha =0.95$. The solid red line and the solid blue line depicted in Figure 9a are compared in Figure 9. The peak value of Spreaders and Removers in ILSR is lower compared to that in classical ILSR. Namely, the scale of rumor propagation has decreased significantly. The presence of media reports and nonlinear inhibition mechanisms can significantly affect the scale of rumor propagation, which is consistent with the above conclusions.

Finally, a model application in an actual situation is presented to verify the model that has been suggested. We examine the platforms of WeChat, MicroBlog, and Network Media about “Tesla’s booth at the Shanghai Auto Show is suspected to be a drive’s right” [61] as the data source for simulation. Then, the number of rumor propagations for a period of 200 h between 20 April to 23 April is fetched. All parameters are denoted as mentioned above, $R_0=0.33$. The appropriate case is fitted to the Model (5) with real data in Figure 10. The simulation results are consistent with real data, accurately reflecting the evolution of Spreaders $S\left(t\right)$. And the most accurate representation of the rumor spread is $\alpha =0.75$. The results demonstrate that the rumor propagation could be precisely captured, which is quite consistent with the proposed model.

8. Conclusions

In this study, the deterministic and stochastic fractional-order ILSR rumor propagate model incorporating media reports and a nonlinear inhibition mechanism is proposed. The presence of positive solutions was extensively confirmed, and the equilibrium states were identified for both the rumor-demise equilibrium and the rumor-permanence equilibrium. The rumor-demise equilibrium $E^0$ is locally asymptotically stable if $R_0<1$. And the unique rumor-permanence equilibrium $E^{*}$ exists under certain conditions and is locally asymptotically stable if $R_0>1$. Moreover, the impact of media reports and the nonlinear inhibition mechanism are fully discussed. Furthermore, we conducted an examination of an optimal control strategy for the rumor propagation model. Finally, we confirmed the previous theoretical investigations by conducting various numerical simulations. It was confirmed that rumor propagation can be effectively prevented by employing media reports and control strategies, which lead to a significant improvement in reducing the risk of rumor-spreading. Then, the deterministic fractional-order system was transformed into the fractional stochastic system combined with white noise. The investigation focuses on the dynamic behavior exhibited by the fractional stochastic model around the rumor-demise equilibrium. The system becomes unstable if the environmental fluctuations are large enough, even though it is originally stable. Again, introducing the model of classical ILSR demonstrates the consistency of the above conclusions. Further, combined with real data, the platform data are used to demonstrate the availability of the proposed model. In future studies, the effects of time delay and denial may be extended under complex networks in a fractional-order system.