A Geometric Approach to the Sundman Transformation and Its Applications to Integrability

Abstract

A geometric approach to the integrability and reduction of dynamical systems, both when dealing with systems of differential equations and in classical physics, is developed from a modern perspective. The main ingredients of this analysis are infinitesimal symmetries and tensor fields that are invariant under the given dynamics. A particular emphasis is placed on the existence of alternative invariant volume forms and the associated Jacobi multiplier theory, and then the Hojman symmetry theory is developed as a complement to the Noether theorem and non-Noether constants of motion. We also recall the geometric approach to Sundman infinitesimal time-reparametrisation for autonomous systems of first-order differential equations and some of its applications to integrability, and an analysis of how to define Sundman transformations for autonomous systems of second-order differential equations is proposed, which shows the necessity of considering alternative tangent bundle structures. A short description of alternative tangent structures is provided, and an application to integrability, namely, the linearisability of scalar second-order differential equations under generalised Sundman transformations, is developed.

1. Introduction: The Meaning of Integrability by Quadratures

Obtaining the solutions of autonomous systems of differential equations appearing in many physical problems is not an easy task. In geometric terms, they are represented by vector fields, whose integral curves are the solutions of the system.

In fact, in order to study an autonomous system of first-order differential equations,

$$\frac{d{x}^i}{dt}=X^i(x^1,\dots ,x^n),i=1,\dots ,n,$$

(1)

use is made of symmetry and reduction techniques [1]. The main parts of these techniques are based on the transformation of the given system into a related one. From a local point of view, sometimes, transformations are seen as coordinate changes (passive point of view). Or, more explicitly, a diffeomorphism $F:M\to M$ of a differentiable manifold changes each local chart $(U,\varphi )$ into a new one $(F\left(U\right),\varphi \circ F^{-1})$.

Note that under a transformation of coordinates,

$${\overline{x}}^i={\phi }^i(x^1,\dots ,x^n)⟺x^i={\psi }^i({\overline{x}}^1,\dots ,{\overline{x}}^n),i=1,\dots ,n,$$

the given system becomes

$$\frac{d{\overline{x}}^i}{dt}={\overline{X}}^i({\overline{x}}^1,\dots ,{\overline{x}}^n),i=1,\dots ,n,$$

with

$${\overline{X}}^i({\overline{x}}^1,\dots ,{\overline{x}}^n)=\frac{\partial {\phi }^i}{\partial x^j}{X}^j\left(\psi \left(({\overline{x}}^1,\dots ,{\overline{x}}^n)\right)\right),$$

where, on the right-hand side, each $x^i$ in the function $X^j$ is replaced by its value in terms of $({\overline{x}}^1,\dots ,{\overline{x}}^n)$, i.e., $x^i={\psi }^i({\overline{x}}^1,\dots ,{\overline{x}}^n)$, and summation on repeated indices is understood. This shows that the functions $X^i$ transform as the components of a vector field X on an n-dimensional manifold. The solutions of the system (1) are then integral curves of such a vector field.

In order to find their solutions, i.e., the flow of the vector fields, as in a generic case, there is no way of writing them in an explicit way, i.e., using fundamental functions, and we are happy if, at least, we can express the solutions in terms of quadratures. More specifically, integrability by quadratures means that one can determine the solutions (i.e., the flow of X) by means of a finite number of algebraic operations (including inversion of functions) and the quadratures of some functions [2].

The characterisation of integrable systems admitting such a type of solution has received a lot of attention, and the answer is always based on the use of Lie algebras of vector fields containing the given one [2,3,4]. In order to study such systems, use is made of symmetry and reduction techniques. The knowledge of some particular solutions of them or related systems may be useful. But symmetry and constants of motion emerge from the existence of compatible geometric structures provided by special tensor fields.

Both concepts, reduction and integrability, appear very often in physics and mathematics and with very different meanings. For instance, students in physics relate the reduction process to infinitesimal symmetries or constants of motion, generally in the framework of Lagrangian or Hamiltonian mechanics, because several reductions in the context of symplectic geometry are well known. Note, however, that reduction processes can be developed in a more general framework and need not be related to symmetry properties, but these only aim to find simpler solvable systems providing at least partial information on the solution of the original problem. The existence of compatible geometric structures on M provided by special tensor fields is also very useful.

The problems in which reduction processes are relevant are the following ones:

• Given a problem that is difficult to solve, we can look for related simpler problems whose solutions provide at least partial information on those of the first one.
• Sometimes, we find geometric structures difficult to handle, for instance, because they have some kind of degeneracy. We then look for a related structure of the same kind that is easier to manage, for instance, a nondegenerate one.
• When the original problem admits some geometric structures, then the reduction procedure tries to preserve such structures.

These are the types of problems we are going to deal with. It is remarked that there is no systematic way of selecting the related reduced systems, and sometimes, there are different possibilities. Of course, in order for the method to be efficient, we should have, in advance, some simple problems for which we know the solutions.

The problem to be analysed here is that of (systems of) first-order differential equations. The higher-order case can be related to a first-order one.

In principle, one tends to assume that a system with fewer unknown variables or a lower-order differential equation is simpler than one with more unknown variables or a higher-order differential equation. The reducibility to a system solvable by quadratures is the final objective. Sometimes, the problem of reduction is related to the so-called coordinate separability.

Usually, reduction processes starting from linear systems may produce nonlinear interacting ones, which, from the physical viewpoint, means that interaction terms can be provided by reduction [5]. Conversely, given a nonlinear system, is it possible to obtain it as a reduction from a simpler linear one?

2. The Reduction of a System of Ordinary Differential Equations

If $F:M\to N$ is a differentiable map, the vector field $X\in \mathfrak{X}\left(M\right)$ is F-related to the vector field $Y\in \mathfrak{X}\left(N\right)$ if, for each point $p\in M$, $F_{\ast p}\left(X_p\right)=Y_{F\left(p\right)}$, i.e., $TF\circ X=Y\circ F$. We say that X is F-projectable. The following diagram is commutative:

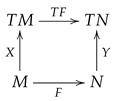
Note that this implies that if $c:I\to M$ is an integral curve of X, then $F\circ c$ is an integral curve of Y (see, e.g., [5]).

The reduction of the dynamics given by the vector field $X\in \mathfrak{X}\left(M\right)$ means finding a manifold N, a differentiable map $F:M\to N$ and an F-related vector field $Y\in \mathfrak{X}\left(N\right)$. The integral curves of Y are F-projections of the integral curves of X. Another problem remains: the reconstruction of the integral curves of $X\in \mathfrak{X}\left(M\right)$ from the integral curves of $Y\in \mathfrak{X}\left(N\right)$.

In the reduction process, the cases to be considered are either when $i:N\to M$ is an immersed submanifold of the n-dimensional manifold M or when $F:M\to N$ is a surjective submersion.

(a) In the first case, the reduction implies that $X_{\left|i\right(N)}$ must be tangent to $i\left(N\right)$, and therefore, there exists a vector field $\overline{X}$ on N such that it is i-related to X. Then, the integral curves of $\overline{X}$ provide us with the integral curves of X. We can suppose that the $(n-k)$-submanifold N is (at least locally) defined by k functions ${\Phi }_1,\dots ,{\Phi }_k$, which should be first integrals for X because of the assumed tangency condition. Note that only some integral curves of X will be obtained in this way, and we need a family of such submanifolds depending on k parameters in order to recover all integral curves of $X\in \mathfrak{X}\left(M\right)$.

This procedure is very commonly used in mechanics: under very general conditions, determining k functionally independent constants of motion reduces the original problem to another problem involving only $(n-k)$ variables but depending on k parameters.

(b) Finding a manifold N and a surjective submersion $F:M\to N$ such that X is a projectable vector field is not an easy task. The map F defines an equivalence relation on M, and N is the space of equivalence classes. The starting point may be the equivalence relation, and then F is the projection map.

Usually, one considers a transformation Lie group G of M that is a symmetry group for X and the equivalence relation associated with the action of G on M: we denote the space of orbits by N, assumed to be a differentiable manifold, with the function F being the natural projection of each element of M on its orbit. The symmetry condition implies that X is a projectable vector field. In this way, the symmetry condition of X is incorporated into the reduction process.

In other situations, the equivalence relation is defined by a foliation (involutive distribution), and the equivalence classes are the leaves. The set of leaves is assumed to have a manifold structure. If the original system has an invariance group, we can consider invariant foliations in such a way that the leaves are preserved.

The above reduction procedures can be used in an iterative way.

In summary, there are two main techniques in the process of solving the system:

• The determination of first integrals for X: First integrals provide us with foliations such that the vector field X is tangent to the leaves, and in this way, the problem reduces to that of a family of lower-dimensional problems, one on each leaf.
• Search for symmetries of the vector field X: The knowledge of infinitesimal groups of symmetries of the vector field (i.e., of the system of differential equations) suggests that we use adapted local coordinates, with the system then decoupling into lower-dimensional subsystems.

More specifically, the knowledge of r functionally independent (i.e., such that $d{F}_1\wedge \cdots \wedge d{F}_r\ne 0$) first integrals, $F_1,\dots ,F_r$, allows us to reduce the problem to that of a family of vector fields ${\tilde{X}}_c$, with $c\in {\mathbb{R}}^r$, defined on the $n-r$-dimensional submanifolds $M_c$ given by the level sets of the vector function of rank r, $(F_1,\dots ,F_r):M\to {\mathbb{R}}^r$.

Of course, the best situation is when $r=n-1$: the leaves are one-dimensional, giving us the solutions to the problem, up to a reparametrisation.

There is another way to reduce the problem. Given an infinitesimal symmetry (i.e., a vector field Y such that $[Y,X]=0$) in a neighbourhood of a point where Y is different from zero, we can choose adapted coordinates, $(y^1,\dots ,y^n)$, for which Y is written as (Straightening out Theorem, see, e.g., [6])

$$Y=\frac{\partial }{\partial y^n}.$$

Then, the symmetry condition $[Y,X]=0$ implies that X has the form

$$X={\overline{f}}^1(y^1,\dots ,y^{n-1})\frac{\partial }{\partial y^1}+\dots +{\overline{f}}^{n-1}(y^1,\cdots ,y^{n-1})\frac{\partial }{\partial y^{n-1}}+{\overline{f}}^n(y^1,\dots ,y^{n-1})\frac{\partial }{\partial y^n},$$

and its integral curves are obtained by solving the system

$$\left\{\begin{array}{ccc}{\displaystyle \frac{d{y}^i}{dt}}& =& {\overline{f}}^i(y^1,\dots ,y^{n-1}),i=1,\dots ,n-1,\hfill \\ {\displaystyle \frac{d{y}^n}{dt}}& =& {\overline{f}}^n(y^1,\dots ,y^{n-1}).\hfill \end{array}\right.$$

We have reduced the problem to a subsystem involving only the first $n-1$ equations, and once this has been solved, the last equation is used to obtain the function $y^n\left(t\right)$ by means of one quadrature. Note that the new coordinates, $y^1,\dots ,y^{n-1}$, are first integrals for Y, and therefore, we cannot easily find such coordinates in a general case.

Moreover, the information provided by two different symmetry vector fields cannot be used simultaneously in the general case, because it is not possible to find local coordinates $(y^1,\dots ,y^n)$ such that

$$Y_1=\frac{\partial }{\partial y^{n-1}},Y_2=\frac{\partial }{\partial y^n},$$

unless $[Y_1,Y_2]=0$.

In terms of adapted coordinates for X, i.e., such that $X=\partial /\partial y^n$, the integration is immediate, the solution being

$$y^k\left(t\right)=y_0^k,k=1,\dots ,n-1,y^n\left(t\right)=y^n\left(0\right)+t.$$

This proves that the concept of integrability by quadratures depends on the choice of initial coordinates. In adapted coordinates, it is always integrable. However, it can be proved that when X is part of a family of vector fields satisfying appropriate conditions, it is integrable by quadratures for any choice of initial coordinates (see, e.g., [2,3]).

We also remark that the set ${\mathfrak{X}}_X\left(M\right)=\{Y\in \mathfrak{X}\left(M\right)\mid [Y,X]=0\}$ of infinitesimal symmetries of $X\in \mathfrak{X}\left(M\right)$ is an $\mathbb{R}$-linear space, and that the flows of such vector fields $Y\in {\mathfrak{X}}_X\left(M\right)$ preserve the set of integral curves of X.

Both constants of motion and infinitesimal symmetries can be used simultaneously if some compatibility conditions are satisfied. We can say that a system admitting $r<n-1$ functionally independent first integrals for X, $F_1,\dots ,F_r$, is integrable when we know that there are s commuting infinitesimal symmetries $Y_1,\dots ,Y_s$, with $r+s=n$, such that

$$[Y_a,Y_b]=0,a,b=1,\dots ,s,\mathrm{and}{Y}_a{F}_{\alpha }=0,\forall a=1,\dots ,s,\alpha =1,\dots ,r.$$

The first integrals determine an s-dimensional foliation, and the latter conditions mean that the restrictions of the s vector fields $Y_a$ to the leaves are tangent to such leaves.

Sometimes, we have additional geometric structures that are compatible with the dynamics. For instance, an interesting example to be studied in Section 4 is that of a symplectic structure $\omega$ on a $2n$-dimensional manifold M. Such a 2-form relates, by contraction, vector fields and 1-forms in a one-to-one manner. The vector fields $X_F$ associated with exact 1-forms $dF$ are said to be Hamiltonian vector fields. The compatibility of $\omega$ means that the vector field X is a Hamiltonian vector field $X=X_H$. The regular Poisson bracket defined by $\omega$ (i.e., $\{F_1,F_2\}=X_{F_2}{F}_1$) allows us to express the tangency conditions as

$$X_{F_b}{F}_a=\{F_a,F_b\}=0;$$

i.e., the first integral functions $F_a$ must be in involution, and the corresponding Hamiltonian vector fields commute. This leads to the particularly interesting Arnold–Liouville definition of (Abelian) complete integrability ($r=s=n$). The vector fields are $X_a=X_{F_a}$ and, for instance, $F_1=H$.

In summary, the problem of integrability by quadratures depends on determining, by quadratures, the necessary first integrals and infinitesimal symmetries and finding adapted coordinates, or, in other words, as shown in the next sections, finding a sufficient number of invariant tensors.

An appropriate set of infinitesimal symmetries of the vector field X provides constants of motion. More specifically, let $\{X_1,\dots ,X_d\}$ be a set of d vector fields that take linearly independent values at every point and that are infinitesimal symmetries of the dynamical vector field X. If they generate an involutive distribution (i.e., there exist functions ${f_{ij}}^k$ such that $[X_i,X_j]={f_{ij}}^k{X}_k$), then, for each triple of numbers $i,j,k$, the functions ${f_{ij}}^k$ are first integrals for X, i.e., $X\left({f_{ij}}^k\right)=0$. In fact, the Jacobi identity for the vector fields $X,X_i$, $X_j$, i.e.,

$$[[X,X_i],X_j]+[[X_i,X_j],X]+[[X_j,X],X_i]=0,$$

leads to

$$[[X_i,X_j],X]=0⟹[{f_{ij}}^k{X}_k,X]=-X\left({f_{ij}}^k\right)X_k=0.$$

Moreover, for any other index l, $X_l\left({f_{ij}}^k\right)$ is also a first integral for X, because as $X_l$ is a symmetry of X, then ${\mathcal{L}}_X\left({\mathcal{L}}_{X_l}\left({f_{ij}}^k\right)\right)={\mathcal{L}}_{X_l}\left({\mathcal{L}}_X\left({f_{ij}}^k\right)\right)=0$. The constants of motion so obtained are not functionally independent, but at least this proves the usefulness of finding these families of vector fields when looking for first integrals.

3. Invariant Tensor Fields and the Integrability of a Vector Field

The main point is that the integrability of a given vector field X on a manifold M is usually studied by means of its compatible geometric structures. Geometric structures are defined by tensor fields t, and they are said to be compatible with X when they are invariant under X, i.e., ${\mathcal{L}}_{X}t=0$.

As an example mentioned before, a function $F\in C^{\infty }\left(M\right)$ invariant under X defines a constant of motion, also called the first integral for X. The corresponding exact 1-form $dF$ defines an $(n-1)$-dimensional foliation (integrable distribution), and the restriction of the vector field X to each leaf is tangent to the leaf, thus defining a family of vector fields on lower-dimensional manifolds, which can be considered reduced systems. This property, where a first integral, i.e., an invariant function, can be used to reduce the integrability of the vector field to a family of lower-dimensional problems, is a particular example of a more general case: the mentioned role of tensor fields invariant under a vector field X on an n-dimensional manifold M in its integrability (see, e.g., [4]).

Another example that we have also considered is that of invariant vector fields $Y\in \mathfrak{X}\left(M\right)$, i.e., such that $Y\in {\mathfrak{X}}_X\left(M\right)=\{Y\in \mathfrak{X}\left(M\right)\mid [Y,X]=0\}$, then giving rise to infinitesimal symmetries of X, whose flows transform solutions into solutions. As the flows of such vector fields $Y\in {\mathfrak{X}}_X\left(M\right)$ preserve the set of integral curves of X, we can also consider a set of vector fields $Y\in \mathfrak{X}\left(M\right)$ whose flows preserve each integral curve of X up to reparametrisations; i.e., they preserve the one-dimensional distribution generated by X, and then the vector field Y is a symmetry of the one-dimensional distribution spanned by X: there exists a function $h\in C^{\infty }\left(M\right)$ such that $[Y,X]=hX$. Such a set of vector fields generating flows preserving the set of integral curves of X up to a reparametrisation is also a real linear space containing ${\mathfrak{X}}_X\left(M\right)$, usually denoted by

$${\mathfrak{X}}^X\left(M\right)=\{Y\in \mathfrak{X}\left(M\right)\mid [Y,X]=f_{Y}X\},f_Y\in C^{\infty }\left(M\right).$$

One can check that ${\mathfrak{X}}^X\left(M\right)$ is a real Lie algebra containing ${\mathfrak{X}}_X\left(M\right)$ as a real Lie subalgebra, but ${\mathfrak{X}}_X\left(M\right)$ is not an ideal in ${\mathfrak{X}}^X\left(M\right)$.

Moreover, if F is a first integral for X, then when Y is a symmetry of the vector field X or, more generally, of the one-dimensional distribution spanned by X, the function $Y\left(F\right)$ is also a first integral, because ${\mathcal{L}}_X\left(Y\left(F\right)\right)=Y\left({\mathcal{L}}_X\left(F\right)\right)-hX\left(F\right)=0$.

Strictly positive symmetric forms g on M invariant under $X\in \mathfrak{X}\left(M\right)$ imply that the given vector field is a Killing vector field whose integrability we have additional information on (see, e.g., [7]), while a nondegenerate closed 2-form $\omega$ on M is invariant under $X\in \mathfrak{X}\left(M\right)$, and such a vector field is a locally Hamiltonian vector field on the symplectic manifold $(M,\omega )$. This is a particularly interesting case that will be studied in the next section.

Later on, we will see several examples of how to find new first integrals when additional tensor fields enter the game. Of course, some invariant multivector fields are also interesting, but the case of Poisson bivector fields is particularly relevant. Differential forms that are invariant under X give rise to absolutely integral invariants, a theory developed by Poincaré in [8]. In particular, invariant 2-forms, for instance, the relevant case in the mechanics of symplectic forms, are very relevant in the study of the integrability of X, and Arnold–Liouville integrability is based on the existence of an appropriate invariant symplectic form.

We now remark that when we have a $(1,1)$-tensor field $\mathcal{R}$ invariant under X, it may be used as a generator of symmetry, in the sense that if Y is a symmetry of X, then ${\mathcal{L}}_X\mathcal{R}=0$ implies that ${\mathcal{L}}_X\left(\mathcal{R}\left(Y\right)\right)=0$, and in this sense, $\mathcal{R}$ generates symmetry; for instance, as X itself is a symmetry, the vector fields ${\mathcal{R}}^k\left(X\right)$, $k\in \mathbb{N}$, are infinitesimal symmetries, too.

Furthermore, if we know such an invariant (1,1)-tensor field $\mathcal{R}$ and choose a local basis of vector fields $\{X_1,\dots ,X_n\}$, then if the matrices A and B are the matrix representatives of $\mathcal{R}$ and ${\mathcal{L}}_X$ in such a basis, respectively, then the invariance condition ${\mathcal{L}}_X\mathcal{R}=0$ is written as

$$\dot{A}=[B,A],$$

(2)

where ${{\dot{A}}_i}^j$ denotes $X\left({A_i}^j\right)$, because if $\mathcal{R}\left(X_i\right)={A_i}^j{X}_j$ and ${\mathcal{L}}_X{X}_i={B_i}^j{X}_j$, as we have ${\mathcal{L}}_X\left[\mathcal{R}\left(X_i\right)\right]={\mathcal{L}}_X\left[{A_i}^j{X}_j\right]={\mathcal{L}}_X\left({A_i}^j\right)X_j+{A_i}^j{B_j}^k{X}_k,$ and $\mathcal{R}\left({\mathcal{L}}_X{X}_i\right)={B_i}^j{A_j}^k{X}_k,$ then, taking into account that the X-invariance of $\mathcal{R}$ is equivalent to ${\mathcal{L}}_X\left[\mathcal{R}\left(X_i\right)\right]=\mathcal{R}\left[{\mathcal{L}}_X\left(X_i\right)\right]$, we find that ${\mathcal{L}}_X\mathcal{R}=0$ is equivalent to ${\mathcal{L}}_X\left({A_i}^j\right)+{A_i}^k{B_k}^j={B_i}^k{A_k}^j$ and, therefore, to the matrix Equation (2), which is called the Lax equation [9,10,11]. Also, note that as the matrix representative of ${\mathcal{R}}^2$ is $A^2$ and ${\mathcal{L}}_X\mathcal{R}=0$ implies that ${\mathcal{L}}_X{\mathcal{R}}^k=0$, with $k\in \mathbb{N}$, we also have

$$\dot{A^k}=[B,A^k],k=1,\dots n.$$

(3)

The importance of these equations is that, as for any pair of matrices, the trace of the commutator is zero, and we have ${\displaystyle \frac{d}{dt}\mathrm{Tr}{A}^k=0}$, and consequently, a $(1,1)$-tensor field $\mathcal{R}$ invariant under X provides us with n constants of motion; in principle, not all of them are functionally independent, as indicated by the Hamilton–Cayley theorem. Another remark is that, as the coefficients of the characteristic equation $\det (A-\lambda I)=0$ can be reconstructed from the traces of powers of A (the Le Verrier method of determining the characteristic equation of a matrix; see, e.g., [12]), the roots of such a characteristic equation, the eigenvalues of A, are constants of motion.

The search for these invariant (1,1)-tensor fields $\mathcal{R}$ is not an easy task and used to come from the existence of alternative structures [5,13,14,15], with the associated constants of motion being called non-Noether constants of motion (see, e.g., [13,16,17]), but they may have a different origin [10,18]. We will come back to this point in Section 5.

Another interesting case is when there exists a volume form invariant under X. This case and an alternative method to find the first integrals associated with symmetries of a one-dimensional distribution spanned by the vector field X will be analysed in Section 5.

4. Invariant Symplectic Structures

We recall that $(M,\omega )$ is a symplectic manifold if M is a finite-dimensional differentiable manifold and $\omega$ is a nondegenerate 2-form that satisfies $d\omega =0$ (that is, $\omega \in Z^2\left(M\right)$). The dimension of M is necessarily even, $\dim M=2n$. General results can be found in reference textbooks, for instance [19,20]. By the nondegeneracy of $\omega$, we mean that for every point $u\in M$, the map ${\widehat{\omega }}_u:T_{u}M\to T_u^{\ast }M$, given by $⟨{\widehat{\omega }}_u\left(v\right),v^{\prime }⟩={\omega }_u(v,v^{\prime })$ with $v,v^{\prime }\in T_{u}M$, has a maximal rank, i.e., ${\left(\omega \right)}^{\wedge n}\ne 0$. Such a map $\widehat{\omega }$ is a base-preserving fibred map, and hence, it induces a mapping between the linear spaces of sections, which, with a slight abuse of notation, we will also write as $\widehat{\omega }:\mathfrak{X}\left(M\right)\to {\bigwedge }^1\left(M\right)$.

The following well-known result completely characterises these symplectic manifolds from the local point of view:

Theorem 1.

(Darboux) Around each point $u\in M$ with $\dim M=2n$, there is a local chart $(U,\varphi )$ such that if $\varphi =(q^1,\dots ,q^n;p_1,\dots ,p_n)$, then ${\omega |}_U=d{q}^i\wedge d{p}_i$.

Such coordinates are called Darboux coordinates.

Since closed and, in particular, exact 1-forms are distinguished elements in ${\bigwedge }^1\left(M\right)$, the corresponding vector fields are called locally Hamiltonian vector fields and Hamiltonian vector fields, respectively. If $H\in C^{\infty }\left(M\right)$, the Hamiltonian vector field $X_H$ associated with the Hamiltonian H is the unique vector field satisfying $\widehat{\omega }\left(X_H\right)=i\left(X_H\right)\omega =dH$. The set of Hamiltonian vector fields will be denoted by ${\mathfrak{X}}_{\mathrm{H}}(M,\omega )$, and that of locally Hamiltonian vector fields by ${\mathfrak{X}}_{\mathrm{LH}}(M,\omega )$, i.e., ${\mathfrak{X}}_{\mathrm{LH}}(M,\omega )={\widehat{\omega }}^{-1}\left(Z^1\left(M\right)\right)$ and ${\mathfrak{X}}_{\mathrm{H}}(M,\omega )={\widehat{\omega }}^{-1}\left(B^1\left(M\right)\right)$. Observe that ${\widehat{\omega }}^{-1}$ is an isomorphism of real vector spaces.

The Cartan homotopy identity, i.e., ${\mathcal{L}}_X\alpha =i\left(X\right)d\alpha +d\left(i\left(X\right)\alpha \right)$, for any $\alpha \in {\bigwedge }^p\left(M\right)$, shows that, given $X\in \mathfrak{X}\left(M\right)$, ${\mathcal{L}}_X\omega =0$ if and only if $i\left(X\right)\omega$ is a closed 1-form, i.e., $X\in {\mathfrak{X}}_{\mathrm{LH}}(M,\omega )$. In particular, ${\mathcal{L}}_{X_H}\omega =0$. In Darboux coordinates, the Hamiltonian vector field $X_H$ corresponding to the function H is given by

$$X_H=\frac{\partial H}{\partial p_i}\frac{\partial }{\partial q^i}-\frac{\partial H}{\partial q^i}\frac{\partial }{\partial p_i},$$

and therefore, the equations determining its integral curves are similar to Hamilton equations.

Note that if $X,Y\in {\mathfrak{X}}_{\mathrm{LH}}(M,\omega )$, the commutator $[X,Y]$ is a Hamiltonian vector field with the Hamiltonian $\omega (Y,X)$, because, from the relation $i\left(X\right){\mathcal{L}}_Y\alpha -{\mathcal{L}}_{Y}i\left(X\right)\alpha =i\left([X,Y]\right)\alpha$, valid for any form $\alpha$, we obtain

$$i\left([X,Y]\right)\omega =i\left(X\right){\mathcal{L}}_Y\omega -{\mathcal{L}}_{Y}i\left(X\right)\omega =-{\mathcal{L}}_{Y}i\left(X\right)\omega =-i\left(Y\right)d\left(i\left(X\right)\omega \right)-d\left(i\left(Y\right)i\left(X\right)\omega \right),$$

and then,

$$i\left(\right[X,Y\left]\right)\omega =-d\left(\omega \right(X,Y\left)\right).$$

(4)

Consequently, the set ${\mathfrak{X}}_{\mathrm{LH}}(M,\omega )$ is a Lie algebra, and ${\mathfrak{X}}_{\mathrm{H}}(M,\omega )$ is an ideal in ${\mathfrak{X}}_{\mathrm{LH}}(M,\omega )$.

As an important property, if $(M,\omega )$ is a symplectic manifold, we can define the Poisson bracket of two functions $F,G\in C^{\infty }\left(M\right)$ as being the function $\{F,G\}$ given by

$$\{F,G\}=\omega (X_F,X_G)=dF\left(X_G\right)=-dG\left(X_F\right).$$

(5)

In Darboux coordinates for $\omega$, the expression for $\{F,G\}$ is the usual one:

$$\{F,G\}=\left(\frac{\partial F}{\partial q^i}\frac{\partial G}{\partial p_i}-\frac{\partial F}{\partial p_i}\frac{\partial G}{\partial q^i}\right).$$

(6)

The aforementioned property (4) means that if $F,G\in C^{\infty }\left(M\right)$, then we have $d\{F,G\}=-i\left([X_F,X_G]\right)\omega$, i.e.,

$$[X_F,X_G]=X_{\{G,F\}}.$$

(7)

This Poisson bracket $\{·,·\}$ is a skew-symmetric $\mathbb{R}$–bilinear map on $C^{\infty }\left(M\right)$ such that it satisfies Jacobi’s identity as a consequence of $\omega$ being closed. In fact, if $F,G,H\in C^{\infty }\left(M\right)$,

$$\begin{array}{cc}\hfill \left(d\omega \right)(X_F,X_G,X_H)& =X_F\omega (X_G,X_H)-X_G\omega (X_F,X_H)+X_H\omega (X_F,X_G)\hfill \\ & -\omega ([X_F,X_G],X_H)+\omega ([X_F,X_H],X_G)-\omega ([X_G,X_H],X_F),\hfill \end{array}$$

and taking into account that $X_F\omega (X_G,X_H)=X_F\{G,H\}=\{\{G,H\},F\}$ and that $\omega ([X_F,X_G]$, $X_H)$ can also be rewritten as $\omega ([X_F,X_G],X_H)=\omega (X_{\{G,F\}},X_H)=\{\{G,F\},H\}$, as well as the corresponding expressions for each cyclic reordering, we find that

$$\left(d\omega \right)(X_F,X_G,X_H)=2\left[\left\{\right\{G,H\},F\}+\left\{\right\{H,F\},G\}+\left\{\right\{F,G\},H\}\right].$$

Finally, we recall that at each point of a neighbourhood of every point of M, the values of the set of Hamiltonian vector fields generate the tangent space, and therefore, $d\omega =0$ if and only if the Jacobi identity holds. Hence, the Poisson bracket endows $C^{\infty }\left(M\right)$ with a real Lie algebra structure, with the Jacobi identity being a consequence of the closedness of $\omega$, and property (7) shows that $-{\widehat{\omega }}^{-1}\circ d:C^{\infty }(M\{·,·\}\to {\mathfrak{X}}_{\mathrm{H}}(M,\omega )$ is a Lie algebra homomorphism.

A Hamiltonian system is a triplet $(M,\omega ,H)$, where $(M,\omega )$ is a symplectic manifold and $H\in C^{\infty }\left(M\right)$. Infinitesimal symmetries of a Hamiltonian system $(M,\omega ,H)$ are vector fields X whose flows are symplectomorphisms, i.e., ${\mathcal{L}}_X\omega =0$, such that they are also symmetries of H, i.e., $XH=0$, and, therefore, they are symmetries of $X_H$, $[X,X_H]=0$, because

$$i\left([X,X_H]\right)\omega ={\mathcal{L}}_X\left(i\left(X_H\right)\left(\omega \right)\right)-i\left(X_H\right)\left({\mathcal{L}}_X\omega \right)={\mathcal{L}}_X\left(dH\right)=d\left({\mathcal{L}}_X\left(H\right)\right)=0.$$

Then, for each $F\in C^{\infty }\left(M\right)$, the relation $X_{H}F=\{F,H\}=-X_{F}H$ shows that $X_F$ is an infinitesimal symmetry of H if and only if F is a first integral for $X_H$ (a result usually known as Noether’s theorem).

It is remarked that, in the case of a Hamiltonian dynamical system, the constants of motion F play a dual role in the reduction process, either as constants of motion (i.e., first integrals for $X_H$) or as generating infinitesimal symmetries $X_F$, because if F is a constant of motion, $\{F,H\}=0$, then the Hamiltonian vector field $X_F$ is an infinitesimal symmetry of H.

Moreover, both $X_H$ and $X_F$ are tangent to the level sets of F, because $X_{H}F=\{F,H\}=0$, and $X_{F}F=\{F,F\}=0$. The restriction of $X_F$ on each leaf of the foliation ${\mathcal{F}}_H$, whose leaves are the level sets of H, can be used to determine adapted coordinates, because $[X_F,X_H]=X_{\{H,F\}}=0$, in such a way that the problem of determining the integral curves of $X_H$ is reduced not just in one but also in two degrees of freedom.

In order to be able to simultaneously use the information given by different constants of motion, $F_1,\dots ,F_r$, it is sufficient that $\{F_i,F_j\}=0,\forall i,j=1,\dots ,r$, because $[X_{F_i},X_{F_j}]=X_{\{F_j,F_i\}}$. If the condition is satisfied, then $[X_{F_i},X_{F_j}]=0$ for any pair of indices i and j, and we can find adapted coordinates such that $X_{F_i}=\partial /\partial y^i$ for $i=1,\dots ,r$. The condition is not necessary because if, for instance, $\{F_i,F_j\}$ is constant for each pair of indices, then it is also true that $[X_{F_i},X_{F_j}]=0$.

The simplest case will be that of Hamiltonian systems in a space of dimension $N=2n$ for which such n functionally independent first integrals, $F_1,\dots ,F_n$, in involution are known: they are called completely integrable systems.

We are now ready to recall the notion of Liouville–Arnold integrability:

Definition 1.

The Hamiltonian dynamical system $(M,\omega ,H)$, with $\dim M=2n$, is said to be completely integrable if there exists a set of n functions $\{F_j\mid j=1,\dots ,n\}$, where $F_j\in C^{\infty }\left(M\right)$, with $F_1=H$, which are first integrals, i.e.,

$$\frac{d{F}_k}{dt}={\mathcal{L}}_{X_H}{F}_k=\{F_k,H\}=0,\forall k=2,\dots ,n,$$

that are functionally independent, i.e., $d{F}_1\wedge \cdots \wedge d{F}_n=/0$, and are pairwise in involution, i.e.,

$$\{F_k,F_j\}=0,\forall j,k=1,\dots n.$$

A completely integrable system that admits more than n functionally independent first integrals is said to be superintegrable, and when the number is the maximum number, $2n-1$, the system is called maximally superintegrable [21]. Many such systems can be found in the physics literature (see, e.g., the recent papers [22,23] and references therein).

The two main examples of Hamiltonian dynamical systems are those of Hamiltonian systems on the cotangent bundle $T^{\ast }Q$ of a manifold Q and those defined by regular Lagrangians on the tangent bundle $TQ$, to be studied in this section. In fact, the cotangent bundle $\pi :T^{\ast }Q\to Q$ is endowed with a canonical 1-form $\theta \in {\bigwedge }^1\left(T^{\ast }Q\right)$, defined by ${\theta }_{\alpha }={\pi }_{\alpha }^{\ast }\alpha$, for all covectors $\alpha$ in Q. Then, $\omega =-d\theta$ is a symplectic form on $T^{\ast }Q$. It is remarked that if $\alpha$ is a 1-form in Q, then as ${\alpha }^{\ast }\theta =\alpha$, we have ${\alpha }^{\ast }\omega ={\alpha }^{\ast }(-d\theta )=-d\left({\alpha }^{\ast }\theta \right)=-d\alpha$.

The geometric framework for the study of Lagrangian mechanics is that of tangent bundles [5,19,20,24,25]. The tangent bundle $\tau :TQ\to Q$ is characterised by two geometric tensors, the vertical endomorphism S, a (1,1)-tensor field on $TQ$, also called a tangent structure, which satisfies $\mathrm{Im}S=\ker S$ and an integrability condition, the vanishing of the Nijenhuis tensor, $N_S=0$, and the Liouville vector field $\Delta$ generating dilations along fibres in $TQ$ [26].

If $(U,\phi )$ is a local chart on Q and ${\mathrm{pr}}^i:{\mathbb{R}}^n\to \mathbb{R}$ are the natural projections on the i-th factor and $q^i={\mathrm{pr}}^i\circ \phi$, we define the coordinate system $(U,q^1,\dots ,q^n)$ on Q, and the corresponding chart in $\mathcal{U}={\tau }^{-1}\left(U\right)$, given by $(\mathcal{U},\phi ,{\phi }_{\ast })$, defines a coordinate system $(q^1,\dots ,q^n,v^1,\dots ,v^n)$ on the open set $\mathcal{U}={\tau }^{-1}\left(U\right)$ of $TQ$. Correspondingly, we consider the coordinate basis of $\mathfrak{X}\left(U\right)$, usually denoted by $\{\partial /\partial q^j\mid j=1,\dots ,n\}$, and its dual basis for ${\bigwedge }^1\left(U\right)$, $\{d{q}^j\mid j=1,\dots ,n\}$. Then, a vector v at a point $q\in U$ is $v=v^j{(\partial /\partial q^j)}_{|q}$, i.e., $v^i=d{q}^i\left(v\right)$, while a covector $\alpha$ at a point $q\in U$ is $\alpha ={\displaystyle {\alpha }_{j}d{q^j}_{|q}}$, with ${\alpha }_i=\alpha \left({(\partial /\partial q^i)}_{|q}\right)$. With this notation, the coordinate expressions of the vertical endomorphism S and the Liouville vector field $\Delta$ are [24,25]

$$S(q,v)=\frac{\partial }{\partial v^i}\otimes d{q}^i,\Delta (q,v)=v^i\frac{\partial }{\partial v^i}.$$

(8)

Similarly, we can introduce a coordinate system $(q^1,\dots ,q^n,p_1,\dots ,p_n)$ in the open set $\overline{\mathcal{U}}={\pi }^{-1}\left(U\right)$ of the cotangent bundle $\pi :T^{\ast }Q\to Q$, and the coordinate expression of the 1-form $\theta$ is

$$\theta (q,p)=p_{i}d{q}^i,$$

(9)

which shows that $\omega =-d\theta$ is a canonical symplectic structure on $T^{\ast }Q$.

Also, recall that a diffeomorphism $\phi$ of the manifold Q induces, in a natural way, a diffeomorphism of its tangent bundle $\Phi \in \mathrm{Diff}\left(TQ\right)$, and it satisfies ${\Phi }_{\ast }\Delta =\Delta$ and $[{\Phi }_{\ast },S]=0$ [24,25].

The vector field $\Delta$ and the tensor field S can be used to select a special kind of vector field whose integral curves are given by the lifting solutions of second-order differential equations. These vector fields, called second-order differential equation vector fields $D\in \mathfrak{X}\left(TQ\right)$ (hereafter shortened to SODE vector fields), are characterised by $S\left(D\right)=\Delta$.

Given a Lagrangian $L\in C^{\infty }\left(TQ\right)$, we can define a 1-form ${\theta }_L=dL\circ S$ and the exact 2-form ${\omega }_L=-d{\theta }_L$. When ${\omega }_L$ is regular, the Lagrangian L is said to be regular: i.e., $(TQ,{\omega }_L)$ is a symplectic manifold. Then, the dynamics are given by the uniquely defined SODE vector field ${\Gamma }_L$ such that

$$i\left({\Gamma }_L\right){\omega }_L=d{E}_L⟺{\mathcal{L}}_{{\Gamma }_L}{\theta }_L-dL=0,$$

(10)

where the energy function $E_L\in C^{\infty }\left(TQ\right)$ is defined by $E_L=\Delta \left(L\right)-L$. This shows that $(TQ,{\omega }_L,E_L)$ is a Hamiltonian dynamical system. The contraction of both sides of the first equation in (10) shows that the energy function is a first integral. Moreover, this implies that ${\mathcal{L}}_{{\Gamma }_L}{\omega }_L=d\left(i\left({\Gamma }_L\right){\omega }_L\right)=0$.

In the usual local tangent bundle coordinates, the expressions of ${\theta }_L$ and $E_L$ are

$${\theta }_L=\frac{\partial L}{\partial v^i}d{q}^i,E_L=v^i\frac{\partial L}{\partial v^i}-L,$$

(11)

while that of ${\omega }_L$ is

$${\omega }_L=\frac{{\partial }^{2}L}{\partial q^j\partial v^i}d{q}^i\wedge d{q}^j+\frac{{\partial }^{2}L}{\partial v^k\partial v^j}d{q}^j\wedge d{v}^k.$$

(12)

It may be of interest to know under what conditions two regular Lagrange functions $L,L^{\prime }\in C^{\infty }\left(TQ\right)$, in $TQ$ produce the same symplectic structure and the same energy function; i.e., $L_0=L-L^{\prime }$ is such that ${\omega }_{L_0}\equiv 0$ and $E_{L_0}=0$.

If $\alpha$ is a 1-form on Q, $\alpha \in {\bigwedge }^1\left(Q\right)$, then $\widehat{\alpha }$ denotes the function $\widehat{\alpha }\in C^{\infty }\left(TQ\right)$ defined by $\widehat{\alpha }\left(u\right)={\alpha }_{\pi \left(u\right)}\left(u\right)$. Such a function is such that $\Delta \widehat{\alpha }=\widehat{\alpha }$ and $d\widehat{\alpha }\circ S={\tau }^{\ast }\alpha$.

Then, a function $L_0\in C^{\infty }\left(TQ\right)$ is such that ${\omega }_{L_0}\equiv 0$ if and only if there exist a closed 1-form $\alpha \in Z^1\left(Q\right)$ and a function $h\in C^{\infty }\left(Q\right)$ such that $L_0=\widehat{\alpha }+h\circ \tau$ (see, e.g., [27]). But, as for such a function $L_0$, we have $E_{L_0}=-h$, we see that $L,L^{\prime }\in C^{\infty }\left(TQ\right)$ in $TQ$ produces the same Hamiltonian dynamical system, i.e., ${\omega }_L={\omega }_{L^{\prime }}$ and $E_L=E_{L^{\prime }}$, if and only if there exists a closed 1-form $\alpha \in Z^1\left(Q\right)$ such that $L^{\prime }=L+\widehat{\alpha }$, and both Lagrangians are then said to be gauge-equivalent.

It is also possible to identify a complete lift vector field $X^c\in \mathfrak{X}\left(TQ\right)$ that is a symmetry of the Hamiltonian dynamical system $(TQ,{\omega }_L,E_L)$ in terms of symmetries of L itself. Recall that if $X\in \mathfrak{X}\left(Q\right)$, its complete lift, denoted by $X^c$, is the vector field on $TQ$, whose flow is given by ${\varphi }_{t\ast }$, where ${\varphi }_t$ is the local flow of the vector field X. If the local coordinate expression of the vector field X in a chart of Q is $X\left(q\right)={\displaystyle }{X}^i\left(q\right)\partial /\partial q^i$, then the corresponding expression for $X^c$ in the associated chart of $TQ$ is $X^c(q,v)={\displaystyle }{X}^i\left(q\right)\partial /\partial q^i+(\partial X^i/\partial q^j)v^j\partial /\partial v^i$.

It is also remarked that if $\Phi \in \mathrm{Diff}\left(TQ\right)$ is a lift of a diffeomorphism $\phi$ of the manifold Q, then ${\Phi }^{\ast }{\theta }_L={\theta }_{{\Phi }^{\ast }L}$, as well as ${\Phi }^{\ast }{E}_L=E_{{\Phi }^{\ast }L}$, as a consequence of ${\Phi }_{\ast }\Delta =\Delta$ and $[{\Phi }_{\ast },S]=0$, because

$${\Phi }^{\ast }{\theta }_L={\Phi }^{\ast }(dL\circ S)=dL\circ S\circ {\Phi }_{\ast }=dL\circ {\Phi }_{\ast }\circ S=d(L\circ \Phi )\circ S={\theta }_{{\Phi }^{\ast }L},$$

(13)

while, as $\Delta$ is $\Phi$-related to itself, $(\Delta L)\circ \Phi =\Delta (L\circ \Phi )$, we have

$${\Phi }^{\ast }{E}_L={\Phi }^{\ast }(\Delta L)-{\Phi }^{\ast }L=\Delta \left({\Phi }^{\ast }L\right)-{\Phi }^{\ast }L=E_{{\Phi }^{\ast }L}.$$

(14)

At the infinitesimal level, (13) and (14) mean that if $X^c\in \mathfrak{X}\left(TQ\right)$ is the complete lift of $X\in \mathfrak{X}\left(Q\right)$, we have

$${\mathcal{L}}_{X^c}{\theta }_L={\theta }_{X^{c}L},X^c{E}_L=E_{X^{c}L}.$$

(15)

All of these properties can be used to derive Noether’s theorem in the Lagrangian formalism:

Theorem 2

(Noether). If the vector field $X\in \mathfrak{X}\left(Q\right)$ is such that there exists a function $h\in C^{\infty }\left(Q\right)$ such that $X^{c}L=\widehat{dh}$, then the function $f=i\left(X^c\right){\theta }_L-{\tau }^{\ast }h$ is a constant of motion.

Proof. 

First, the vector field $X^c$ is Hamiltonian because

$${\mathcal{L}}_{X^c}{\theta }_L={\theta }_{X^{c}L}={\theta }_{\widehat{dh}}={\tau }^{\ast }\left(dh\right)=d\left({\tau }^{\ast }h\right),$$

and then

$$i\left(X^c\right)d{\theta }_L+d\left(i\left(X^c\right){\theta }_L\right)=d\left({\tau }^{\ast }h\right)⟺i\left(X^c\right){\omega }_L=d((i\left(X^c\right){\theta }_L-h)=df.$$

Moreover, $X^c{E}_L=E_{X^{c}L}=E_{\widehat{dh}}=0$, and then if ${\Gamma }_L$ is the dynamical vector field determined by L, i.e., $i\left({\Gamma }_L\right){\omega }_L=d{E}_L$, we have

$${\Gamma }_{L}f=\{f,E_L\}=-\{E_L,f\}=-X^c{E}_L=0.$$

□

Particularly interesting cases are the geodesic Lagrangians defined through a Riemann structure g by $L=\frac{1}{2}g(v,v)$ (see, e.g., [7,28,29]) and the so-called natural Lagrangians defined by means of a Riemann structure g and a function V in Q as follows: $L=\frac{1}{2}g(v,v)-V\left(q\right)$.

A remarkable fact is the possibility of the existence of alternative compatible structures of the same type. For instance, a Hamiltonian vector field $X_H$ on the symplectic manifold $(M,\omega )$ can also be a Hamiltonian vector field with respect to an alternative symplectic structure ${\omega }^{\prime }$; i.e., there exists $H^{\prime }\in C^{\infty }\left(M\right)$ such that $i\left(X_H\right){\omega }^{\prime }=d{H}^{\prime }$. This also implies that ${\mathcal{L}}_{X_H}{\omega }^{\prime }=0$, and we see in this way that ${\omega }^{\prime }$ is an alternative $X_H$-invariant 2-form for $X_H$. But if ${\omega }^{\prime }$ is a 2-form such that ${\mathcal{L}}_{X_H}{\omega }^{\prime }=0$, then ${\mathcal{L}}_{X_H}({\omega }^{\prime }-\lambda \omega )=0$, $\lambda \in \mathbb{R}$, also implies that ${\mathcal{L}}_{X_H}{({\omega }^{\prime }-\lambda \omega )}^{\wedge n}=0$, and as ${({\omega }^{\prime }-\lambda \omega )}^{\wedge n}=f_{\lambda }{\left(\omega \right)}^{\wedge n}$, we see that ${\mathcal{L}}_{X_H}{f}_{\lambda }=0$, and therefore, the function coefficients of powers of $\lambda$ are first integrals. They are usually called non-Noether first integrals [13,16]. Such constants are the same ones as those associated with the invariant (1,1)-tensor field $\mathcal{R}={\widehat{\omega }}^{-1}\circ {\widehat{\omega }}^{\prime }$ in Section 3.

We now mention two particular methods for finding such an $X_H$-invariant 2-form ${\omega }^{\prime }$. First, if a vector field Y is such that $[Y,X_H]=0$ but is not a locally Hamiltonian vector field, then ${\omega }^{\prime }={\mathcal{L}}_Y\left(\omega \right)$ is an $X_H$-invariant closed 2-form, because ${\mathcal{L}}_{X_H}\left({\mathcal{L}}_Y\left(\omega \right)\right)={\mathcal{L}}_Y\left({\mathcal{L}}_{X_H}\left(\omega \right)\right)=0$. Second, if $\varphi \in \mathrm{Diff}\left(M\right)$ is a noncanonical symmetry of the Hamiltonian vector field defined by the Hamiltonian dynamical system $(M,\omega ,H)$, from the relation $i\left({\varphi }_{\ast }\left(X_H\right)\right)\left({\left({\varphi }^{-1}\right)}^{\ast }\left(\omega \right)\right)=d\left({\left({\varphi }^{-1}\right)}^{\ast }H\right)$, we see that if ${\varphi }_{\ast }\left(X_H\right)=X_H$, then $i\left(X_H\right)\left({\left({\varphi }^{-1}\right)}^{\ast }\left(\omega \right)\right)=d\left({\left({\varphi }^{-1}\right)}^{\ast }H\right)$, and therefore, ${\mathcal{L}}_{X_H}\left({\left({\varphi }^{-1}\right)}^{\ast }\left(\omega \right)\right)=0$, and equivalently, ${\mathcal{L}}_{X_H}\left({\varphi }^{\ast }\left(\omega \right)\right)=0$. As it was assumed that ${\omega }^{\prime }={\varphi }^{\ast }\left(\omega \right)\ne \omega$, we can choose such an $X_H$-invariant closed 2-form ${\omega }^{\prime }$ to define, together with $\omega$, the pencil. We also recall that $\varphi \in \mathrm{Diff}\left(M\right)$ is said to be a canonoid transformation of the Hamiltonian dynamical system $(M,\omega ,H)$ when ${\varphi }_{\ast }\left(X_H\right)$ is also a Hamiltonian vector field or, equivalently, when $X_H$ is Hamiltonian with respect to the transformed 2-form ${\varphi }^{\ast }\left(\omega \right)$, and in this case, ${\mathcal{L}}_{X_H}\left({\varphi }^{\ast }\left(\omega \right)\right)=0$ [14,15]; i.e., we can also choose ${\omega }^{\prime }={\varphi }^{\ast }\left(\omega \right)$ as the invariant $X_H$-form.

5. Invariant Volume Forms and Jacobi Multipliers

Another interesting case with many applications, both in the theory of differential equations and in classical mechanics, is that of the existence of a volume form invariant under a given vector field X on an oriented manifold $(M,\Omega )$. Each volume form is of the form $R\Omega$, with $R\in C^{\infty }\left(M\right)$, and the invariance condition is ${\mathcal{L}}_X(R\Omega )=0$, and if we take into account that ${\mathcal{L}}_X(R\Omega )=d\left(i\left(X\right)(R\Omega )\right)=d\left(i\left(RX\right)(\Omega )\right)={\mathcal{L}}_{RX}(\Omega )$, we see that the invariance condition of $R\Omega$ under X is equivalent to the invariance condition of $\Omega$ under $RX$.

Also, recall that for each vector field $X\in \mathfrak{X}\left(M\right)$, the volume form ${\mathcal{L}}_X\Omega$ is proportional to $\Omega$, and the proportionality function is called the divergence of X, i.e.,

$${\mathcal{L}}_X(\Omega )=\mathrm{div}\left(X\right)\Omega ,$$

(16)

and if local coordinates are chosen such that $\Omega =d{x}^1\wedge \cdots \wedge d{x}^n$, when the local expression of X is ${\displaystyle X=X^i\frac{\partial }{\partial x^i}}$, the local expression of $\mathrm{div}\left(X\right)$ is

$$\mathrm{div}\left(X\right)=\frac{\partial X^i}{\partial x^i}.$$

Vector fields X such that $\mathrm{div}\left(X\right)=0$ are called divergence-free vector fields and possess interesting properties (see, e.g., [4]).

Recalling the properties of Lie derivatives, we find that, as for each $f\in C^{\infty }\left(M\right)$, ${\mathcal{L}}_{fX}(\Omega )={\mathcal{L}}_X(f\Omega )=f{\mathcal{L}}_X(\Omega )+\left({\mathcal{L}}_{X}f\right)\Omega$, using the definition (16) of $\mathrm{div}\left(X\right)$, we have

$$\mathrm{div}\left(fX\right)=f\mathrm{div}\left(X\right)+X\left(f\right).$$

(17)

Nonvanishing functions R such that ${\mathcal{L}}_X(R\Omega )={\mathcal{L}}_{RX}(\Omega )=0$, i.e., $\mathrm{div}\left(RX\right)=0$, are called Jacobi multipliers, and (17) shows that the nonvanishing function R is a Jacobi multiplier if and only if (see [30,31] and references therein)

$$R\mathrm{div}\left(X\right)+X\left(R\right)=0⟺\mathrm{div}\left(X\right)+X\left(\log R\right)=0.$$

(18)

Locally defined Jacobi multipliers, obtained as particular solutions of (18), always exist, but in some particular cases, global solutions, giving rise to invariant volume forms, do not exist [32,33].

Note that the relation ${\mathcal{L}}_X(R\Omega )=d\left(i\left(X\right)(R\Omega )\right)=d(i\left(RX\right)\Omega )$ means that, for each positive function f, the function R is a Jacobi multiplier for X on the oriented manifold $(M,\Omega )$ if and only if $fR$ is a Jacobi multiplier for X in the oriented manifold $(M,f^{-1}\Omega )$. Moreover, if two Jacobi multipliers are known, there exist two invariant volume forms, ${\Omega }_1=R_1\Omega$ and ${\Omega }_2=R_2\Omega$, such that ${\Omega }_2=(R_2/R_1){\Omega }_1$, and hence, as ${\mathcal{L}}_X{\Omega }_2={\mathcal{L}}_X(R_2/R_1){\Omega }_1=0$, the quotient $R_2/R_1$ is a first integral.

An interesting case is that of a SODE vector field $\Gamma \in \mathfrak{X}\left(TQ\right)$ admitting a Lagrangian formulation L; i.e., there exists a regular Lagrange function $L\in C^{\infty }\left(TQ\right)$ such that $i(\Gamma ){\omega }_L=d{E}_L$ or, equivalently, ${\mathcal{L}}_{\Gamma }{\theta }_L=dL$. The tangent bundle $TQ$ is orientable, and a local chart of $TQ$ induced by one on Q induces a (local) orientation. As ${\mathcal{L}}_{\Gamma }{\omega }_L=0$, the volume form ${\left({\omega }_L\right)}^{\wedge n}$ is $\Gamma$-invariant, and therefore, if a volume form $\Omega$ was previously fixed, there will be a Jacobi multiplier R such that ${\left({\omega }_L\right)}^{\wedge n}=R\Omega$. If, for instance, $\Omega$ is the volume form determined by a tangent bundle local chart, $\Omega =d{q}^1\wedge \cdots \wedge d{q}^n\wedge d{v}^1\wedge \cdots \wedge d{v}^n$, we find, according to (12), that the determinant of the Hessian matrix W with elements $W_{ij}={\partial }^{2}L/\partial v^i\partial v^j$ is a Jacobi multiplier, because ${\left({\omega }_L\right)}^{\wedge n}$ is a real multiple of $\det Wd{q}^1\wedge \cdots \wedge d{q}^n\wedge d{v}^1\wedge \cdots \wedge d{v}^n$ (see [30] and references therein). Alternative Lagrangian formulations provide different Jacobi multipliers giving rise to constants of motion, which allows the system to be reduced.

Hojman [34] and González-Gascón [35] explored a new approach in the search for first integrals, which has become more and more important over the last several years for its applications to $f\left(R\right)$-gravity and FRW cosmology [36,37,38,39,40,41,42].

The main result is very general and a simple consequence of a geometric relation that, when particularised to specific cases, gives rise to many results scattered throughout the physics literature. So, different relations among vector fields and their divergences can be used to establish first integrals and integral invariants for vector fields on a manifold M.

The following geometric relation plays a fundamental role: if $X,Y$ is an arbitrary pair of vector fields on an oriented manifold $(M,\Omega )$, then

$${\mathcal{L}}_X\left(\mathrm{div}\left(Y\right)\right)-{\mathcal{L}}_Y\left(\mathrm{div}\left(X\right)\right)=\mathrm{div}\left([X,Y]\right),$$

(19)

because as the Lie derivatives of a p-form $\alpha$ satisfy ${\mathcal{L}}_X\left({\mathcal{L}}_Y\alpha \right)-{\mathcal{L}}_Y\left({\mathcal{L}}_X\alpha \right)={\mathcal{L}}_{[X,Y]}\alpha$, then in the particular case $\alpha =\Omega$, we have

$${\mathcal{L}}_X({\mathcal{L}}_Y\Omega )-{\mathcal{L}}_Y({\mathcal{L}}_X\Omega )={\mathcal{L}}_{[X,Y]}\Omega ,$$

(20)

and from the difference between

$${\mathcal{L}}_X({\mathcal{L}}_Y\Omega )={\mathcal{L}}_X(\mathrm{div}\left(Y\right)\Omega )={\mathcal{L}}_X\left(\mathrm{div}\left(Y\right)\right)\Omega +\mathrm{div}\left(Y\right)\mathrm{div}\left(X\right)\Omega$$

and the corresponding relation

$${\mathcal{L}}_Y({\mathcal{L}}_X\Omega )={\mathcal{L}}_Y(\mathrm{div}\left(X\right)\Omega )={\mathcal{L}}_Y\left(\mathrm{div}\left(X\right)\right)\Omega +\mathrm{div}\left(X\right)\mathrm{div}\left(Y\right)\Omega ,$$

we obtain (19).

Consequently, from relation (19), we see that if the vector field $X\in \mathfrak{X}\left(M\right)$ on an oriented manifold $(M,\Omega )$ is divergence-free, then if the vector field Y is an infinitesimal symmetry of X, i.e., $[X,Y]=0$, we find that $\mathrm{div}\left(Y\right)$ is a constant of motion for X. Something similar happens when the vector field Y is an infinitesimal symmetry of the one-dimensional distribution generated by X: i.e., there exists a function h such that $[Y,X]=hX$, because then, in this case, the function $\mathrm{div}\left(Y\right)+h$ is a first integral for X. Actually, if $\mathrm{div}\left(X\right)=0$, then ${\mathcal{L}}_X\Omega =0$, and hence, as $[X,Y]=-hX$,

$${\mathcal{L}}_X({\mathcal{L}}_Y\Omega )={\mathcal{L}}_Y({\mathcal{L}}_X\Omega )+{\mathcal{L}}_{-hX}\Omega =-{\mathcal{L}}_X(h\Omega )=-X\left(h\right)\Omega ,$$

and then, from

$${\mathcal{L}}_X({\mathcal{L}}_Y\Omega )={\mathcal{L}}_X(\mathrm{div}\left(Y\right)\Omega )={\mathcal{L}}_X\left(\mathrm{div}\left(Y\right)\right)\Omega ,$$

we obtain ${\mathcal{L}}_X(\mathrm{div}\left(Y\right)+h)=0$, and therefore, the following function I is a constant of motion for X:

$$I=\mathrm{div}\left(Y\right)+h.$$

(21)

When the vector field $X\in \mathfrak{X}\left(M\right)$ is not divergence-free, because, for any nonvanishing function R, the constants of motion of X coincide with those of $RX$, if we choose R as a Jacobi multiplier for X, then the vector field $\overline{X}=RX$ is such that when $[Y,X]=hX$, we have $[Y,\overline{X}]=\overline{h}\overline{X}$, with $\overline{h}=(Y\left(R\right)/R)+h$, and hence, the preceding result shows that the function $I=\mathrm{div}\left(Y\right)+\overline{h}=\mathrm{div}\left(Y\right)+Y\left(\log R\right)+h$ is a constant of motion for $\overline{X}$ and, therefore, for X [43].

6. A Geometric Approach to a Generalised Sundman Transformation

An infinitesimal time-reparametrisation, usually called a Sundman transformation [44], introduced when looking for an analytic solution to the three-body problem [45,46,47], is very intriguing, at least from a geometric perspective, because its geometric meaning is not clear. So, in the nonautonomous approach, t is not a coordinate but rather a parameter of the integral curve. It was introduced for a second-order differential equation, but it admits a clear geometric generalisation to systems of first-order differential equations.

The geometric approach was developed in [28,48]. This infinitesimal time-reparametrisation is written as

$$\frac{dt}{d\tau }=f\left(x\right).$$

(22)

It has allowed researchers to find solutions to many different problems in the theory of differential equations and related physical problems, for instance, the linearisation of differential equations, or to regularise some equations of motion and to avoid collision singularities. More generally, it is used to transform a given equation into another one of a more appropriate form. Moreover, as a SODE vector field on Q can be seen as a particular case of a vector field on $TQ$, it is enough to consider, for the time being, Sundman transformations for systems of first-order differential equations.

The meaning of infinitesimal time-reparametrisation (22) is based on the following property: if $\gamma \left(t\right)$ is a curve, we carry out the mentioned Sundman transformation by introducing a new parameter $\tau$ into such a curve such that

$$\frac{d\tau }{dt}=\frac{1}{f\left(\gamma \right(t\left)\right)},$$

(23)

and we obtain the reparametrised curve $\overline{\gamma }\left(\tau \right)$, given by $\overline{\gamma }\left(\tau \left(t\right)\right)=\gamma \left(t\right)$, and then

$$\frac{d\gamma }{dt}=\frac{d\overline{\gamma }}{d\tau }\frac{d\tau }{dt}=\frac{1}{f\left(\gamma \right(t\left)\right)}\frac{d\overline{\gamma }}{d\tau }.$$

Consequently, if $\gamma \left(t\right)$ is an integral curve of X, i.e., $d\gamma /dt=X_{\gamma \left(t\right)}$, then

$$\frac{d\overline{\gamma }}{d\tau }=f\left(\gamma \left(t\right)\right)\frac{d\gamma }{dt}=f\left(\gamma \left(t\right)\right)X_{\gamma \left(t\right)}={\left(fX\right)}_{\gamma \left(t\right)}={\left(fX\right)}_{\overline{\gamma }\left(\tau \right)};$$

i.e., the curve $\overline{\gamma }$ is an integral curve of the vector field $fX$.

This implies that we can consider the given Sundman transformation to be a change from the vector field X to the conformally related one $fX$ [28,48], but note that the integral curves of the vector fields $X\in \mathfrak{X}\left(M\right)$ and $fX\in \mathfrak{X}\left(M\right)$ coincide up to their respective reparametrisations. Of course, such infinitesimal time-reparametrisation implies a new velocity $\overline{v}$ with respect to the new time, and then it is related to the old one by ${\overline{v}}^i=f{v}^i$.

It was proven in [49] that for a given incomplete vector field X, it is possible to find a function $f\in C^{\infty }\left(M\right)$ such that the vector field $fX$ is a complete vector field, and this property shows the usefulness of Sundman transformations in the regularisation process. The relevance of the property of replacing a vector field with a conformally related one in the Kustaanheimo–Stiefel regularisation of the Kepler problem was also demonstrated in [49]. Conformally related vector fields have also been considered in the study of superintegrable systems (see, e.g., [22,23]). Moreover, two conformally related vector fields X and $fX$ on a manifold M have the same local first integrals, but, as indicated in [49], this is not true for general tensor fields T, because ${\mathcal{L}}_{fX}T\ne f{\mathcal{L}}_{X}T$. This is an important fact because it provides us with a way to obtain, from a vector field X that does not preserve T, vector fields $fX$ under which a given tensor field T is invariant.

As an example, we can focus on the linearisation of a system of first-order differential equations.

• Linearisation

Recall that a manifold M can be endowed with a linear structure if there exists a complete vector field $\Delta$, playing the role of a Liouville vector field, with only one nondegenerate critical point, such that ${\mathcal{F}}_{\Delta }^{\left(0\right)}=\mathbb{R}$, and ${\mathcal{F}}_{\Delta }^{\left(1\right)}$ separates derivations [5]. Here, ${\mathcal{F}}_{\Delta }^{\left(k\right)}$ denotes the set of functions on the manifold M defined by

$${\mathcal{F}}_{\Delta }^{\left(k\right)}=\{f\in \mathcal{F}\left(M\right)\mid \Delta f=kf\},k\in \mathbb{N}.$$

Linear functions (with respect to $\Delta$) are those defined by $f\in \mathcal{F}\left(M\right)$ such that ${\mathcal{L}}_{\Delta }f=f$, i.e., $f\in {\mathcal{F}}_{\Delta }^{\left(1\right)}$, and linear vector fields $X\in \mathfrak{X}\left(M\right)$ are those preserving the $\mathbb{R}$-linear subspace ${\mathcal{F}}_{\Delta }^{\left(1\right)}$, that is, satisfying ${\mathcal{L}}_X\left({\mathcal{F}}_{\Delta }^{\left(1\right)}\right)\subset {\mathcal{F}}_{\Delta }^{\left(1\right)}$ or, equivalently, ${\mathcal{L}}_X\Delta =[X,\Delta ]=0$.

When X is such that ${\mathcal{L}}_X\Delta \ne 0$, there may exist a positive function f such that ${\mathcal{L}}_{fX}\Delta =0$, because ${\mathcal{L}}_{fX}\Delta =[fX,\Delta ]=f[X,\Delta ]-\Delta \left(f\right)X$. This happens when there exists h such that $[X,\Delta ]=hX$ and the function f is such that $h=\Delta \left(\log f\right)$.

A chart $(U,\phi )$ of M identifies U with an open set of ${\mathbb{R}}^n$, and then U is endowed with the complete vector field $\Delta =x^i\partial /\partial x^i$, and if $X=X^i\left(x\right)\partial /\partial x^i$, we say that the vector field X is linear when $[\Delta ,X]=0$, and as

$$[\Delta ,X]=\left[x^i\frac{\partial }{\partial x^i},X^j\frac{\partial }{\partial x^j}\right]=\left(x^i\frac{\partial X^k}{\partial x^i}-X^k\right)\frac{\partial }{\partial x^k},$$

(24)

$[\Delta ,X]=0$ is equivalent to $X^i\left(x\right)={A^i}_j{x}^j$, with integral curves for X solutions of ${\dot{x}}^i={A^i}_j{x}^j$.

Similarly, vector fields X whose integral curves are solutions of an inhomogeneous linear system, ${\dot{x}}^i={A^i}_j{x}^j+B^i$, are characterised by

$$[\Delta ,[\Delta ,X\left]\right]=-[\Delta ,X].$$

The preceding results can be summarised as follows [48]:

Theorem 3.

Let X be a vector field on a differentiable manifold M endowed with a linear structure Δ.

1. 

${\mathcal{L}}_{\Delta }X=hX$, for some function h, if and only if there exists a nonvanishing positive function f such that the vector field $fX$ satisfies ${\mathcal{L}}_{\Delta }\left(fX\right)=0$.

2. 

${\mathcal{L}}_{\Delta }X=0$ if and only if, for any coordinate system $(U,\phi )$ such that ${\left.\Delta \right|}_U={\displaystyle x^i\frac{\partial }{\partial x^i}}$, the local expression of X is linear.

3. 

${\mathcal{L}}_{\Delta }^{2}X=-{\mathcal{L}}_{\Delta }X$ if and only if for any coordinate system such that ${\left.\Delta \right|}_U={\displaystyle }{x}^i\frac{\partial }{\partial x^i}$, the local expression of X is affine in $x^i$.

• Divergence-free case

If a vector field $X\in \mathfrak{X}\left(M\right)$ on an oriented manifold $(M,\Omega )$ is such that ${\mathcal{L}}_X\Omega \ne 0$, there may be a positive function $f\in C^{\infty }\left(M\right)$ such that ${\mathcal{L}}_{fX}\Omega =0$. These functions are called Jacobi multipliers and play a relevant role in its integrability by quadratures.

Recall that as ${\mathcal{L}}_X\Omega$ is also a volume form, we can define the divergence of X by ${\mathcal{L}}_X\Omega =\mathrm{div}X\Omega$, and then X is divergence-free if and only if ${\mathcal{L}}_X\Omega =0$. Note that as ${\mathcal{L}}_{fX}\Omega ={\mathcal{L}}_X(f\Omega )$, the search for such a Jacobi multiplier is equivalent to the determination of an X-invariant volume form $f\Omega$ (more details can be found in [30,31]).

• Geodesic case

Another possibility would be to consider a Riemannian structure on the manifold M given by a nondegenerate symmetric two-times covariant tensor field g. As ${\mathcal{L}}_{fX}g\ne f{\mathcal{L}}_{X}g$, some non-Killing vector fields X, i.e., such that ${\mathcal{L}}_{X}g\ne 0$, can give rise to Killing ones [7] just by multiplication by a convenient function f.

• Hamiltonian case

Given a closed 2-form $\omega$ that is non-invariant under the vector field X on a manifold, i.e., ${\mathcal{L}}_X\omega \ne 0$, if there is a positive function f such that ${\mathcal{L}}_{fX}\omega =0$, i.e., if $fi\left(X\right)\omega$ is a closed form, then when the nondegeneracy condition $df\wedge \omega =0$ is satisfied, the 2-form $f\omega$ is symplectic, and the vector field X is locally Hamiltonian with respect to this symplectic form $f\omega$. Recall that, in the case where X is also locally Hamiltonian with respect to the original symplectic form $\omega$, such a function f must be a constant of motion for X, $Xf=0$. Moreover, we can make use of the alternative symplectic structure to find non-Noether constants of motion, as explained in Section 4.

The same can be said about bivector fields $\Lambda$, particularly those of Poisson structures, i.e., such that ${[\Lambda ,\Lambda ]}_{\mathrm{S}}=0$, where ${[·,·]}_{\mathrm{S}}$ denotes the Schouten bracket. In this case,

$$\{f,g\}=\Lambda (df,dg),f,g\in C^{\infty }\left(M\right),$$

defines a Poisson bracket. Hamiltonian vector fields $X_f$ on M are those of the form $X_{f}g=\{g,f\}$. Given a vector field X and a Poisson structure $\Lambda$, sometimes, there exists a function f such that $fX$ is Hamiltonian with respect to the Poisson structure $\Lambda$: a Hamiltonisation process.

7. Sundman Transformations for Systems of Second-Order Differential Equations

As indicated above, the Sundman transformation was first introduced to deal with systems of second-order differential equations, such as Newton’s equations of motion. It is well known that an autonomous system

$$\frac{d^2{x}^i}{d{t}^2}=X^i(x^1,\dots ,x^n,{\dot{x}}^1,\dots ,{\dot{x}}^n),i=1,\dots ,n,$$

(25)

is associated with a system of $2n$ first-order differential equations

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{d{x}^i}{dt}}& =& v^i\hfill \\ \hfill {\displaystyle \frac{d{v}^i}{dt}}& =& X^i(x^1,\dots ,x^n,v^1,\dots ,v^n)\hfill \end{array}\right.i=1,\dots ,n,$$

(26)

whose solutions define the integral curves of the SODE vector field $\Gamma$ on $TQ$

$$\Gamma =v^i\frac{\partial }{\partial x^i}+X^i(x,v)\frac{\partial }{\partial v^i};$$

(27)

i.e., a system of second-order differential equations can be dealt with using a SODE vector field on the tangent bundle, $\Gamma \in \mathfrak{X}\left(TQ\right)$, such that $S(\Gamma )=\Delta$.

The theory of Sundman transformations developed for systems of first-order differential equations suggests that we proceed by similarity and define the transformed vector field as obtained by multiplication by the function defining the Sundman transformation. But the appearance of second-order derivatives suggests that this approach may need to be modified. On the other hand, when multiplying by the function f, the SODE characteristic property is lost. This leads us to examine this definition more carefully. It will be shown that we can overcome these two problems in the particularly important case of the function f defining the Sundman transformation, being a constant-sign basic function.

As remarked in [48], when applying a Sundman transformation (22), the new velocities with respect to the new time, $\overline{v}$, are related to the previous ones by ${\overline{v}}^i=f{v}^i$, because

$$v^i=\frac{d{x}^i}{dt}=\frac{d{x}^i}{d\tau }\frac{d\tau }{dt}=\frac{1}{f}{\overline{v}}^i,$$

and therefore,

$$\frac{\partial }{\partial v^i}=\frac{\partial {\overline{v}}^j}{\partial v^i}\frac{\partial }{\partial {\overline{v}}^j}=f\frac{\partial }{\partial {\overline{v}}^i}.$$

This suggests the use of non-natural coordinates on $TQ$, the so-called quasi-velocities [50].

With the change of coordinates to a new coordinate system on the manifold $TQ$

$$(x^i,v^i)\mapsto ({\overline{x}}^i,{\overline{v}}^i),{\overline{x}}^i=x^i,{\overline{v}}^i=f\left(x\right)v^i,$$

(we keep the notation ${\overline{x}}^i$ for clarity), we see, by direct computation, that

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial }{\partial x^j}}& =& {\displaystyle \frac{\partial }{\partial {\overline{x}}^j}}+{\displaystyle \frac{\partial f}{\partial x^j}{v}^i\frac{\partial }{\partial {\overline{v}}^i}}={\displaystyle \frac{\partial }{\partial {\overline{x}}^j}+\frac{1}{f}\frac{\partial f}{\partial {\overline{x}}^j}{\overline{v}}^i\frac{\partial }{\partial {\overline{v}}^i}},\hfill \\ \hfill {\displaystyle \frac{\partial }{\partial v^j}}& =& f{\displaystyle \frac{\partial }{\partial {\overline{v}}^j}}.\hfill \end{array}$$

Consequently, the new coordinate expression of the preceding vector field $\Gamma$ is

$$\Gamma (x,\overline{v})=\frac{{\overline{v}}^i}{f}\frac{\partial }{\partial {\overline{x}}^i}+\left(f{X}^i(x,\overline{v}/f)+{\overline{v}}^i\frac{1}{f^2}\frac{\partial f}{\partial {\overline{x}}^j}{\overline{v}}^j\right)\frac{\partial }{\partial {\overline{v}}^i}.$$

(28)

Under a generalised Sundman transformation of the given system, we can use, as suggested in [48], the operational relations

$$\frac{d}{dt}=\frac{1}{f}\frac{d}{d\tau },\frac{d^2}{d{t}^2}=\frac{1}{f}\frac{d}{d\tau }\left(\frac{1}{f}\frac{d}{d\tau }\right)=\frac{1}{f^2}\frac{d^2}{d{\tau }^2}-\frac{1}{f^3}\frac{df}{d\tau }\frac{d}{d\tau },$$

(29)

and hence, if $x\left(t\right)$ is a solution of the system, and the new parameter $\tau$ is given by

$$\tau \left(t\right)={\int }^t\frac{1}{f\left(\eta \right)}d\eta ,$$

then $\overline{x}\left(\tau \right)$ such that $\overline{x}\left(\tau \left(t\right)\right)=x\left(t\right)$ satisfies the SODE system

$$\frac{d^2\overline{x}}{d{\tau }^2}={\overline{X}}^i\left(\overline{x},\frac{d{\overline{x}}^i}{d\tau }\right),i=1,\dots ,n,$$

with

$${\overline{X}}^i\left(\overline{x},\frac{d\overline{x}}{d\tau }\right)=f^2{X}^i\left(\overline{x},\frac{1}{f}\frac{d\overline{x}}{d\tau }\right)+\frac{d}{d\tau }\left(\log f\right)\frac{d{\overline{x}}^i}{d\tau },$$

(30)

together with ${\overline{v}}^i=f{v}^i$, i.e., $d{\overline{x}}^i/d\tau =fd{x}^i/dt$. The system can be rewritten as

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{d{\overline{x}}^i}{d\tau }}& =& f{v}^i={\overline{v}}^i\hfill \\ \hfill {\displaystyle \frac{d{\overline{v}}^i}{d\tau }}& =& f^2{X}^i\left(\overline{x},{\displaystyle \frac{1}{f}}\overline{v}\right)+{\displaystyle \frac{d}{d\tau }}\left(\log f\right){\overline{v}}^i\hfill \end{array}\right.$$

(31)

This shows that the images under the generalised Sundman transformation of the integral curves of the considered vector field $\Gamma$ are the integral curves of the vector field $\overline{\Gamma }(\overline{x},\overline{v})$

$$\overline{\Gamma }(\overline{x},\overline{v})={\overline{v}}^j\frac{\partial }{\partial {\overline{x}}^j}+\left(\frac{1}{f}{\overline{v}}^j\frac{\partial f}{\partial {\overline{x}}^j}{\overline{v}}^i+f^2{X}^i\left(\overline{x},{\displaystyle \frac{1}{f}}\overline{v}\right)\right)\frac{\partial }{\partial {\overline{v}}^i},$$

(32)

and a simple comparison shows that

$$\overline{\Gamma }(\overline{x},\overline{v})=f\left(\overline{x}\right)\Gamma (\overline{x},\overline{v}).$$

(33)

8. Alternative Tangent Bundle Structures

The relevance and usefulness of the existence of alternative geometric structures in the description of mechanical systems, particularly the tensorial characterisation of linear structures and vector bundle structures, are also well known [5].

We first review the work by Crampin and Thompson on almost-tangent structures on M [26]. An almost-tangent structure on a manifold M is a (1,1)-tensor field S on M such that, at each point $p\in M$, the kernel of the linear map $S_p:T_{p}M\to T_{p}M$ coincides with its image. It follows that $S^2=0$. The almost-tangent structure S is said to be integrable if its Nijenhuis tensor $N_S$ vanishes.

We recall that the Nijenhuis tensor $N_T$ of a (1,1)-tensor field T on a manifold M is a (1,2)-tensor field given by

$$N_T(X_1,X_2)=[T\left(X_1\right),T\left(X_2\right)]+T^2\left([X_1,X_2]\right)-T\left([T\left(X_1\right),X_2]\right)-T\left([X_1,T\left(X_2\right)]\right),$$

where $X_1,X_2\in \mathfrak{X}\left(M\right)$. Therefore, as $S^2=0$,

$$N_S(X_1,X_2)=[S\left(X_1\right),S\left(X_2\right)]-S\left([S\left(X_1\right),X_2]\right)-S\left([X_1,S\left(X_2\right)]\right),\forall X_1,X_2\in \mathfrak{X}\left(M\right).$$

The $N_S=0$ condition implies that the vertical distribution defined by $\ker S=\mathrm{Im}S$ is involutive, because if $X,Y\in \ker S=\mathrm{Im}S$, then there exist $\tilde{X},\tilde{Y}\in \mathfrak{X}\left(M\right)$ such that $S\left(\tilde{X}\right)=X$ and $S\left(\tilde{Y}\right)=Y$, and then

$$[X,Y]=[S\left(\tilde{X}\right),S\left(\tilde{Y}\right)]=S\left([S\left(\tilde{X}\right),\tilde{Y}]\right)+S\left([\tilde{X},S\left(\tilde{Y}\right)]\right);$$

i.e., $[X,Y]$ lies in the image of S, which coincides with $\ker S$, and therefore, the distribution defined by $\ker S$ is involutive and hence integrable in the Darboux sense. The integral submanifolds of such a foliation are the fibres of a fibration $\pi :M\to Q$, where Q is an n-dimensional manifold. The vertical vector fields are those taking values in $\ker S$. Then, if $X\in \mathfrak{X}\left(M\right)$ projects onto a vector field $\overline{X}\in \mathfrak{X}\left(Q\right)$, then $S\left(X\right)$ only depends on $\overline{X}$.

Crampin and Thompson showed [26,51] that there are local coordinates $(x^i,u^i)$ on M such that $S=(\partial /\partial u^i)\otimes d{x}^i$. Here, $(x^1,\dots ,x^n)$ are coordinates on Q, and if $X_1,\dots ,X_n$ are vector fields on M projecting onto $\partial /\partial x^1,\dots ,\partial /\partial x^n$, respectively, as $[S\left(X_i\right),S\left(X_j\right)]=0$, then local coordinates on the fibres can be chosen such that $S\left(X_i\right)=\partial /\partial u^i$. The coordinates $u^i$ are determined only up to an additive constant on each fibre, because they are solutions of the system $S\left(X_i\right)u^j={\delta }_i^j$, and we can change $u^i$ by ${\overline{u}}^i=u^i+f^i\left(x\right)$. The ambiguity is fixed by the choice of the zero section.

Such a choice uniquely determines, for each coordinate system $\left(x^i\right)$ on the base manifold Q, a system of local coordinates $(x^i,u^i)$ such that

$$S=\frac{\partial }{\partial u^i}\otimes d{x}^i.$$

Furthermore, there is a uniquely defined vertical vector field $\Delta$ such that ${\mathcal{L}}_{\Delta }S\left(X\right)=-S\left(X\right)$ and $\Delta =0$ on the zero section. The explicit expression of $\Delta$ is

$$\Delta =u^i\frac{\partial }{\partial u^i}.$$

(34)

Such a vector field $\Delta$ provides a linear space structure to every fibre of $\pi :M\to Q$.

The vector fields associated with systems of second-order differential equations with respect to the new integrable almost-tangent structure are such that $S\left(D\right)=\Delta$, i.e., of the form

$$D(x,u)=u^i\frac{\partial }{\partial x^i}+f^i(x,u)\frac{\partial }{\partial u^i}.$$

It was shown in [48] that, starting with the standard tangent bundle structure given by the vertical endomorphism S and a constant-sign basic function ${\tau }_Q^{\ast }h$ on $TQ$, with $h\in C^{\infty }\left(Q\right)$, we can introduce a new integrable almost-tangent structure $\left({\tau }_Q^{\ast }h\right)S$ on $TQ$, simply denoted by $\overline{S}=hS$, because $\ker \left(hS\right)=\mathrm{Im}\left(hS\right)$, and $N_{hS}=0$. The vertical distribution defined by $\ker \left(hS\right)$ coincides with the usual one defined by $\ker S$, and the set of leaves can be identified with the base manifold Q.

If we choose a local set of coordinates for Q, $(q^1,\dots ,q^n)$, and if $X_1,\dots ,X_n$ are ${\tau }_Q$-projectable vector fields on $TQ$ and ${\tau }_Q$-related to $\partial /\partial q^1,\dots ,\partial /\partial q^n$, respectively, then the vector fields $hS\left(X_1\right),\dots ,hS\left(X_n\right)$ are pairwise commuting, and there exist local coordinates ${\overline{v}}^1,\dots ,{\overline{v}}^n$ such that $S\left(h{X}_i\right)=hS\left(X_i\right)=\partial /\partial {\overline{v}}^i$, and as $S\left(X_i\right)=\partial /\partial v^i$, with the same choice for the zero section, we can see that $\overline{S}=\left({\tau }_Q^{\ast }h\right)S$ has the local expression

$$\overline{S}=\frac{\partial }{\partial {\overline{v}}^i}\otimes d{q}^i=hS,$$

with the fibre coordinates given by $h{\overline{v}}^i=v^i$. The vector field $\overline{\Delta }$ coincides with $\Delta$.

Note that ${\overline{v}}^i$ values are not coordinates adapted to the original tangent bundle structure because the 1-forms ${\alpha }^i$ defining such coordinates of the vector v by ${\overline{v}}^i={\alpha }^i\left(v\right)$ are not exact, with ${\alpha }^i=(1/h)d{q}^i$, and correspond to the so-called quasi-velocities [50]. In summary, we obtain a new tangent bundle structure on $TQ$, with its corresponding Liouville vector field $\overline{\Delta }=\Delta$ and a new concept of a SODE vector field. When $h=f^{-1}$, we see that $\overline{\Gamma }=f\Gamma$ is a SODE vector field with respect to $\overline{S}=(1/f)S$.

If we successively apply two Sundman transformations to a system characterised by the functions $f_1\in C^{\infty }\left(Q\right)$ and $f_2\in C^{\infty }\left(Q\right)$, we obtain a new system by applying the Sundman transformation defined by the product $f_2{f}_1\in C^{\infty }\left(Q\right)$, and we see that the transformed vector field is a SODE vector field with respect to the new tangent bundle structure $\overline{\overline{S}}=f_2^{-1}{f}_1^{-1}S$. As the set of positive real functions is an Abelian multiplicative Lie group, the Sundman transformation corresponding to $f^{-1}$ is the inverse of the Sundman transformation defined by f. More details can be found in [48].

9. Linearisability of Scalar Second-Order Differential Equations

A particularly interesting case is that of systems of second-order differential equations that are linear in a given coordinate system: i.e., the functions $X^i$ are of the form

$$X^i(x,v)=\left({A^i}_j{x}^j+{B^i}_j{v}^j\right),$$

where ${A^i}_j$ and ${B^i}_j$ are real numbers. In geometric terms, this can be written as $[\tilde{\Delta },\Gamma ]=0$, with $\tilde{\Delta }={\Delta }_Q+\Delta$, where

$${\Delta }_Q={\displaystyle }{x}^i(\partial /\partial x^i),\Delta ={\displaystyle }{v}^i(\partial /\partial v^i).$$

Note that the vector field $\tilde{\Delta }$ is not intrinsic, but it depends on the choice of the chart on U. More explicitly, the vector field $\tilde{\Delta }$ is the complete lift of ${\Delta }_Q$. Our aim is to study under which circumstances a given system of second-order differential equations can be transformed by an appropriate Sundman transformation into a linear one.

Consider the simplest case of a one-dimensional autonomous SODE, i.e., $n=1$, and $X^1=F$ is a basic function. The equation of the integral curves of the vector field $\overline{\Gamma }$ transformed under a Sundman transformation of $\Gamma =v\partial /\partial q+F\left(q\right)\partial /\partial v$ is

$$\frac{d\overline{v}}{d\tau }=\frac{1}{f}{f}^{\prime }\left(q\right)\overline{v}\overline{v}+f^{2}F\left(q\right),$$

(35)

and, in the particular case of a system defined by a potential function $\mathcal{V}$, where $F=-{\mathcal{V}}^{\prime }$, the expressions of the SODE vector field $\Gamma$ in coordinates $(q,v)$ and its transformed vector field $\overline{\Gamma }=f\Gamma$ in coordinates $(\overline{q},\overline{v})$ are given, respectively, by

$$\Gamma (q,v)=v\frac{\partial }{\partial q}-{\mathcal{V}}^{\prime }\left(q\right)\frac{\partial }{\partial v},\overline{\Gamma }(\overline{q},\overline{v})=\overline{v}\frac{\partial }{\partial \overline{q}}+\left(\frac{f^{\prime }}{f}{\overline{v}}^2-f^2{\mathcal{V}}^{\prime }\left(\overline{q}\right)\right)\frac{\partial }{\partial \overline{v}}.$$

But as the energy function $E=\frac{1}{2}{v}^2+\mathcal{V}=\frac{1}{2}{(\overline{v}/f)}^2+\mathcal{V}$ is a conserved quantity, if we restrict ourselves to studying the motions for a given energy E,

$$\frac{d\overline{v}}{d\tau }=f{f}^{\prime }\left(q\right)2(E-\mathcal{V})-f^2{\mathcal{V}}^{\prime }\left(q\right)=\frac{d}{dq}\left(f^2(E-\mathcal{V})\right).$$

(36)

This is an inhomogeneous linear differential equation in the variable q if and only if there exist constants A, B and C such that $f^2(E-\mathcal{V})=A{q}^2+Bq+C$, from where

$$\frac{d\overline{v}}{d\tau }=2A\overline{q}+B⟹\frac{d^2\overline{q}}{d{\tau }^2}=2A\overline{q}+B.$$

In the relevant case of the radial equation for a given fixed angular momentum ℓ for the Coulomb–Kepler problem, for which q is the radial variable r and $V\left(r\right)=-k/r$,

$$\mathcal{V}\left(r\right)=-\frac{k}{r}+\frac{{\ell }^2}{2r^2},F\left(r\right)=-{\mathcal{V}}^{\prime }\left(r\right)=\frac{{\ell }^2}{r^3}-\frac{k}{r^2},$$

and from $f^2(E-\mathcal{V})=A{r}^2+B+C$, we obtain

$$f^2\left(E+\frac{k}{r}-\frac{{\ell }^2}{2r^2}\right)=A{r}^2+Br+C,$$

i.e., $f^{2}E=A{r}^2$, $f^{2}k=B{r}^2$ and ${\ell }^2{f}^2=-2C{r}^2$, and therefore, the general solution is a multiple of $f\left(r\right)=r$, with

$$A=E,B=k,C=-\frac{\ell }{2},$$

and then the transformed second-order differential equation is [52]

$$\frac{d^2\overline{r}}{d{\tau }^2}=2Er+k.$$

The Sundman transformation is independent of ℓ, because $f\left(r\right)$ is proportional to r.

In the opposite direction, if we start from the linear SODE vector field $\Gamma$ of the one-dimensional harmonic oscillator, i.e., $\Gamma =v(\partial /\partial x)-{\omega }^{2}x(\partial /\partial v)$, which corresponds to $F\left(x\right)=-{\omega }^{2}x$, i.e., $\mathcal{V}=\frac{1}{2}{\omega }^2{x}^2$, under the Sundman transformation defined by a given function f, it becomes

$$\overline{\Gamma }(\overline{x},\overline{v})=f\left(\overline{x}\right)\Gamma (x,\overline{v})=\overline{v}\frac{\partial }{\partial \overline{x}}+\left(\frac{1}{f}\frac{df}{d\overline{x}}{\overline{v}}^2-f^2{\omega }^2\overline{x}\right)\frac{\partial }{\partial \overline{v}},{\overline{v}}^i=f{v}^i,$$

and the projections onto the base manifold of its integral curves are solutions of

$$\frac{d^2\overline{x}}{d{\tau }^2}-\frac{1}{f}\frac{df}{d\overline{x}}{\left(\frac{d\overline{x}}{d\tau }\right)}^2+f^2{\omega }^2\overline{x}=0;$$

i.e., it appears that an additional quadratic damping term and linearity are lost.

Conversely, an equation of this last type can be reduced to a harmonic oscillator by the Sundman transformation defined by $f^{-1}$. If, for instance, $f\left(x\right)=x^2$, the former equation reduces to

$$\frac{d^2\overline{x}}{d{\tau }^2}+\frac{2}{\overline{x}}{\left(\frac{d\overline{x}}{d\tau }\right)}^2+{\omega }^2\frac{1}{{\overline{x}}^3}=0;$$

i.e., it is the Ermakov–Pinney equation under the action of a damping quadratic term. This is a prototype for linearisable examples.

As indicated in [48], the linear structure on $Q=\mathbb{R}$ depends on the choice of the coordinate y, ${\Delta }_Q=y\partial /\partial y$, and then the linearisability character of a given SODE depends on the choice of y. Therefore, in the study of the linearisation process, we need to first find a coordinate transformation $y=\phi \left(x\right)$ from the original coordinate to the adapted one and then a Sundman transformation, $d\tau =h\left(x\right)dt$, that transforms our original SODE into a linear one in the new coordinate y and its velocity. This will be implemented in several steps by finding several coordinate transformations and Sundman transformations that simplify the form of the SODE. Then, we describe the composition of ordinary changes of coordinates with the Sundman transformation considered so far. We will refer to a transformation of the form $y=x$, $d\tau =h\left(x\right)dt$ as a pure Sundman transformation and to $y=\phi \left(x\right)$, $d\tau =dt$ as a pure coordinate transformation. By composing such types of transformations, we obtain a group of generalised Sundman transformations $(h,\phi )$ defined as

$$y=\phi \left(x\right),d\tau =h\left(x\right)dt,$$

(37)

with the composition law

$$(h_2,{\phi }_2)★(h_1,{\phi }_1)=((h_2\circ {\phi }_1)h_1,{\phi }_2\circ {\phi }_1).$$

This set of generalised Sundman transformations is a semidirect product group whose neutral element is $(1,\mathrm{id})$, and the inverse of $(h,\phi )$ is $((1/h)\circ {\phi }^{-1},{\phi }^{-1}).$ Pure Sundman transformations are those of the form $(h,\mathrm{id})$ and constitute an Abelian invariant subgroup, while the usual coordinate transformations correspond to those of the form $(1,\phi )$ and also make up a subgroup. Finally, each transformation can be factorised as

$$(h,\phi )=(1,\phi )★(h,\mathrm{id})=(h\circ {\phi }^{-1},\mathrm{id})★(1,\phi ).$$

Definition 2.

A SODE is fibre-linearisable (or linearisable in velocities) under a generalised Sundman transformation if it can be transformed to a SODE of the form $\ddot{x}+A\left(x\right)\dot{x}+b\left(x\right)=0$, where A and b are real functions, and a SODE is linearisable under generalised a Sundman transformation if it can be transformed into a SODE of the form $\ddot{x}+\alpha \dot{x}+Bx+C=0$ for some real numbers $\alpha ,B,C\in \mathbb{R}$. Note that when $C\ne 0$, the transformed equation is an inhomogeneous linear equation.

The group properties of the set of generalised Sundman transformations can be used to study the linearisability of a scalar SODE:

$$\frac{d^{2}x}{d{t}^2}=X\left(x,\frac{dx}{dt}\right).$$

(38)

The possible linearising transformations will be factorisable as a composition of a pure coordinate transformation and a pure Sundman transformation. Inverting the process, we can first see the form of the image under a pure Sundman transformation of the prototype linear equation. We can see that its image under the general transformation rule for the one-dimensional case is an equation of the form

$$\frac{d^{2}x}{d{t}^2}+{\gamma }_0\left(x\right){\left(\frac{dx}{dt}\right)}^2+A_0\left(x\right)\frac{dx}{dt}+b_0\left(x\right)=0;$$

(39)

i.e., the function $X(x,v)$ is a polynomial of degree two at most in the variable $v=dx/dt$, ${\partial }^{3}X/\partial v^3=0$. Such a class is invariant under changes of coordinates because if $\overline{x}=\phi \left(x\right)$,

$$\frac{d\overline{x}}{dt}=\frac{d\phi }{dx}\frac{dx}{dt},\frac{d^2\overline{x}}{d{t}^2}=\frac{d^2\phi }{d{x}^2}{\left(\frac{dx}{dt}\right)}^2+\frac{d\phi }{dx}\frac{d^{2}x}{d{t}^2},$$

and therefore, $\overline{x}$ satisfies an equation of the same type. Therefore, we obtain the following:

Theorem 4.

A necessary condition for fibre-linearisability under a generalised Sundman transformation is that the function $X(x,v)$ be a polynomial of degree 2 at most in the variable $v=dx/dt$, or in other words, ${\partial }^{3}X/\partial v^3=0$, and consequently, second-order differential equations linearisable under a generalised Sundman transformation must be of the previous form.

Such a class of equations is invariant under a generalised Sundman transformation and contains a subset of linear equations that correspond to the null function ${\gamma }_0=0$. We must determine which of these equations are linearisable.

Note that the quadratic in the velocity term can always be eliminated by an appropriate pure Sundman transformation, $x_1=x$, $d{t}_1=h\left(x\right)dt$. Under such a transformation, the SODE becomes

$$\frac{d^2{x}_1}{d{t}_1^2}+\left({\gamma }_0+\frac{h^{\prime }}{h}\right){\left(\frac{d{x}_1}{d{t}_1}\right)}^2+\frac{1}{h}{A}_0\frac{d{x}_1}{d{t}_1}+\frac{1}{h^2}{b}_0=0,$$

so that the new coefficients are ${\gamma }_1={\gamma }_0+h^{\prime }/h$, $A_1=A_0/h$ and $b_1=b_0/h^2$. We can choose the function h as a nontrivial solution $h_0\left(x\right)$ of the linear ode

$$\frac{dh}{dx}+{\gamma }_0\left(x\right)h=0,$$

with the general solution $h\left(x\right)=K\exp \left(-{\displaystyle \int }{\gamma }_0\left(x\right)dx\right)$, with K being a constant, which is irrelevant for our purposes. With this choice, under the pure Sundman transformation defined by h, the second-order differential equation becomes the fibre-linear equation

$$\frac{d^2{x}_1}{d{t}_1^2}+A_1\left(x_1\right)\frac{d{x}_1}{d{t}_1}+b_1\left(x_1\right)=0,$$

(40)

with $A_1=A_0/h_0$ and $b_1=b_0/h_0^2$. Therefore, any SODE of the given class is fibre-linearisable by a pure Sundman transformation. If both $A_1$ and $b_1$ vanish identically (i.e., $A_0$ and $b_0$ vanish identically), then we have already obtained a special linear equation, more specifically, $d^2{x}_1/d{t}_1^2=0$.

Note that, in the case where at least one of such functions is not the zero function, once we have obtained an inhomogeneous fibre-linear SODE, we can use only the Sundman transformation preserving the set of inhomogeneous fibre-linear SODEs. These are more general than affine transformations of coordinates, as stated in the following lemma.

Lemma 1.

If a generic Sundman transformation $\overline{x}=\phi \left(x\right),d\overline{t}=h\left(x\right)dt$ preserves the set of inhomogeneous fibre-linear SODEs, then there exists a real constant $c=/0$ such that $d\phi /dx=ch$. Moreover, a Sundman transformation $\overline{x}=\phi \left(x\right),d\overline{t}=h\left(x\right)dt$, such that the condition holds, transforms every inhomogeneous fibre-linear SODE

$$\frac{d^{2}x}{d{t}^2}+A\left(x\right)\frac{dx}{dt}+b\left(x\right)=0$$

(41)

into an analogous one with the coefficients $\overline{A}\left(\overline{x}\right)$ and $\overline{b}\left(\overline{x}\right)$, where

$$\overline{A}\left(\overline{x}\right)=\frac{1}{h\left(x\right)}A\left(x\right)and\overline{b}\left(\overline{x}\right)=\frac{c}{h\left(x\right)}b\left(x\right).$$

(42)

The value of the constant c does not have any influence on the linearisability, and without losing generality, we can take $c=1$ (or $c=-1$ when appropriate).

This shows that we can only transform the fibre-linear SODE by means of a Sundman transformation $x_2=\phi \left(x_1\right)$, and $d{t}_2=h\left(x_1\right)d{t}_1,$ with $\phi \left(x\right)={\displaystyle {\int }^x}h\left(\zeta \right)d\zeta$. As for such a transformation, $d{x}_2/d{t}_2=d{x}_1/d{t}_1$, the expression of the transformed SODE is

$$\frac{d^2{x}_2}{d{t}_2^2}+\frac{1}{h\left(x_1\right)}{A}_1\left(x_1\right)\frac{d{x}_2}{d{t}_2}+\frac{1}{h\left(x_1\right)}{b}_1\left(x_1\right)=0,$$

where the substitution of $x_1$ by ${\phi }^{-1}\left(x_2\right)$ in the last two terms is understood.

This SODE is linear if and only if the function $A_1/h$ is constant and the function $b_1/h$ is affine in the variable $x_2$. There are two different situations:

(a) If $A_1$ vanishes identically (also recall that $A_0$ vanishes identically), we can choose the function h as $h=|b_1|$ in the Sundman transformation, and the transformed SODE is

$$\frac{d^2{x}_2}{d{t}_2^2}+\beta =0,\beta =\mathrm{sign}\left(b\right).$$

The Sundman transformation is $x_2={\displaystyle {\int }^{x_1}}\left|b\left(\zeta \right)\right|d\zeta$, and $d{t}_2=\left|b\left(x_1\right)\right|d{t}_1$.

Alternatively, we can take the generalised Sundman transformation $x_2={\displaystyle {\int }^{x_1}}b\left(\zeta \right)d\zeta$, and $d{t}_2=\left|b\left(x_1\right)\right|d{t}_1$, and the transformed SODE is $d^2{x}_2/d{t}_2^2+1=0$.

(b) If $A_1$ is not the zero function, in order to make the coefficient of $d{x}_2/d{t}_2$ constant, we must take $h\left(x_1\right)=\left|A_1\left(x_1\right)\right|$ (up to an irrelevant multiplicative constant). Thus, the transformation $x_2={\displaystyle {\int }^{x_1}}{A}_1\left(\zeta \right)d\zeta$, and $d{t}_2=\left|A_1\left(x_1\right)\right|d{t}_1$, transforms the given inhomogeneous fibre-linear SODE into the form

$$\frac{d^2{x}_2}{d{t}_2^2}+\alpha \frac{d{x}_2}{d{t}_2}+b_2\left(x_2\right)=0,$$

with $\alpha =\mathrm{sign}\left(A\right)$ (once again, we assume $\alpha$ to be constant) and $b_2\left(x_2\right)=b_1\left(x_1\right)/|A_1\left(x_1\right)|$, where we assume that $x_1$ is replaced by its corresponding value in terms of $x_2$.

A generalised Sundman transformation preserving the form of the above SODE, i.e., inhomogeneous fibre-linear with a constant coefficient $\alpha$, must be of the form $\overline{x}=mx+n$, $d\overline{t}=mdt$, with m and n as constants, and therefore, it is either linear or, otherwise, not linearisable. Obviously, the new SODE is linear if and only if $d{b}_2/d{x}_2$ is constant, $d{b}_2/d{x}_2=B\in \mathbb{R}$.

One can find the conditions in the original data ${\gamma }_0$, $A_0$ and $b_0$ for $b_2\left(x_2\right)$ to be an affine function. The following linearisability condition can be proven [48]: the SODE is linearisable if and only if the functions $A_0$, $b_0$ and ${\gamma }_0$ satisfy

$$\left(A_0\frac{d}{dx}-3A_0^{\prime }\right)\left(A_0\frac{d}{dx}+{\gamma }_0{A}_0-A_0^{\prime }\right)b_0=0.$$

Notice that this condition is also satisfied in the first two cases ($A_0=b_0=0$ and $A_0=/0$, $b_0=0$), and moreover, we can prove that such a condition is invariant under a generalised Sundman transformation.

All of these results can be summarised by the following statement [48]:

Theorem 5.

(i) A second-order differential equation

$$\frac{d^{2}x}{d{t}^2}=X\left(x,\frac{dx}{dt}\right)$$

is fibre-linearisable by a Sundman transformation $y=\phi \left(x\right)$, $d\tau =h\left(x\right)dt$, if and only if it is of the form

$$\frac{d^{2}x}{d{t}^2}+\gamma \left(x\right){\left(\frac{dx}{dt}\right)}^2+A\left(x\right)\frac{dx}{dt}+b\left(x\right)=0.$$

(43)

Moreover, it can always be transformed into a constant-coefficient α form

$$\frac{d^{2}y}{d{\tau }^2}+\alpha \frac{dy}{d\tau }+\beta \left(y\right)=0,$$

with $\alpha =\mathrm{sign}\left(A\right)$ (understanding that $\alpha =0$ if $A=0$).

(ii) A second-order differential equation is linearisable if and only if it is of the preceding form and the coefficients $\gamma \left(x\right)$, $A\left(x\right)$ and $b\left(x\right)$ satisfy

$$Q\equiv \left(A\frac{d}{dx}-3A^{\prime }\right)\left(A\frac{d}{dx}+\gamma A-A^{\prime }\right)b=0.$$

(44)

More specifically, we find the following:

• If $A=0$ and $b=0$, then the SODE can be transformed into the form

  $$\frac{d^{2}y}{d{\tau }^2}=0$$

  (45)

  by the Sundman transformation

  $$y=x,d\tau =\exp \left(-{\int }^x\gamma \left(\zeta \right)d\zeta \right)dt.$$

  (46)
• If $A=0$ and $b=/0$, then the SODE can be transformed into the form

  $$\frac{d^{2}y}{d{\tau }^2}+1=0$$

  (47)

  by the Sundman transformation

  $$y={\int }^{x}b\left(\zeta \right)\exp \left(2{\int }^{\zeta }\gamma \left(\eta \right)d\eta \right)d\zeta ,d\tau =\left|b\left(x\right)\right|\exp \left({\int }^x\gamma \left(\zeta \right)d\zeta \right)dt.$$

  (48)
• If $A=/0$ and the above condition is satisfied, then the SODE can be transformed into the form

  $$\frac{d^{2}y}{d{\tau }^2}+\alpha \frac{dy}{d\tau }+By+C=0,$$

  (49)

  where $\alpha =\mathrm{sign}\left(A\right)$, by the Sundman transformation

  $$y={\int }^{x}A\left(\zeta \right)\exp \left({\int }^{\zeta }\gamma \left(\eta \right)d\eta \right)d\zeta ,d\tau =\left|A\left(x\right)\right|dt.$$

  (50)

To illustrate the theory and for the sake of completeness, we mention several examples, which have been more developed in [48].

1. The Ermakov–Pinney differential equation [53,54]

$$\ddot{x}+\frac{2}{x}{\dot{x}}^2+\frac{{\omega }^2}{x^3}=0,$$

so that $\gamma \left(x\right)=2/x$, $A\left(x\right)=0$ and $b\left(x\right)={\omega }^2/x^3$. Therefore, it is Sundman-linearisable and can be transformed into its canonical form by means of the transformation

$$y={\omega }^2{x}^2,d\tau =\frac{{\omega }^2}{x}dt.$$

2. Geodesics on the sphere: The differential equation is $\ddot{x}=2{\dot{x}}^2\cot x+\sin x\cos x$, so that $\gamma \left(x\right)=-2\cot x$, $A\left(x\right)=0$ and $b\left(x\right)=-\sin x\cos x$. It is Sundman-linearisable into its canonical form by means of the transformation given by

$$y=\frac{1}{2{\sin }^2\left(x\right)},d\tau =\left|\cot \left(x\right)\right|dt.$$

3. The differential equation [55]

$$\ddot{x}+\frac{1}{x}{\dot{x}}^2+x\dot{x}+\frac{1}{2}=0,$$

so that $\gamma \left(x\right)=1/x$, $A\left(x\right)=x$ and $b\left(x\right)=1/2$. The condition $Q=0$ is trivially satisfied because

$$\left(A\frac{d}{dx}+\gamma A-A^{\prime }\right)b=\left(x\frac{d}{dx}\right)(1/2)=0,$$

and therefore, it is Sundman-linearisable. If we consider the interval $x>0$, then the Sundman transformation $y=(1/3)x^3$ and $d\tau =xdt$ transforms the given SODE into its canonical form

$$\frac{d^{2}y}{d{\tau }^2}+\frac{dy}{d\tau }+\frac{1}{2}=0.$$

Notice that this equation is not linearisable by point transformations, as it does not satisfy Lie criteria, but it is Sundman-linearisable.

4. As a generalisation of the preceding example, we consider the differential equation

$$\ddot{x}+\frac{1}{x}{\dot{x}}^2+x\dot{x}+b\left(x\right)=0.$$

The condition $Q=0$ is

$$\left(A\frac{d}{dx}-3A^{\prime }\right)\left(A\frac{d}{dx}+\gamma A-A^{\prime }\right)b=({\Delta }_{\mathbb{R}}-3){\Delta }_{\mathbb{R}}b=0,$$

with ${\Delta }_{\mathbb{R}}=x\partial /\partial x$.

Therefore, $Q=0$ if and only if ${\Delta }_{\mathbb{R}}b$ is homogeneous with degree 3, say, ${\Delta }_{\mathbb{R}}b=3k_1{x}^3$ with $k_1\in \mathbb{R}$, and hence, $b\left(x\right)=k_1{x}^3+k_2$. It follows that the more general Sundman-linearisable SODE of the above form is

$$\ddot{x}+{\displaystyle \frac{1}{x}}{\dot{x}}^2+x\dot{x}+k_1{x}^3+k_2=0.$$

A Sundman transformation linearising this equation is $y=(1/3)x^3$ and $d\tau =\left|x\right|dt$.

5. We can also study the Liénard equation,

$$\ddot{x}+f\left(x\right)\dot{x}+g\left(x\right)=0,$$

(51)

and the existence of generalised Sundman transformations leading from the original equation to the linear equation

$$\frac{d^{2}y}{d{\tau }^2}+\sigma \frac{dy}{d\tau }+y=0$$

can also be found [56], because the Liénard equation is a particular case of the master equation

$$\frac{d^{2}x}{d{t}^2}+\gamma \left(x\right){\left(\frac{dx}{dt}\right)}^2+A\left(x\right)\frac{dx}{dt}+b\left(x\right)=0,$$

with $\gamma \left(x\right)=0$, $A\left(x\right)=f\left(x\right)$ and $b\left(x\right)=g\left(x\right)$. The linearisability condition is

$$Q\equiv \left(A\frac{d}{dx}-3A^{\prime }\right)\left(A\frac{d}{dx}+\gamma A-A^{\prime }\right)b=0,$$

(52)

which, in our particular case, turns out to be

$$\left(f\left(x\right)\frac{d}{dx}-3f^{\prime }\left(x\right)\right)\left(f\left(x\right)\frac{d}{dx}-f^{\prime }\left(x\right)\right)g=0,$$

and therefore,

$$f^2{g}^{″}-f{f}^{″}g-3f{f}^{\prime }{g}^{\prime }+3f^{\prime 2}g=0.$$

Then, given the function f, the function g is any function of the linear space of solutions of the linear second-order differential equation in the variable g. As $g=f$ is a solution of such an equation, we introduce the change of the variable $g=f\zeta$, and the new equation is $f{\zeta }^{″}-f^{\prime }{\zeta }^{\prime }=0$, which shows that the general solution is

$$\zeta =k_1{\int }_0^{x}f\left(\xi \right)d\xi +k_2,$$

and therefore, the linearisability condition implies that the function g is

$$g\left(x\right)=k_{1}f\left(x\right){\int }_0^{x}f\left(\xi \right)d\xi +k_{2}f\left(x\right).$$

Finally, the Liénard-type equation containing a dissipative term studied in [57]

$$\ddot{x}+f\left(x\right){\dot{x}}^2+g\left(x\right)\dot{x}+h\left(x\right)=0$$

(53)

can be reduced by a pure Sundman transformation $d\tau =F\left(x\right)dt$ to a Liénard Equation (51), as more explicitly shown in [48].