Osculating Type Ruled Surfaces with Type-2 Bishop Frame in E³

Abstract

The aim of this work is to investigate osculating type ruled surfaces with a type 2-Bishop frame in $E^3$. We accomplish this by employing the symmetry of osculating curves. We examine osculating type ruled surfaces by taking into account the curvatures of the base curve. We investigate the geometric properties of these surfaces, focusing on their cylindrical and developable characteristics. Moreover, we calculate the Gaussian and mean curvatures and provide the requirements for the surface to be flat and minimal. We determine the requirements for the curves lying on this surface to be geodesic, asymptotic curves, or lines of curvature. Furthermore, relations between osculating type ruled surfaces with central tangent and central normal vectors are given. Finally, some examples of these surfaces are presented.

1. Introduction and Preliminaries

Space curves are one of the most important topics of differential geometry. Curves are characterized by the Frenet frame, which consists of tangent, principal normal, and binormal vectors. However, the Frenet frame is defined only for differentiable curves, and the second derivative of curves can be zero at some points. Because of this, for a more thorough examination of the curve, an alternative to the Frenet frame, known as the Bishop frame, was introduced by Bishop in 1975 [1]. The Bishop frame has been used in biology and has spread to fields such as computer graphics. It is used to predict the structural information of DNA helices and to control virtual cameras in computer graphics. This alternative frame, associated with parallel vector fields and also known as the alternative or parallel frame, is obtained without changing the tangent vector on the Frenet frame and by rotating the principal normal and binormal vectors at an angle. The characterizations of curves using the Bishop frame were obtained in [2,3,4]. Later, a new version of the Bishop frame called the “Type-2 Bishop Frame” was defined by [5]. This other alternative frame, also referred to as the parallel frame, is derived by rotating the tangent and principal normal at an angle while keeping the binormal vector unchanged from the Frenet frame. Subsequently, the characterizations of curves according to the type-2 Bishop frame were studied in [4,5,6,7].

Ruled surfaces are defined as surfaces formed by a one-parameter family of straight lines in Euclidean space. The well-known examples of these surfaces are cylinder and conical surfaces. Their unique geometric properties make them a versatile tool with extensive applications across various engineering disciplines such as manufacturing technology, computer-aided geometric design (CAGD), simulation, rigid body Dynamics, and modern engineering practices [8,9,10]. Izumiya and Takeuchi’s studies on ruled surfaces represent a significant contribution to the field of geometry [11,12,13,14]. Moreover, many researchers have studied different curves on ruled surfaces in [13,14,15,16]. On the other hand, the special ruled surfaces with different direction vectors are called generalized rectifying ruled surfaces, generalized normal ruled surfaces, and osculating-type ruled surfaces in $E^3$, as defined by Önder and Kaya [17,18,19]. Ruled surfaces with the type-2 Bishop frame were studied in [20].

In this paper, we define osculating type ruled surfaces with a type-2 Bishop frame by utilizing the symmetry properties related to osculating curves. We examine these surfaces according to curvatures of the base curve. Moreover, we calculate their Gaussian and mean curvatures and investigate surface curves on osculating-type ruled surfaces. We see that some geometric properties of osculating type ruled surfaces with type-2 Bishop frame in $E^3$ shows similarity with the rectifying ruled surfaces according to Frenet frame in $E^3$ [19]. Interestingly, the consequences slightly show that the osculating type ruled surfaces with the type-2 Bishop frame are associated with the rectifying ruled surfaces according to the Frenet frame in $E^3$. Finally, we present illustrative examples demonstrating the properties and behaviors of these surfaces.

Let $\varsigma$ be a regular curve. $\{T,N,B,\kappa ,\tau \}$ and $\{N_1,N_2,B,k_1,k_2\}$ are the Frenet and type-2 Bishop Frame apparatus of the unit speed curve $\varsigma$, respectively. Then Frenet and type-2 Bishop frame formulas are given by [5,21,22].

$$\left[\begin{array}{c}{T}^{\prime }\\ N^{\prime }\\ B^{\prime }\end{array}\right]=\left[\begin{array}{ccc}0& -\kappa & 0\\ -\kappa & 0& \tau \\ 0& -\tau & 0\end{array}\right]\left[\begin{array}{c}T\\ N\\ B\end{array}\right],\left[\begin{array}{c}{N}_1^{\prime }\\ N_2^{\prime }\\ B^{\prime }\end{array}\right]=\left[\begin{array}{ccc}0& 0& -k_1\\ 0& 0& -k_2\\ k_1& k_2& 0\end{array}\right]\left[\begin{array}{c}{N}_1\\ N_2\\ B\end{array}\right].$$

(1)

The relations between Frenet and type-2 Bishop frames are

$$\left[\begin{array}{c}T\\ N\\ B\end{array}\right]=\left[\begin{array}{ccc}sin\mathsf{\Phi }\left(s\right)& -cos\mathsf{\Phi }\left(s\right)& 0\\ cos\mathsf{\Phi }\left(s\right)& sin\mathsf{\Phi }\left(s\right)& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{N}_1\\ N_2\\ B\end{array}\right].$$

(2)

where $\mathsf{\Phi }$ is the angle between the $N_1$ vector of the Bishop frame and the principal normal vector N of the Frenet frame. The curvatures according to the type 2-Bishop frame are defined by [5]

$$\begin{array}{c}\hfill k_1\left(s\right)=-\tau cos\mathsf{\Phi }\left(s\right),k_2\left(s\right)=-\tau sin\mathsf{\Phi }\left(s\right)\end{array}$$

(3)

where ${\displaystyle \mathsf{\Phi }\left(s\right)=arctan\left(\frac{k_2}{k_1}\right)}$, ${\displaystyle \kappa \left(s\right)={\mathsf{\Phi }}^{\prime }\left(s\right)}$ and $\tau \left(s\right)=\sqrt{k_1^2+k_2^2}$. More information about the type-2 Bishop frame can be found in [5,6,7].

A ruled surface ${\mathsf{\Omega }}_{(\varsigma ,\eta )}$ is defined by

$${\mathsf{\Omega }}_{(\varsigma ,\eta )}=\varsigma \left(s\right)+u\eta \left(s\right)$$

(4)

where $\varsigma :I\subset \mathbb{R}\to {\mathbb{R}}^3$, ${\displaystyle \eta \left(s\right):I\to {\mathbb{R}}^3-\left\{0\right\}}$ are the base curve and ruling, respectively. ${\mathsf{\Omega }}_{(\varsigma ,\eta )}$ is cylindrical if and only if ${\eta }^{\prime }=0$ with $\parallel \eta \parallel =1$. The curve d lying on ${\mathsf{\Omega }}_{(\varsigma ,\eta )}$ satisfying the condition $\langle d^{\prime },{\eta }^{\prime }\rangle =0$ is defined as the striction curve of ${\mathsf{\Omega }}_{(\varsigma ,\eta )}$ [23].

The normal vector n, the Gaussian and mean curvatures of ${\mathsf{\Omega }}_{(\varsigma ,\eta )}$ are defined by [22]

$${\displaystyle n(s,u)=\frac{{\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_s\wedge {\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_u}{∥{\displaystyle {\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_s\wedge {\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_u}∥},}$$

(5)

$$\begin{array}{cc}\hfill K& =\frac{eg-f^2}{EG-F^2},H=\frac{Eg-2Ff+Ge}{2(EG-F^2)}\hfill \end{array}$$

(6)

where

$$\begin{array}{cc}\hfill {\displaystyle E}& =〈{\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_s,{\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_s〉,F=〈{\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_s,{\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_u〉,\hfill \\ \hfill G& =〈{\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_u,{\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_u〉,\hfill \end{array}$$

(7)

$$\begin{array}{c}\hfill e=〈{\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_{ss},n〉,f=〈{\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_{su},n〉,g=〈{\left({\mathsf{\Omega }}_{(\varsigma ,\eta )}\right)}_{uu},n〉.\end{array}$$

(8)

More information about surfaces and ruled surfaces can be found in [11,12,13,14,22,23,24].

2. Osculating Type Ruled Surfaces with Type 2-Bishop Frame

We define an osculating developable surface by $O{D}_{\varsigma }=\varsigma \left(s\right)+u\widetilde{D_0}\left(s\right)$ where $\varsigma :I\to {\mathbb{R}}^3$ is a differentiable unit speed curve with curvatures $k_1\left(s\right)\ne 0$, $k_2\left(s\right)$, type 2-Bishop frame $\{N_1,N_2,B\}$ and where $\widetilde{D_0}\left(s\right)$ is the modified Bishop Darboux vector of $\varsigma \left(s\right)$, which is defined by $\widetilde{D_0}\left(s\right)=-\frac{k_2}{k_1}\left(s\right)N_1\left(s\right)+N_2\left(s\right)$. We define a base curve $\varsigma$ of an osculating type ruled surface where the ruling of the surface always lies in the $\{N_1,N_2\}$ plane of $\varsigma$. The definition of a surface can be given as follows:

Definition 1.

Let $\varsigma \left(s\right)$ be a regular curve in ${\mathbb{R}}^3$ with a type-2 Bishop frame. The ruled surface ${\overrightarrow{\mathsf{\Omega }}}_{(\varsigma ,{\eta }_0)}:Ix\mathbb{R}\to {\mathbb{R}}^3$ defined by

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}=\varsigma \left(s\right)+u{\eta }_o\left(s\right),{\eta }_o=r_1\left(s\right)N_1\left(s\right)+r_2\left(s\right)N_2\left(s\right)\end{array}.$$

(9)

is named an osculating type ruled surface where $r_1 and r_2$ are differentiable functions of the arc length of parameter s.

The osculating type developable surface ${\mathsf{\Omega }}_{(\varsigma ,\widetilde{D_0})}$ is an example of an osculating type ruled surface with ${\displaystyle r_1\left(s\right)=-\frac{k_2}{k_1}\left(s\right)}$ and $r_2\left(s\right)=1$. If we take $r_1\left(s\right)=1$ and $r_2\left(s\right)=0$, then we have a developable tangent surface of ${\mathsf{\Omega }}_{(\varsigma ,N_1)}$. Similarly, taking $r_1\left(s\right)=0$ and $r_2\left(s\right)=1$ gives the principal normal surface ${\mathsf{\Omega }}_{(\varsigma ,N_2)}$ of $\varsigma \left(s\right)$.

Theorem 1.

The surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is not regular if and only if

$$\begin{array}{cc}\hfill & r_1\left(s\right)k_1\left(s\right)+r_2\left(s\right)k_2\left(s\right)=0,\hfill \\ \hfill & 1+u{r}_2\left(s\right){\left(\frac{r_1\left(s\right)}{r_2\left(s\right)}\right)}^{\prime }=0.\hfill \end{array}$$

(10)

Proof. 

From the Equations in (9), we obtain

$$\begin{array}{cc}\hfill & {\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_s=(1+u{r}_1^{\prime })N_1+u{r}_2^{\prime }{N}_2-u(r_1{k}_1+r_2{k}_2)B,\hfill \\ \hfill & {\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_u=r_1{N}_1+r_2{N}_2.\hfill \end{array}.$$

(11)

From the last Equations in (11), we get

$$\begin{array}{cc}\hfill {\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_s\wedge {\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_u& =u{r}_2(r_1{k}_1+r_2{k}_2)N_1-u{r}_1(r_1{k}_1+r_2{k}_2)N_2\hfill \\ \hfill & +r_2\left(1+u{r}_2{\left(\frac{r_1}{r_2}\right)}^{\prime }\right)B.\hfill \end{array}$$

(12)

Then, ${\displaystyle {\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_s\wedge {\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_u=0}$ if and only if $r_1{k}_1+r_2{k}_2=0$ and ${\displaystyle 1+u{r}_2{\left(\frac{r_1}{r_2}\right)}^{\prime }=0}$. □

Proposition 1.

Let ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ have singular points and let the base curve ς not be a plane curve with $r_1,r_2\ne 0$. Then the locus of the singular points of ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is the curve $\varrho \left(s\right)=\varsigma \left(s\right)+u{\eta }_o\left(s\right)$ where $r_1{k}_1+r_2{k}_2=0$ and $u\left(s\right)=-{\left(r_2{\left(\frac{k_2}{k_1}\right)}^{\prime }\right)}^{-1}$.

Proof. 

For the singular points of ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ with the help of Equation (10), we have $u\left(s\right)={\left(r_2{\left(\frac{k_2}{k_1}\right)}^{\prime }\right)}^{-1}$. □

From now on, we will take

$$\begin{array}{ccc}\hfill & \tilde{f}\left(s\right)=r_1{k}_1+r_2{k}_2,\hfill & \hfill \tilde{g}(s,u)=1+u{r}_2{\left(\frac{r_1}{r_2}\right)}^{\prime }.\end{array}$$

(13)

From (9), we have ${\eta }_o^{\prime }=r_1^{\prime }{N}_1+r_2^{\prime }{N}_2-fB$. Then, ${\eta }_o^{\prime }=0$ if and only if $r_i$ and $(i=1,2)$ are non-zero constants and $\tilde{f}=0$. As a result, we find that ${\displaystyle \frac{k_2}{k_1}}$ is constant. If ${\displaystyle \frac{k_2}{k_1}=constant}$, we have a contradiction. So, the surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ cannot be cylindrical.

Corollary 1.

There exists no cylindrical osculating type ruled surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$.

Proposition 2.

For $k_1\ne 0$, osculating type ruled surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is developable if and only if ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}={\mathsf{\Omega }}_{(\varsigma ,\widetilde{D_0})}$.

Proof. 

${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is developable if and only if

$$det({\varsigma }^{\prime },{\eta }_o,{\eta }_o^{\prime })=0\iff -r_2\tilde{f}=0.$$

(14)

From (14), $-r_2\tilde{f}=0$ if and only if $\tilde{f}=0$, which implies that ${\displaystyle r_1=-r_2\frac{k_2}{k_1}}$. Thus, we get ${\eta }_o=r_2\left(\left(-\frac{k_2}{k_1}\right)N_1+N_2\right)=r_2\widetilde{D_0}\left(s\right)$, i.e., ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}={\mathsf{\Omega }}_{(\varsigma ,\widetilde{D_0})}$. □

Proposition 3.

Let $\parallel {\eta }_o\parallel =1$ and $\varsigma \left(s\right)$ be a striction line of ${\mathsf{\Omega }}_{(\varsigma ,q_o)}$. Then, $r_1$ is constant.

Proof. 

The striction parameter of ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is obtained as

$${\displaystyle u\left(s\right)=-\frac{\langle {\varsigma }^{\prime },{\eta }_o^{\prime }\rangle }{\langle {\eta }_o^{\prime },{\eta }_o^{\prime }\rangle }=\frac{r_1^{\prime }}{{\left(r_1^{\prime }\right)}^2+{\left(r_2^{\prime }\right)}^2+{\tilde{f}}^2}.}$$

(15)

From (15), we conclude that the curve $\varsigma \left(s\right)$ is a striction line if and only if $r_1$ is constant. □

Corollary 2.

If $k_1\ne 0$, then for the surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$, the following statements are equivalent.

(i) 

${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is developable.

(ii) 

${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}={\mathsf{\Omega }}_{(\varsigma ,\widetilde{D_0})}$.

From Theorem 1 and Proposition 1, we can give the following corollary.

Corollary 3.

The developable osculating type ruled surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is regular if and only if $\tilde{g}\ne 0$.

Corollary 4.

Let ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ be an osculating type ruled surface. Then

(i) 

$\varsigma \left(s\right)$ is a geodesic.

(ii) 

$\varsigma \left(s\right)$ is not an asymptotic curve.

Proof. 

The unit normal vector n of the surface ${\mathsf{\Omega }}_{\left(\varsigma {\eta }_o\right)}$ can be obtained as

$${\displaystyle n(s,u)=\frac{u{r}_2\tilde{f}{N}_1-u{r}_1\tilde{f}{N}_2+r_2\tilde{g}B}{\sqrt{(r_1^2+r_2^2)u^2{\tilde{f}}^2+r_2^2{\tilde{g}}^2}}.}$$

(16)

By taking $u=0$, the unit normal vector along the base curve $\varsigma \left(s\right)$ on ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ can be obtained as $n_{\varsigma }=B$. Thus, we have $n_{\varsigma }\wedge {\varsigma }^{″}=0$, then $\varsigma \left(s\right)$ is a geodesic and the equality $\langle n_{\varsigma },{\varsigma }^{″}\rangle =0$ implies that $\varsigma \left(s\right)$ is not an asymptotic curve. □

Theorem 2.

The curve ς is a line of curvature on the osculating type ruled surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ with the type-2 Bishop frame if and only if ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is a plane.

Proof. 

The curve $\varsigma$ is a line of curvature on the surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ if and only if

$${\displaystyle n_{\varsigma }^{\prime }\wedge {\varsigma }^{\prime }=0\iff -k_{2}B=0}$$

(17)

where $n_{\varsigma }=B$. From (12), we have $k_2=0$. Then, $\varsigma$ lies on the plane $sp\{N_1,N_2\}$ and binormal vector B is constant. Since $n\perp {\eta }_0$ and $n\perp N_1$, we find $n=\pm B$. Then the unit normal vector of ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is constant, which implies that ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is a plane. For the converse, let a unit normal vector n of ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ be constant and ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ be a plane. Since $n\perp sp\{{\eta }_0,N_1\}$, we get $n\perp sp\{N_1,N_2\}$, which means the vector $n=\pm B$ is constant. Then $n_{\varsigma }^{\prime }\wedge {\varsigma }^{\prime }=-k_{2}B=0$ gives $\varsigma$ is a line of curvature on the surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$. □

The fundamental coefficients of the surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ are calculated as follows:

$$\begin{array}{cc}\hfill E=& {(1+u{r}_1^{\prime })}^2+u^2{\left(r_2^{\prime }\right)}^2+u^2{(r_1{k}_1+r_2{k}_2)}^2,\hfill \\ \hfill F=& r_1+u{r}_1{r}_1^{\prime }+u{r}_2{r}_2^{\prime },G=r_1^2+r_2^2,\hfill \\ \hfill e=& \frac{u^2{\tilde{f}}^2(r_1{k}_2-r_2{k}_1)+u^2\tilde{f}(r_2{r}_1^{″}-r_1{r}_2^{″})-r_2\tilde{g}(k_1(1+u{r}_1^{\prime })+u{k}_2{r}_2^{\prime }+u{\tilde{f}}^{\prime })}{\sqrt{(r_1^2+r_2^2)u^2{\tilde{f}}^2+r_2^2{\tilde{g}}^2}},\hfill \\ \hfill f=& 0,g=\frac{\tilde{f}(u(r_1^{\prime }{r}_2-r_1^{\prime }{r}_2)-r_2\tilde{g})}{\sqrt{(r_1^2+r_2^2)u^2{\tilde{f}}^2+r_2^2{\tilde{g}}^2}}.\hfill \end{array}$$

(18)

By using the fundamental coefficients computed in (18), the Gaussian curvature K and the mean curvature H of ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ are given by

$$\begin{array}{cc}\hfill K=& \frac{{\tilde{f}}^2{(u(r_1^{\prime }{r}_2-r_1^{\prime }{r}_2)-r_2\tilde{g})}^2}{{\left((r_1^2+r_2^2)u^2{\tilde{f}}^2+r_2^2{\tilde{g}}^2\right)}^2},\hfill \\ \hfill H=& \frac{\begin{array}{c}\tilde{f}\left\{u^2\left(r_1^2+r_2^2\right)\left(\tilde{f}(r_1{k}_2-r_2{k}_1)+r_2{r}_1^{″}-r_1{r}_2^{″}\right)\right.\hfill \\ -\left.\left(u(r_1^{\prime }{r}_2-r_2^{\prime }{r}_1)-r_2\tilde{g}\left)\right(2r_1+u{(r_1^2+r_2^2)}^{\prime }\right)\right\}\hfill \\ -r_2\tilde{g}\left(r_1^2+r_2^2\right)\left(k_1(1+u{r}_1^{\prime })+u(k_2{r}_2^{\prime }+{\tilde{f}}^{\prime })\right)\hfill \end{array}}{2{\left((r_1^2+r_2^2)u^2{\tilde{f}}^2+r_2^2{\tilde{g}}^2\right)}^{\frac{3}{2}}}\hfill \end{array}$$

(19)

respectively. We can easily see from (19) and Proposition 2 the Gauss curvature K vanishes if and only if the surface is developable. Then, the following corollary can be given:

Corollary 5.

For $k_1\ne 0$ the osculating type ruled surface with vanishing Gauss curvature K is ${\mathsf{\Omega }}_{(\varsigma ,\widetilde{D_0})}$.

Corollary 6.

Regular points of ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ are minimal if and only if

$$\frac{\tilde{f}}{\tilde{g}}=\frac{r_2\left((r_1^2+r_2^2)(k_1(1+u{r}_1^{\prime })+u(k_2{r}_2^{\prime }+{\tilde{f}}^{\prime }))-\tilde{f}(u{(r_1^2+r_2^2)}^{\prime }+2r_1)\right)}{u^2(r_1^2+r_2^2)(\tilde{f}(r_1{k}_2-r_2{k}_1)+r_2{r}_1^{″}-r_1{r}_2^{″})-u(r_1^{\prime }{r}_2-r_1{r}_2^{\prime })(u{(r_1^2+r_2^2)}^{\prime }+2r_1)}.$$

(20)

Theorem 3.

Let ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ be developable osculating type ruled surface. For $k_1=0$, the ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is minimal and for $k_1\ne 0$, the ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is not minimal.

Proof. 

Let ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ be developable. Then, $\tilde{f}=0$ and from (19), we get

$${\displaystyle H=\frac{-(r_1^2+r_2^2)(k_1(1+u{r}_1^{\prime })+u{k}_2{r}_2^{\prime })}{2r_2^2{\tilde{g}}^2}.}$$

(21)

If $k_1=0$, then $k_2=0$ and we have $H=0$. This result implies that ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is minimal. If $k_1\ne 0$, then by utilizing $\tilde{f}=0$ in (21) we obtain

$${\displaystyle H=\frac{r_1{k}_2-r_2{k}_1}{2r_2\tilde{g}}..}$$

(22)

From (22), ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is minimal if and only if $r_1{k}_2-r_2{k}_1=0$. Hence, we obtain $r_2/r_1=-r_1/r_2$. Then, $r_1^2+r_2^2=0$ gives $r_1=r_2=0$. In that case, ${\eta }_o=0$ which is a contradiction. Therefore, ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is not minimal. □

Corollary 7.

If $k_1\ne 0$, there is no developable osculating type ruled helicoid.

Proof. 

The Catalan Theorem in [24] puts forward that helicoids and pieces of helicoids are the only minimal ruled surfaces and, as a result of Theorem 3, there is no developable osculating type ruled helicoid. □

Under the assumption that ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is developable, the Equations in (11) can be written as

$$\begin{array}{cc}\hfill {\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_s=& (1+u{r}_1^{\prime })N_1+u{r}_2^{\prime }{N}_2,\hfill \\ \hfill {\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_u=& r_1{N}_1+r_2{N}_2\hfill \end{array}.$$

(23)

and the normal vector n of the surface is $\overrightarrow{n}=B$. For the vector ${\overrightarrow{\vartheta }}_p\in T_p{\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$, the Weingarten map of the surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is expressed by ${\displaystyle S_p=-D_p\overrightarrow{\vartheta }:T_p{\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\to T_{{\vartheta }_p}{S}^2}$, where $T_p{\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is tangent space and ${\displaystyle \left\{{\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_s,{\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_u\right\}}$ is its base at $p\in T_p{\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$. Then, we have

$$\begin{array}{cc}\hfill {\displaystyle S_p{\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_s}& {\displaystyle =-\frac{\partial n}{\partial s}=\frac{r_1{k}_2-r_2{k}_1}{r_2\tilde{g}}{\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_s+\frac{u{k}_1{r}_2^{\prime }-k_2(1+u{r}_1^{\prime })}{r_2\tilde{g}}{\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_u,}\hfill \\ \hfill {\displaystyle S_p{\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_u}& {\displaystyle =-\frac{\partial n}{\partial u}=0.}\hfill \end{array}$$

(24)

Then the Weingarten map can be expressed by

$$S=\left[\begin{array}{cc}{\displaystyle \frac{r_1{k}_2-r_2{k}_1}{r_2\tilde{g}}}& 0\\ {\displaystyle \frac{u{k}_1{r}_2^{\prime }-k_2(1+u{r}_1^{\prime })}{r_2\tilde{g}}}& 0\end{array}\right].$$

(25)

Thus, for the surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$, the Gaussian curvature and mean curvature are expressed by

$${\displaystyle K=det\left(S_p\right)=0andH=\frac{1}{2}tr\left(S_p\right)=\frac{r_1{k}_2-r_2{k}_1}{2r_2\tilde{g}},}$$

(26)

respectively. From $det(S_p-\lambda I)=0$, we get the principal curvatures of the surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ as ${\displaystyle {\lambda }_1=\frac{r_1{k}_2-r_2{k}_1}{r_2\tilde{g}}}$, and ${\lambda }_2=0$. Hence, the following corollary can be given:

Corollary 8.

Let ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ be a developable osculating type ruled surface.

(i) 

For $k_1\ne 0$, there exists no umbilical point on the surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$.

(ii) 

For ${\lambda }_1{\lambda }_2=0$ and $k_1\ne {\lambda }_1\ne 0$, the quadratic approach of the surface is a parabolic cylinder.

(iii) 

For ${\lambda }_1={\lambda }_2=0$, the quadratic approach of the surface is a plane.

Since the unit normal vector n of the developable osculating type ruled surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ along the base curve $\varsigma \left(s\right)$ is $n_{\varsigma }=B$, we have

$$S_p\left(N_1\right)=-D_{N_1}{n}_{\varsigma }=-\frac{n_{\varsigma }}{ds}=-k_1{N}_1-k_2{N}_2.$$

(27)

The base curve $\varsigma \left(s\right)$ is a line of curvature, i.e, ($S_{N_1}=\lambda N_1$) if and only if $\varsigma \left(s\right)$ is a plane curve. However, ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ being developable implies that ${\displaystyle k_1=-\left(\frac{r_2}{r_1}\right)k_2}$. Then $r_1\ne 0$ and $k_2=0$ satisfies $k_1=0$ so that $\varsigma \left(s\right)$ is a line. Therefore, the following corollary can be given:

Corollary 9.

The base curve $\varsigma \left(s\right)$ is a line of curvature if and only if $\varsigma \left(s\right)$ is a line.

If $k_1\ne 0$, the equation $S\left({\lambda }_1\right)={\lambda }_1{e}_1$ gives the principal direction $e_1$ as

$$e_1=\left(\frac{r_1{k}_2-r_2{k}_1}{r_2\tilde{g}}\right){\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_s+\left(\frac{u{k}_1{r}_2^{\prime }-k_2(1+u{r}_1^{\prime })}{r_2\tilde{g}}\right){\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_u.$$

(28)

If we assume $r_1{k}_2-r_2{k}_1=0$, it leads to a contradiction. Then the following corollary can be given:

Corollary 10.

Let $k_1\ne 0$ and ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ be a developable osculating type ruled surface.

(i) 

The parameter curve ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}(s,u_0)$ is a line of curvature if and only if $u_0{k}_1{r}_2^{\prime }-k_2(1+u_0{r}_1^{\prime })=0$.

(ii) 

The parameter curve ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}(s_0,u)$ cannot be a line of curvature.

Moreover, using (11) in (28), we get $e_1=-k_1{N}_1-k_2{N}_2$. This result satisfies Corollary 9.

Assume that ${\vartheta }_p\in T_p{\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is a unit tangent vector at a point p on the developable osculating type ruled surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$. Then we express ${\vartheta }_p$ as

$${\displaystyle {\vartheta }_p=A(s,u){\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_s+B(s,u){\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_u}$$

(29)

where A and B are differential functions and $A^2+B^2=1$. Then, we have

$${\displaystyle S_p\left({\vartheta }_p\right)=A(s,u)\left[\left(\frac{r_1{k}_2-r_2{k}_1}{r_2\tilde{g}}\right){\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_s+\left(\frac{u{k}_1{r}_2^{\prime }-k_2(1+u{r}_1^{\prime })}{r_2\tilde{g}}\right){\left({\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}\right)}_u\right].}$$

(30)

Using (11) in (29) and (30), it is obtained that

$$\begin{array}{cc}\hfill & {\vartheta }_p=(A(1+u{r}_1^{\prime })+B{r}_1)N_1+(Au{r}_2^{\prime }+B{r}_2)N_2,\hfill \\ \hfill & S_p\left({\vartheta }_p\right)=-A(k_1{N}_1+k_2{N}_2).\hfill \end{array}$$

(31)

Then the normal curvature can be written as

$$\begin{array}{cc}\hfill k_n\left({\vartheta }_p\right)& =\langle S_p\left(v_p\right),v_p\rangle \hfill \\ \hfill & =-A[k_1(A(1+u{r}_1^{\prime })+B{r}_1)+k_2(Au{r}_2^{\prime }+B{r}_2)].\hfill \end{array}$$

(32)

If $k_1\ne 0$, since ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is developable, ${\displaystyle k_2=-k_1\left(\frac{r_1}{r_2}\right)}$ is obtained. Then, (32) becomes $k_n\left(v_p\right)=-A^2{k}_1\tilde{g}$. If $k_1=0$, we get $k_n\left(v_p\right)=0$. Then the following theorem can be given:

Theorem 4.

Let ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ be a developable osculating type ruled surface.

(i) 

If $k_1\ne 0$, then a unit tangent vector $\vartheta \left(p\right)\in T_p{\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is asymptotic if and only if $\tilde{g}=0$ and ${\vartheta }_p={\eta }_o$.

(ii) 

If $k_1=0$, then ς is a straight line and any tangent vector ${\vartheta }_p$ is asymptotic.

Since the vector ${\eta }_o$ is unit, considering the type-2 Bishop frame of the osculating type ruled surface, we can take ${\eta }_o=cos\psi \left(s\right)N_1\left(s\right)+sin\psi \left(s\right)N_2\left(s\right)$ where $\psi$ is the angle between ${\eta }_o$ and $N_1$. Differentiating the ruling ${\eta }_o$ with respect to s, we obtain

$${\eta }_o^{\prime }=-\left({\psi }^{\prime }sin\psi \right)N_1+\left({\psi }^{\prime }cos\psi \right)N_2-\tilde{f}B$$

(33)

where $\tilde{f}=k_{1}cos\psi +k_{2}sin\psi$. Then, using the definitions in [23], the central normal and central tangent vectors of the surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ are determined by

$$\begin{array}{cc}\hfill h\left(s\right)& =\frac{{\eta }_o^{\prime }\left(s\right)}{\parallel {\eta }_o^{\prime }\left(s\right)\parallel }=\frac{-({\psi }^{\prime }sin\psi )N_1+({\psi }^{\prime }cos\psi )N_2-\tilde{f}B}{\sqrt{{\left({\psi }^{\prime }\right)}^2+{\tilde{f}}^2}},\hfill \\ \hfill a\left(s\right)& ={\eta }_o\left(s\right)\wedge h\left(s\right)=\frac{-(\tilde{f}sin\psi )N_1+(\tilde{f}cos\psi )N_2+{\psi }^{\prime }B}{\sqrt{{\left({\psi }^{\prime }\right)}^2+{\tilde{f}}^2}}\hfill \end{array}$$

(34)

respectively. Then the following corollaries can be given:

Corollary 11.

Let ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ be an osculating type ruled surface. Then the following statements are equivalent:

(i) 

The angle between ${\eta }_o$ and $N_1$ is constant.

(ii) 

The central normal vector $h\left(s\right)$ and the binormal vector of ς are linearly dependent.

(iii) 

The central tangent vector $a\left(s\right)$ lies on the plane $\{N_1,N_2\}$ of ς.

Corollary 12.

For the osculating type ruled surface ${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ the following statements are equivalent:

(i) 

${\mathsf{\Omega }}_{(\varsigma ,{\eta }_o)}$ is developable.

(ii) 

The central normal vector $h\left(s\right)$ lies on the plane $\{N_1,N_2\}$ of ς.

(iii) 

The central tangent vector $a\left(s\right)$ and the binormal vector of ς are linearly dependent.

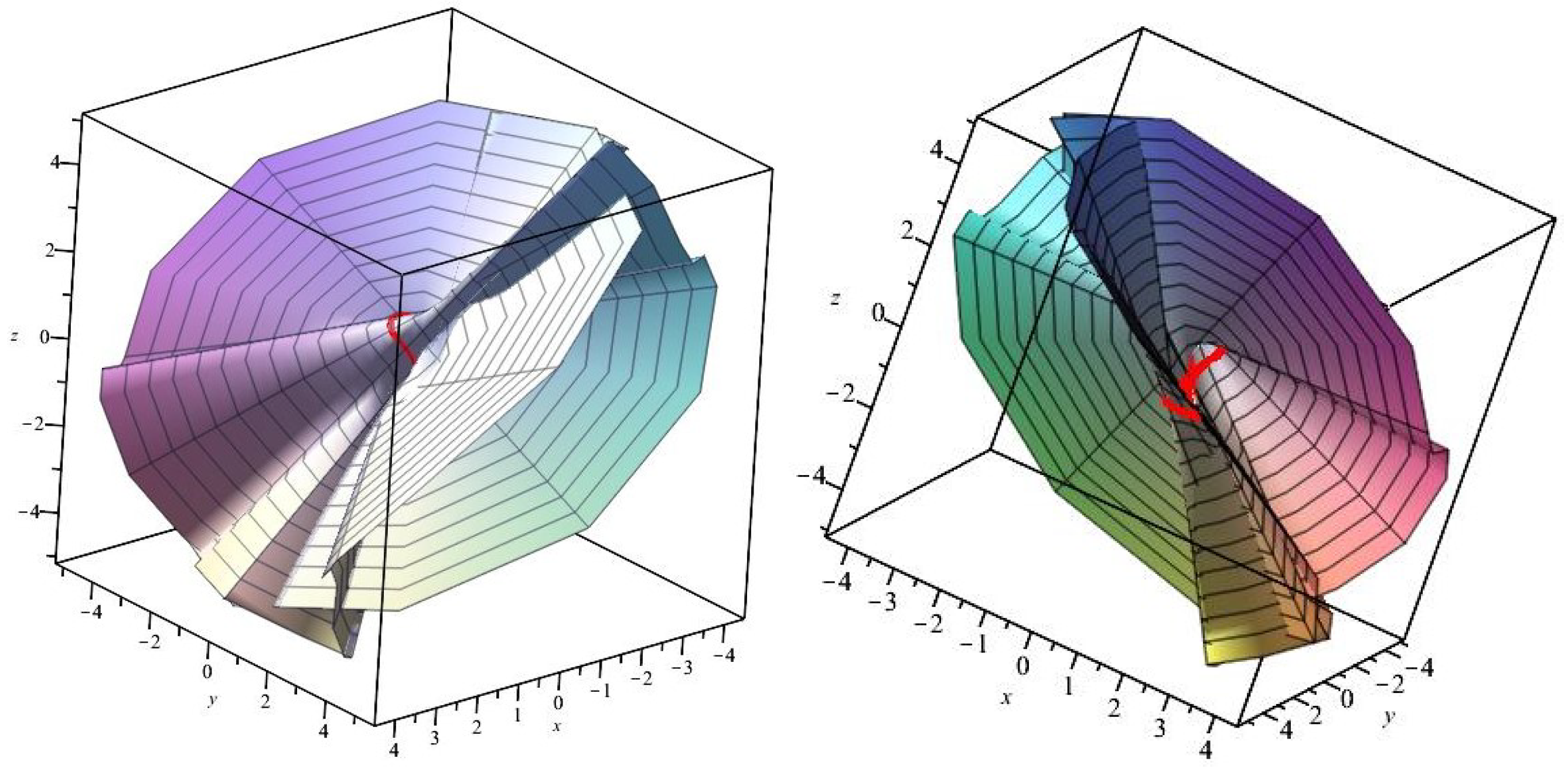
Example 1.

Let $\xi \left(s\right)$ be a unit speed curve of $E^3$ given by

$$\xi \left(s\right)=\left(12cos\frac{s}{13},12sin\frac{s}{13},\frac{5s}{13}\right).$$

(35)

Using (2), the type-2 Bishop frame of $\xi =\xi \left(s\right)$ is written as follows:

$$\begin{array}{cc}\hfill N_1\left(s\right)=& (-\frac{12}{13}sin\frac{12s}{169}sin\frac{s}{13}-cos\frac{12s}{169}cos\frac{s}{13},\hfill \\ \hfill & \frac{12}{13}sin\frac{12s}{169}cos\frac{s}{13}-cos\frac{12s}{169}sin\frac{s}{13},\frac{5}{13}sin\frac{12s}{169}),\hfill \\ \hfill N_2\left(s\right)=& (\frac{12}{13}cos\frac{12s}{169}sin\frac{s}{13}-sin\frac{12s}{169}cos\frac{s}{13},\hfill \\ \hfill & -\frac{12}{13}cos\frac{12s}{169}cos\frac{s}{13}-sin\frac{12s}{169}sin\frac{s}{13},-\frac{5}{13}cos\frac{12s}{169}),\hfill \\ \hfill k_1\left(s\right)=& -\frac{5}{169}cos\frac{12s}{169},k_2\left(s\right)=-\frac{5}{169}sin\frac{12s}{169}\hfill \end{array}$$

(36)

where $\mathsf{\Phi }\left(s\right)={\int }_0^s\frac{12}{169}ds=\frac{12s}{169}$.

By taking ${\displaystyle r_1\left(s\right)=-sin\frac{12s}{169}}$ and ${\displaystyle r_2\left(s\right)=cos\frac{12s}{169}}$, developable osculating type ruled surface ${\mathsf{\Omega }}_{1(\xi ,{\eta }_o)}$ is obtained as (37). The surface is displayed in Figure 1.

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{1(\xi ,{\eta }_o)}=\left(12cos\frac{s}{13},12sin\frac{s}{13},\frac{5s}{13}\right)+u\left(\frac{12}{13}sin\frac{s}{13},-\frac{12}{13}cos\frac{s}{13},-\frac{5}{13}\right).\end{array}$$

(37)

By taking ${\displaystyle r_1\left(s\right)=-cos\frac{12s}{169}}$ and ${\displaystyle r_2\left(s\right)=sin\frac{12s}{169}}$, we obtain a non-developable osculating type ruled surface ${\mathsf{\Omega }}_{2(\xi ,{\eta }_o)}=\xi \left(s\right)+u{\eta }_o\left(s\right)$. The surface is displayed in Figure 2 where

$$\begin{array}{cc}\hfill {\eta }_o\left(s\right)& =(\frac{12}{13}sin\frac{24s}{169}sin\frac{s}{13}+cos\frac{24s}{169}cos\frac{s}{13},\hfill \\ \hfill & cos\frac{24s}{169}sin\frac{s}{13}-\frac{12}{13}sin\frac{24s}{169}cos\frac{s}{13},-\frac{5}{13}sin\frac{24s}{169}).\hfill \end{array}$$

(38)

Example 2.

Let $\rho \left(s\right)$ be a unit speed curve of $E^3$ given by

$$\rho \left(s\right)=\left(\frac{1}{12}sin4s-\frac{1}{3}sin2s,-\frac{1}{12}cos4s+\frac{1}{3}cos2s,\frac{2\sqrt{2}}{3}sins\right).$$

(39)

Using (2), the type-2 Bishop frame of $\rho =\rho \left(s\right)$ is written as follows:

$$\begin{array}{cc}\hfill N_1\left(s\right)& =(sin(2\sqrt{2}coss)\left(\frac{1}{3}cos4s-\frac{2}{3}cos2s\right)+\frac{2\sqrt{2}}{3}cos(2\sqrt{2}coss)cos3s,\hfill \\ \hfill & sin(2\sqrt{2}coss)\left(\frac{1}{3}sin4s-\frac{2}{3}sin2s\right)+\frac{2\sqrt{2}}{3}cos(2\sqrt{2}coss)sin3s,\hfill \\ \hfill & \frac{2\sqrt{2}}{3}sin(2\sqrt{2}coss)coss+\frac{1}{3}cos(2\sqrt{2}coss)),\hfill \\ \hfill N_2\left(s\right)& =(cos(2\sqrt{2}coss)\left(-\frac{1}{3}cos4s+\frac{2}{3}cos2s\right)+\frac{2\sqrt{2}}{3}sin(2\sqrt{2}coss)cos3s,\hfill \\ \hfill & +cos(2\sqrt{2}coss)\left(-\frac{1}{3}sin4s+\frac{2}{3}sin2s\right)+\frac{2\sqrt{2}}{3}sin(2\sqrt{2}coss)sin3s,\hfill \\ \hfill & \frac{1}{3}sin(2\sqrt{2}coss)-\frac{2\sqrt{2}}{3}cos(2\sqrt{2}coss)coss),\hfill \\ \hfill k_1\left(s\right)& =-2\sqrt{2}cosscos(2\sqrt{2}coss),k_2\left(s\right)=-2\sqrt{2}cosssin(2\sqrt{2}coss)\hfill \end{array}$$

(40)

where ${\displaystyle \mathsf{\Phi }\left(s\right)=-2\sqrt{2}{\int }_0^{s}sinsds=2\sqrt{2}coss}$.

By taking $r_1\left(s\right)=-sin(2\sqrt{2}coss)$ and $r_2\left(s\right)=cos(2\sqrt{2}coss)$, a developable osculating type ruled surface ${\mathsf{\Omega }}_{1(\rho ,{\eta }_o)}=\rho \left(s\right)+u{\eta }_o\left(s\right)$ is displayed in Figure 3 where

$$\begin{array}{c}\hfill {\eta }_o\left(s\right)=\left(-\frac{1}{3}cos4s+\frac{2}{3}cos2s,-\frac{1}{3}sin4s+\frac{2}{3}sin2s,-\frac{2\sqrt{2}}{3}coss\right).\end{array}$$

(41)

By taking $r_1\left(s\right)=r_2\left(s\right)=\frac{\sqrt{3}}{3}$, we obtain a non-developable osculating type ruled surface ${\mathsf{\Omega }}_{2(\rho ,{\eta }_o)}=\rho \left(s\right)+u{\eta }_o\left(s\right)$ is displayed in Figure 4 where

$$\begin{array}{cc}\hfill {\eta }_o\left(s\right)& =\frac{\sqrt{3}}{3}(sin(2\sqrt{2}coss)\left(\frac{1}{3}cos4s-\frac{2}{3}cos2s\right)+\frac{2\sqrt{2}}{3}cos3scos(2\sqrt{2}coss),\hfill \\ \hfill & -sin(2\sqrt{2}coss)\left(\frac{1}{3}sin4s+\frac{2}{3}sin2s\right)+\frac{2\sqrt{2}}{3}cos(2\sqrt{2}coss)sin3s,\hfill \\ \hfill & \frac{2\sqrt{2}}{3}sin(2\sqrt{2}coss)coss+\frac{1}{3}cos(2\sqrt{2}coss))\hfill \\ \hfill & +\frac{\sqrt{3}}{3}(cos(2\sqrt{2}coss)\left(-\frac{1}{3}cos4s+\frac{2}{3}cos2s\right)+\frac{2\sqrt{2}}{3}sin(2\sqrt{2}coss)cos3s,\hfill \\ \hfill & -cos(2\sqrt{2}coss))\left(\frac{1}{3}sin4s-\frac{2}{3}sin2s\right)+\frac{2\sqrt{2}}{3}sin3ssin(2\sqrt{2}coss)sin3s,\hfill \\ \hfill & \frac{1}{3}sin(2\sqrt{2}coss)-\frac{2\sqrt{2}}{3}cos(2\sqrt{2}coss)coss).\hfill \end{array}$$

(42)

3. Conclusions

This study examines the construction of osculating type ruled surfaces, whose ruling always lies on the osculating plane of the base curve with the type 2-Bishop frame in ${\mathbb{R}}^3$. The differential geometric features of these surfaces are expressed in terms of the curvatures of the base curve. The conditions for these surfaces to be cylindrical and developable are given. Moreover, the Gaussian and mean curvatures are calculated and examined for conditions to be flat and minimal. Finally, we investigate the conditions for the isoparametric curves to be geodesic, asymptotic curves or lines of curvature. Examples of these surfaces are given and their graphics are drawn. With this research, we offer a new study to the literature by investigating geometric properties of these surfaces according to the type 2-Bishop frame.