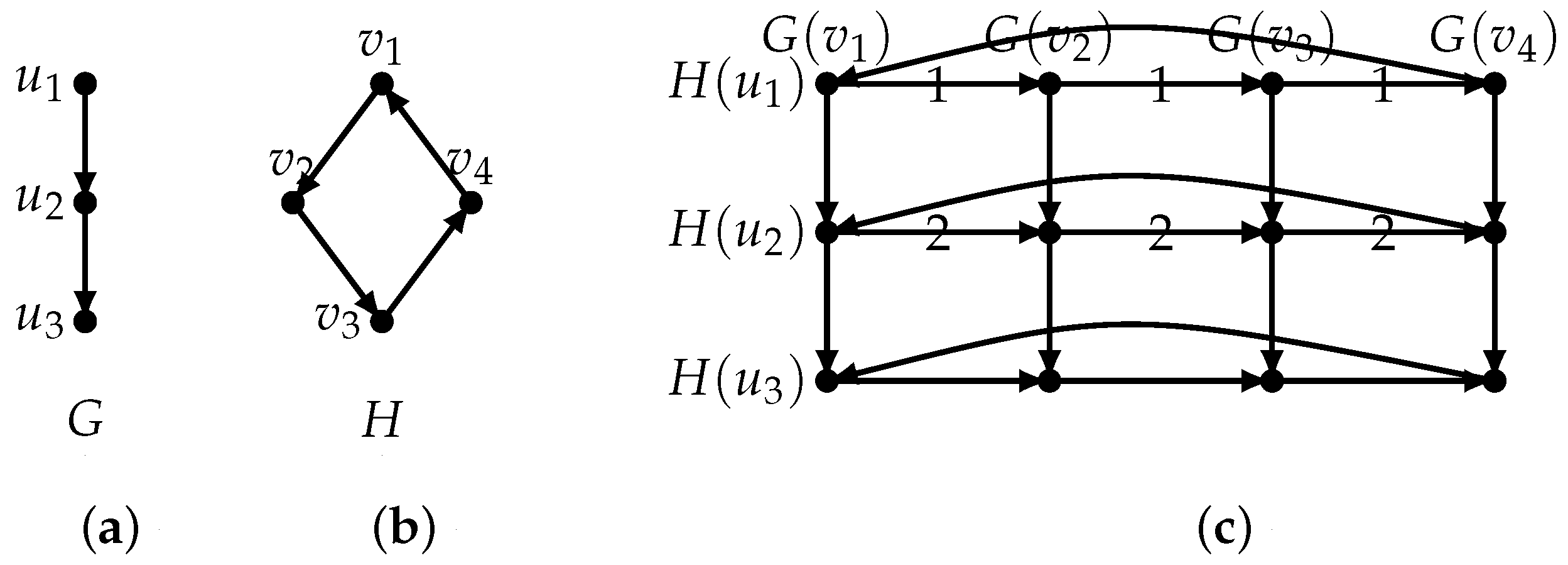
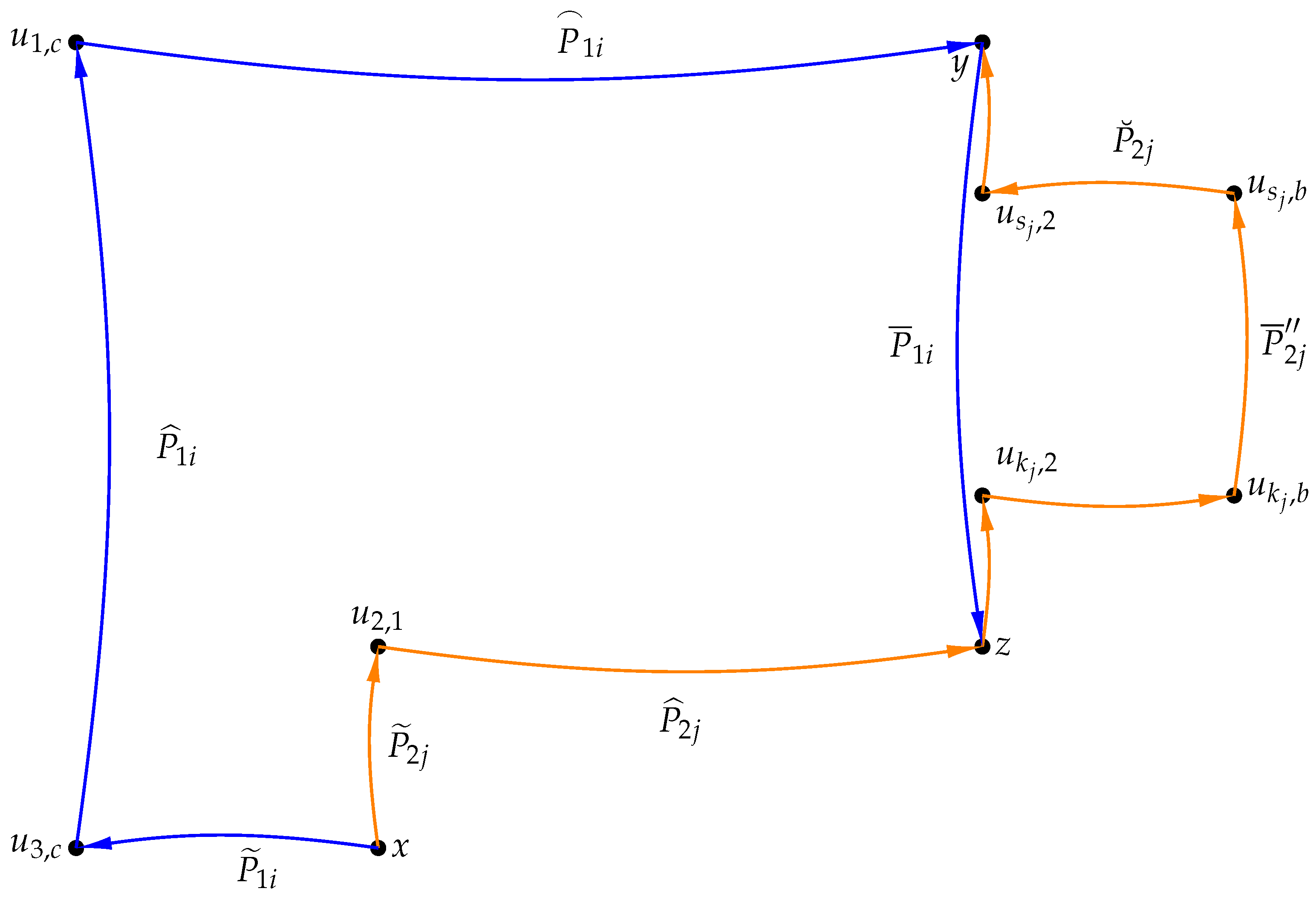
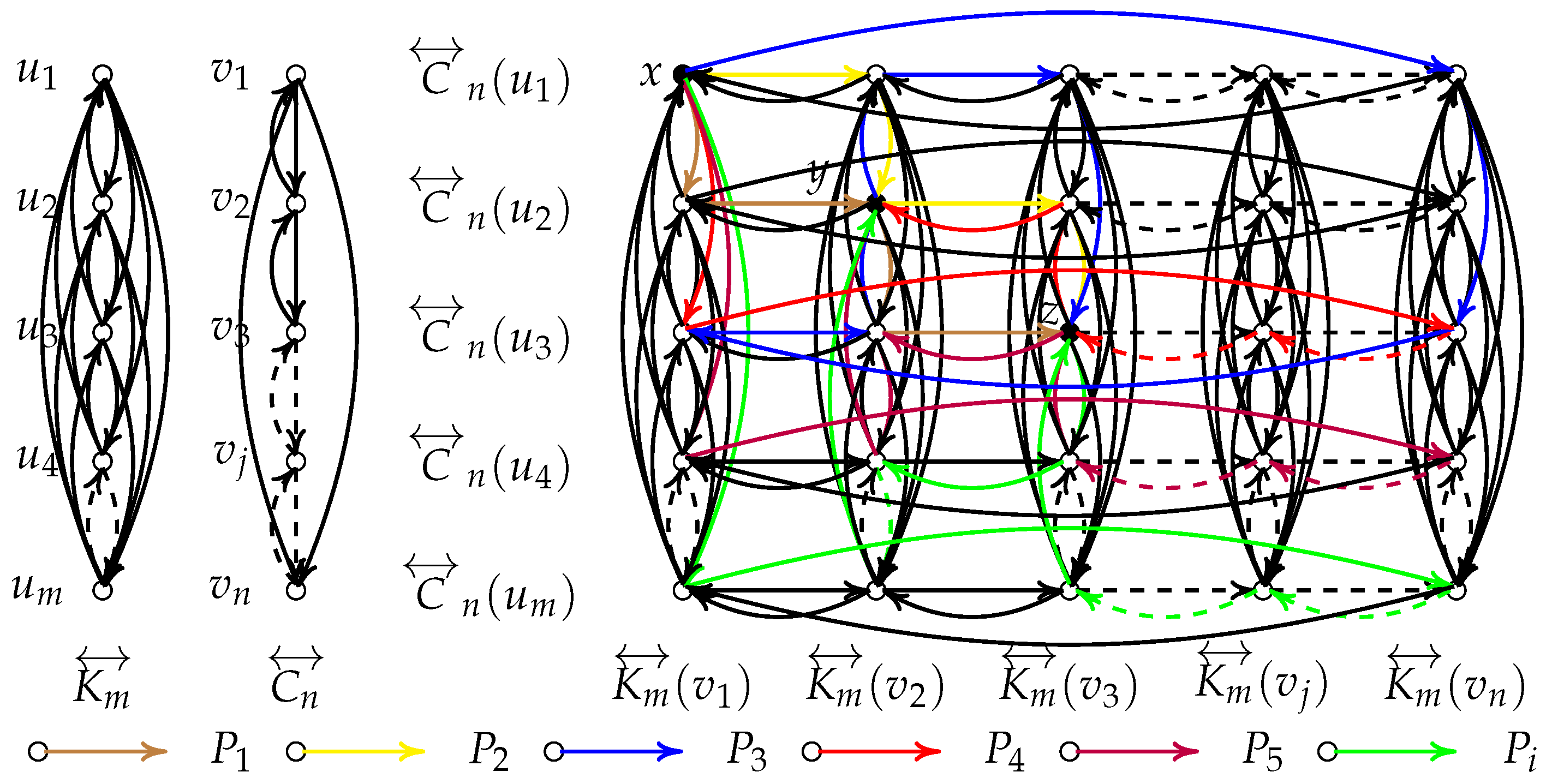
Proof. It suffices to show that there are at least or arc-disjoint -paths for any with , . Let and let . Without loss of generality, we may assume and consider the following six cases.
Case 1. Let
x,
y and
z be in the same
or
for some
,
. Without loss of generality, we may assume that
,
,
. In this case, our overall goal is that we will use arc-disjoint paths between
x and
y in
,
y and
z in
,
x and its out-neighbors in
,
y and its in-neighbors in
,
z and its in-neighbors in
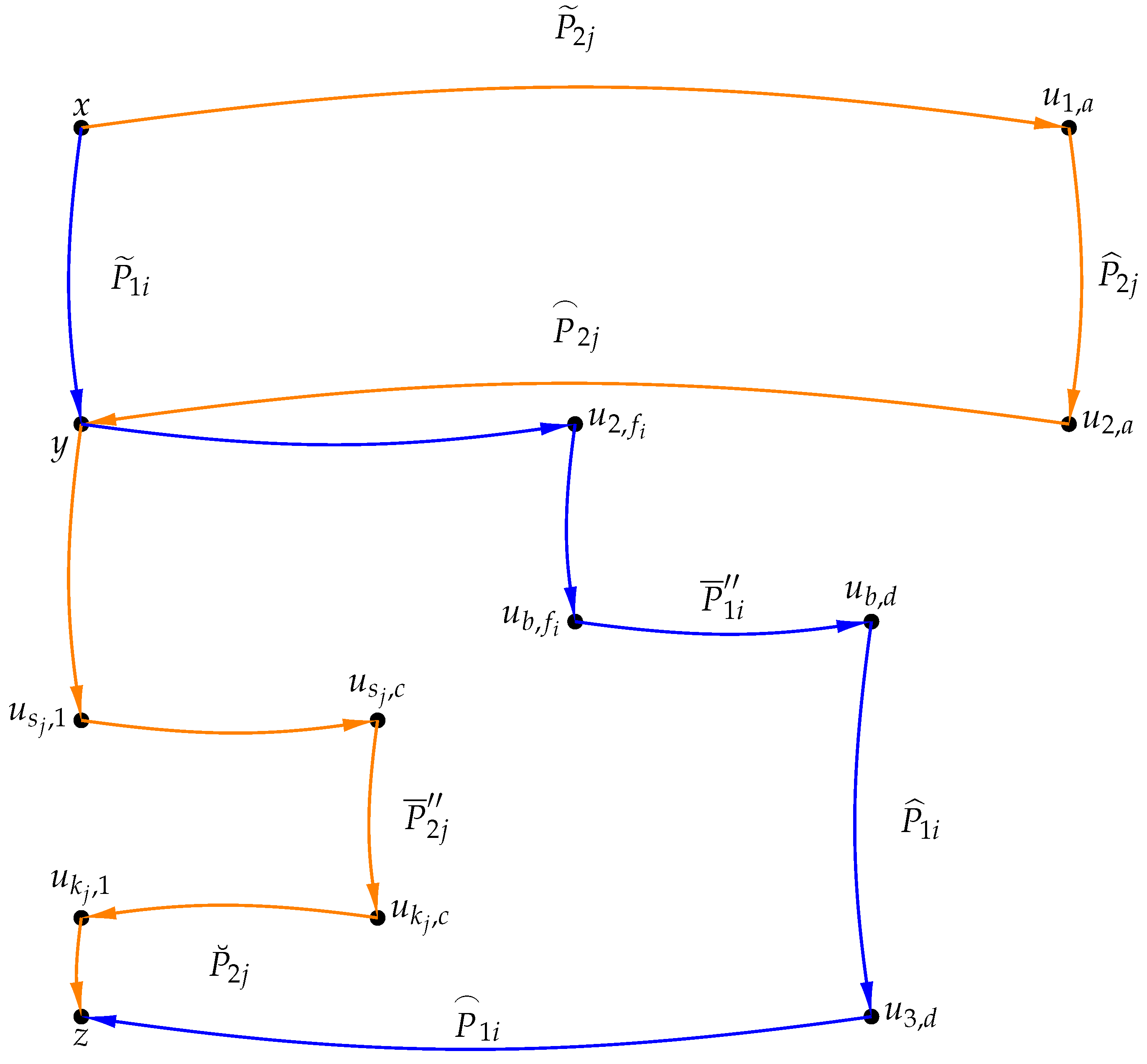
, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in
Figure 2. The vertices and paths contained in
Figure 2 are explained below.
Let , . It is known that there are at least internally disjoint -paths in , denoted as . Considering , , there are at least internally disjoint -paths in , denoted as . For each , let be the out-neighbor of y in ; clearly these out-neighbors are distinct. Similarly, an in-neighbor of z in can be chosen such that these in-neighbors are distinct. In , if there is a vertex that is not an out-neighbor of x, then choose such a vertex as , where . If there is no such vertex, that is, all vertices are out-neighbours of x, then choose any vertex as , where . In , let , , and it is established that there exist at least internally disjoint -paths, say . In , let , , and it is established that there exist at least internally disjoint -paths, say . In , let , , and it is established that there exist at least internally disjoint -paths, say .
In , if there is a vertex that is not an out-neighbor of x in , then choose such a vertex as , with . If there is no such vertex, then choose any vertex as , with . In , with and , it is known that there are at least internally disjoint -paths, denoted as . For each , let be the out-neighbor of y in ; clearly these out-neighbors are distinct. For each , since , an out-neighbor of in , denoted by , can be chosen, with . If there exists a vertex , let . If there is no such vertex, then let . In , is the -path corresponding to , where , and . In , the path from vertex to is denoted as . Let , , and it is established that there exist at least internally disjoint -paths, say . If , then let in . In , let , , and it is established that there exist at least internally disjoint -paths, say .
In , if there is an out-neighbor of x that is not an out-neighbor of x in , then choose such a vertex as , with . If there is no such vertex, then choose any out-neighbor of x as , with . And is an out-neighbor of in . In , is the -path corresponding to , where and . In , the path from vertex to is denoted as . If , then . If , then . If , then . In , with , and , it is known that there exist at least internally disjoint -paths. Then in these paths, one of the paths is chosen, with .
Subcase 1.1. In the set , there is no vertex such that or , and the vertex z is not in path . We now construct the arc-disjoint -paths by letting
.
Then we obtain arc-disjoint -paths.
Subcase 1.2. In the set , there is no vertex such that or , and there exist , but there is no arc in path . Let . The other paths are the same as Subcase 1.1.
Subcase 1.3. There is an arc in path . In the set , there is no vertex x. We can find a path such that . If , then let . If , then let . In and , let and . Let
.
The other paths are the same as Subcase 1.1.
Subcase 1.4. The set contains the vertex and . There is no arc in . In , there is an arc , . In , there exists an out-neighbor of x, where , and this path is denoted by .
Subcase 1.4.1. There is no arc in .
In , the path from vertex to is denoted as . In , with and , it is known that there exist at least internally disjoint -paths. Then in these paths, one of the paths is chosen, with . If , then let . In , the path from vertex to is denoted as . Let
If , then . The other paths are the same as Subcases 1.1–1.3.
Subcase 1.4.2. If there exists an arc in , then in , with and , it is known that there exist at least internally disjoint -paths. Then in these paths, one of the paths is chosen, with . In , the path from vertex to y is denoted as . Let be the same as in Subcase 1.4.1. Let
The other paths are the same as Subcases 1.1–1.3.
Subcase 1.5. In the set , there exists vertex . And there is no arc in .
In , there is an out-neighbor of x such that , and this path is denoted by . In , let , , and we know there exist at least internally disjoint -paths. Then in these paths, we choose one of the paths , and let . In , we denote the path from vertex to as . Let
The other paths are the same as Subcases 1.1–1.3.
Case 2. Let
x and
y be in the same
. Let
x and
z be in the same
for some
,
. Without loss of generality, we may assume that
,
,
. In this case, our overall goal is that we will use arc-disjoint paths between
x and
y in
,
y and its out-neighbors in
,
z and its in-neighbors in
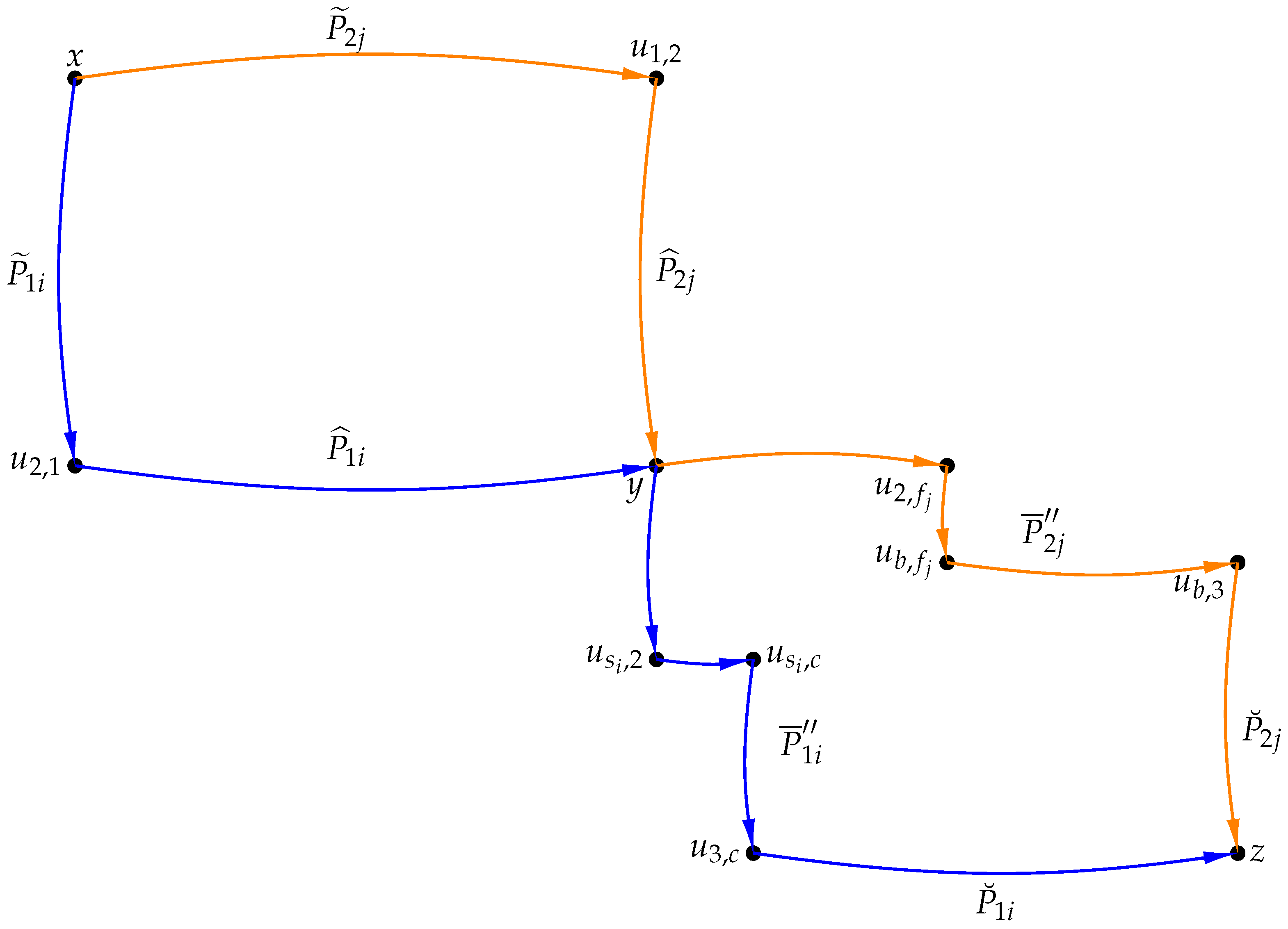
, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in
Figure 3. The vertices and paths contained in
Figure 3 are explained below.
Considering , , it is known that there exist at least internally disjoint -paths in , denoted as . Let , , and there exist at least internally disjoint -paths in , denoted as . For each , let be the out-neighbor of y in ; clearly these out-neighbors are distinct. For each , an out-neighbor of in can be chosen, with . In , with and . is the -path corresponding to . In , the path from vertex to is denoted . With and , it is known that there exist at least internally disjoint -paths in , denoted as . If , then . The arc-disjoint -paths can be constructed as
,
Likewise, we can identify arc-disjoint -paths from x to z and subsequently to y. Consequently, we can derive arc-disjoint -paths.
Case 3. Let
x,
y and
z be in different
and
for some
,
. Without loss of generality, we can assume that
,
,
. In this case, our overall goal is that, we will use arc-disjoint paths between
x and its out-neighbors in
,
y and its out-neighbors in
,
z and its in-neighbors in
,
x and its out-neighbors in
,
y and its out-neighbors in
,
z and its in-neighbors in
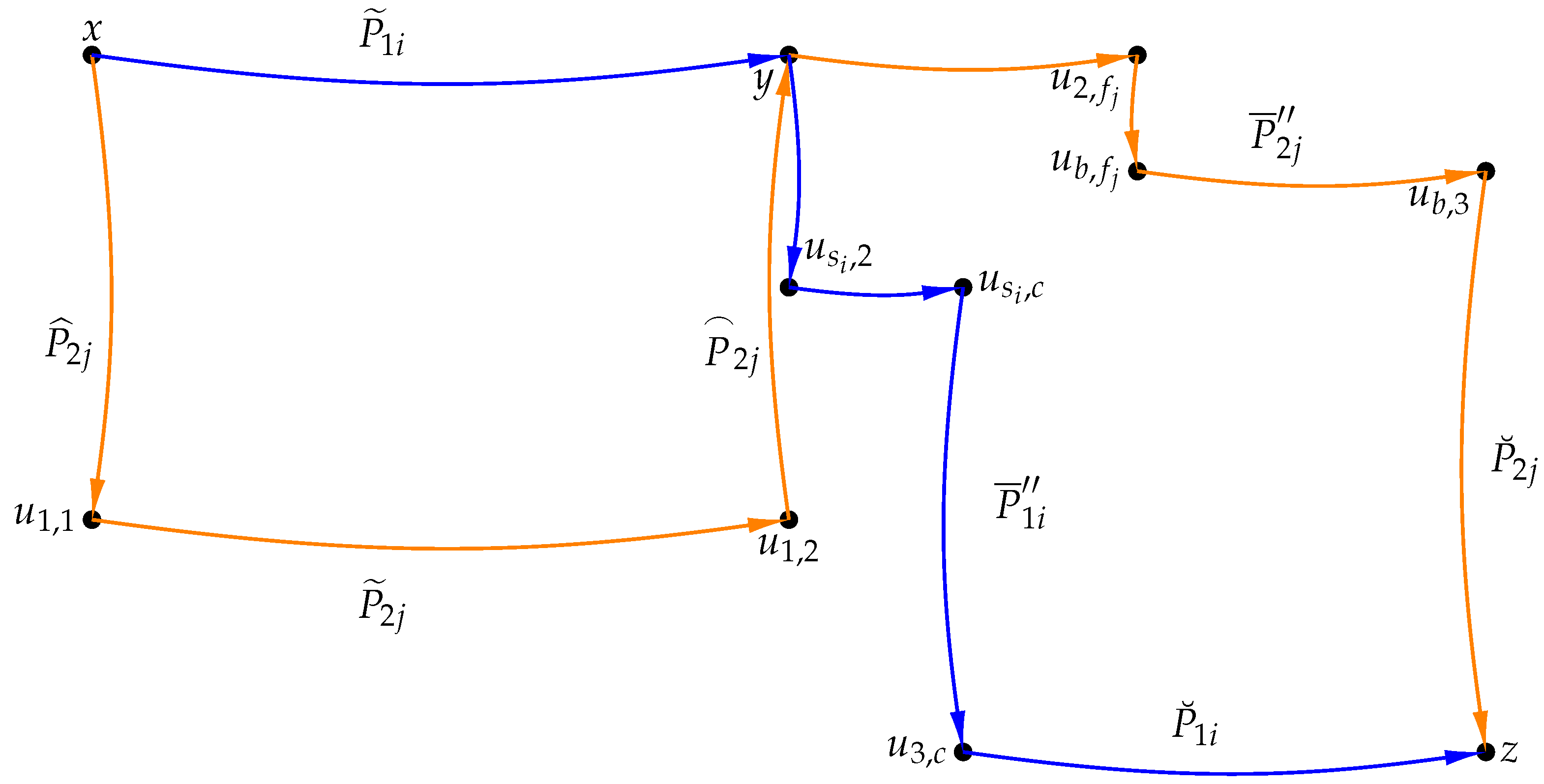
, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in
Figure 4. The vertices and paths contained in
Figure 4 are explained below.
Considering , , it is known that there exist at least internally disjoint -paths in , denoted as . Let , , and there exist at least internally disjoint -paths in , denoted as . Considering , , it is known that there exist at least internally disjoint -paths in , denoted as . Let , , and there exist at least internally disjoint -paths in , denoted as . In , with , , it is known that there exist at least internally disjoint -paths, denoted as . For each , let be the out-neighbor of y in , clearly these out-neighbors are distinct.
In , with , , it is known that there exist at least internally disjoint -paths in , denoted as . For each , let be the out-neighbor of y in , clearly these out-neighbors are distinct. For each , an out-neighbor of in can be chosen, denoted by , with . Similarly, an out-neighbor of in can be chosen, denoted by , with .
In , with , . is the -path corresponding to . In , the path from vertex to is denoted as . In , with , , and it is known that there exist at least internally disjoint -paths, say . In , with , , is the -path corresponding to . In path , the path from vertex to is denoted as . In , with , , and it is known that there exist at least internally disjoint -paths in , say . If , then . If , then . Similarly, if , then . If , then . The arc-disjoint -paths can be constructed as
Then we obtain arc-disjoint -paths.
Case 4. Let
x and
y be in the same
. Let
z,
x, and
y be in different
and let
z,
x be in different
, for some
,
. Without loss of generality, we can assume that
,
,
. In this case, our overall goal is that we will use arc-disjoint paths between
x and
y in
,
y and its out-neighbors in
,
z and its in-neighbors in
,
x and its out-neighbors in
,
y and its out-neighbors in
,
z and its in-neighbors in
, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in
Figure 5. The vertices and paths contained in
Figure 5 are explained below.
Considering , , it is known that there exist at least internally disjoint -paths in , denoted as . In , with , and , it is known that there exist at least internally disjoint -paths, denoted as . In , with , and , it is known that there exist at least internally disjoint -paths, denoted as . In , with , and , it is known that there exist at least internally disjoint -paths, denoted as . Let , , , ,, , and be the same as in Case 3.
If , then . If , then . If , then . If , then . If , then .
Subcase 4.1. If there exists no vertex . Let
Subcase 4.2. If there exists a vertex , then in , there exists an out-neighbor of x. If , this path is denoted by .
In , there exists an out-neighbor of z such that . In , there exists an in-neighbor of y such that . If , this path is denoted by . Then in , with , and , it is known that there are at least internally disjoint -paths. One such -path is chosen, denoted as , with . In , with , and , it is known that there are at least internally disjoint -paths. One such -path is chosen, denoted as , with . Then, is constructed as
The other paths are the same as Subcase 4.1. Then we obtain arc-disjoint -paths.
Case 5. Let
x and
y be in the same
. Let
y and
z be in the same
, for some
,
. Without loss of generality, we can assume that
,
,
. In this case, our overall goal is that we will use arc-disjoint paths between
x and
y in
,
y and
z in
,
x and its out-neighbors in
,
x and its out-neighbors in
,
z and
y in
, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in
Figure 6. The vertices and paths contained in
Figure 6 are explained below.
It is known that there exist at least internally disjoint -paths in , denoted as , where and . In , there exist at least internally disjoint -paths, denoted as , where and . Similarly, in , there exist at least internally disjoint -paths, denoted as , where and . In , there exist at least internally disjoint -paths, denoted as , where and . In , there exist at least internally disjoint -paths, denoted as , where and . For each , let be the in-neighbor of y in , and clearly these in-neighbors are distinct. Similarly, let be the out-neighbor of z in . For each , an out-neighbor of is chosen in , where .
In , with and . is the -path corresponding to . In , the path from vertex to is denoted as . Then, in , with and , it is known that there exist at least internally disjoint -paths. One such -path, denoted as , is chosen, with . The arc-disjoint -paths can be constructed as
If , then . And if , then . This results in obtaining arc-disjoint -paths.
Case 6. Let
y and
z be in the same
. Let
x,
y be in different
and
x,
y,
z be in different
, for some
,
. Without loss of generality, we can assume that
,
,
. Let
,
,
,
,
be the same as in Case 5. In
, with
and
, it is known that there exist at least
internally disjoint
-paths in
, denoted as
. In this case, our overall goal is that we will use arc-disjoint paths between
x and its out-neighbors in
,
y and its in-neighbors in
,
y and
z in
,
x and its out-neighbors in
,
z and its in-neighbors in
,
z and
y in
, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in
Figure 7. The vertices and paths contained in
Figure 7 are explained below.
Subcase 6.1. In the set , there does not exist . Thus, , , , remain the same as in Case 5.
In , with and , it is known that there exist at least internally disjoint -paths in , denoted as . In , with and , it is known that there exist at least internally disjoint -paths in , denoted as . In , with and , it is known that there exist at least internally disjoint -paths in , denoted as . If , then . Let
If , then . And if , then . Now we obtain arc-disjoint -paths.
Subcase 6.2. In the set , only one vertex exists. Thus, , , , remain the same as in Case 5.
If in , then , remain the same as in Subcase 6.1. If an arc is in path , since , then an out-neighbor of can be found in such that and . In , is the -path corresponding to , where , . In , with and , it is known that there exist at least internally disjoint -paths. Then in these paths, one of the paths is chosen, with . and remain the same as in Subcase 6.1. is constructed as
Subcase 6.3. In the set , there is only one vertex .
For each , an in-neighbor of in can be chosen, denoted by , where . In , let be the -path corresponding to , where , . The path from vertex to in path is denoted as . In , let , , and at least internally disjoint -paths are known to exist. Then, one of the paths is chosen, where . If , . And if , . If in the path . Let
.
If an arc is in path , an in-neighbor of can be found in such that and . In , let be the -path corresponding to , where , . In , let , , and at least internally disjoint -paths are known to exist. Then, one of the paths is chosen, and let . Let
Hence, we obtain arc-disjoint -paths.
Now we prove that this bound is sharp. By Proposition 1, By Lemma 2, . So we have , with . Therefore, the lower bound holds and is sharp. □