Directed Path 3-Arc-Connectivity of Cartesian Product Digraphs

Abstract

Let $D=\left(V\right(D),A(D\left)\right)$ be a digraph of order n and let $r\in S\subseteq V\left(D\right)$ with $2\le \left|S\right|\le n$. A directed $(S,r)$-Steiner path (or an $(S,r)$-path for short) is a directed path P beginning at r such that $S\subseteq V\left(P\right)$. Arc-disjoint between two $(S,r)$-paths is characterized by the absence of common arcs. Let ${\lambda }_{S,r}^p\left(D\right)$ be the maximum number of arc-disjoint $(S,r)$-paths in D. The directed path k-arc-connectivity of D is defined as ${\lambda }_k^p\left(D\right)=min\{{\lambda }_{S,r}^p\left(D\right)\mid S\subseteq V\left(D\right),\left|S\right|=k,r\in S\}.$ In this paper, we shall investigate the directed path 3-arc-connectivity of Cartesian product ${\lambda }_3^p(G\square H)$ and prove that if G and H are two digraphs such that ${\delta }^0\left(G\right)\ge 4$, ${\delta }^0\left(H\right)\ge 4$, and $\kappa \left(G\right)\ge 2$, $\kappa \left(H\right)\ge 2$, then ${\lambda }_3^p(G\square H)\ge min\left\{2\kappa \left(G\right),2\kappa \left(H\right)\right\};$ moreover, this bound is sharp. We also obtain exact values for ${\lambda }_3^p(G\square H)$ for some digraph classes G and H, and most of these digraphs are symmetric.

1. Introduction

For a detailed explanation of graph theoretical notation and terminology not provided here, readers are directed to reference [1]. It should be noted that all digraphs discussed in this paper do not contain parallel arcs or loops. The set of all natural numbers from 1 to n is denoted by $\left[n\right]$. If a directed graph D can be obtained from its underlying graph G by replacing each edge in G with corresponding arcs in both directions, then D is said to be symmetric, denoted as $D=\overleftrightarrow{G}$. The notation ${\overleftrightarrow{T}}_n$ is used for a symmetric digraph whose underlying graph forms a tree of order n. The notation ${\overleftrightarrow{C}}_n$ is used for a symmetric digraph whose underlying graph forms a cycle of order n. The cycle digraph of order n is denoted by ${\overrightarrow{C}}_n$. We denote the complete digraph of order n as ${\overleftrightarrow{K}}_n$.

The well-known Steiner tree packing problem is characterized as follows. Given a graph G and a set of terminal vertices $S\subseteq V\left(G\right)$, the goal is to identify as many edge-disjoint S-Steiner trees (i.e., trees T in G with $S\subseteq V\left(T\right)$) as feasible. This particular problem, along with its associated topics, garners significant interest from researchers due to its extensive applications in VLSI circuit design [2,3,4] and Internet Domain [5]. In practical applications, the construction of vertex-disjoint or arc-disjoint paths in graphs holds significance, as they play a crucial role in improving transmission reliability and boosting network transmission rates [6]. This paper will specifically delve into a variant of the directed Steiner tree packing problem, termed the directed Steiner path packing problem, closely interconnected with the Steiner path problem and the Steiner path cover problem [7,8].

We now consider two types of directed Steiner path packing problems and related parameters. Let $D=\left(V\right(D),A(D\left)\right)$ be a digraph of order n and let $r\in S\subseteq V\left(D\right)$ with $2\le \left|S\right|\le n$. A directed $(S,r)$-Steiner path, or simply an $(S,r)$-path, refers to a directed path P originating from r such that S is a subset of the vertices in P. Arc-disjoint between two $(S,r)$-paths implies that they share no common arcs, while two arc-disjoint $(S,r)$-paths are internally disjoint when their common vertex set is precisely S. Let ${\lambda }_{S,r}^p\left(D\right)$ (and ${\kappa }_{S,r}^p\left(D\right)$) represent the maximum number of arc-disjoint (and internally disjoint) $(S,r)$-paths in D, respectively. The Arc-disjoint (or Internally disjoint) Directed Steiner Path Packing problem is formulated as follows. Given a digraph D and letting $r\in S\subseteq V\left(D\right)$, the objective is to maximize the count of arc-disjoint (or internally disjoint) $(S,r)$-paths. The notion of directed path connectivity, which is a derivative of path connectivity in undirected graphs, is intricately linked to the directed Steiner path packing problem and serves as a logical progression from path connectivity in directed graphs (refer to [5] for the initial presentation of path connectivity). The directed path k-connectivity [9] of D is defined as

$${\kappa }_k^p\left(D\right)=min\{{\kappa }_{S,r}^p\left(D\right)\mid S\subseteq V\left(D\right),\left|S\right|=k,r\in S\}$$

Similarly, the directed path k-arc-connectivity [9] of D is defined as

$${\lambda }_k^p\left(D\right)=min\{{\lambda }_{S,r}^p\left(D\right)\mid S\subseteq V\left(D\right),\left|S\right|=k,r\in S\}$$

The concepts of directed path k-connectivity and directed path k-arc-connectivity are synonymous with directed path connectivity. In the context of $k=2$, ${\kappa }_2^p\left(D\right)$ equates to $\kappa \left(D\right)$ and ${\lambda }_2^p\left(D\right)$ equates to $\lambda \left(D\right)$, where $\kappa \left(D\right)$ and $\lambda \left(D\right)$ denote vertex-strong connectivity and arc-strong connectivity of digraphs, respectively. Hence, these parameters can be viewed as extensions of the classical connectivity measures in a digraph. It is pertinent to emphasize the close relationship between strong subgraph connectivity and directed path connectivity; refer to [10,11,12] for further insights on this interconnected topic.

It is a widely recognized fact that Cartesian products of digraphs are of great interest in graph theory and its applications. For a comprehensive overview of various findings on Cartesian products of digraphs, one may refer to a recent survey chapter by Hammack [13]. In this paper, we continue research on directed path connectivity and focus on the directed path 3-arc-connectivity of Cartesian products of digraphs.

In Section 2, we introduce terminology and notation on Cartesian products of digraphs. In Section 3, we prove that if G and H are two digraphs such that ${\delta }^0\left(G\right)\ge 4$, ${\delta }^0\left(H\right)\ge 4$, and $\kappa \left(G\right)\ge 2$, $\kappa \left(H\right)\ge 2$, then

$${\lambda }_3^p(G\square H)\ge min\left\{2\kappa \left(G\right),2\kappa \left(H\right)\right\};$$

moreover, this bound is sharp. Finally, we obtain exact values of ${\lambda }_3^p(G\square H)$ for some digraph classes G and H in Section 4.

2. Cartesian Product of Digraphs

Consider two digraphs G and H with vertex sets $V\left(G\right)=\{u_i\mid i\in \left[n\right]\}$ and $V\left(H\right)=\{v_j\mid j\in \left[m\right]\}$. The Cartesian product of G and H, denoted by $G\square H$, is a digraph with vertex set

$$V(G\square H)=V\left(G\right)\times V\left(H\right)=\{(x,x^{\prime })\mid x\in V\left(G\right),x^{\prime }\in V\left(H\right)\}.$$

The arc set of $G\square H$, denoted by $A(G\square H)$, is given by $\{(x,x^{\prime })(y,y^{\prime })\mid xy\in A\left(G\right),x^{\prime }=y^{\prime },$ or $x=y,x^{\prime }{y}^{\prime }\in A\left(H\right)\}.$ It is worth noting that Cartesian product is an associative and commutative operation. Furthermore, $G\square H$ is strongly connected if and only if both G and H are strongly connected, as shown in a recent survey chapter by Hammack [13].

In the rest of the paper, we will use $u_{i,j}$ to denote $(u_i,v_j)$. Additionally, $G\left(v_j\right)$ will refer to the subgraph of $G\square H$ induced by the vertex set $\{u_{i,j}\mid i\in \left[n\right]\}$ with $j\in \left[m\right]$, while $H\left(u_i\right)$ will denote the subgraph of $G\square H$ induced by the vertex set $\{u_{i,j}\mid j\in \left[m\right]\}$ with $i\in \left[n\right]$. It is evident that $G\left(v_j\right)$ is isomorphic to G and $H\left(u_i\right)$ is isomorphic to H. To illustrate this, refer to Figure 1 (this figure comes from [14]), where it can be observed that $G\left(v_j\right)$ is isomorphic to G for $1\le j\le 4$, and $H\left(u_i\right)$ is isomorphic to H for $1\le i\le 3$.

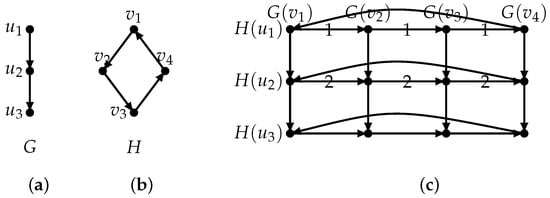
Figure 1. G, H and their Cartesian product [14] (1 denotes arc u_1,1u_1,2, u_1,2u_1,3 and arc u_1,3u_1,4; 2 denotes arc u_2,1u_2,2, u_2,2u_2,3 and arc u_2,3u_2,4).

For distinct indices $j_1$ and $j_2$ with $1\le j_1\ne j_2\le m$, the vertices $u_{i,j_1}$ and $u_{i,j_2}$ belong to the same digraph $H\left(u_i\right)$, where $u_i$ is an element of $V\left(G\right)$. $u_{i,j_2}$ is referred to as the vertex corresponding to $u_{i,j_1}$ in $G\left(v_{j_2}\right)$. Similarly, for distinct indices $i_1$ and $i_2$ with $1\le i_1\ne i_2\le n$, $u_{i_2,j}$ is the vertex corresponding to $u_{i_1,j}$ in $H\left(u_{i_2}\right)$. Analogously, the subgraph corresponding to a given subgraph can also be defined. For instance, in the digraph $\left(c\right)$ depicted in Figure 1, if we label the path 1 as $P_1$ (and the path 2 as $P_2$) in $H\left(u_1\right)$ ($H\left(u_2\right)$), then $P_2$ is identified as the path that corresponds to $P_1$ in $H\left(u_2\right)$.

Sun and Zhang proved some results of directed path connectivity, that is, the following lemma.

Lemma 1

([9]). Let D be a digraph of order n, and let k be an integer satisfying $2\le k\le n$. The following statements are valid:

$\left(1\right)$: ${\lambda }_{k+1}^p\left(D\right)\le {\lambda }_k^p\left(D\right)$ when $k\le n-1$.

$\left(2\right)$: ${\kappa }_k^p\left(D\right)\le {\lambda }_k^p\left(D\right)\le {\delta }^0\left(D\right)=min\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}$.

Lemma 2

([15]). $\kappa \left({\overleftrightarrow{K}}_n\right)=n-1.$

3. A General Lower Bound

Now we will provide a lower bound for ${\lambda }_3^p(G\square H)$.

Theorem 1.

Let G and H be two digraphs such that ${\delta }^0\left(G\right)\ge 4$, ${\delta }^0\left(H\right)\ge 4$, and $\kappa \left(G\right)\ge 2$, $\kappa \left(H\right)\ge 2$. We have

$${\lambda }_3^p(G\square H)\ge min\left\{2\kappa \left(G\right),2\kappa \left(H\right)\right\}.$$

Furthermore, this bound is sharp.

Proof. 

It suffices to show that there are at least $2\kappa \left(G\right)$ or $2\kappa \left(H\right)$ arc-disjoint $(S,r)$-paths for any $S\subseteq V(G\square H)$ with $\left|S\right|=3$, $r\in S$. Let $S=\{x,y,z\}$ and let $r=x$. Without loss of generality, we may assume $\kappa \left(G\right)\le \kappa \left(H\right)$ and consider the following six cases.

Case 1.

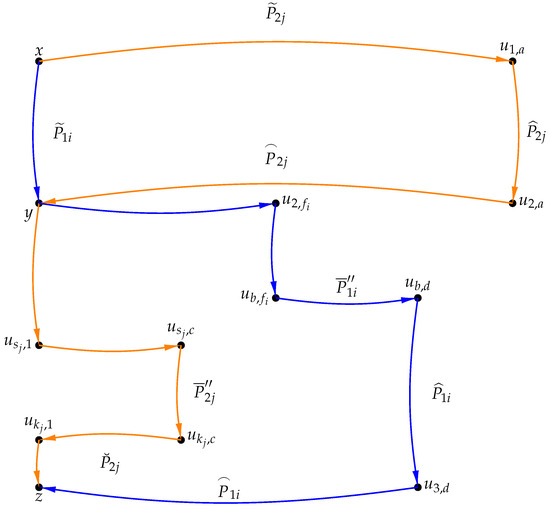
Let x, y and z be in the same $H\left(u_i\right)$ or $G\left(v_j\right)$ for some $i\in \left[n\right]$, $j\in \left[m\right]$. Without loss of generality, we may assume that $x=u_{1,1}$, $y=u_{2,1}$, $z=u_{3,1}$. In this case, our overall goal is that we will use arc-disjoint paths between x and y in $G\left(v_1\right)$, y and z in $G\left(v_1\right)$, x and its out-neighbors in $H\left(u_1\right)$, y and its in-neighbors in $H\left(u_2\right)$, z and its in-neighbors in $H\left(u_3\right)$, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in Figure 2. The vertices and paths contained in Figure 2 are explained below.

Figure 2. Depiction of the arc-disjoint paths found in Case 1 of the proof of Theorem 1.

Let $S_1=\{x,y\}$, $r_1=x$. It is known that there are at least $\kappa \left(G\right)$ internally disjoint $(S_1,r_1)$-paths in $G\left(v_1\right)$, denoted as ${\tilde{P}}_{1i}$$(i\in [\kappa \left(G\right)\left]\right)$. Considering $S_1^{\prime }=\{y,z\}$, $r_1^{\prime }=y$, there are at least $\kappa \left(G\right)$ internally disjoint $(S_1^{\prime },r_1^{\prime })$-paths in $G\left(v_1\right)$, denoted as ${\overline{P}}_{2j}$$(j\in [\kappa \left(G\right)\left]\right)$. For each $j\in \left[\kappa \right(G\left)\right]$, let $u_{s_j,1}$ be the out-neighbor of y in ${\overline{P}}_{2j}$; clearly these out-neighbors are distinct. Similarly, an in-neighbor $u_{k_j,1}$$(j\in [\kappa \left(G\right)\left]\right)$ of z in ${\overline{P}}_{2j}$ can be chosen such that these in-neighbors are distinct. In $H\left(u_1\right)$, if there is a vertex that is not an out-neighbor of x, then choose such a vertex as $u_{1,a}$, where $a\ne 1$. If there is no such vertex, that is, all vertices are out-neighbours of x, then choose any vertex as $u_{1,a}$, where $a\ne 1$. In $H\left(u_1\right)$, let $S_2^{\prime }=\{x,u_{1,a}\}$, $r_2^{\prime }=x$, and it is established that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_2^{\prime },r_2^{\prime })$-paths, say ${\tilde{P}}_{2j}$$(j\in [\kappa \left(G\right)\left]\right)$. In $G\left(v_a\right)$, let $S_3^{\prime }=\{u_{1,a},u_{2,a}\}$, $r_3^{\prime }=u_{1,a}$, and it is established that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_3^{\prime },r_3^{\prime })$-paths, say ${\widehat{P}}_{2j}$$(j\in [\kappa \left(G\right)\left]\right)$. In $H\left(u_2\right)$, let $S_4^{\prime }=\{y,u_{2,a}\}$, $r_4^{\prime }=u_{2,a}$, and it is established that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_4^{\prime },r_4^{\prime })$-paths, say ${\stackrel{⌢}{P}}_{2j}(j\in \left[\kappa \left(G\right)\right])$.

In $H\left(u_1\right)$, if there is a vertex that is not an out-neighbor of x in ${\tilde{P}}_{2j}$, then choose such a vertex as $u_{1,d}$, with $d\notin \{1,a\}$. If there is no such vertex, then choose any vertex as $u_{1,d}$, with $d\notin \{1,a\}$. In $H\left(u_2\right)$, with $S_2=\{y,u_{2,d}\}$ and $r_2=y$, it is known that there are at least $\kappa \left(G\right)$ internally disjoint $(S_2,r_2)$-paths, denoted as ${\overline{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$. For each $i\in \left[\kappa \right(G\left)\right]$, let $u_{2,f_i}$ be the out-neighbor of y in ${\overline{P}}_{1i}$; clearly these out-neighbors are distinct. For each $i\in \left[\kappa \right(G\left)\right]$, since ${\delta }^0\left(G\right)\ge 4$, an out-neighbor of $u_{2,f_i}$ in $G\left(v_{f_i}\right)$, denoted by $u_{b,f_i}(b\in \left[n\right])$, can be chosen, with $b\notin \{1,3\}$. If there exists a vertex $u_{s_j,1}\notin \{u_{1,1},u_{3,1}\}$, let $b=s_j$. If there is no such vertex, then let $b\ne k_j$. In $H\left(u_b\right)$, ${\overline{P}}_{1i}^{\prime }$ is the $(S_3,r_3)$-path corresponding to ${\overline{P}}_{1i}$, where $S_3=\{u_{b,1},u_{b,d}\}$, and $r_3=u_{b,1}$. In ${\overline{P}}_{1i}^{\prime }$, the path from vertex $u_{b,f_i}$ to $u_{b,d}$ is denoted as ${\overline{P}}_{1i}^{″}$. Let $S_4=\{u_{b,d},u_{3,d}\}$, $r_4=u_{b,d}$, and it is established that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_4,r_4)$-paths, say ${\widehat{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$. If $u_{2,f_t}=u_{2,d}(t\in \left[\kappa \left(G\right)\right])$, then let $u_{2,d}\notin {\widehat{P}}_{1t}$ in ${\widehat{P}}_{1t}$. In $H\left(u_3\right)$, let $S_5=\{u_{3,d},z\}$, $r_5=u_{3,d}$, and it is established that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_5,r_5)$-paths, say ${\stackrel{⌢}{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$.

In $H\left(u_1\right)$, if there is an out-neighbor of x that is not an out-neighbor of x in ${\tilde{P}}_{2j}$, then choose such a vertex as $u_{1,c}$, with $c\notin \{a,d\}$. If there is no such vertex, then choose any out-neighbor of x as $u_{1,c}$, with $c\notin \{a,d\}$. And $u_{s_j,c}$ is an out-neighbor of $u_{s_j,1}$ in $H\left(u_{s_j}\right)$. In $G\left(v_c\right)$, ${\overline{P}}_{2j}^{\prime }$ is the $(S_5^{\prime },r_5^{\prime })$-path corresponding to ${\overline{P}}_{2j}$, where $S_5^{\prime }=\{u_{2,c},u_{3,c}\}$ and $r_5^{\prime }=u_{2,c}$. In ${\overline{P}}_{2j}^{\prime }$, the path from vertex $u_{s_j,c}$ to $u_{k_j,c}$ is denoted as ${\overline{P}}_{2j}^{″}$. If $u_{s_t,1}=u_{k_t,1}(t\in \left[\kappa \left(G\right)\right])$, then ${\overline{P}}_{2t}^{″}=\{y{u}_{s_t,1},u_{s_t,1}z\}$. If $u_{s_l,1}=z(l\in \left[\kappa \left(G\right)\right])$, then ${\overline{P}}_{2l}^{″}=\left\{yz\right\}$. If $u_{1,c}\in {\overline{P}}_{2h}^{″}(h\in \left[\kappa \left(G\right)\right])$, then $u_{1,c}\notin {\tilde{P}}_{2h}$. In $H\left(u_{k_j}\right)$, with $S_{6_j}^{\prime }=\{u_{k_j,c},u_{k_j,1}\}$, and $r_{6_j}^{\prime }=u_{k_j,c}$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_{6_j}^{\prime },r_{6_j}^{\prime })$-paths. Then in these paths, one of the paths ${\breve{P}}_{2j}(j\in \left[\kappa \left(G\right)\right])$ is chosen, with $u_{k_j,a}\notin {\breve{P}}_{2j}$.

Subcase 1.1.

In the set $\{u_{s_j,1},u_{k_j,1}\}$, there is no vertex such that $u_{s_j,1}=x$ or $u_{k_j,1}=x$, and the vertex z is not in path ${\tilde{P}}_{1i}$. We now construct the arc-disjoint $(S,r)$-paths by letting

$P_{1i}={\tilde{P}}_{1i}\cup {\overline{P}}_{1i}^{″}\cup {\widehat{P}}_{1i}\cup {\stackrel{⌢}{P}}_{1i}\cup \{y{u}_{2,f_i},u_{2,f_i}{u}_{b,f_i}\},i\in \left[\kappa \left(G\right)\right],$

$P_{2j}={\tilde{P}}_{2j}\cup {\widehat{P}}_{2j}\cup {\stackrel{⌢}{P}}_{2j}\cup {\overline{P}}_{2j}^{″}\cup {\breve{P}}_{2j}\cup \{y{u}_{s_j,1},u_{s_j,1}{u}_{s_j,c},u_{k_j,1}z\},j\in \left[\kappa \left(G\right)\right]\setminus \{t,l\},$

$P_{2t}={\tilde{P}}_{2t}\cup {\widehat{P}}_{2t}\cup {\overline{P}}_{2t}^{″}\cup {\stackrel{⌢}{P}}_{2t},$

$P_{2l}={\tilde{P}}_{2l}\cup {\widehat{P}}_{2l}\cup {\overline{P}}_{2l}^{″}\cup {\stackrel{⌢}{P}}_{2l}$.

Then we obtain $2\kappa \left(G\right)$ arc-disjoint $(S,r)$-paths.

Subcase 1.2.

In the set $\{u_{s_j,1},u_{k_j,1}\}$, there is no vertex such that $u_{s_j,1}=x$ or $u_{k_j,1}=x$, and there exist $z\in {\tilde{P}}_{1h}(h\in \left[\kappa \left(G\right)\right])$, but there is no arc $u_{k_j,1}z$ in path ${\tilde{P}}_{1h}$. Let $P_{1h}={\tilde{P}}_{1h}$. The other paths are the same as Subcase 1.1.

Subcase 1.3.

There is an arc $u_{k_r,1}z$ in path ${\tilde{P}}_{1h}(\{r,h\}\subseteq \left[\kappa \left(G\right)\right])$. In the set $\{u_{s_j,1},u_{k_j,1}\}(j\ne r)$, there is no vertex x. We can find a path ${\stackrel{⌢}{P}}_{2r}$ such that $u_{2,f_h}\notin {\stackrel{⌢}{P}}_{2r}$. If $u_{b,a}\in {\overline{P}}_{1h}^{″}$, then let $u_{b,a}\notin {\widehat{P}}_{2r}$. If $u_{1,d}\in {\widehat{P}}_{1h}$, then let $u_{1,d}\notin {\tilde{P}}_{2r}$. In ${\widehat{P}}_{1h}$ and ${\stackrel{⌢}{P}}_{1h}$, let $u_{2,d}\notin {\widehat{P}}_{1h}$ and $u_{3,a}\notin {\stackrel{⌢}{P}}_{1h}$. Let

$P_{1h}={\tilde{P}}_{1h},$

$P_{2r}={\tilde{P}}_{2r}\cup {\widehat{P}}_{2r}\cup {\stackrel{⌢}{P}}_{2r}\cup {\overline{P}}_{1h}^{″}\cup {\widehat{P}}_{1h}\cup {\stackrel{⌢}{P}}_{1h}\cup \{y{u}_{2,f_h},u_{2,f_h}{u}_{b,f_h}\}$.

The other paths are the same as Subcase 1.1.

Subcase 1.4.

The set $\{u_{s_j,1},u_{k_j,1}\}$ contains the vertex $u_{s_q,1}=x$ and $u_{k_j,1}\ne x$. There is no arc $u_{k_q,1}z$ in ${\tilde{P}}_{1q}$. In ${\overline{P}}_{2q}$, there is an arc $x{u}_{g_1,1}(q\in \left[\kappa \left(G\right)\right]$, $g_1\in \left[n\right])$. In ${\tilde{P}}_{2j}$, there exists an out-neighbor $u_{1,g_2}$ of x, where $g_2\in \left[\kappa \left(G\right)\right]\setminus \{a,c,d\}$, and this path is denoted by ${\tilde{P}}_{2q}$.

Subcase 1.4.1.

There is no arc $x{u}_{g_1,1}$ in ${\tilde{P}}_{1i}$.

In ${\overline{P}}_{2q}^{″}$, the path from vertex $u_{g_1,c}$ to $u_{k_q,c}$ is denoted as ${\overline{P}}_{2q}^{‴}$. In $G\left(v_{g_2}\right)$, with $S_7^{\prime }=\{u_{3,g_2},u_{1,g_2}\}$ and $r_7^{\prime }=u_{3,g_2}$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_7^{\prime },r_7^{\prime })$-paths. Then in these paths, one of the paths ${\tilde{P}}_q$ is chosen, with $u_{k_q,g_2}\notin {\tilde{P}}_q$. If $u_{2,g_2}\in {\tilde{P}}_q$, then let $u_{2,g_2}\notin {\stackrel{⌢}{P}}_{2q}$. In ${\tilde{P}}_{2q}$, the path from vertex $u_{1,g_2}$ to $u_{1,a}$ is denoted as ${\tilde{P}}_{2q}^{\prime }$. Let

$P_{2q}={\overline{P}}_{2q}^{‴}\cup {\breve{P}}_{2q}\cup {\tilde{P}}_q\cup {\tilde{P}}_{2q}^{\prime }\cup {\widehat{P}}_{2q}\cup {\stackrel{⌢}{P}}_{2q}\cup \{x{u}_{g_1,1},u_{g_1,1}{u}_{g_1,c},u_{k_q,1}z,z{u}_{3,g_2}\}.$

If $u_{g_1,1}=u_{k_q,1}$, then $P_{2q}={\tilde{P}}_q\cup {\tilde{P}}_{2q}^{\prime }\cup {\widehat{P}}_{2q}\cup {\stackrel{⌢}{P}}_{2q}\cup \{x{u}_{g_1,1},u_{k_q,1}z,z{u}_{3,g_2}\}$. The other paths are the same as Subcases 1.1–1.3.

Subcase 1.4.2.

If there exists an arc $x{u}_{g_1,1}$ in ${\tilde{P}}_{1g}(g\in \left[\kappa \left(G\right)\right])$, then in $H\left(u_{g_1}\right)$, with $S_6=\{u_{g_1,1},u_{g_1,g_2}\}$ and $r_6=u_{g_1,g_2}$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_6,r_6)$-paths. Then in these paths, one of the paths ${\tilde{P}}_g$ is chosen, with $u_{g_1,d}\notin {\tilde{P}}_g$. In ${\tilde{P}}_{1g}$, the path from vertex $u_{g_1,1}$ to y is denoted as ${\tilde{P}}_{1g}^{\prime }$. Let $P_{2q}$ be the same as in Subcase 1.4.1. Let

$P_{1g}={\tilde{P}}_g\cup {\tilde{P}}_{1g}^{\prime }\cup {\overline{P}}_{1g}^{″}\cup {\widehat{P}}_{1g}\cup {\stackrel{⌢}{P}}_{1g}\cup \{x{u}_{1,g_2},u_{1,g_2}{u}_{g_1,g_2},y{u}_{2,f_g},u_{2,f_g}{u}_{b,f_g}\}.$

The other paths are the same as Subcases 1.1–1.3.

Subcase 1.5.

In the set $\{u_{s_j,1},u_{k_j,1}\}$, there exists vertex $u_{k_p,1}=x$. And there is no arc $u_{k_p,1}z$ in ${\tilde{P}}_{1p}$.

In ${\tilde{P}}_{2j}$, there is an out-neighbor $u_{1,g}$ of x such that $g\in \left[\kappa \right(G\left)\right]\setminus \{a,c,d\}$, and this path is denoted by ${\tilde{P}}_{2p}$. In $G\left(v_g\right)$, let $S_8^{\prime }=\{u_{3,g},u_{1,g}\}$, $r_8^{\prime }=u_{3,g}$, and we know there exist at least $\kappa \left(G\right)$ internally disjoint $(S_8^{\prime },r_8^{\prime })$-paths. Then in these paths, we choose one of the paths ${\tilde{P}}_p$, and let $u_{2,g}\notin {\tilde{P}}_p$. In ${\tilde{P}}_{2p}$, we denote the path from vertex $u_{1,g}$ to $u_{1,a}$ as ${\tilde{P}}_{2p}^{\prime }$. Let

$P_{2p}={\tilde{P}}_p\cup {\tilde{P}}_{2p}^{\prime }\cup {\widehat{P}}_{2p}\cup {\stackrel{⌢}{P}}_{2p}\cup \{xz,z{u}_{3,g}\}.$

The other paths are the same as Subcases 1.1–1.3.

Case 2.

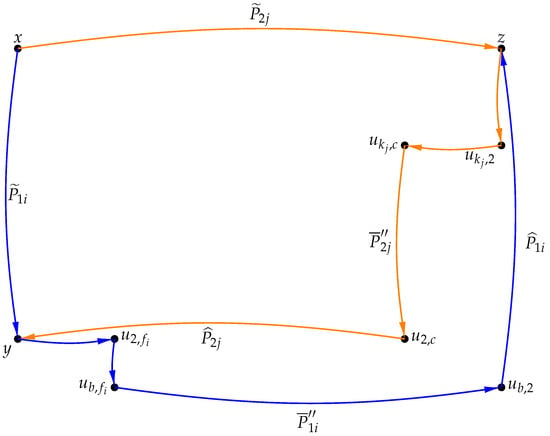
Let x and y be in the same $G\left(v_j\right)$. Let x and z be in the same $H\left(u_i\right)$ for some $i\in \left[n\right]$, $j\in \left[m\right]$. Without loss of generality, we may assume that $x=u_{1,1}$, $y=u_{2,1}$, $z=u_{1,2}$. In this case, our overall goal is that we will use arc-disjoint paths between x and y in $G\left(v_1\right)$, y and its out-neighbors in $H\left(u_2\right)$, z and its in-neighbors in $G\left(v_2\right)$, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in Figure 3. The vertices and paths contained in Figure 3 are explained below.

Figure 3. Depiction of the arc-disjoint paths found in Case 2 of the proof of Theorem 1.

Considering $S_1=\{x,y\}$, $r_1=x$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_1,r_1)$-paths in $G\left(v_1\right)$, denoted as ${\tilde{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$. Let $S_2=\{y,u_{2,2}\}$, $r_2=y$, and there exist at least $\kappa \left(G\right)$ internally disjoint $(S_2,r_2)$-paths in $H\left(u_2\right)$, denoted as ${\overline{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$. For each $i\in \left[\kappa \right(G\left)\right]$, let $u_{2,f_i}$ be the out-neighbor of y in ${\overline{P}}_{1i}$; clearly these out-neighbors are distinct. For each $i\in \left[\kappa \right(G\left)\right]$, an out-neighbor $u_{b,f_i}$ of $u_{2,f_i}$ in $G\left(v_{f_i}\right)$ can be chosen, with $b\ne 1$. In $H\left(u_b\right)$, with $S_3=\{u_{b,1},u_{b,2}\}$ and $r_3=u_{b,1}$. ${\overline{P}}_{1i}^{\prime }$ is the $(S_3,r_3)$-path corresponding to ${\overline{P}}_{1i}$. In ${\overline{P}}_{1i}^{\prime }$, the path from vertex $u_{b,f_i}$ to $u_{b,2}$ is denoted ${\overline{P}}_{1i}^{\prime \prime }$. With $S_4=\{u_{b,2},z\}$ and $r_4=u_{b,2}$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_4,r_4)$-paths in $G\left(v_2\right)$, denoted as ${\widehat{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$. If $u_{2,f_k}=u_{2,2}$, then $u_{2,2}\notin {\widehat{P}}_{1k}$. The arc-disjoint $(S,r)$-paths can be constructed as

$P_{1i}={\tilde{P}}_{1i}\cup {\overline{P}}_{1i}^{″}\cup {\widehat{P}}_{1i}\cup \{y{u}_{2,f_i},u_{2,f_i}{u}_{b,f_i}\}$, $i\in \left[\kappa \right(G\left)\right].$

Likewise, we can identify $\kappa \left(G\right)$ arc-disjoint $(S,r)$-paths from x to z and subsequently to y. Consequently, we can derive $2\kappa \left(G\right)$ arc-disjoint $(S,r)$-paths.

Case 3.

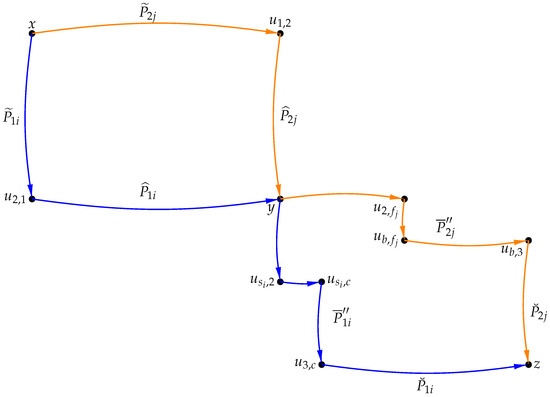
Let x, y and z be in different $H\left(u_i\right)$ and $G\left(v_j\right)$ for some $i\in \left[n\right]$, $j\in \left[m\right]$. Without loss of generality, we can assume that $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. In this case, our overall goal is that, we will use arc-disjoint paths between x and its out-neighbors in $H\left(u_1\right)$, y and its out-neighbors in $H\left(u_2\right)$, z and its in-neighbors in $G\left(v_3\right)$, x and its out-neighbors in $G\left(v_1\right)$, y and its out-neighbors in $G\left(v_2\right)$, z and its in-neighbors in $H\left(u_3\right)$, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in Figure 4. The vertices and paths contained in Figure 4 are explained below.

Figure 4. Depiction of the arc-disjoint paths found in Case 3 of the proof of Theorem 1.

Considering $S_1=\{x,u_{2,1}\}$, $r_1=x$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_1,r_1)$-paths in $G\left(v_1\right)$, denoted as ${\tilde{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$. Let $S_2=\{u_{2,1},y\}$, $r_2=u_{2,1}$, and there exist at least $\kappa \left(G\right)$ internally disjoint $(S_2,r_2)$-paths in $H\left(u_2\right)$, denoted as ${\widehat{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$. Considering $S_1^{\prime }=\{x,u_{1,2}\}$, $r_1^{\prime }=x$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_1^{\prime },r_1^{\prime })$-paths in $H\left(u_1\right)$, denoted as ${\tilde{P}}_{2j}(j\in \left[\kappa \left(G\right)\right])$. Let $S_2^{\prime }=\{u_{1,2},y\}$, $r_2^{\prime }=u_{1,2}$, and there exist at least $\kappa \left(G\right)$ internally disjoint $(S_2^{\prime },r_2^{\prime })$-paths in $G\left(v_2\right)$, denoted as ${\widehat{P}}_{2j}(j\in \left[\kappa \left(G\right)\right])$. In $H\left(u_2\right)$, with $S_3^{\prime }=\{y,u_{2,3}\}$, $r_3^{\prime }=y$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_3^{\prime },r_3^{\prime })$-paths, denoted as ${\overline{P}}_{2j}$. For each $j\in \left[\kappa \right(G\left)\right]$, let $u_{2,f_j}$ be the out-neighbor of y in ${\overline{P}}_{2j}$, clearly these out-neighbors are distinct.

In $G\left(v_2\right)$, with $S_3=\{y,u_{3,2}\}$, $r_3=y$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_3,r_3)$-paths in $G\left(v_2\right)$, denoted as ${\overline{P}}_{1i}$. For each $i\in \left[\kappa \right(G\left)\right]$, let $u_{s_i,2}$ be the out-neighbor of y in ${\overline{P}}_{1i}$, clearly these out-neighbors are distinct. For each $i\in \left[\kappa \right(G\left)\right]$, an out-neighbor of $u_{s_i,2}$ in $H\left(u_{s_i}\right)$ can be chosen, denoted by $u_{s_i,c}(c\in \left[m\right])$, with $c\notin \{1,3\}$. Similarly, an out-neighbor of $u_{2,f_j}$ in $G\left(v_{f_j}\right)$ can be chosen, denoted by $u_{b,f_j}(b\in \left[n\right])$, with $b\notin \{1,3\}$.

In $G\left(v_c\right)$, with $S_4=\{u_{2,c},u_{3,c}\}$, $r_4=u_{2,c}$. ${\overline{P}}_{1i}^{\prime }$ is the $(S_4,r_4)$-path corresponding to ${\overline{P}}_{1i}$. In ${\overline{P}}_{1i}^{\prime }$, the path from vertex $u_{s_i,c}$ to $u_{3,c}$ is denoted as ${\overline{P}}_{1i}^{″}$. In $H\left(u_3\right)$, with $S_5=\{u_{3,c},z\}$, $r_5=u_{3,c}$, and it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_5,r_5)$-paths, say ${\breve{P}}_{1i}$. In $H\left(v_b\right)$, with $S_4^{\prime }=\{u_{b,2},u_{b,3}\}$, $r_4^{\prime }=u_{b,2}$, ${\overline{P}}_{2j}^{\prime }$ is the $(S_4^{\prime },r_4^{\prime })$-path corresponding to ${\overline{P}}_{2j}$. In path ${\overline{P}}_{2j}^{\prime }$, the path from vertex $u_{b,f_j}$ to $u_{b,3}$ is denoted as ${\overline{P}}_{2j}^{″}$. In $G\left(v_3\right)$, with $S_5^{\prime }=\{u_{b,3},z\}$, $r_5^{\prime }=u_{b,3}$, and it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_5^{\prime },r_5^{\prime })$-paths in $G\left(v_3\right)$, say ${\breve{P}}_{2j}$. If $u_{s_k,2}=u_{3,2}$, then $u_{3,2}\notin {\breve{P}}_{1k}(k\in \left[\kappa \left(G\right)\right])$. If $u_{3,1}\in {\tilde{P}}_{1t}$, then $u_{3,1}\notin {\breve{P}}_{1t}(t\in \left[\kappa \left(G\right)\right])$. Similarly, if $u_{2,f_r}=u_{2,3}$, then $u_{2,3}\notin {\breve{P}}_{2r}(r\in \left[\kappa \left(G\right)\right])$. If $u_{1,3}\in {\tilde{P}}_{2h}$, then $u_{1,3}\notin {\breve{P}}_{2h}(h\in \left[\kappa \left(G\right)\right])$. The arc-disjoint $(S,r)$-paths can be constructed as

$P_{1i}={\tilde{P}}_{1i}\cup {\widehat{P}}_{1i}\cup {\overline{P}}_{1i}^{″}\cup {\breve{P}}_{1i}\cup \{y{u}_{s_i,2},u_{s_i,2}{u}_{s_i,c}\},$

$P_{2j}={\tilde{P}}_{2j}\cup {\widehat{P}}_{2j}\cup {\overline{P}}_{2j}^{″}\cup {\breve{P}}_{2j}\cup \{y{u}_{2,f_j},u_{2,f_j}{u}_{b,f_j}\}.$

Then we obtain $2\kappa \left(G\right)$ arc-disjoint $(S,r)$-paths.

Case 4.

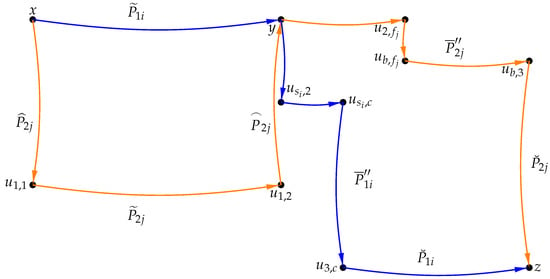
Let x and y be in the same $H\left(u_i\right)$. Let z, x, and y be in different $G\left(v_j\right)$ and let z, x be in different $H\left(u_i\right)$, for some $i\in \left[n\right]$, $j\in \left[m\right]$. Without loss of generality, we can assume that $x=u_{2,1}$, $y=u_{2,2}$, $z=u_{3,3}$. In this case, our overall goal is that we will use arc-disjoint paths between x and y in $H\left(u_2\right)$, y and its out-neighbors in $G\left(v_2\right)$, z and its in-neighbors in $H\left(u_3\right)$, x and its out-neighbors in $G\left(v_2\right)$, y and its out-neighbors in $H\left(u_2\right)$, z and its in-neighbors in $G\left(v_3\right)$, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in Figure 5. The vertices and paths contained in Figure 5 are explained below.

Figure 5. Depiction of the arc-disjoint paths found in Case 4 of the proof of Theorem 1.

Considering $S_1=\{x,y\}$, $r_1=x$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_1,r_1)$-paths in $H\left(u_2\right)$, denoted as ${\tilde{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$. In $G\left(v_1\right)$, with $S_1^{\prime }=\{x,u_{1,1}\}$, and $r_1^{\prime }=x$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_1^{\prime },r_1^{\prime })$-paths, denoted as ${\widehat{P}}_{2j}$. In $H\left(u_1\right)$, with $S_2^{\prime }=\{u_{1,1},u_{1,2}\}$, and $r_2^{\prime }=u_{1,1}$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_2^{\prime },r_2^{\prime })$-paths, denoted as ${\tilde{P}}_{2j}$. In $G\left(v_2\right)$, with $S_3^{\prime }=\{u_{1,2},y\}$, and $r_3^{\prime }=u_{1,2}$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_3^{\prime },r_3^{\prime })$-paths, denoted as ${\stackrel{⌢}{P}}_{2j}$. Let $u_{s_i,2}$, $u_{s_i,c}$, $u_{2,f_j}$, $u_{b,f_j}$,${\breve{P}}_{1i}$, ${\breve{P}}_{2j}$, ${\overline{P}}_{1i}^{″}$ and ${\overline{P}}_{2j}^{″}$ be the same as in Case 3.

If $u_{s_k,2}=u_{3,2}$, then $u_{3,2}\notin {\breve{P}}_{1k}(k\in \left[\kappa \left(G\right)\right])$. If $u_{2,f_r}=u_{2,3}$, then $u_{2,3}\notin {\breve{P}}_{2r}(r\in \left[\kappa \left(G\right)\right])$. If $u_{1,3}\in {\tilde{P}}_{2h}$, then $u_{1,3}\notin {\breve{P}}_{2h}(h\in \left[\kappa \left(G\right)\right])$. If $u_{b,1}\in {\overline{P}}_{2t}^{″}$, then $u_{b,1}\notin {\widehat{P}}_{2t}(t\in \left[\kappa \left(G\right)\right])$. If $u_{1,3}\in {\breve{P}}_{2l}$, then $u_{1,3}\notin {\tilde{P}}_{2l}(l\in \left[\kappa \left(G\right)\right])$.

Subcase 4.1.

If there exists no vertex $u_{2,f_j}=x$. Let

$P_{1i}={\tilde{P}}_{1i}\cup {\overline{P}}_{1i}^{″}\cup {\breve{P}}_{1i}\cup \{y{u}_{s_i,2},u_{s_i,2},u_{s_i,c}\},$

$P_{2j}={\tilde{P}}_{2j}\cup {\overline{P}}_{2j}^{″}\cup {\widehat{P}}_{2j}\cup {\breve{P}}_{2j}\cup {\stackrel{⌢}{P}}_{2j}\cup \{y{u}_{2,f_j},u_{2,f_j}{u}_{b,f_j}\}.$

Subcase 4.2.

If there exists a vertex $u_{2,f_g}=x(g\in \left[\kappa \left(G\right)\right])$, then in $G\left(v_1\right)$, there exists an out-neighbor $u_{b,1}$ of x. If $u_{b,1}\in {\widehat{P}}_{2j}$, this path is denoted by ${\widehat{P}}_{2g}$.

In $H\left(u_3\right)$, there exists an out-neighbor $u_{3,g_1}$ of z such that $g_1\in \left[m\right]\setminus \{c,2,1\}$. In $G\left(v_2\right)$, there exists an in-neighbor $u_{g_2,2}$ of y such that $g_2\in \left[n\right]\setminus \{1,b,3\}$. If $u_{g_2,2}\in {\stackrel{⌢}{P}}_{2j}$, this path is denoted by ${\stackrel{⌢}{P}}_{2g}$. Then in $H\left(u_{g_2}\right)$, with $S_4^{\prime }=\{u_{g_2,g_1},u_{g_2,2}\}$, and $r_4^{\prime }=u_{g_2,g_1}$, it is known that there are at least $\kappa \left(G\right)$ internally disjoint $(S_4^{\prime },r_4^{\prime })$-paths. One such $(S_4^{\prime },r_4^{\prime })$-path is chosen, denoted as ${\widehat{P}}_g$, with $u_{g_2,3}\notin {\widehat{P}}_g$. In $G\left(v_{g_1}\right)$, with $S_5^{\prime }=\{u_{3,g_1},u_{g_2,g_1}\}$, and $r_5^{\prime }=u_{3,g_1}$, it is known that there are at least $\kappa \left(G\right)$ internally disjoint $(S_5^{\prime },r_5^{\prime })$-paths. One such $(S_5^{\prime },r_5^{\prime })$-path is chosen, denoted as ${\overline{P}}_g$, with $u_{b,g_1}\notin {\overline{P}}_g$. Then, $P_{2g}$ is constructed as

$P_{2g}={\overline{P}}_{2g}^{″}\cup {\breve{P}}_{2g}\cup {\overline{P}}_g\cup {\widehat{P}}_g\cup \{x{u}_{b,1},z{u}_{3,g_1},u_{g_2,2}y\}.$

The other paths are the same as Subcase 4.1. Then we obtain $2\kappa \left(G\right)$ arc-disjoint $(S,r)$-paths.

Case 5.

Let x and y be in the same $H\left(u_i\right)$. Let y and z be in the same $G\left(v_j\right)$, for some $i\in \left[n\right]$, $j\in \left[m\right]$. Without loss of generality, we can assume that $x=u_{1,1}$, $y=u_{1,2}$, $z=u_{2,2}$. In this case, our overall goal is that we will use arc-disjoint paths between x and y in $H\left(u_1\right)$, y and z in $G\left(v_2\right)$, x and its out-neighbors in $G\left(v_1\right)$, x and its out-neighbors in $G\left(v_1\right)$, z and y in $G\left(v_2\right)$, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in Figure 6. The vertices and paths contained in Figure 6 are explained below.

Figure 6. Depiction of the arc-disjoint paths found in Case 5 of the proof of Theorem 1.

It is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_1,r_1)$-paths in $H\left(u_1\right)$, denoted as ${\tilde{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$, where $S_1=\{x,y\}$ and $r_1=x$. In $G\left(v_2\right)$, there exist at least $\kappa \left(G\right)$ internally disjoint $(S_2,r_2)$-paths, denoted as ${\overline{P}}_{1i}(i\in \left[\kappa \left(G\right)\right])$, where $S_2=\{y,z\}$ and $r_2=y$. Similarly, in $G\left(v_1\right)$, there exist at least $\kappa \left(G\right)$ internally disjoint $(S_1^{\prime },r_1^{\prime })$-paths, denoted as ${\tilde{P}}_{2j}(j\in \left[\kappa \left(G\right)\right])$, where $S_1^{\prime }=\{x,u_{2,1}\}$ and $r_1^{\prime }=x$. In $H\left(u_2\right)$, there exist at least $\kappa \left(G\right)$ internally disjoint $(S_2^{\prime },r_2^{\prime })$-paths, denoted as ${\widehat{P}}_{2j}(j\in \left[\kappa \left(G\right)\right])$, where $S_2^{\prime }=\{u_{2,1},z\}$ and $r_2=u_{2,1}$. In $G\left(v_2\right)$, there exist at least $\kappa \left(G\right)$ internally disjoint $(S_3^{\prime },r_3^{\prime })$-paths, denoted as ${\overline{P}}_{2j}(j\in \left[\kappa \left(G\right)\right])$, where $S_3^{\prime }=\{z,y\}$ and $r_3^{\prime }=z$. For each $j\in \left[\kappa \right(G\left)\right]$, let $u_{s_j,2}$ be the in-neighbor of y in ${\overline{P}}_{2j}$, and clearly these in-neighbors are distinct. Similarly, let $u_{k_j,2}(j\in \left[\kappa \left(G\right)\right])$ be the out-neighbor of z in ${\overline{P}}_{2j}$. For each $j\in \left[\kappa \right(G\left)\right]$, an out-neighbor $u_{k_j,b}$ of $u_{k_j,2}$ is chosen in $H\left(u_{k_j}\right)$, where $b\ne 1$.

In $G\left(v_b\right)$, with $S_4^{\prime }=\{u_{2,b},u_{1,b}\}$ and $r_4^{\prime }=u_{2,b}$. ${\overline{P}}_{2j}^{\prime }$ is the $(S_4^{\prime },r_4^{\prime })$-path corresponding to ${\overline{P}}_{2j}$. In ${\overline{P}}_{2j}^{\prime }$, the path from vertex $u_{k_j,b}$ to $u_{s_j,b}$ is denoted as ${\overline{P}}_{2j}^{″}$. Then, in $H\left(u_{s_j}\right)$, with $S_{5_j}^{\prime }=\{u_{s_j,b},u_{s_j,2}\}$ and $r_{5_j}^{\prime }=u_{s_j,b}$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_{5_j}^{\prime },r_{5_j}^{\prime })$-paths. One such $(S_{5_j}^{\prime },r_{5_j}^{\prime })$-path, denoted as ${\breve{P}}_{2j}(j\in \left[\kappa \left(G\right)\right])$, is chosen, with $u_{s_j,1}\notin {\breve{P}}_{2j}$. The arc-disjoint $(S,r)$-paths can be constructed as

$P_{1i}={\tilde{P}}_{1i}\cup {\overline{P}}_{1i},$

$P_{2j}={\tilde{P}}_{2j}\cup {\widehat{P}}_{2j}\cup {\overline{P}}_{2j}^{″}\cup {\breve{P}}_{2j}\cup \{z{u}_{k_j,2},u_{s_j,2}y,u_{k_j,2}{u}_{k_j,b}\}.$

If $u_{s_t,2}=u_{k_t,2}(t\in \left[\kappa \left(G\right)\right])$, then $P_{2t}={\tilde{P}}_{2t}\cup {\widehat{P}}_{2t}\cup \{z{u}_{k_t,2},u_{s_t,2}y\}$. And if $u_{k_l,2}=y(l\in \left[\kappa \left(G\right)\right])$, then $P_{2l}={\tilde{P}}_{2l}\cup {\widehat{P}}_{2l}\cup \left\{zy\right\}$. This results in obtaining $2\kappa \left(G\right)$ arc-disjoint $(S,r)$-paths.

Case 6.

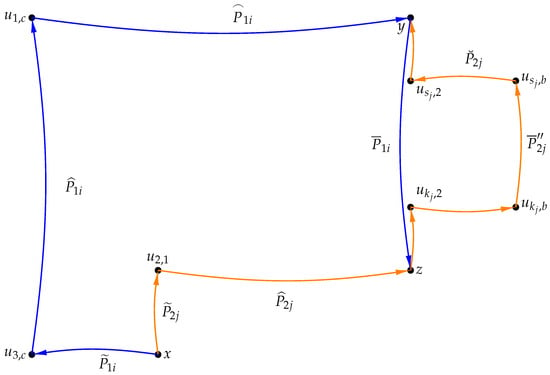
Let y and z be in the same $G\left(v_j\right)$. Let x, y be in different $G\left(v_j\right)$ and x, y, z be in different $H\left(u_i\right)$, for some $i\in \left[n\right]$, $j\in \left[m\right]$. Without loss of generality, we can assume that $x=u_{3,1}$, $y=u_{1,2}$, $z=u_{2,2}$. Let $u_{s_j,2}$$(j\in [\kappa \left(G\right)\left]\right)$, $u_{k_j,2}$, ${\overline{P}}_{1i}$, ${\overline{P}}_{2j}$, ${\widehat{P}}_{2j}$ be the same as in Case 5. In $G\left(v_1\right)$, with $S_1^{\prime }=\{x,u_{2,1}\}$ and $r_1^{\prime }=x$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_1^{\prime },r_1^{\prime })$-paths in $G\left(v_1\right)$, denoted as ${\tilde{P}}_{2j}$. In this case, our overall goal is that we will use arc-disjoint paths between x and its out-neighbors in $H\left(u_3\right)$, y and its in-neighbors in $H\left(u_1\right)$, y and z in $G\left(v_2\right)$, x and its out-neighbors in $G\left(v_1\right)$, z and its in-neighbors in $H\left(u_2\right)$, z and y in $G\left(v_2\right)$, and combine them together to form the required arc-disjoint paths. The general idea of the proof process is briefly described in Figure 7. The vertices and paths contained in Figure 7 are explained below.

Figure 7. Depiction of the arc-disjoint paths found in Case 6 of the proof of Theorem 1.

Subcase 6.1.

In the set $\{u_{s_j,2},u_{k_j,2}\}$, there does not exist $u_{3,2}\in \{u_{s_j,2},u_{k_j,2}\}$. Thus, $u_{s_j,b}$, $u_{k_j,b}$, ${\breve{P}}_{2j}$, ${\overline{P}}_{2j}^{″}$ remain the same as in Case 5.

In $H\left(u_3\right)$, with $S_1=\{x,u_{3,c}\}(c\in \left[m\right]\setminus \{1,2,b\})$ and $r_1=x$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_1,r_1)$-paths in $H\left(u_3\right)$, denoted as ${\tilde{P}}_{1i}$. In $G\left(v_c\right)$, with $S_2=\{u_{3,c},u_{1,c}\}$ and $r_2=u_{3,c}$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_2,r_2)$-paths in $G\left(v_c\right)$, denoted as ${\widehat{P}}_{1i}$. In $H\left(u_1\right)$, with $S_3=\{u_{1,c},y\}$ and $r_3=u_{1,c}$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_3,r_3)$-paths in $H\left(u_1\right)$, denoted as ${\stackrel{⌢}{P}}_{1i}$. If $u_{3,2}\in {\tilde{P}}_{1r}$, then $u_{3,2}\notin {\overline{P}}_{1r}$. Let

$P_{1i}={\tilde{P}}_{1i}\cup {\overline{P}}_{1i}\cup {\widehat{P}}_{1i}\cup {\stackrel{⌢}{P}}_{1i},$

$P_{2j}={\tilde{P}}_{2j}\cup {\overline{P}}_{2j}^{″}\cup {\widehat{P}}_{2j}\cup {\breve{P}}_{2j}\cup \{z{u}_{k_j,2},u_{k_j,2}{u}_{k_j,b},u_{s_j,2}y\}.$

If $u_{s_t,2}=u_{k_t,2}(t\in \left[\kappa \left(G\right)\right])$, then $P_{2t}={\tilde{P}}_{2t}\cup {\widehat{P}}_{2t}\cup \{z{u}_{k_t,2},u_{s_t,2}y\}$. And if $u_{k_l,2}=y(l\in \left[\kappa \left(G\right)\right])$, then $P_{2l}={\tilde{P}}_{2l}\cup {\widehat{P}}_{2l}\cup \left\{zy\right\}$. Now we obtain $2\kappa \left(G\right)$ arc-disjoint $(S,r)$-paths.

Subcase 6.2.

In the set $\{u_{s_j,2},u_{k_j,2}\}$, only one vertex $u_{k_r,2}=u_{3,2}(r\in \left[\kappa \left(G\right)\right])$ exists. Thus, $u_{s_j,b}$, $u_{k_j,b}$, ${\breve{P}}_{2j}$, ${\overline{P}}_{2j}^{″}$ remain the same as in Case 5.

If $u_{k_r,2}{u}_{k_r,b}\notin {\tilde{P}}_{1i}$ in ${\tilde{P}}_{1i}$, then $P_{1i}$, $P_{2j}$ remain the same as in Subcase 6.1. If an arc $u_{k_r,2}{u}_{k_r,b}$ is in path ${\tilde{P}}_{1i}$, since $\delta \left(G\right)\ge 4$, then an out-neighbor $u_{k_r,a}$ of $u_{k_r,2}$ can be found in $H\left(u_3\right)$ such that $u_{k_r,2}{u}_{k_r,a}\notin {\tilde{P}}_{1i}$ and $a\in \left[m\right]\setminus \{c,1\}$. In $G\left(v_a\right)$, ${\overline{P}}_{2r}^{‴}$ is the $(S_3^{\prime },r_3^{\prime })$-path corresponding to ${\overline{P}}_{2r}^{″}$, where $S_3^{\prime }=\{u_{k_r,a},u_{s_r,a}\}$, $r_3^{\prime }=u_{k_r,a}$. In $H\left(u_{s_r}\right)$, with $S_4^{\prime }=\{u_{s_r,a},u_{s_r,2}\}$ and $r_4^{\prime }=u_{s_r,a}$, it is known that there exist at least $\kappa \left(G\right)$ internally disjoint $(S_4^{\prime },r_4^{\prime })$-paths. Then in these paths, one of the paths ${\breve{P}}_{2r}^{\prime }$ is chosen, with $u_{s_r,1}\notin {\breve{P}}_{2r}^{\prime }$. $P_{2j}(j\ne r)$ and $P_{1i}$ remain the same as in Subcase 6.1. $P_{2r}$ is constructed as

$P_{2r}={\tilde{P}}_{2r}\cup {\overline{P}}_{2r}^{‴}\cup {\widehat{P}}_{2r}\cup {\breve{P}}_{2r}^{\prime }\cup \{z{u}_{k_r,2},u_{k_r,2}{u}_{k_r,a},u_{s_r,2}y\}.$

Subcase 6.3.

In the set $\{u_{s_j,2},u_{k_j,2}\}$, there is only one vertex $u_{s_g,2}=u_{3,2}(g\in \left[\kappa \left(G\right)\right])$.

For each $j\in \left[\kappa \right(G\left)\right]$, an in-neighbor of $u_{s_j,1}$ in $H\left(u_{s_j}\right)$ can be chosen, denoted by $u_{s_j,d}(d\in \left[m\right])$, where $d\ne c,1$. In $G\left(v_d\right)$, let ${\overline{P}}_{2j}^{\prime }$ be the $(S_5^{\prime },r_5^{\prime })$-path corresponding to ${\overline{P}}_{2j}$, where $S_5^{\prime }=\{u_{2,d},u_{1,d}\}$, $r_5^{\prime }=u_{2,d}$. The path from vertex $u_{k_j,d}$ to $u_{s_j,d}$ in path ${\overline{P}}_{2j}^{\prime }$ is denoted as ${\overline{P}}_{2j}^{″}$. In $H\left(u_{k_j}\right)$, let $S_{6_j}^{\prime }=\{u_{k_j,2},u_{k_j,d}\}$, $r_{6_j}^{\prime }=u_{k_j,2}$, and at least $\kappa \left(G\right)$ internally disjoint $(S_{6_j}^{\prime },r_{6_j}^{\prime })$-paths are known to exist. Then, one of the paths ${\breve{P}}_{2j}(j\in \left[\kappa \left(G\right)\right])$ is chosen, where $u_{k_j,1}\notin {\breve{P}}_{2j}$. If $u_{s_t,2}=u_{k_t,2}(t\in \left[\kappa \left(G\right)\right])$, $P_{2t}={\tilde{P}}_{2t}\cup {\widehat{P}}_{2t}\cup \{z{u}_{k_t,2},u_{s_t,2}y\}$. And if $u_{k_l,2}=y(l\in \left[\kappa \left(G\right)\right])$, $P_{2l}={\tilde{P}}_{2l}\cup {\widehat{P}}_{2l}\cup \left\{zy\right\}$. If $u_{s_g,d}{u}_{s_g,2}\notin {\tilde{P}}_{1i}$ in the path ${\tilde{P}}_{1i}$. Let

$P_{1i}={\tilde{P}}_{1i}\cup {\overline{P}}_{1i}\cup {\widehat{P}}_{1i}\cup {\stackrel{⌢}{P}}_{1i},$

$P_{2j}={\tilde{P}}_{2j}\cup {\overline{P}}_{2j}^{″}\cup {\widehat{P}}_{2j}\cup {\breve{P}}_{2j}\cup \{z{u}_{k_j,2},u_{s_j,d}{u}_{s_j,2},u_{s_j,2}y\}$.

If an arc $u_{s_g,d}{u}_{s_g,2}$ is in path ${\tilde{P}}_{1i}$, an in-neighbor $u_{s_g,f}$ of $u_{s_g,2}$ can be found in $H\left(u_3\right)$ such that $u_{s_g,f}{u}_{s_g,2}\notin {\tilde{P}}_{1i}$ and $f\in \left[m\right]\setminus \{c,1\}$. In $G\left(v_f\right)$, let ${\overline{P}}_{2g}^{‴}$ be the $(S_7^{\prime },r_7^{\prime })$-path corresponding to ${\overline{P}}_{2g}^{″}$, where $S_7^{\prime }=\{u_{k_g,f},u_{s_g,f}\}$, $r_7^{\prime }=u_{k_g,f}$. In $H\left(u_{k_g}\right)$, let $S_8^{\prime }=\{u_{k_g,2},u_{k_g,f}\}$, $r_8^{\prime }=u_{k_g,2}$, and at least $\kappa \left(G\right)$ internally disjoint $(S_7^{\prime },r_7^{\prime })$-paths are known to exist. Then, one of the paths ${\breve{P}}_{2g}^{\prime }$ is chosen, and let $u_{k_g,1}\notin {\breve{P}}_{2g}^{\prime }$. Let

$P_{2g}={\tilde{P}}_{2g}\cup {\overline{P}}_{2g}^{‴}\cup {\widehat{P}}_{2g}\cup {\breve{P}}_{2g}^{\prime }\cup \{z{u}_{k_g,2},u_{s_g,f}{u}_{s_g,2},u_{s_g,2}y\}.$

Hence, we obtain $2\kappa \left(G\right)$ arc-disjoint $(S,r)$-paths.

Now we prove that this bound is sharp. By Proposition 1, ${\lambda }_3^p({\overleftrightarrow{K}}_n\square {\overleftrightarrow{K}}_m)=n+m-2.$ By Lemma 2, $\kappa \left({\overleftrightarrow{K}}_n\right)=n-1$. So we have ${\lambda }_3^p({\overleftrightarrow{K}}_n\square {\overleftrightarrow{K}}_n)=2\kappa \left({\overleftrightarrow{K}}_n\right)=2n-2$, with $n\ge 5$. Therefore, the lower bound holds and is sharp. □

4. Exact Values for Digraph Classes

In this section, we aim to determine precise values for the directed path 3-arc-connectivity of the Cartesian product of two digraphs within specific digraph classes.

Proposition 1.

We have ${\lambda }_3^p({\overleftrightarrow{K}}_n\square {\overleftrightarrow{K}}_m)=n+m-2.$

Proof. 

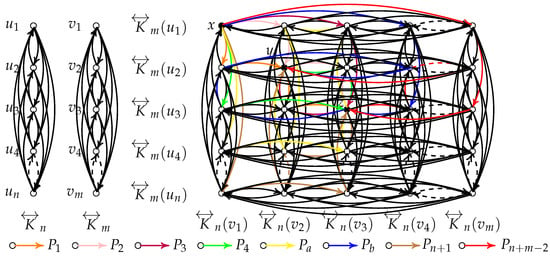
Consider $S=\{x,y,z\}$ and $r=x$. We will focus solely on scenarios where x, y, and z do not all belong to the same ${\overleftrightarrow{K}}_m\left(u_i\right)$ or the same ${\overleftrightarrow{K}}_n\left(v_j\right)$ for any $i\in \left[n\right]$, $j\in \left[m\right]$. The rationale for the remaining cases follows a similar line of argument. Without loss of generality, let us assume $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. It is feasible to derive $n+m-2$ arc-disjoint $(S,r)$-paths in ${\overleftrightarrow{K}}_n\square {\overleftrightarrow{K}}_m$, say $P_1$, $P_2$, ⋯, $P_a(a=min\{i+1,3<i\le n\})$, $P_{i+1}(4<i\le n)$, ⋯, $P_b(b=min\{n+j-2,3<j\le n\})$, $P_{n+j-2}(4<j\le m)$ (as shown in Figure 8) such that

Figure 8. ${\overleftrightarrow{K}}_n\square {\overleftrightarrow{K}}_m$.

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z,$$P_3:x{u}_{1,3}z{u}_{3,2}y,$

$P_4:x{u}_{3,1}z{u}_{2,3}y,$$P_a:x{u}_{4,1}{u}_{4,3}z{u}_{1,3}{u}_{1,2}{u}_{4,2}y,$$P_b:x{u}_{1,4}{u}_{3,4}z{u}_{3,1}{u}_{2,1}{u}_{2,4}y,$

$P_{i+1}:x{u}_{i,1}{u}_{i,3}z{u}_{i-1,3}{u}_{i-1,2}{u}_{i,2}y,$$P_{n+j-2}:x{u}_{1,j}{u}_{3,j}z{u}_{3,j-1}{u}_{2,j-1}{u}_{2,j}y.$

Now, we add two cases to prove that the proposition holds, so as to show that the proposition has no constraint conditions.

First, let $n=m=4$. We can assume that $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. Let

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z,$$P_3:x{u}_{3,1}{u}_{3,2}y{u}_{4,2}{u}_{4,3}z,$

$P_4:x{u}_{4,1}{u}_{4,2}y{u}_{1,2}{u}_{1,3}z,$$P_5:x{u}_{1,3}{u}_{2,3}y{u}_{2,4}{u}_{3,4}z,$$P_6:x{u}_{1,4}{u}_{2,4}y{u}_{2,1}{u}_{3,1}z.$

Furthermore, let $n=2$, $m=4$. We can assume that $x=u_{1,1}$, $y=u_{1,2}$, $z=u_{1,3}$. Let

$P_1:xyz,$$P_2:xzy,$$P_3:x{u}_{1,4}z{u}_{2,3}{u}_{2,2}y,$$P_4:x{u}_{2,1}{u}_{2,3}z{u}_{1,4}y.$

Then we have $n+m-2=$ min $\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}\ge {\lambda }_3^p({\overleftrightarrow{K}}_n\square {\overleftrightarrow{K}}_m)\ge n+m-2$. This concludes the proof. □

Proposition 2.

We have ${\lambda }_3^p({\overleftrightarrow{C}}_n\square {\overleftrightarrow{K}}_m)=m+1,$ with $n\ge 3$.

Proof. 

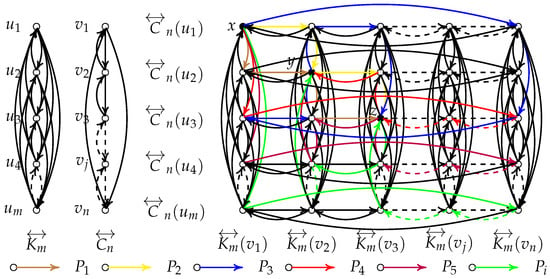
Let $S=\{x,y,z\}$, $r=x$, and we only examine the case where x, y, and z are not all within the same ${\overleftrightarrow{C}}_n\left(u_i\right)$ or the same ${\overleftrightarrow{K}}_m\left(v_j\right)$ for any $i\in \left[n\right]$, $j\in \left[m\right]$. The rationale for the remaining cases follows a similar line of argument. Without loss of generality, let us assume $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. We can obtain $m+1$ arc-disjoint $(S,r)$-paths in ${\overleftrightarrow{C}}_n\square {\overleftrightarrow{K}}_m$, say $P_1$, $P_2$, ⋯, $P_{i+1}(4<i\le m)$, $P_{m-1}$, $P_m$ (as shown in Figure 9) such that

Figure 9. $\overleftrightarrow{C_n}\square {\overleftrightarrow{K}}_m$.

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z,$$P_3:x{u}_{1,n}{u}_{3,n}{u}_{3,1}{u}_{3,2}y{u}_{1,2}{u}_{1,3}z,$

$P_4:x{u}_{3,1}{u}_{3,n}\dots u_{3,j}\dots z{u}_{2,3}y,$$P_5:x{u}_{4,1}{u}_{4,n}\cdots u_{4,j}\cdots u_{4,3}z{u}_{3,2}{u}_{4,2}y,$

$P_{i+1}:x{u}_{i,1}{u}_{i,n}\cdots u_{i,j}\cdots u_{i,3}z{u}_{i-1,3}{u}_{i-1,2}{u}_{i,2}y.$

Now, we add two cases to prove that the proposition holds, so as to show that the proposition has no constraint conditions.

First, let $n=3,$$m=4$. We can assume that $x=u_{1,1}$, $y=u_{2,1}$, $z=u_{3,1}$. Let

$P_1:xyz,$$P_2:xzy,$$P_3:x{u}_{4,1}z{u}_{3,2}{u}_{2,2}y,$$P_4:x{u}_{1,3}{u}_{2,3}y{u}_{2,2}{u}_{3,2}{u}_{3,3}z.$

Furthermore, let $n=3$, $m=2$. We can assume that $x=u_{1,1}$, $y=u_{1,2}$, $z=u_{1,3}$. Let

$P_1:xyz,$$P_2:xz{u}_{2,3}{u}_{2,2}y,$$P_3:x{u}_{2,1}{u}_{2,3}zy.$

Then we have $m+1=min\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}\ge {\lambda }_3^p({\overleftrightarrow{C}}_n\square {\overleftrightarrow{K}}_m)\ge m+1$. This concludes the proof. □

Proposition 3.

We have ${\lambda }_3^p({\overrightarrow{C}}_n\square {\overleftrightarrow{K}}_m)=m.$

Proof. 

Let $S=\{x,y,z\}$, $r=x$, and we only examine the case where x, y, and z are not all within the same ${\overrightarrow{C}}_n\left(u_i\right)$ or the same ${\overleftrightarrow{K}}_m\left(v_j\right)$ for any $i\in \left[n\right]$, $j\in \left[m\right]$. The rationale for the remaining cases follows a similar line of argument. Without loss of generality, let us assume $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. We can obtain m arc-disjoint $(S,r)$-paths in ${\overrightarrow{C}}_n\square {\overleftrightarrow{K}}_m$.

First assume that m is even number, let

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z,$$P_3:x{u}_{3,1}{u}_{3,2}y{u}_{2,3}z,$

$P_4:x{u}_{4,1}{u}_{4,2}y{u}_{1,2}{u}_{1,3}z,$$P_{i-1}:x{u}_{i-1,1}{u}_{i-1,2}y{u}_{i,2}{u}_{i,3}z,$

$P_i:x{u}_{i,1}{u}_{i,2}y{u}_{i-1,2}{u}_{i-1,3}z$, $4<i\le m,$ and i is an even number.

Conversely assume that m is odd number, let

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z,$$P_3:x{u}_{3,1}{u}_{3,2}y{u}_{1,2}{u}_{1,3}z,$

$P_{i-1}:x{u}_{i-1,1}{u}_{i-1,2}y{u}_{i,2}{u}_{i,3}z,$

$P_i:x{u}_{i,1}{u}_{i,2}y{u}_{i-1,2}{u}_{i-1,3}z$, $3<i\le m,$ and i is an odd number. Then we have $m=min\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}\ge {\lambda }_3^p({\overrightarrow{C}}_n\square {\overleftrightarrow{K}}_m)\ge m$. This completes the proof. □

Proposition 4.

We have ${\lambda }_3^p({\overleftrightarrow{T}}_n\square {\overleftrightarrow{K}}_m)=m.$

Proof. 

Let $S=\{x,y,z\}$, $r=x$, and we only examine the case where x, y, and z are not all within the same ${\overleftrightarrow{T}}_n\left(u_i\right)$ or the same ${\overleftrightarrow{K}}_m\left(v_j\right)$ for any $i\in \left[n\right]$, $j\in \left[m\right]$. The rationale for the remaining cases follows a similar line of argument. Without loss of generality, let us assume $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. We can obtain m arc-disjoint $(S,r)$-paths in ${\overleftrightarrow{T}}_n\square {\overleftrightarrow{K}}_m$, say $P_1$, $P_2$, ⋯, $P_i(4<i\le m)$, $P_{m-1}$, $P_m$ such that

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z,$$P_3:x{u}_{1,3}{u}_{2,3}y{u}_{2,1}{u}_{3,1}z,$

$P_4:x{u}_{1,4}{u}_{2,4}{u}_{3,4}z{u}_{3,2}y,$$P_i:x{u}_{1,i}{u}_{2,i}{u}_{3,i}z{u}_{3,i-1}{u}_{2,i-1}y.$

Then we have $m=min\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}\ge {\lambda }_3^p({\overleftrightarrow{T}}_n\square {\overleftrightarrow{K}}_m)\ge m$. This completes the proof. □

Proposition 5.

We have ${\lambda }_3^p({\overrightarrow{C}}_n\square {\overrightarrow{C}}_m)=2.$

Proof. 

Let $S=\{x,y,z\}$, $r=x$, and we only examine the case where x, y, and z are not all within the same ${\overrightarrow{C}}_n\left(u_i\right)$ or the same ${\overrightarrow{C}}_m\left(v_j\right)$ for any $i\in \left[n\right]$, $j\in \left[m\right]$. The rationale for the remaining cases follows a similar line of argument. Without loss of generality, let us assume $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. We can obtain two arc-disjoint $(S,r)$-paths in ${\overrightarrow{C}}_n\square {\overrightarrow{C}}_m$, say $P_1$ and $P_2$ such that

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z.$

Then we have $2=min\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}\ge {\lambda }_3^p({\overrightarrow{C}}_n\square {\overrightarrow{C}}_m)\ge 2$. This completes the proof. □

Proposition 6.

We have ${\lambda }_3^p({\overrightarrow{C}}_n\square {\overleftrightarrow{C}}_m)=3,$ with $m\ge 3$.

Proof. 

Let $S=\{x,y,z\}$, $r=x$, and we only examine the case where x, y, and z are not all within the same ${\overrightarrow{C}}_n\left(u_i\right)$ or the same ${\overleftrightarrow{C}}_m\left(v_j\right)$ for any $i\in \left[n\right]$, $j\in \left[m\right]$. The rationale for the remaining cases follows a similar line of argument. Without loss of generality, let us assume $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. We can obtain three arc-disjoint $(S,r)$-paths in ${\overrightarrow{C}}_n\square {\overleftrightarrow{C}}_m$, say $P_1$, $P_2$, $P_3$ such that

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z,$

$P_3:x{u}_{m,1}{u}_{m,2}{u}_{m-1,2}\cdots u_{3,2}y{u}_{1,2}{u}_{1,3}{u}_{m,3}{u}_{m-1,3}\cdots z.$

Then we have $3=min\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}\ge {\lambda }_3^p({\overrightarrow{C}}_n\square {\overleftrightarrow{C}}_m)\ge 3$. This completes the proof. □

Proposition 7.

We have ${\lambda }_3^p({\overleftrightarrow{C}}_n\square {\overleftrightarrow{C}}_m)=4,$ with $n\ge 3$, $m\ge 3$.

Proof. 

Let $S=\{x,y,z\}$, $r=x$, and we only examine the case where x, y, and z are not all within the same ${\overleftrightarrow{C}}_n\left(u_i\right)$ or the same ${\overleftrightarrow{C}}_m\left(v_j\right)$ for any $i\in \left[n\right]$, $j\in \left[m\right]$. The rationale for the remaining cases follows a similar line of argument. Without loss of generality, let us assume $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. We can obtain four arc-disjoint $(S,r)$-paths in ${\overleftrightarrow{C}}_n\square {\overleftrightarrow{C}}_m$, say $P_1$, $P_2$, $P_3$, $P_4$ such that

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z,$

$P_3:x{u}_{m,1}{u}_{m,2}{u}_{m,3}{u}_{m-1,3}\cdots z{u}_{3,2}y,$$P_4:x{u}_{1,n}{u}_{2,n}{u}_{3,n}z{u}_{2,3}y.$

Then we have $4=min\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}\ge {\lambda }_3^p({\overleftrightarrow{C}}_n\square {\overleftrightarrow{C}}_m)\ge 4$. This completes the proof. □

Proposition 8.

We have ${\lambda }_3^p({\overrightarrow{C}}_n\square {\overleftrightarrow{T}}_m)=2.$

Proof. 

Let $S=\{x,y,z\}$, $r=x$, and we only examine the case where x, y, and z are not all within the same ${\overrightarrow{C}}_n\left(u_i\right)$ or the same ${\overleftrightarrow{T}}_m\left(v_j\right)$ for any $i\in \left[n\right]$, $j\in \left[m\right]$. The rationale for the remaining cases follows a similar line of argument. Without loss of generality, let us assume $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. We can obtain three arc-disjoint $(S,r)$-paths in ${\overrightarrow{C}}_n\square {\overleftrightarrow{T}}_m$, say $P_1$ and $P_2$ such that

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z.$

Then we have $2=min\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}\ge {\lambda }_3^p({\overrightarrow{C}}_n\square {\overleftrightarrow{T}}_m)\ge 2$. This completes the proof. □

Proposition 9.

We have ${\lambda }_3^p({\overleftrightarrow{C}}_n\square {\overleftrightarrow{T}}_m)=3,$ with $n\ge 3$.

Proof. 

Let $S=\{x,y,z\}$, $r=x$, and we only examine the case where x, y, and z are not all within the same ${\overleftrightarrow{C}}_n\left(u_i\right)$ or the same ${\overleftrightarrow{T}}_m\left(v_j\right)$ for any $i\in \left[n\right]$, $j\in \left[m\right]$. The rationale for the remaining cases follows a similar line of argument. Without loss of generality, let us assume $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. We can obtain three arc-disjoint $(S,r)$-paths in ${\overleftrightarrow{C}}_n\square {\overleftrightarrow{T}}_m$, say $P_1$, $P_2$, $P_3$ such that

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z,$$P_3:x{u}_{m,1}{u}_{m,2}{u}_{m,3}{u}_{m-1,3}\cdots z{u}_{3,2}y.$

Then we have $3=min\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}\ge {\lambda }_3^p({\overleftrightarrow{C}}_n\square {\overleftrightarrow{T}}_m)\ge 3$. This completes the proof. □

Proposition 10.

We have ${\lambda }_3^p({\overleftrightarrow{T}}_n\square {\overleftrightarrow{T}}_m)=2.$

Proof. 

Let $S=\{x,y,z\}$, $r=x$, and we only examine the case where x, y, and z are not all within the same ${\overleftrightarrow{T}}_n\left(u_i\right)$ or the same ${\overleftrightarrow{T}}_m\left(v_j\right)$ for any $i\in \left[n\right]$, $j\in \left[m\right]$. The rationale for the remaining cases follows a similar line of argument. Without loss of generality, let us assume $x=u_{1,1}$, $y=u_{2,2}$, $z=u_{3,3}$. We can obtain three arc-disjoint $(S,r)$-paths in ${\overleftrightarrow{T}}_n\square {\overleftrightarrow{T}}_m$, say $P_1$ and $P_2$ such that

$P_1:x{u}_{2,1}y{u}_{3,2}z,$$P_2:x{u}_{1,2}y{u}_{2,3}z.$

Then we have $2=min\{{\delta }^{+}\left(D\right),{\delta }^{-}\left(D\right)\}\ge {\lambda }_3^p({\overleftrightarrow{T}}_n\square {\overleftrightarrow{T}}_m)\ge 2$. This completes the proof. □

According to Propositions 1–9, we find that the directed path 3-arc-connectivity of some Cartesian products of digraphs is equal to the minimum semi-degrees. Based on this discovery, we can consider under what conditions the directed path 3-arc-connectivity of Cartesian products of digraphs can be equal to the minimum semi-degrees, which is a problem we can consider next.

5. Conclusions

In this paper, we prove that if G and H are two digraphs such that $\delta \left(G\right)\ge 4$, $\delta \left(H\right)\ge 4$, and $\kappa \left(G\right)\ge 2$, $\kappa \left(H\right)\ge 2$, then ${\lambda }_3^p(G\square H)\ge min\left\{2\kappa \left(G\right),2\kappa \left(H\right)\right\},$ and moreover, this bound is sharp. Finally, we obtain exact values of ${\lambda }_3^p(G\square H)$ for some digraph classes G and H. In practical terms, constructing vertex-disjoint or arc-disjoint paths in graphs is crucial. These paths play a significant role in improving transmission reliability and boosting network transmission speeds.