A Globally Convergent Iterative Method for Matrix Sign Function and Its Application for Determining the Eigenvalues of a Matrix Pencil

Abstract

In this research article, we propose a new matrix iterative method with a convergence order of five for computing the sign of a complex matrix by examining the different patterns and symmetry of existing methods. Analysis of the convergence of the method was explored on a global scale, and attraction basins were demonstrated. In addition to this, the asymptotic stability of the scheme was explored.Then, an algorithm for determing thegeneralized eigenvalues for the case of regular matrix pencils was investigated using the matrix sign computation. We performed a series of numerical experiments using numerous matrices to confirm the usefulness and superiority of the proposed method.

1. Introduction

Over the past several years, the efficient computing of matrix functions has emerged as a prominent area of research. Symmetry plays a significant role in the study of matrix functions, particularly in understanding their properties, behavior, and computational methods. Symmetry principles are widely used in physics and engineering to analyze and solve problems involving matrix functions. For instance, in quantum mechanics, symmetric matrices often arise in the context of Hamiltonians, and efficient computation of matrix functions is crucial for simulating quantum systems and predicting their behavior. In order to compute matrix functions, various iterative schemes have been suggested, which include methods for the evaluation of matrix sign function. The scalar sign function defined for $z\in \mathbb{C}$ such that $Re\left(z\right)\ne 0$ which is given as,

$$sign\left(z\right)=\left\{\begin{array}{c}1,Re\left(z\right)>0,\hfill \\ -1,Re\left(z\right)<0.\hfill \end{array}\right.$$

(1)

is extended to form the matrix sign function. Roberts [1] introduced the Cauchy integral representation of the matrix sign function in 1980, given by

$$sign\left(A\right)=\frac{2}{\pi }A{\int }_0^{\infty }{(t^{2}I+A^2)}^{-1}dt,$$

(2)

which can be applied in model reduction and in solving algebraic Riccati and Lyapunov equations. Recall the definition of matrix sign function $sign\left(A\right)$ via the Jordan canonical form [2], in which if $A=PJ{P}^{-1}$ is the Jordan decomposition of A such that $J=diag(J_1,J_2)$, then

$$sign\left(A\right)=P\left[\begin{array}{cc}-I_p& 0\\ 0& I_{n-p}\end{array}\right]P^{-1},$$

(3)

where $A\in {\mathbb{C}}^{n\times n}$ has no eigenvalue on the imaginary axis, P is a nonsingular matrix, and p and $n-p$ are sizes of Jordan blocks $J_1$, $J_2$ corresponding to eigenvalues lying in left half plane $\left({\mathbb{C}}^{-}\right)$ and right half plane $\left({\mathbb{C}}^{+}\right)$, respectively.

In the pursuit of evaluating $sign\left(A\right)$ as a solution of

$$W^2-I=0,$$

(4)

Roberts applied Newton’s method ($NM$) resulting into the following iterative formula:

$$W_{l+1}=\frac{1}{2}(W_l+W_l^{-1}),l=0,1,2,\dots ,$$

(5)

with the initial matrix $W_0=A$ and convergence of order two.

Another alternative is accelerated Newton’s method ($ANM$) that can be achieved via norm scaling parameter in (5) given by,

$$\left\{\begin{array}{cc}{W}_0\hfill & =A,\hfill \\ {\mu }_l\hfill & =\sqrt{\frac{\parallel W_l^{-1}\parallel }{\parallel W_l\parallel }},\hfill \\ W_{l+1}\hfill & =\frac{1}{2}({\mu }_l{W}_l+{\mu }_l^{-1}{W}_l^{-1}).\hfill \end{array}\right.$$

(6)

In order to improve the convergence, acceleration and scaling of iteration (5), Kenney and Laub [3,4] suggested a family of matrix iterations by employing the Padé approximant to the function

$$H\left(x\right)={(1-x)}^{-1/2},$$

(7)

where $x=1-z^2$ and taking into the consideration

$$sign\left(z\right)=\frac{z}{{(1-x)}^{1/2}}.$$

(8)

Let $(r,s)$-Padé approximant to $H\left(x\right)$ with $r+s\ge 1$ is denoted as $\frac{P_{r,s}\left(x\right)}{Q_{r,s}\left(x\right)}$, then

$$w_{l+1}=\frac{w_l{P}_{r,s}(1-w_l^2)}{Q_{r,s}(1-w_l^2)}={\psi }_{2r+1,2s},$$

(9)

converges to $\pm 1$ if $r\ge s-1$ and it has convergence rate equal to $r+s+1$. So, the $(r,s)$-Padé approximant iteration ($P{A}_{r,s}$) for computing $sign\left(A\right)$ is

$$W_{l+1}=W_l\left[P_{r,s}(1-W_l^2)\right]{\left[Q_{r,s}(1-W_l^2)\right]}^{-1}.$$

(10)

These iterations were later investigated by Gomilko et al. [5]. Other popular iterative approaches for $sign\left(A\right)$, such as the Newton-Schulz method $\left(NSM\right)$ [6]

$$W_{l+1}=\frac{1}{2}{W}_l(3I-W_l^2),$$

(11)

and Halley’s method $\left(HM\right)$ [2]

$$W_{l+1}=[I+3W_l^2]{\left[W_l(3I+W_l^2)\right]}^{-1}.$$

(12)

are either members of the Padé family (10) or its reciprocal family.

A recent fifth order iterative method [7] (represented as Lotfi’s Method ($LM$)) for $sign\left(A\right)$ can be investigated and is given by

$$W_{l+1}=\left[W_l(18I-20W_l^2-30W_l^4)\right]{[5I+15W_l^2-45W_l^4-7W_l^6]}^{-1}.$$

(13)

For more recent literature on matrix sign function, one can go through references [8,9,10].

Motivated by constructing efficient iterative methods like the methods discussed above and to overcome on some of the drawbacks of the existing iterative methods, here we aim to propose a globally convergent iterative method for approximation of $sign\left(A\right)$. Matrix sign function has several application in scientific computing (see e.g., [11,12]). Another applications of matrix sign function include solving various matrix equations [13], solving stochastic differential equations [14] and many more.

In this article, we present a fifth order iterative scheme for evaluation of $sign\left(A\right)$. The outline for the rest of the article is defined here: In Section 2, the construction of new iterative scheme for evaluating matrix sign function has been concluded. In Section 3, basins of attraction guarantees the global convergence of developed method. Also, convergence analysis for the fifth rate of convergence is discussed along with stability analysis. Then the proposed method is extended to determine the generalized eigenvalues of a regular matrix pencil in Section 4. Computational complexity is examined in Section 5. Numerical examples are provided to evaluate the performance and to demonstrate the numerical precision of suggested method in Section 6. The final conclusion is presented in Section 7.

2. A Novel Iterative Method

In this section, we have developed an iterative method for evaluation of $sign\left(A\right)$. The primary goal is to develop the scheme by examining the factorization patterns and symmetry of existing schemes rather than using a non-linear equation solver [13]. We aim to design an iterative formula that does not conflict with the Padé family members (9) or its reciprocals.

If we assume the eigenvalues to converge to 1 or $-1$, and we aim to get a higher convergence order five, then the iterative formula will satisfy the equation

$$\frac{w_{l+1}-1}{w_{l+1}+1}=\frac{{(w_l-1)}^5}{{(w_l+1)}^5}.$$

(14)

If we solve Equation (14) for $w_{l+1}$, then we get

$$w_{l+1}=\frac{w_l(5+10w_l^2+w_l^4)}{1+10w_l^2+5w_l^4}.$$

(15)

Nevertheless, the formula mentioned above is not a novel one, as it is a member of Padé family (9). So, we make some modifications in (14) so that the formula becomes better in terms of converegnce as follows:

$$\frac{w_{l+1}-1}{w_{l+1}+1}=\frac{{(w_l-1)}^5(-4+w_l)}{{(w_l+1)}^5(-4-w_l)},$$

(16)

provided that $∥\frac{-4+w_l}{-4-w_l}∥<1$. Solving (16) for $w_{l+1}$, we get

$$w_{l+1}=\frac{w_l(21+50w_l^2+9w_l^4)}{4+45w_l^2+30w_l^4+w_l^6},$$

(17)

which contains a polynomial of degree 5 in the numerator and a polynomial of degree 6 in the denominator. From (9), it is clear that Padé family has a unique member with a polynomial of degree $2r+1$ in numerator and a polynomial of degree $2s$ in denominator for each $r,s\ge 0$. So $2r+1=5$ and $2s=6$ will result into $r=2$ and $s=3$, i.e., $P{A}_{2,3}$ and will have order $2+3+1=6$ which is different from the order 5 that we are achieving. So, the above formula (17) is not a part of the family (9) or reciprocals of (9) and therefore our proposed method ($PM$) is as follows:

$$W_{l+1}=\left[W_l(21I+50W_l^2+9W_l^4)\right]{[4I+45W_l^2+30W_l^4+W_l^6]}^{-1},$$

(18)

where $W_0$ is the appropriate initial guess which we discuss in Section 3.

Remark 1.

Convergence can be slow if $\parallel W_l\parallel >>1$ for some l. In that situation, it is advisable to introduce the scaling parameter ${\mu }_l$ [15] given as,

$${\mu }_l=\left\{\begin{array}{c}\sqrt{\frac{\parallel W_l^{-1}\parallel }{\parallel W_l\parallel }}(\mathit{norm}\mathit{scaling}),\hfill \\ \sqrt{\frac{\rho \left(W_l^{-1}\right)}{\rho \left(W_l\right)}}(\mathit{spectral}\mathit{scaling}),\hfill \\ \sqrt{{\left|det\left(W_l\right)\right|}^{-1/n}}(\mathit{determinant}\mathit{scaling}).\hfill \end{array}\right.$$

(19)

to speed up the convergence [16] of the scheme.

Hence, we also present the accelerated proposed method ($APM$) which is accelerated version of (18) given by

$$\left\{\begin{array}{cc}{W}_0\hfill & =A,\hfill \\ {\mu }_l\hfill & =\mathrm{Scaling}\mathrm{parameter}\mathrm{computed}\mathrm{by}\left(\mathrm{19}\right),\hfill \\ W_{l+1}\hfill & =\left[{\mu }_l{W}_l(21I+50{\mu }_l^2{W}_l^2+9{\mu }_l^4{W}_l^4)\right]{[4I+45{\mu }_l^2{Z}_l^2+30{\mu }_l^4{W}_l^4+{\mu }_l^6{W}_l^6]}^{-1},\hfill \end{array}\right.$$

(20)

where ${lim}_{l\to \infty }{\mu }_l=1$ and ${lim}_{l\to \infty }{W}_l=S=sign\left(A\right)$.

3. Convergence and Stability Analysis

In this section, we discuss the convergence analysis to ensure that the sequence generated from (18) converges to $sign\left(A\right)$ for a matrix $A\in {\mathbb{C}}^{n\times n}$. We draw the basins of attraction to confirm the global convergence of the proposed scheme and compared with the existing schemes for solving $w^2-1=0$ [17].

We consider a region $R=[-2,2]\times [-2,2]\in \mathbb{C}$. The region has grid size of $256\times 256$ and has two simple roots $-1$ and 1. The convergence was determined by the stopping criteria $\parallel f\left(w_l\right)\parallel \le {10}^{-2}$. The exact location of roots is shown by two white dots within the basins. The dark blue color (left side of basins) represent the convergence region corresponding to the root $w=-1$ and the light blue color (right side of basins) represent the convergence region corresponding to the root $w=1$.

Figure 1 illustrates the basins for $NM$ (5), $NSM$ (11), $HM$ (12), $P{A}_{r,s}$ (10), and the proposed method $PM$ (18). It is evident from Figure 1b,d that methods $NSM$ and $P{A}_{3,1}$ exhibit local convergence, while the other methods exhibit the global convergence. Moreover, Figure 1e,f illustarte broader and lighter basins of attraction because of higher convergence order of $P{A}_{2,2}$ and $PM$ as compared to the basins of $NM$ and $HM$ as shown in Figure 1a,c. One can notice the symmetry in convergence region of each method. The convergence regions are symmetric about imaginary axis.

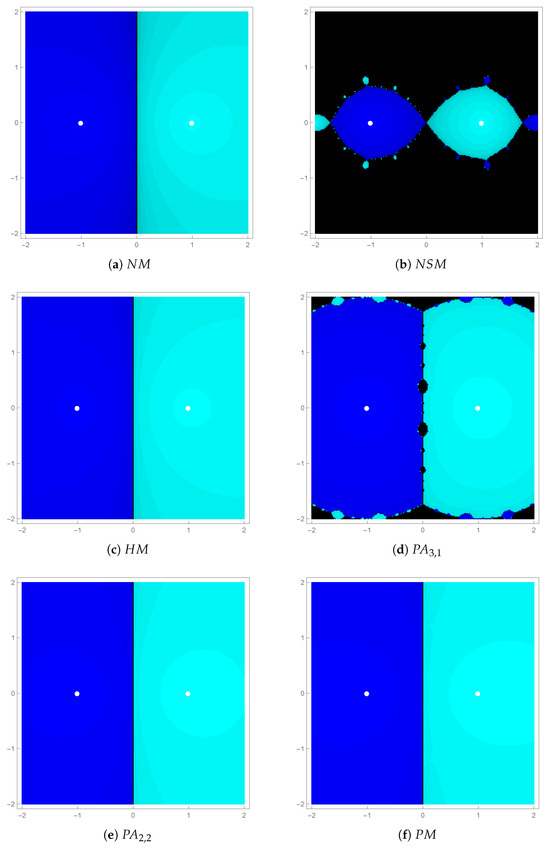
Figure 1. Attraction basins of various methods for equation $w^2-1=0$.

After achieving global convergence of the proposed method, it is important to examine certain critical factors related to matrix iterations, including convergence rate and numerical stability.

3.1. Convergence Analysis

Theorem 1.

Suppose that the initial matrix $W_0=A\in {\mathbb{C}}^{n\times n}$ has no eigenvalue on the imaginary axis, then the sequence of matrices ${\left\{W_l\right\}}_{l=0}^{\infty }$ generated from (18) converges to $sign\left(A\right)=S$.

Proof. 

Let $W=PJ{P}^{-1}$ be Jordan decomposition of matrix $W\in {\mathbb{C}}^{n\times n}$ and consider

$$R\left(W\right)=PR\left(J\right)P^{-1}.$$

(21)

where R is the rational function linked to (18). Consequently, this will lead to the mapping of an eigenvalue $\lambda$ of $W_l$ to an eigenvalue $R\left(\lambda \right)$ of $W_{l+1}$. Also, R will satisfy the properties given as follows:

• $sign\left(R\right(w\left)\right)=sign\left(w\right)$∀$w\in \mathbb{C}$.
• $w_{l+1}=R\left(w_l\right)$ with $w_0=w$ converges to $sign\left(w\right)$, where $Re\left(w\right)\ne 0$.

To achieve this objective, consider $A=P\Lambda P^{-1}$ as the Jordan decomposition of A that can be modified as [2]

$$P^{-1}AP=\Lambda =\left[\begin{array}{cc}C& 0\\ 0& N\end{array}\right],$$

(22)

where P is a non singular matrix while Jordan blocks C and N are associated to the eigenvalues in ${\mathbb{C}}^{-}$ and ${\mathbb{C}}^{+}$ respectively. Let the principal diagonals of blocks C and N have values ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_p$ and ${\lambda }_{p+1},{\lambda }_{p+2},\dots ,{\lambda }_n$ respectively. Then

$$sign\left(A\right)=P\left[\begin{array}{cc}-I_p& 0\\ 0& I_{n-p}\end{array}\right]P^{-1}.$$

(23)

Therefore,

$$\begin{array}{cc}\hfill sign(\Lambda )& =sign\left(P^{-1}AP\right)=P^{-1}sign\left(A\right)P\hfill \\ \hfill & =\left[\begin{array}{cccccc}sign\left({\lambda }_1\right)& & & & & \\ & \ddots & & & & \\ & & sign\left({\lambda }_p\right)& & & \\ & & & sign\left({\lambda }_{p+1}\right)& & \\ & & & & \ddots & \\ & & & & & sign\left({\lambda }_n\right)\end{array}\right]\hfill \end{array}$$

(24)

Now, define a sequence $D_l=P^{-1}{W}_{l}P$ with $D_0=P^{-1}AP$. Then from (18), we get

$$D_{l+1}=\left[D_l(21I+50D_l^2+9D_l^4)\right]{[4I+45D_l^2+30D_l^4+D_l^6]}^{-1}.$$

(25)

Mathematical induction states that all $D_l$’s for $l=1,2,3\dots$ will be diagonal if $D_0$ is diagonal. When $D_0$ is not diagonal, the proof may be considered in the similar methodology as stated at the end of the proof.

Now, (25) can be written for scalar case $f\left(w\right)=w^2-1=0$ as follows:

$$d_{l+1}^i=\frac{d_l^i(21+50{d_l^i}^2+9{d_l^i}^4)}{4+45{d_l^i}^2+30{d_l^i}^4+{d_l^i}^6},$$

(26)

where $d_l^i={\left(D_l\right)}_{i,i}$ and $1\le i\le n$. Furthermore, $sign\left({\lambda }_i\right)=s_i$, with $s_i=\pm 1$ and therefore from (26),

$$\frac{d_{l+1}^i-s_i}{d_{l+1}^i+s_i}={\left(\frac{-s_i+d_l^i}{s_i+d_l^i}\right)}^5\left(\frac{4s_i-d_l^i}{4s_i+d_l^i}\right).$$

(27)

The factor $\frac{4s_i-d_l^i}{4s_i+d_l^i}$ is bounded for $1\le i\le n$ and does not affect the convergence. Furthermore, by selecting the right initial matrix $W_0=A$ and $\left|\frac{d_0^i-s_i}{d_0^i+s_i}\right|<1$, we get

$$\underset{l\to \infty }{lim}\left|\frac{d_{l+1}^i-s_i}{d_{l+1}^i+s_i}\right|=0,$$

(28)

implying that ${lim}_{l\to \infty }\left(d_l^i\right)=s_i=sign\left({\lambda }_i\right)$ and hence ${lim}_{l\to \infty }\left(D_l\right)=sign(\Lambda )$.

In the case when $D_0$ is not a diagonal matrix, it is essential that we investigate the relation between the eigenvalues of $W_i$’s which was briefly explained at the starting of the proof.

$${\lambda }_{l+1}^i=[{\lambda }_l^i(21I+50{{\lambda }_l^i}^2+9{{\lambda }_l^i}^4)]{[4I+45{{\lambda }_l^i}^2+30{{\lambda }_l^i}^4+{{\lambda }_l^i}^6]}^{-1}.$$

(29)

In a comparable approach, it is clear from (29) that ${\lambda }_i$’s will converge to $s_i=\pm 1$, i.e.,

$$\underset{l\to \infty }{lim}\left|\frac{{\lambda }_{l+1}^i-s_i}{{\lambda }_{l+1}^i+s_i}\right|=0.$$

(30)

As a result, it is easy to conclude that

$$\underset{l\to \infty }{lim}{W}_l=P(\underset{l\to \infty }{lim}{D}_l)P^{-1}=Psign(\Lambda )P^{-1}=sign\left(A\right),$$

(31)

which finishes the proof.    □

Theorem 2.

Considering the assumptions of Theorem 1, the matrix sequence ${\left\{W_l\right\}}_{l=0}^{\infty }$ generated from (18) has convergence rate five to $sign\left(A\right)=S$.

Proof. 

Since, $W_l$ depends on matrix A∀$l\ge 0$ and the matrix A commutes with S, so $W_l$ also commutes with S∀$l\ge 0$. Taking into consideration the substitution

$$B_l=4I+45W_l^2+30W_l^4+W_l^6,$$

(32)

we get,

$$\begin{array}{cc}\hfill W_{l+1}-S& =\left[W_l(21I+50W_l^2+9W_l^4)\right]B_l^{-1}-S\hfill \\ \hfill & =[21W_l+50W_l^3+9W_l^5-S{B}_l]B_l^{-1}\hfill \\ \hfill & =[21W_l+50W_l^3+9W_l^5-4S-45S{W}_l^2-30S{W}_l^4-S{W}_l^6]B_l^{-1}\hfill \\ \hfill & =[-4S^5+21S^4{W}_l-45S^3{W}_l^2+50S^2{W}_l^3-30S{W}_l^4+9W_l^5-S{W}_l^6]B_l^{-1}\hfill \\ \hfill & ={(W_l-S)}^5(4I-S{W}_l)B_l^{-1}\hfill \end{array}$$

(33)

Apply any type of matrix norm to the both sides of (33),

$$∥W_{l+1}-S∥\le \left(∥4I-S{W}_l∥∥B_l^{-1}∥\right){∥W_l-S∥}^5.$$

(34)

This completes the proof.    □

3.2. Stability Issues

Theorem 3.

Considering the assumptions of Theorem 1, the sequence of matrix iterations ${\left\{W_l\right\}}_{l=0}^{\infty }$ generated from (18) is stable asymptotically.

Proof. 

The iterate obtained from (18) is a function of A because of $W_0=A$, and hence commutes with A. Let ${\Delta }_l$ be the perturbation generated at $l^{th}$ iterate in (18). Then

$${\tilde{W}}_l=W_l+{\Delta }_l.$$

(35)

Based on the results of the error analysis of order one, we may consider that ${\left({\Delta }_l\right)}^j\approx 0$, $j\ge 2$. As long as ${\Delta }_l$ is small enough, this usual adjustment will work. Also suppose that $W_l\approx sign\left(A\right)=S$ for larger l, then we get

$$\begin{array}{cc}\hfill {\tilde{W}}_{l+1}& =[{\tilde{W}}_l(21I+50{\tilde{W}}_l^2+9{\tilde{W}}_l^4)]{[4I+45{\tilde{W}}_l^2+30{\tilde{W}}_l^4+{\tilde{W}}_l^6]}^{-1}\hfill \\ \hfill & =[(W_l+{\Delta }_l)(21I+50{(W_l+{\Delta }_l)}^2+9{(W_l+{\Delta }_l)}^4)][4I+45{(W_l+{\Delta }_l)}^2\hfill \\ \hfill & +30{(W_l+{\Delta }_l)}^4+{(W_l+{\Delta }_l)}^6{]}^{-1}\hfill \\ \hfill & \approx [80S+148{\Delta }_l+68S{\Delta }_{l}S]{[80I+108S{\Delta }_l+108{\Delta }_{l}S]}^{-1}\hfill \\ \hfill & \approx \left[S+\frac{37}{20}{\Delta }_l+\frac{17}{20}S{\Delta }_{l}S\right]\left[I-\frac{27}{20}S{\Delta }_l-\frac{27}{20}{\Delta }_{l}S\right]\hfill \\ \hfill & \approx S+\frac{1}{2}{\Delta }_l-\frac{1}{2}S{\Delta }_{l}S.\hfill \end{array}$$

(36)

Here, the identity [18] given by

$${(B+C)}^{-1}=B^{-1}-B^{-1}C{B}^{-1}+O\left(C^2\right).$$

(37)

has been applied, where B is any nonsingular matrix and C is any matrix. Also, considering ${\Delta }_{l+1}={\tilde{W}}_{l+1}-W_{l+1}$, we get

$${\Delta }_{l+1}\approx \frac{1}{2}{\Delta }_l-\frac{1}{2}S{\Delta }_{l}S.$$

(38)

At this point, it is possible to deduce that ${\Delta }_{l+1}$ is bounded, i.e.,

$$∥{\Delta }_{l+1}∥\le \frac{1}{2}∥{\Delta }_0-S{\Delta }_{0}S∥,$$

(39)

which completes the proof.    □

4. Extension to Determine Generalized Eigenvalues of a Matrix Pencil

Let $A,B\in {\mathbb{C}}^{n\times n}$. Then $\lambda \in \mathbb{C}$ is said to be a generalized eigenvalue of a matrix pencil $A-\lambda B$ if there exists a non-zero vector $\mathbf{x}\in {\mathbb{C}}^n$ such that

$$A\mathbf{x}=\lambda B\mathbf{x}.$$

(40)

Here $\mathbf{x}$ will be a generalized eigenvector corresponding to $\lambda$ and (40) is referred as a generalized eigenvalue problem. This can be determined by finding the zeros of characteristic polynomial $det(A-\lambda B)$.

Complex problem solving in physics was the first scenario for the appearance of the characteristic polynomial and the eigenproblem. For a recent coverage of the topic one can see [19]. When more generality is needed, generalized eigenvalue problem is taking the place of the classical approach [20].

Problem (40) arises in several fields of numerical linear algebra. However, the dimensions of matrices A and B are typically quite enormous, hence further complicating the situation. There are a lot of different approaches that claim to be able to solve (40) including the necessary eigenvectors in a smaller subspace or series of matrix pencils [21,22,23] or using matrix decomposition [24,25,26]. Our interest is in employing the matrix sign function which involves evaluating certain matrix sign computations based on the given matrix pencil to compute the required decomposition and hence to solve the problem (40).

To solve the problem (40) for the case of regular matrix pencils using matrix sign function, we consider rank revealing $QR$$\left(RRQR\right)$ decomposition [27] after computing sign of two matrices depending on the given matrix pencil.

Theorem 4.

Let $A,B\in {\mathbb{C}}^{n\times n}$ such that $A-\lambda B$ be a regular matrix pencil and let $U_1$ and $U_2$ are defined as

$$\begin{array}{c}\hfill U_1=\frac{I-S_1}{2},U_2=\frac{I-S_2}{2},\end{array}$$

(41)

where $S_1$ and $S_2$ are sign functions given by

$$\begin{array}{cc}\hfill S_1& =sign({(A-B)}^{-1}(A+B)),\hfill \\ \hfill S_2& =sign((A+B){(A-B)}^{-1}).\hfill \end{array}$$

(42)

If $U_1{\Pi }_1=Q_1{R}_1$ and $U_2{\Pi }_2=Q_2{R}_2$ are $RRQR$ decompositions of $U_1$ and $U_2$ such that $Q_2^{*}A{Q}_1$ and $Q_2^{*}B{Q}_1$ are upper triangular, then

$${\lambda }_i=\frac{{\alpha }_{ii}}{{\beta }_{ii}},$$

(43)

where ${\lambda }_i$’s are eigenvalues of $A-\lambda B$, ${\alpha }_{ii}$ and ${\beta }_{ii}$ are the diagonal entries of $Q_2^{*}A{Q}_1$ and $Q_2^{*}B{Q}_1$ respectively for $i=1,2,\dots ,n$. Moreover, if B is non-invertible, then ${\beta }_{ii}=0$ for some i which implies that some eigenvalues of $A-\lambda B$ will be infinity.

Let $\tau$ denotes tolerance value and $max$ be the maximum iterations. Then, in accordance with the proposed method (18) and Theorem 4, we propose Algorithm 1 to find out the eigenvalues of a regular matrix pencil $A-\lambda B$.

Algorithm 1 Evaluating generalized eigenvalues of $A-\lambda B$

Require: $A,B,max,\tau$ Ensure: $S_1,S_2,{\lambda }_i^{\prime }s$   1: Initialize $W_0={(A-B)}^{-1}(A+B)$.   2: while $l\le max$ and $\parallel W_l^2{-I\parallel }_{*}>\tau$ do   3:         Apply method (18).   4:         return $W_{\infty }=sign({(A-B)}^{-1}(A+B))=S_1$.   5: end while   6: Construct $RRQR$ decomposition of $U_1=\frac{I-S_1}{2}$ as follows: $\hspace{1em}\hspace{1em}\hspace{1em} U_1{\Pi }_1=Q_1{R}_1$.   7: Initialize $W_0=(A+B){(A-B)}^{-1}$.   8: Repeat step 2–5 to return $W_{\infty }=sign((A+B){(A-B)}^{-1})=S_2$.   9: Construct $RRQR$ decomposition of $U_2=\frac{I-S_2}{2}$ as follows: $\hspace{1em}\hspace{1em}\hspace{1em} U_2{\Pi }_2=Q_2{R}_2$. 10: Compute two matrices $Q_2^{*}A{Q}_1=\left[{\alpha }_{ij}\right]$ and $Q_2^{*}B{Q}_1=\left[{\beta }_{ij}\right]$, where $1\le i,j\le n$. 11: if ${\alpha }_{ij}={\beta }_{ij}=0$ ∀ $i>j$ then 12:      for i=1:n do 13:           ${\lambda }_i=\frac{{\alpha }_{ii}}{{\beta }_{ii}}$. 14:      end for 15: end if

5. Computational Complexity

The computational efficiency index ($CEI$) [28] of an iterative method can be defined as follows:

$$CEI=p^{\frac{1}{C}}.$$

(44)

Here p denotes convergence order and C denotes computational cost per iteration.

The approximate cost of matrix multiplications in current programming packages is $2.373$ [29]. For a matrix of size n, we therefore consider that the cost of one matrix-matrix multiplication is $n^{\frac{2373}{1000}}$ and cost of one matrix inverse is $\frac{2n^3}{3}$. Additionally, we do not take into account the cost per iteration of norm computation (in $ANM$ (6)), addition and subtraction. Then, $CEI$’s for the methods $NM$ (5), $ANM$ (6), $HM$ (12) and $PM$ (18) to compute $sign\left(A\right)$ are given in Table 1.

Table 1. $CEI$’s for various methods along with their convergence orders.

Method	Convergence Order	$\mathit{CEI}$
$NM$	2	$2^{\frac{1}{n^{2373/1000}+\frac{2n^3}{3}}}$
$ANM$	$\sqrt{3}+1$	${(\sqrt{3}+1)}^{\frac{1}{n^{2373/1000}+\frac{2n^3}{3}}}$
$HM$	3	$3^{\frac{1}{3n^{2373/1000}+\frac{2n^3}{3}}}$
$PM$	5	$5^{\frac{1}{5n^{2373/1000}+\frac{2n^3}{3}}}$

Figure 2 presents a comparison of the efficiencies of several approaches, demonstrating the greater efficiency index of the suggested method.

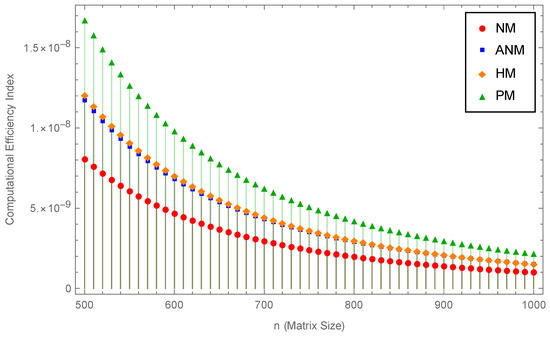
Figure 2. Comparative analysis of efficiency indices for different methods.

6. Numerical Aspects

In this section, we have examined a variety of examples to evaluate our proposed method by comparing it with various existing techniques. For this study, we have assumed the following stopping criteria:

$$\parallel W_l^2{-I\parallel }_{*}\le \tau ,$$

(45)

where $\tau$ stands for the tolerance value and ${\parallel .\parallel }_{*}$ will be suitable matrix norm. Also, $l_{\infty }$ and $l_2$ norms are considered for real and complex input matrices, respectively [14].

For the sake of comparison, we only consider the methods that exhibit global convergence and we do not include any methods that have local convergence. The methods that are being compared will be $NM$ (5), $ANM$ (6), $HM$ (12), $P{A}_{2,2}$ ((10) for $r=s=2$), $LM$ (13), $PM$ (18) and $APM$ (20) with spectral scaling (19). All simulations are done in Mathematica using system specifications “Windows 11 Home Intel(R) Core(TM) i7-1255U CPU running at 1.70 GHz processor having 16.0 RAM (64-bit operating system)”.

Example 1.

Here, we perform the eigenvalue clustering of a random real $500\times 500$ matrix given as

SeedRandom[100]; A = RandomReal[{-5,5},{500,500}];

The outcomes are shown in Figure 3 using the stopping criteria (45) with $l_{\infty }$ norm and $\tau ={10}^{-4}$. We can see that eigenvalues of $W_0$ are scattered at the initial stage as shown in Figure 3a, while proceeding for the next iterations $W_i$ in Figure 3b–g for $i=1,2,\dots ,6$ respectively using $PM$ (18), the eigenvalues are converging towards 1 or $-1$. Then in Figure 3h, all eigenvalues converge to 1 or $-1$ (based on the stopping criteria) implying that the sequence of matrices ${\left\{W_l\right\}}_{l=0}^{\infty }$ converges to $sign\left(A\right)$. The result of Theorem 1 is therefore confirmed.

Figure 3. Eigenvalue clustering of $500\times 500$ matrix at every iterate in Example 1.

Example 2.

In this example, convergence of many different methods for computing $sign\left(A\right)$ has been compared, where A is a random $1000\times 1000$ complex square matrix given as follows:

SeedRandom[101];

A = RandomComplex[{-1 - 1.5 I, 1 + 1.5 I}, {1000, 1000}]

The comparison is shown in Figure 4 with $\tau ={10}^{-4}$ and $l_2$ norm which illustrates the results with regard to the number of iterations and the absolute error and demonstrates the consistent behavior of both $PM$ and $APM$.

Figure 4. Convergence history of different methods for Example 2.

Example 3.

This example presents a comparison on convergence of many different methods for computing $sign\left(A\right)$, where A is a random $2000\times 2000$ real square matrix given as

 

SeedRandom[111];

A = RandomReal[{-25, 25}, {2000, 2000}];

The comparison is presented in Figure 5 with $\tau ={10}^{-4}$ and $l_{\infty }$ norm which illustrates the results with respect to the number of iterations and the absolute error and demonstrates the consistent behavior of both $PM$ and $APM$ for evaluating $sign\left(A\right)$.

Figure 5. Convergence history of different methods for Example 3.

Example 4.

Here, we examine the convergence of various methods with regard to the iteration number and the timings of CPU for evaluating the sign function of ten random matrices:

 

SeedRandom[121]; number = 10; tolerance = 10^(-5);

Table[A[j] = RandomComplex[{-3 - 2 I, 3 + 2 I}, {50j, 50j}];, {j, number}];

The comparative analysis based on iteration number and CPU timings for matrices of various sizes, are presented in Table 2 and Table 3 respectively using $\tau ={10}^{-5}$ and $l_2$-norm. The implementation of new methods $\left(PM\right)$ and $\left(APM\right)$ result in an improvement in the average iteration number and the amount of time spent by CPU. The outcomes demonstrate that the suggested method $\left(PM\right)$ is significantly better as compared to other fifth order methods like $P{A}_{2,2}$ and $LM$.

Table 2. Comparative analysis for the iteration number in Example 4.

Matrix	$\mathit{NM}$	$\mathit{ANM}$	$\mathit{HM}$	$\mathit{LM}$	${\mathit{PA}}_{2,2}$	$\mathit{PM}$	$\mathit{APM}$
$A_{50\times 50}$	12	11	8	6	6	5	4
$A_{100\times 100}$	15	13	9	7	7	6	5
$A_{150\times 150}$	15	15	10	8	7	6	5
$A_{200\times 200}$	15	15	9	8	7	6	5
$A_{250\times 250}$	15	17	10	8	7	6	5
$A_{300\times 300}$	14	15	9	7	6	6	5
$A_{350\times 350}$	15	16	10	8	7	6	5
$A_{400\times 400}$	17	19	11	10	7	7	5
$A_{450\times 450}$	14	15	9	7	6	6	5
$A_{500\times 500}$	18	21	12	9	8	7	6
Mean	15	15.7	9.7	7.8	6.8	6.1	5

Table 3. Comparative analysis for the CPU-time (in seconds) in Example 4.

Matrix	$\mathit{NM}$	$\mathit{ANM}$	$\mathit{HM}$	$\mathit{LM}$	${\mathit{PA}}_{2,2}$	$\mathit{PM}$	$\mathit{APM}$
$A_{50\times 50}$	0.03	0.02	0.01	0.01	0.02	0.01	0.01
$A_{100\times 100}$	0.07	0.15	0.05	0.05	0.09	0.05	0.10
$A_{150\times 150}$	0.16	0.23	0.12	0.15	0.21	0.10	0.24
$A_{200\times 200}$	0.29	0.40	0.19	0.26	0.34	0.18	0.40
$A_{250\times 250}$	0.47	0.67	0.32	0.39	0.53	0.25	0.60
$A_{300\times 300}$	0.58	0.87	0.44	0.55	0.63	0.44	1.02
$A_{350\times 350}$	0.82	1.29	0.70	0.88	1.21	0.63	1.44
$A_{400\times 400}$	1.20	2.04	1.46	1.78	1.62	0.99	1.70
$A_{450\times 450}$	1.31	2.06	1.08	1.40	1.87	1.16	2.29
$A_{500\times 500}$	2.06	3.58	1.91	2.32	3.07	1.60	3.32
Mean	0.70	1.13	0.63	0.78	0.96	0.54	1.11

Now, in Examples 5 and 6, we aim to evaluate generalized eigenvalues of matrix pencils using matrix sign function for which we use Algorithm 1 for different methods by replacing (18) with existing methods in Step 3.

Example 5.

Let $A-\lambda B$ be a matrix pencil, where matrices A and B are given by [30]

$$A={\left[\begin{array}{ccccc}\frac{99}{100}& \frac{1}{100}& 0& \cdots & 0\\ 0& \frac{98}{100}& \ddots & & 0\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& \cdots & 0& \frac{1}{100}& \frac{1}{100}\\ 0& \cdots & 0& 0& \frac{0}{100}\end{array}\right]}_{100\times 100},B={\left[\begin{array}{cccc}0& & & \\ & \ddots & & \\ & & 0& \\ & & & I_{20}\end{array}\right]}_{100\times 100},$$

where $I_{20}$ is the identity matrix of size 20.

The eigenvalues of given pencil $A-\lambda B$ are ${\lambda }_i=\frac{i-1}{100}$ for $i=1,2,\dots 20$ and remaining eigenvalues are infinite. We verify these eigenvalues using proposed method and Algorithm 1. We compute the matrices $Q_2^{*}A{Q}_1={\left[{\alpha }_{ij}\right]}_{100\times 100}$ and $Q_2^{*}B{Q}_1={\left[{\beta }_{ij}\right]}_{100\times 100}$ and then calculate ${\lambda }_i^{\prime }s$ from Algorithm 1. The outcomes are presented in Table 4 for $i=1,2,\dots 20$.

Table 4. Eigenvalues (${\lambda }_i$’s) of matrix pencil $A-\lambda B$ in Example 5.

i	1	2	3	4	5	6	7	8	9	10
${\alpha }_{ii}$	0.189762	0.18	−0.17	0.16	0.15	−0.14	0.13	−0.12	−0.11	0.1
${\beta }_{ii}$	0.99875	1	−1	1	1	−1	1	−1	−1	1
${\lambda }_i$	0.19	0.18	0.17	0.16	0.15	0.14	0.13	0.12	0.11	0.1
$\mathit{i}$	11	12	13	14	15	16	17	18	19	20
${\alpha }_{ii}$	−0.09	0.08	−0.07	0.05	−0.03	0.02	0.01	0	−0.06	0.04
${\beta }_{ii}$	−1	1	−1	1	−1	1	1	−1	−1	1
${\lambda }_i$	0.09	0.08	0.07	0.05	0.03	0.02	0.01	0	0.06	0.04

Moreover, ${\beta }_{ii}=0$ for $21\le i\le 100$ which implies that ${\lambda }_i=\infty$ for $21\le i\le 100$. Hence this example verifies the results given in Theorem 4.

Example 6 (Bounded finline dielectric waveguide problem).

The generalized eigenvalue problem (40) arises in the finite element analysis for finding the propagating modes of a rectangular waveguide. We consider three cases for the pairs of matrices A and B as $BFW62A,BFW62B$; $BFW398A, BFW398B$ and $BFW782A, BFW782B$ from the Matrix Market [31].

Table 5 shows the outcomes depending on the iteration numbers $l_1$ and $l_2$ for computing $S_1=sign({(A-B)}^{-1}(A+B))$ and $S_2=sign((A+B){(A-B)}^{-1})$ with corresponding absolute errors ${ϵ}_{l_1}={\parallel W_{l_1}^2-I\parallel }_{\infty }$ and ${ϵ}_{l_2}={\parallel W_{l_2}^2-I\parallel }_{\infty }$ using stopping criterion (45) with $\tau ={10}^{-10}$. Also, total computational time in seconds taken for computing $S_1$ and $S_2$ has been compared in Figure 6. The outcomes demonstrate that the suggested method is better with respect to errors and timings.

Table 5. Comparison of results obtained from various methods in Example 6.

Matrices	Method	${\mathit{l}}_1$	${\mathit{ϵ}}_{{\mathit{l}}_1}$	${\mathit{l}}_2$	${\mathit{ϵ}}_{{\mathit{l}}_2}$
BFW62A, BFW62B	$NM$	2	$5.79607\times {10}^{-11}$	2	$5.79607\times {10}^{-11}$
	$HM$	2	$4.44089\times {10}^{-16}$	2	$4.44089\times {10}^{-16}$
	$P{A}_{2,2}$	1	$1.65201\times {10}^{-13}$	1	$1.64757\times {10}^{-13}$
	$LM$	1	$9.80327\times {10}^{-13}$	1	$9.81437\times {10}^{-13}$
	$PM$	1	$9.90319\times {10}^{-14}$	1	$1.00364\times {10}^{-13}$
BFW398A, BFW398B	$NM$	2	$6.18883\times {10}^{-12}$	2	$6.18883\times {10}^{-12}$
	$HM$	2	$4.44089\times {10}^{-16}$	2	$4.44089\times {10}^{-16}$
	$P{A}_{2,2}$	1	$1.50990\times {10}^{-14}$	1	$1.50990\times {10}^{-14}$
	$LM$	1	$9.08162\times {10}^{-14}$	1	$9.23706\times {10}^{-14}$
	$PM$	1	$1.11022\times {10}^{-14}$	1	$1.11022\times {10}^{-14}$
BFW782A, BFW782B	$NM$	2	$5.82201\times {10}^{-13}$	2	$5.82201\times {10}^{-13}$
	$HM$	2	$4.44089\times {10}^{-16}$	2	$4.44089\times {10}^{-16}$
	$P{A}_{2,2}$	1	$6.43929\times {10}^{-15}$	1	$3.99680\times {10}^{-15}$
	$LM$	1	$7.99361\times {10}^{-15}$	1	$7.99361\times {10}^{-15}$
	$PM$	1	$5.32907\times {10}^{-16}$	1	$5.32907\times {10}^{-16}$

Figure 6. Comparison of CPU time for various methods to compute $S_1$ and $S_2$ in Example 6.

7. Conclusions

This paper has discussed an iterative approach for evaluation of sign of a matrix. Our proposed iterative method attains a convergence order of five, showcasing its efficiency in evaluation of the sign of complex matrices. Through comprehensive convergence analysis discussed globally and the demonstration of asymptotic stability, we have established the robustness and reliability of the proposed approach. Then an algorithm has been designed for determining the generalized eigenvalues of a regular matrix pencil utilizing matrix sign computation. Furthermore, extensive numerical experiments performed on matrices of different sizes have validated the effectiveness and superiority of our method over existing techniques.