Quantum-Number Projected Generator Coordinate Method for 21Ne with a Chiral Two-Nucleon-Plus-Three-Nucleon Interaction
Abstract
1. Introduction
2. The PGCM for an Odd-Mass Nucleus
2.1. Nuclear Hamiltonian
2.2. Nuclear Wave Functions
2.3. Evaluation of Norm and Hamiltonian Overlaps
- The contribution of the one-body term is simply given bywhere . The reduced matrix element is defined as , and the one-body density operator with the two angular momenta coupled to zero [13]with .
- The energy by the two-body term consists of termand termwhere the J-coupled mixed density and pairing density are defined as,Here, we introduce the symbol . The symmetry of Clebsch–Gordan coefficient implies the relation . The -type two-body interaction matrix elements in the J-coupled form are related to those of -type via the Pandya transformation [35],where the unnormalized -type two-body matrix elements in the J-coupled form are related to those in M-scheme as follows:
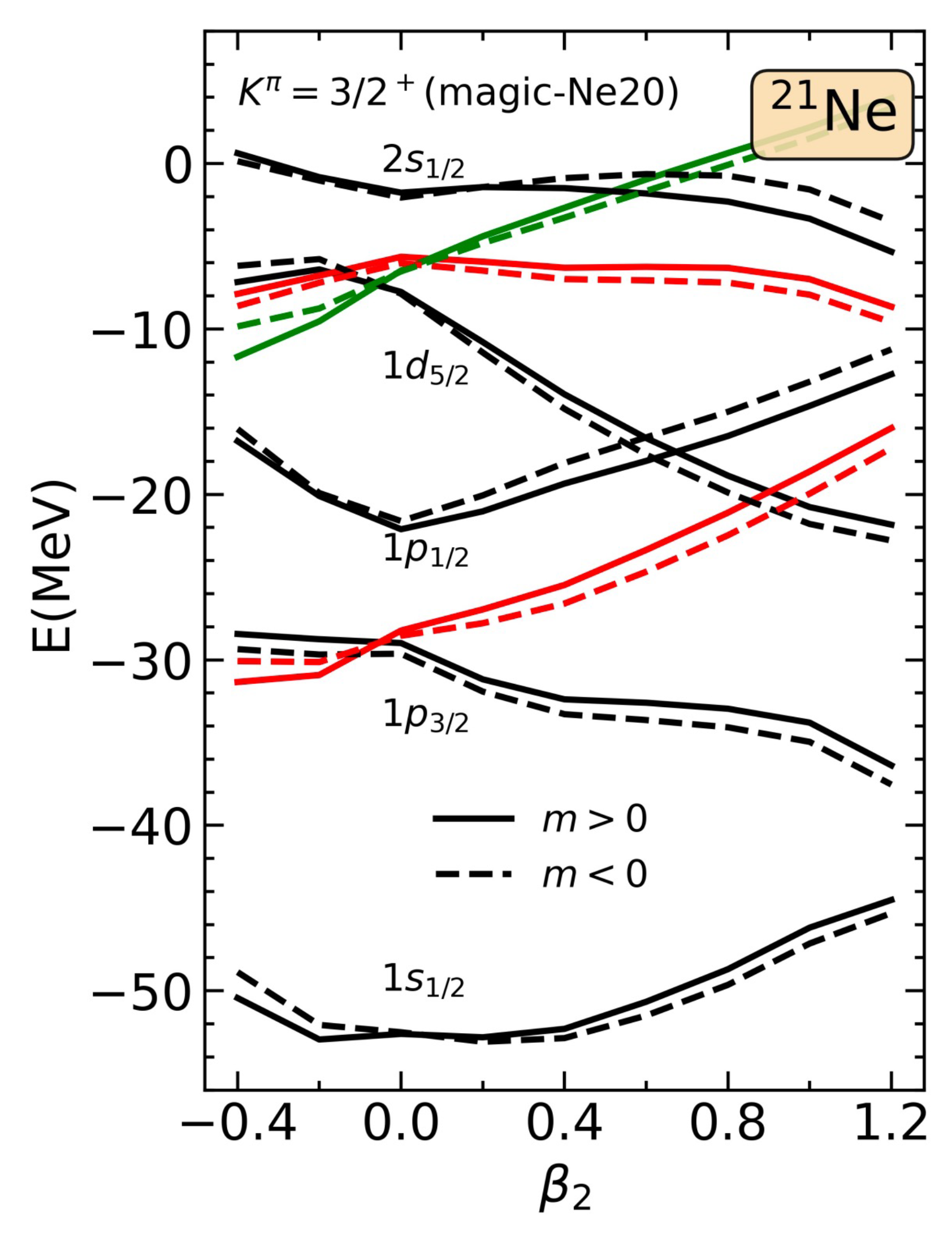
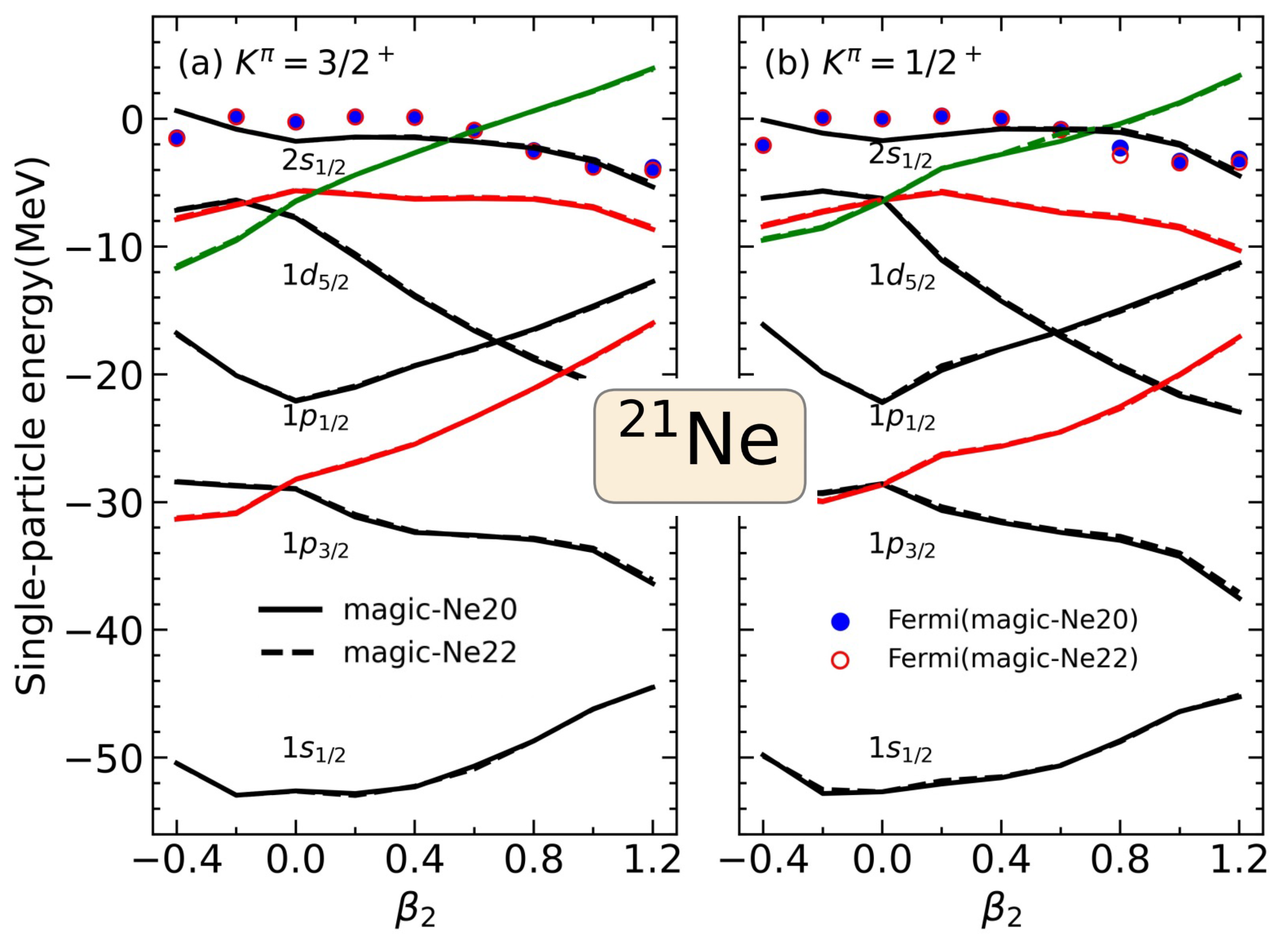
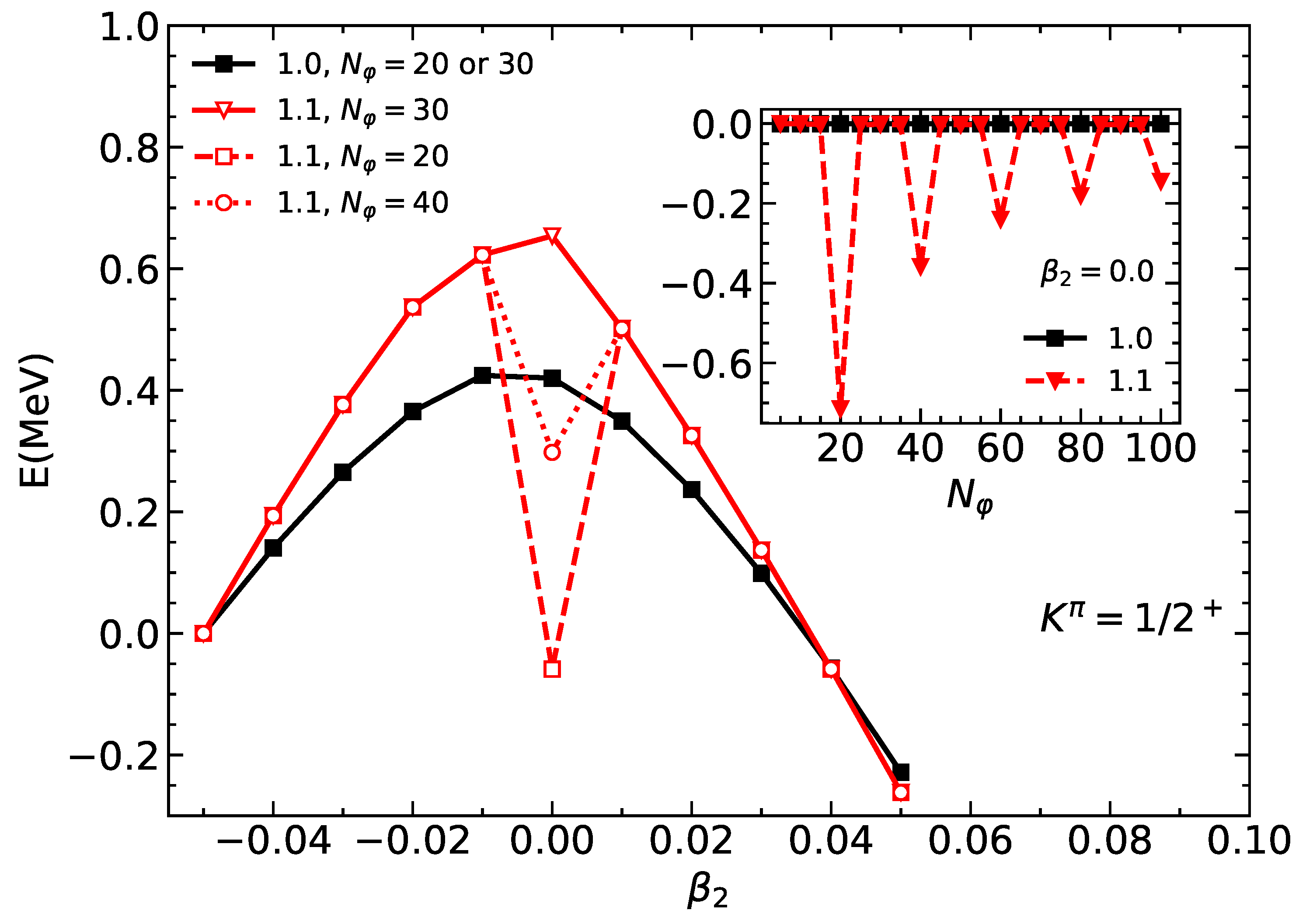
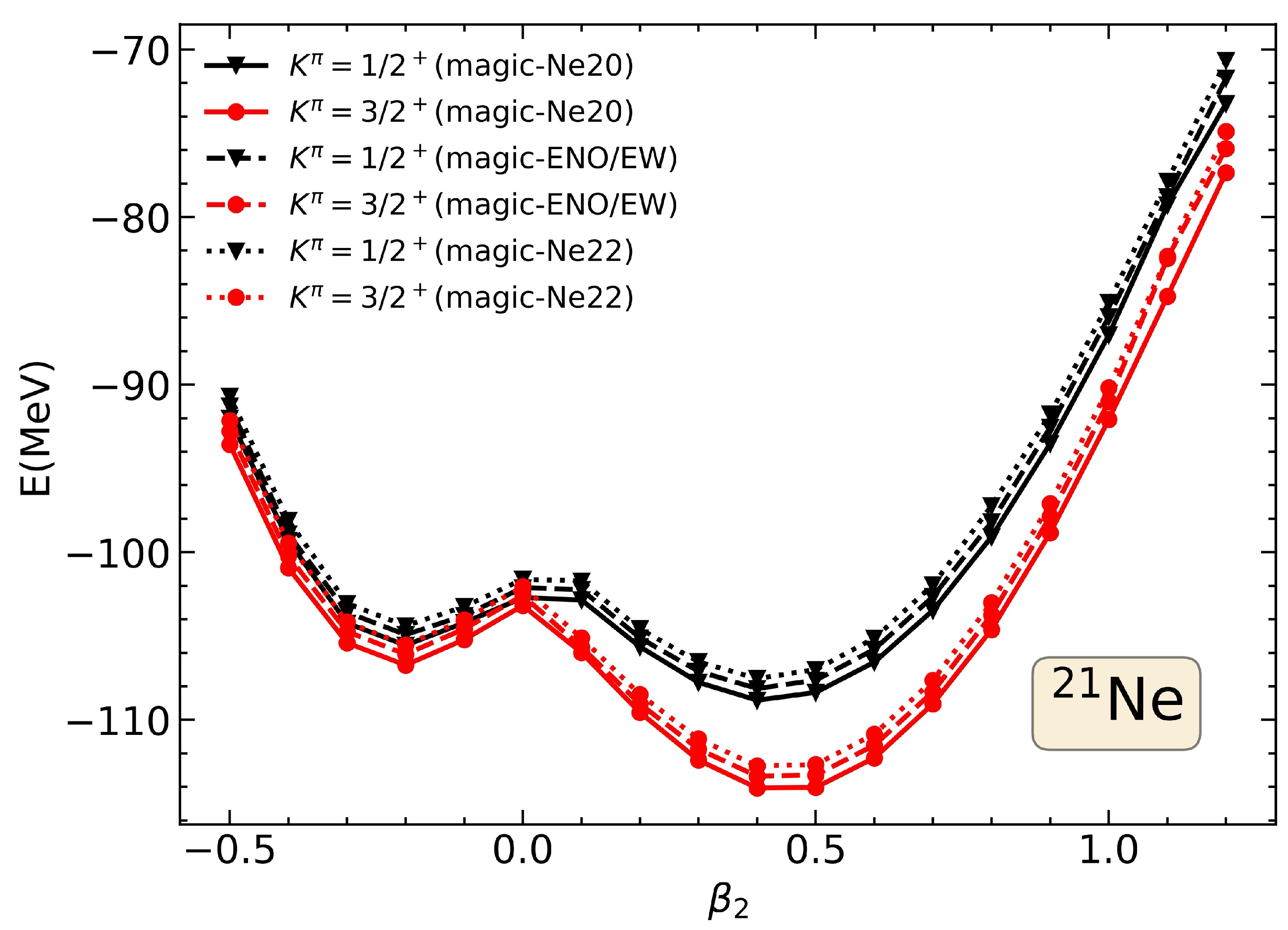
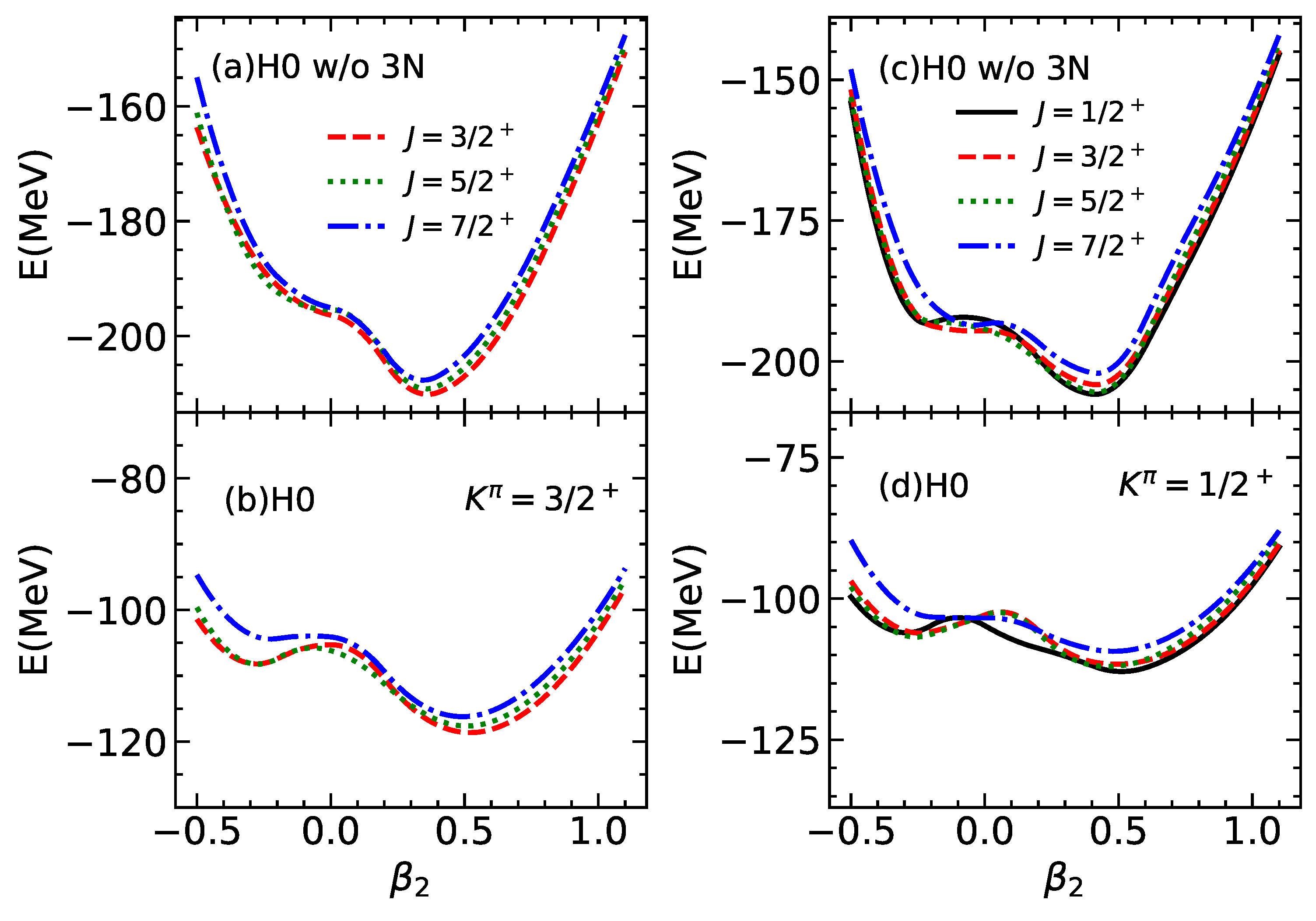
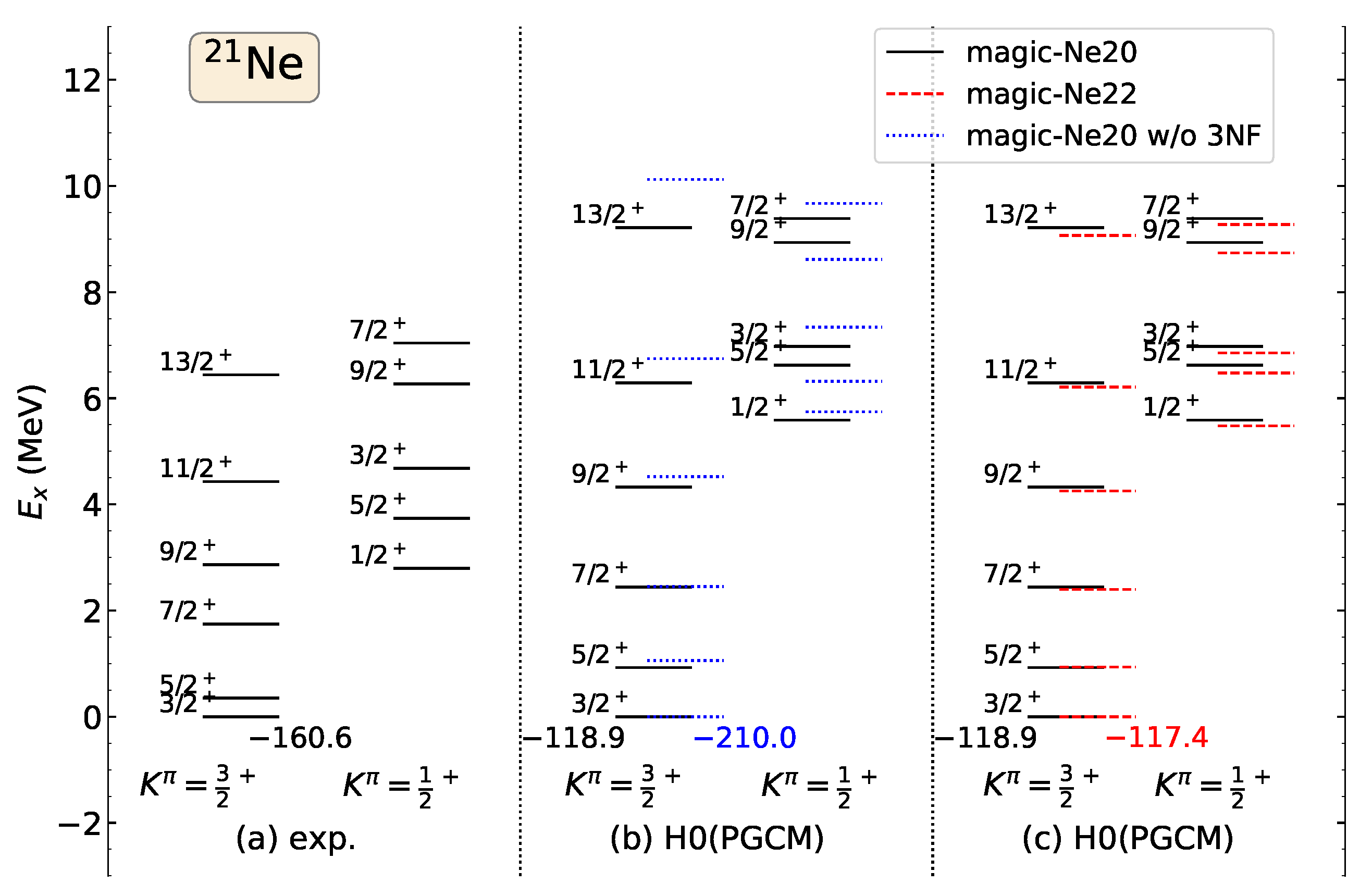
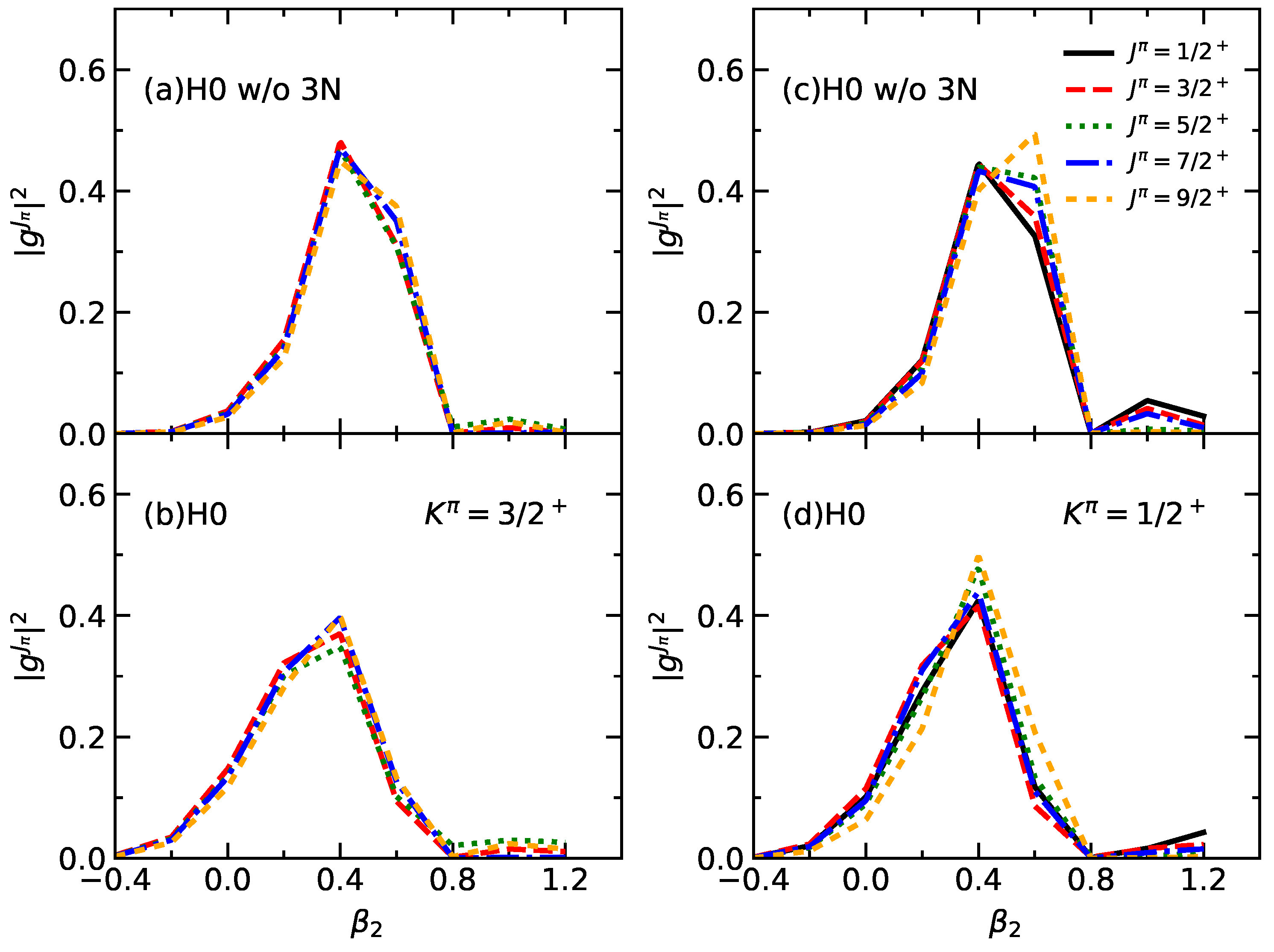
3. Results and Discussion
Effective Hamiltonians
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EFT | Effective field theory |
| IMSRG | In-medium similarity renormalization group |
| PGCM | Projected generator coordinate method |
| IM-GCM | In-medium generator coordinate method |
| MR-CDFT | Multi-reference covariant density functional theory |
| HWG | Hill–Wheeler–Griffin |
References
- Bohr, A.; Mottelson, B.R. Nuclear Structure. Volume II. Nuclear Deformations; Word Scientific: Singapore, 1998. [Google Scholar]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: New York, NY, USA, 1980. [Google Scholar]
- Engel, J.; Ramsey-Musolf, M.J.; van Kolck, U. Electric Dipole Moments of Nucleons, Nuclei, and Atoms: The Standard Model and Beyond. Prog. Part. Nucl. Phys. 2013, 71, 21–74. [Google Scholar] [CrossRef]
- Arrowsmith-Kron, G.; Athanasakis-Kaklamanakis, M.; Au, M.; Ballof, J.; Berger, R.; Borschevsky, A.; Breier, A.A.; Buchinger, F.; Budker, D.; Caldwell, L.; et al. Opportunities for Fundamental Physics Research with Radioactive Molecules. arXiv 2023, arXiv:2302.02165. [Google Scholar]
- Brodeur, M.; Buzinsky, N.; Caprio, M.A.; Cirigliano, V.; Clark, J.A.; Fasano, P.J.; Formaggio, J.A.; Gallant, A.T.; Garcia, A.; Gandolfi, S.; et al. Nuclear β decay as a probe for physics beyond the Standard Model. arXiv 2023, arXiv:2301.03975. [Google Scholar]
- Yao, J.M.; Meng, J.; Niu, Y.F.; Ring, P. Beyond-mean-field approaches for nuclear neutrinoless double beta decay in the standard mechanism. Prog. Part. Nucl. Phys. 2022, 126, 103965. [Google Scholar] [CrossRef]
- Hill, D.L.; Wheeler, J.A. Nuclear constitution and the interpretation of fission phenomena. Phys. Rev. 1953, 89, 1102–1145. [Google Scholar] [CrossRef]
- Griffin, J.J.; Wheeler, J.A. Collective Motions in Nuclei by the Method of Generator Coordinates. Phys. Rev. 1957, 108, 311–327. [Google Scholar] [CrossRef]
- Bender, M.; Heenen, P.H.; Reinhard, P.G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121–180. [Google Scholar] [CrossRef]
- Niksic, T.; Vretenar, D.; Ring, P. Relativistic Nuclear Energy Density Functionals: Mean-Field and Beyond. Prog. Part. Nucl. Phys. 2011, 66, 519–548. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Dobaczewski, J.; Ring, P.; Robledo, L.M.; Yannouleas, C. Symmetry restoration in mean-field approaches. J. Phys. G 2021, 48, 123001. [Google Scholar] [CrossRef]
- Liu, L.; Otsuka, T.; Shimizu, N.; Utsuno, Y.; Roth, R. No-core Monte Carlo shell-model calculation for 10Be and 12Be low-lying spectra. Phys. Rev. C 2012, 86, 014302. [Google Scholar] [CrossRef]
- Yao, J.M.; Engel, J.; Wang, L.J.; Jiao, C.F.; Hergert, H. Generator-coordinate reference states for spectra and 0νββ decay in the in-medium similarity renormalization group. Phys. Rev. C 2018, 98, 054311. [Google Scholar] [CrossRef]
- Yao, J.M.; Bally, B.; Engel, J.; Wirth, R.; Rodríguez, T.R.; Hergert, H. Ab Initio Treatment of Collective Correlations and the Neutrinoless Double Beta Decay of 48Ca. Phys. Rev. Lett. 2020, 124, 232501. [Google Scholar] [CrossRef]
- Frosini, M.; Duguet, T.; Ebran, J.P.; Somà, V. Multi-reference many-body perturbation theory for nuclei: I. Novel PGCM-PT formalism. Eur. Phys. J. A 2022, 58, 62. [Google Scholar] [CrossRef]
- Frosini, M.; Duguet, T.; Ebran, J.P.; Bally, B.; Mongelli, T.; Rodríguez, T.R.; Roth, R.; Somà, V. Multi-reference many-body perturbation theory for nuclei: II. Ab initio study of neon isotopes via PGCM and IM-NCSM calculations. Eur. Phys. J. A 2022, 58, 63. [Google Scholar] [CrossRef]
- Frosini, M.; Duguet, T.; Ebran, J.P.; Bally, B.; Hergert, H.; Rodríguez, T.R.; Roth, R.; Yao, J.; Somà, V. Multi-reference many-body perturbation theory for nuclei: III. Ab initio calculations at second order in PGCM-PT. Eur. Phys. J. A 2022, 58, 64. [Google Scholar] [CrossRef]
- Kimura, M. The Intruder feature of Mg-31 and the coexistence of many particle and many hole states. Phys. Rev. C 2007, 75, 041302. [Google Scholar] [CrossRef]
- Kimura, M. Spectroscopy and intruder configurations of 33Mg and 31Ne studied with antisymmetrized molecular dynamics. arXiv 2011, arXiv:1105.3281. [Google Scholar]
- Bally, B.; Avez, B.; Bender, M.; Heenen, P.H. Beyond Mean-Field Calculations for Odd-Mass Nuclei. Phys. Rev. Lett. 2014, 113, 162501. [Google Scholar] [CrossRef]
- Bally, B.; Giacalone, G.; Bender, M. Structure of 128,129,130Xe through multi-reference energy density functional calculations. Eur. Phys. J. A 2022, 58, 187. [Google Scholar] [CrossRef]
- Bally, B.; Giacalone, G.; Bender, M. The shape of gold. Eur. Phys. J. A 2023, 59, 58. [Google Scholar] [CrossRef]
- Borrajo, M.; Egido, J.L. A symmetry-conserving description of odd nuclei with the Gogny force. Eur. Phys. J. A 2016, 52, 277, Erratum in Eur. Phys. J. A 2017, 53, 38. [Google Scholar] [CrossRef]
- Borrajo, M.; Egido, J.L. Ground-state properties of even and odd Magnesium isotopes in a symmetry-conserving approach. Phys. Lett. B 2017, 764, 328–334. [Google Scholar] [CrossRef]
- Borrajo, M.; Egido, J.L. Symmetry Conserving Configuration Mixing description of odd mass nuclei. Phys. Rev. C 2018, 98, 044317. [Google Scholar] [CrossRef]
- Zhou, E.F.; Wu, X.Y.; Yao, J.M. Multireference covariant density-functional theory for the low-lying states of odd-mass nuclei. Phys. Rev. C 2024, 109, 034305. [Google Scholar] [CrossRef]
- Anguiano, M.; Egido, J.L.; Robledo, L.M. Particle number projection with effective forces. Nucl. Phys. A 2001, 696, 467–493. [Google Scholar] [CrossRef]
- Bender, M.; Duguet, T.; Lacroix, D. Particle-number restoration within the energy density functional formalism. Phys. Rev. C 2009, 79, 044319. [Google Scholar] [CrossRef]
- Duguet, T.; Bender, M.; Bennaceur, K.; Lacroix, D.; Lesinski, T. Particle-number restoration within the energy density functional formalism: Nonviability of terms depending on noninteger powers of the density matrices. Phys. Rev. C 2009, 79, 044320. [Google Scholar] [CrossRef]
- Hergert, H. In-Medium Similarity Renormalization Group for Closed and Open-Shell Nuclei. Phys. Scr. 2017, 92, 023002. [Google Scholar] [CrossRef]
- Egido, J.L.; Lessing, J.; Martin, V.; Robledo, L.M. On the solution of the Hartree-Fock-Bogoliubov equations by the conjugate gradient method. Nucl. Phys. A 1995, 594, 70–86. [Google Scholar] [CrossRef]
- Bally, B.; Sánchez-Fernández, A.; Rodríguez, T.R. Symmetry-projected variational calculations with the numerical suite TAURUS: I. Variation after particle-number projection. Eur. Phys. J. A 2021, 57, 69, Erratum in Eur. Phys. J. A 2021, 57, 124. [Google Scholar] [CrossRef]
- Yao, J.M.; Meng, J.; Ring, P.; Vretenar, D. Configuration mixing of angular-momentum projected triaxial relativistic mean-field wave functions. Phys. Rev. C 2010, 81, 044311. [Google Scholar] [CrossRef]
- Balian, R.; Brezin, E. Nonunitary bogoliubov transformations and extension of wick’s theorem. Nuovo Cim. B 1969, 64, 37–55. [Google Scholar] [CrossRef]
- Pandya, S.P. Nucleon-Hole Interaction in jj Coupling. Phys. Rev. 1956, 103, 956–957. [Google Scholar] [CrossRef]
- Bertsch, G.F.; Robledo, L.M. Symmetry restoration in Hartree-Fock-Bogoliubov based theories. Phys. Rev. Lett. 2012, 108, 042505. [Google Scholar] [CrossRef] [PubMed]
- Avez, B.; Bender, M. Evaluation of overlaps between arbitrary fermionic quasiparticle vacua. Phys. Rev. C 2012, 85, 034325. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys. Rev. C 2003, 68, 041001. [Google Scholar] [CrossRef]
- Bogner, S.K.; Furnstahl, R.J.; Schwenk, A. From low-momentum interactions to nuclear structure. Prog. Part. Nucl. Phys. 2010, 65, 94–147. [Google Scholar] [CrossRef]
- Hebeler, K.; Bogner, S.K.; Furnstahl, R.J.; Nogga, A.; Schwenk, A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys. Rev. C 2011, 83, 031301. [Google Scholar] [CrossRef]
- Fomenko, V.N. Projection in the occupation-number space and the canonical transformation. J. Phys. A Gen. Phys. 1970, 3, 8–20. [Google Scholar] [CrossRef]
- Hergert, H.; Bogner, S.K.; Morris, T.D.; Schwenk, A.; Tsukiyama, K. The In-Medium Similarity Renormalization Group: A Novel Ab Initio Method for Nuclei. Phys. Rept. 2016, 621, 165–222. [Google Scholar] [CrossRef]
- Firestone, R. Nuclear Data Sheets for A = 21. Nucl. Data Sheets 2015, 127, 1–68. [Google Scholar] [CrossRef]
| Interactions | |||||
|---|---|---|---|---|---|
| Ne20 | 6 | 211.205 | 50.093 | ||
| ENO/EW | 6 | 225.067 | 54.706 | ||
| Ne22 | 6 | 242.241 | 57.339 | ||
| Ne20(w/o 3N) | 6 | 506.122 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.; Zhou, E.; Yao, J.; Hergert, H. Quantum-Number Projected Generator Coordinate Method for 21Ne with a Chiral Two-Nucleon-Plus-Three-Nucleon Interaction. Symmetry 2024, 16, 409. https://doi.org/10.3390/sym16040409
Lin W, Zhou E, Yao J, Hergert H. Quantum-Number Projected Generator Coordinate Method for 21Ne with a Chiral Two-Nucleon-Plus-Three-Nucleon Interaction. Symmetry. 2024; 16(4):409. https://doi.org/10.3390/sym16040409
Chicago/Turabian StyleLin, Wei, Enfu Zhou, Jiangming Yao, and Heiko Hergert. 2024. "Quantum-Number Projected Generator Coordinate Method for 21Ne with a Chiral Two-Nucleon-Plus-Three-Nucleon Interaction" Symmetry 16, no. 4: 409. https://doi.org/10.3390/sym16040409
APA StyleLin, W., Zhou, E., Yao, J., & Hergert, H. (2024). Quantum-Number Projected Generator Coordinate Method for 21Ne with a Chiral Two-Nucleon-Plus-Three-Nucleon Interaction. Symmetry, 16(4), 409. https://doi.org/10.3390/sym16040409





