Abstract
The present study explores the symmetries associated with the cluster structure of light nuclei and draws the connection between solutions of the Schrödinger equation for the harmonic oscillator and the quasi-crystalline arrangements of α-particles, which gives rise to a series of collective behaviors. The double-center harmonic oscillator is used to formulate the collisions of two nuclei described by harmonic oscillator solutions and traces out the evolution of the cluster structure in the dynamics of the collision process and demonstrates that the symmetries are preserved in this process. The connection between this study and stellar nucleosynthesis is described.
1. Nuclear Clustering and Symmetries
Since the beginning of the introduction of the nuclear shell model, it has been known that symmetries play a fundamental role in nuclei [1,2]. These symmetries relate to the spin and orbital angular momentum of the nucleus and the approximate isospin symmetry, which involves neutrons and protons. However, there are other symmetries that involve how nucleons organize themselves inside nuclei, associated with the phenomenon of nuclear clustering [3,4,5].
The nucleus is often depicted as a homogeneous distribution of protons and neutrons. However, details of the nucleon–nucleon interaction, mediated by the strong nuclear force, mean that the structure of the nucleus is far from this simple picture. At a macroscopic level, the impact of the strong interaction can be felt through the binding energies of nuclei. Binding energies provide a determination of the amount of energy required to separate the nucleons bound inside the nucleus to their free, unbound counterparts. As such, this quantity is a direct measure of the average force nucleons experience within the nucleus. This has been parameterized through the semi-empirical mass formula [6], which has the following form:
where N and Z represent the numbers of neutrons and protons, and A = N + Z. The five terms correspond to different features of a nucleus, as represented by a liquid drop of nuclear matter. In order, the terms correspond to a volume energy (), associated with the interactions felt by the A nucleons and accounting for the saturation of the nuclear force (i.e., nucleons only interact with those in close proximity). From this, correction terms associated with the deficit of nucleons at the surface (, nucleons at the surface have ~50% fewer nucleons to interact with), the Coulomb repulsion of protons (), and the imbalance of protons and neutrons () are subtracted, and then finally, a pairing term is added.
The first three terms reveal nothing surprising in the nature of the strong and electromagnetic interaction; however, the last two do. There is an energy associated with the asymmetry in the numbers of protons and neutrons, with the term vanishing when . This indicates that a nucleus has the highest binding when neutrons and protons reside in identical quantum levels, or orbits. The last term is the pairing term, , which is positive when both neutron and proton numbers are even, zero when only one of N or Z are even, and negative when both are odd. This can be traced to pairs of protons/neutrons with their spins anti-aligned in counter-propagating orbits with their angular momentum, spin, and orbital angular momentum coupled to zero.
These details impact nuclear structure and impose both correlations in momentum and physical space, and are most noticeable in light nuclear systems where the energy associated with these correlations are of a similar scale to the volume energy. This is seen in Figure 1, where nuclei with N = Z and even proton and neutron numbers are most tightly bound, which is most obvious in the case of the 4He nucleus. In fact, the binding of 4He is so large that the 8Be nucleus finds itself unbound to decay into two 4He nuclei. This is a feature that is important in limiting the rate of helium burning in the red giant phase of stars and subsequently the rate of formation of 12C [7]. As nuclei such as 8Be, 12C, 16O,… can be decomposed into α-particles, 4He nuclei subunits invite the idea that these nuclei might be described in terms of α-particle clusters.

Figure 1.
Binding energy per nucleon (BE/A) plotted as a function of nucleon number. Different isotopes have different color lines, e.g., the helium isotopes are red, and lithium and beryllium isotopes are green and yellow, respectively.
The question arises as to whether these clusters arise only in the momentum correlations associated with the manifestation of the nuclear strong interaction or if it is appropriate to consider these clusters to be spatial arrangements of α-particles. The first real glimpse of this was found in the study of Hafstadt and Teller [8], as shown in Figure 2. This illustrated how the binding energies could be understood in terms of the number of interactions between α-particles and an α–α interaction energy. This invites a view of these nuclei in which the α-particle structure plays a significant role and that the momentum correlations associated with the nucleon–nucleon interaction, in turn, induces spatial arrangements of the α-particles. The other important feature of the α-particle is the very high energy of the first excited state, which lies at ~20 MeV. Compared with other nuclei, this is very high and attests to the strength of the correlations and the inertness of the α-particle. As such, once formed within the nuclear environment, one can expect the α-particle to have a significant lifetime. The structures shown in Figure 2 have particular symmetries that then invite an interpretation of their excited states in terms of collective rotations.
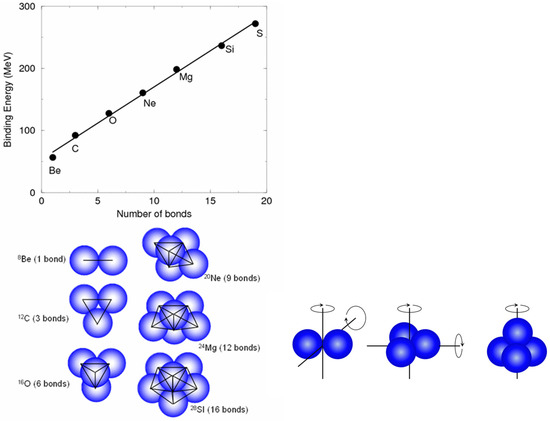
Figure 2.
(Left-hand side): Binding energy plotted as a function of the number of bonds between alpha-particles and the corresponding geometric arrangements [8,9]. (Right-hand side): Collective rotations of the 2α (dumbbell), 3α (triangle), and 4α (tetrahedron) systems.
In the case of 8Be, there are two identical axes around which the rotations may occur, and the equation for the rotational energy is [8]:
where is the moment of inertia of two touching α-particles. This produces a set of quantum states ,… up to a maximum angular momentum that the system can sustain. In the case of the 8Be nucleus, there are four particles in p-orbitals (l = 1); then, the maximum total angular momentum that can be generated is
For 12C, there are two different symmetry axes. The first has a three-fold rotational symmetry (perpendicular to the plane of the triangle) and the second has a two-fold symmetry (in the plane of the triangle). The second of these corresponds to a rotation of the two α-particles in the base of the triangle, i.e., the moment of inertia is given by . This symmetry is designated . The rotations around the three-fold symmetry axis are labelled by the quantum number K, and can take values of … Collective rotations are labelled by the and J values and the rotational energy is given by [8]:
For = , the rotations will be around an axis that lies in the plane of the three α-particles (in fact, passing through the center of one α- particle and between the other two), generating a series of states The in the denominator in the second term arises from the moment of a triangle of three touching spheres around the triangle center being approximately equal to twice the moment of inertia of two touching spheres. The next set of rotations are associated with the rotation around an axis perpendicular to the plane of the triangle, with each α-particle having one unit of angular momentum (, giving L = 3 × 1ℏ and =. Rotations around this axis and that parallel to the plane combine to give a series of states The next set of collective states then corresponds to each α-particle, with = 2ℏ and corresponding to L = 3 × 2ℏ.
For the tetrahedral arrangement of clusters in 16O, there is one common symmetry axis and the rotational energies are given by:
Here, the relevant symmetry is Td.
A more contemporary description of these symmetries is found in the algebraic cluster model, which accounts for both the rotational and vibrational symmetries of these nuclei and has been performed for the 12C and 16O systems [10,11]. These cluster symmetries assume that the α-particles are boson-like and that the internal structure can be neglected. However, one should recognize that the full wavefunction of the system needs to be fully antisymmetrized, given the fermionic nucleon components. This process of antisymmetrization precludes certain states that would appear otherwise, as demonstrated in Refs. [12,13].
Up to this point, the symmetries that arise from the point and rotational symmetries grow from an assumption of a crystalline arrangement of clusters. However, a successful description of nuclei should recognize that the individual nucleons move in a mean field formed by the average interaction that a nucleon experiences within the nucleus. This is typically represented by a Woods–Saxon potential with an additional spin–orbit interaction to give the nuclear shell model solutions of the Schrödinger equation. Here, the nucleons are then associated with standing wave solutions for the given potential. It is then not immediately obvious how these might map onto those realized from the α-particle geometric arrangements.
It is possible to realize analytic solutions of the deformed harmonic oscillator, which illustrate the connection. It is clear that the deformed harmonic oscillator potential is only an approximation to more realistic nuclear potentials, but that the conclusions reached in the following are robust and map to more complex nuclear models [14]. The solutions of the deformed harmonic oscillator are given by:
where are the characteristic angular frequencies in the three Cartesian coordinate directions, and are the associated oscillator quanta. Here,
and for axial symmetry , the nuclear/oscillator deformation parameter is then given by:
The energy levels of the deformed harmonic oscillator are illustrated in Figure 3. In nuclei, the presence of a shell structure, or equivalent regions of high-density states, is associated with stability. For example, spherical nuclei such as 4He, 16O, and 40Ca have high binding energies and comparatively high excitation energies for the first excited state. These are associated with magic proton and neutron numbers 2, 8, and 20. Figure 3 illustrates that at high levels of degeneracy, shell gaps appear in the deformed energy level scheme at both prolate and oblate deformations associated with integer ratios of axial deformation parameters/frequencies. This produces new sets of magic numbers particular to that deformation. As demonstrated in Ref. [15], these new magic numbers can be represented by a single sequence of numbers, 2, 6, 12, 20, 30,…, as illustrated in Figure 4.
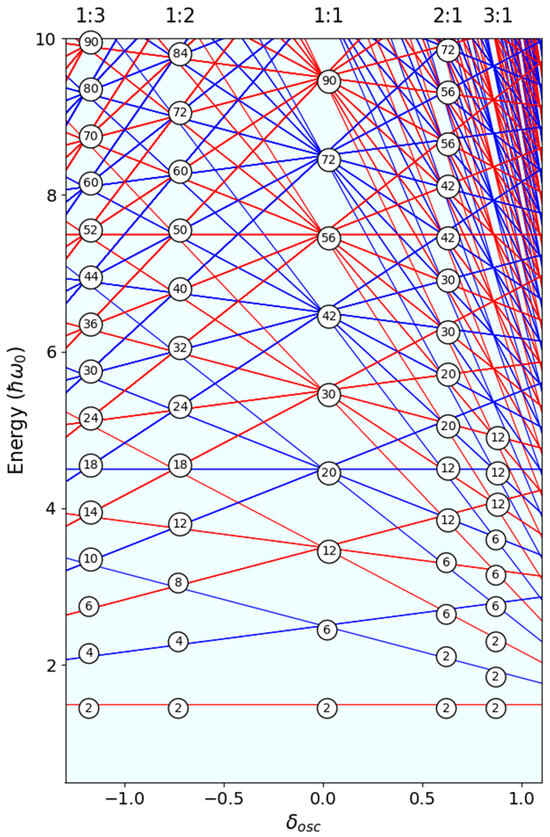
Figure 3.
The energy levels of the deformed harmonic oscillator as a function of deformation, , in units of . The red and blue lines correspond to even and odd total oscillator quanta and the numbers in the circles represent the numbers of protons, or neutrons, that can be placed in the levels at the points of high degeneracy [15].
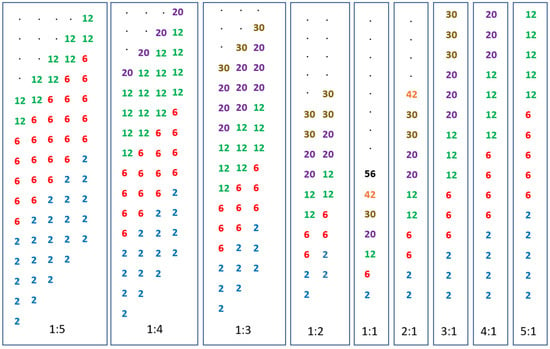
Figure 4.
The symmetries of the deformed harmonic oscillator. The spherical pattern of degeneracies (how many protons or neutrons may be placed in orbits) 2, 6, 12, 20, 30, 42… are seen to repeat at integer deformations of the HO potential [15].
This sequence is that found for the spherical solutions; 1:1 is found to be repeated at each deformation of the system with a slightly different set of systematics either side of sphericity. For n:1 prolate deformations, the sequence of numbers is stacked such that all of the 2s appear first, then the 6s, etc., …, whereas on the oblate side at a deformation of 1:n, the sequences linked to the prolate n:1 deformations are repeated n times. There is thus an underlying symmetry that can be traced back to the spherical harmonic oscillator.
The interpretation of this symmetry is as follows: For a 2:1 prolate deformation, the shell structure and degeneracy is represented by filling two harmonic oscillators, and at n:1, there are n harmonic oscillators. Crucially, from a geometric perspective, these oscillators would all be aligned along the deformation axis. Thus, from a cluster perspective, the interpretation would be n clusters aligned along a common axis. In its simplest form, this would reproduce the α+α clustering associated with 8Be. For the 1:2 oblate deformation, it is seen that the sequence of degeneracies is created by combining two 2:1 prolate sequences, but with one offset by 1. As discussed in Ref. [15], this sequence can reproduce the structure of oblate, deformed, clustered nuclei such as 12C and 28Si and the associated D3h structure of 12C. The Td structure of 16O corresponds to the spherical 1:1 deformation with an α-particle stacked on top of the 3α, triangular, D3h structure of 12C.
The assembly of the individual clusters into the composite system, such that the resulting structures respect the Pauli exclusion principle, can be described by the Harvey model [16]. The methodology extending from 2 to n centers is explained in Ref. [17]. The Harvey model is a method for combining the oscillator quanta from a multi-center system into a single center. It ensures that the Pauli exclusion principle is observed when levels from multi-centers are combined. For a two center system with levels labelled by , merged along the -axis, then the resulting levels are associated by the quantum numbers 2 and 2. Extending to N centers, the merged levels have quantum numbers N, , … N These principles preserve the number of internal nodes of the wavefunctions being combined in merging from N centers to one center.
In summary, both from a perspective of considering light, alpha-conjugate nuclei to be constructed from arrangements of α-particles arranged into geometric structures and that of solutions of the Schrödinger equation associated with the deformed harmonic oscillator, clustering is evident in the structure of light nuclei. These geometric structures have characteristic point symmetries that then, in turn, are associated with collective rotational behavior, which appear as rotational bands. These observations tally well with the available experimental evidence, e.g., as demonstrated in the case of the rotations of 12C [10].
2. Clustering and Collisions
The aim of the present contribution is to explore how the symmetries associated with the appearance of clustering in light nuclei translate into the dynamics of collisions of clustered nuclei and the nature of the composite system if the clusters fuse. There is a long history of heavy-ion, molecular resonances that are well summarized in Refs. [18,19,20]. The collisions of nuclei such as 12C + 12C, 12C + 16O, and 16O + 16O reveal a series of resonances associated with the intermediate nuclei 24Mg, 28Si, and 32S, respectively. The widths of these resonances are keV, indicating lifetimes that are much greater than the collision time and point to the formation of a series of special states, which preserve the original structure of the colliding partners, exciting di-nuclear structures in the intermediate system with a series of rotational bands identified. The 12C + 12C resonances have been interpreted in terms of an array of cluster-like structures, which can be found in both the mean-field [21,22] and the alpha cluster models [23] with resonances observed in different reaction channels being ascribed to different types of cluster structures [20,24].
The Double-Center Oscillator
In order to describe the evolution of the collision of two nuclei, the framework of the double-center harmonic oscillator (DCHO) is used [25] (see Figure 5).
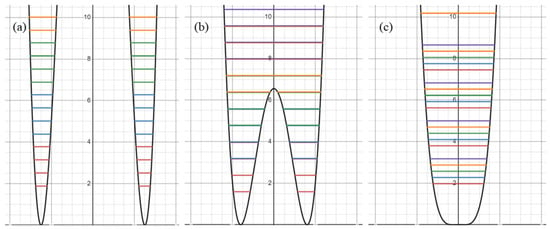
Figure 5.
The DCO potential shape (arbitrary axes): the colors indicate different values for ( = 0). is given by red; is given by blue; is given by green. During deformation of the potential, these energy level positions move (with respect to one another). (a) shows when the potential acts as two independent (D)Hos, (b) shows partial merging of these potentials in the true DCO regime, and (c) shows how the (D)HO is recovered in the limit .
In this instance, the potential is modelled as two interacting deformed harmonic oscillator (DHO) potentials, where deformation arises naturally due to their separation. The key parameter describing the interaction of the two potentials evolves from the deformation, δ, of the fused potential to the positions of the two centers of the interacting DHOs, . In the case of symmetric nuclei, e.g., 12C + 12C, the location of the two potentials along the collision, , axis is given by (the centers are the same distance from the origin), and for asymmetric cases, . This can be solved analytically, as shown by Holzer [25], and the derivation here closely follows the original derivation. The Hamiltonian used is a direct generalization of the Nilsson Hamiltonian for two centers:
Here,
where and are the angular momentum operators with respect to the two centers: and , and both the Hamiltonian and potential are in cylindrical co-ordinates. The parameters C and D ensure that the transition between single-center and double-center shell models is appropriate: for small separation of the centers, a single DHO is recovered, and as the center separation increases, there is a proper transition to the DCHO before a transition at very large separation to two independent DHO potentials. For the symmetric case, which we will focus on here, , whereas for the asymmetric case, . For simplicity, the derivation outlined below follows the symmetric solution.
As is indeed the case for the single-center DHO case and without non-local terms of orbital angular momentum and the spin–orbit interaction, the volume of the nucleus described in the DCHO must be constant throughout deformation and separation. This constraint is applied to the equipotential surface that coincides with the nuclear surface. The characteristic oscillation frequency, ω, is found through this volume conservation as:
with r the root of
The HO constants have the form:
where R is the approximate nuclear radius, found via the liquid drop model and the assumption of the nucleus being modelled as a dense sphere () being proportional to the number of nucleons, A. In this approach, the constant of proportionality, , can be thought of as the Compton wavelength of the proton: (via the proton, where A = 1), and can be determined experimentally.
By applying the Schrödinger equation to the symmetric-case Hamiltonian, and through the standard approach of applying the ansatz: three ordinary differential equations are obtained for the wavefunctions χ(ρ), φ(z), and ν(ϕ). Physically relevant solutions for ν(ϕ) and χ(ρ) are essential to find and , which are given as:
The prime focus here is the solution as a function of z. The solution follows from a standard differential equation that takes solutions of the form containing confluent hypergeometric functions, . Before imposing physical constraints, the z wavefunction solutions have the form:
where
so that the wavefunction is defined for and , and , are constants found through the eigenvalue equations and normalization. A physical solution is ensured by using Born’s conditions, or more explicitly meeting the following criteria:
- (i)
- The two functions must be single valued (unique for any given value). This ensures a single probability for a given state. This is naturally satisfied as does not contain any branch points (in contrast to , which does).
- (ii)
- The two functions must be continuous at z = 0.
- (iii)
- The first derivatives of the two functions must be continuous at z = 0.
- (iv)
- The functions must be square integrable and therefore have the correct asymptotic values such that they vanish as This is ensured through the asymptotic definition of the confluent hypergeometric function.
By accounting for these four conditions, the wavefunction (Equation (14)) becomes:
where is a generalised hypergeometric function and appears through the asymptotic definition of the confluent hypergeometric function. In the limit the eigenvalue equations for are found:
and the values of can be extracted when are fixed through normalization. It should be noted that , and it need not be an integer, as in the DHO; only the values and large values are known with certainty.
In the symmetric case, [H, Π] = 0, meaning that the Hamiltonian, H, commutes with the parity operator, Π. Because of this, the eigenfunctions of H are also the eigenfunctions of Π, i.e., , meaning that for each parity, the relations for are as follows:
- Positive parity: and
- Negative parity: and
For negative parity at , the eigenvalue equation for (Equation (17)) becomes:
This is only valid when , where . These are the standard HO eigenstates for negative parity. The energy levels as a function of are obtained by substituting the wavefunction φ(z) into the ordinary differential equation for φ(z) to produce:
Following a likewise procedure for the asymmetric case gives the following wavefunctions:
Here, implies and implies for the asymmetric centers. The eigenvalue equations are then:
Giving
Here, and are related through energy conservation as:
3. Results
The solutions of the DCHO are shown in Figure 6 and Figure 7 for the values and the associated energy levels. There are some simple rules.
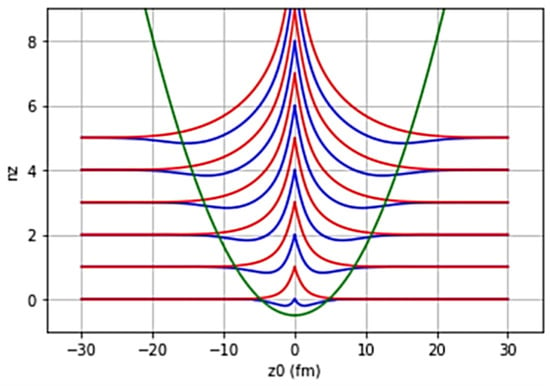
Figure 6.
The evolution of the values as a function of the separation of the two DHO potentials. In this representation the two potentials merge at with potential 1 approaching the origin from the negative z-direction and potential 2 from the positive z-direction. The blue and red lines show the evolution of the values such that when the two potentials are merged then the asymptotic values become and The green line illustrates the point when the two separate potentials begin to merge.
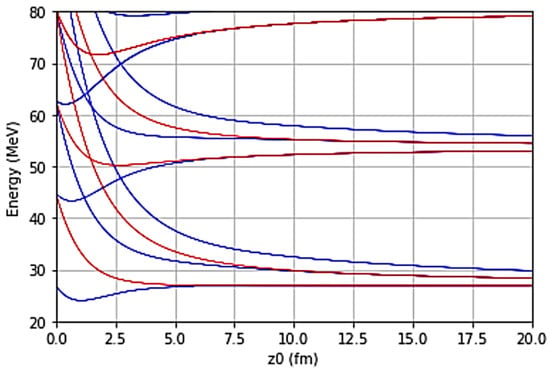
Figure 7.
The energy levels of the DCHO given by Equations (19) and (24). The blue lines provide the symmetric solutions and the red lines provide asymmetric solutions as a function of the separation of the two potentials (z0).
The solutions for the DCHO demonstrate some guiding principles of the evolution of two harmonic oscillator potentials as they evolve from infinite separation to zero separation. As is shown in Figure 6, there is a change in the values at infinite separation to and at zero separation. This evolution reflects the change in the wavefunctions such that the final single center wavefunction preserves the number of nodes in the system and introduces an additional node according to the linear combinations:
Thus, in Figure 6, the merging of the potentials from the negative and positive z-direction results in protons and neutrons either following the blue line or red line from either side, but not both blue and red together. The green line in Figure 6 illustrates the approximate variation in the location at which levels in the separate HO potentials overlap and the system changes from two separate HO potentials to solutions of the double-center harmonic oscillator.
The rules of the DCHO are encoded in the Harvey rules [16]. These are illustrated in Figure 8 for the fusion of two 12C nuclei.
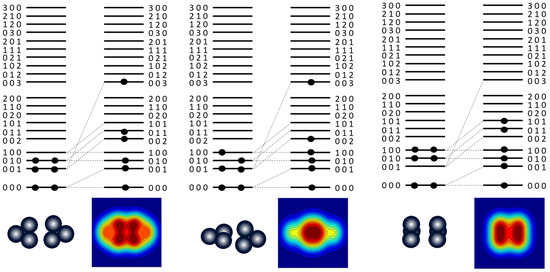
Figure 8.
Harvey characterization of the fusion of two 12C nuclei with three different relative orientations. See the text for details.
The 12C nucleus in its ground state can be represented by the HO configuration (0,0,0)4, (0,0,1)4, and (0,1,0)4, which is associated with a triangular structure orientated in the y–z plane. Different orientations of the 3α structure can be created by populating the (1,0,0), (0,1,0), and (0,0,1) levels with different pairs. As is shown in Figure 8, when these nuclei merge, following solutions of the DCHO and as depicted by the Harvey scheme, different final 24Mg structures are produced. The interesting observation is that the final structure that is produced, as represented by the DHO densities, retains the symmetries of the original arrangements of the 12C clusters. For example, the left-hand side of Figure 8 shows the merger of two 12C nuclei with all α-particles in the y–z plane and this results in a 24Mg cluster structure in which 6α-particles are arranged, where two 3α triangles are clear. Different orientations give different cluster structures with the central example corresponding to an α + 16O + α structure and the right-hand image would be a compact 24Mg structure associated with an arrangement similar to the 24Mg ground state.
Another thing to note is that for different orientations, the circles that represent 2p+2n (α-particle) combinations, are promoted to orbits of different energies associated with the different orientations. In other words, the potential energy associated with different orientations is different, with that of the more compact structure being lowest and the planar structure being the highest (the α + 16O + α structure is intermediate). This can be thought of as a Pauli repulsion effect, which would add to the Coulomb repulsion associated with the like proton charges in the two 12C nuclei. Thus, the formation of the compact structure would proceed at lower energies and the planar structure at higher energies, and the difference in barriers would drive re-orientation of the 12C nuclei in the collision process. This has been demonstrated, for example, in coupled-reaction-channel calculations by Boztosun and Rae [26].
The calculations in Figure 8 are performed with the DHO in the limit of zero separation of the two 12C nuclei. However, using the DCHO and the two-center wavefunctions, it is possible to calculate the evolution of the densities from the point where the two potentials begin to merge, through the point of closest contact and the formation of the intermediate structure to the point where the two nuclei move apart. In these calculations there is full consideration of the incident kinetic energy and the repulsive effect of the Pauli repulsion as particles trace out orbitals that climb in energy and the repulsive effect of the Coulomb repulsion. This is shown in Figure 9. Here, it is assumed that in the DCHO calculations, the line joining the two 12C nuclei remains as the z-axis.
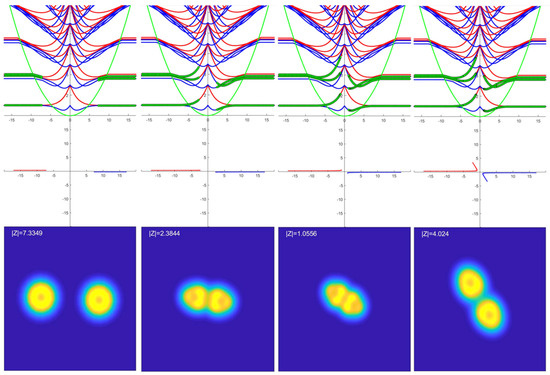
Figure 9.
Collision of two 12C nuclei calculated using DCHO wavefunctions for a small impact parameter. The bottom panels show the evolving densities, and for different separations of the two potentials (labelled by ), the middle panel shows the classical trajectories in the center-of-mass frame for the two nuclei and the top panel shows how the particles follow the energy solutions of the DCHO via the green dots.
It is observed in these calculations that the 3α structure of 12C and the 6α structure of 24Mg is preserved, and the symmetries described earlier in this paper not only affect the static properties of nuclei, but also the dynamical ones as well.
4. Discussion and Conclusions
The results presented here illustrate how the DCHO can be used to combine the dynamics of a collision process with the symmetries that arise from the standing wave solutions in the HO potentials and the cluster structures that arise. The symmetries that occur in the original nuclei are preserved in the collision process and thus materialize in the composite system. In this way, one can trace how different cluster states are produced in nuclear reactions. There is an implicit assumption here that the evolution of collision dynamics is on a timescale indicating that the reaction is adiabatic. In other words, once the particles are locked into particular orbitals, they remain so for the duration of the collision. But, as explored in Reference [26] and elsewhere, it may be possible for the nuclei to orientate themselves in the collision process and particle hop from one orbital to another. In principle, such effects can be calculated within the DCHO by tracing out the lowest energy configuration in the merger of the two nuclei. This is equivalent to tracking the lowest energy path across the dynamical potential energy surface representing the collision.
Understanding the behavior of two 12C nuclei in the collision is particularly important in understanding 12C + 12C burning in massive stars; changes to the structure that create low-energy resonances could lower the temperature and density required to ignite carbon burning, and change the burning rate. The rate of carbon burning (along with the stellar mass) can dictate whether the star will stay as a white dwarf or evolve into a type 1A supernova: a standard candle. In 12C+12C burning, the two primary reaction channels are 12C(12C, α)20Ne and 12C(12C, p)23Na, with the former calculated using antisymmetrized molecular dynamics (AMD) highlighting the α substructure of 12C [27]. Similar conclusions have been reached in time-dependent Hartree Fock (TDHF) calculations [28]. The emergence of similar conclusions from these more complex models and the more simplified DCHO method demonstrates the robustness of the symmetries in the calculations and their deeper impact on the synthesis of elements in stars.
Author Contributions
Both authors have contributed equally to the development of the ideas presented. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Elliott, J.P.; Flowers, B.H.; Cockcroft, J.D. The Structure of the Nuclei of Mass 18 and 19. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1997, 229, 536–563. [Google Scholar] [CrossRef]
- Arima, A. Elliott’s SU(3) Model and Its Developments in Nuclear Physics. J. Phys. G Nucl. Part. Phys. 1999, 25, 581. [Google Scholar] [CrossRef]
- Lombardo, I.; Dell’Aquila, D. Clusters in Light Nuclei: History and Recent Developments. Riv. Nuovo Cimento 2023, 46, 521–618. [Google Scholar] [CrossRef]
- Kanada-En’yo, Y.; Horiuchi, H. Structure of Light Unstable Nuclei Studied with Antisymmetrized Molecular Dynamics. Prog. Theor. Phys. Suppl. 2001, 142, 205–263. [Google Scholar] [CrossRef]
- Fulton, B.R.; Rae, W.D.M. Fission of Light Nuclei. J. Phys. G Nucl. Part. Phys. 1990, 16, 333. [Google Scholar] [CrossRef]
- von Weizsäcker, C.F. Zur Theorie der Kernmassen. Z. Phys. 1935, 96, 431–458. [Google Scholar] [CrossRef]
- Freer, M.; Fynbo, H.O.U. The Hoyle State in 12C. Prog. Part. Nucl. Phys. 2014, 78, 1–23. [Google Scholar] [CrossRef]
- Hafstad, L.R.; Teller, E. The Alpha-Particle Model of the Nucleus. Phys. Rev. 1938, 54, 681–692. [Google Scholar] [CrossRef]
- Freer, M. Clusters in Nuclei. Scholarpedia 2010, 5, 9652. [Google Scholar] [CrossRef]
- Marín-Lámbarri, D.J.; Bijker, R.; Freer, M.; Gai, M.; Kokalova, T.; Parker, D.J.; Wheldon, C. Evidence for Triangular D3h Symmetry in 12C. Phys. Rev. Lett. 2014, 113, 012502. [Google Scholar] [CrossRef]
- Bijker, R.; Iachello, F. Evidence for Tetrahedral Symmetry in 16O. Phys. Rev. Lett. 2014, 112, 152501. [Google Scholar] [CrossRef]
- Hess, P.O. 12C within the Semi-Microscopic Algebraic Cluster Model. Eur. Phys. J. A 2018, 54, 32. [Google Scholar] [CrossRef]
- Hess, P.O.; Berriel-Aguayo, J.R.M.; Chávez-Nuñez, L.J. 16O within the Semi-Microscopic Algebraic Cluster Model and the Importance of the Pauli Exclusion Principle. Eur. Phys. J. A 2019, 55, 71. [Google Scholar] [CrossRef]
- Freer, M.; Horiuchi, H.; Kanada-En’yo, Y.; Lee, D.; Meißner, U.-G. Microscopic Clustering in Light Nuclei. Rev. Mod. Phys. 2018, 90, 035004. [Google Scholar] [CrossRef]
- Freer, M.; Marsh, T.; Souter, J. Symmetries of the Oblate Deformed Harmonic Oscillator. J. Phys. G Nucl. Part. Phys. 2022, 49, 055105. [Google Scholar] [CrossRef]
- Harvey, M. Many nucleon correlations in light nuclei. In Proceedings of the 2nd International Conference on Clustering Phenomena in Nuclei USDERA Report ORO-4856-26, College Park, MD, USA, 21–25 April 1975. [Google Scholar]
- Freer, M. Nucleon Clustering in Light Nuclei. In Oxford Research Encyclopedia of Physics; Oxford University Press: Oxford, UK; American Institute of Physics: College Park, MD, USA, 2023; ISBN 978-0-19-087199-4. [Google Scholar]
- Bromley, D.A.; Erb, K.A. Treatise on Heavy-Ion Science; Plenum Press: New York, NY, USA; London, UK, 1985; Volume 3. [Google Scholar]
- Betts, R.R.; Wuosmaa, A.H. Nuclear Molecules. Rep. Prog. Phys. 1997, 60, 819. [Google Scholar] [CrossRef]
- Freer, M.; Merchant, A.C. Developments in the Study of Nuclear Clustering in Light Even—Even Nuclei. J. Phys. G Nucl. Part. Phys. 1997, 23, 261. [Google Scholar] [CrossRef]
- Leander, G.; Larsson, S.E. Potential-Energy Surfaces for the Doubly Even N = Z Nuclei. Nucl. Phys. A 1975, 239, 93–113. [Google Scholar] [CrossRef]
- Flocard, H.; Heenen, P.H.; Krieger, S.J.; Weiss, M.S. Configuration Space, Cranked Hartree-Fock Calculations for the Nuclei 16O, 24Mg and 32S. Prog. Theor. Phys. 1984, 72, 1000–1016. [Google Scholar] [CrossRef]
- Marsh, S.; Rae, W.D.M. The Structure of 24Mg Using the Cranked Cluster Model. Phys. Lett. B 1986, 180, 185–190. [Google Scholar] [CrossRef]
- Freer, M. The Clustered Nucleus—Cluster Structures in Stable and Unstable Nuclei. Rep. Prog. Phys. 2007, 70, 2149. [Google Scholar] [CrossRef]
- Holzer, P.; Mosel, U.; Greiner, W. Double-Centre Oscillator and Its Application to Fission. Nucl. Phys. A 1969, 138, 241–252. [Google Scholar] [CrossRef]
- Boztosun, I.; Rae, W.D.M. Analysis of the 12C+12C Reaction Using a New Type of Coupling Potential. Phys. Rev. C 2001, 63, 054607. [Google Scholar] [CrossRef]
- Taniguchi, Y.; Kimura, M. 12C+12C Fusion S⁎-Factor from a Full-Microscopic Nuclear Model. Phys. Lett. B 2021, 823, 136790. [Google Scholar] [CrossRef]
- Godbey, K.; Simenel, C.; Umar, A.S. Absence of Hindrance in a Microscopic 12C+12C Fusion Study. Phys. Rev. C 2019, 100, 024619. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).