The Testing Procedure for the Overall Lifetime Performance Index of Rayleigh Products in Multiple Production Lines Based on the Progressive Type I Interval Censored Sample
Abstract
1. Introduction
2. The Overall Lifetime Performance Index and the Conforming Rate
3. The Testing Procedure for the Overall Lifetime Performance Index
3.1. Maximum Likelihood Estimator of the Lifetime Performance Index
3.2. The Testing Procedure for the Overall Lifetime Performance Index and Power Analysis
| Algorithm 1. Testing procedure for the overall lifetime performance index |
| Step 1: For the pre-assigned target level for the overall lifetime performance index, the required target level for each individual lifetime performance index is determined as for each production line. Then the testing hypothesis for some i vs. are constructed. Step 2: Under the known lower specification observe the progressive type I interval censored sample at the observation times with censoring schemes of from the Rayleigh distribution. Step 3: Compute the value of the test statistic where is obtained by solving Equation (14). Step 4: For significance level of we can calculate the critical value , is defined in Equation (18). Step 5: If , we can concluded that the overall lifetime performance index of the products adhered the required level. |
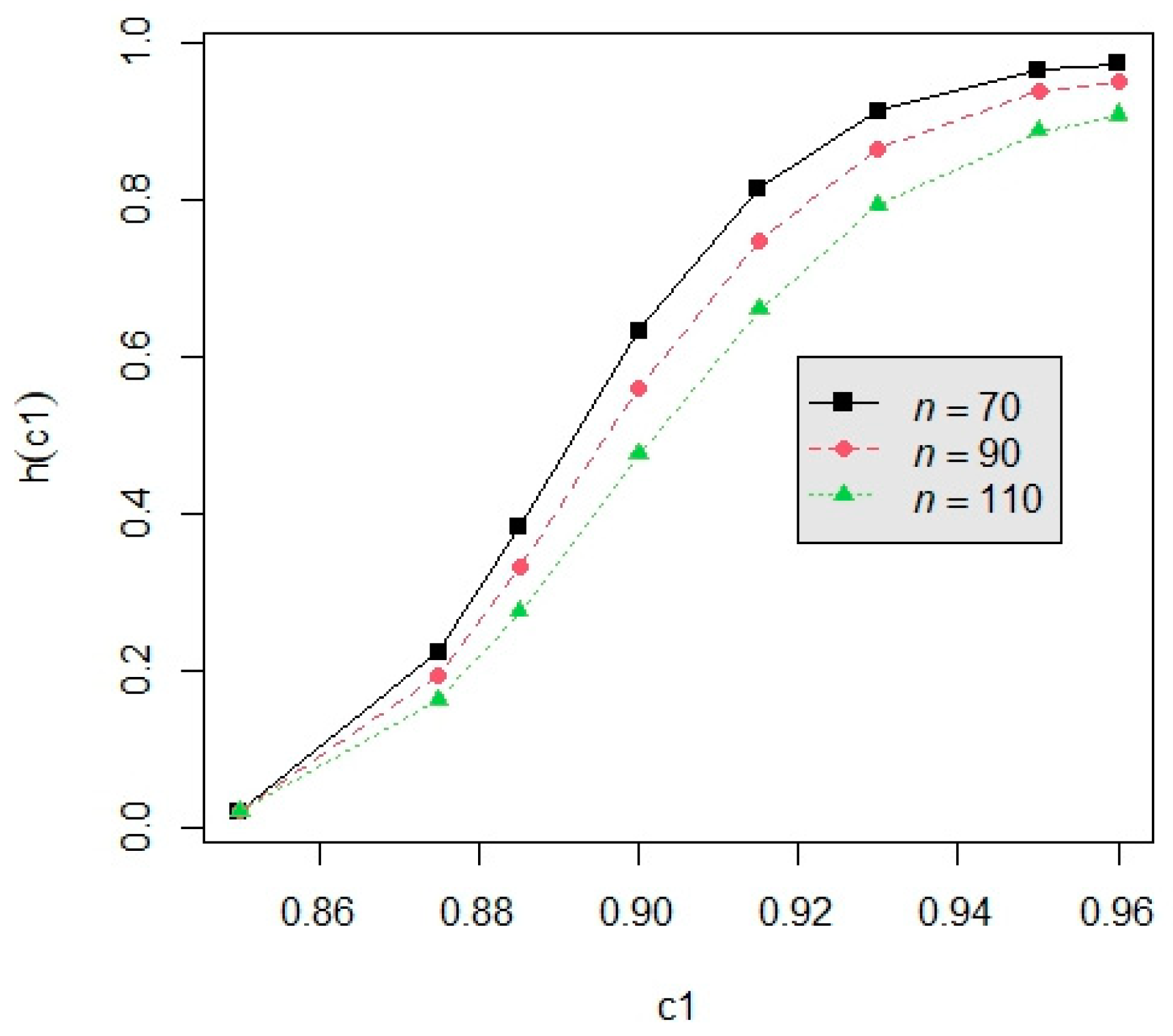
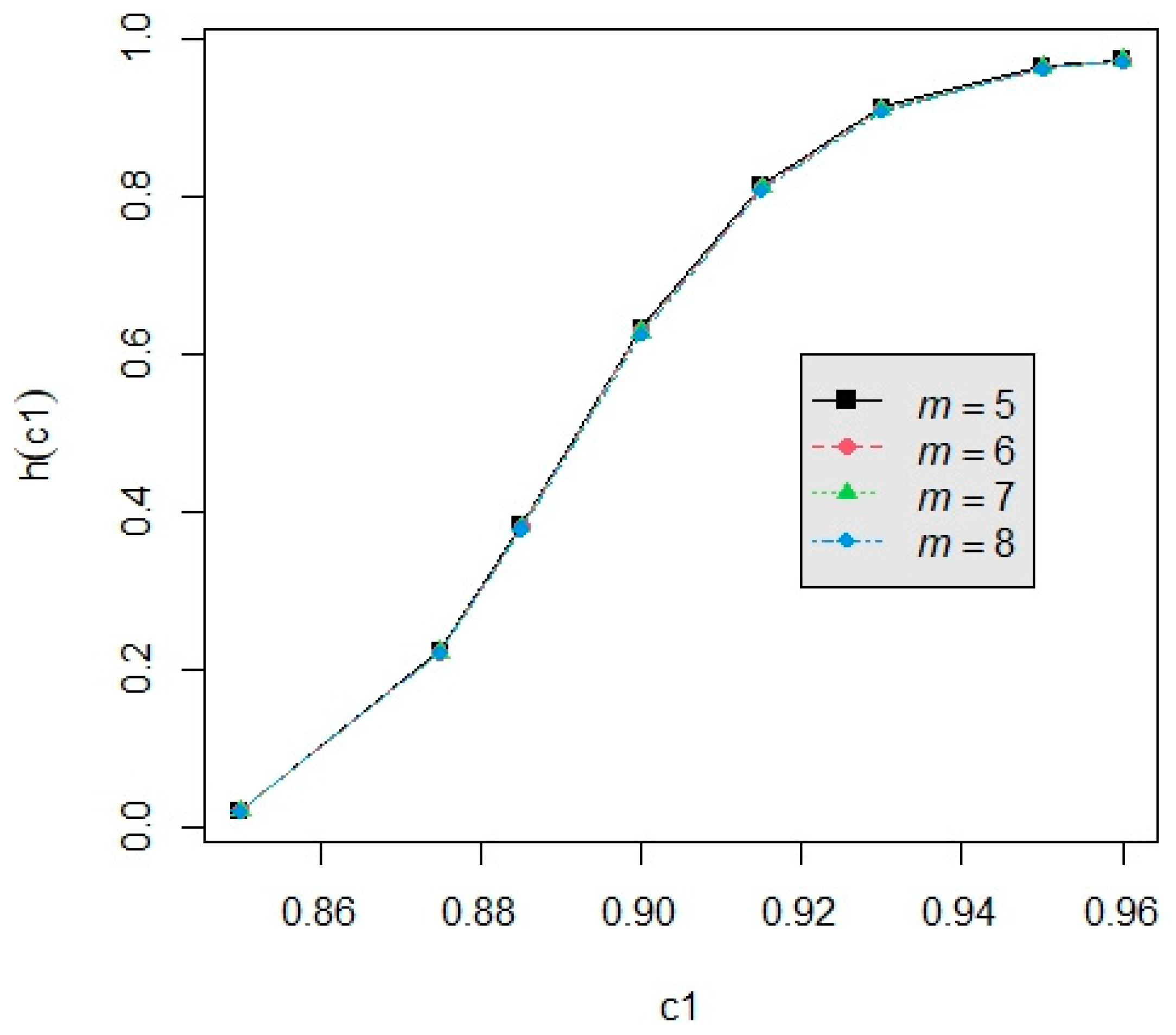
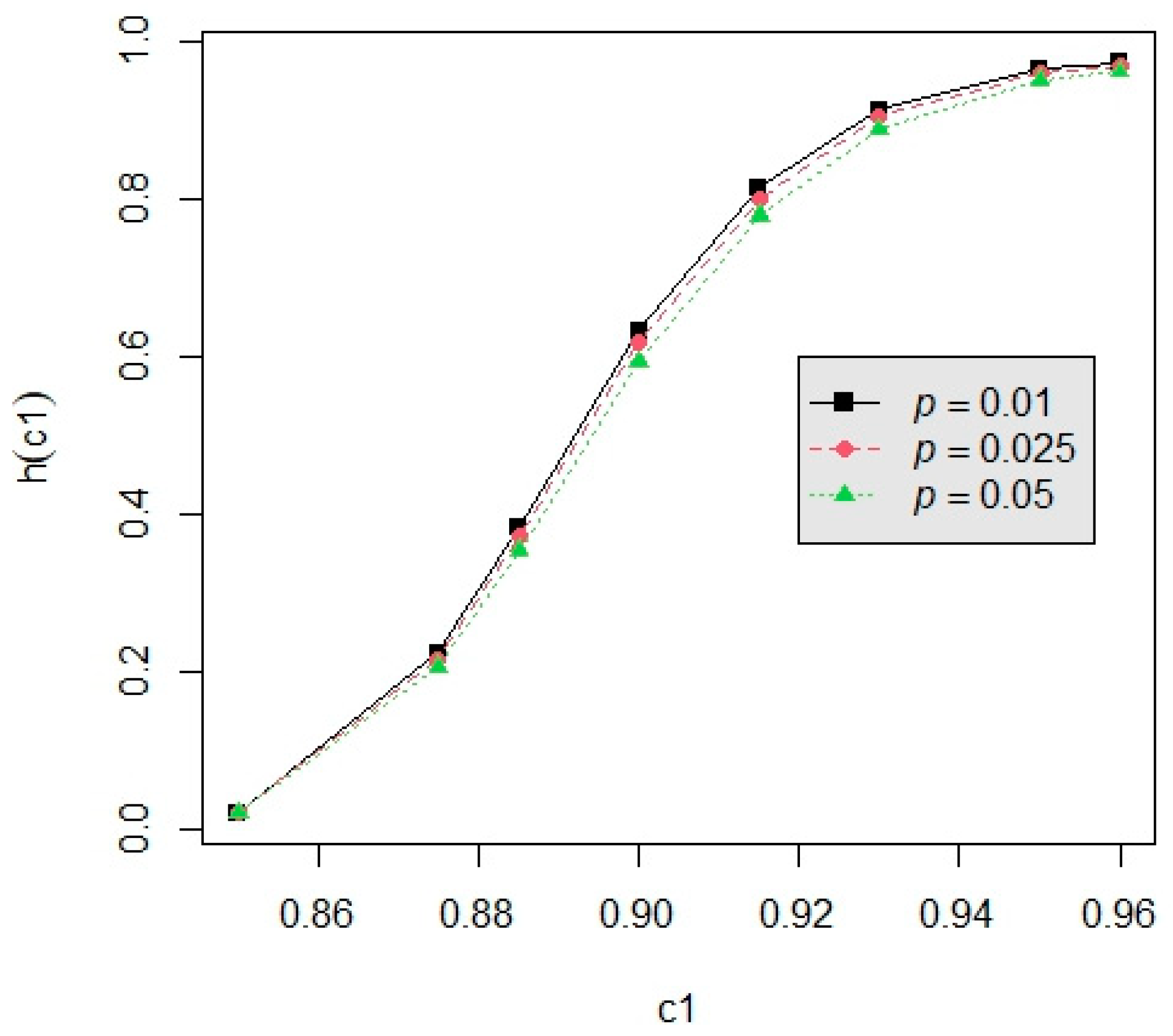
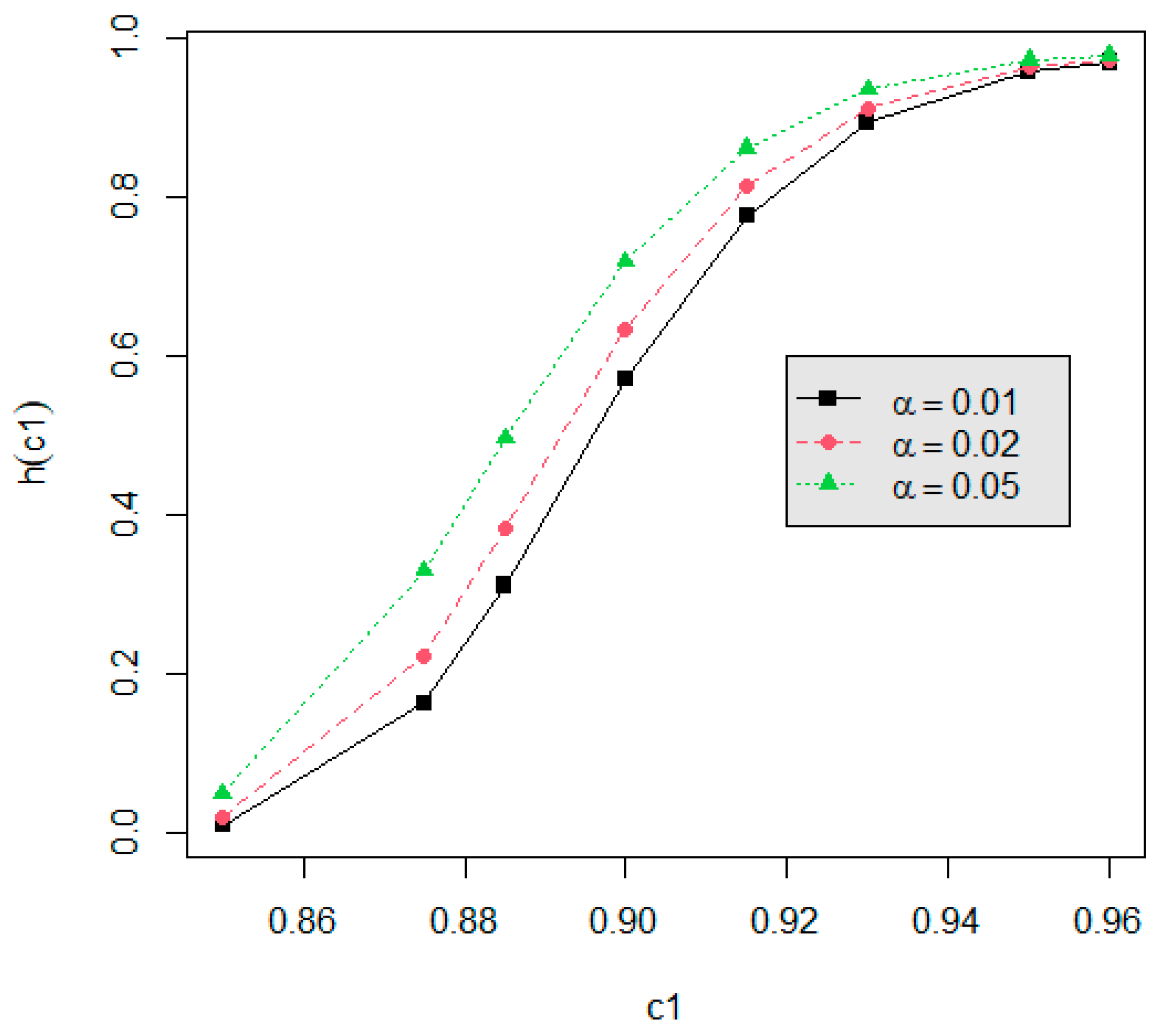
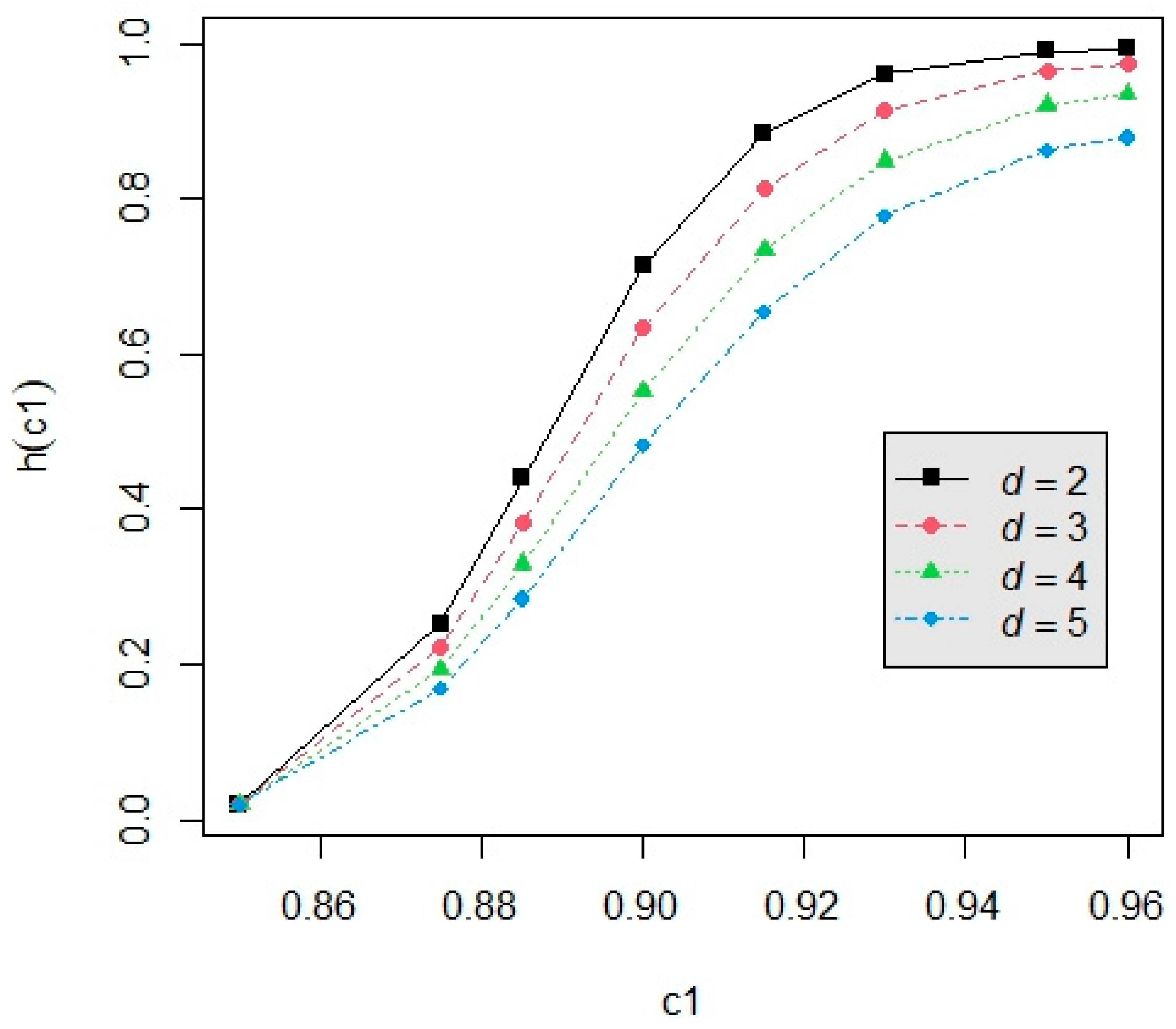
3.3. Example
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| c1 | ||||||||
| m | n | p | 0.85 | 0.885 | 0.9 | 0.915 | 0.93 | 0.96 |
| 6 | 70 | 0.05 | 0.0100 | 0.2580 | 0.4975 | 0.7178 | 0.8612 | 0.9636 |
| 0.075 | 0.0100 | 0.2479 | 0.4803 | 0.6997 | 0.8474 | 0.9577 | ||
| 0.1 | 0.0100 | 0.2318 | 0.4523 | 0.6691 | 0.8229 | 0.9465 | ||
| 90 | 0.05 | 0.0100 | 0.3163 | 0.5887 | 0.8041 | 0.9200 | 0.9844 | |
| 0.075 | 0.0100 | 0.3036 | 0.5697 | 0.7873 | 0.9094 | 0.9811 | ||
| 0.1 | 0.0100 | 0.2835 | 0.5385 | 0.7583 | 0.8901 | 0.9745 | ||
| 110 | 0.05 | 0.0100 | 0.3721 | 0.6657 | 0.8649 | 0.9540 | 0.9933 | |
| 0.075 | 0.0100 | 0.3573 | 0.6461 | 0.8504 | 0.9465 | 0.9915 | ||
| 0.1 | 0.0100 | 0.3337 | 0.6135 | 0.8246 | 0.9321 | 0.9878 | ||
| 7 | 70 | 0.05 | 0.0100 | 0.2568 | 0.4953 | 0.7155 | 0.8595 | 0.9629 |
| 0.075 | 0.0100 | 0.2447 | 0.4749 | 0.6939 | 0.8428 | 0.9557 | ||
| 0.1 | 0.0100 | 0.2260 | 0.4421 | 0.6575 | 0.8132 | 0.9418 | ||
| 90 | 0.05 | 0.0100 | 0.3147 | 0.5863 | 0.8020 | 0.9187 | 0.9840 | |
| 0.075 | 0.0100 | 0.2997 | 0.5638 | 0.7819 | 0.9059 | 0.9800 | ||
| 0.1 | 0.0100 | 0.2763 | 0.5270 | 0.7471 | 0.8822 | 0.9716 | ||
| 110 | 0.05 | 0.0100 | 0.3703 | 0.6632 | 0.8631 | 0.9531 | 0.9931 | |
| 0.075 | 0.0100 | 0.3527 | 0.6399 | 0.8457 | 0.9439 | 0.9909 | ||
| 0.1 | 0.0100 | 0.3251 | 0.6012 | 0.8144 | 0.9260 | 0.9861 | ||
| 8 | 70 | 0.05 | 0.0100 | 0.2555 | 0.4931 | 0.7132 | 0.8578 | 0.9622 |
| 0.075 | 0.0100 | 0.2417 | 0.4695 | 0.6881 | 0.8383 | 0.9537 | ||
| 0.1 | 0.0100 | 0.2205 | 0.4321 | 0.6460 | 0.8035 | 0.9369 | ||
| 90 | 0.05 | 0.0100 | 0.3130 | 0.5839 | 0.7999 | 0.9174 | 0.9836 | |
| 0.075 | 0.0100 | 0.2958 | 0.5578 | 0.7764 | 0.9023 | 0.9788 | ||
| 0.1 | 0.0100 | 0.2693 | 0.5156 | 0.7358 | 0.8741 | 0.9685 | ||
| 110 | 0.05 | 0.0100 | 0.3684 | 0.6607 | 0.8613 | 0.9522 | 0.9929 | |
| 0.075 | 0.0100 | 0.3482 | 0.6337 | 0.8408 | 0.9413 | 0.9902 | ||
| 0.1 | 0.0100 | 0.3168 | 0.5891 | 0.8040 | 0.9197 | 0.9842 | ||
| c1 | ||||||||
| m | n | p | 0.85 | 0.885 | 0.9 | 0.915 | 0.93 | 0.96 |
| 6 | 70 | 0.05 | 0.0200 | 0.3276 | 0.5662 | 0.7644 | 0.8854 | 0.9685 |
| 0.075 | 0.0200 | 0.3163 | 0.5493 | 0.7479 | 0.8733 | 0.9633 | ||
| 0.1 | 0.0200 | 0.2982 | 0.5216 | 0.7199 | 0.8517 | 0.9533 | ||
| 90 | 0.05 | 0.0200 | 0.3910 | 0.6537 | 0.8409 | 0.9357 | 0.9868 | |
| 0.075 | 0.0200 | 0.3774 | 0.6358 | 0.8262 | 0.9268 | 0.9839 | ||
| 0.1 | 0.0200 | 0.3556 | 0.6059 | 0.8006 | 0.9102 | 0.9781 | ||
| 110 | 0.05 | 0.0200 | 0.4499 | 0.7248 | 0.8930 | 0.9639 | 0.9944 | |
| 0.075 | 0.0200 | 0.4344 | 0.7070 | 0.8807 | 0.9577 | 0.9929 | ||
| 0.1 | 0.0200 | 0.4095 | 0.6768 | 0.8586 | 0.9458 | 0.9897 | ||
| 7 | 70 | 0.05 | 0.0200 | 0.3262 | 0.5641 | 0.7623 | 0.8839 | 0.9679 |
| 0.075 | 0.0200 | 0.3128 | 0.5440 | 0.7426 | 0.8693 | 0.9615 | ||
| 0.1 | 0.0200 | 0.2917 | 0.5113 | 0.7091 | 0.8431 | 0.9491 | ||
| 90 | 0.05 | 0.0200 | 0.3893 | 0.6514 | 0.8391 | 0.9346 | 0.9864 | |
| 0.075 | 0.0200 | 0.3732 | 0.6301 | 0.8215 | 0.9238 | 0.9829 | ||
| 0.1 | 0.0200 | 0.3477 | 0.5948 | 0.7906 | 0.9035 | 0.9756 | ||
| 110 | 0.05 | 0.0200 | 0.4479 | 0.7226 | 0.8915 | 0.9632 | 0.9942 | |
| 0.075 | 0.0200 | 0.4296 | 0.7013 | 0.8767 | 0.9556 | 0.9924 | ||
| 0.1 | 0.0200 | 0.4004 | 0.6653 | 0.8498 | 0.9407 | 0.9882 | ||
| 8 | 70 | 0.05 | 0.0200 | 0.3248 | 0.5619 | 0.7602 | 0.8824 | 0.9672 |
| 0.075 | 0.0200 | 0.3093 | 0.5387 | 0.7374 | 0.8653 | 0.9597 | ||
| 0.1 | 0.0200 | 0.2854 | 0.5012 | 0.6984 | 0.8344 | 0.9446 | ||
| 90 | 0.05 | 0.0200 | 0.3875 | 0.6492 | 0.8372 | 0.9335 | 0.9861 | |
| 0.075 | 0.0200 | 0.3690 | 0.6244 | 0.8167 | 0.9207 | 0.9819 | ||
| 0.1 | 0.0200 | 0.3400 | 0.5838 | 0.7805 | 0.8965 | 0.9728 | ||
| 110 | 0.05 | 0.0200 | 0.4459 | 0.7203 | 0.8900 | 0.9624 | 0.9940 | |
| 0.075 | 0.0200 | 0.4248 | 0.6956 | 0.8726 | 0.9534 | 0.9918 | ||
| 0.1 | 0.0200 | 0.3915 | 0.6540 | 0.8408 | 0.9354 | 0.9866 | ||
| c1 | ||||||||
| m | n | p | 0.85 | 0.885 | 0.9 | 0.915 | 0.93 | 0.96 |
| 6 | 70 | 0.05 | 0.0500 | 0.4432 | 0.6648 | 0.8254 | 0.9158 | 0.9749 |
| 0.075 | 0.0500 | 0.4309 | 0.6492 | 0.8117 | 0.9061 | 0.9706 | ||
| 0.1 | 0.0500 | 0.4110 | 0.6233 | 0.7880 | 0.8887 | 0.9622 | ||
| 90 | 0.05 | 0.0500 | 0.5098 | 0.7425 | 0.8870 | 0.9546 | 0.9897 | |
| 0.075 | 0.0500 | 0.4958 | 0.7269 | 0.8754 | 0.9479 | 0.9874 | ||
| 0.1 | 0.0500 | 0.4729 | 0.7006 | 0.8549 | 0.9352 | 0.9827 | ||
| 110 | 0.05 | 0.0500 | 0.5687 | 0.8024 | 0.9268 | 0.9754 | 0.9958 | |
| 0.075 | 0.0500 | 0.5535 | 0.7876 | 0.9176 | 0.9709 | 0.9946 | ||
| 0.1 | 0.0500 | 0.5285 | 0.7622 | 0.9007 | 0.9621 | 0.9920 | ||
| 7 | 70 | 0.05 | 0.0500 | 0.4416 | 0.6629 | 0.8237 | 0.9146 | 0.9744 |
| 0.075 | 0.0500 | 0.4270 | 0.6443 | 0.8073 | 0.9029 | 0.9691 | ||
| 0.1 | 0.0500 | 0.4037 | 0.6136 | 0.7788 | 0.8817 | 0.9586 | ||
| 90 | 0.05 | 0.0500 | 0.5080 | 0.7405 | 0.8855 | 0.9538 | 0.9895 | |
| 0.075 | 0.0500 | 0.4914 | 0.7219 | 0.8717 | 0.9456 | 0.9866 | ||
| 0.1 | 0.0500 | 0.4645 | 0.6906 | 0.8468 | 0.9299 | 0.9807 | ||
| 110 | 0.05 | 0.0500 | 0.5668 | 0.8006 | 0.9257 | 0.9749 | 0.9956 | |
| 0.075 | 0.0500 | 0.5487 | 0.7829 | 0.9145 | 0.9694 | 0.9942 | ||
| 0.1 | 0.0500 | 0.5193 | 0.7524 | 0.8939 | 0.9584 | 0.9909 | ||
| 8 | 70 | 0.05 | 0.0500 | 0.4401 | 0.6609 | 0.8220 | 0.9134 | 0.9738 |
| 0.075 | 0.0500 | 0.4232 | 0.6394 | 0.8028 | 0.8997 | 0.9675 | ||
| 0.1 | 0.0500 | 0.3966 | 0.6040 | 0.7696 | 0.8746 | 0.9549 | ||
| 90 | 0.05 | 0.0500 | 0.5062 | 0.7386 | 0.8841 | 0.9529 | 0.9892 | |
| 0.075 | 0.0500 | 0.4870 | 0.7170 | 0.8678 | 0.9432 | 0.9858 | ||
| 0.1 | 0.0500 | 0.4563 | 0.6806 | 0.8386 | 0.9245 | 0.9784 | ||
| 110 | 0.05 | 0.0500 | 0.5648 | 0.7987 | 0.9245 | 0.9744 | 0.9955 | |
| 0.075 | 0.0500 | 0.5439 | 0.7781 | 0.9114 | 0.9678 | 0.9937 | ||
| 0.1 | 0.0500 | 0.5102 | 0.7426 | 0.8868 | 0.9544 | 0.9896 | ||
| c1 | ||||||||
| m | n | p | 0.85 | 0.885 | 0.9 | 0.915 | 0.93 | 0.96 |
| 6 | 70 | 0.05 | 0.0100 | 0.2114 | 0.4071 | 0.6057 | 0.7572 | 0.8961 |
| 0.075 | 0.0100 | 0.2026 | 0.3912 | 0.5864 | 0.7393 | 0.8842 | ||
| 0.1 | 0.0100 | 0.1888 | 0.3657 | 0.5546 | 0.7085 | 0.8628 | ||
| 90 | 0.05 | 0.0100 | 0.2613 | 0.4924 | 0.7010 | 0.8389 | 0.9435 | |
| 0.075 | 0.0100 | 0.2502 | 0.4741 | 0.6815 | 0.8231 | 0.9351 | ||
| 0.1 | 0.0100 | 0.2327 | 0.4443 | 0.6487 | 0.7954 | 0.9193 | ||
| 110 | 0.05 | 0.0100 | 0.3101 | 0.5679 | 0.7747 | 0.8935 | 0.9692 | |
| 0.075 | 0.0100 | 0.2969 | 0.5481 | 0.7563 | 0.8805 | 0.9635 | ||
| 0.1 | 0.0100 | 0.2759 | 0.5156 | 0.7245 | 0.8570 | 0.9525 | ||
| 7 | 70 | 0.05 | 0.0100 | 0.2103 | 0.4051 | 0.6032 | 0.7550 | 0.8946 |
| 0.075 | 0.0100 | 0.1999 | 0.3863 | 0.5803 | 0.7335 | 0.8803 | ||
| 0.1 | 0.0100 | 0.1839 | 0.3565 | 0.5427 | 0.6967 | 0.8542 | ||
| 90 | 0.05 | 0.0100 | 0.2599 | 0.4901 | 0.6985 | 0.8369 | 0.9425 | |
| 0.075 | 0.0100 | 0.2468 | 0.4683 | 0.6753 | 0.8180 | 0.9323 | ||
| 0.1 | 0.0100 | 0.2264 | 0.4334 | 0.6362 | 0.7845 | 0.9128 | ||
| 110 | 0.05 | 0.0100 | 0.3084 | 0.5654 | 0.7724 | 0.8919 | 0.9685 | |
| 0.075 | 0.0100 | 0.2928 | 0.5419 | 0.7503 | 0.8762 | 0.9616 | ||
| 0.1 | 0.0100 | 0.2684 | 0.5036 | 0.7123 | 0.8476 | 0.9478 | ||
| 8 | 70 | 0.05 | 0.0100 | 0.2091 | 0.4030 | 0.6008 | 0.7527 | 0.8931 |
| 0.075 | 0.0100 | 0.1972 | 0.3814 | 0.5743 | 0.7276 | 0.8763 | ||
| 0.1 | 0.0100 | 0.1791 | 0.3475 | 0.5310 | 0.6849 | 0.8454 | ||
| 90 | 0.05 | 0.0100 | 0.2585 | 0.4877 | 0.6961 | 0.8349 | 0.9414 | |
| 0.075 | 0.0100 | 0.2434 | 0.4627 | 0.6691 | 0.8128 | 0.9294 | ||
| 0.1 | 0.0100 | 0.2203 | 0.4228 | 0.6239 | 0.7735 | 0.9061 | ||
| 110 | 0.05 | 0.0100 | 0.3067 | 0.5629 | 0.7700 | 0.8902 | 0.9678 | |
| 0.075 | 0.0100 | 0.2887 | 0.5357 | 0.7443 | 0.8718 | 0.9596 | ||
| 0.1 | 0.0100 | 0.2611 | 0.4917 | 0.7000 | 0.8379 | 0.9428 | ||
| c1 | ||||||||
| m | n | p | 0.85 | 0.885 | 0.9 | 0.915 | 0.93 | 0.96 |
| 6 | 70 | 0.05 | 0.0200 | 0.2729 | 0.4727 | 0.6574 | 0.7903 | 0.9066 |
| 0.075 | 0.0200 | 0.2629 | 0.4565 | 0.6391 | 0.7738 | 0.8957 | ||
| 0.1 | 0.0200 | 0.2470 | 0.4304 | 0.6086 | 0.7454 | 0.8758 | ||
| 90 | 0.05 | 0.0200 | 0.3286 | 0.5576 | 0.7459 | 0.8637 | 0.9499 | |
| 0.075 | 0.0200 | 0.3163 | 0.5396 | 0.7280 | 0.8497 | 0.9423 | ||
| 0.1 | 0.0200 | 0.2968 | 0.5101 | 0.6976 | 0.8248 | 0.9279 | ||
| 110 | 0.05 | 0.0200 | 0.3814 | 0.6303 | 0.8123 | 0.9115 | 0.9730 | |
| 0.075 | 0.0200 | 0.3672 | 0.6114 | 0.7958 | 0.9003 | 0.9680 | ||
| 0.1 | 0.0200 | 0.3445 | 0.5801 | 0.7673 | 0.8797 | 0.9580 | ||
| 7 | 70 | 0.05 | 0.0200 | 0.2716 | 0.4707 | 0.6550 | 0.7882 | 0.9053 |
| 0.075 | 0.0200 | 0.2598 | 0.4515 | 0.6333 | 0.7685 | 0.8921 | ||
| 0.1 | 0.0200 | 0.2413 | 0.4208 | 0.5972 | 0.7344 | 0.8678 | ||
| 90 | 0.05 | 0.0200 | 0.3270 | 0.5553 | 0.7436 | 0.8619 | 0.9490 | |
| 0.075 | 0.0200 | 0.3125 | 0.5339 | 0.7223 | 0.8451 | 0.9397 | ||
| 0.1 | 0.0200 | 0.2898 | 0.4992 | 0.6860 | 0.8150 | 0.9220 | ||
| 110 | 0.05 | 0.0200 | 0.3795 | 0.6279 | 0.8102 | 0.9101 | 0.9724 | |
| 0.075 | 0.0200 | 0.3628 | 0.6055 | 0.7905 | 0.8965 | 0.9662 | ||
| 0.1 | 0.0200 | 0.3363 | 0.5684 | 0.7561 | 0.8713 | 0.9538 | ||
| 8 | 70 | 0.05 | 0.0200 | 0.2703 | 0.4686 | 0.6527 | 0.7861 | 0.9039 |
| 0.075 | 0.0200 | 0.2567 | 0.4465 | 0.6275 | 0.7631 | 0.8884 | ||
| 0.1 | 0.0200 | 0.2357 | 0.4114 | 0.5859 | 0.7234 | 0.8597 | ||
| 90 | 0.05 | 0.0200 | 0.3254 | 0.5530 | 0.7414 | 0.8602 | 0.9481 | |
| 0.075 | 0.0200 | 0.3088 | 0.5283 | 0.7166 | 0.8404 | 0.9371 | ||
| 0.1 | 0.0200 | 0.2829 | 0.4885 | 0.6744 | 0.8050 | 0.9158 | ||
| 110 | 0.05 | 0.0200 | 0.3777 | 0.6255 | 0.8081 | 0.9087 | 0.9718 | |
| 0.075 | 0.0200 | 0.3584 | 0.5995 | 0.7851 | 0.8927 | 0.9644 | ||
| 0.1 | 0.0200 | 0.3283 | 0.5569 | 0.7450 | 0.8628 | 0.9493 | ||
| c1 | ||||||||
| m | n | p | 0.85 | 0.885 | 0.9 | 0.915 | 0.93 | 0.96 |
| 6 | 70 | 0.05 | 0.0500 | 0.3788 | 0.5717 | 0.7294 | 0.8346 | 0.9210 |
| 0.075 | 0.0500 | 0.3674 | 0.5560 | 0.7131 | 0.8205 | 0.9114 | ||
| 0.1 | 0.0500 | 0.3493 | 0.5301 | 0.6856 | 0.7959 | 0.8938 | ||
| 90 | 0.05 | 0.0500 | 0.4398 | 0.6518 | 0.8059 | 0.8958 | 0.9585 | |
| 0.075 | 0.0500 | 0.4266 | 0.6351 | 0.7908 | 0.8843 | 0.9520 | ||
| 0.1 | 0.0500 | 0.4053 | 0.6074 | 0.7646 | 0.8637 | 0.9396 | ||
| 110 | 0.05 | 0.0500 | 0.4950 | 0.7171 | 0.8608 | 0.9342 | 0.9780 | |
| 0.075 | 0.0500 | 0.4804 | 0.7004 | 0.8474 | 0.9253 | 0.9738 | ||
| 0.1 | 0.0500 | 0.4566 | 0.6723 | 0.8238 | 0.9088 | 0.9654 | ||
| 7 | 70 | 0.05 | 0.0500 | 0.3773 | 0.5697 | 0.7273 | 0.8328 | 0.9199 |
| 0.075 | 0.0500 | 0.3639 | 0.5510 | 0.7079 | 0.8159 | 0.9082 | ||
| 0.1 | 0.0500 | 0.3427 | 0.5205 | 0.6751 | 0.7863 | 0.8867 | ||
| 90 | 0.05 | 0.0500 | 0.4381 | 0.6496 | 0.8040 | 0.8944 | 0.9577 | |
| 0.075 | 0.0500 | 0.4225 | 0.6298 | 0.7859 | 0.8805 | 0.9498 | ||
| 0.1 | 0.0500 | 0.3975 | 0.5970 | 0.7545 | 0.8554 | 0.9344 | ||
| 110 | 0.05 | 0.0500 | 0.4931 | 0.7150 | 0.8591 | 0.9331 | 0.9775 | |
| 0.075 | 0.0500 | 0.4758 | 0.6951 | 0.8430 | 0.9223 | 0.9723 | ||
| 0.1 | 0.0500 | 0.4479 | 0.6616 | 0.8145 | 0.9020 | 0.9618 | ||
| 8 | 70 | 0.05 | 0.0500 | 0.3758 | 0.5677 | 0.7252 | 0.8310 | 0.9187 |
| 0.075 | 0.0500 | 0.3604 | 0.5461 | 0.7027 | 0.8113 | 0.9050 | ||
| 0.1 | 0.0500 | 0.3362 | 0.5111 | 0.6647 | 0.7766 | 0.8795 | ||
| 90 | 0.05 | 0.0500 | 0.4364 | 0.6475 | 0.8021 | 0.8930 | 0.9569 | |
| 0.075 | 0.0500 | 0.4184 | 0.6246 | 0.7810 | 0.8767 | 0.9475 | ||
| 0.1 | 0.0500 | 0.3899 | 0.5868 | 0.7443 | 0.8470 | 0.9290 | ||
| 110 | 0.05 | 0.0500 | 0.4912 | 0.7129 | 0.8574 | 0.9320 | 0.9770 | |
| 0.075 | 0.0500 | 0.4712 | 0.6897 | 0.8386 | 0.9193 | 0.9708 | ||
| 0.1 | 0.0500 | 0.4393 | 0.6510 | 0.8051 | 0.8951 | 0.9579 | ||
| c1 | ||||||||
| m | n | p | 0.85 | 0.885 | 0.9 | 0.915 | 0.93 | 0.96 |
| 6 | 70 | 0.05 | 0.0100 | 0.1756 | 0.3361 | 0.5095 | 0.6552 | 0.8072 |
| 0.075 | 0.0100 | 0.1680 | 0.3218 | 0.4905 | 0.6352 | 0.7903 | ||
| 0.1 | 0.0100 | 0.1562 | 0.2990 | 0.4595 | 0.6016 | 0.7609 | ||
| 90 | 0.05 | 0.0100 | 0.2187 | 0.4141 | 0.6065 | 0.7506 | 0.8800 | |
| 0.075 | 0.0100 | 0.2090 | 0.3970 | 0.5860 | 0.7314 | 0.8662 | ||
| 0.1 | 0.0100 | 0.1937 | 0.3695 | 0.5521 | 0.6984 | 0.8415 | ||
| 110 | 0.05 | 0.0100 | 0.2614 | 0.4856 | 0.6863 | 0.8206 | 0.9253 | |
| 0.075 | 0.0100 | 0.2496 | 0.4665 | 0.6658 | 0.8033 | 0.9147 | ||
| 0.1 | 0.0100 | 0.2311 | 0.4355 | 0.6311 | 0.7730 | 0.8950 | ||
| 7 | 70 | 0.05 | 0.0100 | 0.1746 | 0.3343 | 0.5070 | 0.6527 | 0.8051 |
| 0.075 | 0.0100 | 0.1657 | 0.3174 | 0.4845 | 0.6288 | 0.7848 | ||
| 0.1 | 0.0100 | 0.1520 | 0.2908 | 0.4481 | 0.5890 | 0.7495 | ||
| 90 | 0.05 | 0.0100 | 0.2174 | 0.4119 | 0.6039 | 0.7482 | 0.8783 | |
| 0.075 | 0.0100 | 0.2060 | 0.3916 | 0.5795 | 0.7252 | 0.8617 | ||
| 0.1 | 0.0100 | 0.1883 | 0.3595 | 0.5395 | 0.6858 | 0.8316 | ||
| 110 | 0.05 | 0.0100 | 0.2598 | 0.4832 | 0.6837 | 0.8184 | 0.9240 | |
| 0.075 | 0.0100 | 0.2460 | 0.4605 | 0.6592 | 0.7977 | 0.9111 | ||
| 0.1 | 0.0100 | 0.2245 | 0.4241 | 0.6180 | 0.7611 | 0.8870 | ||
| 8 | 70 | 0.05 | 0.0100 | 0.1737 | 0.3324 | 0.5046 | 0.6501 | 0.8030 |
| 0.075 | 0.0100 | 0.1634 | 0.3130 | 0.4786 | 0.6224 | 0.7793 | ||
| 0.1 | 0.0100 | 0.1479 | 0.2829 | 0.4370 | 0.5765 | 0.7380 | ||
| 90 | 0.05 | 0.0100 | 0.2162 | 0.4097 | 0.6012 | 0.7458 | 0.8765 | |
| 0.075 | 0.0100 | 0.2030 | 0.3864 | 0.5731 | 0.7190 | 0.8571 | ||
| 0.1 | 0.0100 | 0.1830 | 0.3498 | 0.5270 | 0.6731 | 0.8215 | ||
| 110 | 0.05 | 0.0100 | 0.2583 | 0.4807 | 0.6811 | 0.8163 | 0.9227 | |
| 0.075 | 0.0100 | 0.2424 | 0.4546 | 0.6526 | 0.7920 | 0.9075 | ||
| 0.1 | 0.0100 | 0.2181 | 0.4130 | 0.6050 | 0.7491 | 0.8786 | ||
| c1 | ||||||||
| m | n | p | 0.85 | 0.885 | 0.9 | 0.915 | 0.93 | 0.96 |
| 6 | 70 | 0.05 | 0.0200 | 0.2305 | 0.3977 | 0.5629 | 0.6939 | 0.8230 |
| 0.075 | 0.0200 | 0.2217 | 0.3827 | 0.5443 | 0.6749 | 0.8071 | ||
| 0.1 | 0.0200 | 0.2077 | 0.3587 | 0.5137 | 0.6430 | 0.7792 | ||
| 90 | 0.05 | 0.0200 | 0.2796 | 0.4776 | 0.6560 | 0.7826 | 0.8911 | |
| 0.075 | 0.0200 | 0.2687 | 0.4603 | 0.6366 | 0.7649 | 0.8783 | ||
| 0.1 | 0.0200 | 0.2513 | 0.4322 | 0.6042 | 0.7343 | 0.8552 | ||
| 110 | 0.05 | 0.0200 | 0.3269 | 0.5486 | 0.7304 | 0.8461 | 0.9329 | |
| 0.075 | 0.0200 | 0.3140 | 0.5298 | 0.7115 | 0.8305 | 0.9231 | ||
| 0.1 | 0.0200 | 0.2935 | 0.4990 | 0.6791 | 0.8030 | 0.9050 | ||
| 7 | 70 | 0.05 | 0.0200 | 0.2293 | 0.3958 | 0.5605 | 0.6915 | 0.8210 |
| 0.075 | 0.0200 | 0.2189 | 0.3780 | 0.5384 | 0.6689 | 0.8019 | ||
| 0.1 | 0.0200 | 0.2027 | 0.3499 | 0.5024 | 0.6309 | 0.7683 | ||
| 90 | 0.05 | 0.0200 | 0.2782 | 0.4754 | 0.6535 | 0.7804 | 0.8895 | |
| 0.075 | 0.0200 | 0.2653 | 0.4549 | 0.6304 | 0.7592 | 0.8741 | ||
| 0.1 | 0.0200 | 0.2451 | 0.4219 | 0.5920 | 0.7225 | 0.8459 | ||
| 110 | 0.05 | 0.0200 | 0.3252 | 0.5462 | 0.7280 | 0.8441 | 0.9317 | |
| 0.075 | 0.0200 | 0.3100 | 0.5239 | 0.7054 | 0.8254 | 0.9199 | ||
| 0.1 | 0.0200 | 0.2861 | 0.4876 | 0.6668 | 0.7921 | 0.8975 | ||
| 8 | 70 | 0.05 | 0.0200 | 0.2282 | 0.3938 | 0.5581 | 0.6891 | 0.8190 |
| 0.075 | 0.0200 | 0.2163 | 0.3734 | 0.5326 | 0.6628 | 0.7967 | ||
| 0.1 | 0.0200 | 0.1979 | 0.3414 | 0.4912 | 0.6189 | 0.7573 | ||
| 90 | 0.05 | 0.0200 | 0.2768 | 0.4731 | 0.6510 | 0.7781 | 0.8879 | |
| 0.075 | 0.0200 | 0.2619 | 0.4495 | 0.6243 | 0.7534 | 0.8698 | ||
| 0.1 | 0.0200 | 0.2390 | 0.4119 | 0.5799 | 0.7107 | 0.8364 | ||
| 110 | 0.05 | 0.0200 | 0.3236 | 0.5438 | 0.7256 | 0.8422 | 0.9305 | |
| 0.075 | 0.0200 | 0.3061 | 0.5180 | 0.6993 | 0.8203 | 0.9165 | ||
| 0.1 | 0.0200 | 0.2790 | 0.4764 | 0.6545 | 0.7811 | 0.8898 | ||
| c1 | ||||||||
| m | n | p | 0.85 | 0.885 | 0.9 | 0.915 | 0.93 | 0.96 |
| 6 | 70 | 0.05 | 0.0500 | 0.3280 | 0.4945 | 0.6407 | 0.7481 | 0.8453 |
| 0.075 | 0.0500 | 0.3177 | 0.4792 | 0.6232 | 0.7311 | 0.8308 | ||
| 0.1 | 0.0500 | 0.3013 | 0.4544 | 0.5943 | 0.7021 | 0.8052 | ||
| 90 | 0.05 | 0.0500 | 0.3838 | 0.5733 | 0.7253 | 0.8260 | 0.9064 | |
| 0.075 | 0.0500 | 0.3715 | 0.5565 | 0.7080 | 0.8107 | 0.8951 | ||
| 0.1 | 0.0500 | 0.3519 | 0.5289 | 0.6786 | 0.7840 | 0.8744 | ||
| 110 | 0.05 | 0.0500 | 0.4351 | 0.6403 | 0.7902 | 0.8796 | 0.9432 | |
| 0.075 | 0.0500 | 0.4213 | 0.6228 | 0.7739 | 0.8666 | 0.9347 | ||
| 0.1 | 0.0500 | 0.3991 | 0.5937 | 0.7457 | 0.8434 | 0.9188 | ||
| 7 | 70 | 0.05 | 0.0500 | 0.3267 | 0.4925 | 0.6384 | 0.7460 | 0.8435 |
| 0.075 | 0.0500 | 0.3145 | 0.4744 | 0.6177 | 0.7256 | 0.8261 | ||
| 0.1 | 0.0500 | 0.2953 | 0.4453 | 0.5834 | 0.6910 | 0.7952 | ||
| 90 | 0.05 | 0.0500 | 0.3822 | 0.5711 | 0.7231 | 0.8240 | 0.9050 | |
| 0.075 | 0.0500 | 0.3677 | 0.5512 | 0.7024 | 0.8057 | 0.8913 | ||
| 0.1 | 0.0500 | 0.3448 | 0.5187 | 0.6675 | 0.7735 | 0.8660 | ||
| 110 | 0.05 | 0.0500 | 0.4333 | 0.6380 | 0.7882 | 0.8780 | 0.9421 | |
| 0.075 | 0.0500 | 0.4170 | 0.6172 | 0.7686 | 0.8624 | 0.9318 | ||
| 0.1 | 0.0500 | 0.3909 | 0.5828 | 0.7349 | 0.8341 | 0.9122 | ||
| 8 | 70 | 0.05 | 0.0500 | 0.3254 | 0.4905 | 0.6362 | 0.7438 | 0.8417 |
| 0.075 | 0.0500 | 0.3114 | 0.4697 | 0.6122 | 0.7201 | 0.8213 | ||
| 0.1 | 0.0500 | 0.2895 | 0.4364 | 0.5727 | 0.6799 | 0.7850 | ||
| 90 | 0.05 | 0.0500 | 0.3806 | 0.5690 | 0.7209 | 0.8221 | 0.9036 | |
| 0.075 | 0.0500 | 0.3640 | 0.5460 | 0.6969 | 0.8007 | 0.8875 | ||
| 0.1 | 0.0500 | 0.3378 | 0.5087 | 0.6564 | 0.7630 | 0.8575 | ||
| 110 | 0.05 | 0.0500 | 0.4315 | 0.6358 | 0.7861 | 0.8764 | 0.9411 | |
| 0.075 | 0.0500 | 0.4127 | 0.6117 | 0.7633 | 0.8580 | 0.9289 | ||
| 0.1 | 0.0500 | 0.3830 | 0.5721 | 0.7240 | 0.8246 | 0.9053 | ||
References
- Juran, J.M. Juran’s Quality Control Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Kane, V.E. Process capability indices. J. Qual. Technol. 1986, 18, 41–52. [Google Scholar] [CrossRef]
- Hsiang, T.C.; Taguchi, G. A tutorial on quality control and assurance—The Taguchi mthods. In Proceedings of the Joint Meetings of the American Statistical Association—ASA Annual Meeting, Las Vegas, NV, USA, 5–8 August 1985; p. 188. [Google Scholar]
- Pearn, W.L.; Kotz, S.; Johnson, N.L. Distributional and inferential properties of process capability indices. J. Qual. Technol. 1992, 24, 216–231. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley and Sons Inc.: New York, NY, USA, 1985. [Google Scholar]
- Tong, L.I.; Chen, K.S.; Chen, H.T. Statistical testing for assessing the performance of lifetime index of electronic components with exponential distribution. Int. J. Qual. Reliab. Manag. 2002, 19, 812–824. [Google Scholar] [CrossRef]
- Aggarwala, R. Progressive interval censoring: Some mathematical results with applications to inference. Commun. Stat.-Theory Methods 2001, 30, 1921–1935. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods and Applications; Birkhäuser: Boston, MA, USA, 2000. [Google Scholar]
- Hong, C.W.; Lee, W.C.; Wu, J.W. Computational Procedure of Performance Assessment of Lifetime Index of Products for the Weibull Distribution with the Progressive First-Failure-Censored Sampling Plan. J. Appl. Math. 2012, 2012, 717184. [Google Scholar] [CrossRef]
- Wu, J.W.; Lee, W.C.; Lin, L.S.; Hong, M.L. Bayesian test of lifetime performance index for exponential products based on the progressively type II right censored sample. J. Quant. Manag. 2011, 8, 57–77. [Google Scholar]
- Sanjel, D.; Balakrishnan, N. A Laguerre polynomial approximation for a goodness-of-fit test for exponential distribution based on progressively censored data. J. Stat. Comput. Simul. 2008, 78, 503–513. [Google Scholar] [CrossRef]
- Lee, W.C.; Wu, J.W.; Hong, C.W. Assessing the lifetime performance index of products with the exponential distribution under progressively type II right censored samples. J. Comput. Appl. Math. 2009, 231, 648–656. [Google Scholar] [CrossRef]
- Lee, H.M.; Wu, J.W.; Lei, C.L. Assessing the Lifetime Performance Index of Exponential Products With Step-Stress Accelerated Life-Testing Data. IEEE Trans. Reliab. 2013, 62, 296–304. [Google Scholar] [CrossRef]
- Wu, S.F.; Lin, Y.T.; Chang, W.J.; Chang, C.W.; Lin, C. A computational algorithm for the evaluation on the lifetime performance index of products with Rayleigh distribution under progressive type I interval censoring. J. Comput. Appl. Math. 2018, 328, 508–519. [Google Scholar] [CrossRef]
- Wu, S.F.; Liu, T.H.; Lai, Y.H.; Chang, W.T. A study on the experimental design for the lifetime performance index of Rayleigh lifetime distribution under progressive type I interval censoring. Mathematics 2022, 10, 517. [Google Scholar] [CrossRef]
- Wu, S.F.; Wu, Y.C.; Wu, C.H.; Chang, W.T. Experimental design for the lifetime performance Index of Weibull products based on the progressive type I interval censored sample. Symmetry 2021, 13, 1691. [Google Scholar] [CrossRef]
- Wu, S.F.; Song, M.Z. The experimental design for the progressive type I interval censoring on the lifetime performance index of Chen lifetime distribution. Mathematics 2023, 11, 1554. [Google Scholar] [CrossRef]
- Guillermo, M.F.; Roger, T.F.; Marvin, J.N. Likelihood-Based Inference for the Asymmetric Beta-Skew Alpha-Power Distribution. Symmetry 2020, 12, 613. [Google Scholar]
- Seong, Y.; Lee, K. Exact Likelihood Inference for Parameter of Exponential Distribution under Combined Generalized Progressive Hybrid Censoring Scheme. Symmetry 2022, 14, 1764. [Google Scholar] [CrossRef]
- Jäntschi, L. Binomial Distributed Data Confidence Interval Calculation: Formulas, Algorithms and Examples. Symmetry 2022, 14, 1104. [Google Scholar] [CrossRef]
- Félix, A.A.; Hortensia, R.C.; Marcos, M.C. A comparison of some confidence intervals for a binomial proportion based on a shrinkage estimator. Open Math. 2023, 21, 20220588. [Google Scholar]
- Caroni, C. Modeling the reliability of ball bearings. J. Stat. Educ. 2002, 10, 1–8. [Google Scholar] [CrossRef][Green Version]
- Gail, M.H.; Gastwirth, J.L. A sacle-free goodness-of-fit Test for the Exponential Distribution Based on the Gini Statistic. J. R. Stat. Soc. Ser. B (Methodol.) 1978, 40, 350–357. [Google Scholar]
- Aarset, M.V. How to identify a bathtub hazard rate. IEEE Trans. Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.-F.; Huang, P.-T. The Testing Procedure for the Overall Lifetime Performance Index of Rayleigh Products in Multiple Production Lines Based on the Progressive Type I Interval Censored Sample. Symmetry 2024, 16, 195. https://doi.org/10.3390/sym16020195
Wu S-F, Huang P-T. The Testing Procedure for the Overall Lifetime Performance Index of Rayleigh Products in Multiple Production Lines Based on the Progressive Type I Interval Censored Sample. Symmetry. 2024; 16(2):195. https://doi.org/10.3390/sym16020195
Chicago/Turabian StyleWu, Shu-Fei, and Pei-Tzu Huang. 2024. "The Testing Procedure for the Overall Lifetime Performance Index of Rayleigh Products in Multiple Production Lines Based on the Progressive Type I Interval Censored Sample" Symmetry 16, no. 2: 195. https://doi.org/10.3390/sym16020195
APA StyleWu, S.-F., & Huang, P.-T. (2024). The Testing Procedure for the Overall Lifetime Performance Index of Rayleigh Products in Multiple Production Lines Based on the Progressive Type I Interval Censored Sample. Symmetry, 16(2), 195. https://doi.org/10.3390/sym16020195







