Abstract
Today, rope access systems (RASs) and fall arrest systems (FASs) incorporate significant technological innovations. This research aims to determine the safest knot to be used in RASs. The most secure knots are those that leave the most resistance in the rope. Static laboratory tests, followed by an extensive statistical analysis of the obtained data, were carried out under controlled conditions. Five types of anchor knots were selected and studied using three rope models with similar diameters, and we analysed the symmetrical versions in the dextrorotational direction. Thirty break tests were performed for each rope model. The total number of breakage tests was 90. The double overhand knot proved to be the safest knot with an average efficiency of 61.82%. A better understanding of the behaviour of knots and their correct use in FASs will be key to accident prevention.
1. Introduction
The continuous improvement of safety standards to prevent accidents is a legal and moral obligation. Accidents have socioeconomic impacts that affect business, commerce, education, and public policy [1,2]. Improving the elements of individual fall protection systems will have positive effects on the number of serious accidents. Falls from a height are one of the leading causes of fatalities. In the United States (US) construction industry, these accidents caused 5701 fatalities between 2003 and 2018, with 1102 fatalities in 2019, the highest value since 2011 [3]. According to the data acquired by the Center for Construction Research and Training in 2018, the US construction industry reported 633 fatalities and 51 hospitalizations [4,5]. Safe Work Australia compiles deaths due to work-related injuries, specifically those caused by falls from a height. In 2021, the organisation determined that such falls were the third highest cause of occupational mortality, with 22 deaths accounting for 11% of all fatalities [6]. For 2020, Spanish statistics reflect similar data to those of Australia, with 86 deaths due to falls, representing 11.39% of the total number of fatal accidents [7]. According to the Health and Safety Executive in Construction in Great Britain, falls from a height constitute the main cause of mortality and represent 50% of all fatal injuries [8].
Fall arrest systems (FASs) are included in the European Standard (EN) 363 [9]. Rope access systems (RASs) are FASs in which the worker is positioned by ropes at the operation point. Ropes are the main element of an RAS. Figure 1 represents the main RAS components. Using a carabiner (1 in Figure 1), the knots connect the rope to the structure (2 in Figure 1) [10,11,12,13,14,15,16,17].
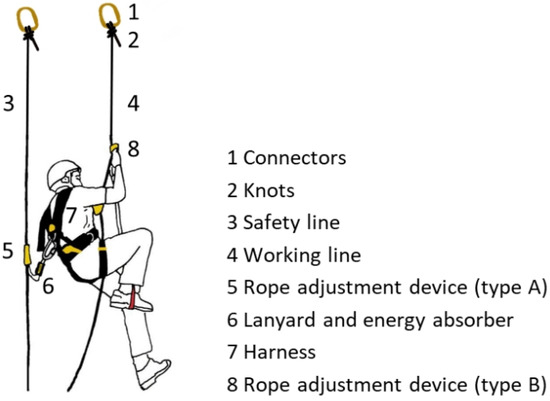
Figure 1.
Example of an RAS. Figure according to the standard in [9].
There are more than 3800 types of knots [18]. Some knots have been studied by other authors, but these previous works have serious shortcomings in terms of the methodology used and the treatment of the obtained data. Moreover, previously analysed knots are those used in sports. As a result, some knots that could be used as anchor knots, such as the double overhand knot, have not yet been studied [19,20]. Advances in technology and the use of new materials in rope manufacturing mean that the effects of knot selection on these new types of rope need to be re-examined [21,22,23,24]. The overhand sling, figure eight sling, figure nine sling, clove hitch, and double overhand sling are anchoring knots. These knots are used in rope access systems in the construction sector for the maintenance of skyscrapers, power pylons, dams, and unique high-rise projects [10,11,12,25,26,27,28,29].
Knots reduce the static breaking strain of ropes [18,19,29,30,31,32,33] by 35–50%, depending on the diameter and type of rope and knot. A summary of the wide range of results in this field [34,35,36,37] is shown in Figure 2. This lack of homogeneity in the results can be explained by the fact that some authors did not consider important test parameters such as the loading rate, the acclimatisation of the specimens, the need for loading cycles prior to failure, or the minimum number of tests.
Authors such as Boron, Drohan, Merchant, Diamond, and Gómez [25,34,38,39,40] used the manufacturer’s breaking strength data in their studies. Manufacturers provide a minimum knotless tensile strength of the rope. However, the data provided by manufacturers are usually much lower than the real breaking strength. Brown, Milne, Aldazábal, and Simon [26,35,36,41] have determined this value experimentally using tests in which the real value of the break is obtained.
To obtain reliable results in static tests, it is important to establish a low loading speed close to the equilibrium, since in quasistatic and dynamic tests, it cannot be assumed that the ropes exhibit a homogeneous regular behaviour. It is necessary to perform the previous loading cycles in tests with new ropes to simulate their use and achieve more homogeneous mechanical response behaviours in both the core and sheath assembly.
To evaluate the loss of static rope strength due to the presence of knots, the efficiency term (η) of a knot is used. This term is defined as the quotient of the breaking load of the rope with a knot (x) and the breaking load of the rope without a knot (y), the magnitude of which is usually expressed as a percentage via Equation (1):
Measuring the efficiency as a function of knotless rope strength stems from work by Šimon [41] (p. 404), who, for the first time, proposed the following concept: “Loop knot efficiency is not a constant, but depends at least on the static breaking strength of a rope”. In addition, manufacturers indicate a minimum knotless tensile strength for their ropes, but the provided data are usually much lower than the actual breaking strength. Manufacturers also do not provide static breaking strength values for ropes with different knots. Consequently, the efficiency value must be obtained in the laboratory for each rope and knot assembly. Figure 2 shows the average efficiency values of the main anchoring knots obtained from the studies carried out in the last two decades. The technological progress of these materials remains rapid and constant.
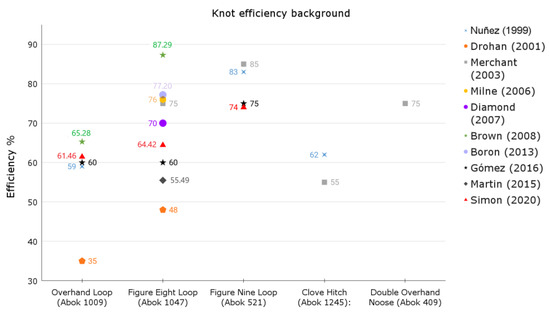

Figure 2.
Efficiencies () of various knots obtained by authors in previous research [25,26,29,34,35,38,39,40,41,42].
Table 1 provides a schematic overview of the main characteristics of previous investigations, including the type of rope, the standard used, the experimental procedure, and the source of the knotless breaking load.

Table 1.
Main methodologies and experimental procedures used with knots.
From a strictly statistical perspective, several authors stated that tests should be repeated at least five times for each specimen, especially for systems that affect employee safety and life [35,41]. These recommendations are in line with the American NFPA 1 [49]. Drohan [34] stressed the importance of conditioning samples 72 h prior to testing and performed an atmospheric control test at 20 °C under 65% humidity, as specified in ISO 139:2005/A1 [29,42,53]. Some authors consider the number of cycles before the breaking load to have a significant effect on the obtained results. Baszczyński [54] observed significant differences between the load-elongation characteristics obtained in the first load cycle and those obtained in subsequent cycles and concluded that the organisation of the textile structure was more strongly affected during the first load. After working with new ropes, Gómez [40] concluded that ropes break at lower loads when new.
In short, the required information to assess the most appropriate knot for use in RASs is lacking. The aim of this research was to carry out rigorous laboratory tests considering the variables that affect the test: humidity, temperature, speed, load cycles, and sample conditioning. Complemented by a rigorous statistical study of five breaks per configuration, including knotless breaks, reliable data were obtained to determine which knot is the safest anchor knot for FASs and RASs. Selecting the correct anchorage knot significantly contributes to safety when working at a height and reduces the probability of a fall-from-height accident.
2. Materials and Methods
2.1. Ropes and Test Samples
The regulations applicable to ropes used in RASs in Europe are Directive 2001/45/EC of the European Parliament and of the Council of the European Union [55]. As personal protective equipment (PPE), ropes are also affected by EU Regulation 2016/425 of the Official Journal of the European Union [56]. RAS ropes are products with an international standard certification. European regulations for low-stretch kernmantle ropes and dynamic ropes establish technical specifications that provide a presumption of conformity for applying the CE mark according to EU Regulation 2016/425 on PPE [56]. Compliance with the technical requirements of this regulation presupposes compliance with the essential safety requirements of Directive 2001/45/EC [55].
Three types of rope were selected from different manufacturers with international reputations in the RAS sector. Table 2 shows the main technical characteristics of the tested ropes. All ropes were new, low-elongation kernmantle type A ropes in accordance with EN 1891 [43]. All ropes were made from synthetic textile fibres and consisted of a braided core and sheath with a low elongation coefficient. These are the types of ropes used in RASs [10,12,25,26,27,29,41,57]. The range of diameters was between 10.5 and 11 mm, which is the range commonly used in RASs and allows for a reliable comparison of results. The textile materials used for these ropes were polyamide (PA) and polyester (PES) with low-stretch core sheathing [53]. Notably, the λ rope has double normative certification and complies with the requirements of EN 1891 [43] for low-stretch core ropes and EN 892 [46] for dynamic ropes. A study on this type of rope with double certification is, therefore, a milestone. Types A and Ψ are certified by the National Fire Protection Association (NFPA), the Eurasian Economic Union (EAC), and the International Mountaineering and Climbing Association (UIAA) [49,58,59].

Table 2.
Technical specifications in accordance with the manufacturer’s user manual.
The tested specimens (Figure 3) were made using sections of the three rope models. Six specimens were taken from the same rope sample, with five for knot tests and one for knotless tests. The lengths of the five samples with knots ranged from a minimum of 2.5 m to a maximum of 4 m, depending on the type of knot. In this way, the rope could be wound around the test bollard three times. The knot was tied at one end of the rope, while the other end of the rope was left untied. In the test specimen reserved for evaluating the resistance of the rope, no end or knot type was made. Instead, the rope was simply coiled around the two bollards.
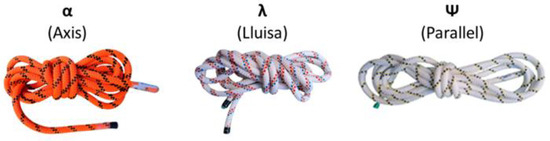
Figure 3.
Rope models used during the tests.
2.2. Knots
Based on the available documentation, we tested five of the most commonly used loading knots (Figure 4) in RASs [11,38]: the figure nine loop, figure eight loop, double overhand noose, clove hitch, and overhand loop. All knots were configured using the symmetrical dextrorotatory versions (see Figure 5).

Figure 4.
Tested knots.
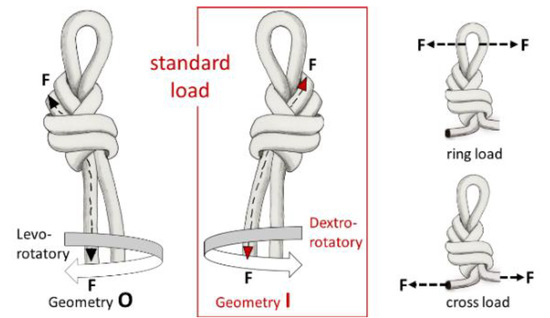
Figure 5.
Possible loading of a knot, and the symmetrical realisation of a loop knot.
The knots in this paper were studied by applying a load longitudinally to the rope axis (standard load), as this is how knots are loaded when used in RASs. From a geometrical perspective, each knot has two symmetrical versions in its construction. In this study, we examine the I-geometry (see Figure 5, red centre); i.e., a symmetrical version of knot construction with the loops in a dextrorotational direction. A well-made knot is particularly important to ensure the homogeneity of the results and draw the correct conclusions. To this end, all knots in this work were made by the same person who is an expert in fall protection systems, a specialist in RASs, a firefighter, and a rescuer with more than 30 years of experience.
2.3. Experiment Setup and Procedure
The rupture tests described in this paper were carried out at the Geotextiles and Geosynthetics Laboratory of the AITEX/Research and Innovation Centre. An INSTRON model 5984HK8242 dynamometer with a maximum capacity of 150 kN was used. This machine allows both the force and displacement to be controlled (Figure 6). The force was recorded with an INSTRON load cell, using a full scale of 150 kN and a measurement frequency of 50 Hz. Data management was carried out using Bluehill software (Bluehill version: Universal V4.15), also from INSTRON (INSTRON version: 5984). The knotless rope tests were carried out using a Zwick Roell Z600E (Manufacturer: Instron, City: Barcelona, Country: Spain) maximum-capacity dynamometer with an integrated cell. A bollard (13 cm in diameter) was used to hold the free end (without a knot or sewn end). The free end was wrapped around the bollard at least three times to ensure sufficient friction between the rope and the bollard to prevent the rope from slipping (Figure 6a,b). The last section of rope was secured with a clamp stopper to prevent slippage. The testing machine and a croquis of the bollard used are shown in Figure 6. The smaller the diameter, the higher the stress concentration; thus, a smaller diameter may cause a breaking point to contact the bollard. To measure the tensile breakage correctly, the rope should theoretically break when the first loaded knot becomes strangulated [11,26,32,50]. If the knot breaks on contact with the bollard, the test method is incorrect, and the true tensile break is not obtained. Once the specimen has been conditioned, the knot is installed in the loading gantry. Then, the cylinder is inserted through the core of the knot and secured with a locking mechanism. The setup and procedure of the experiment are shown in the flow chart in Figure 6c.
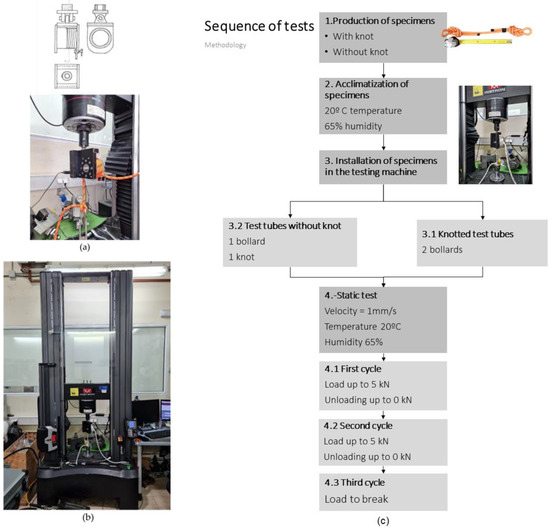
Figure 6.
Encounter between the terminals and a bollard (a). Detail of the test machine (b). Test sequence (c).
The test procedure consisted of placing a specimen in the test gantry and breaking it. Five breaks were made for each knot type and rope model selected. To acclimatise them, the samples were placed in a conditioning chamber for 72 h prior to testing. A temperature of 20.0 °C (±2.0 °C) and relative humidity of 65% (±4.0%) were maintained in the room in which the tests were carried out, as specified in ISO 139:2005/A1 [53]. In all tests carried out, the load was applied at a speed of 1 mm/s, which is the maximum speed allowed by the EN 364 [60]. The test specimens were 40 cm in length between the bollards.
Although the EN 364 standard [60] specifies a few tests (between two and four) for each set of samples, the most restrictive criterion established by the NFPA 1 standard [49] was used in this research. This standard states that at least five tests must be carried out whenever the lives of workers are at stake. The requirements of ISO 7500-1 [61] were also considered. Two bollards with identical characteristics were used to determine the knotless rope strength. Each end of the rope was wound onto the bollards. The sample was placed in the tester (Figure 6). The diameter of the bollard holding the knotless rope was 13 cm. A smaller diameter can cause the rope to break when it encounters the bollard, because the smaller the diameter, the higher the stress concentration. To measure the tensile breakage correctly, the rope should theoretically break when the loaded knot becomes strangulated for the first time [11,26,32,50]. After conditioning the sample, the knot was placed on the loading gantry. Then, the cylinder was inserted through the coke of the knot and secured with a pin. The terminal was wrapped around the bollard three times. The terminal stop was secured to prevent any slippage (Figure 6). Each specimen was subjected to three cycles: two previous loading/unloading cycles up to 5 kN and a final cycle until breaking. Figure 7 shows the cycles each specimen was subjected to. Previous authors, such as Boron, Martin, Drohan, and Aldazabal [25,29,34,36] did not carry out preloading cycles in their tests. However, these preload cycles were performed by Milne [35]. Šimon [41] explains that this omission was due to using testing ropes that were not new. In the present research, these prestress cycles were essential, as new ropes were used.
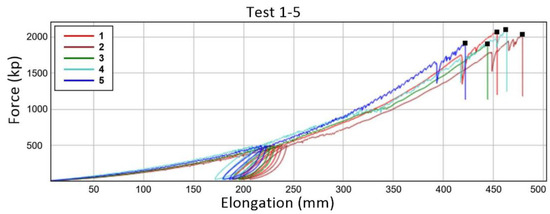
Figure 7.
Results obtained for the knot overland loop with rope α.
Overall, three different rope models were used: five sets of knotted tests and a final set of knotless tests. Each test series consisted of five breaks. In total, 25 knotted breaks and five knotless breaks were carried out.
3. Results and Discussion
3.1. Statistical Analysis
The Kolmogorov–Smirnov and Shapiro tests were used to validate the normality assumption. The quantitative parametric data were presented as the mean ± standard deviation. To study the influence of the two categorical variables (rope and knot) on the resistance, a two-way analysis of variance (ANOVA) test was carried out. To build a predictive model and analyse the influence of the rope breaking force on the knot efficiency, a linear regression was performed. An estimation of the measured values using the solid approximation of the knot efficiency probability distribution function (PDF) was performed following the results presented in Šimon [62]. The R software package version 4.2.3 was used for the analyses.
3.2. Knotless Rope Breaks: Efficiency
As defined in Equation (1), to obtain the knot efficiency (η), it was essential to measure the resistance of the ropes without knots, since the resistances given by the manufacturers were unreliable (Table 3).

Table 3.
Knotless static strength. Manufacturer data vs. experimentally obtained data.
The effect of each rope and knot on the efficiency was analysed using the ANOVA after obtaining the efficiency values for each rope and knot. Table 4 shows the estimated effects of the knot and rope on the efficiency when no interaction was included in the model [63].

Table 4.
ANOVA results for efficiencies.
Including an additive model in the ANOVA yielded results like those obtained when interactions were considered. In this case, the R2 was 0.8814. The hypothesis of the normality of the residuals was satisfied with a p-value of 0.70 after applying the Shapiro test. The interaction present in the model was not significant at a 0.01 level, which was also the case for the static breaking strength.
An interaction graph (Figure 8) was created to assess the presence of any interactions between the rope and knot varieties. As shown in the graph, the behaviours of different ropes were the same for different knot types. The knot type and rope type had a significant effect on the efficiency and breaking strength. Table 5 shows the estimated effects of each factor (knot and rope).
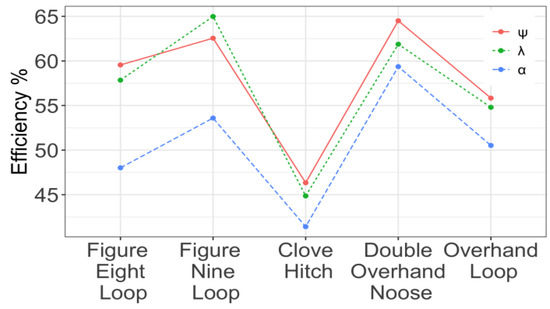
Figure 8.
Efficiency: interactions between the rope model and knot type.

Table 5.
Estimation of the knot effect and rope effect on efficiency.
The results in Figure 9a,b show that the greatest efficiency was obtained for the knots with a larger volume, specifically, the double overhand knot and the figure nine loop. Marturello and Muffly [64,65] presented similar results and suggested increasing the number of turns (i.e., knot size) to improve the knot efficiency. The observed effect of the number of turns of the knot on the loss of strength in the rope can be explained by the process that the rope experiences during the breaking process. Tension forces are transferred along the whole length of the rope. In the area of the knot, this traction causes the knot to tighten. At the entrance of the knot, the rope is then constricted. As the tension in the rope is inversely proportional to the cross-sectional area, reducing the cross-sectional area at the entrance of the knot greatly increases the tension in this area. Breaks always occur at the knot entrance in knotted ropes. Notably, the rope with the smallest diameter ψ was the rope with the highest efficiency among the tested rope models shown in Figure 9c,d. To estimate the efficiency of each rope/knot separately, the scheme presented by Šimon [62] was considered due to the lack of symmetry in the PDF of efficiency. Two knots had an average efficiency above 60%: the double overhand knot and the figure nine loop. The figure eight loop and the overhand loop yielded average efficiency results between 48% and 60%, respectively. The clove hitch had the lowest efficiency, with less than 45%. The least-squares approximation of these two parameters was used to determine if there was a trend in the knot efficiency as a function of the breaking load of the rope on which the knot was tied.
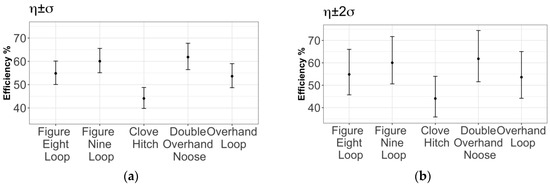
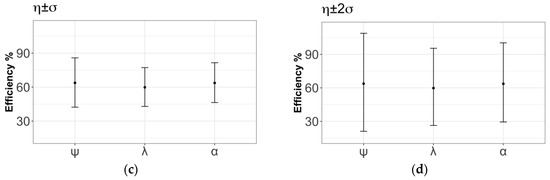
Figure 9.
Efficiencies for each knot type and rope model: (a–d).
The results presented the efficiency of each knot as a linear decreasing function dependent on the static breaking load of the rope (Figure 10). The graph shows two types of lines with slopes that are clearly distinguishable from each other: (1) knots of the figure eight and figure nine families and (2) all other knots. Among previous authors, only Marturello [64] and, in particular, Šimon [62], carried out valuable, rigorous statistical analyses. We compared the results of the slopes published by these two authors with those presented in this work.
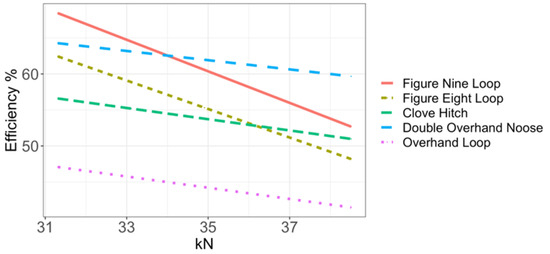
Figure 10.
Efficiency of the knot as a function of the breaking load of the rope.
The double overhand knot had a mean efficiency of 61.82%. The confidence intervals were 1σ (56.45, 67.76) and 2σ (51.55, 74.41). In Figure 11a, the efficiency of this knot is plotted as a linear decreasing function of the knotless breaking strength: η (y) = −0.78 (y − 34.996) + 44.202%. The best efficiency was observed when using this knot.
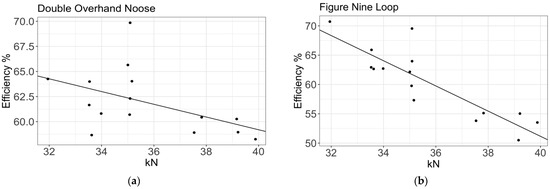
Figure 11.
Presentation of efficiency: (a) double overhand noose; (b) figure nine loop.
A mean efficiency of 60.05% with confidence intervals of 1σ (55.11, 65.54) and 2σ (50.62, 71.72) was obtained for the figure nine loop (see Figure 11b). The decreasing function obtained was η (y) = −2.19 (y − 34.996) + 60.375%. The efficiency (74%) was almost identical to that observed by Šimon [62] on a single rope. However, the range used by Šimon, with 2σ (71.19–76.81) obtained using a single rope, was more focused. The range of values obtained in this paper was much broader, using three ropes with different diameters and manufacturers. The following data were reported by other authors using less detailed experimental procedures and less statistical rigour: Merchant [38]: 85% efficiency for used ropes and breaking strength obtained from the manufacturer; Núñez [42]: 83% efficiency; and Gómez [40]: 75% efficiency using new/used ropes and breaking strength obtained from manufacturer.
Figure 12a shows the data for the figure eight knot, with a mean efficiency of 54.84% and confidence intervals of 1σ (50.07, 60.11) and 2σ (45.72, 66.02). This is undoubtedly the most commonly studied knot and that with the largest number of results available from previous studies. Higher efficiency values have been obtained by many authors. For example, Diamond [39] reported an average efficiency of 70%. However, he did not report important aspects of the test methodology, such as whether the rope was used or new, the test speed, or whether the samples were acclimatised. Šimon [41] found a mean efficiency of 64.42%. The resulting confidence interval was considerably lower than that obtained here, because Šimon used only one type of rope, whereas this study used three different rope models. Merchant [38] obtained a 75% efficiency for used ropes. However, he did not clearly define the experimental procedure or the manufacturer’s breaking strength. Milne [35] found an efficiency of 76% for new ropes and used his own tests to assess the ropes’ breaking strengths. Boron [25] reported an efficiency of 77% for new ropes using a well-defined methodology but used the manufacturer’s breaking load as a reference.
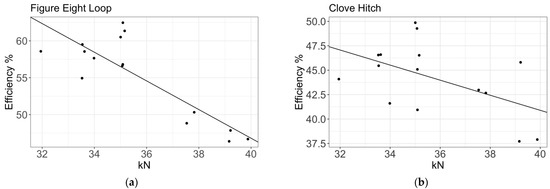
Figure 12.
Presentation of efficiency: (a) figure eight loop; (b) clove hitch.
Finally, the highest average efficiency value obtained prior to the present work was that of Brown [26] at 87.29%. However, this study did not define whether the rope was new or used, nor did it provide relevant details on the experimental procedure. Nevertheless, the reported efficiencies were derived from the tested data.
Efficiency values like those obtained in the present study were achieved by the analysed authors. Martin [29] did not indicate where the breaking strength of the rope was obtained but reported an efficiency of 55.49% for new ropes. Gómez [40] reported a 60% efficiency with new and used ropes, but the experimental procedure was too undefined, and the breaking strength values were those of the manufacturers. In addition, no confidence intervals were provided. Drohan [34] reported an efficiency of 48% for used ropes. The breaking strength values of the ropes were those given by the manufacturers. Some previous studies stated that the figure eight is one of the best knots [26,35]. A number of these studies did not include other very important knots, including the figure nine loop and the double overhand knot. The efficiency results obtained in this research contradict the claims of Milne [35], who obtained an average efficiency of 61.82% for the double overhand noose knot. A detailed study of the results showed that efficiency was a decreasing function of knotless rope resistance, which was satisfied as follows: η(y)= −1.98 (y − 34.996) + 55.138%. Compared to the function obtained by Šimon [41], η(y) ≅ −0.77 (y − 32.79) + 66.4%, the obtained function decreased with a greater slope.
The clove hitch shown in Figure 12b had the lowest efficiency data of all the knots tested, with a mean efficiency of 44.08% and confidence intervals of 1σ (39.80, 48.78) and 2σ (35.84, 53.98). The decreasing function obtained corresponds to η(y) = −0.64 (y − 34.996) + 61.91%. Nuñez [42] and Merchant [38] gave efficiency results of 62% and 55%, respectively, for the efficiency of this knot. Nuñez [42] performed laboratory tests according to the EN 919 [44]. However, he did not give details on important experimental procedures such as the test speed or sample conditioning. Merchant [38] carried out tests on new ropes (11 mm in diameter) but did not adequately describe the test methodology.
The average efficiency for the overhand loop was 53.60%, while the confidence intervals were 1σ (48.70, 59.00) and 2σ (44.19, 65.02). The regression gave the following expression: η(y)= −0.78 (y – 34.996) + 53.717% (Figure 13). Šimon [41] reported a result similar to that obtained in this study for this type of knot, using five ropes and 108 trials (η (y)= −0.62 (y − 32.79) + 60.67%). Šimon reported a mean efficiency of 56.92% when testing only one type of rope. The confidence interval was slightly lower but remained within the expected values. Drohan [34] reported an average efficiency of 65% with an 11 mm low-stretch kernmantle rope. Drohan ran six tests on samples that were preconditioned at 20 °C and 65% humidity but did not perform any preload cycles. The breaking strength value was that which was provided by the manufacturer. Similar to Drohan [34], Brown [26] reported an efficiency of 65.28% and used 10 mm dynamic ropes. Brown also included the results of tests using a knot tied around a metal tube, increasing the efficiency by reducing the rope curvature at the knot [63]. Considering past studies, the present results seem reasonable, as previously reported efficiencies tend to cluster around the values in the present study.
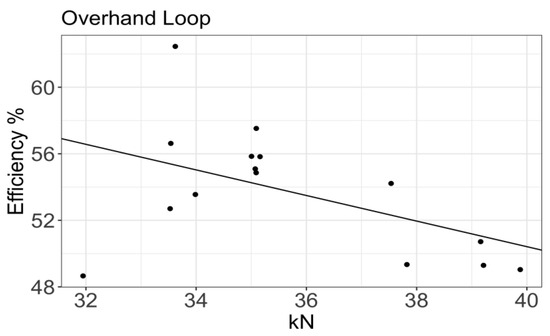
Figure 13.
Presentation of efficiency: overhand loop.
4. Conclusions and Contributions
This research offers relevant data to determine knot efficiency more accurately in fall arrest systems, ultimately improving worker safety. Every knot reduces the tensile strength of a rope, but not all knots cause the same reduction in strength. The rope strength can vary by more than 6 kN depending on the type of knot chosen. The results obtained in this article are valid for a low-elongation core sheath rope of type A, EN 1891 [43], with a diameter of 10.7 ± 0.3 mm and a breaking load of 30–35 kN. The knots were tested in a standard load configuration, with the I-geometry knot construction already described in detail by other authors such as García and Castaño [11], Šimon [41], and Gómez [40]. The symmetry of the dextrorotational version was used for all knots. We observed the breaking point of the rope to be located at the knot. Indeed, the breaking point occurred at exactly the first strangulation point of the loaded rope. Knots with a greatest resistance to breakage are those with a greater volume, more loops, and a greater turning radius in the rope section where the breaking occurs, such as the figure eight loop and the double overhand knot. These knots behave much more efficiently than knot types with a smaller volume and less rope consumption, such as the clove hitch.
The resistance values obtained in the tests showed that each of the analysed knots, regardless of the type of rope, could resist a slow traction force above the injury threshold (12 kN). The minimum resistance values obtained with each of the knots and ropes tested were within the relevant safety limits, making such knots suitable for static rope access and positioning work. The most efficient results were obtained using the combination of an overhand knot and ψ rope with a smaller diameter and, theoretically, a lower resistance. The α rope has a larger diameter and is the strongest without a knot. However, this rope type yielded the poorest efficiency. From the results obtained, it is possible to establish a taxonomy from the most to least efficient: the double overhand knot, figure nine loop, figure eight loop, overhand knot, and carnation knot.
The obtained knot efficiency can be empirically represented as a decreasing line depending on the static breaking load of the rope. In the same way, a decrease in the knot efficiency can be observed as the rope diameter increases. The interaction data showed that a favourable or unfavourable knot behaviour occurred independently of the type of rope used from the perspectives of strength and efficiency. There was also a large variation in tensile strength depending on the choice of knot type. The rope type selection had no such significant influence. The figure eight- and figure nine-family knots were affected by a much more rapid loss of efficiency as the breaking strength of the rope increased. For the other knots, this phenomenon was less pronounced.
After analysing the results, we concluded that the best anchorage knot to use in RASs is the double overhand knot, in terms of efficiency and strength. The main contribution of this research, and its greatest novelty, is its identification of the double overhand knot as the safest knot to use in fall arrest systems.
These findings will have important implications in both sports and the workplace, particularly in construction, wind turbines, industry, rescue, climbing, canyoning, and caving. Indeed, the present results could have implications in any activity where rope access systems are used.
It is highly advisable for future authors to include technical specifications relating to knot efficiency in applicable regulations so that the knot behaviour against loads can be known. Establishing a good classification system for safe knots could help establish safety criteria for the elements and components of FASs.
In future work, it will be necessary to improve the knowledge of knots by analysing other characteristics such as the knot behaviour during dynamic tests. Future work could also explore hypotheses related to the relevance of knot construction and geometry (with levorotatory symmetry), as well as knot functionality and the complexity of untying after loading.
Author Contributions
Conceptualization, P.I.S. and E.Á.C.; methodology, P.I.S., E.Á.C., B.F. and J.F.M.; validation, P.I.S., E.Á.C., B.F., E.G. and J.F.M.; formal analysis, E.Á.C. and J.F.M.; investigation, P.I.S., E.Á.C., B.F. and E.G.; writing—original draft preparation, P.I.S., E.Á.C. and J.F.M.; writing—review and editing, P.I.S., E.Á.C., B.F., E.G. and J.F.M.; supervision, P.I.S., E.Á.C., B.F. and E.G.; project administration, B.F. and E.G.; funding acquisition, P.I.S., E.Á.C., B.F. and E.G. This article is part of the doctoral thesis of P.I.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University of Alicante and Centro de Innovación Vertical S.A.C., grant numbers PC20-01A and GRE 20-07-A.
Data Availability Statement
The data presented in this study are available upon request to the corresponding author. The data are not publicly available because possible misinterpretation of the data could cause fall from height accidents.
Acknowledgments
The authors are particularly grateful to the CIV Vertical Innovation Centre of Perú and the University of Alicante.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Luo, F.; Li, R.Y.M.; Crabbe, M.J.C.; Pu, R. Economic development and construction safety research: A bibliometrics approach. Saf. Sci. 2022, 145, 105519. [Google Scholar] [CrossRef]
- Zeng, L.; Li, R.Y.M.; Yigitcanlar, T.; Zeng, H. Public Opinion Mining on Construction Health and Safety: Latent Dirichlet Allocation Approach. Buildings 2023, 13, 927. [Google Scholar] [CrossRef]
- Dong, X.S.; Brown, S.; Brooks, R.D. Trends of fatal falls in the U.S. Construction Industry. In Proceedings of the 21st Congress of the International Ergonomics Association (IEA 2021), Online, 13–18 June 2021; Volume 309. [Google Scholar] [CrossRef]
- Dong, X.S.; Largay, J.A.; Choi, S.D.; Wang, X.; Cain, C.T.; Romano, N. Fatal falls and PFAS use in the construction industry: Findings from the NIOSH FACE reports. Accid. Anal. Prev. 2017, 102, 136–143. [Google Scholar] [CrossRef]
- Dong, X.S.; Jackson, R.; Varda, D.; Bunting, J. Trends of Fall Injuries and Prevention in the Construction Industry. Available online: https://www.cpwr.com/wp-content/uploads/publications/Quarter2-QDR-2019.pdf (accessed on 8 March 2022).
- Safe Work Australia. Work-Related Injury Fatalities/Key WHS Statistics Australia. 2021. Available online: https://www.safeworkaustralia.gov.au/sites/default/files/2021-10/Key%20work%20health%20and%20safety%20statistics%20Australia%202021.pdf (accessed on 5 March 2022).
- Ministry of Labor and Social Economy (MITES). Occupational Accident Statistics. Available online: https://www.mites.gob.es/estadisticas/eat/eat20/Resumen_resultados_ATR_2020.pdf (accessed on 8 February 2022).
- Health and Safety Executive. Health and Safety in Construction in Great Britain (HSE). Construction Statistics in Great Britain. 2022. Available online: https://www.hse.gov.uk/statistics/industry/construction.pdf (accessed on 30 January 2022).
- EN-363:2018; Personal Fall Protection Equipment-Personal Fall Protection Systems. European Committee for Standardization: Brussels, Belgium, 2018.
- Carrión, E.A.; Menchacatorre, P.I.; García, R.T. Individual Fall Protection Systems: Legislation, Definitions and Equipment; Publications of the University of Alicante: Alicante, Spain, 2014; ISBN 978-84-9717-321-6. [Google Scholar]
- Garcia-Dils de la Vega, S.; Castaño Lacruz, J. Some notes on knots. Subterránea 2005, 23, 42–44. Available online: https://www.efiemer.com/wp-content/uploads/2019/02/Algunas_notas_sobre_nudos.pdf (accessed on 16 March 2022).
- Guinot, S.; Sáez, P. Sistemas de Protección Individual Contra Caídas en Bomberos; Ediciones Desnivel: Madrid, Spain, 2015; ISBN 978-84-9829-330-2. [Google Scholar]
- Tourte, B.; Marbach, G. Técnicas de Espeleologia Alpina; Ediciones Desnivel: Madrid, Spain, 2003; ISBN 978-84-9576-095-1. [Google Scholar]
- Sulowski, A.C. How good is the 8 kN Maximum Arrest Force limit in industrial Fall Arrest Systems. In Proceedings of the International Symposium on Fall Protection—IFPS’06, Seattle, WA, USA, 14–15 June 2006. [Google Scholar]
- Pomares, J.C.; Irles, R.; Segovia, E.; Ferrer, B. Acceleration and Deflection Analysis for Class C Edge Protection Systems in Construction Work. J. Constr. Eng. Manag. 2014, 8, 140. [Google Scholar] [CrossRef]
- Zuluaga, C.M.; Albert, A.; Winkel, M.A. Improving Safety, Efficiency, and Productivity: Evaluation of Fall Protection Systems for Bridge Work Using Wearable Technology and Utility Analysis. J. Constr. Eng. Manag. 2020, 146, 04019107. [Google Scholar] [CrossRef]
- Rico, S.; Matthew, H.; Rajagopalan, B.; Siddharth, B. Safety Risk Tolerance in the Construction Industry: Cross-Cultural Analysis. J. Constr. Eng. Manag. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Ashley, C.W. The Ashley Book of Knots, 12th ed.; Doubleday and Company, Inc.: New York, NY, USA, 1944. [Google Scholar]
- Marbach, G.; Tourte, B. Alpine Caving Techniques: A Complete Guide to Safe and Efficient Caving, 1st ed.; Speleo Projects: Allschwil, Switzerland, 2002. [Google Scholar]
- Turner, J.C.; Griend, P.V.; Warner, C. History and Science of Knot; Series on Knots and Everything; World Scientific Publishing Co Pte Ltd.: Singapore, 1996; p. 464. [Google Scholar]
- BEAL. Available online: https://www.beal-planet.com/en (accessed on 31 January 2022).
- Cuenot, S.; Bodeau, H. Petzl, la Promesse des Profondeurs; Guérin, Ed.; Editions Paulsen: Chamonix, France, 2012. [Google Scholar]
- MSA. The Safety Company. Available online: https://us.msasafety.com/Fall-Protection/Rescue-%26-Descent-Products/FP-Rescue-Ropes/p/000230001200001001 (accessed on 8 February 2022).
- PETZL. PETZL-Professional. Available online: https://www.petzl.com/GB/en/Professional/Ropes (accessed on 28 January 2022).
- Boron, K.; Obstalecki, M.; Kurath, P.; Horn, G.P. Utilizing Knots to Reduce Dynamic Loads in Fire Service Rope Systems. Conf. Proc. Soc. Exp. Mech. Ser. 2013, 1, 433–439. [Google Scholar] [CrossRef]
- Brown, A. The Strength of Knots in Dynamic Climbing Rope. Available online: http://personal.strath.ac.uk/andrew.mclaren/alasdair_brown_2008.pdf (accessed on 2 February 2022).
- Carrión, E.; Ferrer, B.; Monge, J.; Sáez, P.; Pomares, J.; González, A. Minimum Clearance Distance in Fall Arrest Systems with Energy Absorber Lanyards. Int. J. Environ. Res. Public Health 2021, 18, 5823. [Google Scholar] [CrossRef]
- López, E.; Julián, R.; Reising, M. Evaluation and analysis of climbing knots. In Proceedings of the 13th Argentine and 8th Latin American Congress of Physical Education and Sciences, Ensenada, Mexico, 30 September–4 October 2019; Available online: http://congresoeducacionfisica.fahce.unlp.edu.ar/ (accessed on 1 January 2023).
- Martin, D.A.; Boron, K.; Obstalecki, M.; Kurath, P.; Horn, G.P. Feasibility of Knots to Reduce the Maximum Dynamic Arresting Load in Rope Systems. J. Dyn. Behav. Mater. 2015, 1, 214–224. [Google Scholar] [CrossRef][Green Version]
- Arai, Y.; Yasuda, R.; Akashi, K.-I.; Harada, Y.; Miyata, H.; Kinosita, K., Jr.; Itoh, H. Tying a molecular knot with optical tweezers. Nature 1999, 399, 446–448. [Google Scholar] [CrossRef]
- Marbach, G.; Rocourt, J.L. Techniques de la Spéléologie Alpine; Techniques Sportives Appliquées: Choranche, France, 1980. [Google Scholar]
- Pieranski, P.; Kasas, S.; Dietler, G.; Dubochet, J.; Stasiak, A. Localization of breakage points in knotted strings. New J. Phys. 2001, 3, 10. [Google Scholar] [CrossRef]
- Stasiak, A.; Dobay, A.; Dubochet, J. Knotted Fishing Line, Covalent Bonds, and Breaking Points. Science 1999, 286, 11. [Google Scholar] [CrossRef]
- Drohan, D. Preferred Knots for Use in Canyons. Available online: http://www.paci.com.au/downloads_public/knots/06_Joining-knots_DDrohan.pdf (accessed on 8 March 2022).
- Milne, K.A.; McLaren, A.J. An Assessment of the Strength of Knots and Splices Used as Eye Terminations in a Sailing Environment. Sports Eng. 2006, 9, 1–13. [Google Scholar] [CrossRef]
- Aldazabal, J.; Meizoso, A.M.; Muniategui, A.; Ibarzabal, A.; Urcaregui, M. Tensile Strength of Knotted Ropes. An. De La Mecánica De Fract. 2007, 2, 563–566. [Google Scholar]
- Nuñez, T. Los Mejores Nudos de Escalada; Ediciones Desnivel: Madrid, Spain, 2011. [Google Scholar]
- Merchant, D. Life on a Line. The Underground Rope Rescue Manual, 2nd ed.; Lulu Enterprises, UK Ltd.: North Wales, UK, 2007; Volume 2, Available online: http://www.lifeonaline.com/legal (accessed on 3 January 2023).
- Diamond, W. An Assessment of the Strength of Rope Splices and Knots in Sailing Ropes. Available online: http://Personal.Strath.Ac.Uk/Andrew.Mclaren/William_Diamond_2007.Pdf (accessed on 8 March 2022).
- Gómez, P. Breaking Knots, 2nd ed.; Valencian School of Speleology: Valencia, Spain, 2016. [Google Scholar]
- Šimon, J.; Dekýš, V.; Palcek, P. Revision of Commonly Used Loop Knots Efficiencies. Acta Phys. Pol. A 2020, 138, 404–420. [Google Scholar] [CrossRef]
- Nuñez, T. Something More about Knots; Ediciones Desnivel: Madrid, Spain, 1999. [Google Scholar]
- UNE-EN 1891; Personal Protective Equipment for the Prevention of Falls from a Height—Low Stretch Kernmantle Ropes. Asociación Española de Normalización: Madrid, Spain, 1999.
- EN 919:1995; Fibre Ropes for General Service. Determination of Certain Physical and Mechanical Properties. European Committee for Standardization: Brussels, Belgium, 1995.
- AS 4142.3; Fibre Ropes, Part 3: Man-Made Fibre Rope for Static Life Rescue Lines. Australia Standards: Homebush, Australia, 1993.
- EN 892:2012; Mountaineering Equipment-Dynamic Mountaineering Ropes-Safety Requirements and Test Methods. European Committee for Standardization: Brussels, Belgium, 2012.
- BS:3104:1970; Polyamide (Nylon) Mountaineering Ropes. British Standards Institution: London, UK, 1970.
- BS EN 892:2004; Mountaineering Equipment. Dynamic Mountaineering Ropes. Safety Requirements and Test Methods. British Standards Institution: London, UK, 2004.
- National Fire Protection Association. NFPA 1. Fire Code, 2012th ed.; NFPA Publications: Quincy, MA, USA, 2011. [Google Scholar]
- Saitta, A.M.; Soper, P.D.; Wasserman, E.; Klein, M.L. Influence of a knot on the strength of a polymer strand. Nature 1999, 399, 46–48. [Google Scholar] [CrossRef] [PubMed]
- Horn, G.P.; Kurath, P. In Failure of firefighter escape rope under dynamic loading and elevated temperatures. In Dynamic Behavior of Materials, Proceedings of the 2010 Annual Conference on Experimental and Applied Mechanics, Indianapolis, Indiana, 7–10 June 2010; Springer: New York, NY, USA, 2011; Volume 1, pp. 353–359. [Google Scholar] [CrossRef]
- Fontenot, N.; Stenvers, D.; Gilmore, J.; Solomon, A.; van Berkel, B.; Grabandt, O.; Kong, D. In Use of synthetic rope in high-temperature or fire environments. In OCEANS 2009; IEEE: Biloxi, MS, USA, 2009; pp. 1–6. [Google Scholar] [CrossRef]
- EN ISO 139:2005/A1; Textiles—Standard Atmospheres for Conditioning and Testing. European Committee for Standardization: Brussels, Belgium, 2005.
- Baszczyński, K. Effect of Repeated Loading on Textile Rope and Webbing Characteristics in Personal Equipment Protecting against Falls from a Height. Fibres Text. East. Eur. 2015, 23, 110–118. [Google Scholar] [CrossRef]
- European Parliament and the Council of the European Union. Directive 2001/45/EC of the European Parliament and of the Council of 27 June 2001. Amending Council Directive 89/655/EEC Concerning the Minimum Safety and Health Requirements for the Use of Work Equipment by Workers at Work; Official Journal of the European Communities: Luxembourg, 2001. [Google Scholar]
- European Parliament and the Council of the European Union. Regulation (EU) 2016/425 of the European Parliament and of the Council of 9 March 2016 on Personal Protective Equipment and Repealing Council Directive 89/686/EEC. Available online: http://data.europa.eu/eli/reg/2016/425/oj (accessed on 28 January 2024).
- Carrión, E.; Sáez, P.; Pomares, J.; González, A. Average Force of Deployment and Maximum Arrest Force of Energy Absorbers Lanyards. Int. J. Environ. Res. Public Health 2020, 17, 7647. [Google Scholar] [CrossRef] [PubMed]
- Eurasian Economic Union (EAC). Available online: https://www.ccis-expertise.com/en/eurasian-economic-union-export (accessed on 19 January 2024).
- UIAA 107; Safety Standards. Available online: https://www.theuiaa.org/safety/safety-standards/ (accessed on 8 May 2023).
- EN-364/AC; Personal Protective Equipment against Falls from a Height Test Methods. European Committee for Standardization: Brussels, Belgium, 1993.
- EN ISO 7500-1:2018; Metallic Materials. Calibration and Verification of Static Uniaxial Testing Machines. Part 1: Tension/Compression Testing Machines. Calibration and Verification of the Force-Measuring System. European Committee for Standardization: Brussels, Belgium, 2018.
- Šimon, J.; Ftorek, B. Basic Statistical Properties of the Knot Efficiency. Symmetry 2022, 14, 1926. [Google Scholar] [CrossRef]
- Zhu, X.; Li, R.Y.M.; Crabbe, M.J.C.; Sukpascharoen, K. Can a chatbot enhance hazard awareness in the construction industry? Front. Public Health 2022, 10, 993700. [Google Scholar] [CrossRef] [PubMed]
- Marturello, D.M.; McFadden, M.S.; Bennett, R.A.; Ragetly, G.R.; Horn, G. Knot Security and Tensile Strength of Suture Materials. Vet. Surg. 2014, 43, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Muffly, T.M.; Boyce, J.; Kieweg, S.L.; Bonham, A.J. Tensile Strength of a Surgeon’s or a Square Knot. J. Surg. Educ. 2010, 67, 222–226. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





