A Hierarchy of Covariant Generalized Schwarz Maps in M₂(ℂ)

Abstract

A class of linear maps in $M_2\left(\mathbb{C}\right)$ displaying diagonal unitary and orthogonal symmetries is analyzed. Using a notion of $\omega$-duality, we prove that a map which is $\omega$-dual to a generalized Schwarz map is again generalized Schwarz. We introduce an infinite hierarchy of generalized Schwarz maps and study the property of an asymptotic limiting map. Interestingly, it is shown that the first example of Schwarz but not completely positive map found by Choi is an example of an asymptotic map.

1. Introduction

Consider a unitary n-dimensional representation $U_g$ of a compact Lie group G. A linear map $\mathrm{\Phi }:M_n\left(\mathbb{C}\right)\to M_n\left(\mathbb{C}\right)$ (where $M_n\left(\mathbb{C}\right)$ denotes an algebra of $n\times n$ complex matrices) is G-covariant if

$$U_g\mathrm{\Phi }\left(X\right)U_g^{†}=\mathrm{\Phi }\left(U_{g}X{U}_g^{†}\right),$$

(1)

for all $X\in M_n\left(\mathbb{C}\right)$ and all elements $g\in G$. One calls $\mathrm{\Phi }$ to be conjugate G-covariant if

$$U_g\mathrm{\Phi }\left(X\right)U_g^{†}=\mathrm{\Phi }\left({\overline{U}}_{g}X{U}_g^{\mathrm{T}}\right),$$

(2)

where $U_g^{\mathrm{T}}$ denotes the transposition and ${\overline{U}}_g$ the complex conjugation. If the map $\mathrm{\Phi }$ is also completely positive and trace-preserving (CPTP), then one calls $\mathrm{\Phi }$ a covariant quantum channel. Covariant quantum channels play an important role in various problems in quantum information theory. Prominent examples of covariant channels include depolarizing channels and transpose depolarizing channels. The covariance property of quantum channels was originally analyzed by Scutaru [1] who derived the Stinespring-type theorem for covariant completely positive maps and then developed by Holevo [2,3] (for more recent analysis cf., e.g., [4,5,6,7]).

In this paper, we analyze linear maps satisfying an operator Schwarz inequality [8,9,10,11]

$$\mathrm{\Phi }\left(X^{†}X\right)\ge \mathrm{\Phi }\left(X^{†}\right)\mathrm{\Phi }\left(X\right).$$

(3)

A map $\mathrm{\Phi }:M_n\left(\mathbb{C}\right)\to M_m\left(\mathbb{C}\right)$ is unital if $\mathrm{\Phi }\left({1\mathrm{l}}_n\right)={1\mathrm{l}}_m$. A unital map is called a Schwarz map if (3) holds for all $X\in M_n\left(\mathbb{C}\right)$. Any unital completely positive map satisfies (3) and any Schwarz map is necessarily positive. A transposition map provides a simple example of a unital positive map which is not Schwarz, and the first example of a Schwarz map $\mathrm{\Phi }:M_2\left(\mathbb{C}\right)\to M_2\left(\mathbb{C}\right)$, which is not completely positive, was provided by Choi [12].

It is well known [8,9,10,11] that unital positive maps satisfy (3) for all $X=X^{†}$. Actually, any positive unital map satisfies (3) for normal operators, i.e., $X{X}^{†}=X^{†}X$. In this case, it is called Kadison inequality [13]. Schwarz maps were recently analyzed in [14,15,16,17,18].

In a recent paper [19], authors proposed the following:

Definition 1.

A linear map $\mathrm{\Phi }:M_n\left(\mathbb{C}\right)\to M_m\left(\mathbb{C}\right)$ is called a generalized Schwarz map if

$$\left(\begin{array}{cc}\mathrm{\Phi }\left({1\mathrm{l}}_n\right)& \mathrm{\Phi }\left(X\right)\\ \mathrm{\Phi }{\left(X\right)}^{†}& \mathrm{\Phi }\left(X^{†}X\right)\end{array}\right)\ge 0,$$

(4)

for all $X\in M_n\left(\mathbb{C}\right)$.

One immediately shows that $\mathrm{\Phi }$ is generalized Schwarz if and only if

$$\mathrm{\Phi }\left(X^{†}X\right)\ge \mathrm{\Phi }{\left(X\right)}^{†}\mathrm{\Phi }{\left({1\mathrm{l}}_n\right)}^{+}\mathrm{\Phi }\left(X\right),$$

(5)

where $A^{+}$ denotes a generalized Moore–Penrose inverse of A [20,21]. Clearly, if $\mathrm{\Phi }$ is unital, then (5) reduces to the original Schwarz inequality (3). In a recent paper [18], we analyzed both Schwarz and generalized Schwarz maps in $M_2\left(\mathbb{C}\right)$ covariant with respect to a group of diagonal $2\times 2$ unitaries $\mathcal{D}\mathcal{U}\left(2\right)$ and diagonal $2\times 2$ orthogonal matrices $\mathcal{D}\mathcal{O}\left(2\right)$. Interestingly, the generalized Schwarz property, contrary to positivity and completely positivity, is not preserved when passing to the dual map. Recall that given a map $\mathrm{\Phi }:M_n\left(\mathbb{C}\right)\to M_m\left(\mathbb{C}\right)$ one defines its Hilbert–Schmidt dual (adjoint) ${\mathrm{\Phi }}^{\ast }:M_m\left(\mathbb{C}\right)\to M_n\left(\mathbb{C}\right)$ via

$${({\mathrm{\Phi }}^{\ast }\left(X\right),Y)}_{\mathrm{HS}}:={(X,\mathrm{\Phi }\left(Y\right))}_{\mathrm{HS}},$$

(6)

where the Hilbert–Schmidt inner product reads ${(X,Y)}_{\mathrm{HS}}:=\mathrm{Tr}\left(X^{†}Y\right)$. In what follows we introduce a new inner product and a new notion of duality which does preserve the very property to be generalized Schwarz when applied to generalized covariant Schwarz maps i $M_2\left(\mathbb{C}\right)$.

The paper is organized as follows: Section 2 provides a brief introduction to the class of covariant qubit maps we analyze. In Section 3, we introduce the very notion of $\omega$-duality where $\omega :=\mathrm{\Phi }\left(1\mathrm{l}\right)$ and prove that if $\mathrm{\Phi }$ is covariant generalized Schwarz, so is its $\omega$-dual map ${\mathrm{\Phi }}^{\ast \omega }$. Then, the next Section defines and analyzes an infinite hierarchy of covariant generalized Schwarz maps. The properties of a limiting map ${\mathrm{\Phi }}_{\infty }$ are presented in Section 4. Final conclusions are collected in Section 5.

2. Materials and Methods

In this paper, we consider linear maps $\mathrm{\Phi }$ satisfying

$$\mathcal{O}\mathrm{\Phi }\mathcal{O}=\mathrm{\Phi }$$

(7)

for all diagonal orthogonal matrices, i.e., ${\mathcal{O}}_{kl}=\pm {\delta }_{kl}$. A linear map $\mathrm{\Phi }:M_2\left(\mathbb{C}\right)\to M_2\left(\mathbb{C}\right)$ is covariant with respect to diagonal orthogonal matrices, i.e., satisfies (7), if [18,22,23],

$$\mathrm{\Phi }\left(X\right)=\left(\begin{array}{cc}a{X}_{11}+a^{\prime }{X}_{22}& \lambda X_{12}+\overline{\mu }{X}_{21}\\ \overline{\lambda }{X}_{21}+\mu X_{12}& b^{\prime }{X}_{11}+b{X}_{22}\end{array}\right),$$

(8)

where $X_{ij}$ are matrix elements of $X\in M_2\left(\mathbb{C}\right)$. Additionally, $\mathrm{\Phi }$ is covariant with respect to diagonal unitary matrices if $\mu =0$. Hence, $\mathrm{\Phi }$ is uniquely determined by a $2\times 2$ complex matrix

$$A=\left(\begin{array}{cc}a& a^{\prime }\\ b^{\prime }& b\end{array}\right)$$

(9)

and two complex parameters $(\lambda ,\mu )$. $\mathrm{\Phi }$ preserves Hermiticity if A is a real matrix. Now,

• $\mathrm{\Phi }$ is unital iff $a+a^{\prime }=b+b^{\prime }=1$,
• $\mathrm{\Phi }$ is trace-preserving if $a+b^{\prime }=b+a^{\prime }=1$,
• $\mathrm{\Phi }$ is positive if $a,a^{\prime },b,b^{\prime }\ge 0$ and

  $$\left|\lambda \right|+\left|\mu \right|\le \sqrt{ab}+\sqrt{a^{\prime }{b}^{\prime }},$$

  (10)
• $\mathrm{\Phi }$ is completely positive iff $a,a^{\prime },b,b^{\prime }\ge 0$ and

  $$\left|\lambda \right|\le \sqrt{ab},\left|\mu \right|\le \sqrt{a^{\prime }{b}^{\prime }}.$$

  (11)

In [18], it was shown

Proposition 1.

Φ defined in (8) is generalized Schwarz iff $a,a^{\prime },b,b^{\prime }\ge 0$ and

$${\displaystyle \frac{{\left|\lambda \right|}^2}{a}}+{\displaystyle \frac{{\left|\mu \right|}^2}{a^{\prime }}}\le b+b^{\prime },{\displaystyle \frac{{\left|\lambda \right|}^2}{b}}+{\displaystyle \frac{{\left|\mu \right|}^2}{b^{\prime }}}\le a+a^{\prime }.$$

(12)

In particular, if $\mathrm{\Phi }$ is unital then Inequalities (12) reduce to

$${\displaystyle \frac{{\left|\lambda \right|}^2}{a}}+{\displaystyle \frac{{\left|\mu \right|}^2}{1-a}}\le 1,{\displaystyle \frac{{\left|\lambda \right|}^2}{b}}+{\displaystyle \frac{{\left|\mu \right|}^2}{1-b}}\le 1.$$

(13)

Note that Conditions (10)–(12) are invariant under

$$\left(\begin{array}{cc}a& a^{\prime }\\ b^{\prime }& b\end{array}\right)\to \left(\begin{array}{cc}ra& r{a}^{\prime }\\ b^{\prime }/r& b/r\end{array}\right),$$

(14)

with arbitrary $r>0$.

A map ${\mathrm{\Phi }}^{\ast }$ dual to $\mathrm{\Phi }$ belongs to the same class (8), i.e., it is covariant, and it is defined by a transpose matrix $A^{\mathrm{T}}$ together with parameters $(\overline{\lambda },\mu )$. It is, therefore, clear that Proposition 1 implies

Proposition 2.

A dual map ${\mathrm{\Phi }}^{\ast }$ is generalized Schwarz if and only

$${\displaystyle \frac{{\left|\lambda \right|}^2}{a}}+{\displaystyle \frac{{\left|\mu \right|}^2}{b^{\prime }}}\le b+a^{\prime },{\displaystyle \frac{{\left|\lambda \right|}^2}{b}}+{\displaystyle \frac{{\left|\mu \right|}^2}{a^{\prime }}}\le a+b^{\prime }.$$

(15)

3. Results

The two basic questions we pose are the following: If $\mathrm{\Phi }$ is Schwarz, is ${\mathrm{\Phi }}^{\ast }$ also Schwarz? The same question is formulated for generalized Schwarz maps. For unital maps, we prove the following:

Theorem 1.

If Φ is a covariant unital Schwarz, then its dual ${\mathrm{\Phi }}^{\ast }$ is a covariant generalized Schwarz map.

Proof. 

Note that elliptic Conditions (12) define a closed convex set $S_{ab}$ on the $\left(\right|\lambda |,|\mu \left|\right)$ plane. Similarly, Conditions (15) define a closed convex set $S_{ab}^{\ast }$ on the same plane. To prove the theorem, one has to show that $S_{ab}\subset S_{ab}^{\ast }$. Note that four ellipses (12) and (15) intersect in $(\sqrt{ab},\sqrt{a^{\prime }{b}^{\prime }})$. Let us assume that $a\le b$ (equivalently $b^{\prime }\le a^{\prime }$). Then $S_{ab}$ intersect $\left|\lambda \right|$-axis at $\sqrt{a}$ and $\left|\mu \right|$-axis at $\sqrt{b^{\prime }}$. On the other hand, $S_{ab}^{\ast }$ intersect $\left|\lambda \right|$-axis at $min\{\sqrt{a(b+a^{\prime })},\sqrt{b(a+b^{\prime })}\}$ and $\left|\mu \right|$-axis at $min\{\sqrt{b^{\prime }(b+a^{\prime })},\sqrt{a^{\prime }(a+b^{\prime })}\}$. Therefore, $S_{ab}\subset S_{ab}^{\ast }$ if and only if

$$a\le min\{a(b+a^{\prime }),b(a+b^{\prime })\},$$

(16)

together with

$$b^{\prime }\le min\{b^{\prime }(b+a^{\prime }),a^{\prime }(a+b^{\prime })\}.$$

(17)

One immediately checks that, indeed, Conditions (16) and (17) are satisfied. Clearly, similar analysis works if one assumes that $b\le a$.   □

One may pose a natural question: assuming that $\mathrm{\Phi }$ is a covariant generalized Schwarz map, is it true that its dual ${\mathrm{\Phi }}^{\ast }$ is generalized Schwarz as well? In general, it is no longer true.

Example 1.

Let Φ be characterized by

$$A=\left(\begin{array}{cc}1& 1\\ 2& 3\end{array}\right),\lambda =\sqrt{a(b+b^{\prime })}=\sqrt{5},\mu =0.$$

Then its dual characterized by

$$A^{\mathrm{T}}=\left(\begin{array}{cc}1& 2\\ 1& 3\end{array}\right),\lambda =\sqrt{5},\mu =0,$$

is no longer generalized Schwarz since $\sqrt{5}>min\{\sqrt{4},\sqrt{9}\}=2$.

Let $\mathrm{\Phi }$ be a covariant generalized Schwarz map. Define

$$\omega :=\mathrm{\Phi }\left(1\mathrm{l}\right)=\left(\begin{array}{cc}{\omega }_1& 0\\ 0& {\omega }_2\end{array}\right)=\left(\begin{array}{cc}a+a^{\prime }& 0\\ 0& b+b^{\prime }\end{array}\right).$$

(18)

Clearly, for unital maps $\omega =1\mathrm{l}$. Let us define a new inner product in $M_2\left(\mathbb{C}\right)$ via

$${(X,Y)}_{\omega }:=\mathrm{Tr}\left({\omega }^{{\displaystyle \frac{1}{2}}}{X}^{†}{\omega }^{{\displaystyle \frac{1}{2}}}Y\right).$$

(19)

Note that if $\omega =1\mathrm{l}$, then (19) reduces to the Hilbert–Schmidt inner product.

Definition 2.

Given Φ, one defines its ω-dual map ${\mathrm{\Phi }}^{\ast \omega }$ via

$${({\mathrm{\Phi }}^{\ast \omega }\left(X\right),Y)}_{\omega }:={(X,\mathrm{\Phi }\left(Y\right))}_{\omega },$$

(20)

that is,

$$\mathrm{Tr}\left({\mathrm{\Phi }}^{\ast \omega }\left(X^{†}\right){\omega }^{{\displaystyle \frac{1}{2}}}Y{\omega }^{{\displaystyle \frac{1}{2}}}\right):=\mathrm{Tr}\left({\omega }^{{\displaystyle \frac{1}{2}}}{X}^{†}{\omega }^{{\displaystyle \frac{1}{2}}}\mathrm{\Phi }\left(Y\right)\right),$$

(21)

for all $X,Y\in M_2\left(\mathbb{C}\right)$.

It is clear that if $\mathrm{\Phi }$ is unital, then ${\mathrm{\Phi }}^{\ast \omega }={\mathrm{\Phi }}^{\ast }$.

Remark 1.

The inner Product (19) is well known in the theory of quantum Markovian semigroups [24,25,26,27] in the analysis of quantum detailed balance. Actually, given state ω, one defines one-parameter family of inner products

$${(X,Y)}_s:=\mathrm{Tr}\left({\omega }^s{X}^{†}{\omega }^{1-s}Y\right),s\in [0,1].$$

(22)

If $s={\displaystyle \frac{1}{2}}$, the above formula reduces to (19). Usually, it is called the KMS (after Kubo–Martin–Schwinger) inner product. Another popular choice corresponds to $s=1$. In this case, it is usually called the GNS (after Gelfand–Naimark–Segal) inner product.

Proposition 3.

If Φ is a covariant generalized Schwarz, then its ω-dual map ${\mathrm{\Phi }}^{\ast \omega }$ is a covariant generalized Schwarz map.

Proof. 

Let us observe that the $\omega$-dual map ${\mathrm{\Phi }}^{\ast \omega }$ is again covariant and it is characterized by ‘$\omega$-transposition’ of the matrix A,

$$\tilde{A}=\left(\begin{array}{cc}\tilde{a}& {\tilde{a}}^{\prime }\\ {\tilde{b}}^{\prime }& \tilde{b}\end{array}\right)=\left(\begin{array}{cc}a& {\displaystyle \frac{{\omega }_1}{{\omega }_2}}{b}^{\prime }\\ {\displaystyle \frac{{\omega }_2}{{\omega }_1}}{a}^{\prime }& b\end{array}\right),$$

(23)

together with $\tilde{\lambda }={\lambda }^{\ast }$ and $\tilde{\mu }=\mu$. If $\omega =1\mathrm{l}$, i.e., the map $\mathrm{\Phi }$ is unital, then $\tilde{A}=A^{\mathrm{T}}$.   □

Theorem 2.

Maps Φ and its ω-dual ${\mathrm{\Phi }}^{\ast \omega }$ satisfy the following properties:

• Φ is positive if ${\mathrm{\Phi }}^{\ast \omega }$ is positive,
• Φ is completely positive if ${\mathrm{\Phi }}^{\ast \omega }$ is completely positive,
• if Φ is generalized Schwarz, then ${\mathrm{\Phi }}^{\ast \omega }$ is generalized Schwarz.

Proof. 

Note that $\tilde{a}\tilde{b}=ab$ and ${\tilde{a}}^{\prime }\tilde{b}=a^{\prime }{b}^{\prime }$. Hence, conditions for positivity (10) and complete positivity for $\mathrm{\Phi }$ and its dual ${\mathrm{\Phi }}^{\ast \omega }$ coincide. Now, since ${\mathrm{\Phi }}^{\ast \omega }$ is covariant, it is clear that ${\mathrm{\Phi }}^{\ast \omega }$ is generalized Schwarz if

$${\displaystyle \frac{{\left|\lambda \right|}^2}{a}}+{\displaystyle \frac{{\left|\mu \right|}^2}{\frac{{\omega }_1}{{\omega }_2}{b}^{\prime }}}\le b+{\displaystyle \frac{{\omega }_2}{{\omega }_1}}{a}^{\prime },{\displaystyle \frac{{\left|\lambda \right|}^2}{b}}+{\displaystyle \frac{{\left|\mu \right|}^2}{\frac{{\omega }_2}{{\omega }_1}{a}^{\prime }}}\le a+{\displaystyle \frac{{\omega }_1}{{\omega }_2}}{b}^{\prime }.$$

(24)

Note that four Ellipses (15) and (24) intersect at $(\sqrt{ab},\sqrt{a^{\prime }{b}^{\prime }})$ on the plane $\left(\right|\lambda |,|\mu \left|\right)$. Let S denote a closed convex set constrained by (15), and $\tilde{S}$ be a corresponding set constrained by (24). To prove the theorem, one has to show that $S\subset \tilde{S}$. It means that the following conditions have to be satisfied:

$$min\{a(b+b^{\prime }),b(a+a^{\prime })\le min\left\{{\displaystyle \frac{a({\omega }_{1}b+{\omega }_2{a}^{\prime })}{{\omega }_1}},{\displaystyle \frac{b({\omega }_{2}a+{\omega }_1{b}^{\prime })}{{\omega }_1}}\right\},$$

(25)

and

$$min\{a^{\prime }(b+b^{\prime }),b^{\prime }(a+a^{\prime })\}\le min\left\{{\displaystyle \frac{b^{\prime }({\omega }_{1}b+{\omega }_2{a}^{\prime })}{{\omega }_2}},{\displaystyle \frac{a^{\prime }({\omega }_{2}a+{\omega }_{1}b)}{{\omega }_2}}\right\}.$$

(26)

Note that if $\mathrm{\Phi }$ is unital, then (25) and (26) reduce to (16) and (17). Now, to check (25), let us assume that $a^{\prime }(b+b^{\prime })\le b^{\prime }(a+a^{\prime })$ or, equivalently, $a^{\prime }b\le a{b}^{\prime }$. Inserting ${\omega }_1=a+a^{\prime }$ and ${\omega }_2=b+b^{\prime }$, one easily proves that

$$a^{\prime }(b+b^{\prime })\le {\displaystyle \frac{b^{\prime }({\omega }_{1}b+{\omega }_2{a}^{\prime })}{{\omega }_2}},a^{\prime }(b+b^{\prime })\le {\displaystyle \frac{a^{\prime }({\omega }_{2}a+{\omega }_1{b}^{\prime })}{{\omega }_2}}.$$

Similarly, one proves the remaining inequalities.   □.

Example 2.

Consider again the map from Example 2 corresponding to ${\omega }_1=2$ and ${\omega }_2=5$. Its ω-dual is characterized by

$$\tilde{A}=\left(\begin{array}{cc}1& {\displaystyle \frac{4}{5}}\\ {\displaystyle \frac{5}{2}}& 3\end{array}\right),\tilde{\lambda }=\sqrt{5},\tilde{\mu }=0,$$

and it is indeed generalized Schwarz due to

$$\sqrt{5}\approx 2.23607<min\{\sqrt{11/2},\sqrt{27/5}\}\approx 2.32379.$$

Summarising: a map dual (with respect to the standard Hilbert–Schmidt inner product) to a covariant Schwarz map is always generalized Schwarz. However, it is no longer true for generalized Schwarz map. We find it rather very unsatisfactory. Note, however, that such generalized map is no longer unital and hence the standard Hilbert–Schmidt inner product does not play any distinguished role. Introducing a new Inner Product (19) and defining the corresponding $\omega$-duality, we showed that if $\mathrm{\Phi }$ is generalized Schwarz, then its $\omega$-dual is also generalized Schwarz.

The procedure proposed in the previous section enables one to define the following infinite series of covariant generalized Schwarz maps: let ${\mathrm{\Phi }}_0$ be such a map and define ${\mathrm{\Phi }}_1:={\mathrm{\Phi }}_0^{\ast {\omega }_0}$, where ${\omega }_0={\mathrm{\Phi }}_0\left(1\mathrm{l}\right)$. It is, therefore, clear that one may define an infinite series of maps via

$${\mathrm{\Phi }}_{n+1}:={\mathrm{\Phi }}^{\ast {\omega }_n}={\left({\left({\left({\mathrm{\Phi }}_0^{\ast {\omega }_0}\right)}^{\ast {\omega }_1}\right)}^{\dots }\right)}^{\ast {\omega }_n},$$

(27)

where ${\omega }_n={\mathrm{\Phi }}_n\left(1\mathrm{l}\right)$, i.e., ${\mathrm{\Phi }}_{n+1}$ is ${\omega }_n$-dual to ${\mathrm{\Phi }}_n$. Evidently, each ${\mathrm{\Phi }}_n$ is a covariant generalized Schwarz map. Equivalently, the recurrent relation may be defined in terms of the matrix $A_n$ characterizing the map ${\mathrm{\Phi }}_n$. One finds

$$A_n=\left(\begin{array}{cc}a& a_n^{\prime }\\ b_n^{\prime }& b\end{array}\right),$$

(28)

with the following recurrent relations:

$$a_{n+1}^{\prime }=a+{\displaystyle \frac{a+a_{n-1}^{\prime }}{b+b_{n-1}^{\prime }}}{b}_{n-1}^{\prime },b_{n+1}^{\prime }=b+{\displaystyle \frac{b+b_{n-1}^{\prime }}{a+a_{n-1}^{\prime }}}{a}_{n-1}^{\prime },$$

(29)

and parameters $(a_0^{\prime },b_0^{\prime })$ correspond to the map ${\mathrm{\Phi }}_0$. Let $S_n$ be a closed convex set on the $\left(\right|\lambda |,|\mu \left|\right)$-plane constrained by the corresponding ellipses,

$${\displaystyle \frac{{\left|\lambda \right|}^2}{a}}+{\displaystyle \frac{{\left|\mu \right|}^2}{a_n^{\prime }}}\le b+b_n^{\prime },\mathrm{and}{\displaystyle \frac{{\left|\lambda \right|}^2}{b}}+{\displaystyle \frac{{\left|\mu \right|}^2}{b_n^{\prime }}}\le a+a_n^{\prime }.$$

(30)

One obviously has

$$S_0\subset S_1\subset S_2\subset \dots .$$

(31)

Note that due to $a_n^{\prime }{b}_n^{\prime }=a_0^{\prime }{b}_0^{\prime }$, all pairs of Ellipses (30) intersect at $(\sqrt{ab},\sqrt{a_0^{\prime }{b}_0^{\prime }})$.

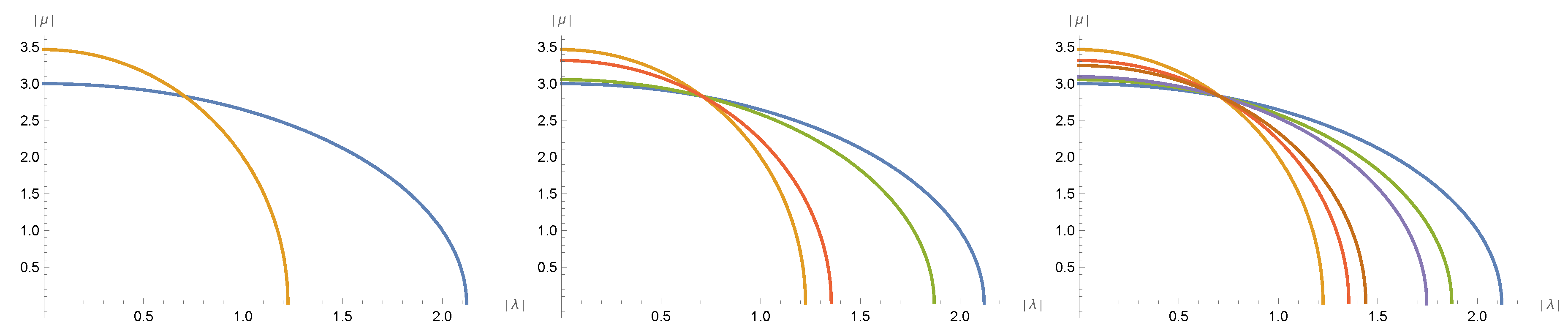
Example 3.

To illustrate how this procedure works, let us consider a map ${\mathrm{\Phi }}_0$ characterized by

$$A_0=\left(\begin{array}{cc}1& 2\\ 4& {\displaystyle \frac{1}{2}}\end{array}\right).$$

(32)

In Figure 1, we plot the corresponding pairs of ellipses for ${\mathrm{\Phi }}_0$, ${\mathrm{\Phi }}_1$, and ${\mathrm{\Phi }}_2$. Note that ellipses corresponding to ${\mathrm{\Phi }}_1$ lie between ellipses of ${\mathrm{\Phi }}_0$, and these of ${\mathrm{\Phi }}_2$ lie between ellipses of ${\mathrm{\Phi }}_1$.

Figure 1. (Color online) (left): ellipses of ${\mathrm{\Phi }}_0$, (middle): ellipses of ${\mathrm{\Phi }}_0$ and ${\mathrm{\Phi }}_1$, (right): ellipses of ${\mathrm{\Phi }}_0$, ${\mathrm{\Phi }}_1$, and ${\mathrm{\Phi }}_2$. All ellipses intersect at $(0.71,2.82)$.

Does a sequence of maps $\{{\mathrm{\Phi }}_0,{\mathrm{\Phi }}_1,{\mathrm{\Phi }}_2,\dots \}$ converge to some limiting map ${\mathrm{\Phi }}_{\infty }$? Simple analysis of recurrent Relations (29) leads to the following:

Proposition 4.

A sequence $\{{\mathrm{\Phi }}_0,{\mathrm{\Phi }}_1,{\mathrm{\Phi }}_2,\dots \}$ converges to a map ${\mathrm{\Phi }}_{\infty }$ characterized by

$$A_{\infty }=\left(\begin{array}{cc}a& a_{\infty }^{\prime }\\ b_{\infty }^{\prime }& b\end{array}\right),$$

(33)

with

$$a_{\infty }^{\prime }=\sqrt{{\displaystyle \frac{a}{b}}}\sqrt{a_0^{\prime }{b}_0^{\prime }},b_{\infty }^{\prime }=\sqrt{{\displaystyle \frac{b}{a}}}\sqrt{a_0^{\prime }{b}_0^{\prime }}.$$

(34)

In Figure 2 we illustrate the convergence of ellipses corresponding to maps ${\mathrm{\Phi }}_n$ to the limiting ellipse corresponding to ${\mathrm{\Phi }}_{\infty }$. Moreover, if the parameters $\lambda$ and $\mu$ are real, then a limiting map is ${\omega }^{\infty }$-selfdual (where ${\omega }^{\infty }:={\mathrm{\Phi }}_{\infty }\left(1\mathrm{l}\right)$). One finds

$${\omega }_1^{\infty }=a+a_{\infty }^{\prime }=\sqrt{{\displaystyle \frac{a}{b}}}\left(\sqrt{ab}+\sqrt{a_0^{\prime }{b}_0^{\prime }}\right),{\omega }_2^{\infty }=b+b_{\infty }^{\prime }=\sqrt{{\displaystyle \frac{b}{a}}}\left(\sqrt{ab}+\sqrt{a_0^{\prime }{b}_0^{\prime }}\right),$$

(35)

and hence

$${\displaystyle \frac{{\omega }_1^{\infty }}{{\omega }_2^{\infty }}}={\displaystyle \frac{a}{b}}.$$

(36)

Figure 2. (Color online) A central light blue ellipse corresponds to the limiting map ${\mathrm{\Phi }}_{\infty }$.

Remark 2.

Note that if $a=b$, then

$$A_n\to A_{\infty }=\left(\begin{array}{cc}a& \sqrt{a_0^{\prime }{b}_0^{\prime }}\\ \sqrt{a_0^{\prime }{b}_0^{\prime }}& a\end{array}\right),$$

(37)

and hence ${\omega }^{\infty }\propto 1\mathrm{l}$. In particular, if ${\mathrm{\Phi }}_0$ is unital and self-dual, i.e., $a=b$ and $a_0^{\prime }=b_0^{\prime }=1-a$, then ${\mathrm{\Phi }}_n={\mathrm{\Phi }}_0$ for $n=1,2,3,\dots$ and hence ${\mathrm{\Phi }}_{\infty }={\mathrm{\Phi }}_0$.

Remark 3.

Note that positivity Condition (10) implies

$$\left|\lambda \right|+\left|\mu \right|\le \sqrt{ab}+\sqrt{a_0^{\prime }{b}_0^{\prime }}\le {\displaystyle \frac{1}{2}}\mathrm{Tr}{\omega }^{\infty },$$

(38)

and the last inequality is saturated only if $a=b$.

4. Discussion

The map characterized by $A_{\infty }$ is generalized Schwarz if and only if

$${\displaystyle \frac{{\left|\lambda \right|}^2}{a}}+{\displaystyle \frac{{\left|\mu \right|}^2}{a_{\infty }^{\prime }}}\le b+b_{\infty }^{\prime },{\displaystyle \frac{{\left|\lambda \right|}^2}{b}}+{\displaystyle \frac{{\left|\mu \right|}^2}{b_{\infty }^{\prime }}}\le a+a_{\infty }^{\prime },$$

(39)

where $(a_{\infty }^{\prime },b_{\infty }^{\prime })$ are defined in (34). Interestingly, both ellipses in (39) coincide and hence the asymptotic map is controlled by a single elliptic condition. Note that the above condition is invariant with respect to the following rescaling transformation:

$$a\to ra,b\to {\displaystyle \frac{1}{r}}b,$$

(40)

with arbitrary $r>0$. Let $S(a,a^{\prime },b,b^{\prime })$ denote a convex set on the $\left(\right|\lambda |,|\mu \left|\right)$-plane constrained by (39). One has

$$S(a,a^{\prime },b,b^{\prime })=S(ra,r{a}^{\prime },b/r,b^{\prime }/r),$$

(41)

for any $r>0$. Taking $r=\sqrt{{\displaystyle \frac{b}{a}}}$, one finds

$$S(a,a_{\infty }^{\prime },b,b_{\infty }^{\prime })=S(\sqrt{ab},\sqrt{a_0^{\prime }{b}_0^{\prime }},\sqrt{ab},\sqrt{a_0^{\prime }{b}_0^{\prime }})$$

(42)

and hence both $A_{\infty }$ and the following symmetric matrix

$$A_{\infty }^{\mathrm{sym}}=\left(\begin{array}{cc}\sqrt{ab}& \sqrt{a_0^{\prime }{b}_0^{\prime }}\\ \sqrt{a_0^{\prime }{b}_0^{\prime }}& \sqrt{ab}\end{array}\right)=:\left(\begin{array}{cc}\alpha & \beta \\ \beta & \alpha \end{array}\right),$$

(43)

give rise to the same asymptotic ellipse

$${\displaystyle \frac{{\left|\lambda \right|}^2}{\alpha }}+{\displaystyle \frac{{\left|\mu \right|}^2}{\beta }}\le \alpha +\beta .$$

(44)

It is, therefore, clear that the asymptotic ellipse depends only upon ($\alpha :=\sqrt{ab}$, $\beta :=\sqrt{a_0^{\prime }{b}_0^{\prime }}$).

Corollary 1.

A covariant map corresponding to symmetric Matrix (43) is

1. 

unital and trace preserving if $\alpha +\beta =1$,

2. 

positive iff $\left|\lambda \right|+\left|\mu \right|\le \alpha +\beta$,

3. 

completely positive if $\left|\lambda \right|\le \alpha$ and $\left|\mu \right|\le \beta$,

4. 

generalized Schwarz if (44) holds.

Example 4.

The first example of a Schwarz map in $M_2\left(\mathbb{C}\right)$ which is not dual-positive was provided by Choi [12],

$$\mathrm{\Phi }\left(X\right)={\displaystyle \frac{1}{4}}1\mathrm{l}\mathrm{Tr}X+{\displaystyle \frac{1}{2}}{X}^{\mathrm{T}}.$$

(45)

It corresponds to

$$A=\left(\begin{array}{cc}3/4& 1/4\\ 1/4& 3/4\end{array}\right),\lambda =0,\mu =\sqrt{1-a}=1/2.$$

(46)

It is clear that it has a form of (43) and saturates (44).

5. Conclusions

We analyzed a class of Schwarz and generalized Schwarz maps in $M_2\left(\mathbb{C}\right)$. A map dual (with respect to the standard Hilbert–Schmidt inner product) to a covariant Schwarz map is always generalized Schwarz. However, it is no longer true for generalized Schwarz map. We found it rather unsatisfactory and proposed a simple remedy. A generalized Schwarz map is no longer unital and hence the standard Hilbert–Schmidt inner product does not play any distinguished role. Introducing a new inner product (19) and defining the corresponding $\omega$-duality we showed that if $\mathrm{\Phi }$ is generalized Schwarz then its $\omega$-dual is also generalized Schwarz. This procedure gives rise to the whole infinite hierarchy of maps $\left\{{\mathrm{\Phi }}_n\right\}$ which are generalized Schwarz whenever ${\mathrm{\Phi }}_0$ is generalized Schwarz. It is shown that sequence $\left\{{\mathrm{\Phi }}_n\right\}$ converges to an asymptotic map ${\mathrm{\Phi }}_{\infty }$ which is generalized Schwarz if (44) holds.

It would be interesting to generalize this simple observation for other classes of maps, in particular to consider maps in $M_n\left(\mathbb{C}\right)$ with $n>2$.