Hyperbolic Non-Polynomial Spline Approach for Time-Fractional Coupled KdV Equations: A Computational Investigation
Abstract
1. Introduction
2. Constructing the Hyperbolic Non-Polynomial Spline
3. Assessment of Error with Truncation
4. Application of Time-Fractional Coupled KdV Equations with Conformable HNPSM
- 1.
- for .
- 2.
- for all .
- 3.
- if is a constant function.
- 4.
- .
- 5.
- .
- 6.
- should exhibit differentiability.
5. CHNPSM Stabilities
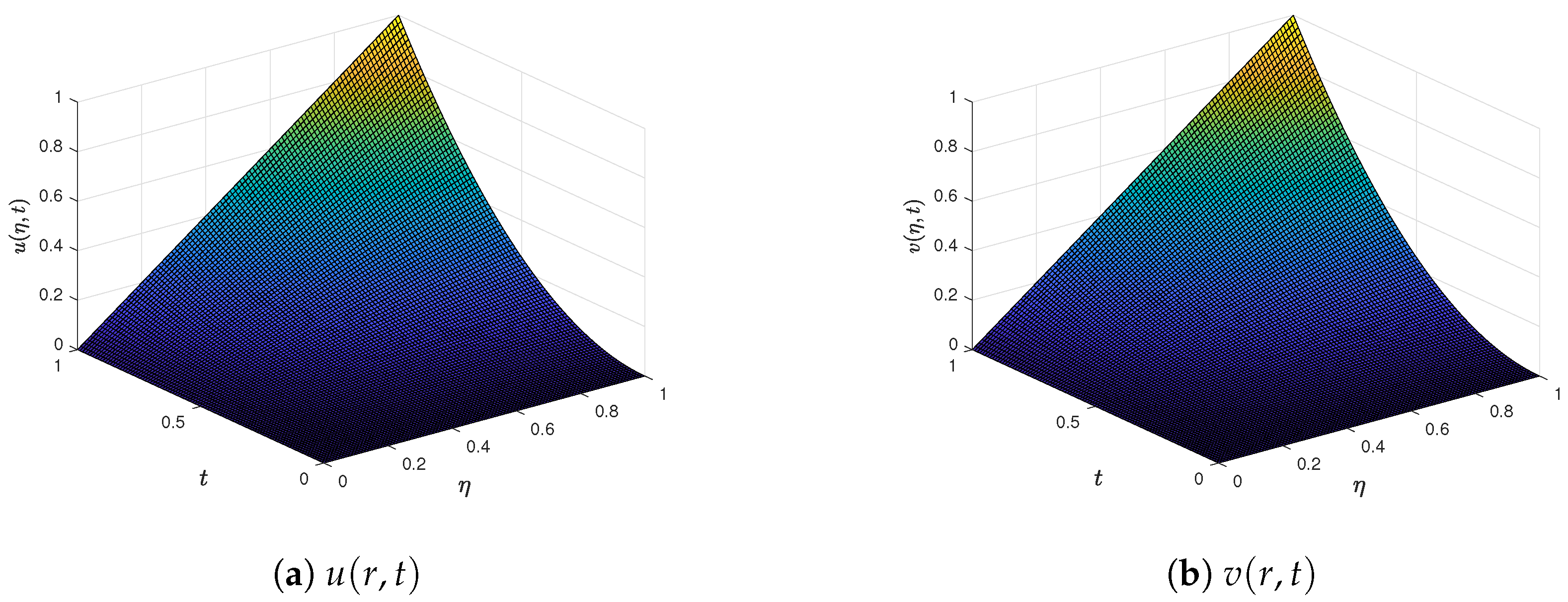
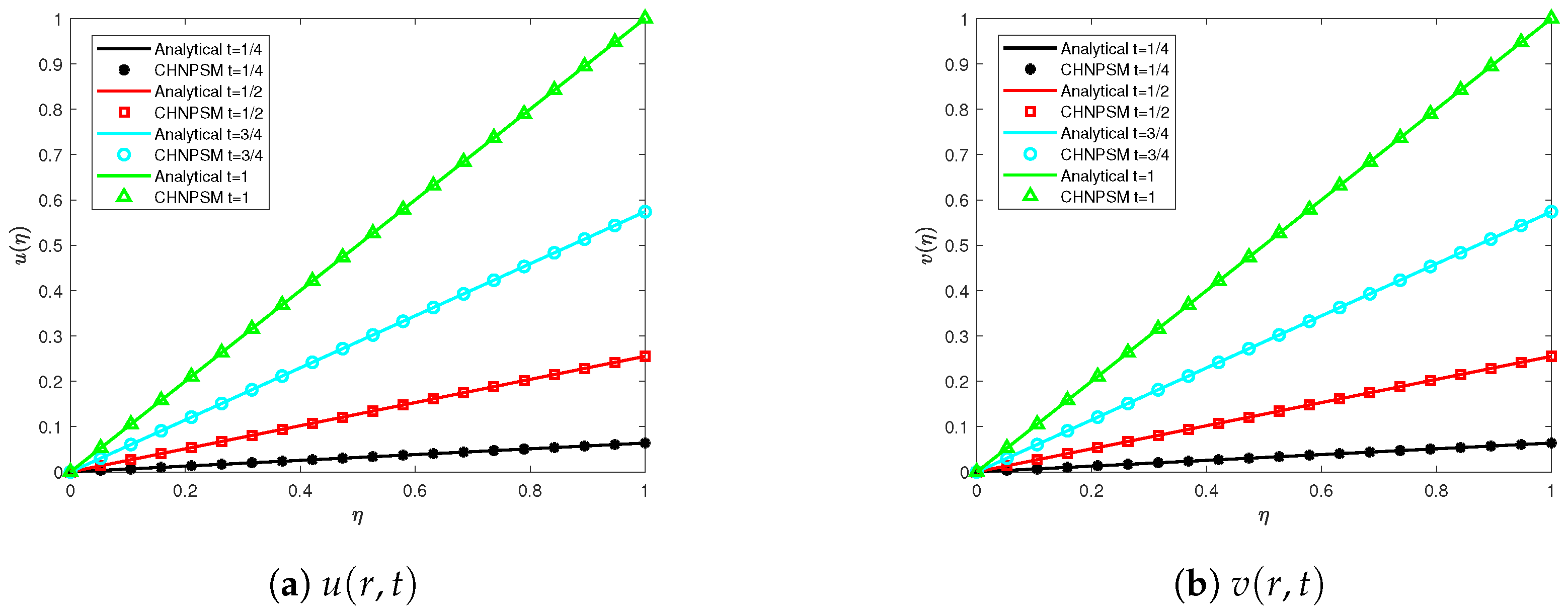
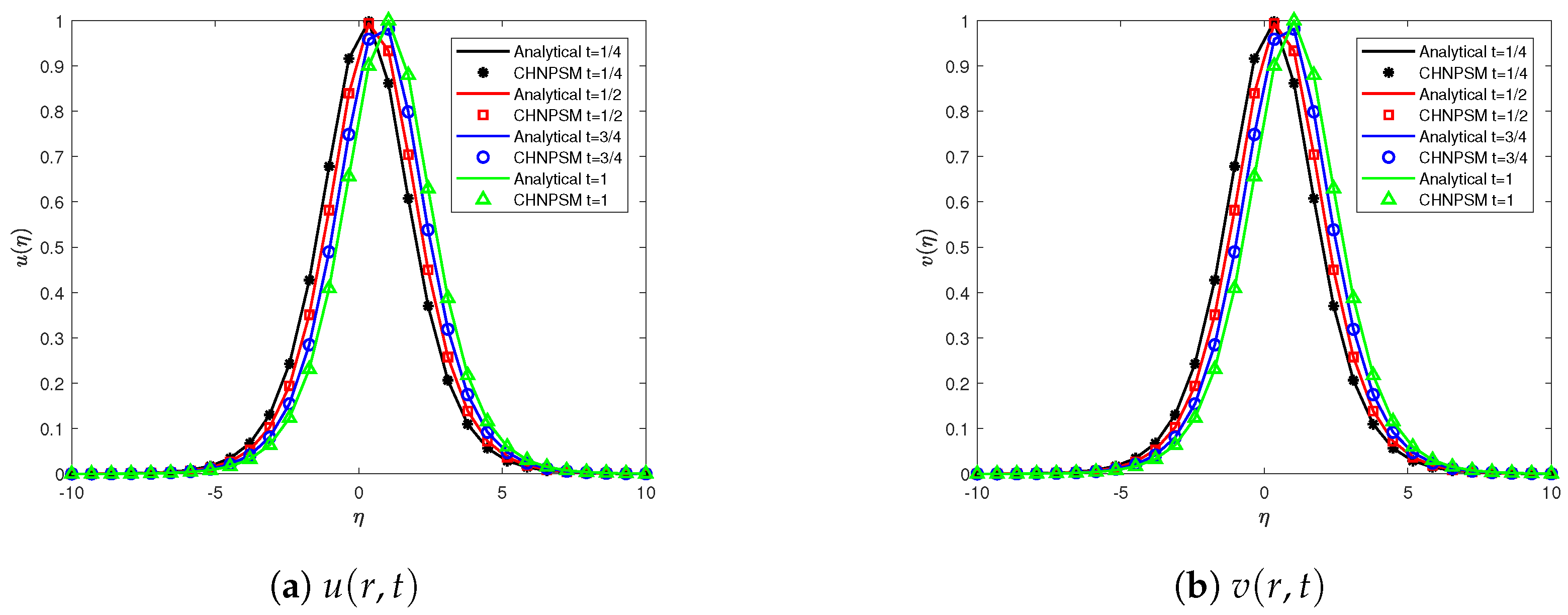
6. Evaluation of Numerical Performance
7. Computational Efficiency and Symmetry Analysis
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Debnath, L. A brief historical introduction to fractional calculus. Int. J. Math. Educ. Sci. Technol. 2004, 35, 487–501. [Google Scholar] [CrossRef]
- Abu Arqub, O. Numerical solutions for the Robin time-fractional partial differential equations of heat and fluid flows based on the reproducing kernel algorithm. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 828–856. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional derivatives for physicists and engineers. Chaos 2013, 27, 214–220. [Google Scholar]
- Agarwal, P.; Baleanu, D.; Chen, Y.; Momani, S.; Machado, T. Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier/North-Holland: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Noureen, R.; Naeem, M.N.; Baleanu, D.; Mohammed, P.O.; Almusawa, M.Y. Application of trigonometric B-spline functions for solving Caputo time fractional gas dynamics equation. AIMS Math. 2023, 8, 25343–25370. [Google Scholar] [CrossRef]
- Sadiya, U.; Inc, M.; Arefin, M.A.; Uddin, M.H. Consistent travelling waves solutions to the non-linear time fractional Klein–Gordon and Sine-Gordon equations through extended tanh-function approach. J. Taibah Univ. Sci. 2022, 16, 594–607. [Google Scholar] [CrossRef]
- Li, M.; Ding, X.; Xu, Q. Non-polynomial spline method for the time-fractional nonlinear Schrödinger equation. Adv. Differ. Equ. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Yousif, M.A.; Hamasalh, F.K. The fractional non-polynomial spline method: Precision and modeling improvements. Math. Comput. Simul. 2024, 218, 512–525. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M.; Hamanah, W.M. Certain new models of the multi-space fractal-fractional Kuramoto-Sivashinsky and Korteweg-de Vries equations. Mathematics 2022, 10, 1089. [Google Scholar] [CrossRef]
- Zou, G. Numerical solutions to time-fractional stochastic partial differential equations. Numer. Algorithms 2019, 82, 553–571. [Google Scholar] [CrossRef]
- Mohamed, M.Z.; Hamza, A.E.; Sedeeg, A.K.H. Conformable double Sumudu transformations: An efficient approximation solutions to the fractional coupled Burger’s equation. Ain Shams Eng. J. 2023, 14, 101879. [Google Scholar] [CrossRef]
- El-Ajou, A.; Al-Smadi, M.; Oqielat, M.N.; Momani, S.; Hadid, S. Smooth expansion to solve high-order linear conformable fractional PDEs via residual power series method: Applications to physical and engineering equations. Ain Shams Eng. J. 2020, 11, 1243–1254. [Google Scholar] [CrossRef]
- Ragula, K.; Soujanya, G.B.S.L.; Swarnakar, D. Computational approach for a singularly perturbed differential equations with mixed shifts using a non-polynomial spline. Int. J. Anal. Appl. 2023, 21, 1–20. [Google Scholar] [CrossRef]
- Mahdy, A.M.S. Numerical solutions for solving model time-fractional Fokker–Planck equation. Numer. Methods Partial Differ. Equ. 2021, 37, 1120–1135. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Mandal, H.; Bira, B. Lie symmetry and exact solution of the time-fractional Hirota-Satsuma Korteweg-de Vries system. Russ. J. Math. Phys. 2021, 28, 284–292. [Google Scholar] [CrossRef]
- Khan, K.; Ali, A.; De la Sen, M.; Irfan, M. Localized modes in time-fractional modified coupled Korteweg-de Vries equation with singular and non-singular kernels. AIMS Math. 2022, 7, 1580–1602. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S. A reliable technique to study nonlinear time-fractional coupled Korteweg–de Vries equations. Adv. Differ. Equ. 2020, 2020, 169. [Google Scholar] [CrossRef]
- Arifeen, S.U.; Haq, S. Petrov–Galerkin approximation of time-fractional coupled Korteweg–de Vries equation for propagation of long wave in shallow water. Math. Comput. Simul. 2023, 207, 226–242. [Google Scholar] [CrossRef]
- Hussain, M.; Haq, S. Radial basis functions collocation method for numerical solution of coupled Burgers’ and Korteweg-de Vries equations of fractional order. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 707–725. [Google Scholar] [CrossRef]
- Albuohimad, B.; Adibi, H.; Kazem, S. A numerical solution of time-fractional coupled Korteweg-de Vries equation by using spectral collection method. Ain Shams Eng. J. 2018, 9, 1897–1905. [Google Scholar] [CrossRef]
- Alzahrani, A.B.M.; Alhawael, G. Novel computations of the time-fractional coupled Korteweg–de Vries equations via non-singular kernel operators in terms of the natural transform. Symmetry 2023, 15, 2010. [Google Scholar] [CrossRef]
- Hussain, M.; Haq, S.; Ghafoor, A. Meshless spectral method for solution of time-fractional coupled KdV equations. Appl. Math. Comput. 2019, 341, 321–334. [Google Scholar] [CrossRef]
- Kawala, A.M.; Abdelaziz, H.K. Crank–Nicolson finite difference method for time-fractional coupled KdV equation. Int. J. Comput. Math. 2021, 98, 2564–2575. [Google Scholar] [CrossRef]
- Saad, K.M.; Srivastava, H.M. Numerical solutions of the multi-space fractional-order coupled Korteweg-de Vries equation with several different kernels. Fractal Fract. 2023, 7, 716. [Google Scholar] [CrossRef]
- Yaşar, E.; Yıldırım, Y.; Khalique, C.M. Lie symmetry analysis, conservation laws and exact solutions of the seventh-order time fractional Sawada–Kotera–Ito equation. Results Phys. 2016, 6, 322–328. [Google Scholar] [CrossRef][Green Version]
- Hu, J.; Ye, Y.; Shen, S.; Zhang, J. Lie symmetry analysis of the time fractional KdV-type equation. Appl. Math. Comput. 2014, 233, 439–444. [Google Scholar] [CrossRef]
- Akbulut, A.; Taşcan, F. Lie symmetries, symmetry reductions and conservation laws of time fractional modified Korteweg–de Vries (mkdv) equation. Chaos Solitons Fractals 2017, 100, 1–6. [Google Scholar] [CrossRef]
- Yu, J.; Feng, Y. Symmetry analysis, exact solutions and conservation laws of time fractional Caudrey–Dodd–Gibbon equation. Ex. Counterexamples 2024, 6, 100166. [Google Scholar] [CrossRef]
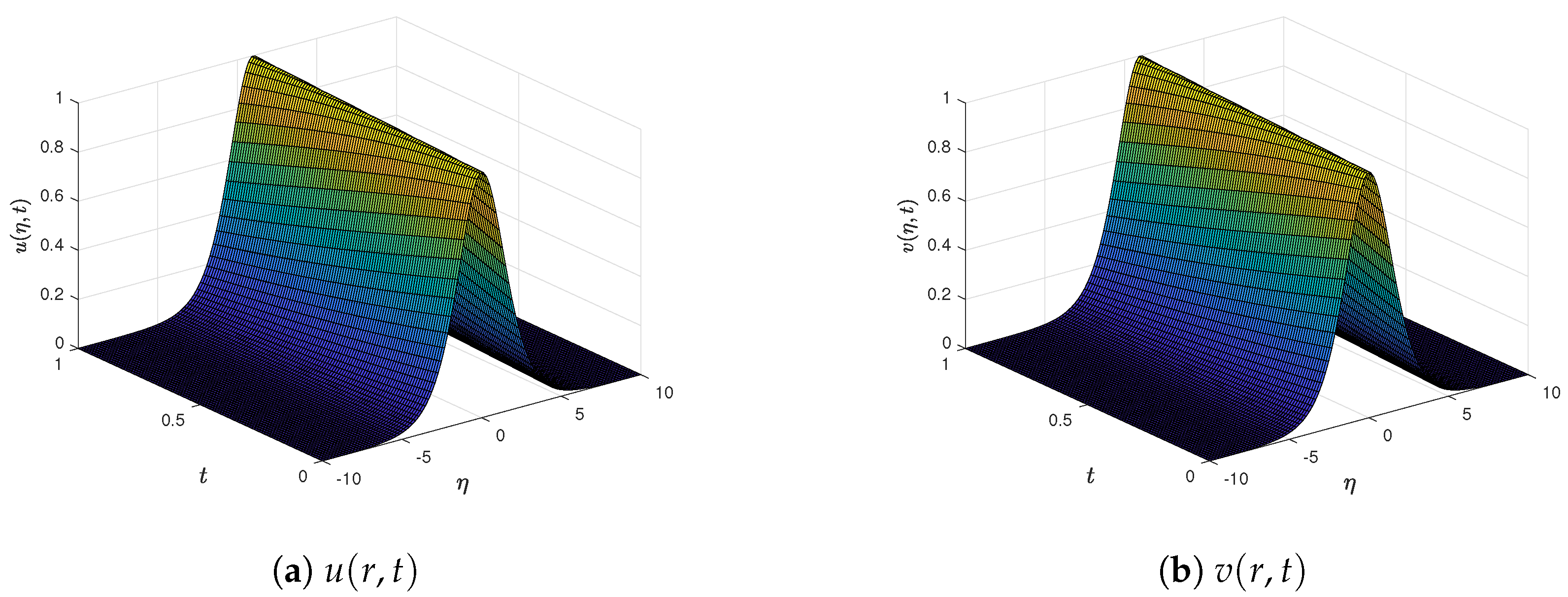
| CHNPSM | [26] | ||||
|---|---|---|---|---|---|
| CHNPSM | [22] | ||||
|---|---|---|---|---|---|
| 1 | |||||
| 1 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vivas-Cortez, M.; Yousif, M.A.; Mohammed, P.O.; Lupas, A.A.; Ibrahim, I.S.; Chorfi, N. Hyperbolic Non-Polynomial Spline Approach for Time-Fractional Coupled KdV Equations: A Computational Investigation. Symmetry 2024, 16, 1610. https://doi.org/10.3390/sym16121610
Vivas-Cortez M, Yousif MA, Mohammed PO, Lupas AA, Ibrahim IS, Chorfi N. Hyperbolic Non-Polynomial Spline Approach for Time-Fractional Coupled KdV Equations: A Computational Investigation. Symmetry. 2024; 16(12):1610. https://doi.org/10.3390/sym16121610
Chicago/Turabian StyleVivas-Cortez, Miguel, Majeed A. Yousif, Pshtiwan Othman Mohammed, Alina Alb Lupas, Ibrahim S. Ibrahim, and Nejmeddine Chorfi. 2024. "Hyperbolic Non-Polynomial Spline Approach for Time-Fractional Coupled KdV Equations: A Computational Investigation" Symmetry 16, no. 12: 1610. https://doi.org/10.3390/sym16121610
APA StyleVivas-Cortez, M., Yousif, M. A., Mohammed, P. O., Lupas, A. A., Ibrahim, I. S., & Chorfi, N. (2024). Hyperbolic Non-Polynomial Spline Approach for Time-Fractional Coupled KdV Equations: A Computational Investigation. Symmetry, 16(12), 1610. https://doi.org/10.3390/sym16121610












