Abstract
Coalitional game with uncertain payoffs driven by uncertain variables stands for uncertain coalitional game. A -pessimistic Shapley value as the solution of uncertain coalitional game is proposed in this paper, which can be played an important role in solving the problem of profit allocation. Moreover, the -pessimistic Shapley value is proved to be the only value satisfying symmetry, dummy and additivity. Based on the -pessimistic Shapley value, a new method of teaching quality evaluation in the institutions of higher learning is presented. In order to obtain the index of teaching quality evaluation in uncertain environments, an -pessimistic multilinear extension is defined. Meanwhile, some properties of -pessimistic multilinear extension are investigated successfully. Moreover, the problem of teaching quality evaluation are considered in this paper.
1. Introduction
Modern game theory was pioneered by von Neumann [1]. As we consider the enforcement of cooperation, the coalitional game was provided by von Neumann et al. [2], which only studied two fields, one that we must consider how to construct the coalition, and another fields that, when the coalition was built, we must figure out how to assign the profit. Many methods have been proposed to solve the profit allocation, such as Shapley value [3], stable set [2], core [4] and kernel [5]. The Shapley value was first proposed by Shapley [3]; it has been applied in many areas, such as the social network [6], the population cost reduction [7] and the cooperative ventures [8].
In order to count the Shapley value of the coalitional game with larger members, one of the principal difficulties is obtaining the sum with a very large number of terms by its definition.Thus, a multilinear extension of an n-person game was introduced to count the Shapley value by Owen [9]. Later on, the multilinear extension was offered to computer the Banzhaf value by Owen [10], where the Banzhaf value was proposed to measure the power for the coalitional game by Banzhaf [11]. Moreover, the modified multiliner extension was provided to calculate the coalitional structure value by Owen and Winter [12], the Johnston index by Johnston [13], the Deegan–Packel index by Deegan and Packel [14] and the Public Good index (Holler [15]) by Alonso-Meijide et al. [16], respectively.
As the payoffs of the coalitional game affected by “noise” were modeled by uncertain variables in uncertainty theory, two kinds of uncertain Shapley values were proposed by Gao et al. [17]. The uncertain variable was defined by Liu [18], which has been extensively developed in many fields, such as finance [19], statistic [20] and time series [21]. Uncertainty theory was first applied in game theory by Gao [22], which provided an uncertain bimatrix game. Thereafter, uncertain differential games were provided by Yang and Gao [23]. Moreover, uncertainty theory was also applied in other different styles of games; for example, the uncertain bimatrix game was given by Yang and Gao [24] and the uncertain extensive game was presented by Wang et al. [25]. Moreover, the uncertain core of the uncertain coalitional game was proposed by Yang et al. [26].
Teaching quality evaluation has been investigated by many scholars; for example, Wen et al. [27] solved the cloud matter-element evaluation on the classroom teaching quality of postgraduates based on game theory, Xia [28] presented the study on the system weakness of teaching evaluation and evaluation from the perspective of game theory and Pieter and Bert [29] considered the the validity of student evaluation of teaching by using game theory. At present, the system of teaching quality evaluation is based on the real number. But there exist many uncertain factors in the process of education, which can be described by uncertain variables, and the process of teaching quality evaluation can be modeled by uncertain coalitional game. In this paper, a -pessimistic Shapley value as the solution of uncertain coalitional game is proposed, the -pessimistic Shapley value is proved to be the only value satisfying symmetry, dummy and additivity. Based on the -pessimistic Shapley value, a new method of teaching quality evaluation in the institutions of higher learning is presented. In order to obtain the index of teaching quality evaluation in uncertain environments, an -pessimistic multilinear extension is defined and some properties of -pessimistic multilinear extension are investigated successfully.
The structure of this paper is designed as follows. The definition of -pessimistic Shapley value and the properties of -pessimistic Shapley value are presented in Section 2. The definition of -pessimistic multilinear extension and the properties of -pessimistic multilinear extension are investigated in Section 3. The new method of teaching quality evaluation based on the -pessimistic Shapley value is given in Section 4. Finally, the conclusions are shown in Section 5.
2. An -Pessimistic Shapley Value
The concept of the -pessimistic Shapley value is proposed in this section. Moreover, the -pessimistic Shapley value is proved to be the only value satisfying symmetry, dummy and additivity.
Definition 1.
The of uncertain coalitional game satisfying the following condition:
is called the α-pessimistic Shapley value, where w is a uncertain variable, and
where is the inverse uncertainty distribution of uncertain variable w in the work of Liu [18]. u is the number of players in U, , stands for the α-pessimistic marginal contribution of player n to coalition U.
Definition 2.
If the following condition is established:
then the player n is called a dummy in uncertain coalition game for each coalition U that includes n.
Definition 3.
If the following condition is established:
then the players n and m are called the interchangeable in uncertain coalitional game .
Now, the characterization of the -pessimistic Shapley value is introduced as follows:
- Symmetry: If n and m are interchangeable in uncertain coalitional game , then ;
- Dummy: If n is a dummy in uncertain coalitional game , then ;
- Additivity: For any two uncertain coalition games and , there isfor all , where is defined as
Theorem 1.
The α-pessimistic Shapley value of uncertain coalition game is the only value that satisfies symmetry, dummy and additivity.
Proof.
The process of proof is similar to the Theorem 3.1 in the work of Gao et al. [17]. So we omit it here. □
3. An -Pessimistic Multilinear Extension
From the Definition 1, we see that -pessimistic Shapley value is a real valued function of , where and . We can also interpret as the set of all vectors (), whose components are either 0 or 1. Thus, it also seems reasonable to try to extend it through the cube
According to the above analysis, we can define the -pessimistic multilinear extension.
Definition 4.
Let uncertain payoff w be an n-person uncertain coalitional game with carrier . The α-pessimistic multilinear extension of w is a function defined by
for , .
According to Definition 4, we can give a probabilistic interpretation for . Assume that a coalition is to be formed at random, we set ℑ to be random coalition, and let the event
have probability (). Moreover, we assume that the events are independent, and for any fixed , we obtain the probability of the event U,
Thus,
Under the given randomization scheme, can be thought of as the random expectation of . To better understand the -pessimistic multilinear extension, we also provide two theorems as follows:
Theorem 2.
Assume that is the α-pessimistic multilinear extension, then
- (1)
- is linear in each ;
- (2)
- be coincides with ;
- (3)
- is unique with respect to the above two properties.
Proof.
(1), From the shape of the , each of the terms
is linear in each . Hence, the sum of such terms is also linear in each .
(2), For , let be the U-corner of the cube,
Then,
It is easy to see that, if , then the term in
vanishes. If there is some , the corresponding ; if there is some , the corresponding . In either case, at least one of the factors vanishes, so the entire product vanishes. If , then the term in braces is equal to 1. Thus,
and coincide with .
(3), We first point out that a -pessimistic multilinear function of n variables, being a polynomial, has the form
and depends on the constants . According to the Equation (1) of , Equation (2) reduces to
so that the condition reduces to
for all . This is a system of linear equations in the unknowns . But for a linear system, this means that the corresponding matrix of coefficients is nonsingular, and so the system always has a unique solution. Therefore, we conclude that has a unique . □
Theorem 3.
Let v and w be the uncertain payoff for the coalitional games with the same player set S, and let and be the corresponding α-pessimistic multilinear extension. Then, for any scalars a and b, the game has the .
Proof.
Assume that
for , and
for . Let be the -pessimistic multilinear extension of , so,
□
Theorem 4.
Assume that is the n-th partial derivative of ; then, we have the relationship between the α-pessimistic Shapley value and the α-pessimistic multilinear extension,
Proof.
Let be the n-th partial derivative of , we have
Assume that ; this will reduce to
In particular, we set , and have
where u is the cardinality of U. Integrating this, we obtain
Thus, the -pessimistic Shapley value is obtained with a totally different way by integrating the partial derivatives of along the main diagonal of the cube . Next, we provide an example to present how to count the -pessimistic Shapley value by the -pessimistic multilinear extension. □
Example 1.
In a three-person uncertain coalitional game, their uncertain payoffs are given as
As we consider taking the α-pessimistic value criterion, their -pessimistic values are obtained:
According to the definition of the α-pessimistic multilinear extension, we have
and the partial derivative of ,
By means of Theorem 4, we can obtain the α-pessimistic Shapley value
Thus, we can computer the α-pessimistic Shapley value by the α-pessimistic multilinear extension.
4. A New Method of Teaching Quality Evaluation
The index of teaching quality evaluation includes slides, blackboard, cartoon, game, etc. The teaching method of slides means that slide equipment is used to present images of teaching contents, and presents complex concepts and theories becoming concrete, which use slides to assist teaching, and display teaching content through visual elements (such as pictures, charts, animations, etc.) to help students better understand and remember. The teaching method of the blackboard is an indispensable part of teaching; through different design methods and types, it effectively conveys knowledge, helping students understand and remember. The animation teaching method is an innovative teaching method in order to improve students’ learning effect and interest by animation. The teaching method of the game is an innovative teaching strategy, which integrates the form and principle of games into teaching activities, aiming at stimulating students’ learning interest and initiative, and promoting students’ active participation and active learning.
Theorem 5.
Assume that the index of teaching quality evaluation is the uncertain coalitional game , , then the single index of teaching quality evaluation is
where is the n-th partial derivative of the α-pessimistic multilinear extension, w stands for the uncertain variable and
where is the inverse uncertainty distribution of uncertain variable w in the work of Liu [18].
Case 1.
In fact, the teaching quality evaluation is a coalitional game, which can be solved by the Shapley value. Then, , 1: Slides, 2: Blackboard, 3: Cartoon. In the specific teaching environment, the index of teaching quality evaluation for the alliance are zigzag uncertain variables denoted by, where a, b, c are real numbers with in reference [18]. The inverse uncertainty distribution of zigzag uncertain variable is
They are presented as below:
Firstly, we take the -pessimistic criterion; then, the -pessimistic index of teaching quality evaluation for the alliance is given as follows:
Then, the index of teaching quality evaluation is counted by means of the -pessimistic multilinear extension
Case 2.

Through experiments, it has been demonstrated that there are many types of education in the institutions of higher learning, the success of which must be approved by at least: 1. Online education and offline education; 2. Two of the four teaching tools; 3. Either class lecture and one of the teaching methods, or all three of the teaching methods. Setting this as a simple game, we note that we have a natural division of the education in the institutions of higher learning into three subsets. There are the teaching locations
the teaching tools
and the teaching methods
Moreover, we find the game of the education can be represented as
where is a two-player simple game with members in which the larger coalitional is the only winning coalition; is a four-player simple game with members in which any two-player coalition (or larger) wins; and is a four-player simple game with members . In order to analyze the index of each area, we assume that v is a zigzag uncertain variable
Therefore, we can consider the game of the education as an uncertain composition game. For here, we have the -pessimistic multilinear extension
and its partial derivative at the points (),
For , we obtain the -pessimistic multilinear extension
and its partial derivative at the points (),
Next, for , we have
and its partial derivative at the points (),
Moreover, the -pessimistic values of v are provided as
Then, we can obtain the -pessimistic multilinear extension
and its partial derivatives,
At the points (),

Table 1.
Index for each area.
Thus, we have the index for each area, in order to simplify the name of area, we set to represent the online education, offline education, slide, blackboard, cartoon, game, class lecture, questions and answers in class, group discussion and teaching in project.
As we take the -pessimstic value criterion, the changes from 0.1 to 0.9 and we obtain the -pessimistic Shapley value for each area, and present it in Table 2 and Figure 1.

Table 2.
-pessimistic Shapley value with different .
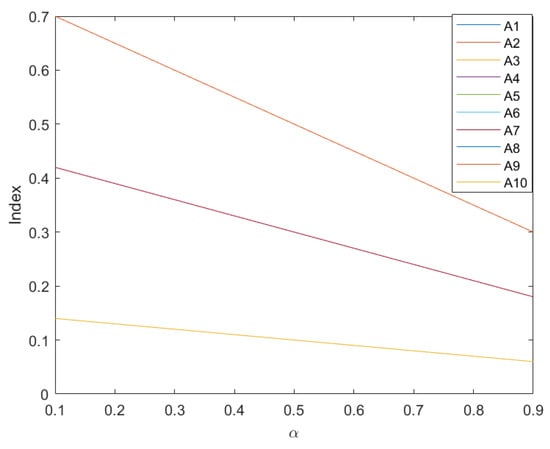
Figure 1.
-pessimistic Shapley value with different from 0.1 to 0.9.
Based on the above table, we found that and have the same power index, while , , , , , , and also have the same power index. In order to consider how the risk affects the index of the education, we give the curve graph of the -pessimistic Shapley value with different from 0.1 to 0.9. We can obtain from the above curve that the -pessimistic value of each area decrease with the confidence level . That is to say, when the risk is decreasing, the confidence level will be decreasing; then, the index will be higher. If each area wants to obtain a higher index, they should adjust their confidence level to be smaller.
5. Conclusions
The -pessimistic Shapley values were defined, and their properties were discussed in this paper. Based on the -pessimistic Shapley value, a new method of teaching quality evaluation is proposed. In order to obtain the index of teaching quality evaluation, an -pessimistic multilinear extension was provided, and the properties of the -pessimistic multilinear extension were presented. Moreover, the relationship between the -pessimistic Shapley value and the -pessimistic multilinear extension were given, which could be applied to count the -pessimistic Shapley value by means of the -pessimistic multilinear extension. Finally, the problem of teaching quality evaluation in uncertain environments was solved in this paper.
Based on the process of exploring the -pessimistic Shapley value, -pessimistic core, -pessimistic stable set, -pessimistic Bargaing set, -pessimistic Kernel and -pessimistic Nucleolus for the solutions of uncertain coalitional games can be investigated in the future.
Funding
This work was supported by the Science and Technology Innovation Project of Beijing Forestry University (BLX202244).
Institutional Review Board Statement
This paper does not contain any studies with human participants or animals performed by any of the authors.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Neumann, J.V. Zur Theorie der Gesellschaftsspiele. Math. Ann. 1928, 100, 295–320. [Google Scholar] [CrossRef]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Shapley, L. A value for n-person games. Ann. Math. Stud. 1953, 28, 307–318. [Google Scholar]
- Aumann, R.; Maschler, M. The bargainning set for cooperative games. Adv. Game Theory 1964, 52, 443–476. [Google Scholar]
- Davis, M.; Maschler, M. The kernel of a cooperative game. Nav. Res. Logist. Q. 1965, 12, 223–259. [Google Scholar] [CrossRef]
- Suri, N.; Narahari, Y. A Shapley value based approach to discover influential nodes in social networks. IEEE Trans. Autom. Sci. Eng. 2011, 8, 130–147. [Google Scholar]
- Petrosjan, L.; Zaccour, G. Time-consistent Shapley value allocation of pollution cost reduction. J. Econ. Dyn. Control 2003, 27, 381–398. [Google Scholar] [CrossRef]
- Brink, R.; Levinsky, R.; Zeleny, M. The Shapley value, the proper Shapley value, and sharing rules for cooperative ventures. Oper. Res. Lett. 2020, 48, 55–60. [Google Scholar] [CrossRef]
- Oven, G. Multilinear extensions of games. Manag. Sci. 1972, 18, 64–79. [Google Scholar] [CrossRef]
- Owen, G. Multilinear extensions and the Banzhaf value. Nav. Res. Logist. Q. 1975, 22, 741–750. [Google Scholar] [CrossRef]
- Banzhaf, J. Weighted voting doesn’t work: A mathematical analysis. Rutgers Law Rev. 1964, 19, 317–343. [Google Scholar]
- Owen, G.; Winter, E. The multilinear extension and the coalition structure value. Games Econ. Behav. 1992, 4, 582–587. [Google Scholar] [CrossRef]
- Johnston, R. On the measurement of power: Some reactions to Laver. Environ. Plan. A 1978, 10, 907–914. [Google Scholar] [CrossRef]
- Deegan, J.; Packel, E. A new index of power for simple n-person games. Int. J. Game Theory 1978, 7, 113–123. [Google Scholar] [CrossRef]
- Holler, M. Forming coalitions and measuring voting power. Political Stud. 1982, 30, 262–271. [Google Scholar] [CrossRef]
- Alonso-Meijide, J.; Casas-M<i>e</i>´ndez, B.; Holler, M.; Lorenzo-Freire, S. Computing power indices: Multilinear extensions and new characterizations. Eur. J. Oper. Res. 2008, 188, 540–554. [Google Scholar] [CrossRef][Green Version]
- Gao, J.W.; Yang, X.F.; Liu, D. Uncertain Shapley value of coalitional game with application to supply chain alliance. Appl. Soft Comput. 2017, 56, 551–556. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory, 2nd ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Liu, B. Some research problems in uncertainty theory. J. Uncertain Syst. 2009, 3, 3–10. [Google Scholar]
- Lio, W.; Liu, B. Residual and confidence interval for uncertain regression model with imprecise observations. J. Intell. Fuzzy Syst. 2018, 35, 2573–2583. [Google Scholar] [CrossRef]
- Yang, X.F.; Liu, B. Uncertain time series analysis with imprecise observation. Fuzzy Optim. Decis. Mak. 2019, 18, 263–278. [Google Scholar] [CrossRef]
- Gao, J.W. Uncertain bimatrix game with applications. Fuzzy Optim. Decis. Mak. 2013, 12, 65–78. [Google Scholar] [CrossRef]
- Yang, X.F.; Gao, J.W. Linear-Quadratic uncertain differential game with application to resource extration problem. IEEE Trans. Fuzzy Syst. 2016, 24, 819–826. [Google Scholar] [CrossRef]
- Yang, X.F.; Gao, J.W. Bayesian equilibria for uncertain bimatrix game with asymmetric information. J. Intell. Manuf. 2017, 28, 515–525. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, S.; Gao, J.W. Uncertain extensive game with application to resource allocation of national security. J. Ambient. Intell. Humaniz. Comput. 2017, 8, 797–808. [Google Scholar] [CrossRef]
- Yang, X.F.; Gao, J.W. Uncertain core for coalitional game with uncertain payoffs. J. Uncertain Syst. 2014, 8, 13–21. [Google Scholar]
- Wen, J.; Zhu, L.; Ma, S.; Fan, Z.; Sun, Y.; Chen, Z. Cloud matter-element evaluation on the classroom teaching quality of postgraduate based on game theory. J. Civ. Aviat. Flight Univ. China 2023, 34, 38–43. [Google Scholar]
- Xia, S. Study on the system weakness of teaching evaluation and evaluation from the perspective of game theory. Educ. Sci. 2012, 26, 58–61. [Google Scholar]
- Pieter, S.; Bert, B.; Dimitri, M. On the validity of student evaluation of teaching: The state of the art. Rev. Educ. Res. 2013, 83, 598–642. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).