Abstract
In this article, we introduce a new three-parameter distribution called the discrete Weibull exponential (DWE) distribution, based on the use of a discretization technique for the Weibull-G family of distributions. This distribution is noteworthy, as its probability mass function presents both symmetric and asymmetric shapes. In addition, its related hazard function is tractable, exhibiting a wide range of shapes, including increasing, increasing–constant, uniform, monotonically increasing, and reversed J-shaped. We also discuss some of the properties of the proposed distribution, such as the moments, moment-generating function, dispersion index, Rényi entropy, and order statistics. The maximum likelihood method is employed to estimate the model’s unknown parameters, and these estimates are evaluated through simulation studies. Additionally, the effectiveness of the model is examined by applying it to three real data sets. The results demonstrate that, in comparison to the other considered distributions, the proposed distribution provides a better fit to the data.
1. Introduction
The use of statistical distributions is crucial in fitting various types of data. Traditional distributions do not always capture the diverse shapes and behaviors found in natural data, leading to the development of new families of distributions to accommodate more complex data. On the other hand, discrete distributions are essential for measuring quantities (e.g., the lifetime of products) on a non-continuous scale, prompting researchers to introduce new discrete distributions. These distributions, however, have limitations in modeling complex data, encouraging the development of more flexible options. As a result, interest has increased in discretizing existing continuous models to achieve a better fit for a larger range of data sets. A statistical method relying on creating new discrete G classes of probability models from existing continuous classes has recently been derived. For instance, Ref. [1] presented and defined the discrete Gompertz-G family of distributions following [2]. A new G family of continuous distributions, named the exponential generalized-G family, was presented in [3]. Following [4], Ref. [5] introduced and discussed the discrete Rayleigh G family of distributions, whereas [6] suggested a discrete analogue of the Weibull-G family.
Recently, Ref. [7] presented a new method, called transformed-transformer, to generate new families of distributions. They chose the weight function , where is a cumulative distribution function of any baseline distribution with parameter vector , in order to introduce the Weibull-G, beta-exponential-G, and gamma-G families of distributions.
In this paper, , which has been discussed in [7,8,9], is specifically considered. The cumulative distribution function (CDF) of the Weibull-G distribution is defined as
with corresponding probability density function (PDF):
The survival function (SF) and the hazard rate function (HRF) are, respectively, given by
Over the last few decades, several discretized forms of continuous distributions have been derived to model different discrete data sets. The most notable discretization approach is the survival discretization method proposed by [10]. It is a novel technique that utilizes the survival function of any continuous distribution to develop a new discrete distribution. The probability mass function of a discrete distribution has been defined in [10] as follows:
where is the survival function of the continuous distribution, defined as
where is a CDF of the continuous distribution and is a vector of parameters.
This approach has recently been extended to define some new discrete families of probability distributions. For example, Ref. [1] introduced the discrete Gompertz-G family of distributions and studied the discrete Gompertz exponential, discrete Gompertz–Weibull, and discrete Gompertz–inverse Weibull distributions; Ref. [5] studied the discrete Rayleigh family of distributions and proposed the discrete Rayleigh–Weibull distribution; Ref. [11] presented the odd Perks-G family of distributions and presented the discrete odd Perks exponential distribution; Ref. [12] introduced a discrete exponential generalized-G family of distributions and introduced the discrete exponential generalized Weibull distribution; and Ref. [13] proposed a discrete analogue of the odd Weibull-G family of distributions and studied the discrete odd Weibull–Geometric and the discrete odd Weibull–Inverse Weibull distributions.
Therefore, the main focus of this paper is to utilize the discretization technique proposed in [10] to construct a new discrete distribution that is more flexible in fitting data. To illustrate this, in this study, we use the survival discretization technique to convert the continuous Weibull-G (W-G) family to a discrete family, named the discrete Weibull-G (DW-G) family, in order to develop a three-parameter distribution, which is called the discrete Weibull exponential (DWE) distribution.
Starting with the continuous Weibull-G family proposed in [7], and utilizing the discretization approach from [10], the CDF of THE discrete Weibull-G (DW-G) family can be formulated as follows:
and the corresponding SF of the DW-G family can be derived as follows:
Therefore, the probability mass function (PMF) of the DW-G family can be expressed as follows:
and based on Equations (8) and (9), the HRF can then be written as follows:
The remainder of this article is organized as follows: Section 2 introduces the DWE distribution as well as its survival and hazard rate functions. Section 3 explores some fundamental statistical properties of the DWE distribution. Section 4 discusses the estimation of its distribution parameters using the method of maximum likelihood estimation (MLE). Section 5 supplies a simulation study in order to evaluate the estimates. Section 6 provides three real data applications which exemplify the adequacy of the proposed distribution. Finally, Section 7 concludes this paper.
2. Discrete Weibull Exponential Distribution (DWE)
If X is the exponential random variable with parameter , then its CDF is given by
Substituting in Equations (7) and (9), the DWE distribution has the following CDF and PMF, respectively:
Moreover, the SF and HRF are, respectively, given as
Some PMF and HRF plots for the DWE model generated under selected parameter values are shown in Figure 1 and Figure 2. From Figure 1, it can be seen that the PMF plots of the DWE distribution exhibit various shapes, which include symmetric, right skewed, increasing, decreasing, J-shaped, and reversed J-shaped curves. Additionally, Figure 2 reveals that the HRF of the DWE distribution presents a variety of shapes. In particular, it can be increasing, increasing–constant, decreasing, uniform, or monotonically increasing. These observations strongly suggest the great flexibility of the DWE distribution in fitting data.
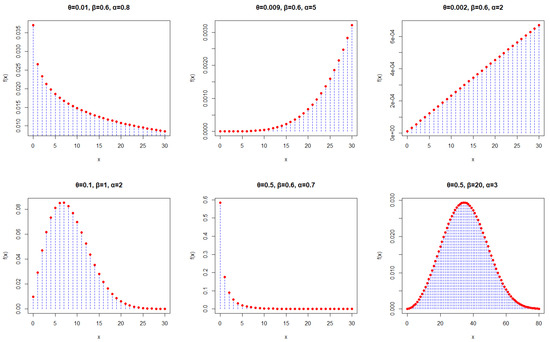
Figure 1.
PMF plots of the DWE model.
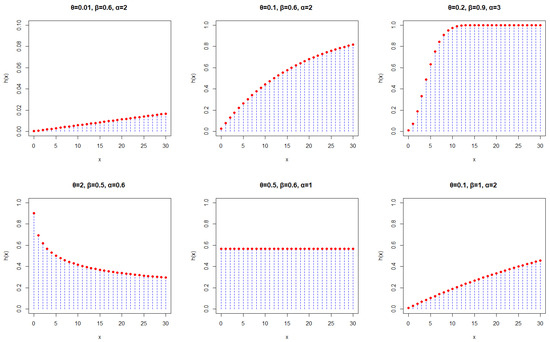
Figure 2.
HRF plots of the DWE model.
3. Statistical Properties of the DWE Distribution
Some properties of the DWE distribution are detailed in this section, including the quantile function, moments, moment-generating function, dispersion index, coefficient of variation, Rényi entropy, and order statistics.
3.1. The Quantile Function and the Median
The quantile of DWE distribution can be obtained by
where is the ceiling function, which returns the smallest integer greater than or equal to its argument.
In particular, if we set q = 0.5, we obtain the value of the median of the proposed distribution; in particular, the median M is given as:
3.2. Moments
The rth moment of a random variable X, which follows the DWE distribution, can be calculated as
where is the PMF of DWE distribution.
Therefore,
Thus, the variance of the DWE distribution is obtained as follows:
Moreover, the skewness and kurtosis can be found, respectively, as follows:
3.3. The Moment-Generating Function
Assume that X is a non-negative random variable (RV), which follows the DWE distribution. Then, the moment-generating function of the RV X can be derived as follows:
3.4. The Dispersion Index and Coefficient of Variation
The dispersion index (DSI) of the DWE distribution is defined as
Furthermore, the coefficient of variation (COV) of the DWE distribution is calculated as follows
Some numerical results for the mean, variance, skewness (sk), kurtosis (K), DSI, and COV are presented in Table 1.

Table 1.
Numerical results for mean, variance (var), skewness (sk), kurtosis (K), dispersion index (DSI), and coefficient of variation (COV).
From Table 1, The following is clear: As increases under fixed values of and , the mean and variance decrease, whereas the sk and K increase. As increases under fixed values of and , the mean, variance, sk, and K increase. As increases under fixed values of and , the mean, variance, sk, and K decrease. In addition, the DSI can be less or greater than 1, which means that it is suitable for representing under-or over-dispersed phenomena.
3.5. The Rényi Entropy
The Rényi Entropy (RE), proposed in [14], is a fundamental entropy function. It is obtained as follows:
where and .
Substituting Equation (12) into the entropy function, we obtain
3.6. The Order Statistic
Assume that are randomly sampled from the DWE distribution and let denote the rth order statistic.
Consider ; the CDF of the ith order statistic for a random sample from the DWE distribution is given by
using the binomial expansion equation,
and, substituting Equation (13) into Equation (19), the CDF of the order statistic can be presented as
The corresponding PMF of the rth order statistic can be obtained by applying the formula discussed in [15]:
Thus,
In particular, setting and in Equation (26), we can obtain the PMFs of the minimum and maximum order statistics, respectively.
4. Parameter Estimation for DWE Distribution
The MLE approach was used to estimate the parameters for the DWE distribution. The steps are as follows: First, define the log-likelihood function. Second, consider the three parameters and , and differentiate the log-likelihood function with respect to each parameter. Finally, set the derivative equations to zeros. The likelihood function for the DWE distribution is given as follows
Then, the log-likelihood function for the DWE distribution can be defined as
The derivatives of Equation (27), with respect to the DWE distribution parameters, are obtained as follows:
Hence, the MLEs of the parameters and can be obtained by equating Equations (28)–(30) to zero, and solving them either analytically or numerically, using a method such as the Newton–Raphson iteration method. Moreover, using an R function like optim and nim, the estimators can automatically be obtained by maximizing Equation (27).
5. Simulation Study
In this section, three cases are presented to examine the performance of the MLEs of the DWE distribution parameters. Some values were considered for the parameters, as follows:
- Case I:
- .
- Case II:
- .
- Case III:
- .
The mean square error (MSE) was applied to evaluate the MLE, for every parameter. The number of iterations for each case in the simulation was nsim = 10,000. The mean square error (MSE) can be calculated as
The Monte Carlo simulation method was used. The MLEs of the parameters and their corresponding MSEs are listed in Table 2.

Table 2.
Simulation results for the DWE MLEs and MSEs with different sample sizes for the three considered cases.
From Figure 3, Figure 4 and Figure 5, and Table 2, the MSE clearly becomes smaller as the sample size increases, and the MLEs become nearer to the true parameters.
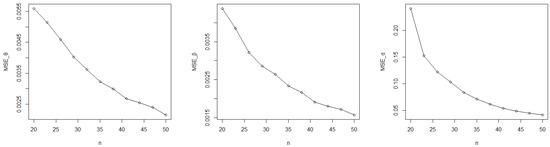
Figure 3.
The MSE of for the DWE (0.5, 0.6, 1.1).
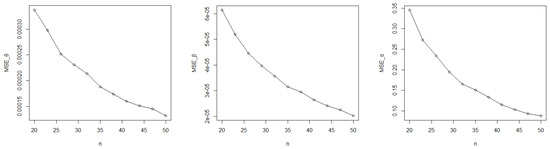
Figure 4.
The MSE of for the DWE (0.2, 0.5, 2.4).
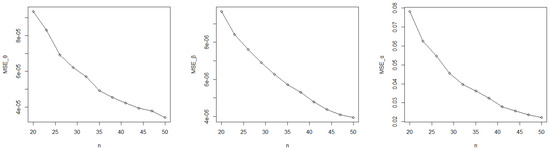
Figure 5.
The MSE of for the DWE (0.05, 0.4, 1.3).
6. Application
In this section, the flexibility of the DWE distribution is illustrated by fitting three real data sets using six different distributions, in addition to the proposed DWE distribution. The PMFs for the six distributions used in the comparison are as follows:
- (1)
- Geometric Distribution (Geom)
- (2)
- Poisson distribution (Pois)
- (3)
- Discrete Weibull–Geometric Distribution (DWGeom) [16]:
- (4)
- Discrete fréchet (dfréchet) [17]:
- (5)
- Discrete extended odd Weibull exponential distribution (DEOWE) [18]:
- (6)
- Discrete Weibull Distribution (DWD) [19]:
The parameters of fitted distributions were estimated using the maximum likelihood method (i.e., maximizing the log-likelihood). Goodness-of-fit (GOF) criteria, including the Corrected Akaike Information Criterion (AICc) [20], Akaike’s Information Criterion (AIC) [21], Bayesian Information Criterion (BIC) [22], and Hannan–Quinn Information Criterion (HQIC) [23], were used to discriminate the best model. Plots were generated for comparison between the DWE distribution and the other distributions, and the Kolmogorov–Simornov (K-S) test was conducted to determine the p-value for each distribution. The formulas for the GOF criteria are listed below:
where ℓ is the log-likelihood function evaluated for the MLEs, h is the number of estimated parameters for the model, and n is the sample size.
6.1. First Data Set
The first data set is presented in [24]. It contains 26 observations that indicate the failure times for a specific product. This information has also been used in [11,25]. Figure 6 and Figure 7 show the p-p plot of the fitted distributions and the empirical CDFs for this data set. A summary of the MLE results for the parameters, along with the SEs, log-likelihood, AICc, AIC, BIC, and HQIC for each distribution is provided in Table 3.
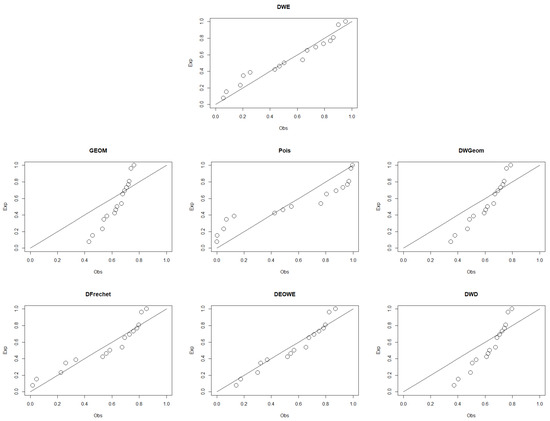
Figure 6.
p-p plots for the DWE and other considered distributions for the first data set.
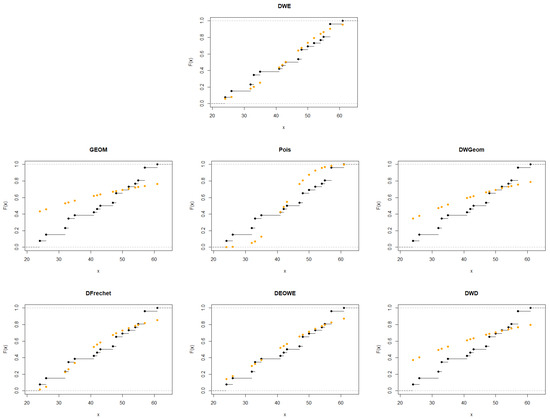
Figure 7.
Plots of the empirical CDFs of the DWE and other considered distributions for the first data set.

Table 3.
MLEs (with their corresponding SEs in parentheses ) and GOF criteria for the first data set.
6.2. Second Data Set
The second data set was reported in [26] and provides 61-day COVID-19 data recorded between 13 June and 12 August of 2021 in Italy. This data set includes newly reported cases on a daily basis. Figure 8 and Figure 9 show the p-p plots of the fitted distributions and the empirical CDFs for the second data set, respectively. A summary of the results of the MLEs of the parameters along with the SEs, the log-likelihood, AICc, AIC, BIC, and HQIC for each distribution is provided in Table 4.
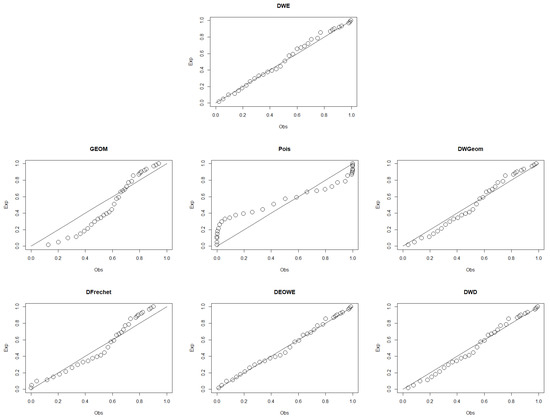
Figure 8.
p-p plots of the DWE and other considered distributions for the second data set.
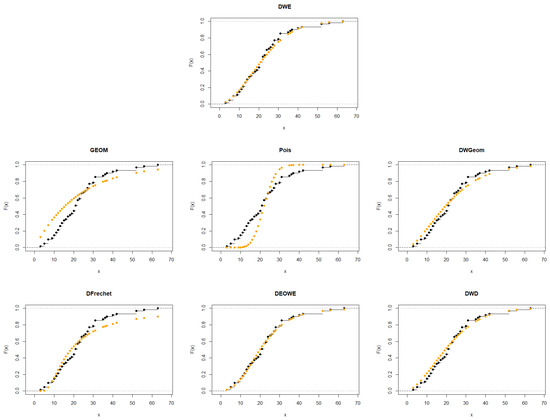
Figure 9.
Plots of the empirical CDFs of the DWE and other considered distributions for the second data set.

Table 4.
MLEs (with their corresponding SEs in parentheses ) and GOF criteria for the second data set.
6.3. Third Data Set
The third data set was reported in [27], and provides 101 observations. It includes the fatigue life (at 18 cycles per second) of 6061-T6 aluminum coupons that were cut parallel to the direction of rolling and oscillated. Figure 10 and Figure 11 show the p-p plots of the fitted distributions and the empirical CDFs for the third data set, respectively. A summary of the results of the MLEs of the parameters along with the SEs, the log-likelihood, AICc, AIC, BIC, and HQIC for each distribution is provided in Table 5.
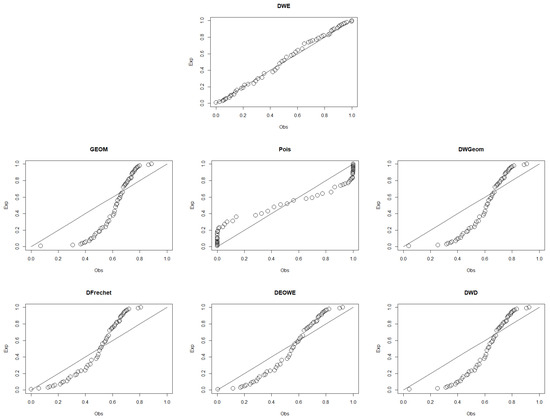
Figure 10.
p-p plots of the DWE and other considered distributions for the third data set.
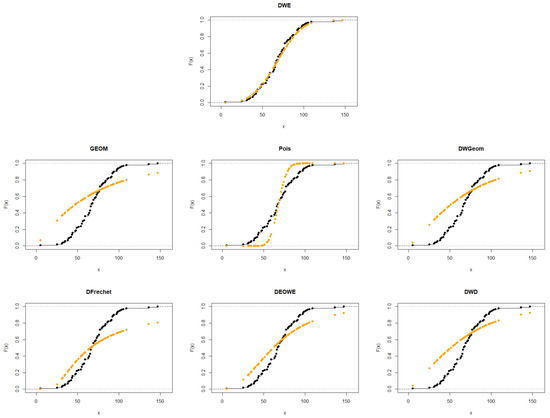
Figure 11.
Plots of the empirical CDFs of the DWE and other considered distributions for the third data set.

Table 5.
MLEs (with their corresponding SEs in parentheses) and GOF criteria for the third dataset.
7. Conclusions
In this work, discretization of a continuous family of distributions was studied. This discretized family of distributions is called the discrete Weibull-G family of distributions, and the three-parameter DWE distribution is presented as a member of this family. Both the PMF and HRF of the DWE distribution have shapes that appear to be promising for capturing the various behaviors of data. Furthermore, some of the statistical properties of this distribution were studied. Its three parameters were estimated using the maximum likelihood method. Three cases with different sample sizes and different DWE parameter values were used to assess the performance of the MLEs of the DWE distribution parameters. Three real data sets were utilized to examine the efficiency of the DWE distribution, in comparison with various commonly used distributions. The presented figures demonstrate the usefulness of the proposed distribution. The obtained results indicate that the proposed DWE distribution represents a highly flexible distribution with good potential for modeling real data.
Author Contributions
Conceptualization, D.A. and H.K.; methodology, A.B. and D.A.; software, A.B.; validation, D.A. and H.K.; formal analysis, A.B.; investigation, A.B., D.A. and H.K.; resources, A.B.; data curation, A.B.; writing—original draft preparation, A.B.; writing—review and editing, D.A. and H.K.; visualization, A.B.; supervision, D.A. and H.K.; project administration, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Eliwa, M.; Alhussain, Z.; El-Morshedy, M. Discrete Gompertz-G family of distributions for over-and under-dispersed data with properties, estimation, and applications. Mathematics 2020, 8, 358. [Google Scholar] [CrossRef]
- Steutel, F.W.; Van Harn, K. Infinite Divisibility of Probability Distributions on the Real Line; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Yousof, H.M.; Majumder, M.; Jahanshahi, S.; Masoom Ali, M.; Hamedani, G. A new Weibull class of distributions: Theory, characterizations and applications. J. Stat. Res. Iran JSRI 2018, 15, 45–82. [Google Scholar] [CrossRef]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G family of probability distributions. J. Data Sci. 2014, 12, 53–68. [Google Scholar] [CrossRef]
- Aboraya, M.; M. Yousof, H.; Hamedani, G.; Ibrahim, M. A new family of discrete distributions with mathematical properties, characterizations, Bayesian and non-Bayesian estimation methods. Mathematics 2020, 8, 1648. [Google Scholar] [CrossRef]
- Ibrahim, M.; Ali, M.M.; Yousof, H.M. The discrete analogue of the Weibull G family: Properties, different applications, Bayesian and non-Bayesian estimation methods. Ann. Data Sci. 2021, 10, 1069–1106. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Ghosh, I. On the Weibull-X family of distributions. J. Stat. Theory Appl. 2015, 14, 169–183. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; M. Ortega, E.M.; Ramires, T.G. A new generalized Weibull family of distributions: Mathematical properties and applications. J. Stat. Distrib. Appl. 2015, 2, 13. [Google Scholar] [CrossRef]
- Kemp, A.W. Classes of Discrete Lifetime Distributions. Commun. Stat.—Theory Methods 2004, 33, 3069–3093. [Google Scholar] [CrossRef]
- Elbatal, I.; Alotaibi, N.; Almetwally, E.M.; Alyami, S.A.; Elgarhy, M. On Odd Perks-G Class of Distributions: Properties, Regression Model, Discretization, Bayesian and Non-Bayesian Estimation, and Applications. Symmetry 2022, 14, 883. [Google Scholar] [CrossRef]
- Eliwa, M.S.; El-Morshedy, M.; Yousof, H.M. A Discrete Exponential Generalized-G Family of Distributions: Properties with Bayesian and Non-Bayesian Estimators to Model Medical, Engineering and Agriculture Data. Mathematics 2022, 10, 3348. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.; Tyagi, A. A discrete analogue of odd Weibull-G family of distributions: Properties, classical and Bayesian estimation with applications to count data. J. Appl. Stat. 2022, 49, 2928–2952. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; University of California Press: Berkeley, CA, USA, 1961; Volume 4, pp. 547–562. [Google Scholar]
- Arnold, B.C.; Balakrishnan, N.; Nagaraja, H.N. A First Course in Order Statistics; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Jayakumar, K.; Babu, M.G. Discrete Weibull geometric distribution and its properties. Commun. Stat.—Theory Methods 2018, 47, 1767–1783. [Google Scholar] [CrossRef]
- Nadarajah, S.; Lyu, J. New discrete heavy tailed distributions as models for insurance data. PLoS ONE 2023, 18, e0285183. [Google Scholar] [CrossRef]
- Nagy, M.; Almetwally, E.M.; Gemeay, A.M.; Mohammed, H.S.; Jawa, T.M.; Sayed-Ahmed, N.; Muse, A.H. The new novel discrete distribution with application on covid-19 mortality numbers in Kingdom of Saudi Arabia and Latvia. Complexity 2021, 2021, 7192833. [Google Scholar] [CrossRef]
- Augusto Taconeli, C.; Rodrigues de Lara, I.A. Discrete Weibull distribution: Different estimation methods under ranked set sampling and simple random sampling. J. Stat. Comput. Simul. 2022, 92, 1740–1762. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Hannan, E.J.; Quinn, B.G. The determination of the order of an autoregression. J. R. Stat. Soc. Ser. B Methodol. 1979, 41, 190–195. [Google Scholar] [CrossRef]
- Gacula, M., Jr.; Kubala, J. Statistical models for shelf life failures. J. Food Sci. 1975, 40, 404–409. [Google Scholar] [CrossRef]
- Nassar, M.; Kumar, D.; Dey, S.; Cordeiro, G.M.; Afify, A.Z. The Marshall–Olkin alpha power family of distributions with applications. J. Comput. Appl. Math. 2019, 351, 41–53. [Google Scholar] [CrossRef]
- Almetwally, E.M.; Abdo, D.A.; Hafez, E.; Jawa, T.M.; Sayed-Ahmed, N.; Almongy, H.M. The new discrete distribution with application to COVID-19 Data. Results Phys. 2022, 32, 104987. [Google Scholar] [CrossRef] [PubMed]
- Birnbaum, Z.W.; Saunders, S.C. Estimation for a family of life distributions with applications to fatigue. J. Appl. Probab. 1969, 6, 328–347. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).