Abstract
In this paper, an ancient Babylonian algorithm for calculating the square root of 2 is unveiled, and the potential link between this primitive technique and an ancient Chinese method is explored. The iteration process is a symmetrical property, whereby the approximate root converges to the exact one through harmonious interactions between two approximate roots. Subsequently, the algorithm is extended in an ingenious manner to solve algebraic equations. To demonstrate the effectiveness of the modified algorithm, a transcendental equation that arises in MEMS systems is considered. Furthermore, the established algorithm is adeptly adapted to handle differential equations and fractal-fractional differential equations. Two illustrative examples are presented for consideration: the first is a nonlinear first-order differential equation, and the second is the renowned Duffing equation. The results demonstrate that this age-old Babylonian approach offers a novel and highly effective method for addressing contemporary problems with remarkable ease, presenting a promising solution to a diverse range of modern challenges.
1. Introduction
The old Babylonian algorithm is an ancient method for computing various mathematical values. One of its notable applications is in calculating the square root of a number.
This algorithm works by making an initial guess and then refining it through a series of iterations. For example, to find the square root of a number N, an initial guess x0 is chosen. Then, in each iteration, a new approximation xn+1 is calculated using the formula xn+1 = (xn + N/xn)/2. As the iterations progress, the value of xn gets closer and closer to the actual square root of N.
This algorithm is surprisingly effective and efficient. It shows the ingenuity of ancient mathematicians in developing practical methods for solving complex mathematical problems. Although developed thousands of years ago, the old Babylonian algorithm still has relevance today and can be used as an alternative approach to modern computational methods in certain situations.
The evolution of ancient mathematics unfolded in a multitude of ways across a diverse array of geographical regions, as evidenced by the extant evidence [1,2,3]. Prior to the publication of Euclid’s Elements [4], the mathematical tradition of ancient China exerted the greatest influence [5,6,7]. The most striking difference between the two is undoubtedly the axiomatic framework of Euclid’s work and its abstract, formal character, which stands in stark contrast to the ancient Chinese mathematics, which was developed for practical applications.
The contrast between these two mathematical traditions is quite remarkable. Euclid’s work is characterized by its axiomatic framework and highly abstract, formal nature. On the other hand, ancient Chinese mathematics was primarily developed for practical applications. This difference is evident in the way problems were approached and solved. In ancient China, mathematics was often used to address real-world issues, such as engineering, astronomy, and commerce. The focus was on finding solutions that could be directly applied to practical situations.
In contrast, Euclid’s approach aimed at establishing a logical and systematic foundation for mathematics. His axioms and theorems provided a framework for deductive reasoning and the development of abstract mathematical concepts. This formal approach laid the groundwork for much of modern mathematics. Despite their differences, both traditions have made invaluable contributions to the history and development of mathematics.
Prior to its widespread adoption in the West after 1202 AD, the double false position method [8], also known as the Ying Buzu Shu [9], had been utilized in ancient China for over a millennium. Newton’s 1670 iteration algorithm, which is the most widely used in modern numerical simulation, was already in use by ancient Chinese mathematicians in more sophisticated forms for over a millennium [10].
The double false position method is a clever approach that allows for the approximation of solutions to various mathematical problems. It involves making two initial guesses and then refining the solution through a series of calculations. This technique showcases the ingenuity and advanced thinking of ancient Chinese mathematicians.
On the other hand, Newton’s 1670 iteration algorithm, which is extremely popular and widely used in modern numerical simulation, is a more recent development in the Western mathematical tradition. However, it is astonishing to note that ancient Chinese mathematicians had been using similar if not more sophisticated forms of this algorithm for over a millennium. This highlights the remarkable achievements and foresight of ancient Chinese mathematics. It also emphasizes the fact that mathematical knowledge and techniques have developed and spread across different cultures and time periods, each contributing to the overall growth and evolution of the field.
The Nine Chapters [11], an ancient Chinese mathematical treatise, may be considered a Chinese counterpart to Euclid’s Elements, which exerted a dominant influence on Western mathematics for centuries. Similarly, the Nine Chapters came to be regarded as the foundational text of ancient Chinese mathematics for many millennia [12]. When ancient mathematics is re-examined from a modern mathematical perspective, it can provide a novel perspective on the applications of mathematics to practical problems [13].
The study of ancient Chinese mathematics is a well-established field of research. In a review article [14], some ancient Chinese algorithms were introduced, and their modern applications to solve nonlinear differential equations were elucidated. Additionally, a frequency formulation was proposed [14]. The formulation’s simplicity and effectiveness have led to its widespread use for rapidly and reliably obtaining insights into the periodic properties of nonlinear vibration systems. Elías-Zúñiga et al. used the concept to study a fractal vibration system [15] and gave a modified frequency formulation [16]; Zhang et al. extended the concept to nonlinear oscillators with generalized initial conditions [17]; Yang et al. extended it to fractional vibration systems [18]; and various modified frequency formulations have appeared [19,20]. Chun-Hui He further developed the ancient Chinese mathematical algorithm into a modern numerical method [21], which was subsequently named the Chun-Hui He algorithm or Chun-Hui He iteration method in the literature [22,23].
Another topic of considerable interest in the field of ancient Chinese mathematics is the He Chengtian inequality, which was extended to facilitate the solution of nonlinear oscillators [24]. This approach, which is known as the max–min approach [25,26], has been the subject of considerable research.
In this paper, we briefly introduce an ancient Babylonian algorithm [27,28]. The calculation of the square root has been a topic of considerable interest among scholars of ancient mathematics [29,30]; it was the focus of the ancient Chinese, Sanskrit mathematics, Mediterranean practical arithmetic, and the old Babylonian algorithm [31]. Here, we first introduce the Smyrna algorithm [29]; its iteration process is
When N = 2, we have the following series converging to √2:
1/1, 3/2, 7/5, 17/13, 43/30, 103/73, 249/176, 601/425, 1451/1026, 3513/2487. This is a limiting process and not an exact equality for every iteration. The ancient Babylonian algorithm for finding square roots can be considered invalid in certain extreme cases, for example, when dealing with extremely small numbers close to zero. Due to the limitations of numerical precision and rounding errors, the Babylonian algorithm might not converge accurately to the expected square root. For instance, if attempting to find the square root of a number like 10−20, the algorithm might encounter difficulties in accurately converging to the true square root value.
The old method exhibits a distinctive symmetrical quality, which is both intriguing and harmoniously pleasing from a mathematical perspective. It is noteworthy that the square root of 2 can be represented by a fraction with an arbitrarily high degree of precision. This phenomenon is even more intriguing when one considers that the irrational approximation can be expressed by a fraction of two prime numbers, specifically 17/13, 103/73, and 3513/2487.
With different initial guesses, we can obtain the following approximate root:
2/1, 4/3, 10/7, 24/17, 58/41, 140/99, 338/239, 816/577, 1970/1393
3/1, 5/4, 13/9, 31/22, 75/53, 181/128, 437/309, 1055/746, 2547/1801
5/3, 11/8, 27/19, 65/46, 157/111, 379/268, 1016/647, 2320/1673, 6313/3993
3/5, 13/8, 29/21, 71/50, 171/121, 463/292, 1047/755, 2555/1802, 6161/4359
There are additional primes that can be identified, e.g., 2547/1801.
The Smyrna algorithm is also called Theon’s Ladder [29]. The √2 ratio was also widely used in ancient architecture [32,33], especially in ancient China; the concept of a round Heaven and square Earth was used to design various architectures.
Now, we must first consider the following algebraic equation:
Here, a is a positive constant. The old Babylonian algorithm is [27,28].
Quadratic equations occupied a significant place in Babylonian mathematics [34]. There are also some variants [35,36]. Calkin and others revealed the possible connection between the Newton iteration method and the ancient Babylonian algorithm [26]. Surprisingly, this ancient algorithm is still in use and has applications in modern times [37,38,39]. Here, we will show its connection to an ancient Chinese algorithm called the He Chengtian average [40]. This will be discussed in Section 2. After that, a general algebraic equation is considered in Section 3. As an example, a micro-electromechanical system (MEMS) is considered in Section 4. Then, the old method is extended to solve differential equations in Section 5. Finally, in the last section, the future research frontiers are pointed out.
2. He Chengtian Average
A simple sight into old Babylonian algorithm, we find that
where ; here, a is a real number, and xn and a/xn are two approximates.
The He Chengtian average [40] is
where p and q are positive nature numbers. Equation (4) can be written in the form
Here, β = p/(p + q). It is important to note that the initial guess must be different from x1 = a. When β = 1/2, Equation (5) is Equation (2). This might have shown a possible link between the old Babylonian algorithm and the old He Chengtian average. A modified He Chengtian average was suggested in Ref. [41]. When β = (n − 1)/n, Equation (5) becomes the Newton method.
3. Cube Root and Beyond
In a modern mathematics view, the old Babylonian algorithm can be easily extended to solve a cube root:
Similar to Equation (6), we have
We recommend β = 2/3 for the cube root:
We consider a simple case where a = 2 and begin with the initial guess of x0 = 1; three iterations lead to 1.33333333, 1.26388889, and 1.25993349, respectively, while the exact root is 1.25992105. The relative error is only 0.00098% for the third iteration result.
For a more general case,
where m is a real number. We have the following iteration algorithm:
Here, we recommend β = (m − 1)/m. We consider a simple case of a = 2 and m = 7; we begin with x0 = 1, and the three iterations are 1.14285714, 1.10781907, and 1.10412697, respectively, while the exact one is 1.104089513673812, with only a relative error of 0.0034% for the third iteration result.
Now, we consider a general algebraic equation
We re-write Equation (11) in the form
The iteration algorithm is
We can construct other iteration formulations, which will be discussed in a forthcoming paper.
4. MEMS System
As a practical application, we consider a transcendental equation that arises in MEMS systems [42]:
The root of Equation (14) is the threshold value for the applied voltage; when x is smaller than the root, a periodic solution [43] is predicted, while when x is larger than the root, the so-called pull-in instability [44,45] occurs. The MEMS system is now widely used as sensors with extremely high sensitivity [46]. Zhang et al. suggested a method for the estimation of the frequency of a MEMS system [47]. Lv studied the MEMS system in a fractal space [48]. The dynamic characteristics of MEMS systems were studied in Refs. [49,50].
We introduce a new variable, u, defined as
Equation (14) becomes
By Equation (13), we have
We commence with u0 = 1, and the initial two iterations yield the following outcomes: u1 = 1.19314718 and u2 = 1.47046999. The exact root is 1.43066373, with a relative error of 2.78% for the second iteration result. This level of accuracy is sufficient for practical applications, although it may be possible to achieve greater precision by continuing the iteration process.
5. Differential Equations
The above section shows that the modified old Babylonian algorithm is suitable for solving algebraic equations, but this is not enough. Most engineering problems are modelled by differential equations, so this section applies the old method to solve nonlinear differential equations.
Consider the following nonlinear differential equation:
Its exact solution is u(x) = 1/(1 + x). We have the following iteration formulation:
where is an approximate value of the first-order derivative, and the initial guess should satisfy the initial condition.
Equation (18) shows so we choose β = 1/2 and begin with
where b is an unknown constant. Equation (20) is the trial solution; its choice is similar to that in the variational-based methods, e.g., the Ritz method [51].
The approximation of the first-order derivative is
The first iteration gives
By the initial condition, we have
So, we find b = 1, and we obtain the exact solution.
Another example is the following well-known Duffing equation arising in the nonlinear vibration system [52,53,54]:
We construct the following iteration algorithm:
where is an approximate value of the second-order derivative. Note that the initial guess should satisfy the initial conditions.
We begin with
It comes from the approximate solution ; is the unknown frequency. According to Equation (25), the approximation of the second-order derivative can be obtained as
The first iteration gives the following result:
It should satisfy the initial conditions, so we have
From Equation (29), we obtain the following frequency–amplitude relation:
So, the approximate solution is
Figure 1 illustrates that the agreement between the approximate solution and the exact solution for weak nonlinearity is indeed valid. As the value of the parameter η approaches infinity, the discrepancy between the approximate and exact frequencies increases, reaching a maximum of 18.03%.
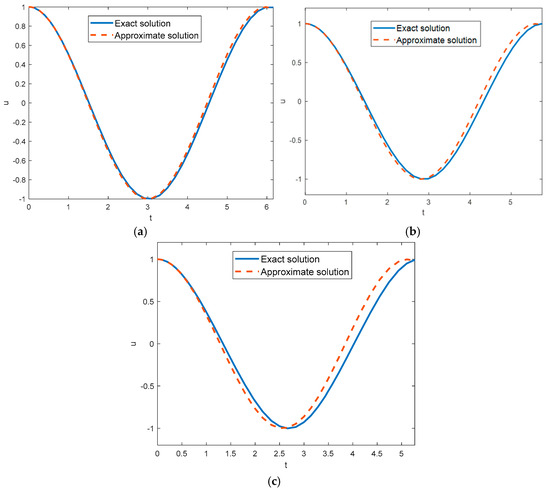
Figure 1.
Comparison of the approximate solutions of Equation (29) with the exact ones for the cases of (a) A = 1, η = 0.1; (b) A = 1, η = 0.25; and (c) A = 1, η = 0.5.
To enhance the precision of the approximation, it is advisable to seek an approximate solution in the following form:
a and b are unknown constants satisfying the following relationship:
According to Equation (32), we begin with
According to Equation (34), the approximation of the second-order derivative can be obtained as
The first iteration yields the following result:
According to the initial conditions and Equation (24), we have
That means
By simultaneously solving Equations (33), (38), and (39), one can determine the values of a, b, and ω. It is recommended that β be set to 1/2.
6. Discussion and Conclusions
This brief article presents an overview of the Babylonian algorithm, originally developed to solve the equation x2 = 2, and explores its potential applications to modern mathematical problems.
For a general algebraic equation
Its iteration algorithm can be expressed as
We recommend = 1/2. Consider the following example [40]:
Beginning with x0 = 1, the first three iteration results are
The precise root is 0.67019, and the relative error of the third approximate solution is 1.89%. This is an acceptable level of precision given that only three iterations were performed.
For a general differential equation,
where L and N are, respectively, the linear differential operator and the nonlinear operator. An iteration algorithm can be constructed as
where u0 is such chosen so that it satisfies all boundary and initial conditions; it should involve an unknown parameter. For nonlinear oscillators, we can choose u0 in the form
where A and are determined by the initial conditions; is determined by the following equation:
where is a location point.
For (24), we can assume
By Equation (47), we have
The location point is chosen as
That means
From Equation (48), we have
This is exactly same as that obtained by the homotopy perturbation method [53].
For fractal oscillators [55,56,57], we consider the following example
where is the two-scale fractal derivative [58,59,60], is the two-scale fractal dimensions [61].
We begin with
By Equation (47), we have
Similar to the above example, the location point is chosen as
and
From Equation (48), we have
So, the approximate solution of Equation (55) is
It is exactly the same as that in Ref. [55].
Now, we re-study Equation (18); the iteration formulation is
We begin with u0 = 1/(1 + bx) and obtain the following result:
Locating at x = 0, we have
We can determine b = 1; this leads to the exact solution.
The old Babylonian algorithm is an amazingly effective way to solve the root of 2, even more so than the well-known Newton iteration method. When the old method is re-studied in view of modern mathematics, it can solve more complex problems. The ability to solve nonlinear differential equations offers a promising scenario for both mathematicians and engineers. Its convergence and reliability in practical applications require further research, and this work paves the way for scientists to use ancient achievements for modern applications. It is our expectation that this preliminary study on the old Babylonian algorithm will serve as a foundation for more advanced research into its iteration robustness and potential applications.
This article proposes a modified version of the old Babylonian algorithm that can be applied to modern problems, e.g., nonlinear vibration systems, fractal oscillators, and nonlinear differential equations. The modification is straightforward and effective in addressing the examples presented. However, the author acknowledges that, regardless of its effectiveness, the new iteration algorithm’s convergence should be rigorously demonstrated. In practical terms, this paper can be regarded as an exemplar of a successful paradigm.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Leung, F.K.S. Jewish culture, Chinese culture, and mathematics education. Educ. Stud. Math. 2021, 107, 405–423. [Google Scholar] [CrossRef]
- Chemla, K. Reviving Ancient Chinese Mathematics: Mathematics, History, and Politics in the Work of Wu Wen-Tsun. ISIS 2016, 107, 894–896. [Google Scholar] [CrossRef]
- Liu, P. The Traditional Academy of Mathematics at the Fenglong Mountain of China. Math. Intell. 2021, 43, 45–49. [Google Scholar] [CrossRef]
- Saito, K. Re-examination of the different origins of the arithmetical books of Euclid’s Elements. Hist. Math. 2019, 47, 39–53. [Google Scholar] [CrossRef]
- Kline, M. Mathematical Thought From Ancient to Modern Times; Oxford University Press: New York, NY, USA, 1972. [Google Scholar]
- Eves, H. An Introduction to the History of Mathematics, 5th ed.; CBS College Publishing: New York, NY, USA, 1983. [Google Scholar]
- Eves, H. Great Moments in Mathematics; The Mathematical Association of America: New York, NY, USA, 1983. [Google Scholar]
- Papakonstantinou, J.M.; Tapia, R.A. Origin and Evolution of the Secant Method in One Dimension. Am. Math. Mon. 2013, 120, 500–518. [Google Scholar] [CrossRef]
- Manimegalai, B.; Swaminathan, R.; Lyons, M.E.G.; Rajendran, L. Application of Taylor’s series with Ying Buzu Shu algorithm for the nonlinear problem in amperometric biosensors. Int. J. Electrochem. Sci. 2022, 17, 22074. [Google Scholar] [CrossRef]
- He, C.H. A simple analytical approach to a nonlinear equation arising in porous catalyst. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 861–866. [Google Scholar] [CrossRef]
- Cullen, C. Can we make the history of mathematics historical? The case of ancient China. Stud. Hist. Philos. Sci. Part A 2006, 37, 515–525. [Google Scholar] [CrossRef]
- Dauben, J.W. Ancient Chinese mathematics: The (Jiu Zhang Suan Shu) vs Euclid’s Elements. Aspects of proof and the linguistic limits of knowledge. Int. J. Eng. Sci. 1998, 36, 1339–1359. [Google Scholar] [CrossRef]
- Zhang, H.L.; Qin, L.J. An ancient Chinese mathematical algorithm and its application to nonlinear oscillators. Comput. Math. Appl. 2011, 61, 2071–2075. [Google Scholar] [CrossRef]
- He, J.H. Some asymptotic methods for strongly nonlinear equations. Int. J. Mod. Phys. B 2006, 20, 1141–1199. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Martínez-Romero, O.; Trejo, D.O.; Palacios-Pineda, L.M. Analysis of a damped fractal system using the ancient Chinese algorithm and the two-scale fractal dimension transform. Fractals 2022, 30, 2250173. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Palacios-Pineda, L.M.; Jiménez-Cedeño, I.H.; Martínez-Romero, O.; Olvera-Trejo, D. Enhanced He’s frequency-amplitude formulation for nonlinear oscillators. Results Phys. 2020, 19, 103626. [Google Scholar] [CrossRef]
- Zhang, J.G.; Song, Q.R.; Zhang, J.Q.; Wang, F. Application of He’s frequency formula to nonlinear oscillators with generalized initial conditions. Facta Univ. Ser. Mech. Eng. 2023, 21, 701–712. [Google Scholar] [CrossRef]
- Yang, Y.J.; Han, G.L.; Yuan, Y.Z. Local fractional damped non-linear oscillation: Frequency Estimation and Energy Consumption. Therm. Sci. 2024, 28, 2143–2151. [Google Scholar] [CrossRef]
- Shen, Y. The Lagrange interpolation for He’s frequency formulation. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1387–1391. [Google Scholar] [CrossRef]
- He, C.H.; Liu, C. A modified frequency-amplitude formulation for fractal vibration systems. Fractals 2022, 30, 2250046. [Google Scholar] [CrossRef]
- He, C.H. An introduction to an ancient Chinese algorithm and its modification. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2486–2491. [Google Scholar] [CrossRef]
- Khan, W.A. Numerical simulation of Chun-Hui He’s iteration method with applications in engineering. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 944–955. [Google Scholar] [CrossRef]
- Khan, W.A.; Arif, M.; Mohammed, M.; Farooq, U.; Farooq, F.B.; Elbashir, M.K.; Rahman, J.U.; AlHussain, Z.A. Numerical and Theoretical Investigation to Estimate Darcy Friction Factor in Water Network Problem Based on Modified Chun-Hui He’s Algorithm and Applications. Math. Probl. Eng. 2022, 2022, 8116282. [Google Scholar] [CrossRef]
- Wang, J. He’s Max-Min Approach for Coupled Cubic Nonlinear Equations Arising in Packaging System. Math. Probl. Eng. 2013, 2013, 382509. [Google Scholar] [CrossRef]
- Durmaz, S.; Demirbag, S.A.; Kaya, M.O. Approximate solutions for nonlinear oscillation of a mass attached to a stretched elastic wire. Comput. Math. Appl. 2011, 61, 578–585. [Google Scholar] [CrossRef][Green Version]
- Bayat, M.; Bayat, M.; Kia, M.; Ahmadi, H.R.; Pakar, I. Nonlinear frequency analysis of beams resting on elastic foundation using max-min approach. Geomech. Eng. 2018, 16, 355–361. [Google Scholar]
- Knuth, D.E. Ancient Babylonian algorithm. Commun. ACM 1972, 15, 671–677. [Google Scholar] [CrossRef]
- Fowler, D.; Robson, E. Square root approximations in Old Babylonian mathematics: YBC 7289 in context. Hist. Math. 1998, 25, 366–378. [Google Scholar] [CrossRef]
- Kainzinger, A. The Mathematics of the Viereckschanzen of the La Tene Culture. Nexus Netw. J. 2021, 23, 337–393. [Google Scholar] [CrossRef]
- Bailey, D.H.; Borwein, J.M. Ancient Indian Square Roots: An Exercise in Forensic Paleo-Mathematics. Am. Math. Mon. 2012, 119, 646–657. [Google Scholar] [CrossRef][Green Version]
- Hoyrup, J. When is the algorithm concept pertinent—And when not? Thoughts about algorithms and paradigmatic examples, and about algorithmic and non-algorithmic mathematical cultures. AIMS Math. 2018, 3, 211–232. [Google Scholar] [CrossRef]
- Kainzinger, A. The mathematics in the structures of Stonehenge. Arch. Hist. Exact Sci. 2011, 65, 67–97. [Google Scholar] [CrossRef]
- Cha, J.; Kim, Y.J. Reconsidering a proportional system of timber-frame structures through ancient mathematics books: A case study on the Muryangsujon Hall at Pusoksa Buddhist Monastery. J. Asian Archit. Build. 2019, 18, 457–471. [Google Scholar] [CrossRef]
- Friberg, J. Geometric division problems, quadratic equations, and recursive geometric algorithms in Mesopotamian mathematics. Arch. Hist. Exact Sci. 2014, 68, 1–34. [Google Scholar] [CrossRef][Green Version]
- Ilic, S.; Petkovic, M.S.; Herceg, D. A note on Babylonian square root algorithm and related variants. Novi Sad J. Math 1996, 26, 155–162. [Google Scholar]
- Calkin, N.J.; Davis, K.; Haithcock, E.; Kenyon, C.M.; Wu, S. What Newton Might Have Known: Experimental Mathematics in the Classroom. Am. Math. Mon. 2021, 128, 845–855. [Google Scholar] [CrossRef]
- Gayathri, S.S.; Kumar, R.; Haghparast, M.; Dhanalakshmi, S. A Novel and Efficient square root Computation Quantum Circuit for Floating-point Standard. Int. J. Theor. Phys. 2022, 61, 234. [Google Scholar]
- Parise, M. Improved Babylonian Square Root Algorithm-Based Analytical Expressions for the Surface-to-Surface Solution to the Sommerfeld Half-Space Problem. IEEE Trans. Antennas Propag. 2015, 63, 5832–5837. [Google Scholar] [CrossRef]
- Parise, M. An exact series representation for the EM field from a vertical electric dipole on an imperfectly conducting half-space. J. Electromagn. Waves Appl. 2014, 28, 932–942. [Google Scholar] [CrossRef]
- Liu, Y.Q.; He, J.H. On relationship between two ancient Chinese algorithms and their application to flash evaporation. Results Phys. 2017, 7, 320–322. [Google Scholar] [CrossRef]
- Lin, L.; Yu, D.N.; He, C.H.; Liu, Y.P. A short remark on the solution of Rachford-Rice equation. Therm. Sci. 2018, 22, 1849–1852. [Google Scholar] [CrossRef]
- Skrzypacz, P.; Kadyrov, S.; Nurakhmetov, D.; Wei, D. Analysis of dynamic pull-in voltage of a graphene MEMS model. Nonlinear Anal. Real World Appl. 2019, 45, 581–589. [Google Scholar] [CrossRef]
- He, J.H. Periodic solution of a micro-electromechanical system. Facta Univ. Ser. Mech. Eng. 2024, 22, 187–198. [Google Scholar] [CrossRef]
- Yang, Q. A mathematical control for the pseudo-pull-in stability arising in a micro-electromechanical system. J. Low Freq. Noise Vib. Act. Control 2023, 42, 927–934. [Google Scholar] [CrossRef]
- Tian, D.; Ain, Q.T.; Anjum, N.; He, C.-H.; Cheng, B. Fractal N/MEMS: From pull-in instability to pull-in stability. Fractals 2021, 29, 2150030. [Google Scholar] [CrossRef]
- He, J.H.; He, C.H.; Qian, M.Y.; Alsolami, A.A. Piezoelectric Biosensor based on ultrasensitive MEMS system. Sens. Actuators A Phys. 2024, 376, 115664. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Tian, D.; Pang, J. A fast estimation of the frequency property of the microelectromechanical system oscillator. J. Low Freq. Noise Vib. Act. Control 2022, 41, 160–166. [Google Scholar] [CrossRef]
- Lv, G. Dynamic behaviors for the graphene nano/microelectromechanical system in a fractal space. J. Low Freq. Noise Vib. Act. Control 2023, 42, 1107–1116. [Google Scholar] [CrossRef]
- Faghidian, S.A.; Tounsi, A. Dynamic characteristics of mixture unified gradient elastic nanobeams. Facta Univ. Ser. Mech. Eng. 2022, 20, 539–552. [Google Scholar] [CrossRef]
- He, J.H.; Yang, Q.; He, C.H.; Alsolami, A.A. Pull-down instability of the quadratic nonlinear oscillator. Facta Univ. Ser. Mech. Eng. 2023, 21, 191–200. [Google Scholar] [CrossRef]
- Wang, K.J. Variational approach for the fractional exothermic reactions model with constant heat source in porous medium. Therm. Sci. 2023, 27, 2879–2885. [Google Scholar] [CrossRef]
- He, C.H.; Amer, T.S.; Tian, D.; Abolila, A.F.; Galal, A.A. Controlling the kinematics of a spring-pendulum system using an energy harvesting device. J. Low Freq. Noise Vib. Act. Control 2022, 41, 1234–1257. [Google Scholar] [CrossRef]
- He, C.H.; El-Dib, Y.O. A heuristic review on the homotopy perturbation method for non-conservative oscillators. J. Low Freq. Noise Vib. Act. Control 2022, 41, 572–603. [Google Scholar] [CrossRef]
- He, C.H.; Tian, D.; Moatimid, G.M.; Salman, H.F.; Zekry, M.H. Hybrid rayleigh-van der pol-duffing oscillator: Stability analysis and controller. J. Low Freq. Noise Vib. Act. Control 2022, 41, 244–268. [Google Scholar] [CrossRef]
- Lu, J.F.; Ma, L. Analysis of a fractal modification of attachment oscillator. Therm. Sci. 2024, 28, 2153–2163. [Google Scholar] [CrossRef]
- Feng, G.Q. He’s frequency formula to fractal undamped Duffing equation. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1671–1676. [Google Scholar] [CrossRef]
- Ren, F. Non-linear oscillation of a mass attached to a stretched elastic wire in a fractal space. Therm. Sci. 2024, 28, 2165–2169. [Google Scholar] [CrossRef]
- Tian, D.; He, C.H. A fractal micro-electromechanical system and its pull-in stability. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1380–1386. [Google Scholar] [CrossRef]
- He, C.H. A variational principle for a fractal nano/microelectromechanical (N/MEMS) system. Int. J. Numer. Methods Heat Fluid Flow 2023, 33, 351–359. [Google Scholar] [CrossRef]
- El-Dib, Y.O.; Elgazery, N.S.; Alyousef, H.A. The up-grating rank approach to solve the forced fractal duffing oscillator by non- perturbative technique. Facta Univ. Ser. Mech. Eng. 2024, 22, 199–216. [Google Scholar] [CrossRef]
- He, C.H.; Liu, C. Fractal dimensions of a porous concrete and its effect on the concrete’s strength. Facta Univ. Ser. Mech. Eng. 2023, 21, 137–150. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).