Lossless Recompression of Vector Quantization Index Table for Texture Images Based on Adaptive Huffman Coding Through Multi-Type Processing

Abstract

With the development of the information age, all walks of life are inseparable from the internet. Every day, huge amounts of data are transmitted and stored on the internet. Therefore, to improve transmission efficiency and reduce storage occupancy, compression technology is becoming increasingly important. Based on different application scenarios, it is divided into lossless data compression and lossy data compression, which allows a certain degree of compression. Vector quantization (VQ) is a widely used lossy compression technology. Building upon VQ compression technology, we propose a lossless compression scheme for the VQ index table. In other words, our work aims to recompress VQ compression technology and restore it to the VQ compression carrier without loss. It is worth noting that our method specifically targets texture images. By leveraging the spatial symmetry inherent in these images, our approach generates high-frequency symbols through difference calculations, which facilitates the use of adaptive Huffman coding for efficient compression. Experimental results show that our scheme has better compression performance than other schemes.

1. Introduction

Ever since people realized the convenience artificial intelligence (AI) brought us, many AI-based tools and applications have been developed at an amazingly fast speed to leverage the quality of our lives. While the third industrial revolution is approaching, many new developments depending on AI are engaged. Evolutionary robots are not only built to assist in manufacturing, transportation, and healthcare but also built to accommodate modern smart homes. With all these advanced technologies, the traffic of future telecommunications becomes heavier than ever. Traditional cellular networks could not keep up the speed of transmitting data, but the possibility of industry revolution becomes a reality when Fifth-Generation (5G) communication technology comes into play. The ability to handle huge amounts of data through the internet is a major milestone to achieve and it increases the demand on digital cloud utilization.

The benefits of using 5G infrastructure [1,2] are that it can transmit data faster because of its higher bandwidth and it can connect to more devices to make internet-of-things (IoT) and machine-to-machine communication possible. Even though 5G can transmit big data, it is critical to improve data compression mechanisms to decrease the sizes of transmitted files. The smaller a file size, the faster the transmission speed and the smaller the cloud storage required.

Images, videos, and audio are common data formats transmitted through networks in our daily lives. Image compression can be categorized as either lossy or lossless, depending on whether the original images can be fully restored. Most of the time, people choose lossy compression for better web performance. Although lossy image compression cannot fully restore the original images, the recovered images are generally visually recognizable with only minor distortions. Vector quantization (VQ) [3,4] is a widely used and fundamental image compression technique in academia. To maintain high image quality, obtaining a well-trained codebook is essential. When an image has strong symmetry, the vectors in the codebook can be reused more frequently, improving compression efficiency. The Linde–Buzo–Gray (LBG) algorithm [5], introduced in 1980, is a well-known method for training codebooks. It divides an image into blocks, converts the data sequences of these blocks into codewords, and replaces these codewords with the indices from a well-trained codebook to compress the image. Improving image compression techniques [6,7,8,9,10,11,12,13,14,15,16,17] is a key issue that many scholars have focused on. VQ compression technology [6,7,8] has been widely used in various fields in recent years. Any improvements in VQ schemes could potentially be applied to other compression techniques in the future.

VQ compression can be categorized into memory VQ and memoryless VQ. The primary difference between the two is whether the correlations are among adjacent blocks or among neighbor pixels in a block. There are many well-known memory VQ compression algorithms, such as finite-state VQ (FSVQ) [9], side match VQ (SMVQ) [10], and predictive VQ (PVQ) [11,12]. Memory VQ schemes require more computation cost than memoryless VQ ones in general. Several favored memoryless VQ compression algorithms, such as Predictive Mean Search (PMS) [13], Search-Order Coding (SOC) [14], and Index Compression VQ (ICVQ) [17], have been proposed. Subsequently, some algorithms [16,17] based on SOC for VQ index tables were developed. In 2009, Chang et al. [16] used a state codebook to recompress the VQ index table. In 2024, Lin et al. [17] applied the concept of side match to recompress the VQ index table. When compression is based on the correlation of neighboring indices of an index table, the index values can be treated as the neighboring pixel values. If the adjacent pixels are highly correlated in an image, it can help the compression of the image. Similarly, to an index table, the compression rate will be higher if the adjoined indices are close in value. In order to achieve this purpose, sorting a codebook is used to make neighboring indices close in value. Since there are more and more applications that require reversibility, it is necessary to be able to retrieve the original index table after decompression to keep the visual quality of the images at VQ level. Previous schemes for recompressing the VQ index table perform poorly on texture images. To achieve a high compression rate for the index table, we propose a scheme that combines principal component analysis (PCA) [18] and Huffman coding [19]. The real challenge in compressing texture images is finding the right balance between compression efficiency and preserving quality. Specifically, it is about determining how much the VQ data can be reduced without noticeable quality loss. Most importantly, the goal is to ensure that any degradation in image quality is imperceptible to the human eye. The contributions of our proposed scheme are:

• We propose a recompression scheme for a VQ index table of texture images, which achieves better compression effectiveness compared to other similar schemes.
• Our proposed scheme enables lossless decompression after compression, allowing the restoration of the original VQ index table.

This paper is structured as follows: Section 2 describes the fundamental concepts of the methods related to our scheme; Section 3 details the flow of algorithms used in the proposed scheme; the experiments and results are analyzed in Section 4; and, at the end of the research, we conclude our thoughts in Section 5.

2. Related Work

Our proposed scheme involves a few common techniques, such as vector quantization (VQ), principal component analysis (PCA), and Huffman coding. To better understand essential concepts of these processes, they are described in the subsections below.

2.1. Vector Quantization Compression

After LBG Algorithm [5] was first proposed by Linde, Buzo, and Gray back in 1980, the block-based method became a common and widely used technique in image compression. Much research and many studies conducted co-operated with the VQ technique in their schemes to compress images effectively afterwards.

There are three parts involved in a VQ compression:

Part 1: Codebook Training

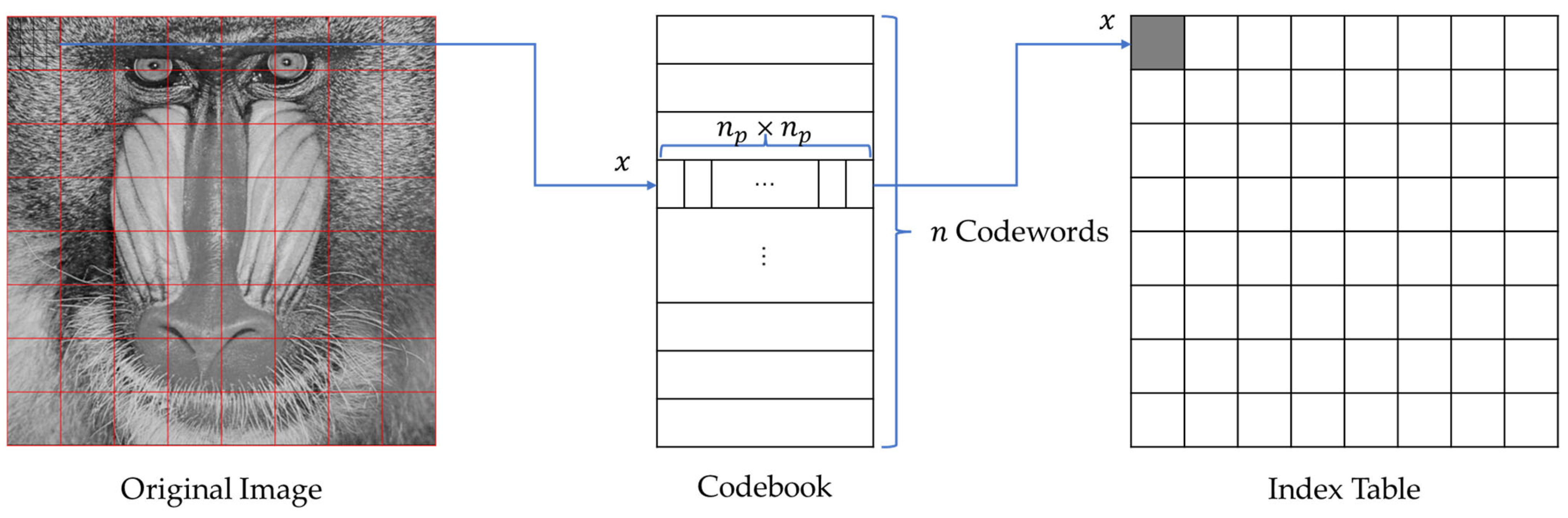
An image in a training set is divided into $n_b\times n_b$ nonoverlapped blocks. Each block has $n_p\times n_p$ pixels and is considered as an $n_p^2$-dimensional codeword. By processing a reasonable-sized image training set, a well-trained codebook consisting of the most representative codewords can be obtained. The size of a codebook varies depending on the specifications of an application.

Part 2: Encoding

After obtaining a well-trained codebook, the original image $\mathit{I}$ is divided into $n_b\times n_b$ blocks to meet the codeword dimension of the codebook. A set of vectors is represented as $\mathit{V}=\left\{ v_1, v_2, \cdots , v_{n_b^2} \right\}$ and $\mathit{C}\mathit{B}$ is a codebook of size $n$, $\mathit{C}\mathit{B}=\left\{ \mathit{c}{\mathit{w}}_1, \mathit{c}{\mathit{w}}_2, \cdots , \mathit{c}{\mathit{w}}_n \right\}$. If $k$ represents the codeword being processed, each codeword $\mathit{c}{\mathit{w}}_k$ can be represented as $\mathit{c}{\mathit{w}}_k=\left(p_{j1}, p_{j2}, \cdots , p_{j{n}_p^2}\right)$, where $j$ represents the vector being processed. The minimized Euclidean distance $d_{j\mathit{V}}$ between an input vector ${\mathit{v}}_j$ and $\mathit{c}{\mathit{w}}_k$ is calculated for each pixel block in the image $\mathit{I}$ by going through the codewords in the codebook using Equation (1). Setting $d_{j\mathit{V}}$ to the minimum distance limits the distortion of the input image.

$$d_{j\mathit{V}}=mi{n}_{k=1}^n\sqrt{{{\displaystyle \sum }}_{i=1}^{n_p\times n_p}{\left({({\mathit{v}}_{\mathit{j}})}_i-{(\mathit{c}{\mathit{w}}_k)}_i\right)}^2}$$

(1)

where $i$ represents the vector dimension being processed.

An index table mapping to the image $\mathit{I}$ is generated by using the codeword indices in the codebook, which represent the closest distances to the image pixel blocks. A pixel block is replaced by an index of a codeword in the mapped index table. The encoding process is demonstrated in Figure 1.

Figure 1. Encoding process of VQ.

Since the index table is then transmitted rather than the pixel values in $n_p\times n_p$ square blocks, the VQ approach reduces the image size radically. A high compression rate is achieved because the bit size of a codeword’s index is much smaller than that of a $n_p\times n_p$-dimensional vector.

Part 3: Decoding

The index table generated by the encoder and the well-trained codebook are sent to the decoder. The codebook for decoding must be the same one used for encoding. Retrieval of the original image with little distortion can simply be a table look-up. The computational time is fast and the image quality can be controlled by the size of the codebook used. However, there is a tradeoff between the size of the codebook and the compression rate. The computation time can increase because there are more Euclidean distance calculations.

2.2. Principal Component Analysis

When dealing with a codebook containing $n_p\times n_p$-dimensional codewords, it is important to sort the codebook to enhance compression efficiency. To achieve this, we can sort the codewords so that similar codewords are located near each other. Principal component analysis (PCA) is a technique that helps identify an optimal axis and allows us to preserve the maximum variance among codewords. By applying PCA, we can reduce the dimensionality of the data while ensuring that similar codewords remain close to each other. A sorting can be accomplished by projecting the $n_p\times n_p$-dimensional codewords onto a specific axis that maintains the relationships between similar codewords. The optimal axis is called the first principal component direction $\mathit{l}$, which is a direction with a maximized variance of projected points. Let $\mathit{C}$ be the covariance matrix calculated from the set of codewords $\left\{{\mathit{c}}_1, {\mathit{c}}_2, \cdots , {\mathit{c}}_n\right\}$, where $n$ represents the number of codewords in the codebook. When projecting these codewords onto the directions defined by the $m$ eigenvectors ${\mathit{l}}_1, {\mathit{l}}_2, \cdots , {\mathit{l}}_m$, $m$ is the codeword dimension. The $m$ eigenvalues ${\mathit{\lambda }}_1, {\mathit{\lambda }}_2, \cdots , {\mathit{\lambda }}_m$ correspond to the variance of each direction. The $m$ eigenvectors ${\mathit{l}}_1, {\mathit{l}}_2, \cdots , {\mathit{l}}_m$ are the $m$ principal components in the covariance matrix $\mathit{C}$. ${\mathit{l}}_1$ is the direction of the first principal component and explains the most variance in the data. Therefore, we denote $\mathit{l}={\mathit{l}}_1$ as the first principal component direction that we are looking for.

In order to obtain a sorted codebook and achieve index correlation through PCA, the steps are as follows:

Step 1: Obtain the optimal direction $\mathit{l}$ and calculate the projected values using Equation (2) for all codewords. Here, $k$ denotes the index of the codeword.

$${\alpha }_k=\mathit{l}·{\mathit{c}}_k$$

(2)

Step 2: Sort the codewords based on their projected values ${\alpha }_k$ to obtain the sorted codebook.

Step 3: Update the index table by finding the corresponding indices in the sorted codebook.

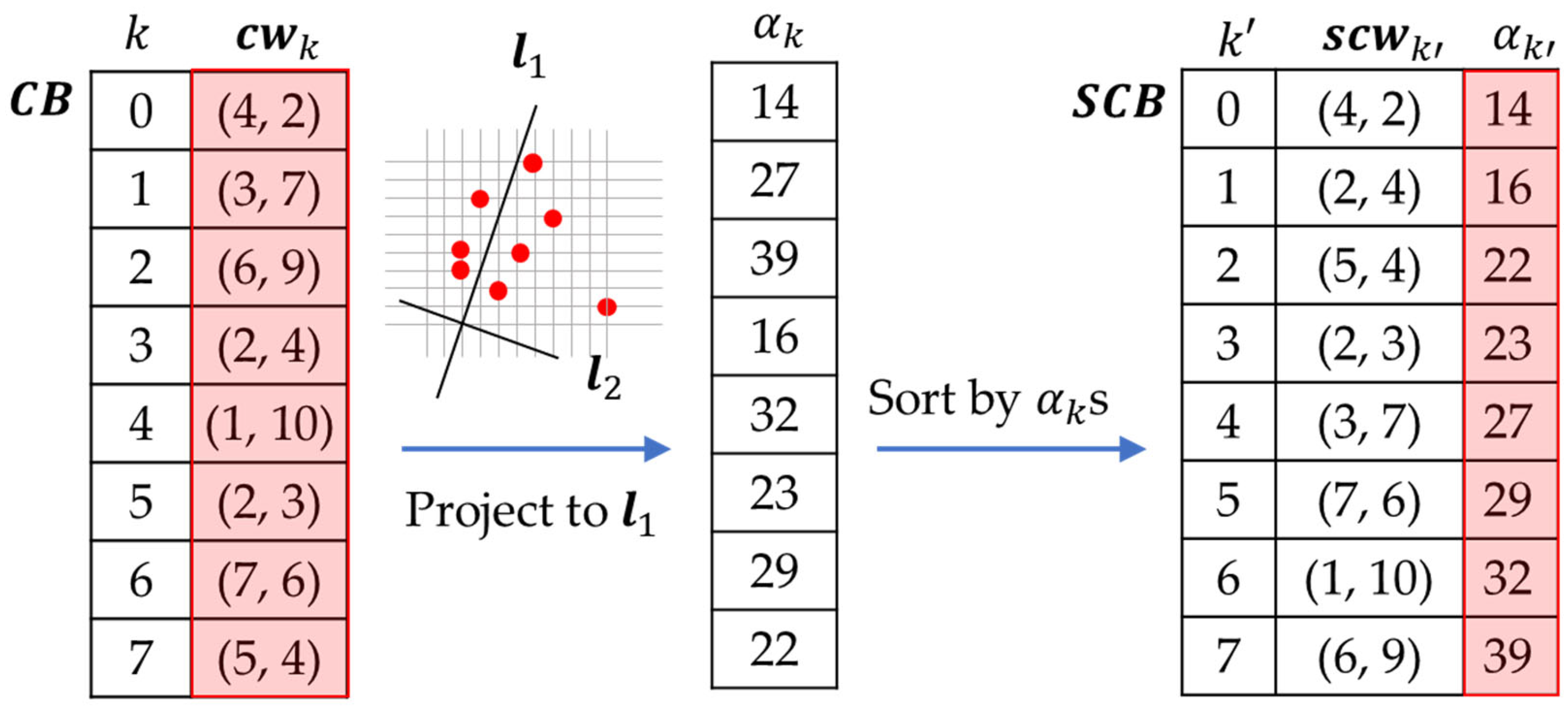
Figure 2 shows an example of PCA sorting. Let a codebook $\mathit{C}\mathit{B}$ consist of eight 2D codewords $\mathit{C}\mathit{B}=\left\{\left(4,2\right),\left(3, 7\right),\left(6, 9\right),\left(2, 4\right),\left(1, 10\right),\left(2, 3\right),\left(7, 6\right),\left(5, 4\right)\right\}$. PCA lines ${\mathit{l}}_1$ and ${\mathit{l}}_2$ are adjusted from the center of codewords to the origin. ${\mathit{l}}_1$ and ${\mathit{l}}_2$ are perpendicular to each other. Allocate the PCA line ${\mathit{l}}_1$, which has the maximum variance of codewords projected to it. Obtain the codeword projected values ${\alpha }_k$s to the PCA line ${\mathit{l}}_1$: 14, 27, 39, 16, 32, 23, 29, and 22. We can then sort the codewords according to their projected values and obtain the sorted codebook $\mathit{S}\mathit{C}\mathit{B}$. An index table constructed by using the sorted codebook can better correlate the neighboring blocks.

Figure 2. An example of PCA sorting.

2.3. Huffman Coding

A Huffman coding is a common encoding algorithm used for data compression. The algorithm was developed by David A. Huffman [19] back in 1952 to represent data by variable-length codes. The key concept of the method is to represent highly used symbols with fewer bits. Based on this concept, a frequency-based binary tree is built from the bottom up and the tree is converged to a Huffman code table eventually.

The inputs to the Huffman coding are a symbol table $s=\left\{s_1, s_2, \cdots , s_a\right\}$ of size $a$ and a corresponding frequency table $f=\left\{f_1, f_2, \cdots , f_a\right\}$. The output of the algorithm is a Huffman code table $hc=\left\{h{c}_1, h{c}_2, \cdots , h{c}_a\right\}$, which can be used to convert symbols into bit streams.

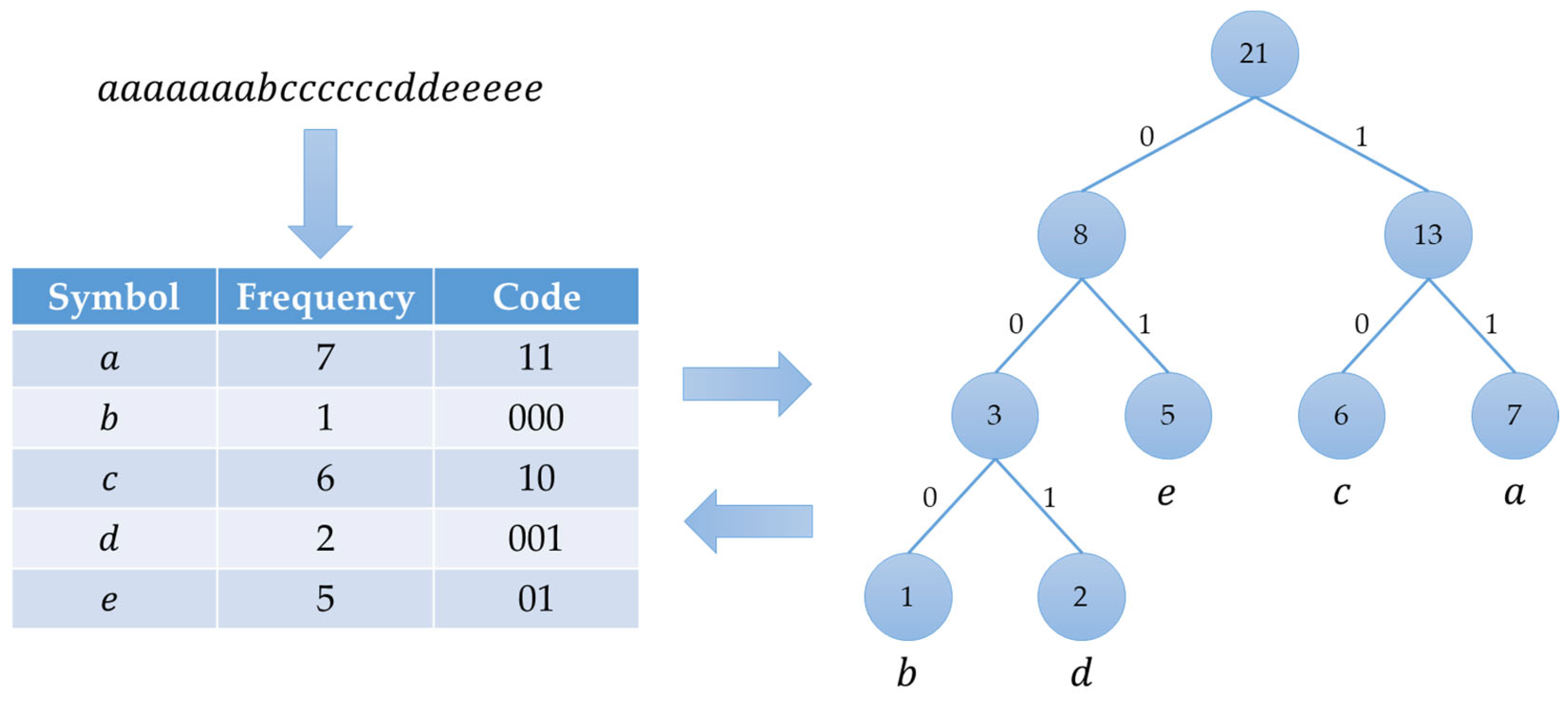
Figure 3 is an example of Huffman code building. If a symbol stream is defined as $S=\left\{aaaaaabccccccddeeeee\right\}$, every symbol is a child node in the Huffman tree and the tree is built from the bottom up according to the frequencies of symbols in the stream $S$. After the tree is built, the left-child is coded with 0 and the right-child is coded with 1. The codes of a symbol are constructed by walking through nodes from the top-most node until reaching a child node matching the desired symbol.

Figure 3. An example of Huffman tree and code table.

3. Proposed Scheme

In this section, we propose a novel recompression scheme based on Huffman coding of index changes between neighboring blocks. First, we obtain a well-ordered new codebook by applying the PCA algorithm to the pretrained VQ codebook. Due to the texture of the image, after sorting with the PCA algorithm, the codebook indices of neighboring blocks are often highly correlated with each other. Based on this characteristic, we calculate the differences or XOR values between neighboring blocks along specified paths, resulting in a processed index table. We observe that the processed index table contains some high-frequency symbols, allowing us to further compress it using Huffman coding.

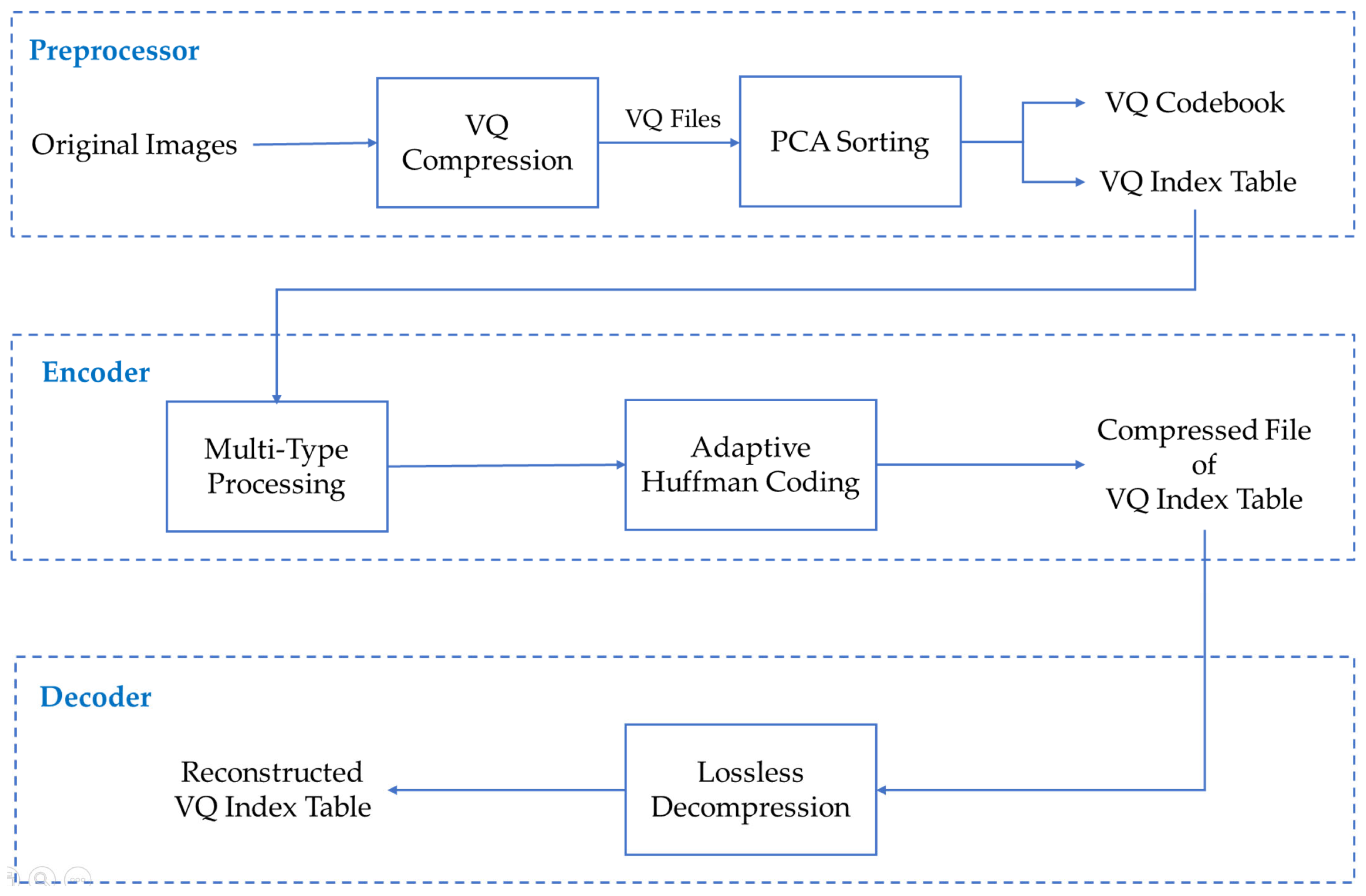
Figure 4 shows the flow of our proposed scheme. Inside of the preprocessor, we apply VQ compression to the original images, generating the VQ codebook and VQ index table. We then sort the VQ codebook using PCA and obtain the corresponding VQ codebook and its updated VQ index table. The VQ index table is the input to the encoder. Through multi-type processing using different paths and methods, various types of processed index tables are obtained. Due to the immersion of numerous high-frequency symbols after processing, they undergo compression using adaptive Huffman coding to generate compressed files of all VQ index table types. The type with the smallest file size, indicating the best compression result, is selected and recorded using an indicator. Upon receiving the compressed VQ index table file, the decoder extracts the indicator first and then performs the corresponding reverse process of lossless decompression to reconstruct the original VQ index table.

Figure 4. The flow of our proposed scheme.

3.1. Multi-Type Processing Phase

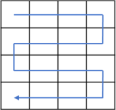
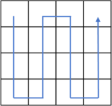
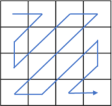
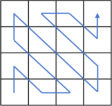
The core of our research is this multi-type processing aiming to optimize the compression results. As shown in Table 1, there are eight processing types: a total of four different serpentine or zigzag paths combined with either a difference calculation method $difference$ or an XOR method $XOR$. After obtaining a processed index table, it is compressed using adaptive Huffman coding. To achieve the best compression results, we compare the results of all compression types and select one by using a 3-bit indicator to denote the selected processing type. It should be noted that a path in Table 1 is only a schematic representation of the direction. Different block sizes for LBG training and different sizes of VQ compressed images will lead to variations in the size of the index table, which is not necessarily the $4\times 4$ size shown under the path of Table 1.

Table 1. Processing types with corresponding paths and methods.

Type	Indicator	Path	Method
1	000		$difference$
2	001		$difference$
3	010		$difference$
4	011		$difference$
5	100		$XOR$
6	101		$XOR$
7	110		$XOR$
8	111		$XOR$

Firstly, we need to retain the index value of the first step position to ensure that the VQ index table can be reconstructed without any loss. For all other positions, they are calculated based on the index value of the previous position relative to the current one according to the selected path. The processed index values are obtained using Equation (3). The index value of the starting position in the path retains its original value, while subsequent positions use either difference calculations or XOR operations depending on the specified method. Here, $\mathit{P}\mathit{I}\mathit{T}$ represents the processed index table, $\mathit{I}\mathit{T}$ represents the original VQ index table, $ps$ represents the step in the path, and $\mathcal{M}$ represents the processed method.

$$\mathit{P}\mathit{I}{\mathit{T}}_{step}=\left\{\begin{array}{c}\mathit{I}{\mathit{T}}_{ps},\\ \mathit{I}{\mathit{T}}_{ps}-\mathit{I}{\mathit{T}}_{ps-1}, \\ \mathit{I}{\mathit{T}}_{ps}\oplus \mathit{I}{\mathit{T}}_{ps-1},\end{array}\right.\begin{array}{c}if ps=1\\ if \mathcal{M} is difference\\ if \mathcal{M} is XOR\end{array}$$

(3)

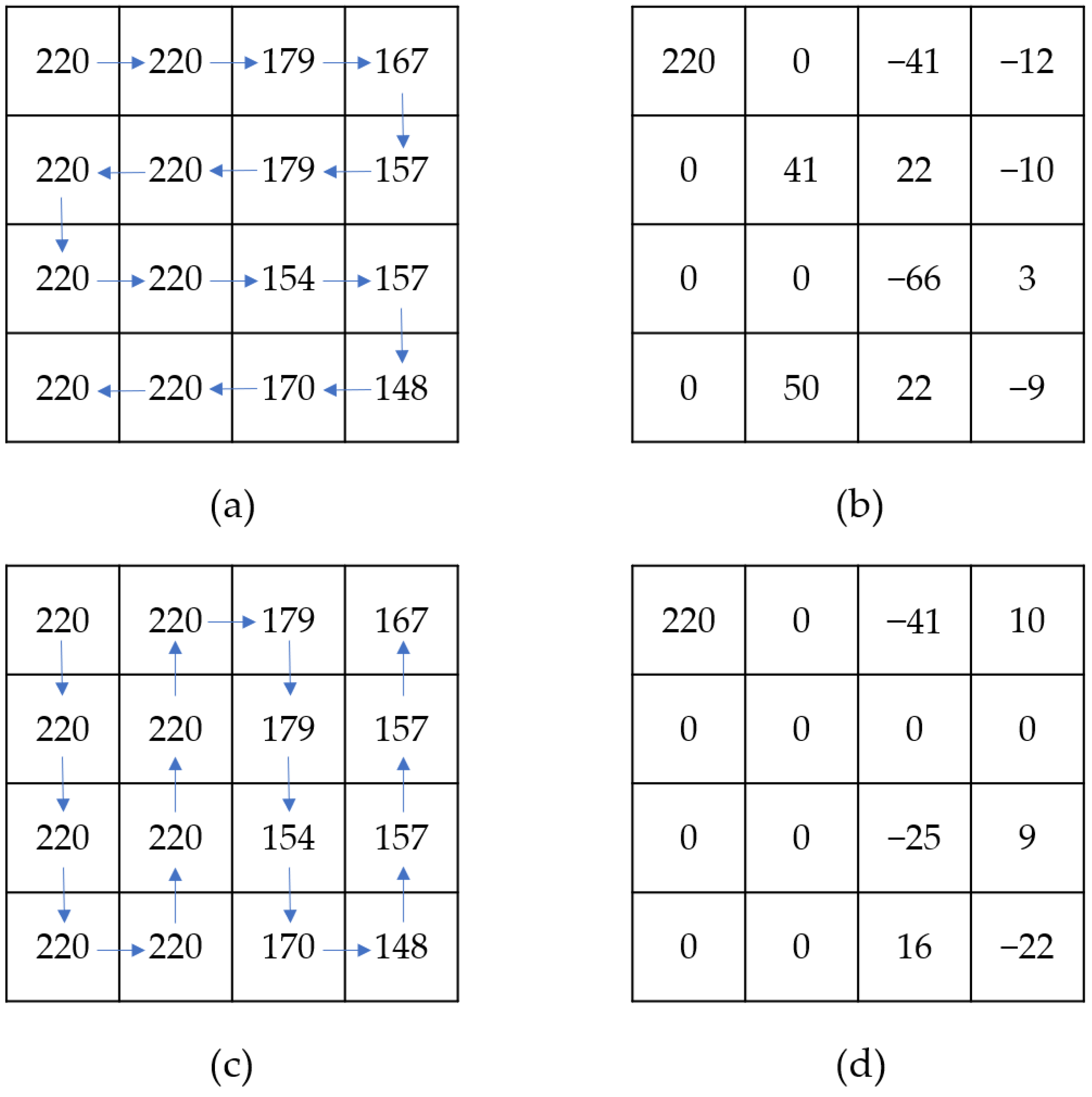
Figure 5 shows examples for two different types: (a) and (c) represent the original indices of the VQ compressed image for $type 1$ and $type 2$, respectively, while (b) and (d) represent the processed index tables for $type 1$ and $type 2$ after using difference calculations. We observe that the index value of the starting point, which is 220, remains unchanged, while the values at other positions indicate relative changes to their respective previous positions. Results of other types are similar to the shown examples. In other words, an image VQ compressed index table corresponds to eight processed index tables depending on types.

Figure 5. Examples of different processing paths. (a) The original indices of the VQ compressed image $type 1$. (b) The processed index table for $type 1$ using the difference method. (c) The original indices of the VQ compressed image for $type 2$. (d) The processed index table for $type 2$ using the difference method.

3.2. Adaptive Huffman Coding Phase

Since there is a certain correlation between the changes in adjacent indices in texture images, there will be some high-frequency changed values. We can use this characteristic feature to compress using Huffman coding. Finally, we choose the type that produces the shortest compression code and record it with a 3-bit indicator.

Due to varying texture features in different images, we construct an independent Huffman coding table for each image instead of using a shared Huffman coding table. Therefore, our scheme involves adaptively constructing Huffman coding tailored to each texture image. Algorithm 1 describes the adaptive Huffman coding. First, input the processed index table $\mathit{P}\mathit{I}\mathit{T}$ to the encoder; then, count the number of changed values in $\mathit{P}\mathit{I}\mathit{T}$, that is, to obtain the number of unique symbols and the counts of each symbol that constitute the frequency table $\mathit{F}\mathit{T}$. Then, convert the frequency into probability, construct the Huffman tree, and, finally, use the Huffman code $HC$ to represent the compressed $\mathit{P}\mathit{I}\mathit{T}$ based on the constructed Huffman tree. To summarize, we obtain the Huffman code $HC$ and the frequency table at the end of the process. The reason for storing the frequency table instead of the Huffman tree is that the storage space occupied by the frequency table will be smaller than that of the Huffman tree, which can achieve a better compression effect.

Algorithm 1. Adaptive Huffman Coding
Input	Processed index table PIT.
Output	Huffman codes HC, frequency table FT.
Step 1	Calculate frequencies:     symbols = unique(PIT)     //Get unique symbols in the processed index table.     counts = histcounts(PIT, [symbols, max(symbols) + 1])     //Count the frequency of each symbol.     FT = [symbols’, counts’]     //Combine symbols and counts into a frequency table.
Step 2	Build Huffman tree:     prob = counts/sum(counts)     //Normalize frequencies to probabilities.     huffmanTree = huffmandict(symbols, prob)     //Construct the Huffman tree using the symbols and their probabilities.
Step 3	Generate codes:     HC = huffmanenco(PIT, huffmanTree)     //Encode the symbols in the PIT using the Huffman tree.
Step 4	Output Huffman codes HC, frequency table FT.

We perform adaptive Huffman coding on the processed index tables corresponding to the eight types, obtaining eight sets of Huffman codes HC and frequency table FT. To obtain the best compression effect, we then choose the path type with the smallest storage space for HC and FT and represent it with a 3-bit indicator. Assuming that type 2 has the best compression effect, “001” is recorded as the indicator. Finally, the compressed file of the VQ index table includes the indicator, frequency table, and Huffman code.

3.3. Lossless Decompression Phase

In the lossless decompression phase, the decoder first identifies the type of processing through the indicator after receiving the compressed file of the VQ index table. Then, it uses the frequency table to build a Huffman tree in the same way as the encoder and decodes the Huffman code to retrieve the processed index table. Since the processing type is known, the VQ index table can be reconstructed using the corresponding path and method. Equation (4) shows the formula of VQ index table reconstruction. At the starting step of the path, the index value is the same as the processed index value. For other positions, the processed index value of the current step is added to the processed index value of the previous step to reconstruct the original VQ index value if the method is $difference$. When the method is $XOR$, the processed index value of the current step is XORed with the processed index value of the previous step to reconstruct the original VQ index value. After processing all steps of the entire path, the VQ index table can be reconstructed.

$$\mathit{I}{\mathit{T}}_{ps}=\left\{\begin{array}{c}\mathit{P}\mathit{I}{\mathit{T}}_{ps},\\ \mathit{P}\mathit{I}{\mathit{T}}_{ps}+\mathit{P}\mathit{I}{\mathit{T}}_{ps-1}, \\ \mathit{P}\mathit{I}{\mathit{T}}_{ps}\oplus \mathit{P}\mathit{I}{\mathit{T}}_{ps-1},\end{array}\right.\begin{array}{c}if ps=1\\ if \mathcal{M} is difference\\ if \mathcal{M} is XOR\end{array}$$

(4)

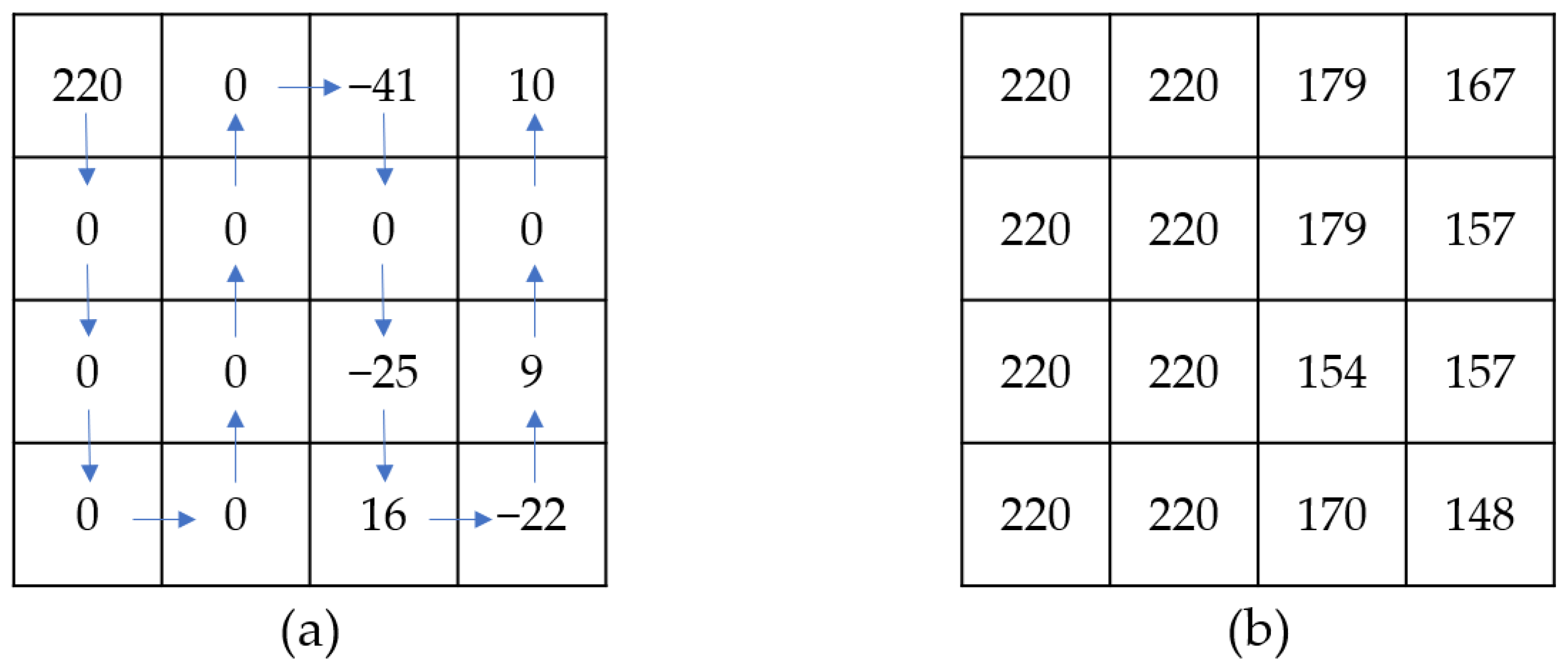
Figure 6 is a specific example. First, assume that the indicator extracted by the decoder is “001”, which corresponds to $type 2$. Figure 6a shows the processed index table with the $type 2$ path. Because the method of $type 2$ is “difference”, according to Equation (4), the reconstructed original VQ index table is shown in Figure 6b.

Figure 6. An example of reconstructing a VQ index table: (a) the processed index table of $type 2$; (b) the reconstructed VQ index table.

4. Experimental Results

To verify the performance of our proposed scheme on texture images, we compare it with other algorithms that also compress the VQ index table, namely the search order coding (SOC) algorithm [14], the SOC-based state codebook (SOC+SC) algorithm [16], and the SOC-based side match (SOC+SM) algorithm [17]. Our experimental environment consists of a Windows 11 laptop with a 3.20 GHz AMD Ryzen 7 CPU and 16 GB RAM. The software used is MATLAB R2024a.

We use bit rate ($BR$), i.e., bits per pixel, as a metric to compare compression performance with other schemes. Equation (5) shows how bit rate is calculated, where $total bits$ represents the size of the compressed file of a VQ index table and $M\times N$ represents the dimensions of the VQ image.

$$BR={\displaystyle \frac{total bits}{M\times N}}$$

(5)

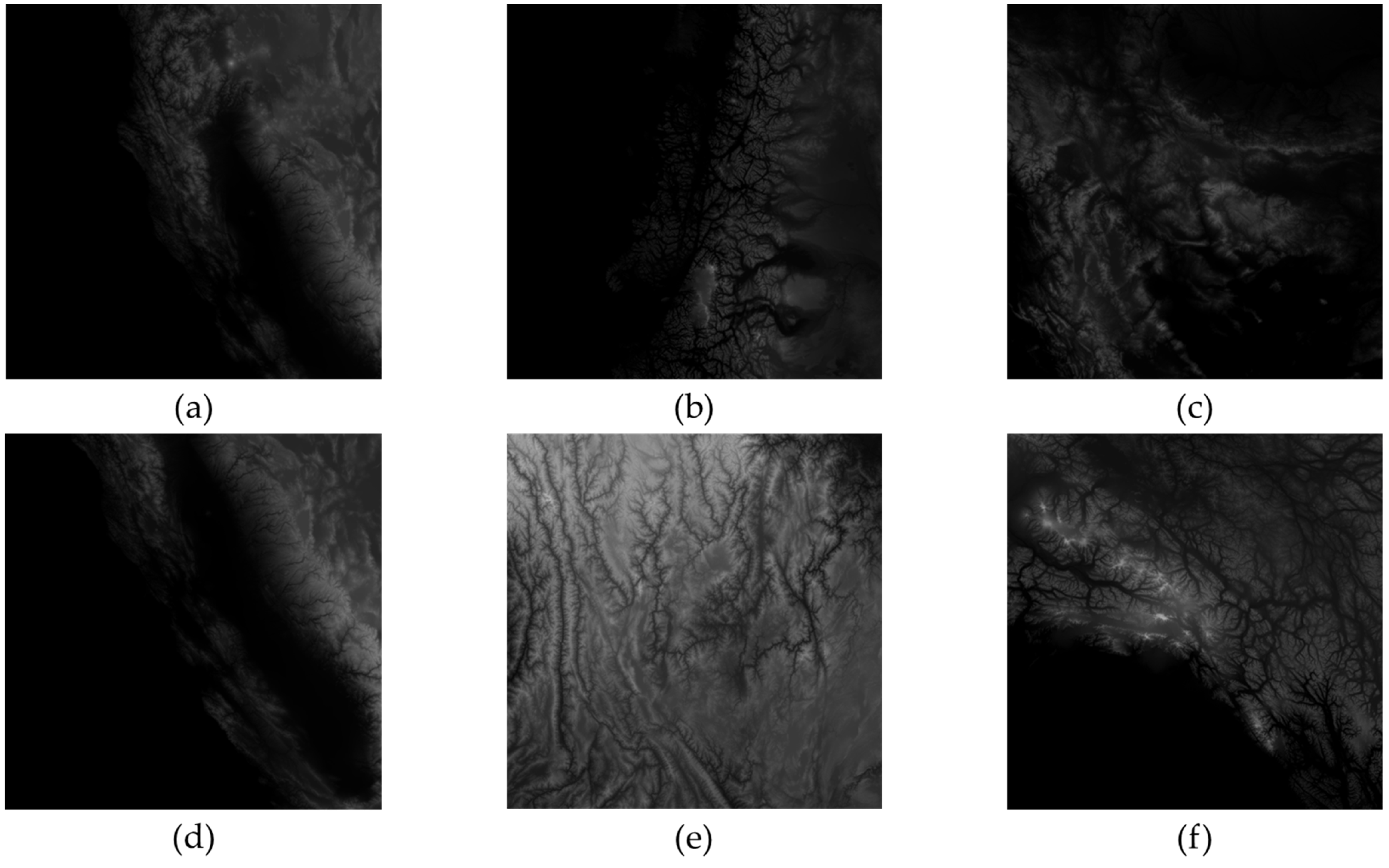
To explore potential limitations of the proposed method, we designed experiments to investigate the impacts of texture images on compression efficiency. In fact, texture images have influence on VQ compression and, consequently, impact the efficiency of recompression. Therefore, we conducted experiments on different images and with varying codebook sizes to obtain comprehensive results. Figure 7 shows six $512\times 512$ monochrome texture images from the USC-SIPI image database [20], which we use as test images. We divided an image into $4\times 4$ blocks and then used LBG algorithm [5] to obtain a VQ codebook and its index table. 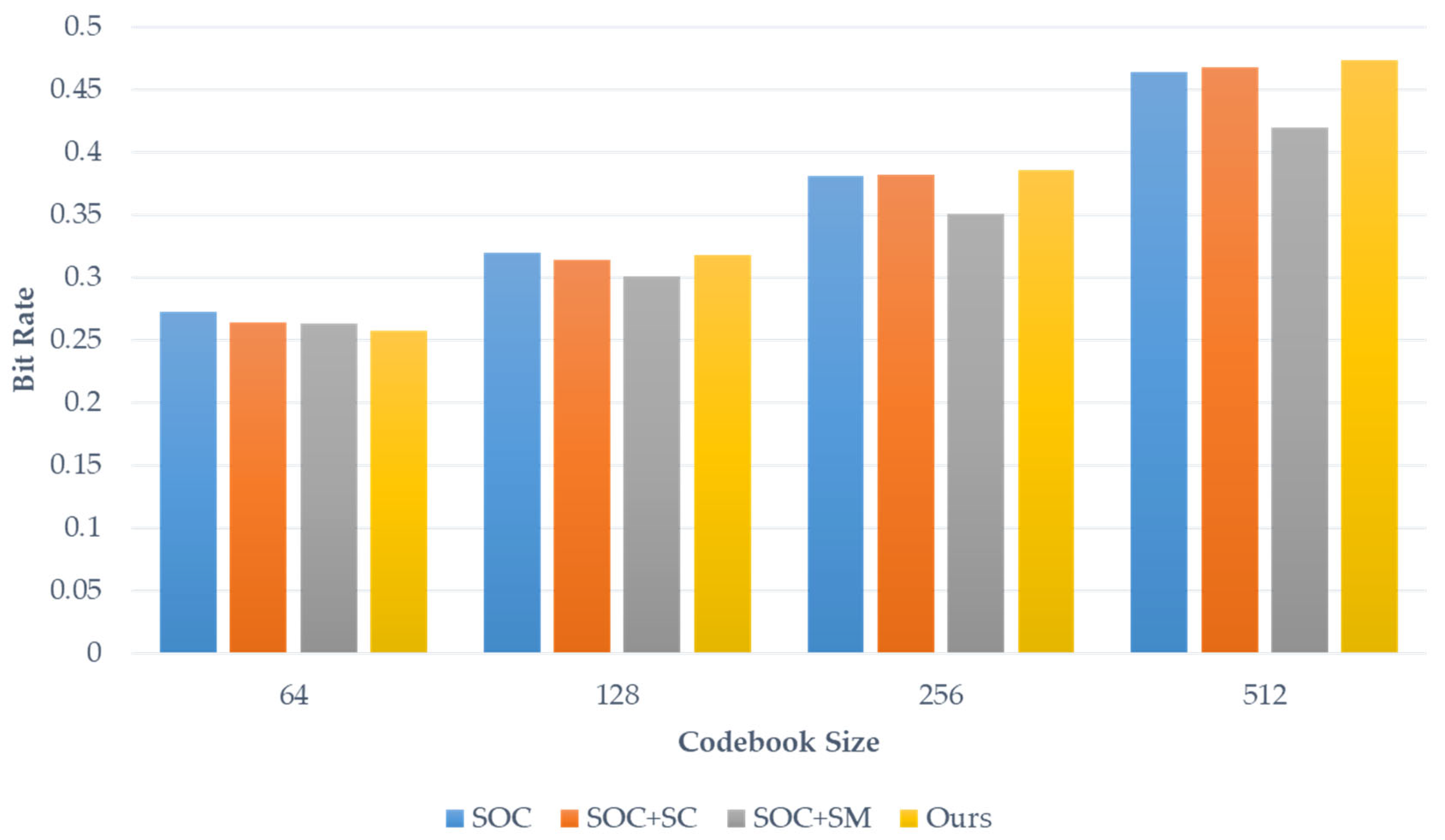Table 2, Table 3, Table 4 and Table 5 show the bit rate and improvement rate of our proposed scheme compared to other schemes using index table recompression in the monochrome texture images while VQ codebook sizes were 64, 128, 256, and 512, respectively. The three schemes [14,16,17] we used in comparisons are all based on the SOC algorithm. In this experiment, we set the number of bits to $n=2$ for all three schemes and set the matching range to $r=4$ for the scheme proposed by Lin et al. [17]. The bit rates for all VQ images across all codebook sizes using our proposed scheme are lower than those of other schemes, demonstrating that our proposed scheme provides better compression performance for texture images. Notably, the bit rate of the Wood Grain image reaches 0.2188, which is more than 22% higher than the other three schemes, if there are 64 codewords in the VQ codebook.

Figure 7. Monochrome texture images: (a) “Herringbone Weave”, (b) “Woolen Cloth”, (c) “Pressed Calf Leather”, (d) “Beach Sand”, (e) “Water”, and (f) “Wood Grain”.

Table 2. Comparison of bit rate and improvement rate with other schemes in monochrome texture images using a VQ codebook containing 64 codewords.

Images	SOC [14]	Improvement Rate	SOC+SC [16]	Improvement Rate	SOC+SM [17]	Improvement Rate	Ours
Herringbone Weave	0.4156	12.34%	0.4220	13.66%	0.4294	15.14%	0.3643
Woolen Cloth	0.3718	4.96%	0.3780	6.53%	0.3594	1.70%	0.3533
Pressed Calf Leather	0.4028	10.55%	0.4090	11.92%	0.4165	13.50%	0.3603
Beach Sand	0.3989	6.33%	0.4111	9.10%	0.3964	5.74%	0.3737
Water	0.2824	11.40%	0.2765	9.51%	0.2665	6.11%	0.2502
Wood Grain	0.2828	22.64%	0.2813	22.24%	0.2815	22.28%	0.2188

Table 3. Comparison of bit rate and improvement rate with other schemes in monochrome texture images using a VQ codebook containing 128 codewords.

Images	SOC [14]	Improvement Rate	SOC+SC [16]	Improvement Rate	SOC+SM [17]	Improvement Rate	Ours
Herringbone Weave	0.4862	12.27%	0.4999	14.68%	0.5078	16.01%	0.4265
Woolen Cloth	0.4520	6.02%	0.4702	9.66%	0.4365	2.68%	0.4248
Pressed Calf Leather	0.4783	10.53%	0.4957	13.68%	0.4994	14.32%	0.4279
Beach Sand	0.4761	7.97%	0.4988	12.15%	0.4775	8.24%	0.4382
Water	0.3531	11.01%	0.3525	10.86%	0.3226	2.60%	0.3142
Wood Grain	0.3445	18.37%	0.3380	16.81%	0.3352	16.11%	0.2812

Table 4. Comparison of bit rate and improvement rate with other schemes in monochrome texture images using a VQ codebook containing 256 codewords.

Images	SOC [14]	Improvement Rate	SOC+SC [16]	Improvement Rate	SOC+SM [17]	Improvement Rate	Ours
Herringbone Weave	0.5546	10.43%	0.5875	15.44%	0.5855	15.15%	0.4968
Woolen Cloth	0.5318	6.41%	0.5635	11.66%	0.5273	5.59%	0.4978
Pressed Calf Leather	0.5482	8.93%	0.5784	13.68%	0.5771	13.50%	0.4992
Beach Sand	0.5481	6.97%	0.5830	12.54%	0.5607	9.07%	0.5099
Water	0.4280	10.20%	0.4444	13.51%	0.3964	3.03%	0.3844
Wood Grain	0.4137	14.74%	0.4191	15.82%	0.4021	12.28%	0.3527

Table 5. Comparison of bit rate and improvement rate with other schemes in monochrome texture images using a VQ codebook containing 512 codewords.

Images	SOC [14]	Improvement Rate	SOC+SC [16]	Improvement Rate	SOC+SM [17]	Improvement Rate	Ours
Herringbone Weave	0.6198	7.59%	0.6629	13.59%	0.6586	13.03%	0.5728
Woolen Cloth	0.6040	4.20%	0.6462	10.47%	0.6157	6.03%	0.5786
Pressed Calf Leather	0.6158	6.24%	0.6565	12.06%	0.6528	11.56%	0.5774
Beach Sand	0.6147	4.29%	0.6593	10.77%	0.6404	8.13%	0.5883
Water	0.5115	10.01%	0.5367	14.24%	0.4869	5.47%	0.4603
Wood Grain	0.4885	12.03%	0.5027	14.52%	0.4816	10.77%	0.4297

We found that earth height map images also exhibited texture features. Therefore, we selected six height map images from the Earth Terrain, Height, and Segmentation Map Images dataset [21] as test images, shown in Figure 8, for experiments as well. Table 6, Table 7, Table 8 and Table 9 display the bit rate and improvement rate of our proposed scheme compared to other schemes using earth height map images with VQ codebooks of sizes 64, 128, 256, and 512, respectively. Our scheme demonstrated better compression effectiveness across all codebook sizes. In particular, as shown in Table 6, the bit rates are only 0.1556 for Height map 1 and 0.1503 for Height map 4, achieving an improvement rate of more than 30% over other schemes. We observed that it also had high improvement rates for other sizes. This demonstrates that our scheme applied to texture images, including earth height map images, is more effective.

Figure 8. Earth height map images: (a) “Height map 1”, (b) “Height map 2”, (c) “Height map 3”, (d) “Height map 4”, (e) “Height map 5”, and (f) “Height map 6”.

Table 6. Comparison of bit rate and improvement rate with other schemes in Earth Height Map images using a VQ codebook containing 64 codewords.

Images	SOC [14]	Improvement Rate	SOC+SC [16]	Improvement Rate	SOC+SM [17]	Improvement Rate	Ours
Height map 1	0.2394	34.98%	0.2276	31.63%	0.2274	31.56%	0.1556
Height map 2	0.2512	27.25%	0.2389	23.48%	0.2393	23.62%	0.1828
Height map 3	0.2620	16.96%	0.2474	12.04%	0.2465	11.71%	0.2176
Height map 4	0.2336	35.66%	0.2234	32.75%	0.2229	32.59%	0.1503
Height map 5	0.3166	24.27%	0.2887	16.97%	0.2876	16.64%	0.2397
Height map 6	0.2837	18.05%	0.2645	12.12%	0.2642	12.02%	0.2325

Table 7. Comparison of bit rate and improvement rate with other schemes in Earth Height Map images using a VQ codebook containing 128 codewords.

Images	SOC [14]	Improvement Rate	SOC+SC [16]	Improvement Rate	SOC+SM [17]	Improvement Rate	Ours
Height map 1	0.2749	29.36%	0.2555	23.99%	0.2517	22.83%	0.1942
Height map 2	0.2898	20.88%	0.2736	16.19%	0.2727	15.91%	0.2293
Height map 3	0.3180	12.58%	0.2939	5.42%	0.2878	3.40%	0.2780
Height map 4	0.2665	29.87%	0.2497	25.16%	0.2448	23.65%	0.1869
Height map 5	0.3905	22.20%	0.3485	12.83%	0.3434	11.53%	0.3038
Height map 6	0.3440	16.30%	0.3171	9.20%	0.3165	9.01%	0.2880

Table 8. Comparison of bit rate and improvement rate with other schemes in Earth Height Map images using a VQ codebook containing 256 codewords.

Images	SOC [14]	Improvement Rate	SOC+SC [16]	Improvement Rate	SOC+SM [17]	Improvement Rate	Ours
Height map 1	0.3169	25.20%	0.3042	22.09%	0.2897	18.17%	0.2370
Height map 2	0.3302	17.24%	0.3210	14.88%	0.3124	12.52%	0.2733
Height map 3	0.3792	11.25%	0.3620	7.03%	0.3413	1.37%	0.3366
Height map 4	0.3068	25.93%	0.2946	22.86%	0.2791	18.60%	0.2272
Height map 5	0.4704	21.71%	0.4437	17.00%	0.4248	13.29%	0.3683
Height map 6	0.4023	14.40%	0.3911	11.95%	0.3773	8.73%	0.3443

Table 9. Comparison of bit rate and improvement rate with other schemes in Earth Height Map images using a VQ codebook containing 512 codewords.

Images	SOC [14]	Improvement Rate	SOC+SC [16]	Improvement Rate	SOC+SM [17]	Improvement Rate	Ours
Height map 1	0.3602	21.30%	0.3595	21.14%	0.3344	15.24%	0.2835
Height map 2	0.3764	12.40%	0.3774	12.63%	0.3576	7.79%	0.3297
Height map 3	0.4485	10.13%	0.4443	9.29%	0.4074	1.08%	0.4030
Height map 4	0.3478	21.59%	0.3458	21.13%	0.3218	15.26%	0.2727
Height map 5	0.5561	20.97%	0.5534	20.59%	0.5198	15.46%	0.4395
Height map 6	0.4618	11.52%	0.4683	12.74%	0.4449	8.16%	0.4086

The reason our scheme is better than the traditional SOC-based schemes is that the blocks of texture images are very similar, leading to many similar VQ codewords. Without a sorted codebook, the visual appearances can be similar but the adjacent index values are very different. Our proposed scheme does not rely on this entirely; it counts on using adaptive coding to compress based on the high frequencies of changed symbols as well. 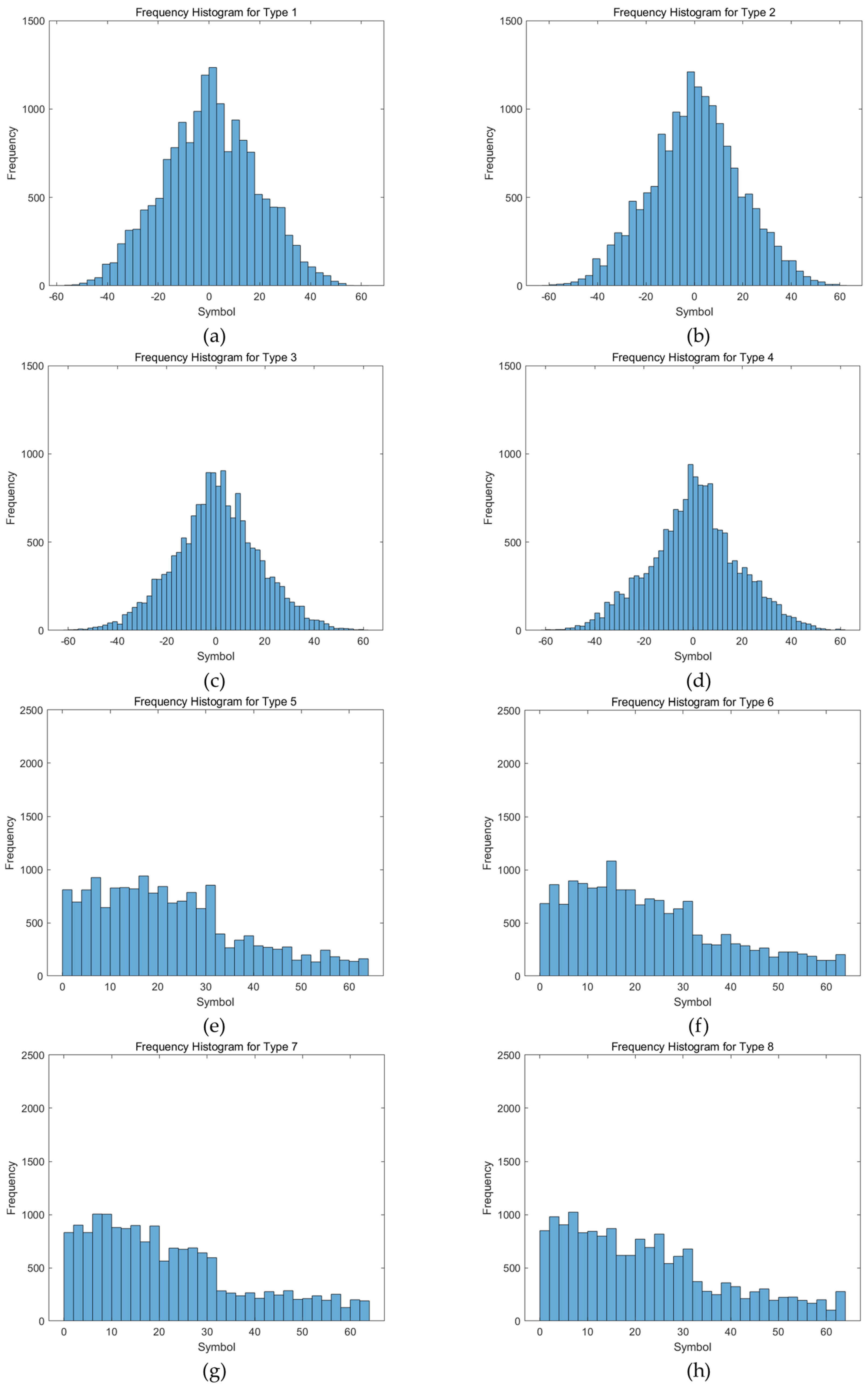Figure 9 shows the histogram of the processed index frequencies for different processing types of “Herringbone Weave” using a VQ codebook containing 64 codewords. We can observe that the types coped with the $difference$ method have more symbols concentrated at the high-frequency area near 0 and the frequency distribution trends are more obvious. In contrast, the processing types using the $XOR$ method have fewer symbols, and the high-frequency areas are spread out around smaller values. Due to these differences in numbers of symbols and their frequencies, each method exhibits its own advantages when compressing various types of images. In summary, such frequency distributions are conducive to further compression using adaptive Huffman coding.

Figure 9. The processed index frequencies for different types of “Herringbone Weave” using a VQ codebook containing 64 codewords. (a) $type 1$. (b) $type 2$. (c) $type 3$. (d) $type 4$. (e) $type 5$. (f) $type 6$. (g) $type 7$. (h) $type 8$.

To evaluate the performance of our proposed scheme on different images beyond texture images, we used six common images shown in Figure 10. Figure 11 presents the results of our scheme and other schemes when using codebook sizes of 64, 128, 256, and 512. The experimental results show that, with a codebook of 64 codewords, the compression rates of our method are superior to other methods. For other codebook sizes, although our scheme does not achieve the best compression performance, it is only slightly behind. This demonstrates that our method performs well on various images, not just texture images.

Figure 10. Common images: (a) “Airplane”, (b) “Baboon”, (c) “Boat”, (d) “Goldhill”, (e) “Lake”, and (f) “Peppers”.

Figure 11. Comparison of bit rates with other schemes in common images.

Table 10 presents p-values comparing our proposed scheme with other methods. The p-value is a statistical measure that helps determine the significance of results; a smaller p-value indicates a more significant result. It can be observed that all p-values for the other methods are below 0.05 when compared to our method, demonstrating the statistical significance of our results. This finding provides strong support for our research conclusions.

Table 10. Comparison of p-values with other schemes.

SOC [14] vs. Ours	SOC+SC [16] vs. Ours	SOC+SM [17] vs. Ours
0.0075	0.0201	0.0206

Table 11 and Table 12, respectively, present the time complexities of the proposed scheme. The time complexity is $O\left(n\log n\right)$ for the encoder and $O\left(n\right)$ for the decoder. With different codebook sizes trained using various test images, the fastest execution time occurs at a codebook size of 64, which is approximately 0.1 s. This demonstrates one of the advantages of our proposed scheme. Additionally, we observe that a larger codebook size does result in longer execution time. This is because there are more symbols to encode in the Huffman coding stage, which results in increasing the processing time. Therefore, shorter execution time usually indicates fewer symbols.

Table 11. Time complexity of our proposed scheme.

Encoder	Decoder
$O\left(n\log n\right)$	$O\left(n\right)$

Table 12. Execution time of our proposed scheme.

Codebook Size	Monochrome Texture Images		Earth Height Map Images		Common Images
	Encoder	Decoder	Encoder	Decoder	Encoder	Decoder
64	0.12	0.15	0.07	0.08	0.12	0.12
128	0.25	0.19	0.12	0.11	0.22	0.15
256	0.54	0.24	0.21	0.14	0.47	0.20
512	1.33	0.32	0.40	0.18	1.11	0.28

5. Conclusions

This paper presents an effective recompression scheme for VQ-compressed index tables of texture images. The encoder performs a multi-type process on a VQ index table. The processing types are formed by different scanning paths and calculation methods; each type, then, is evaluated by applying adaptive Huffman coding. After evaluation, we select the type with the best compression effect and use a 3-bit indicator to record the type. The decoder only needs to extract the indicator first to determine the processing type and then perform the inverse operation of the encoder to reconstruct the original VQ index table. Compared with other schemes designed for compressing VQ index tables, our scheme demonstrates better compression performance on both datasets. Significant improvements across different codebook sizes and various VQ-compressed images reflect the superior compression performance of our scheme as well. Our research positively impacts image compression technology in fields such as telemedicine, remote sensing, and multimedia storage and transmission. In the future, we will test different datasets and explore more effective compression algorithms.