Abstract
A bicluster consists of a subset of rows and columns of a given matrix, whose intersection defines the region (bicluster) of values of precisely defined condition. Through the decades, a variety of biclustering techniques have been successfully developed. Recently, it was proved that many possible patterns defined in two-dimensional data could be found with the application of Boolean reasoning. The provided theorems showed that any existing pattern in the data could be unequivocally encoded as an implicant of a proper Boolean function. Moreover, a prime implicant of that function encoded the inclusion-maximal (non-extendable) pattern. On the other hand, the definition of some two-dimensional patterns may be easily extended to three-dimensional patterns (triclusters) as well as to any number of dimensions (n-clusters). This paper presents a new approach for searching for three- and higher-dimensional simple patterns in continuous data with Boolean reasoning. Providing the definition of the Boolean function for this tasks, it is shown that the similar correspondence—implicants encode patterns, and prime implicants encode inclusion-maximal patterns—has a strong mathematical background: the proofs of appropriate theorems are also presented in this paper.
1. Introduction
When we think about data analysis, the most intuitive aspects that come to mind are clustering, prediction, classification, pattern recognition, and many others. Biclustering seems to be a hidden sibling. However, as it was defined in the 1960s [1], it became more popular several decades later when it was applied to biomedical purposes [2]. What is a bicluster? Having two-dimensional homogeneous data, we may be interested in searching for a submatrix: a subset of rows and columns, whose intersection would point such a set of cells to follow a well-defined condition for some values.
The notion of a bicluster, just representing a kind of pattern in the data, is originally related to two-dimensional data. However, it is very easy to extend it to three, four, or even an unlimited number of dimensions. That would lead us to triclusters, quadriclusters, and finally, n-clusters.
In this paper, a generalized mathematical background for searching for n-clusters in n-dimensional data is presented. The approach applies the Boolean reasoning paradigm, the paradigm that was successfully adopted in biclustering [3,4,5], triclustering [6], or binary n-clustering [7]. Here again, the task of searching for the pattern is expressed as a Boolean formula analysis, and again, proper theorems that bind these results with the required patterns are formulated and proved.
The paper is organized as follows: It starts with a brief description of Boolean reasoning, the explanation of biclustering and triclustering (including the difference between biclustering and clustering), and current results of Boolean reasoning application in such an area of data analysis. Then, it is followed by the introduction of two quite necessary notions: exactness and inclusion maximality. Later, the proof of concept of triclustering continuous data with Boolean reasoning is discussed step by step; the core part of the paper consists of theorems that bind exact patterns (triclusters, n-clusters) in the data with implicants of well-defined and data-dependent Boolean variables; further, these theorems are proved. The paper ends with some conclusions and perspectives of further works in this area.
2. Context of Searching Patterns with Boolean Reasoning
To understood the idea of the application of Boolean reasoning for searching biclusters, triclusters, n-clusters, and many more, a general description of Boolean reasoning is presented, followed by a brief review of other bi(tri)clustering approach; afterwards, a summary of past results on the application Boolean reasoning for pattern search is provided.
2.1. Boolean Reasoning
Boolean reasoning [8] is a paradigm of data processing that assumes that it is possible to express (encode) a source issue as a Boolean function, which can be later processed, and the results can be decoded as the solution of the original problem. Such an approach is very common in the domain of rough sets [9,10]. However, it was also proved that such an approach may be useful in many types of pattern induction, which is described in more detail in Section 2.3.
2.2. Biclustering and Triclustering
When one hears the word “biclustering”, it is very intuitive but wrong to think about clustering of two-dimensional data. Nothing could be further from the truth. The goal of clustering is to find subgroups of objects (described with many, usually more than two, features) more similar to each other than to objects from other found groups. Moreover, features describing the objects may have completely different and incomparable domains such as age, height, weight, monthly salary, number of children, and so on. What is more, clustering provides—from a mathematical point of view—the partition of the set of objects (we keep away from fuzzy approach results before their defuzzyfication). On the other hand, biclustering means searching for submatrices of a given input matrix, when all its values come from the same domain. Such an assumption is crucial, as we take into consideration differences between any cells of the input data (please try to imagine, in reference to clustering, how to interpret the difference between height in kg and number of children: the subtraction is technically possible, but the result cannot be interpreted). The found submatrix is then called a bicluster, as it is described (defined) by two clusters of row and column indices. The intersection of these rows and columns defines which cells belong to the bicluster. It is obvious that for the same input data, the patterns one can find may vary as we change their expected properties. They may be different for binary, discreet, and continuous data.
Staying in this frame of reference of the strong bind between clustering and set partitioning, it is also worth emphasizing that biclustering results may violate any (or even all) of three partitioning requirements: found biclusters may overlap each other, they do not have to cover all the input data, and finally, the empty biclusters may also satisfy well-specified pattern requirements (the existence of empty but correct biclusters was already discussed in [3,4]).
The difference between clustering and biclustering becomes more intuitive with the following comparison. Let us consider two different sets of four objects, described with four features. The clustering technique may be applied to find similar objects as well as to find comparable features. Figure 1 shows possible results of both approaches.
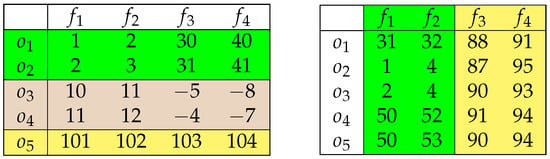
Figure 1.
Possible results of object (left) and feature (right) clustering.
In each case, the objects (Figure 1 left) and the features (Figure 1 right) were partitioned into subsets of more similar feature values/feature statistics. On the other hand, when the two-dimensional array of continuous values becomes the point of interest, we look for a pattern whose inner maximal difference does not exceed the assumed level . The obvious, however not-satisfiable solution, is to consider each cell a single-value bicluster. This is not a proper approach, as we usually expect that any method of data analysis will bring us more generous (object aggregating) results. Figure 2 shows biclusters of different levels of (single-cell patterns were not colored to make the figure more legible).
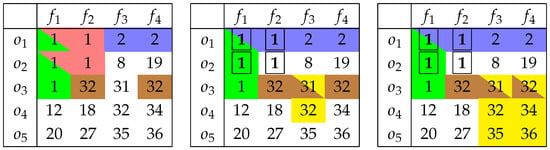
Figure 2.
Biclustering results for different levels of : 1 (left), 2 (middle), and 5 (right).
Even for , we may observe that two patterns— and —have two cells ( and ) that belong to each of them, respectively. When we increase , we should expect a further pattern extension in any direction, and it is easily observable in the above figure.
Over the years, many biclustering techniques, solving particular biclustering aims, have been developed. They include the following, grouped by the nature of their approach:
- Uncovering structures by eigenvectors [11];
- Evolutionary computation [12,13,14,15,16];
- Graphs [17,18,19];
- Ensemble methods [20];
- Scatter search [21,22].
The separate branch of biclustering techniques based on Boolean reasoning is described in the following subsection.
Biclustering refers to a two-dimensional data analysis. However, it is very easy to extend such an approach into three dimensions. Very early studies of three-dimensional (and higher) data were carried out as early as the 1970s [23]. Later studies are described in [24,25,26].
Triclustering was applied successfully in many fields of application, including gene expression analysis [27,28,29], climate data processing [30], or graph analysis [31].
2.3. Boolean Reasoning in Pattern Search
The first paper that paid attention to the fact that Boolean reasoning may be successfully applied in biclustering was published in 2018 [3]. The attempts were focused on discrete and binary data biclustering. The nature of the data required a pattern that contained only such cells that had the same value. The paper provided the definitions of data-encoding Boolean formulas (the first step of the Boolean reasoning paradigm—to express the analyzed data as a Boolean formula). The formulas were built from row/column indices corresponding to variables and were conjunctions of disjunctions of literals. Such a formula is commonly known as CNF—conjunctive normal form. The secondary goal of the analysis was to find prime implicants of these functions, the so-called DNF: disjunctive normal form. Having prime implicants, it was easy to decode them into patterns. It was possible because two theorems (weak and strong) related to each issue (discrete and binary data analysis, separately) were introduced and proved. The general form of the weak theorem said: “An implicant of the Boolean function corresponds to the pattern in the data in such a way that the pattern is built from all row/column corresponding variables that are not present in the implicant”. The strong version of the theorem said that prime implicants encoded inclusion maximal patterns in the data (the notion of the inclusion maximality is described in a more detail in Section 3.2).
Afterwards, this approach was extended for continuous data, as well as for many other types of patterns, and finally even for n-dimensional binary data. At this moment, it is possible to search the following patterns with Boolean reasoning:
- Constant values in discrete data [3];
- Constant values in binary data [3];
- Constant values in n-dimensional binary data [7];
- -Limited (inner maximal difference) biclusters in continuous data [4];
- -Limited (inner minimal difference) biclusters in continuous data [4];
- Center-based biclusters (values not greater/smaller than a defined center and assumed margin) [32];
- -Shifting patterns (only the in-row difference in a pattern is limited) [33].
For any of the above-mentioned tasks, a data-encoding Boolean formula definition was provided, and weak and strong theorems were presented and proved.
One may wonder about the purpose of providing weak theorems in all of these cases. The first reason is that a weak theorem helps to prove a strong theorem (that will become clear in Section 6). The second motivation refers to the computational complexity of the Boolean function satisfiability analysis. It is much less time consuming to find an implicant of the Boolean function (we know from weak theorems that such implicants also encode a demanded pattern) than to find a prime one. Based on the weak theorems, it became possible to apply (with some modifications) well-known strategies of implicant search into biclustering [5,34].
3. Additional Notions
This section clarifies two already-mentioned notions: exactness and inclusion maximality.
3.1. Pattern Exactness
As already discussed, having any dimensional input data, it is possible to define a variety of conditions that the pattern (bicluster, tricluster, n-cluster) should satisfy. Independently of the dimensionality of the data and the pattern condition, we may determine precisely whether the pattern fulfills the criteria or not. The pattern satisfying the criteria is called exact.
Let us consider a small continuous data matrix as presented in Figure 3.
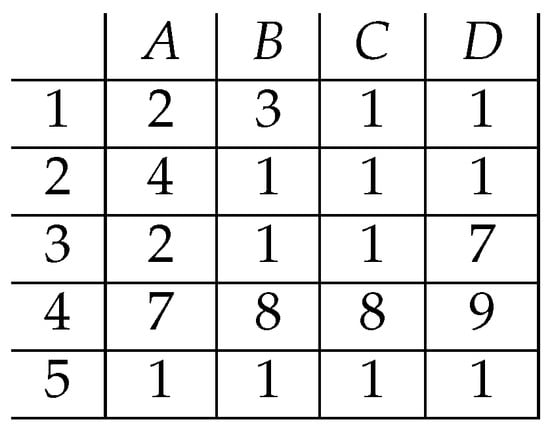
Figure 3.
A sample matrix of continuous data.
Considering the first two patterns of ones (left and center) of Figure 4, both of them are exact (there is no cell with a value different than one), while the right one is not “right”, as it contains three and seven.
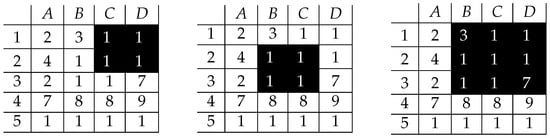
Figure 4.
Exact (left and center) and non-exact (right) patterns of 1’s in the input matrix.
3.2. Inclusion Maximality
The recalled strong versions of theorems refer to the inclusion maximality. Let us go back to the generous definition of a pattern as an n-tuple of subsets of each input data direction. We know from the theory of sets that two sets may be completely disjoint (e.g., and ), may have a non-empty intersection (e.g., and ), and one of them may be a proper subset (proper means that sets are not equal to each other) of the other (e.g., is a proper subset of ). That leads us to the notion of a partially ordered set. From the two sets, the first one is higher in order if the second one is the proper subset of the first one.
As also suggested before, the goal of any data analysis is to provide as general solutions as possible. Considering single-cell patterns is not satisfactory. In opposition to such an intuitive solution, it is required to search for such patterns that could not be extended in any dimension without violating the above-mentioned exactness.
Let us still focus on the data presented in Figure 3, and let us discuss a single-value pattern of ones as presented in Figure 5.
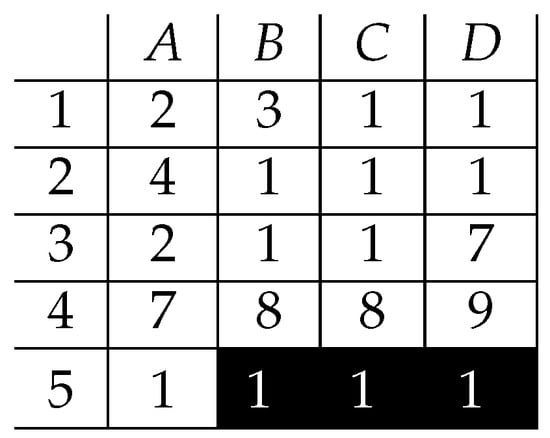
Figure 5.
Bicluster of 1’s—.
This is obvious that it is an exact pattern. However, it cannot be called an inclusion-maximal one, as it is possible to extend it in any of both dimensions but still keeping it exact (Figure 6).
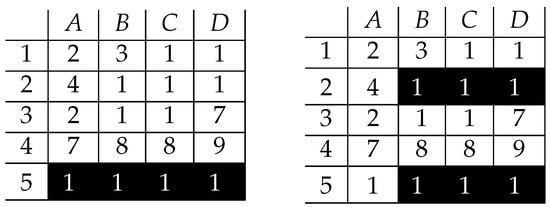
Figure 6.
Bicluster of 1’s extended by column (left) and row (right).
The two newly created patterns are now inclusion-maximal, as it is impossible to extend them in any direction (row or column) without violating their exactness—any new row or any new column contain values different than ones.
4. A Proof of Concept
This section extends the example already presented in [6]. Let us consider the following three-dimensional data as presented in Figure 7. The original cube is decomposed into three slices—denoted as , , and —and each slice consists of rows (1, 2, 3) and columns (A, B, C).
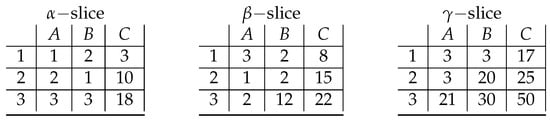
Figure 7.
A sliced representation of the cube .
The formal criterion for the tricluster of cells, whose values do not exceed an assumed level , would look as follows:
Following the rule of building a Boolean formula for searching for biclusters in the continuous data presented in [4] as the encoding of all pairs of cells whose difference exceeds the assumed level , the formal definition of the Boolean formula corresponding to the data would look as follows:
where
such that
Having 27 cells, the cube provides different pairs. Over 200 of them should be encoded as Boolean function clauses. Differences between all 27 cells are presented in Figure 8.
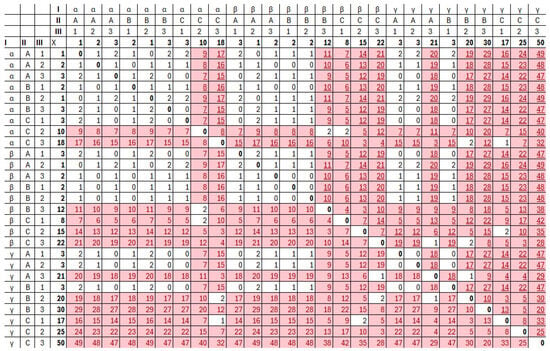
Figure 8.
Differences between all cells of the considered cube.
Three coordinates—slice, column, and row—are denoted as I, II, and III row/column header, respectively. Additionally, the value of the corresponding cell is in bold font. The presented matrix is symmetric and has zeros on the main diagonal, which comes directly from the symmetry of the difference in values. The highlighted and underlined cells refer to pairs of cube elements whose difference exceeds the assumed level .
A manual transformation of the formula from CNF into DNF and shortening it to the prime-implicant-only representation results in the following final formula:
The found prime implicant consists of such Boolean variables whose corresponding rows/columns/slices are not present in the inclusion-maximal tricluster. That means that the following prime implicant should be decoded into the following tricluster: . This tricluster can be easily visualized as presented in Figure 9.
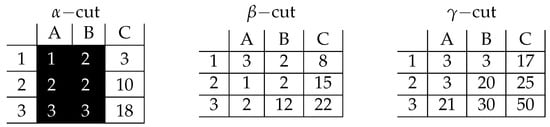
Figure 9.
Visualization of prime implicant corresponding the inclusion-maximal bicluster: .
The found pattern contains only 1, 2, and 3 values. That means that it satisfies the condition of the maximal inner difference being less than 2. Now, let us analyze whether the pattern is inclusion-maximal or not. If it was not, that would mean that we could add at least one row, or one column, or one slice having still a pattern of inner difference not greater than 2. It is impossible to add any row, as the pattern contains all possible rows. Column C (of values 3, 10, and 18) cannot be added either as it would violate the above-mentioned condition: e.g., the difference between 18 and 1 breaks the limit significantly. For the same reason, any of remaining slices— and —cannot be added. The value 12 from the slice (in row 3 and column B already present in the pattern) avoids it. The same reasoning excludes the slice from the pattern. We have already shown that it is impossible to extend the pattern in any direction, so it is inclusion-maximal.
The list of all prime implicants with their corresponding triclusters and an optional annotation is presented in Table 1.

Table 1.
Prime implicants of the function f and the corresponding inclusion-maximal triclusters.
Visualization of all other inclusion maximal and non-trivial (i.e. wider than only one cell) triclusters, corresponding to non-empty prime implicants, is provided in Appendix A.
5. Boolean Reasoning-Based Triclustering Formalism
The above example showed that it was possible to apply Boolean reasoning to search for triclusters. However, at the moment, we cannot generalize such an approach to any continuous data. That step—the generalization—requires providing appropriate theorems and their proofs.
Two theorems—called weak and strong—bind implicants with patterns in the following way: the weak theorem binds implicants with patterns of required properties, while the strong theorem states that prime implicants correspond to inclusion-maximal patterns.
5.1. Weak Theorem of Triclustering Continuous Data
Let be a three-dimensional cube of continuous values, and let us search for patterns (triclusters) of inner maximal difference not greater than . Let us encode all pairs of cells with the formula according to (2) under the conditions (3) and (4).
Theorem 1.
, where is a conjunction of row-corresponding Boolean variables, is a conjunction of column-corresponding Boolean variables, and is a conjunction of slice-corresponding Boolean variables, is an implicant of iff is a pattern in , satisfying the σ condition.
- Let be an implicant of and let not be an exact pattern in . That means that there exists at least one pair of cells in such that their absolute difference exceeds the assumed level . This leads to the statement that cannot be an implicant of as it was assumed that covered all pairs in of the absolute difference greater that .
- Let be an exact pattern in and let not be an implicant of . That means that there exists a clause in that does not cover. This, in turn, means that this clause codes such a pair of cells from that violates the condition, which is in contradiction with the assumption that is an exact pattern.
5.2. Strong Theorem of Triclustering Continuous Data
Theorem 2.
, where is a conjunction of row-corresponding Boolean variables, is a conjunction of column-corresponding Boolean variables, and is a conjunction of slice-corresponding Boolean variables, is a prime implicant of iff is an inclusion-maximal pattern in , satisfying the σ condition.
- Let be the prime implicant of . From the above theorem, is the exact pattern in . Let us assume that is not an inclusion-maximal pattern, so at least one of the three following ways of its expansion are possible:
- An extension with the row r so is also an exact pattern in ;
- An extension with the column c so is also an exact pattern in ;
- An extension with the slice s so is also an exact pattern in .
However, also from the above theorem, we conclude that any of the extended patterns has a corresponding implicant of , which has a shortened conjunction of row/column/slice-corresponding variables, which is in contradiction with the assumption that is a prime implicant.
- Let be an inclusion-maximal exact pattern in . From the above theorem, we know that is an implicant of . Let us assume that is not a prime implicant of . This, in turn, means that at least one row/column/slice-corresponding Boolean variable may be removed from . The shortened implicant—also from the above theorem—codes a pattern extended by a row/column/slice. This is in contradiction with the assumption that is inclusion-maximal (not extendable).
6. Generalization and Its Correctness
As we have already proved the weak and strong theorems of continuous data triclustering based on Boolean reasoning, we may try to generalize such an approach to any data dimensionality and provide proper theorems—weak and strong again—for the purpose of n-clustering.
Let be an n-dimensional hypercube of continuous values. As an n-cluster, an n-tuple would be denoted, such that . Assuming that the maximal inner difference in the pattern should be not greater than , the condition for the pattern values would look as follows:
The data-corresponding Boolean formula would look as follows:
where are first-dimension indices corresponding to variables, are second-dimension indices corresponding to variables, and so on, such that:
6.1. Weak Theorem of n-Clustering Continuous Data
Let be an n-dimensional cube of continuous values, and the patterns (n-clusters) of inner maximal difference not greater than are searched for. Let us encode all pairs of cells with the formula according to definition (6) under the above-mentioned conditions.
Theorem 3.
, where is a conjunction of ith dimension indices corresponding to Boolean variables, is an implicant of iff is a pattern in , satisfying the σ condition.
- Let be an implicant of , and let P not be an exact pattern in . That means that there exists at least one pair of cells in such that their absolute difference exceeds the assumed level . This leads to the statement that cannot be an implicant of as it was assumed that covered all pairs in of the absolute difference greater than .
- Let be an exact pattern in , and let not be an implicant of . That means that there exists a clause in that does not cover. This, in turn, means that this clause codes such a pair of cells from that violates the condition, which is in contradiction with the assumption that is an exact pattern.
6.2. Strong Theorem of n-Clustering the Continuous Data
Theorem 4.
A , where is a conjunction of ith dimension indices corresponding to Boolean variables, is a prime implicant of iff is an inclusion-maximal pattern in , satisfying the σ condition.
- Let be the prime implicant of . From the above theorem, is the exact pattern in . Let us assume that is not an inclusion-maximal pattern; thus, there exists at least one direction i, such that the following extension of the pattern is possible:However, also from the above theorem, we conclude that any of the extended patterns will have a corresponding implicant of , that would have a shortened conjunction of ith dimension indices corresponding to variables, which is in contradiction with the assumption that is a prime implicant.
- Let be an inclusion maximal exact pattern in . From the above theorem, we know that is an implicant of . Let us assume that is not a prime implicant of . This, in turn, means that at least one ith dimension indices corresponding to Boolean variable may be removed from . The shortened implicant—also from the above theorem—codes a pattern extended in the ith direction. This would be in contradiction with the assumption that is inclusion-maximal (not extendable).
7. Conclusions and Further Works
This paper provided a new approach to analyze three- or higher-dimensional data. The novelty came from the fact that Boolean reasoning was used. Following a working idea of searching for triclusters in continuous data presented in [6], this work provided not only a mathematical proof for the idea correctness but also extended the application for data of any dimensionality, presenting proper and proved theorems.
The theoretical benefits of providing a complete set of weak and strong theorems give two ways of processing the data. For few data, we may proceed in an exhaustive way by searching for all prime implicants of a data-corresponding Boolean function. Several proposals were presented in [35,36].
However, it is very important to remember that even for the three-dimensional issues, an initial CNF of the function consists of up to six literal clauses. That, in turn, means that the satisfiability of the six-CNF needs to be checked, while the problem of three-CNF functions’ satisfiability checking is one of the Karp’s 21 NP-complete problems [37]. This is why the weak theorem has a second benefit. Recall that it says that each implicant (not necessarily a prime one) encodes an exact pattern in the data. Thanks to that, it becomes possible to apply well-known—possibly with the requirement of some small modifications—implicant search heuristics, e.g., in [5], a modified version of Johnson’s strategy [38] (the main reason of the modification was to avoid empty pattern finding) was introduced, and in [7], a mixed heuristic strategy for binary data biclustering was proposed: the upper level of heuristics was responsible for changing the input data in the search tree, while the lower level of heuristics used the above-mentioned strategy [5].
Concluding, the paper showed the potential of Boolean reasoning in biclustering; however, the increasing size of single clauses will inspire new heuristics development.
Funding
This work was supported by the Department of Computer Networks and Systems (RAu9) at Silesian University of Technology.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
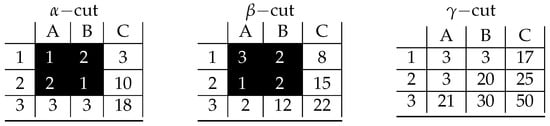
Figure A1.
Visualization of prime implicant corresponding to inclusion-maximal bicluster: .
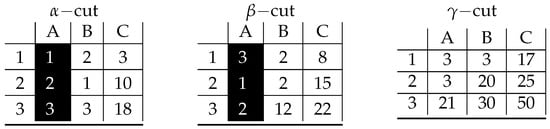
Figure A2.
Visualization of prime implicant corresponding to inclusion-maximal bicluster: .
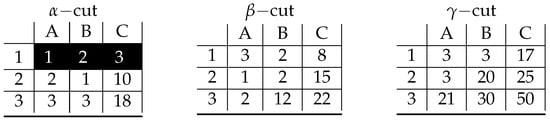
Figure A3.
Visualization of prime implicant corresponding to inclusion-maximal bicluster: .
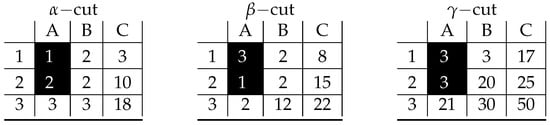
Figure A4.
Visualization of prime implicant corresponding to inclusion-maximal bicluster: .
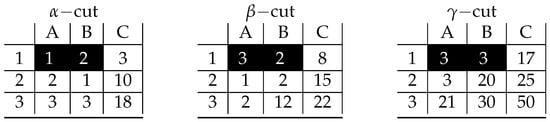
Figure A5.
Visualization of prime implicant corresponding to inclusion-maximal bicluster: .
References
- Morgan, J.; Sonquist, J. Problems in the analysis of survey data, and a proposal. J. Am. Stat. Assoc. 1963, 58, 415–434. [Google Scholar] [CrossRef]
- Cheng, Y.; Church, G.M. Biclustering of Expression Data. In Proceedings of the Eighth International Conference on Intelligent Systems for Molecular Biology, La Jolla, CA, USA, 16–23 August 2000; AAAI Press: Washington, DC, USA, 2000; pp. 93–103. [Google Scholar]
- Michalak, M.; Ślȩzak, D. Boolean Representation for Exact Biclustering. Fundam. Informaticae 2018, 161, 275–297. [Google Scholar] [CrossRef]
- Michalak, M.; Ślȩzak, D. On Boolean Representation of Continuous Data Biclustering. Fundam. Informaticae 2019, 167, 193–217. [Google Scholar] [CrossRef]
- Michalak, M.; Jaksik, R.; Ślȩzak, D. Heuristic Search of Exact Biclusters in Binary Data. Int. J. Appl. Math. Comput. Sci. 2020, 30, 161–171. [Google Scholar] [CrossRef]
- Michalak, M. Triclustering based on Boolean reasoning—A proof–of–concept. Procedia Comput. Sci. 2024, in press. [Google Scholar]
- Michalak, M. Theoretical Backgrounds of Boolean Reasoning Based Binary n–clustering. Knowl. Inf. Syst. 2022, 64, 2171–2188. [Google Scholar] [CrossRef]
- Brown, F.M. Boolean Reasoning; Springer: Boston, MA, USA, 1990. [Google Scholar]
- Pawlak, Z.; Skowron, A. Rough Sets and Boolean Reasoning. Inf. Sci. 2007, 177, 41–73. [Google Scholar] [CrossRef]
- Ślȩzak, D.; Janusz, A. Ensembles of Bireducts: Towards Robust Classification and Simple Representation. Lect. Notes Comput. Sci. 2011, 7105, 64–77. [Google Scholar]
- Kluger, Y.; Basri, R.; Chang, J.T.; Gerstein, M. Spectral biclustering of microarray data: Coclustering genes and conditions. Genome Res. 2003, 13, 703–716. [Google Scholar] [CrossRef]
- Aguilar-Ruiz, J.S.; Divina, F. Evolutionary computation for biclustering of gene expression. In Proceedings of the 2005 ACM Symposium on Applied Computing (SAC), Santa Fe, NM, USA, 13–17 March 2005; ACM: New York, NY, USA, 2005; pp. 959–960. [Google Scholar]
- Mitra, S.; Banka, H. Multi-objective evolutionary biclustering of gene expression data. Pattern Recognit. 2006, 39, 2464–2477. [Google Scholar] [CrossRef]
- Divina, F.; Aguilar–Ruiz, J.S. Biclustering of expression data with evolutionary computation. IEEE Trans. Knowl. Data Eng. 2006, 18, 590–602. [Google Scholar] [CrossRef]
- Pontes, B.; Divina, F.; Giráldez, R.; Aguilar-Ruiz, J.S. Improved biclustering on expression data through overlapping control. Int. J. Intell. Comput. Cybern. 2009, 2, 477–493. [Google Scholar] [CrossRef]
- Pontes, B.; Giráldez, R.; Aguilar-Ruiz, J.S. Configurable pattern-based evolutionary biclustering of gene expression data. Algorithms Mol. Biol. 2013, 8, 4. [Google Scholar] [CrossRef] [PubMed]
- Tanay, A.; Sharan, R.; Shamir, R. Discovering statistically significant biclusters in gene expression data. Bioinformatics 2002, 18, S136–S144. [Google Scholar] [CrossRef]
- Denitto, M.; Farinelli, A.; Figueiredo, M.; Bicego, M. A biclustering approach based on factor graphs and the max–sum algorithm. Pattern Recognit. 2017, 62, 114–124. [Google Scholar] [CrossRef]
- Denitto, M.; Bicego, M.; Farinelli, A.; Figueiredo, M. Spike and slab biclustering. Pattern Recognit. 2017, 72, 186–195. [Google Scholar] [CrossRef]
- Hanczar, B.; Nadif, M. Ensemble methods for biclustering tasks. Pattern Recognit. 2012, 45, 3938–3949. [Google Scholar] [CrossRef]
- Nepomuceno, J.A.; Troncoso, A.; Aguilar-Ruiz, J.S. Biclustering of Gene Expression Data by Correlation-Based Scatter Search. BioData Min. 2011, 4, 3. [Google Scholar] [CrossRef]
- Nepomuceno, J.A.; Troncoso, A.; Aguilar-Ruiz, J.S. Scatter search-based identification of local patterns with positive and negative correlations in gene expression data. Appl. Soft Comput. 2015, 35, 637–651. [Google Scholar] [CrossRef]
- Caroll, J.D.; Chang, J.J. Analysis of individual differences in multidimensional scaling via an n-way generalization of “Eckart-Young” decomposition. Psychometrika 1970, 35, 283–319. [Google Scholar] [CrossRef]
- Krolak-Schwerdt, S.; Orlik, P.; Ganter, B. TRIPAT: A Model for Analyzing Three-Mode Binary Data. In Proceedings of the Information Systems and Data Analysis; Bock, H.H., Lenski, W., Richter, M.M., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 298–307. [Google Scholar] [CrossRef]
- Lehmann, F.; Wille, R. A triadic approach to formal concept analysis. In Proceedings of the Conceptual Structures: Applications, Implementation and Theory; Ellis, G., Levinson, R., Rich, W., Sowa, J.F., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 32–43. [Google Scholar] [CrossRef]
- Zhao, L.; Zaki, M.J. TRICLUSTER: An effective algorithm for mining coherent clusters in 3D microarray data. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, MA, USA, 14–16 June 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 694–705. [Google Scholar] [CrossRef]
- Siswantining, T.; Bustamam, A.; Sarwinda, D.; Soemartojo, S.M.; Latief, M.A.; Octaria, E.A.; Siregar, A.T.M.; Septa, O.; Al-Ash, H.S.; Saputra, N. Triclustering method for finding biomarkers in human immunodeficiency virus-1 gene expression data. Math. Biosci. Eng. 2022, 19, 6743–6763. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, H.A.; Mahanta, P.; Bhattacharyya, D.K.; Kalita, J.K.; Ghosh, A. Intersected coexpressed subcube miner: An effective triclustering algorithm. In Proceedings of the 2011 World Congress on Information and Communication Technologies, Mumbai, India, 1–14 December 2011. [Google Scholar] [CrossRef]
- Siswantining, T.; Saputra, N.; Sarwinda, D.; Al-Ash, H.S. Triclustering Discovery Using the δ-Trimax Method on Microarray Gene Expression Data. Symmetry 2021, 13, 437. [Google Scholar] [CrossRef]
- Wu, X.; Raul Zurita-Milla, E.I.V.; Kraak, M.J. Triclustering Georeferenced Time Series for Analyzing Patterns of Intra-Annual Variability in Temperature. Ann. Am. Assoc. Geogr. 2018, 108, 71–87. [Google Scholar] [CrossRef]
- Guigourès, R.; Boullé, M.; Rossi, F. A Triclustering Approach for Time Evolving Graphs. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining Workshops, Brussels, Belgium, 10 December 2012; pp. 115–122. [Google Scholar] [CrossRef]
- Michalak, M. Induction of Centre–Based Biclusters in Terms of Boolean Reasoning. Adv. Intell. Syst. Comput. 2020, 1061, 239–248. [Google Scholar]
- Michalak, M.; Aguilar-Ruiz, J.S. Shifting Pattern Biclustering and Boolean Reasoning Symmetry. Symmetry 2023, 15, 1977. [Google Scholar] [CrossRef]
- Michalak, M. Hierarchical heuristics for Boolean-reasoning-based binary bicluster induction. Acta Inform. 2022, 59, 673–685. [Google Scholar] [CrossRef]
- Déharbe, D.; Fontaine, P.; Le Berre, D.; Mazure, B. Computing prime implicants. In Proceedings of the 2013 Formal Methods in Computer-Aided Design, Portland, OR, USA, 20–23 October 2013; pp. 46–52. [Google Scholar] [CrossRef]
- Strzemecki, T. Polynomial-time algorithms for generation of prime implicants. J. Complex. 1992, 8, 37–63. [Google Scholar] [CrossRef]
- Karp, R.M. Reducibility among Combinatorial Problems. In Complexity of Computer Computations: Proceedings of a Symposium on the Complexity of Computer Computations, Held March 20–22, 1972, at the IBM Thomas J. Watson Research Center, Yorktown Heights, New York, and sponsored by the Office of Naval Research, Mathematics Program, IBM World Trade Corporation, and the IBM Research Mathematical Sciences Department; Miller, R.E., Thatcher, J.W., Bohlinger, J.D., Eds.; Springer: Boston, MA, USA, 1972; pp. 85–103. [Google Scholar] [CrossRef]
- Johnson, D.S. Approximation algorithms for combinatorial problems. J. Comput. Syst. Sci. 1974, 9, 256–278. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).