Asymmetries Caused by Nonparaxiality and Spin–Orbit Interaction during Light Propagation in a Graded-Index Medium
Abstract
1. Introduction
2. Basic Equations
3. Simulation Results
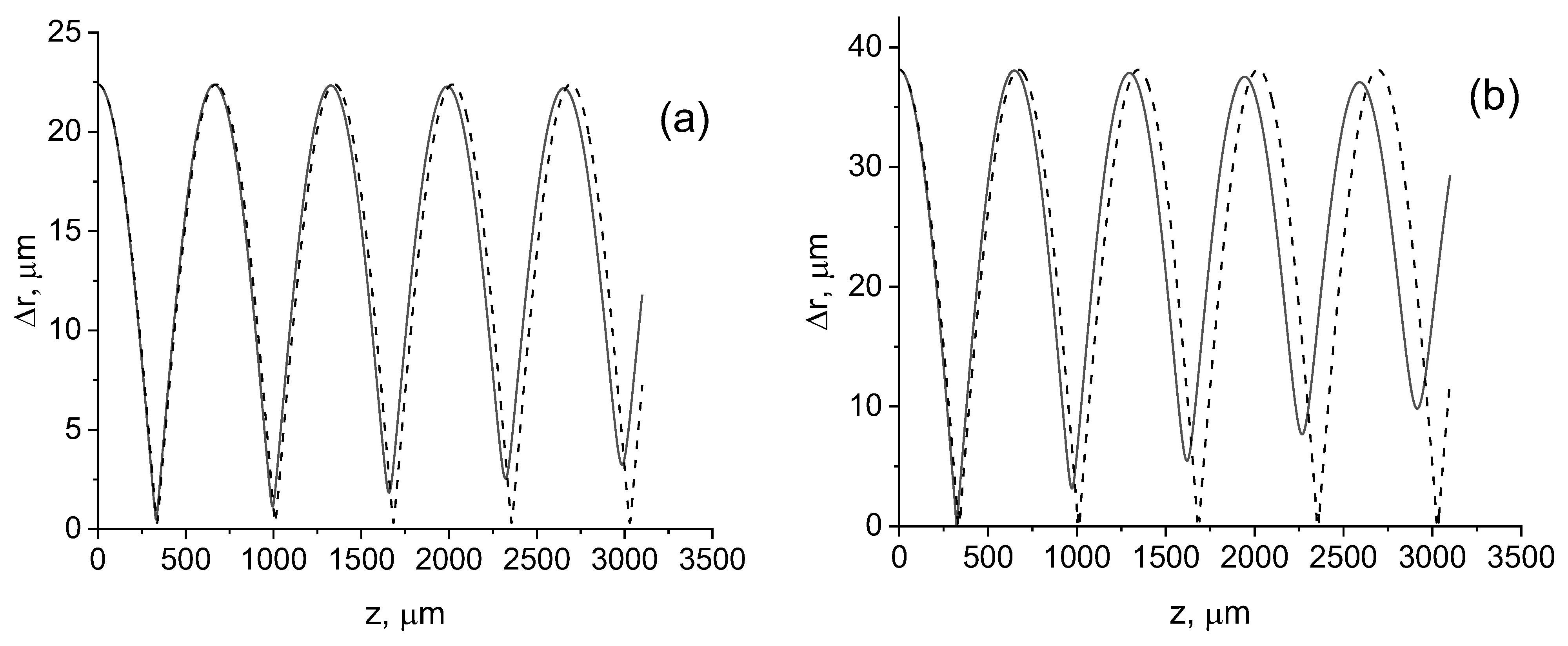
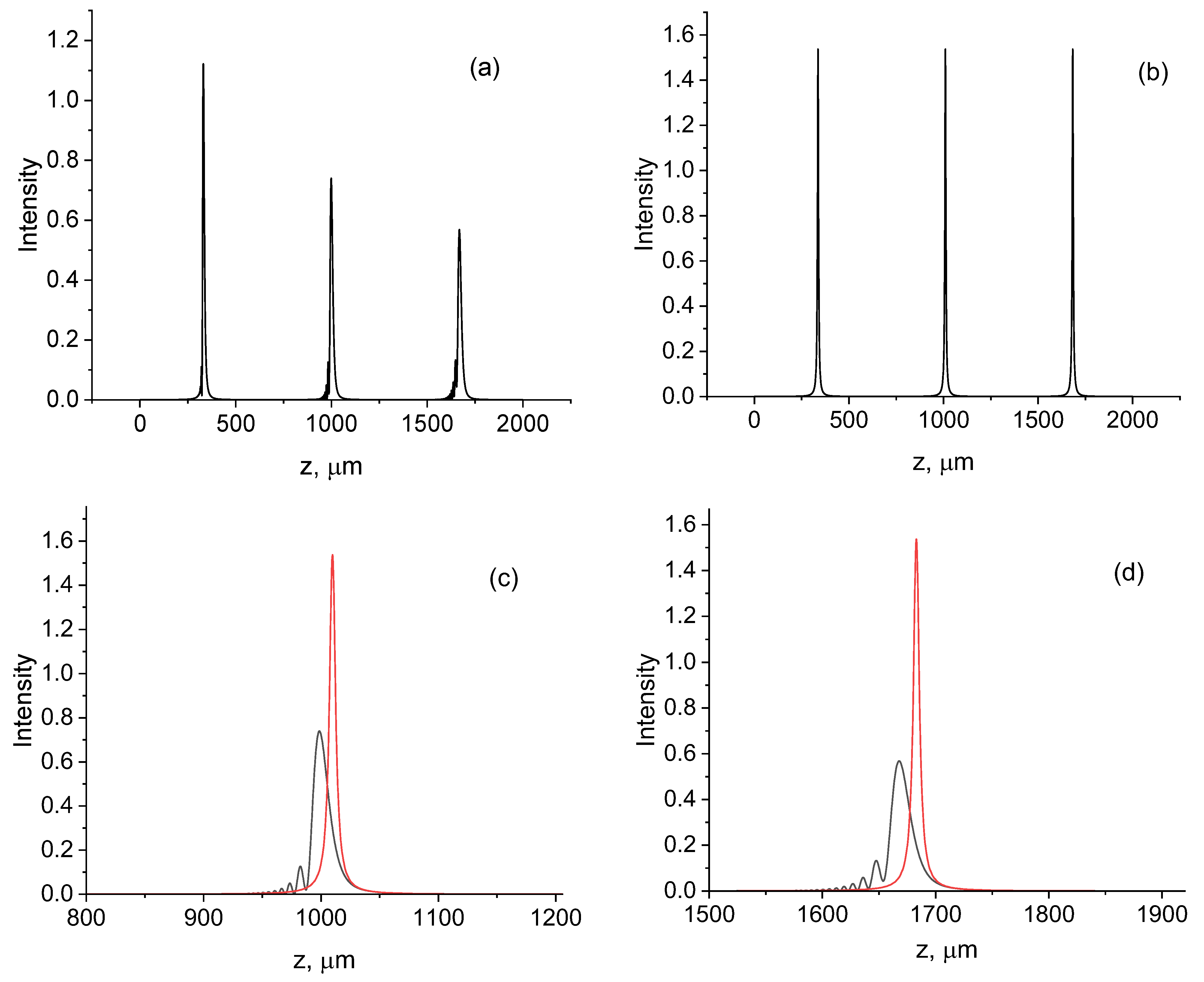
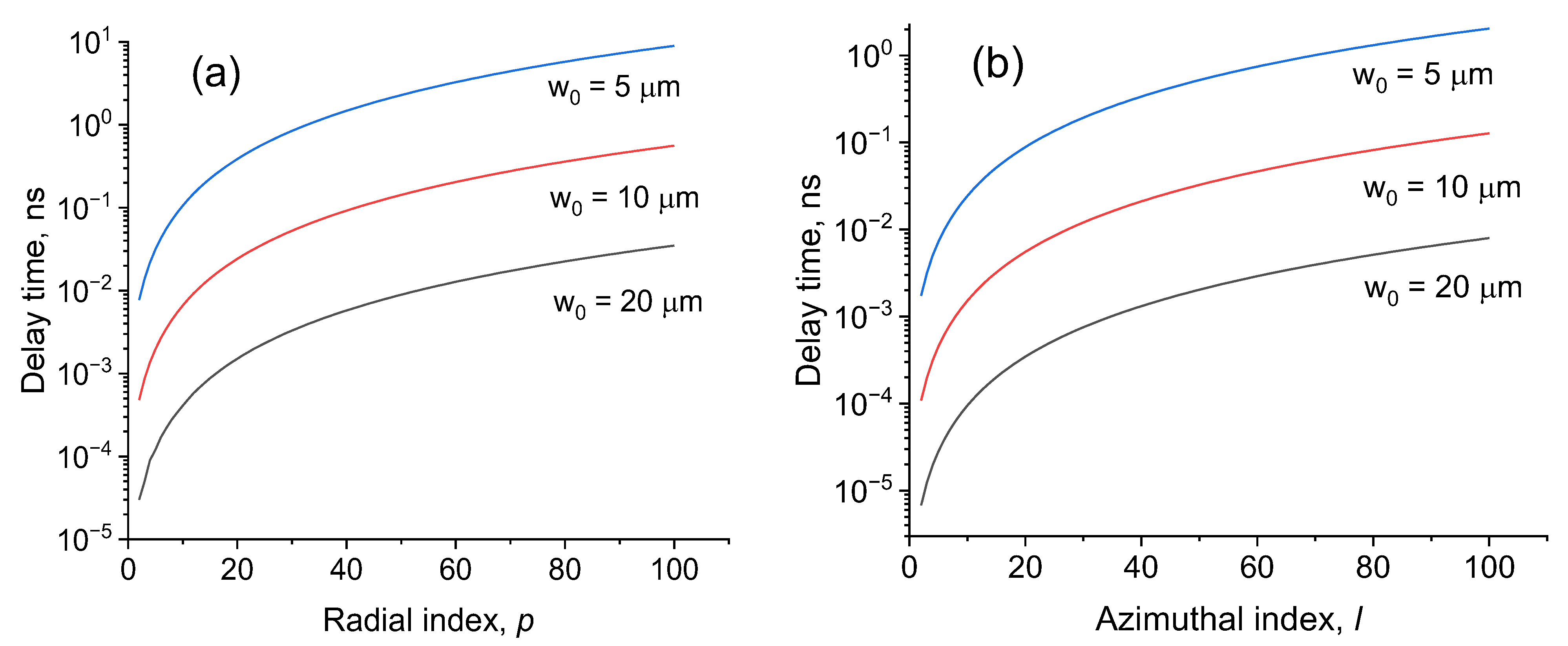
3.1. Effect of Nonparaxiality on the Beam Width and Axial Intensity Distribution
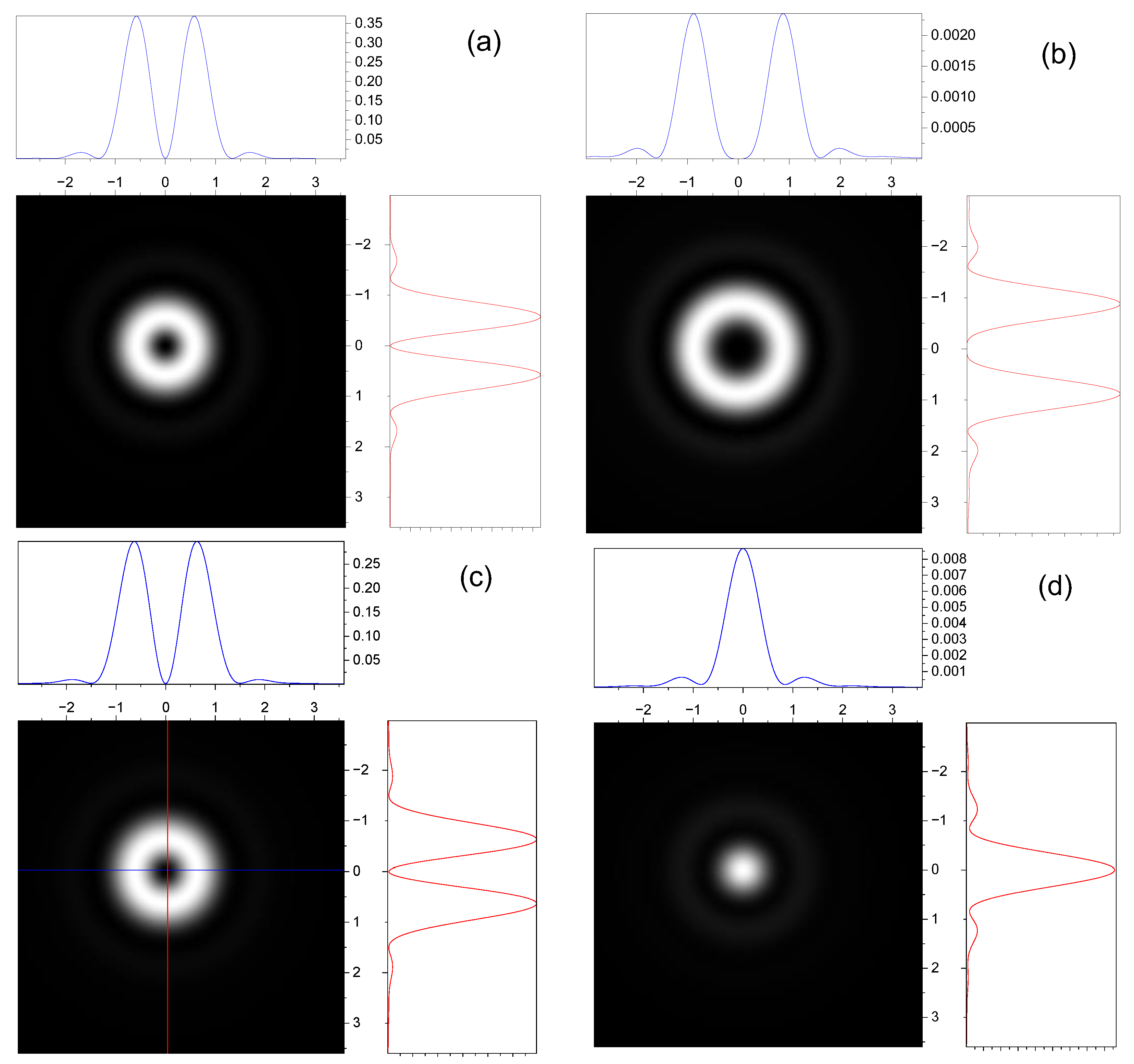
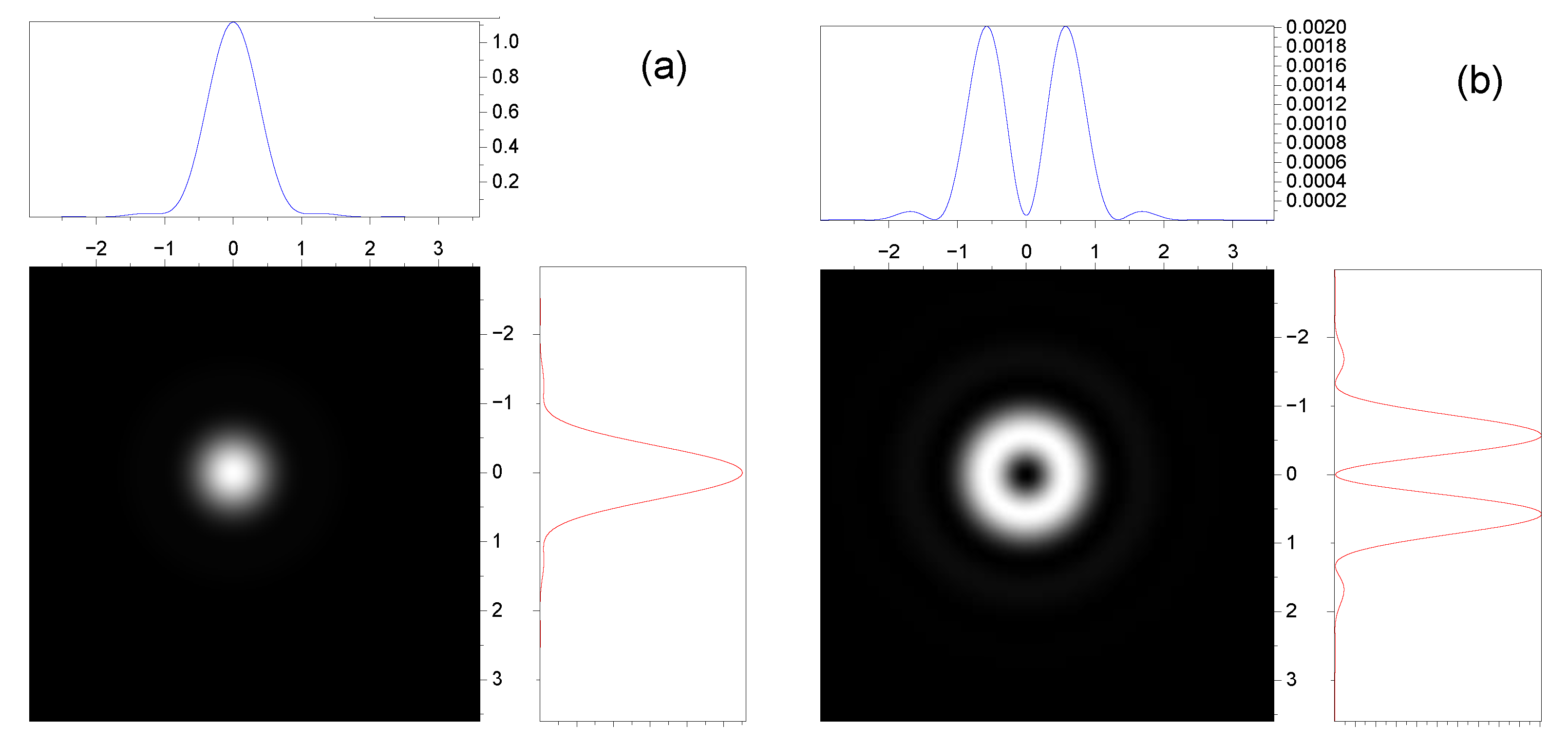
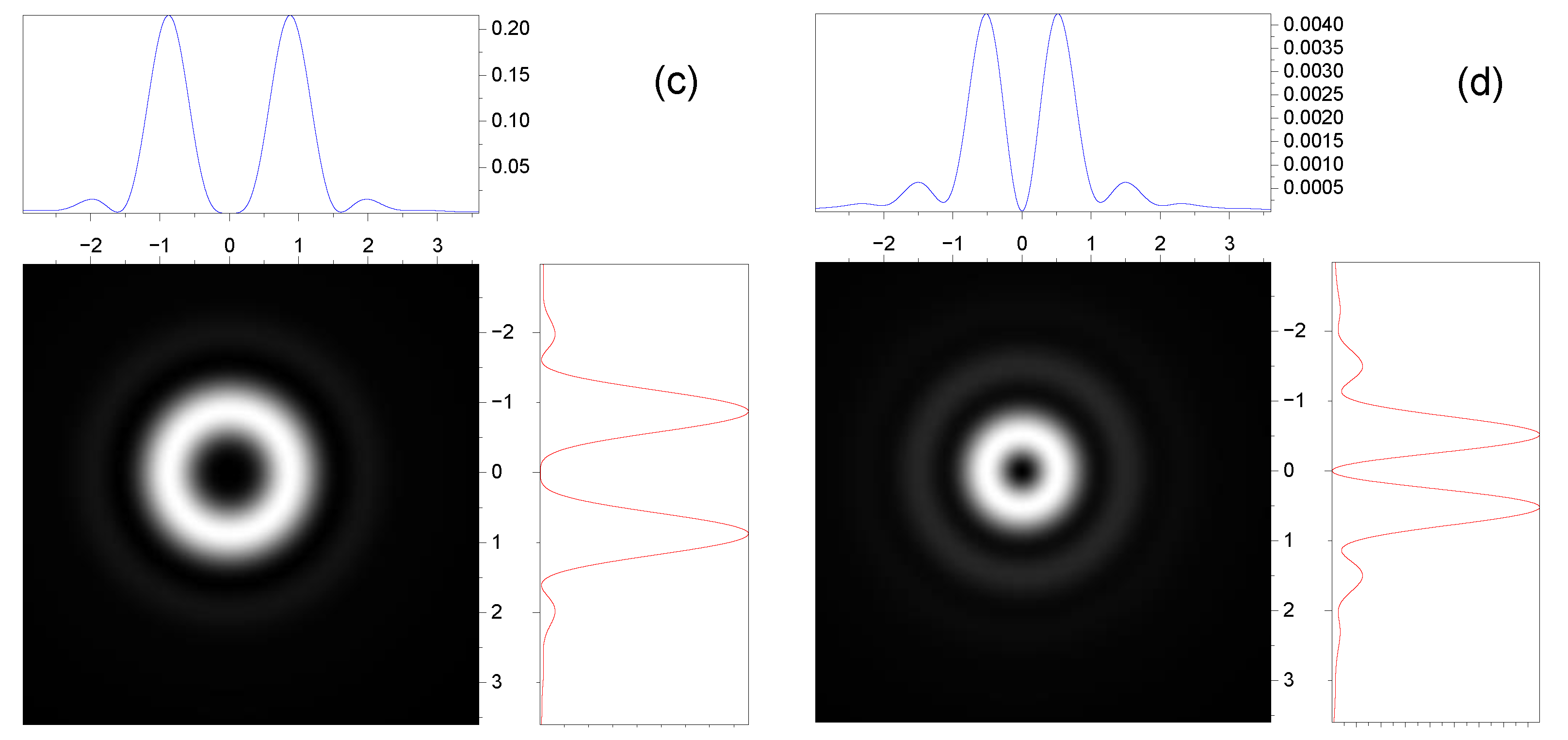
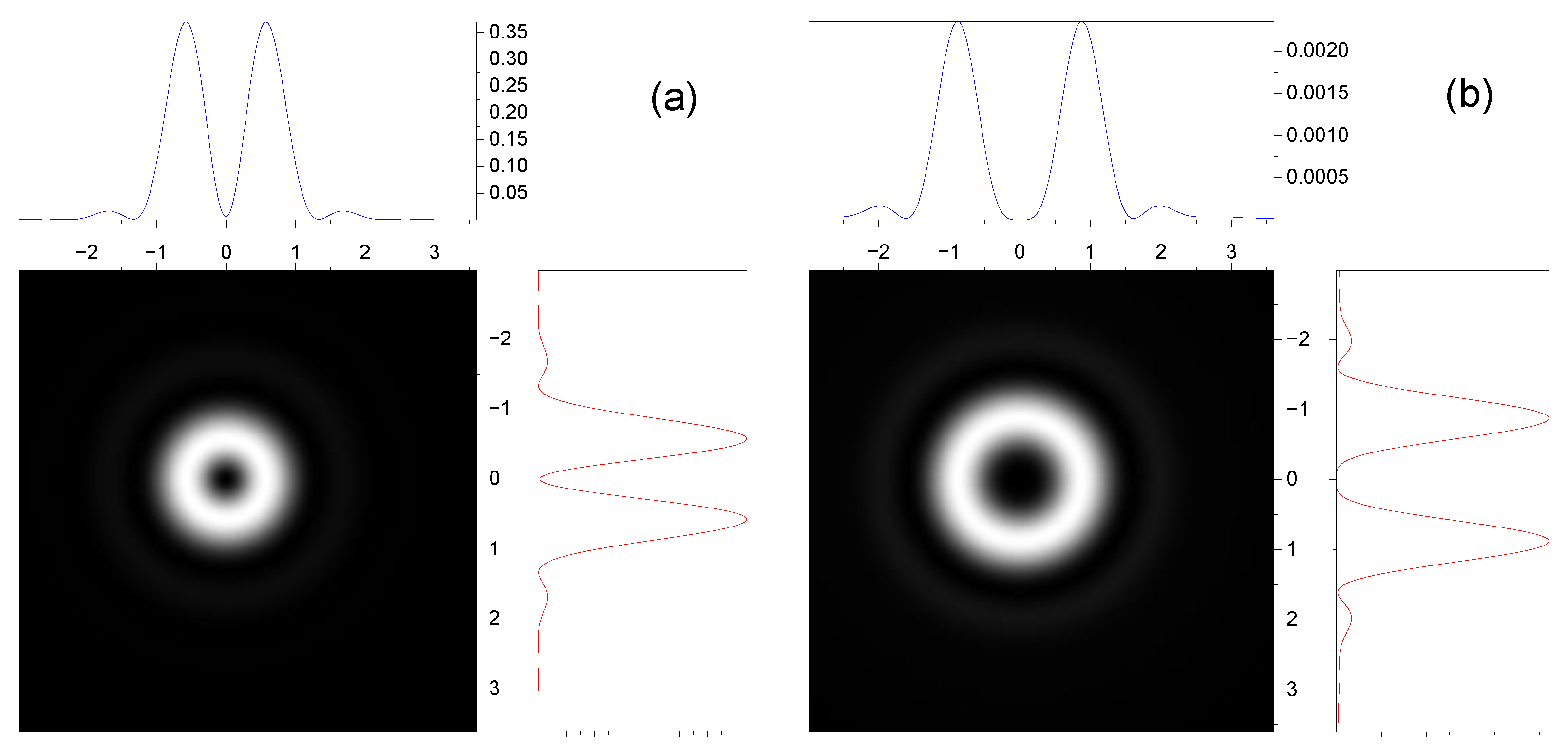
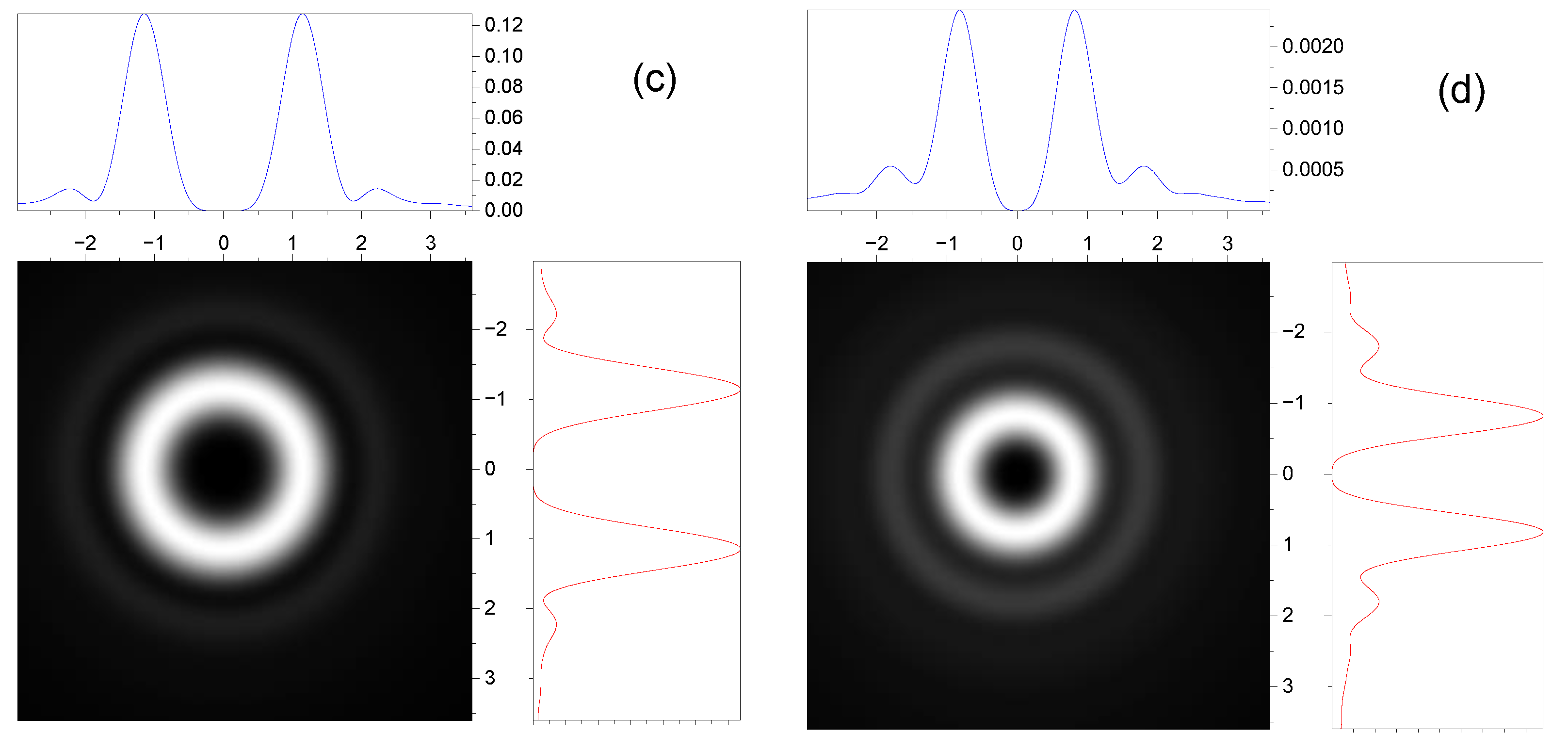
3.2. Effect of Spin–Orbit Interaction on the Intensity Distribution
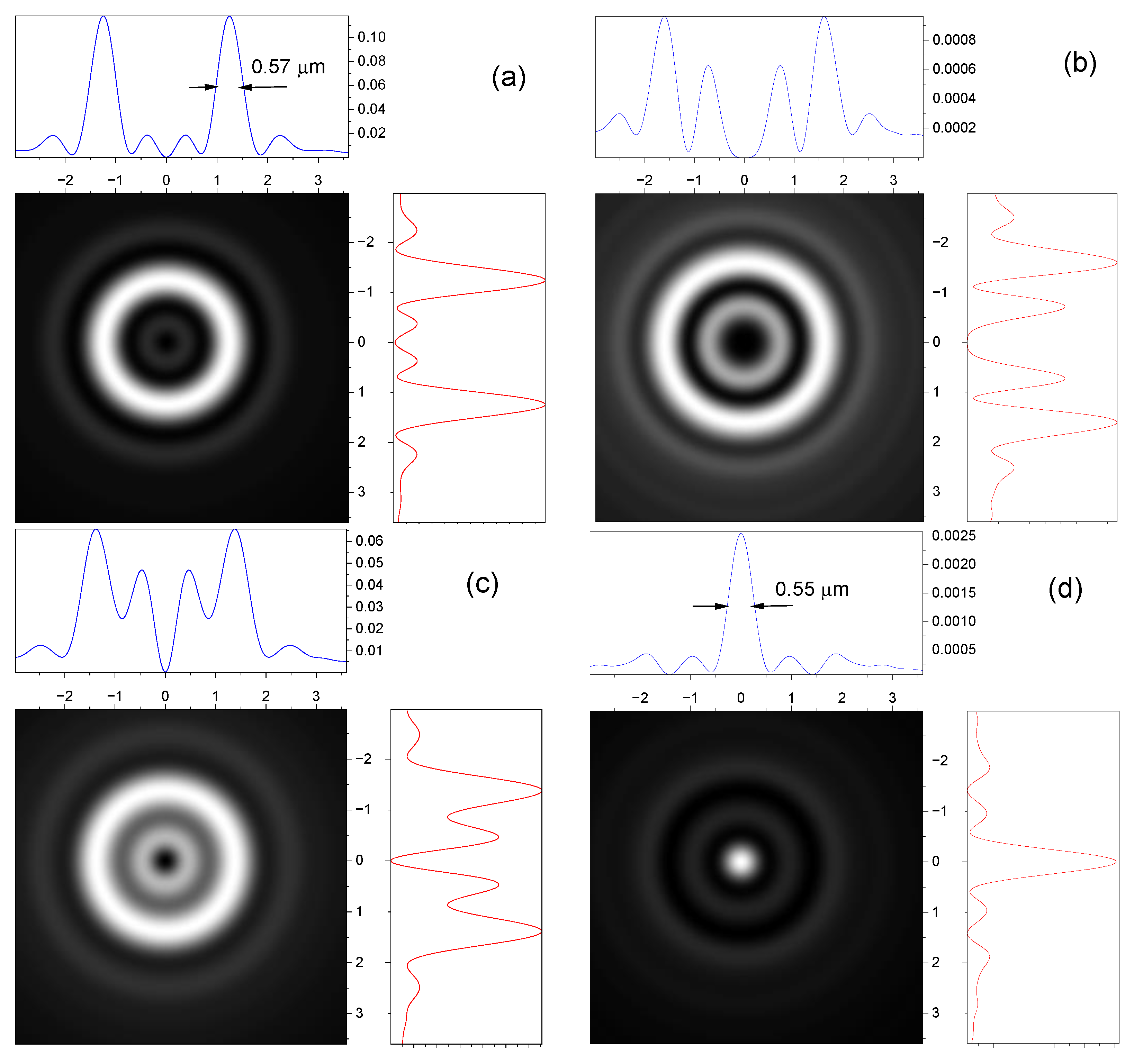
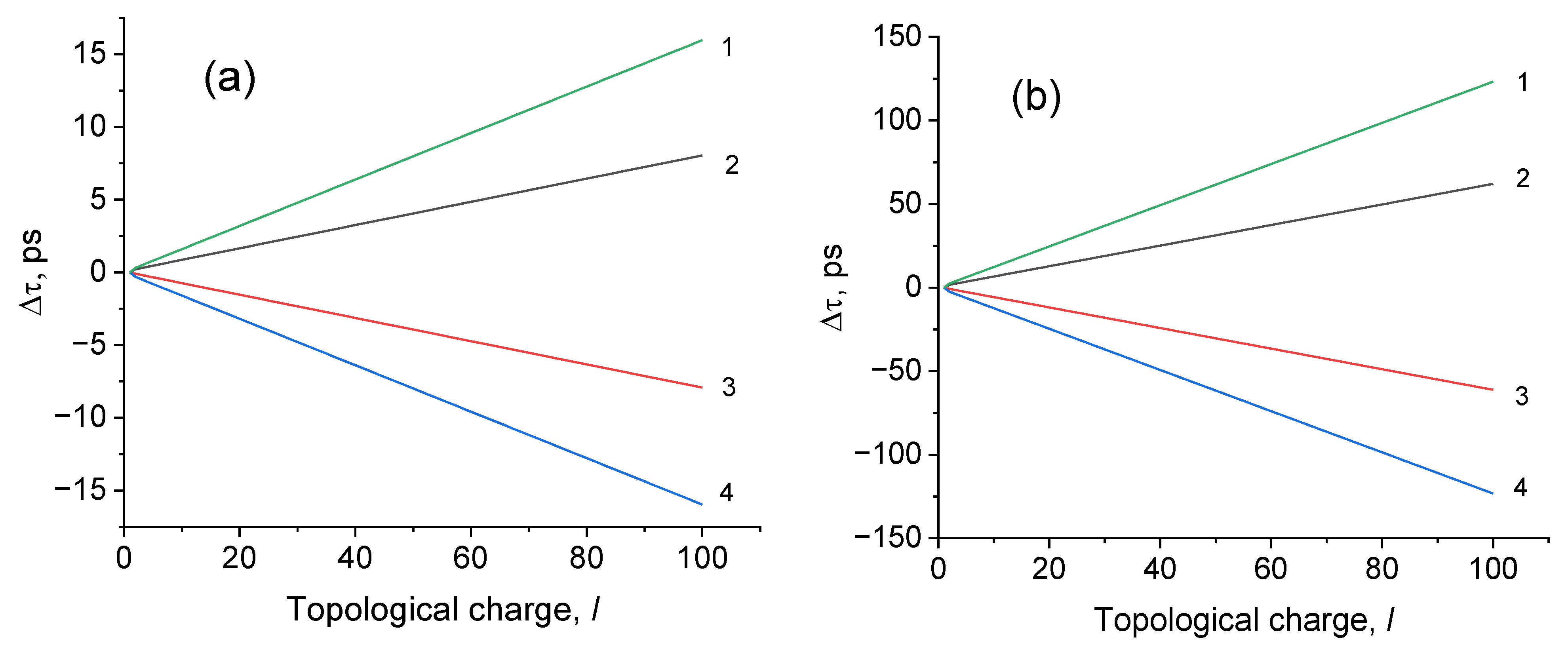
3.3. Effect of Spin–Orbit Interaction on the Speed of Vortex Beams in Optical Fiber
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fedotov, V.A.; Mladyonov, P.I.; Prosvirnin, S.I.; Rogacheva, A.V.; Chen, Y.; Zheludev, N.I. Asymmetric Propagation of Electromagnetic Waves through a Planar Chiral Structure. Phys. Rev. Lett. 2006, 97, 167401. [Google Scholar] [CrossRef]
- Xu, Y.; Shi, Q.; Zhu, Z.; Shi, J. Mutual conversion and asymmetric transmission of linearly polarized light in bilayered chiral metamaterial. Opt. Expr. 2014, 22, 25679–25688. [Google Scholar] [CrossRef] [PubMed]
- Plum, R.; Lin, X.X.; Fedotov, V.; Chen, Y.; Tsai, D.P.; Zheludev, N.I. Metamaterials: Optical Activity without Chirality. Phys. Rev. Lett. 2009, 102, 113902. [Google Scholar] [CrossRef] [PubMed]
- Goos, F.; Hanchen, H. Ein neuer und fundamentaler versuch zur total reflexion. Ann. Phys. 1947, 1, 333–345. [Google Scholar] [CrossRef]
- Imbert, C. Calculation and experimental proof of the transverse shift induced by total internal reflection of a circularly polarized light beam. Phys. Rev. D 1972, 5, 787–796. [Google Scholar] [CrossRef]
- Gorodetsky, Y.; Niv, A.; Kleiner, V.; Hasman, E. Observation of the Spin-Based Plasmonic Effect in Nanoscale Structures. Phys. Rev. Lett. 2008, 101, 043903. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Gorodetski, Y.; Kleiner, V.; Hasman, E. Coriolis effect in optics: Unified geometric phase and spin-Hall effect. Phys. Rev. Lett. 2008, 101, 030404. [Google Scholar] [CrossRef]
- Petrov, N.I.; Sokolov, Y.M.; Stoiakin, V.V.; Danilov, V.A.; Popov, V.V.; Usievich, B.A. Observation of Giant Angular Goos-Hanchen Shifts Enhanced by Surface Plasmon Resonance in Subwavelength Grating. Photonics 2023, 10, 180. [Google Scholar] [CrossRef]
- Gorodetski, Y.; Shitrit, N.; Bretner, I.; Kleiner, V.; Hasman, E. Observation of optical spin symmetry breaking in nanoapertures. Nano Lett. 2009, 9, 3016–3019. [Google Scholar] [CrossRef]
- Vuong, L.T.; Adam, A.J.L.; Brok, J.M.; Planken, P.C.M.; Urbach, H.P. Electromagnetic spin-orbit interactions via scattering of subwavelength apertures. Phys. Rev. Lett. 2010, 104, 083903. [Google Scholar] [CrossRef]
- Rytov, S.M. On transition from wave to geometrical optics. Dokl. Akad. Nauk USSR 1938, 18, 263–266. [Google Scholar]
- Vladimirsky, V.V. On rotation of polarization plane in twisted ray of light. Dokl. Akad. Nauk USSR 1941, 31, 222–225. [Google Scholar]
- Tomita, A.; Chiao, R.Y. Observation of Berry’s Topological Phase by Use of an Optical Fiber. Phys. Rev. Lett. 1986, 57, 937–940. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45–57. [Google Scholar]
- Zel’dovich, B.Y.; Kundikova, N.D. Intrafibre rotation of the plane of polarization. Quant. Electron. 1995, 25, 172–174. [Google Scholar] [CrossRef]
- Zel’dovich, B.Y.; Liberman, V.S. Rotation of the plane of a meridional beam in a graded-index waveguide due to the circular nature of the polarization. Sov. J. Quant. Electron. 1990, 20, 427–428. [Google Scholar] [CrossRef]
- Zel’dovich, B.Y.; Kitaevskaya, I.V.; Kundikova, I.D. Inhomogeneity of the optical Magnus effect. Quant. Electron. 1996, 26, 87–88. [Google Scholar] [CrossRef]
- Petrov, N.I. Depolarization of light in a graded-index isotropic medium. J. Mod. Opt. 1996, 43, 2239–2249. [Google Scholar] [CrossRef]
- Petrov, N.I. Evolution of polarization in an inhomogeneous isotropic medium. JETP 1997, 85, 1085–1093. [Google Scholar] [CrossRef]
- Petrov, N.I. Evolution of Berry’s phase in a graded-index medium. Phys. Lett. A 1997, 234, 239–250. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Niv, A.; Kleiner, V.; Hasman, E. Geometrodynamics of spinning light. Nat. Photon. 2008, 2, 748–753. [Google Scholar] [CrossRef]
- Liberman, V.S.; Zel’dovich, B.Y. Spin-orbit interaction of a photon in an inhomogeneous medium. Phys. Rev. A 1992, 46, 5199–5207. [Google Scholar] [CrossRef] [PubMed]
- Onoda, M.; Murakami, S.; Nagaosa, N. Hall Effect of Light. Phys. Rev. Lett. 2004, 93, 083901. [Google Scholar] [CrossRef] [PubMed]
- Kavokin, A.; Malpuech, G.; Glazov, M. Optical Spin Hall Effect. Phys. Rev. Lett. 2005, 95, 136601. [Google Scholar] [CrossRef] [PubMed]
- Snyder, A.W.; Love, J.D. Optical Waveguide Theory; Chapman and Hall: London, UK, 1983. [Google Scholar]
- Bliokh, K.Y.; Desyatnikov, A.S. Spin and orbital Hall effects for diffracting optical beams in gradient-index media. Phys. Rev. A 2009, 79, 011807. [Google Scholar] [CrossRef]
- Bliokh, K.Y. Geometrodynamics of polarized light: Berry phase and spin Hall effect in a gradient-index medium. J. Opt. A Pure Appl. Opt. 2009, 11, 094009. [Google Scholar] [CrossRef]
- Dugin, A.; Zel’dovich, B.; Kundikova, N.; Liberman, V. Effect of circular polarization on the propagation of light through an optical fiber. J. Exp. Theor. Phys. Lett. 1991, 53, 197–199. [Google Scholar]
- Cao, Z.; Zhai, C.; Xu, S.; Chen, Y. Propagation of on-axis and off-axis Bessel beams in a gradient-index medium. J. Opt. Soc. Am. A 2018, 35, 230–235. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Ostrovskaya, E.A.; Alonso, M.A.; Rodriguez-Herrera, O.G.; Lara, D.; Dainty, C. Spin-to-orbital angular momentum conversion in focusing, scattering, and imaging systems. Optics Express 2011, 19, 26132–26149. [Google Scholar] [CrossRef]
- Petrov, N.I. Spin-orbit and tensor interactions of light in inhomogeneous isotropic media. Phys. Rev. A 2013, 88, 023815. [Google Scholar] [CrossRef]
- Petrov, N.I. Spin-dependent transverse force on a vortex light beam in an inhomogeneous medium. JETP Lett. 2016, 103, 443–448. [Google Scholar] [CrossRef]
- Zhao, R.; Deng, F.; Yu, W.; Huang, J.; Deng, D. Propagation properties of Airy–Gaussian vortex beams through the gradient-index medium. J. Opt. Soc. Am. A 2016, 33, 1025–1031. [Google Scholar] [CrossRef]
- Petrov, N.I. Vector Laguerre–Gauss beams with polarization-orbital angular momentum entanglement in a graded-index medium. J. Opt. Soc. Am. A 2016, 33, 1363–1369. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Hao, P.; Zhang, Y.; Zhao, Z.; Wu, J.; Li, J. Propagation of noninteger cylindrical vector vortex beams in a gradient-index fiber. Opt. Lett. 2023, 48, 2484–2487. [Google Scholar] [CrossRef] [PubMed]
- Pei, S.; Xu, S.; Cui, F.; Pan, Q.; Cao, Z. Propagation of a Bessel–Gaussian beam in a gradient-index medium. Appl. Opt. 2019, 58, 920–926. [Google Scholar] [CrossRef]
- Chakravarthy, T.P.; Viswanatham, N.K. Direct and reciprocal spin-orbit interaction effects in a graded-index medium. OSA Contin. 2019, 2, 1576–1589. [Google Scholar] [CrossRef]
- Sodha, M.S.; Ghatak, A.K. Inhomogeneous Optical Waveguides; Plenum Press: New York, NY, USA, 1977. [Google Scholar]
- Loffler, W.; van Exter, M.P.; Hooft, G.W.; Eliel, E.R.; Hermans, K.; Broer, D.J.; Woerdman, J.P. Polarization-dependent Goos–Hänchen shift at a graded dielectric interface. Opt. Commun. 2010, 283, 3367–3370. [Google Scholar] [CrossRef]
- Petrov, N.I. Beam shift in a graded-index optical fiber. J. Opt. 2013, 15, 014011. [Google Scholar] [CrossRef]
- Fock, V.A.; Leontovich, M.A. Solution of the Problem of Propagation of Electromagnetic Waves along the Earth’s Surface by Method of Parabolic Equations. J. Phys.—USSR, 1946; 10, 13–23. [Google Scholar]
- Petrov, N.I. Vector and tensor polarizations of light beams. Las. Phys. 2008, 18, 522–525. [Google Scholar] [CrossRef]
- Pachava, S.; Dixit, A.; Srinivasan, B. Modal decomposition of Laguerre Gaussian beams with different radial orders using optical correlation technique. Opt. Exp. 2019, 27, 13182–13193. [Google Scholar] [CrossRef]
- Petrov, N.I. Splitting of levels in a cylindrical dielectric waveguide. Opt. Lett. 2013, 38, 2020–2022. [Google Scholar] [CrossRef]
- Eide, H.A.; Stamnes, J.J. Exact and approximate solutions for focusing of two-dimensional waves. J. Opt. Soc. Am. A 1998, 15, 1285–1319. [Google Scholar]
- Petrov, N.I. Focusing of beams into subwavelength area in an inhomogeneous medium. Opt. Exp. 2001, 9, 658–673. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Du, S.; Dong, Y.; Wang, F.; Zhao, C.; Cai, Y. Nonparaxial propagation properties of a vector partially coherent dark hollow beam. JOSA A 2013, 30, 1358–1372. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.I. Macroscopic quantum effects for classical light. Phys. Rev. A 2014, 90, 043814. [Google Scholar] [CrossRef]
- Matsuhara, M. Analysis of electromagnetic-wave modes in lens-like media. JOSA 1973, 63, 135–138. [Google Scholar] [CrossRef]
- Thyagarajan, R.; Chatak, A.K. Perturbation theory for studying the effect of the ∇ε term in lens-like media. Optics Commun. 1974, 11, 417–421. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Frolov, D.Y. Spin-orbit interaction of photons and fine splitting of levels in ring dielectric resonator. Optics Commun. 2005, 250, 321–327. [Google Scholar] [CrossRef][Green Version]
- Petrov, N.I. Depolarization of Light in Optical Fibers: Effects of Diffraction and Spin-Orbit Interaction. Fibers 2021, 9, 34. [Google Scholar] [CrossRef]
- Bouchard, F.; Harris, J.; Mand, H.; Boyd, R.W.; Karimi, E. Observation of subluminal twisted light in vacuum. Optica 2016, 3, 351–354. [Google Scholar] [CrossRef]
- Petrov, N.I. Speed of structured light pulses in free space. Sci. Rep. 2019, 9, 18332. [Google Scholar] [CrossRef]
- Marcuse, D. Light Transmission Optics; Van Nostrand Reinhold: New York, NY, USA, 1982. [Google Scholar]
- Guo, Y.; Pu, M.; Zhang, F.; Xu, M.; Li, X.; Ma, X.; Luo, X. Classical and generalized geometric phase in electromagnetic metasurfaces. Photonics Insights 2022, 1, R03. [Google Scholar] [CrossRef]
- Agrawal, G.P. Physics and Engineering of Graded-Index Media, 1st ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Dong, M.; Bai, Y.; Yao, J.; Zhao, Q.; Yang, Y. Propagation properties of partially coherent modified Bessel-Gauss beams through the gradient-index medium. Appl. Opt. 2020, 59, 8023–8028. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, M.; Guo, Z.; Feng, Z.; Li, J. Change in phase singularities of a partially coherent Gaussian vortex beam propagating in a GRIN fiber. Opt. Expr. 2020, 28, 4661–4673. [Google Scholar] [CrossRef] [PubMed]
- Wadood, S.A.; Liang, K.; Agrawal, G.P.; Visser, T.D.; Stroud, C.R.; Vamivakas, A.N. Propagation of Gaussian Schell-model beams in modulated graded-index media. Opt. Expr. 2021, 29, 21240–21251. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Wang, J.; Guo, M.; Qin, Z.; Li, J. Propagation properties of Gaussian vortex beams through the gradient-index medium. Opt. Commun. 2020, 465, 125559. [Google Scholar] [CrossRef]
- Petrov, N.I. Sharp focusing of partially coherent Bessel-correlated beams by a graded-index lens. Opt. Lett. 2023, 48, 6048–6051. [Google Scholar] [CrossRef]
- Petrov, N.I. Remote focusing of a light beam. Las. Phys. Lett. 2016, 13, 015101. [Google Scholar] [CrossRef]
- Eismann, J.S.; Nicholls, L.H.; Roth, D.J.; Alonso, M.A.; Banzer, P.; Rodríguez-Fortuño, F.J.; Zayats, A.V.; Nori, F.; Bliokh, K.Y. Transverse spinning of unpolarized light. Nat. Photonics 2021, 15, 156–161. [Google Scholar] [CrossRef]
- Ketara, M.L.; Kobayashi, H.; Brasselet, E. Sensitive vectorial optomechanical footprint of light in soft condensed matter. Nat. Photon. 2021, 15, 121–124. [Google Scholar] [CrossRef]
- Cardano, F.; Marrucci, L. Longitudinal fields and transverse rotations. Nat. Photonics 2021, 15, 72–74. [Google Scholar] [CrossRef]
- Qin, Z.; Zhang, L.; Zhang, R.; Zhang, P.; Qi, R.; Zhang, Q.; Ren, L.; Jiang, L. Effect of the incident polarization on in-plane and out-of-plane spin splitting near the critical angle. Opt. Exp. 2023, 31, 853–863. [Google Scholar] [CrossRef]
- Lee, Y.U.; Wu, J.W. Visualization of the optical spin Hall effect in out-of-plane refraction. Opt. Lett. 2023, 48, 5988–5991. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrov, N.I. Asymmetries Caused by Nonparaxiality and Spin–Orbit Interaction during Light Propagation in a Graded-Index Medium. Symmetry 2024, 16, 87. https://doi.org/10.3390/sym16010087
Petrov NI. Asymmetries Caused by Nonparaxiality and Spin–Orbit Interaction during Light Propagation in a Graded-Index Medium. Symmetry. 2024; 16(1):87. https://doi.org/10.3390/sym16010087
Chicago/Turabian StylePetrov, Nikolai I. 2024. "Asymmetries Caused by Nonparaxiality and Spin–Orbit Interaction during Light Propagation in a Graded-Index Medium" Symmetry 16, no. 1: 87. https://doi.org/10.3390/sym16010087
APA StylePetrov, N. I. (2024). Asymmetries Caused by Nonparaxiality and Spin–Orbit Interaction during Light Propagation in a Graded-Index Medium. Symmetry, 16(1), 87. https://doi.org/10.3390/sym16010087






