Abstract
Reinterpretation of mathematics behind the exactly solvable Calogero’s A-particle quantum model is used to propose its generalization. Firstly, it is argued that the strongly singular nature of Calogero’s particle–particle interactions makes the original permutation-invariant Hamiltonian tractable as a direct sum of isospectral components, which are mutually independent. Secondly, after the elimination of the center-of-mass motion, the system is reconsidered as existing in the reduced Euclidean space of relative coordinates and decaying into a union of subsets called Weyl chambers. The mutual independence of the related reduced forms of operators enables us to makes them nonisospectral. This breaks the symmetry and unfolds the spectral degeneracy of H. A new multiparametric generalization of the conventional A-body Calogero model is obtained. Its detailed description is provided up to .
1. Introduction
The well-known [1,2,3] quantum Hamiltonian
invented by Calogero [4,5,6] and written here in units , plays an important methodical role in nuclear, atomic, and molecular physics, and in quantum chemistry [7]. It is a truly remarkable one-dimensional A-particle-chain alias linear-molecule model that combines non-numerical solvability [8] with a nontrivial and multibranched phenomenological relevance [9,10]. Its symmetry with respect to the permutations of coordinates is accompanied by a fairly realistic shape of its two-body interaction potentials, mimicking not only the expected asymptotic attraction but also a frequently encountered repulsion at short distances [11].
Equally strongly, the impact of the model can be felt in mathematics. The wealth of related innovations ranges from the upgrades of the applications of Lie algebras [12,13,14] and of orthogonal polynomials [15,16] up to the amendments of paradigms known as Wigner–Dunkl quantum mechanics [17,18], quasi-Hermitian quantum mechanics [19,20,21,22,23,24], or -symmetric quantum mechanics [25,26,27,28,29,30,31].
In our paper, we propose a multiparametric but still exactly solvable generalization of model (1). For introduction, it is sufficient to consider the most elementary two-particle special case
The well-known additional merit of the model emerges after one defines the two new “relative-motion” alias Jacobi coordinates [3]
After, one manages to separate the center-of-mass motion [32,33]. This leads to the reduction in and replacement of the initial partial differential Schrödinger equation by another, ordinary differential bound-state problem in ,
The positive corresponds to the ordering (with the first particle lying on the real line to the right from the second one), while the negative choice of represents our pair of particles as positioned inside a complementary half-plane of where .
The two half-lines may be called Weyl chambers. In the literature, such a name is used for any number of particles A. After the standard elimination of the center of mass [34,35], the -particle-coordinate space becomes reduced to its subspace . This is performed in full analogy with the change in coordinates (3) so that at any higher , the space remains parametrized by the relative Jacobi coordinates [3,36,37].
In terms of the latter coordinates, the singular repulsion must be considered, and the reduced space becomes split, in a way generalizing the case, into a union of -dimensional Weyl chambers , i.e., . Unfortunately, a return to and to the reduced Schrödinger Equation (4) reveals the existence of a subtle mathematical problem. Emphasized, e.g., by Landau and Lifshitz [38], the short-range force is strongly singular in the origin so that Calogero’s system existing on the real line becomes tractable as composed of two completely dynamically independent quantum systems existing on the respective permutation-characterized Weyl-chamber half-lines or . All of the meaningful phenomenological predictions (i.e., of the structure of the spectrum or of the wave functions) are then encoded in any one of its Weyl chambers. In this sense, the reference to “global” Hamiltonians (2) or (1) can be considered (perhaps, unintentionally) misleading.
Such an observation has several consequences, some of which are explained and described in what follows. The presentation of our results is preceded by a brief review of some of the basic properties of the most elementary conventional Calogero;s model in Section 2. As a core and guide to our study, the “asymmetrization” preserving the solvability is proposed at . In Section 3, the details of analogous asymmetrization are described for . After transition to arbitrary A, our innovative Calogero-like model is finally analyzed and discussed in Section 4 and Section 5 and in Appendix A.
2. Spectral Degeneracy and Its Unfolding at A = 2
The singularity in Equation (4) resembles the centrifugal term in the radial Schrödinger equation of a centrally symmetric harmonic oscillator in a specific ℓth partial wave. Formally, we may reparametrize and reconstruct the real (though, in general, noninteger and/or nonpositive) angular-momentum-like parameter ℓ from a given value of coupling constant C,
A decisive difference from the radial Schrödinger equation is that our present Equation (4) has to exist, by definition, on the whole real line of . In Calogero’s operator in Equation (2), the two particle coordinates and are independent variables, so that one has to represent the motion in both the left Weyl chamber of and the right Weyl chamber of .
2.1. Singularity in the Origin
Due to the singularity at , our reduced Hamiltonian is merely essentially self-adjoint [39]. In the origin, some additional boundary conditions have to be imposed in order to make the problem mathematically well-defined. An explicit specification of physics behind these boundary conditions is necessary. Only then one can speak about a consistent quantum theory and a unique operator associated with the differential expressions of Equation (1) or, at , in Equations (2) and (4).
As such, we accept, at , the most common convention through which one requires
This is equivalent to the suppression of the dominant component of the wave function near the origin (see a few related comments in [40]). Calogero’s reduced symmetric-interaction Equation (4) can be then perceived as existing on the full real line. In spite of the presence of the barrier, the bound states are made well defined by constraint (6).
In a more consequent and physics-oriented conceptual setting, the interpretation of the role of the barriers is less clear. The tunneling between the two neighboring half-line alias Weyl chambers is fully suppressed. One could speak about a direct sum of the two independent quantum systems. Moreover, once we recall the even-parity symmetry of the potential in (4), we have the full freedom of redirecting our attention from the model defined on the whole real line to just one of the independent submodels. Both of these submodels are isospectral so that the spectrum of the complete system is doubly degenerate.
In many applications, people decide to ignore the impenetrability of the barrier (i.e., the absence of any meaningful contact between the subsystems), preferring reference to the full-line Hamiltonian (1). Such a slightly manipulative decision is presented as well motivated by the possibility of working, mostly in the context of statistical physics, with the two alternative versions of the wave functions, which are constructed as spatially symmetrized or antisymmetrized,
In spite of the complete absence of tunneling, the respective wave-function superpositions (7) are declared tractable as mimicking a system of two indistinguishable “bosons” (due to the Pauli-principle-simulating symmetry ) or “fermions” (with spatial antisymmetry sampling the fermionic statistics).
Due to the degeneracy in combination with the absence of tunneling, one could equally decide to consider some more sophisticated full-line requirements with, say, wave functions such that , using an arbitrary complex . Nevertheless, in spite of being mathematically acceptable, such a generalization is not used. In the overall pragmatic context of the applied quantum mechanics, even the two most elementary specifications of are thought to make the most elementary one-dimensional two-particle version (4) of the conventional Calogero model sufficiently appealing, intuitive, and useful, as well as all of its descendants.
In this paper, we advocate for a different philosophy.
2.2. Asymmetric Barrier
During the recent developments of quantum theory, the Pauli-principle-rooted paradigm seems to be shattered. The first, purely mathematical, reason is that once we have zero tunneling through Calogero’s barrier, there is no reason for keeping this barrier formally left-right symmetric. In Equation (4), with , we can therefore “asymmetrize” the singular term,
Precisely, such an idea of asymmetrization of the impenetrable barrier at served as an inspiration for our study.
The idea appeared to be supported, independently, by some very recent developments in applications. The necessity of working with an asymmetric singular barriers emerged, for example, in the context of relativistic quantum mechanics [41]. The presence of interactions containing an asymmetric impenetrable barrier has been found productive, especially for certain systems described by one-dimensional Dirac equations (cf. [42]). In another paper (cf. [43]), the same authors introduced and solved the Dirac equation in which the impenetrable barrier was kept left-right symmetric. The routine reduction of the equation led to an equivalent Schrödinger-type differential equation defined along the whole real line in which the effective barrier reappeared in a manifestly asymmetric form of Equation (8) (also see a few more comments on this topic in Appendix A).
Let us now accept the idea and let us replace, in our reduced Calogero–Schrödinger Equation (4), the conventional symmetric barrier with its two-parametric asymmetric generalization (8). Such a model (i.e., two decoupled radial harmonic oscillators with different angular momenta) is exactly solvable [44]. Its spectrum can be written in closed form as
The degeneracy as encountered when becomes, up to accidental confluences, removed when .
Due to the simplicity of the model, it becomes entirely straightforward to deduce the basic consequences. In a methodically motivated analysis, let us consider just a special case of Equation (8) in which the asymmetry is kept one-parametric and maximal,
After we recall Equation (4) and out-scale the inessential spring constant , we arrive at a drastically asymmetric one-parametric toy-model potential
the shape of which is shown in Figure 1.
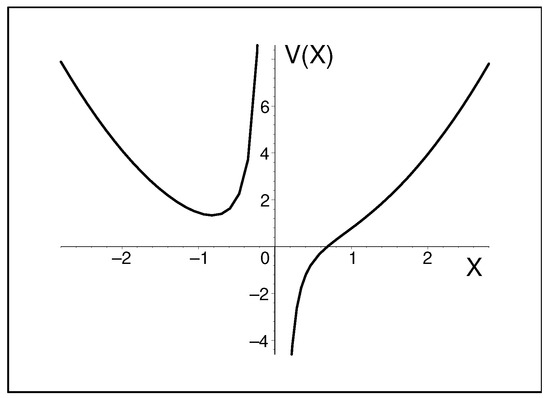
Figure 1.
Potential (11) at .
The explicit non-numerical form of the spectrum immediately follows from Equation (9), and its -dependence is displayed in Figure 2. The only instant of degeneracy occurs at . The spectrum even becomes equidistant at . One only has to add that the price to be paid for the unfolding of the degeneracy is not too small.
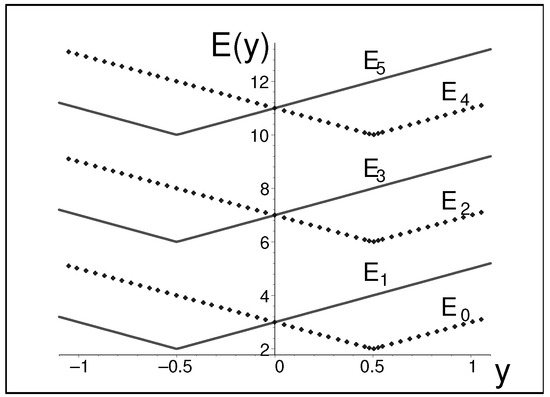
Figure 2.
Bound-state energies in (11). Full/dotted lines mark the left-/right-well subspectra.
Lemma 1.
Analogous consequences can be drawn after the more general two-parametric asymmetrization of the barrier (cf. (8)), or after transition to a larger number of particles. With the details explained below, let us only mention here that once we, at any A, asymmetrize the boundary between some two Weyl chambers and by choice of the respective couplings , we reveal that, in a way shown in Lemma 1 and Figure 2, the composition of the two subspectra may remain nondegenerate. Up to the accidental degeneracies, therefore, the -supported wave function necessarily vanishes in and vice versa.
Within the limit of , the spectrum becomes degenerate so that we may return to the wave–function superpositions as shown in Equation (7). Due to the absence of tunneling, there is still no reason for leaving the Weyl-chamber-dependent direct-sum interpretation of Hamiltonians (1).
We may now return to the two-body case in which the following statement is required:
Theorem 1.
Strictly speaking, the couplings and may need not be different. In both of these scenarios, the main message delivered by Theorem 1 is that if we wish to understand and break the symmetry of the system (represented, in this section, by the Hamiltonian in Equation (4)) and if we wish to introduce its consistently asymmetrized generalization (sampled, say, via Figure 1), we just have to take the two different versions of the Hamiltonian, and we have to restrict them to the respective single Weyl chamber. In the way prescribed in Equation (12), and in a way that is generalized below, a similar conclusion applies to the asymmetrized Calogero-like systems of more particles.
As long as the related analysis is technically less transparent, it makes sense to proceed more slowly and move, first, to the very next special case with three particles.
3. Spectral Degeneracy and its Unfolding at A = 3
For some purposes (and, in particular, for methodical purposes), the original symmetric Calogero model (1) as well as its present asymmetric Calogero-like generalization are too elementary at . In both of these regimes, fortunately, the pedagogical merits of these models are only partially lost after transition to [20].
3.1. Weyl Chambers
In Calogero’s symmetric model, (1) with the change in variables
enables us to eliminate the center-of-mass motion and to arrive at the reduced but still partial differential Schrödinger equation in the plane ,
At any nonvanishing coupling constant , the three impenetrable barriers divide the plane into as many as six Weyl-chamber sectors. Their shapes are displayed in Figure 3. We define them there not only by the inequalities imposed upon X and Y (in which stands for the set of two elements) but also, equivalently, by the subscripts in , which refer to the respective particle orderings .
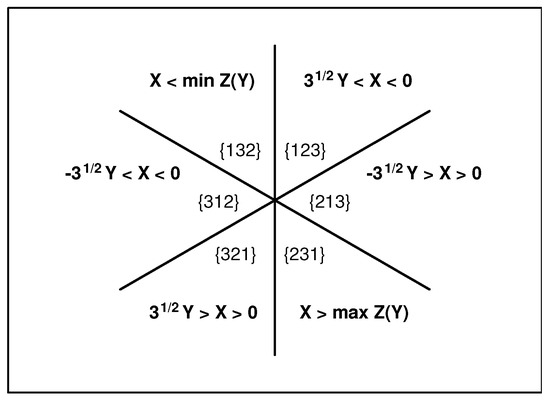
Figure 3.
Six wedge−shaped Weyl chambers in plane at .
A third, equally -specific but formally independent definition of the Weyl chambers, is based on a spherical-coordinate reparametrization and of the plane. After such a change in perspective, our Calogero–Schrödinger Equation (14) is found to be solvable by the separation of variables. This appeared to be a decisive discovery in [4], where the ansatz led to angular equation
The impenetrable barriers in Figure 3 are now localized simply as lying along the constant-angle lines with .
The split of the two-dimensional plane into six Weyl chambers is presented, in a slightly modified manner, in Figure 4. The three solid lines of the preceding picture are reinterpreted as separating those subscripts of the Weyl chambers (i.e., triplets of integers ), which only differ by a single elementary transposition. The line that represents the two-body repulsion barrier and that stands for the transposition is now marked by symbol “”, etc.
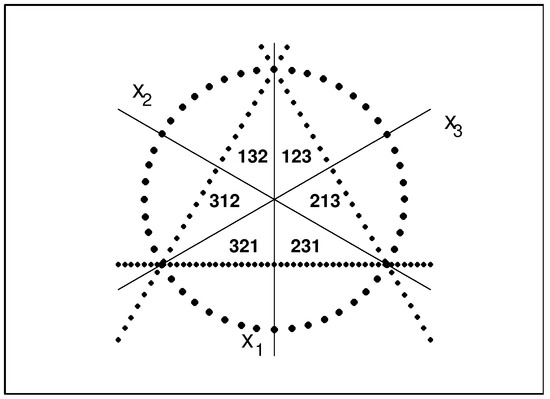
Figure 4.
Weyl-chamber projections on the eye-guiding circle and triangle.
3.2. Nonequal Barriers vs. Loss of Solvability
By far the most important formal merit of the conventional symmetric (i.e., equal-coupling) Calogero–Schrödinger Equation (14) is that after the separation of variables, both the angular Equation (15) and its more common harmonic-oscillator radial-equation partner prove solvable in closed form. This yields the spectrum
exhibiting multiple accidental degeneracies plus a global sextuple degeneracy reflecting the split of the plane into the six dynamically independent Weyl chambers. In this sense, every energy level in Equation (16) can be assigned six independent wave functions. Due to the impenetrability of the barriers, every one of these functions may be chosen as exclusively supported by one of the eligible Weyl chambers,
In the opposite direction, one could argue that the admissibility of the choice (17) (where index runs over all six permutations of triplet 123) is a consequence of the impenetrability of the Weyl-chamber boundaries, implying that every one of the levels in Equation (16), “locally” (i.e., inside ) degenerate or not, is also six times degenerate, as well as “globally” (i.e., inside ).
Let us now remind the readers that our study aimed aimed, first of all, at an unfolding of the “global” spectral degeneracy. The goal is achieved by means of an asymmetrization of the Hamiltonian. In the special case, one of our guiding ideas is that the strength of the singularities of Hamiltonian (1) is only controlled by a single coupling constant C.
Preliminarily, one of the most natural tentative generalizations of model (14) might be sought via an ad hoc replacement of the single coupling constant C with a triplet of independent parameters,
The denominators in (18) and, hence, the localization of all of the Weyl-chamber boundaries would remain the same. In combination with the loss of symmetry, their impenetrability would imply the loss of the coincidence of the six Weyl-chamber-related subspectra .
As long as the potentials inside the chambers can now be treated as a set of independent, isolated two-dimensional quantum dots, only the accidental “local” degeneracy between the bound-state subspectra survives.
Remark 1.
The sextuple degeneracy of the energy levels (16) can be unfolded using the three-parametric asymmetrization (18) of the reduced Calogero-like Schrödinger Equation (14). In such a case, the standard proof of the exact solvability of the model does not apply. In the future, indeed, the system might still be found solvable. With the present level of knowledge, the full exact solvability has to be declared, with all probability, lost.
Incidentally, the latter methodical uncertainty may be related to the well-known fact that in several generalized Calogero-type models, the not-quite-expected exact solvability was found to be restricted to a finite subset of certain anomalous, “anharmonic” bound states [45]. A connection of such an incomplete “quasi-exact” form of solvability with our present approach is nontrivial. Although the possible comparisons already lie beyond the scope of our present study, interested readers may find more details and inspiration in the comprehensive review paper [46] published in 2005 as a part of the Birthday Issue dedicated to Francesco Calogero on the occasion of his 70th birthday.
Another observation related to Remark 1 is that up to an accidental occurrence of a degeneracy, and in sharp contrast to the symmetric scenario, virtually all of the bound states of the asymmetric model with an unfolded spectrum necessarily have to obey the single-chamber-support restriction (17) imposed upon wave functions.
3.3. Reinstallation of Solvability: Asymmetric Barriers
The validity and constructive nature of Theorem 1 at might have to be extended to all of the models with . In particular, the degeneracy of Calogero’s spectrum has to be unfolded. This degeneracy can be attributed to the particle–permutation symmetry of the Hamiltonian. Thus, as long as we wish to weaken the degeneracy in a way different from the preceding tentative method (18), we have to find another method of breaking that symmetry.
Naturally, we wish to do so without the loss of the exact, closed-form solvability of the original symmetric model. The overall strategy of doing so was already indicated above. We have to pick six different coupling strengths and introduce six reparametrized versions of Calogero’s exactly solvable Hamiltonian in Equation (1), . Now, although all of these operators are defined over the whole unrestricted range range of the coordinates, the impenetrability of the barriers enables us restrict their respective actions to the functions over a single Weyl chamber.
In this manner, we complement the properly asymmetrized model (12) with its exactly solvable descendant.
Theorem 2.
Calogero-like quantum system with Hamiltonian
is exactly solvable, provided only that
at .
Proof.
Such a model is a direct sum over all six permutations of integers . Every one of its independent components (20) is obtained from the conventional model (1) after the elimination of the center-of-mass degree of freedom. Hence, up to the loss of the “global” degeneracy, the bound-state solutions remain “locally” unchanged even after the range of coordinates is restricted by to , and after the coupling is chosen to be equal to . □
Six independent coupling constants in Equation (20) (alias the “colors” of the chambers) may but need not be all mutually different. Serving for an exhaustive classification of all of the asymmetric generalizations of the symmetric model. The classification can be given the form of a list of all of the possible nontrivial colorings of the six wedges in Figure 3 or Figure 4.
As long as the explicit formulation of the list of the colorings is conceptually elementary, it may be left to the readers. Let us only note that in addition to the original Calogero’fully symmetric case (using just a single color C) and the maximally asymmetrized six-color system admitting a maximal reduction in the degeneracy, some of the other special colorings might prove to be of enhanced interest for application. For example, we could be interested in the form of boundaries between neighboring Weyl chambers and . The reason is that these boundaries in are pull-downs of the microscopic particle–particle repulsion-force singularities in . Various “realistic” subclassifications might then be motivated by the need for being given a phenomenological input knowledge of dynamics on the microscopic level, with the emphasis put upon the difference between the symmetric barriers (when ) and their asymmetric repulsion-force alternatives (when ). Thus, in particular, whenever only some of the particle–particle barriers remain symmetric, we can speak about hybrid models. In these cases, the unfolding of the “global” spectral degeneracy is just partial.
Alternatively, one could demand that even when all of the particle–particle barriers become left–right asymmetric, the breakdown of symmetry may be incomplete, leading again to the partial removal of the model’s spectral degeneracy. Once we recall Figure 4, such an arrangement might be immediately visualized via coloring(s) in which one only uses a minimum (i.e., say, two) different colors. In these cases, the wave function of the system can (i.e., are allowed to) remain nonvanishing in more than one Weyl chamber, i.e., in principle, in the whole union of all of the Weyl chambers carrying the same color.
4. Spectral Degeneracy and Its Unfolding Beyond A = 3
4.1. Exact Solvability
The systems with different As share formal analogies. In all of them, in particular, the Weyl chambers may be numbered using the configuration alias permutations of the particles. We abbreviate and denote if and only if . Next, the singularities occur in whenever . After we eliminate the center of mass [33], these singularities also cut and split the reduced space into its Weyl-chamber subsets . The points of their boundaries are precisely the points at which the microscopic particle–particle interaction becomes singular.
For all of these reasons, many of the above-mentioned considerations can be generalized to any A. In particular, the generalizations of Equation (19) and of Theorem 2 to any A are immediate.
Theorem 3.
At any integer , the Calogero-like quantum system with Hamiltonian
is exactly solvable, provided only that
at .
At any A, in other words, the ultimate asymmetrized Calogero-like Hamiltonian remains formally defined as a direct sum of its mutually noninteracting particle-ordering-dependent components. Every such model remains solvable. Even the limiting transition to the symmetric special case is smooth.
The only remaining open problem seems to be the formulation of an explicit list of all of the structurally nonequivalent colorings . Thus, the qualitative characterization of the set of the repulsive-barrier coupling constants is a crucial task. The task only requires a manageable visualization of the -dimensional space of the relative coordinates after its decomposition .
In such a framework, we are now prepared to give our preceding result an alternative formulation.
Theorem 4.
This observation provides the background and reason why our preceding constructive analyses are instructive and have to be complemented by their extension beyond .
In our ultimate illustration, the choice of forms a certain “feasibility bridge” connecting the easy models, where , with the overcomplicated ones, where . Thus, it makes sense to show that also the four-particle Calogero-like asymmetrized models in Equation (21) admit a feasible, compact, and more or less explicit descriptive analysis.
4.2. Weyl-Chamber Boundaries and Their Cartography at A = 4
One of the key formal advantages of the conventional as well as generalized Calogero-like models with is the separability of the initial partial differential Schrödinger equation, i.e., its reducibility to a set of ordinary differential eigenvalue problems. Such a feature is lost at so that the simplest elements of this class with deserve our constructive attention. Moreover, in a way advocated in the literature, the choice of as made in the two preceding sections need not be sufficiently representative in a broader methodical context at least [47,48]. As we already mentioned, the enumeration of the colorings in Figure 3 or Figure 4 is next to trivial. We be found it desirable to extend our discussion beyond .
4.2.1. Colorings at
At the task of the split of the plane by the sextuplet of the wedge-shaped Weyl chambers as well as the related classification alias coloring problems are comparatively easy to settle. All of the half-line Weyl-chamber boundaries share a common vertex and form a planar star. This makes the coloring of the wedges easy, leading immediately to an exhaustive classification of all of the unfoldings of the degeneracies, i.e., of all of the spectrally nonequivalent models. Moreover, it is sufficient to classify just the colorings of the six segments of an auxiliary circle or, equivalently, of an auxiliary triangle (cf. Figure 4).
The situation at is perceivably more complicated. Indeed, we have to replace, first of all, the change in variables (13) with its analogue. Nevertheless, the details of the change in variables as well as an explicit discussion of a deep algebraic discussion of its consequences is skipped here, for three reasons. Besides the first one (viz., the sake of brevity: their form is well known) and the second one (viz., a redundancy for our present purposes: the algebraic formulae already become far from transparent), our third and main reason is that in a way shown in Figure 4, at , it is sufficient to know, in its graphical form, just the topology (i.e., the neighborhoods) of the Weyl chambers.
4.2.2. Projection on a Central Sphere
Interested readers may find deeper insight into the formulae and multiple deep algebraic structures in the dedicated literature [3,49,50]. At , in particular, one has to deal with as many as eligible Weyl chambers. Thus, a replacement of the formulae with their graphical alternatives seems well founded. It enhances the efficiency of the analysis. In particular, the description becomes facilitated when we recall and adapt the graphical tricks as used for . In the first step, the centralized dotted-curve auxiliary planar circle in Figure 4 can be replaced at with a sphere in three dimensions. In full analogy, this enables one to project the three-dimensional objects on the spherical triangles of the form displayed in Figure 5.
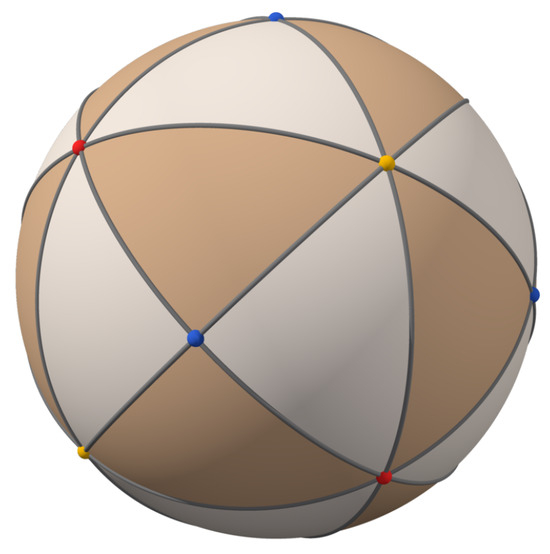
Figure 5.
Three-dimensional Weyl chambers in projection on an eye-guiding central sphere (source of the picture: [51], author: Tilman Piesk, licence: Watchduck—Own work, CC BY 4.0).
4.2.3. Projections on a Central Cube
The role of the dotted-line triangle in Figure 4 can readily be transferred at , to a central tetrakishexahedron in Ref. [52] and Figure 6. A key advantage of such an upgrade of projection is that it further simplifies the representation of the three-dimensional Weyl chamber pyramids . It replaces their projections on the spherical triangles in Figure 5 with the flat, planar triangles of the surface in Figure 6.
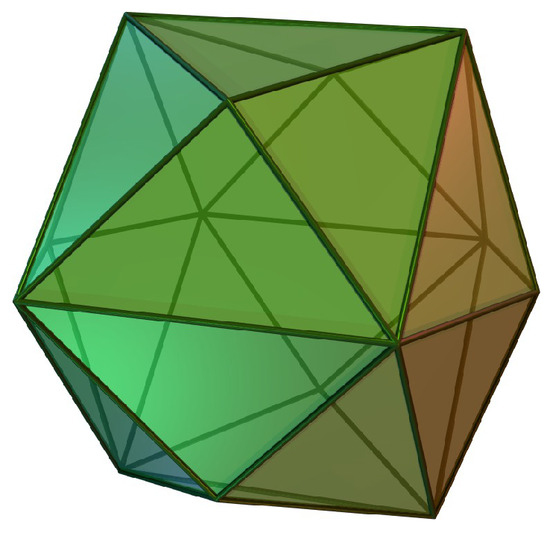
Figure 6.
Rectified projection of 24 Weyl chambers on the surface of a tetrakishexahedron (source: [52], author: T. Piesk, licence: Watchduck–Own work, CC BY 4.0).
Although the colorings of the planar triangular faces of the tetrakishexahedron look feasible, let us introduce another, last simplification converting the tetrakishexahedron in Figure 6 into a cube, with its six faces divided into quadruplets of the neighboring -representing triangles. For completeness, interested readers can find the three-dimensional picture of such a cube with subdivided faces on the internet [53]. In Figure 7, we present its planar, two-dimensional unfold.
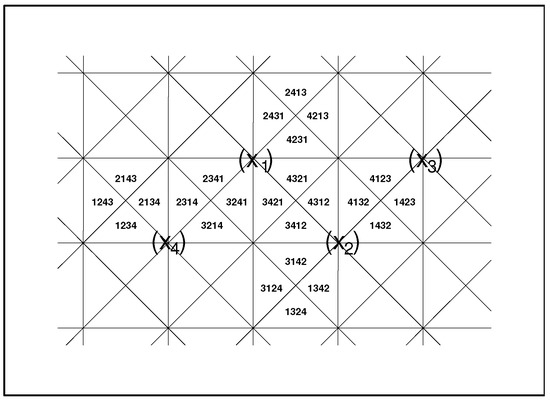
Figure 7.
Twenty-four Weyl chambers in projection on a central cube.
4.2.4. Numbering by Permutations
For our present purposes, we cut and display the surface of the cube in the planar-cartography representation in Figure 7. We only have to remember that such a planar picture might require, for some purposes, a reconstruction of the three-dimensional surface of the cube by bending and gluing some of the edges.
The union has to be taken over all of the permutations of the particles. It is only important for us to know that before the projection, as shown in Figure 7, the geometric shape of the individual three-dimensional Weyl chambers again has a pyramidal form, with their top fixed in the origin. We may expect that in comparison with the three-particle model, the generalization of the “cartography” to (and, in principle, to any larger ) is straightforward.
After the projection on the cube, we have to deal with the planar representation of the surface. The vertices of the cube coincide with the intersections of the six singularity lines (i.e., of the three lines standing for the adjacent edges and the other three representing the face diagonals). One only has to remember that these vertices are defined as the octuplet of points in at which the circumscribed auxiliary sphere is intersected by the four straight lines representing the original particle-coordinate axes of , , and . These intersections are also identified in Figure 7.
In this figure, the surface of the inscribed cube is represented by six concatenated squares. The symbols mark the intersections of outwards-running axes with the sphere and with the cube (at its vertices). The planar triangular projections of all of the twenty-four three-dimensional Weyl chambers on the walls of the cube are finally numbered here by the quadruplets of integers such that . In this manner, we again obtain a transparent schematic two-dimensional representation of the Calogero-model kinematics at .
In the same figure, the straight lines mark the singularities (i.e., the barriers), and the numbers characterize the (projections of the) chambers . One can easily check that whenever one crosses the line, the quadruplet of integers is changed just by an elementary permutation of its neighboring elements. This permutation (i.e., a rearrangement of the particles) can be perceived as a consequence of the crossing of the barrier alias singularity line.
As a serendipitious byproduct of these topological considerations, we may deduce the following, not quite expected, combinatorial result.
Lemma 2.
Once we localize the positive half-line intersections , , , and on the auxiliary cube’s surface, the allocation of the permutations ijkl to the triangles of the cube’s surface is unique.
This observation returns us to the model with where we marked, in Figure 4, the projections of the triplet of the original Cartesian particle-coordinate axes , , and . These lines intersected the auxiliary circle at the six “barrier-sampling” points. At , the idea remains applicable because, now, the intersections of the sphere with the axes , , , and form an octuplet of the “marked” points in the diagram in Figure 7.
We may identify the latter points with the vertices of our auxiliary cube defined as inscribed in the auxiliary sphere. This enables us to project the boundaries of the separate Weyl chambers on the walls of the cube yielding the singularity lines in Figure 7. Summarizing, the twenty-four Weyl chambers are mapped on the set of spherical triangles covering the auxiliary sphere. They are, incidentally, rectangular. Their planar projections cover the surface of the above-mentioned inscribed cube, with the rectangularity preserved. What is important is that the one-to-one correspondence between the topology of the three-dimensional Weyl chambers and the topology of the “numbered” triangles in Figure 7 is achieved and guaranteed.
4.3. Alternative Cartography at A = 4
Let us repeat that after a routine elimination of the center-of-mass degree of freedom, the constructions have to be simplified by the reduction in the initial partial differential Schrödinger equation in four coordinates to its three-dimensional effective version [37]. As long as we are mainly interested in the structure of the decomposition of into a union of the Weyl chambers, we do not need the explicit formulae for the wave functions. These formulae may already be fairly complicated, see [3,54]. Fortunately, our present task is just the specification of the Weyl chamber or chambers in which the wave function of a relevant bound state can be nontrivial, .
Such a specification should be based on a visualization of the decomposition of and on the phenomenologically motivated assignment of the equal or different couplings to the respective chambers at all of the position permutations . Naturally, an exhaustive and systematic account of all of the possibilities would be too long. For a selection of a sample, we propose combining a “minimal” nontrivial coloring (using just two colors ) with a “maximal” asymmetry of the barriers (meaning that none of the barriers remains symmetric, i.e., invariant under the exchange of particles ). A sample of the maximally asymmetric arrangement (using just two colors called “left” and “right”) is displayed in Figure 8.
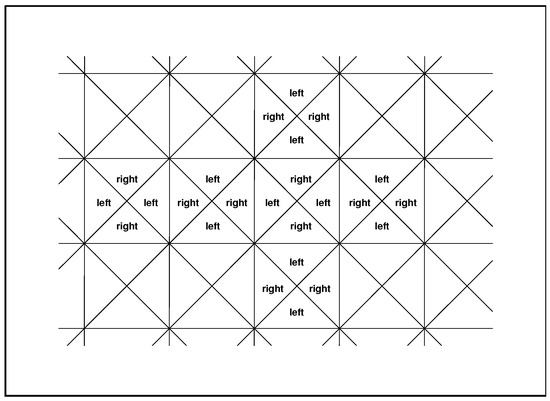
Figure 8.
The coloring with unique (viz., left–right) asymmetry of all of the barriers.
4.3.1. Projections of the Set of Weyl Chambers on a Tetrahedron
The surface of the cube in the preceding paragraph is a three-dimensional object. Its cut and straightening were used, yielding Figure 7 and Figure 8. An alternative approach to the visualization of the same three-dimensional cube is shown in Figure 9, where just half of its surface is presented, as shown after the cube is rotated in such a way that the vertex marked with symbol “” appears in front and in the center of the figure.
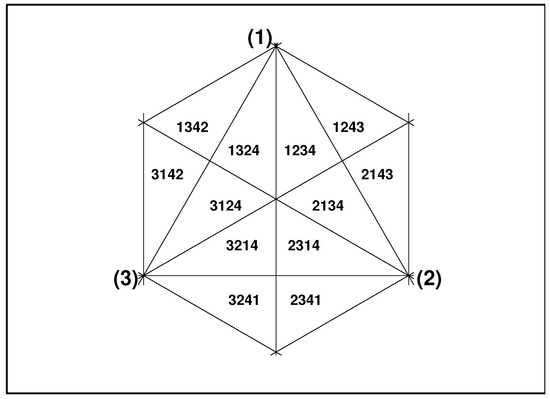
Figure 9.
The upper half of the auxiliary cube in Figure 7 as seen from vertex “”.
Although the latter planar view represents a three-dimensional cube, we might re-read the same picture as a flat triangle with vertices , , and , endowed with the three planar extensions that could be bent along the edges and turned down. A new three-dimensional surface emerges. Its complementary “invisible” lower half could be reconstructed given the same shape glued to the upper half.
Admissibly, this type of reconstruction of the missing part in Figure 9 is oversophisticated. Nevertheless, its minor reinterpretation yields another, much more regular, Platonic-body representation of the topology, i.e., of the representation of the Weyl-chamber neighborhoods. Explicitly, it is presented in Figure 10. The Weyl chambers (numbered there by the triplets of integers) are organized into three triangles. The upper one (with vertices , , and ) remains unchanged while the other three triangles are all bent down, with their respective circle-marked “outer” vertices A, B, and C to be glued together, forming the fourth vertex of a tetrahedron, which should be endowed with symbol .
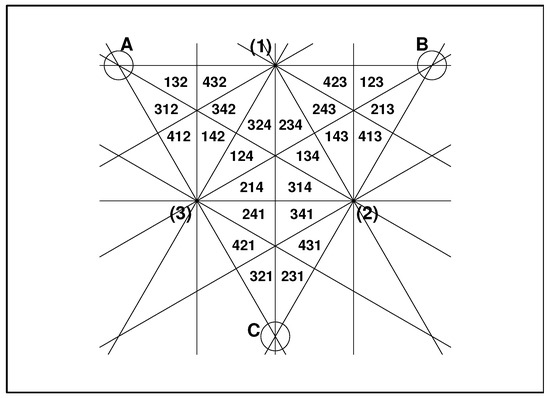
Figure 10.
A tetrahedral alternative to Figure 7 (the surface unfolded into triangle ).
In Figure 10, the three intersections marked as , , and have to be interpreted as the three vertices of one of the four triangular sides of an auxiliary central tetrahedron. Its remaining three sides are triangles , , and . In the figure, the surface of the tetrahedron is unfolded so that after its refolding (in three dimensions), the three “outermost” vertices of the large triangle (marked with small circles and letters A, B, and C) coincide.
In a marginal remark, let us add that, for the sake of brevity, we numbered all of the small Weyl-chamber-representing triangles by the triplets of integers . The reason for this is that for a return to the full-fledged notation , the “missing” value of i is provided by the nearest vertex . The rule becomes sufficient after the symbols A, B, and C are all re-read as . Incidentally, in such a simplification, we can move one step further. This is explained in Figure 11, in which we attach the new quadruplet of symbols to the remaining four vertices. Then, as long as all of the neighboring Weyl chambers share the last integer l with vertex , two digits suffice for the labeling.
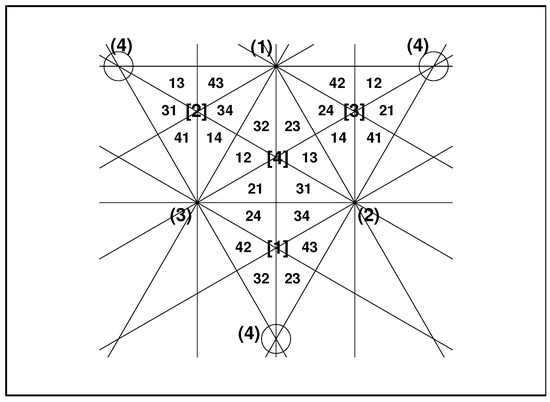
Figure 11.
An alternative version of Figure 10 (a shortened Weyl-chamber classification).
4.3.2. An Ultimate Classification of the Barriers
In addition to a purely formal appeal of the shortened notation, it directly indicates which particles are exchanged when crossing some of the singular boundary lines. Due to this, the combinatorics of coloring becomes easier, also simplifying our ultimate understanding of the correspondence between the microscopic symmetries/asymmetries of the particle–particle repulsion and the structure of the macroscopic bound-state spectrum.
Any phenomenologically motivated and exhaustive “tetrahedral-surface” classification of all of the 24 Weyl chambers (and of their shared singular boundaries), as provided in Figure 10 and Figure 11, can be reinterpreted as a completion of Figure 9 with its “invisible” half added. The four-digit particle orderings in Figure 9 are shortened to the three-digit symbols in Figure 10. The reason for this is that for the full identification of the chambers in our notation, the knowledge of the trailing triplet is sufficient. The “missing” value of i (always equal to 1, 2, 3, or 4) coincides with the one given in the parenthesized symbol marking the adjacent vertex. The validity of this coincidence can immediately be checked via the inspection of the “incomplete” Figure 9.
An alternative to Figure 10 is presented in Figure 11, where the remaining four “anonymous” sextuple intersections of the singularity lines (localized in the centers of the sides of the tetrahedron) are marked with the symbols , , , and . Again, having noticed that the adjacent chambers-marking triplets of integers share vertex with , we introduce our ultimate index-shortening convention in Figure 11.
Under the latter convention, one can finally decide to set the tetrahedron’s edges equal to one and to subsequently distinguish between the “long”, “middle”, and “short” Weyl-chamber singular boundaries of the respective lengths , , and . Using this notation, one can conclude that among the total number of 36 singular boundaries, we have to deal with 12 short ones, 12 middle ones, and 12 long ones, with the long ones always having end points of the form , while representing the lines of the reordering of the remaining two integers j and k in our ultimate chamber-classification scheme in Figure 11.
5. Summary
One of the characteristic features of the conventional Calogero model (1), which describes the one-dimensional motion of a system of A quantum particles, is the symmetry of the Hamiltonian with respect to the reordering of the particles. Remarkably, such symmetry can be spontaneously broken because the details of the dynamics are such that whenever one fixes the ordering in advance, it is, during the evolution, conserved. The system can be perceived as composed of multiple (i.e., of as many as ) independent subsystems.
In such a situation, it is natural to ask the question about the feasibility of manifestly breaking the above-mentioned symmetry. The motivation appears sound: in the symmetric model, the spectrum is multiply degenerate, and it was not too clear how one could unfold this degeneracy. At the same time, a promising methodical guidance seemed to lie in a manifest violation of the symmetry in the way illustrated in Figure 1, and by the “validating” small-A examples as thoroughly described in Section 2 and Section 3.
Along this line, we found and described one of the possible answers. A modification of the model was proposed, in which the class of the forces that control the evolution was extended. The basic idea of the innovation may be seen in the dynamic nature of the conservation of the ordering. It appeared to be caused by the original Calogero’s particle-particle-repulsion forces which were simply too strong. Their strength made any exchange of the neighboring particles prohibited.
We argued that the main reason for a complete suppression of the rearrangements had to be seen, first of all, in the strongly singular behavior of Calgero’s original repulsion forces at short distances. From this, we deduced that the whole rearrangement suppression paradox can be identified as a mere misunderstanding. We think that the puzzle is now clarified.
We recollected that the conventional interpretation of Calogero’s quantum system (as currently accepted by the majority of authors) is that its Hamiltonian H is a direct sum of all of the eligible ordering-dependent operators , where the subscript denotes and defines such an ordering. We imagined that, from this point of view, one can and should reinterpret the singular particle–particle repulsion as an impenetrability of the boundaries of the Weyl chambers .
This is a decisive step. It gave birth to the main idea of our present study: we proposed that one can construct a fairly large family of new Calogero-like Hamiltonians in which a central role is played by the turn of our model-building attention from the complete kinematical Euclidean space (comprising all of the individual particle coordinates with ) to its decomposition into a union of the ad hoc -dimensional submanifolds.
Routinely, after the standard and trivial decoupling of the independent center-of-mass motion, the decomposition was reduced to the space defined as a union of the -dimensional wedge-shaped Weyl chambers . Then, the rest and the largest part of the paper had to be devoted to an explicit description and discussion of some consequences of the main idea.
One of the phenomenologically most interesting consequences of the decomposition of the set parametrized by the -plet of relative coordinates concerns the boundaries between the neighboring Weyl chambers. These (repulsive) boundaries just correspond, from the microscopic point of view, to the mutual (repulsive) particle–particle interactions. Thus, in the language of mathematics, both of these representations of the (impenetrable) boundaries (not admitting any tunneling) appear to be allowed left–right asymmetric.
The consequences of asymmetrization of such an “input” information about dynamics were discussed, in detail, for , , and at . In all of these examples, the loss of symmetry was shown to lead to a higher flexibility (which is due to the emergence of many new and freely variable parameters) as well as to a partial or complete suppression of the “global” degeneracy of the spectrum of the original Calogero model.
One of the most important challenges appeared to be the preservation of the exact solvability of the model after its asymmetrization. Due to an (at least partial) suppression of the degeneracy of the spectrum of the conventional symmetric model, the related unfolding of the wave functions was expected to prove useful, say, during some further future amendment of the model using, say, perturbation theory.
In our text, we pointed out that in the symmetric-model special case the exact solvability of quantum Hamiltonian (1) is a nontrivial consequence of its Lie-algebraic symmetry [1]. The existence of this symmetry is only rendered possible by the idealized picture of dynamics: the motion of the multiplet of particles is one-dimensional. Moreover, the mutual two-body interactions between individual particles are represented by the quartic plus inverse quartic potentials and , respectively. In this paper, from this point of view, the generalization was be characterized as making the shape of the forces asymmetric, i.e., different for and for . This rendered the new Calogero-like model multiparametric.
Another important aspect of the innovation is that in spite of the emergence of new free parameters, the resulting Calogero-like model remains solvable exactly. Although such a statement may sound surprising, the explanation is not too difficult, requiring just a more consequent use of the concept of the Weyl chambers. Incidentally, we could borrow the definition from the conventional Calogero model. Thus, what we only had to add was the emphasis upon the strongly singular nature of the particle–particle short-range interactions . We only had to reread the well-known impenetrability of these barriers as a ban of particle exchanges.
During the unitary time evolution of our generalized quantum system, the ordering of the particles can be perceived as conserved. This is the most immediate consequence of the full-scale suppression of the tunneling between the neighboring Weyl chambers. Thus, any bound state of any Calogero-like quantum system can be understood as represented by the wave function supported by a single Weyl-chamber subdomain of coordinates. The only difference between the original and the present (i.e., “asymmetrized”) models is that, in the former case, due to the uniqueness of their coupling C, every bound-state energy level is particle-ordering-independent.
We showed how the “global” degeneracy of the levels can systematically be removed. What is sufficient is that in Hamiltonian (1) the coupling constant C is made configuration-dependent. Thus, along all of the inner boundaries of one of the Weyl chambers (say, of characterized by the arrangement of the particle coordinates), we require that . In another Weyl chamber (say, in , characterized by another ordering alias permutation of the particles), we set , etc. In general, one then has to distinguish between two scenarios: either the respective singular coupling strengths coincide (i.e., we have ) or not.
In the latter case of our present interest, we had to generalize, “asymmetrize”, the form of the Hamiltonian in Equation (1) by making it configuration-dependent. In particular, once we wished to keep the model solvable, we had to make all of the choices of the parameters mutually compatible. In this context, we found the criterion. Naturally, for an ultimate explicit construction of thenew solvable multiparametric Calogero-like model, such a guarantee is a crucial mathematical ingredient. So, we showed that such a guarantee is just a combinatorial exercise, provided only that we take into consideration the impenetrability of the singular particles-separating barriers.
The absence of tunneling allowed us to infer that the conventional Calogero’s choice of the spatially symmetric alias particle-exchange invariant is not sufficiently general. In a systematic search for its more general spatially asymmetric and configuration-dependent alternatives, we started our analysis with the two-particle scenario. We replaced the conventional Calogero’s choice of repulsion with the spatially asymmetric Formula (8) and outlined the consequences. At , we displayed all of the six wedge-shaped Weyl chambers in Figure 3. In Figure 4, we showed that and how the two-dimensional Weyl-chamber wedges can be projected, for simplification purposes, on the segments of an auxiliary circle or on the sides of an auxiliary triangle. The idea was subsequently transferred to . We emphasized that the role of the circle and triangle at becomes inherited by a sphere and a cube or, alternatively, by a tetrahedron at , etc. This was our last illustration and argument in support of the consistency of the process of asymmetrization at any A.
Summarizing, we established, first of all, that what can and should be asymmetric are the boundaries between the Weyl chambers. Secondly, we emphasized that a return to the generic form of Calogero’s Hamiltonian (1) is possible, provided only that this operator is reinterpreted as particle-ordering-dependent. Thirdly, its form of a direct sum over subsystems was shown to open the possibility of an unfolding of the “global” spectral degeneracy. Last but not least we pointed out that due to the absence of tunneling, the unfolding of levels can be mediated simply by the choice of a suitable multiplet of the particle-repulsion couplings , leading to a classification via a coloring of the Weyl chambers. For a really elementary illustration, a return to Figure 1 is recommended.
Funding
This research received no external funding.
Data Availability Statement
No new data were created.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. The Occurrence of Asymmetric Impenetrable Barriers in Relativistic Quantum Mechanics
The conventional nonrelativistic quantum theory admits, in contrast to its classical limit, the existence of bound states even in a strongly singular attractive potential , provided only that the coupling is not too large [38]. In [43], Ishkhanyan and Krainov turned their attention to analogous singular-potential problems in relativistic quantum mechanics. Some of their results might find a not quite expectable nonrelativistic counterpart in our present paper.
In their study of a stationary one-dimensional Dirac equation, they considered, in particular, a specific pseudoscalar screened Coulomb potential exhibiting a conventional spatial symmetry,
In a way reported during a recent conference [41], they revealed that in addition to its well-motivated phenomenological origin, the model could prove methodically relevant because it can be made conditionally exactly solvable (CES; for concise information on the latter concept, see our older comment [40]).
From our present point of view, the essence of the Ishkhanyan’s and Krainov’s message is that after one rewrites Dirac equation in a mathematically equivalent nonrelativistic bound-state form, one just has to solve the effective Schrödinger equation with a spatially manifestly asymmetric potential
with parameter . In particular, their model possesses a spatially manifestly asymmetric central singularity with which the mathematically desirable CES property was found to occur at a special value of .
We have to add that the authors of [43] worked with an extreme, phenomenologically ambitious asymmetry of their potential. In our present notation, they used just Equation (8) with two independent couplings,
They were of an opposite sign and of different sizes, and there were no free parameters left. Indeed, once we return to the units , their CES constraint (A2) acquired the form of our present Equation (10) with .
For us, the latter results are encouraging, demonstrating that it makes sense to work with asymmetric singular forces. By relations (A2), we also felt inspired toa replace the ansatz (8) with the more elementary one-parametric convention (11). We came to the conclusion that the CES-based necessity of working with a fixed value of in (A2) is too high a price for the technical advantage of the user-friendliness of the model. Thus, we turned attention to the harmonic-oscillator confinement (11) because, qualitatively, the asymmetric shape of our two-body potentials, as shown in Figure 1, is, after all, not too different from the shape of the CES potential in Equation (A1) as displayed in Figure 2 in paper [43].
In [41], the authors emphasized that it makes good sense to search for a deeper understanding of the connection between the flexibility of the spectral properties and the absence of the tunneling caused by the singular nature of the barriers. They noticed that the choice of the matching condition at “must be adjusted according to the specific physical context under consideration” [43]. In our present paper, the latter point has attracted due attention. We managed to disentangle several related technical challenges. In particular, we shortened the argumentation by omitting all of the phenomenologically motivated references to the relativistic quantum dynamics. After all, even in [43], we read that the “results show a significant difference between the Schródinger and Dirac cases” and that “it is clear that the reason for the discrepancy [between the Schródinger and Dirac models] is that the boundary conditions we [=they] use for these two cases are [different, i.e.,] due to different considerations”. For this reason, we kept the scope of our present study restricted to the strictly nonrelativistic systems, promising still very broad potential applicability [11].
References
- Olshanetsky, M.A.; Perelomov, A.M. Quantum completely integrable systems connected with semi-simple Lie algebras. Lett. Math. Phys. 1977, 2, 7–13. [Google Scholar] [CrossRef]
- Olshanetsky, M.A.; Perelomov, A.M. Quantum integrable systems related to Lie algebras. Phys. Rept. 1983, 94, 313–404. [Google Scholar] [CrossRef]
- Turbiner, A. Hidden algebra of the N-body Calogero problem. Phys. Lett. B 1994, 320, 281–286. [Google Scholar] [CrossRef]
- Calogero, F. Solution of a three-body problem in one dimension. J. Math. Phys. 1969, 10, 2191–2196. [Google Scholar] [CrossRef]
- Calogero, F. Ground state of a one-dimensional N-body problem. J. Math. Phys. 1969, 10, 2197–2200. [Google Scholar] [CrossRef]
- Calogero, F. Solution of the one-dimensional N-body problem with quadratic and/or inversely quadratic pair potentials. J. Math. Phys. 1971, 12, 419–436. [Google Scholar] [CrossRef]
- Van Diejen, J.F.; Vinet, L. (Eds.) Calogero-Moser- Sutherland Models (CRM Series in Mathematical Physics); Springer: New York, NY, USA, 2000. [Google Scholar]
- Rühl, W.; Turbiner, A.V. Exact solvability of the Calogero and Sutherland models. Mod. Phys. Lett. A 1995, 10, 2213–2222. [Google Scholar] [CrossRef]
- Sutherland, B. Beautiful Models: 70 Years of Exactly Solved Quantum Many-Body Problems; World Scientific: Singapore, 2004. [Google Scholar]
- Polychronakos, A.P. Physics and mathematics of Calogero particles. J. Phys. A Math. Gen. 2006, 39, 12793. [Google Scholar] [CrossRef]
- Calogero, F. Calogero-Moser system. Scholarpedia 2008, 3, 7216. [Google Scholar] [CrossRef][Green Version]
- Ghosh, P.K.; Khare, A.; Sivakumar, M. Supersymmetry, shape invariance, and solvability of AN-1 and BCN Calogero-Sutherland model. Phys. Rev. A 1998, 58, 821. [Google Scholar] [CrossRef]
- Khastgir, S.P.; Pocklington, A.J.; Sasaki, R. Quantum Calogero-Moser Models: Integrability for all Root Systems. J. Phys. A Math. Gen. 2000, 33, 9033–9064. [Google Scholar] [CrossRef][Green Version]
- Boreskov, K.G.; Turbiner, A.V.; Vieyra, J.C.L. Solvability of the Hamiltonians related to exceptional root spaces: Rational case. Commun. Math. Phys. 2005, 260, 17–44. [Google Scholar] [CrossRef]
- Dunkl, C.F.; Hu, Y. Orthogonal Polynomials of Several Variables; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Van Diejen, J.F. Confluent hypergeometric orthogonal polynomials related to the rational quantum Calogero system with harmonic confinement. Commun. Math. Phys. 1997, 188, 467–497. [Google Scholar] [CrossRef]
- Chung, W.S.; Hassanabadi, H. One-dimensional quantum mechanics with Dunkl derivative. Mod. Phys. Lett. A 2019, 34, 1950190. [Google Scholar] [CrossRef]
- Sedaghatnia, P.; Hassanabadi, H.; Junker, G.; Kříž, J.; Hassanabadi, S.; Chung, W.S. Investigation of the generalised Wigner-Dunkl harmonic oscillator and its coherent states. Ann. Phys. 2023, 458, 169445. [Google Scholar] [CrossRef]
- Scholtz, F.G.; Geyer, H.B.; Hahne, F.J.W. Quasi-Hermitian Operators in Quantum Mechanics and the Variational Principle. Ann. Phys. 1992, 213, 74–101. [Google Scholar] [CrossRef]
- Znojil, M.; Tater, M. Complex Calogero model with real energies. J. Phys. A Math. Gen. 2001, 34, 1793–1803. [Google Scholar] [CrossRef]
- Znojil, M.; Tater, M. Exactly solvable three-body Calogero-type model with translucent two-body barriers. Phys. Lett. A 2001, 284, 225–230. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Gupta, K.S. On the real spectra of Calogero model with complex coupling. Phys. Lett. A 2004, 323, 29–33. [Google Scholar] [CrossRef]
- Assis, P.E.G.; Fring, A. From real fields to complex Calogero particles. J. Phys. A Math. Gen. 2009, 42, 425206. [Google Scholar] [CrossRef]
- Fring, A.; Smith, M. Antilinear deformations of Coxeter groups, an application to Calogero models. J. Phys. A Math. Gen. 2010, 43, 325201. [Google Scholar] [CrossRef]
- Bagarello, F.; Gazeau, J.-P.; Szafraniec, F.; Znojil, M. (Eds.) Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Znojil, M. PT symmetric harmonic oscillators. Phys. Lett. A 1999, 259, 220–223. [Google Scholar] [CrossRef]
- Jakubsky, V. PT-symmetric Calogero-type model. Czechosl. J. Phys. 2004, 54, 67–69. [Google Scholar] [CrossRef]
- Brihaye, Y.; Nininahazwe, A. On PT symmetric extensions of the Calogero model. Int. J. Mod. Phys. A 2004, 19, 4391–4400. [Google Scholar] [CrossRef]
- Fring, A.; Znojil, M. PT-symmetric deformations of Calogero models. J. Phys. A Math. Gen. 2008, 41, 194010. [Google Scholar] [CrossRef]
- Fring, A. PT-symmetric deformations of integrable models. Phil. Trans. Roy. Soc. Lond. A 2013, 371, 20120046. [Google Scholar] [CrossRef] [PubMed]
- Correa, F.; Lechtenfeld, O. Algebraic integrability of PT-deformed Calogero models. J. Phys. Conf. Ser. 2021, 2038, 012007. [Google Scholar] [CrossRef]
- Jakubsky, V.; Znojil, M.; Luis, E.A.; Kleefeld, F. Trigonometric identities, angular Schrödinger equations and a new family of solvable models. Phys. Lett. A 2005, 334, 154–159. [Google Scholar] [CrossRef]
- Hakobyan, T.; Nersessian, A.; Yeghikyan, V. The cuboctahedric Higgs oscillator from the rational Calogero model. J. Phys. A Math. Theor. 2009, 42, 205206. [Google Scholar] [CrossRef]
- Feigin, M.V. Intertwining relations for the spherical parts of generalized Calogero operators. Theor. Math. Phys. 2003, 135, 497–509. [Google Scholar]
- Hakobyan, T.; Lechtenfeld, O.; Nersessian, A. The spherical sector of the Calogero model as a reduced matrix model. Nucl. Phys. B 2012, 858, 250–266. [Google Scholar] [CrossRef][Green Version]
- Feigin, M.; Lechtenfeldl, O.; Polychronakos, A. The quantum angular Calogero-Moser model. J. High Energy Phys. 2013, 1307, 162. [Google Scholar] [CrossRef]
- Correa, F.; Lechtenfeld, O. The tetrahexahedric angular Calogero model. J. High Energy Phys. 2015, 1510, 191. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Pergamon: New York, NY, USA, 1977. [Google Scholar]
- Lapointe, L.; Vinet, L. Exact Operator Solution of the Calogero-Sutherland Model. Commun. Math. Phys. 1996, 178, 425–452. [Google Scholar] [CrossRef]
- Znojil, M. Comment on conditionally exactly soluble class of quantum potentials. Phys. Rev. A 2000, 61, 066101. [Google Scholar] [CrossRef]
- Ishkhanyan, A.M. Conditionally exactly solvable Dirac potential, including x1/3 pseudoscalar interaction. In Proceedings of the International Conference of Analytic and Algebraic Methods in Physics XX (FNSPE), Prague, Czech Republic, 28–31 August 2023. [Google Scholar]
- Ishkhanyan, A.M.; Kreinov, V.P. Exact solution of the 1D Dirac equaiton for a pseudoscalar interaction potential with the inverse-square-root variation law. Sci. Rep. 2023, 13, 13482. [Google Scholar] [CrossRef]
- Ishkhanyan, A.M.; Kreinov, V.P. Conditionally exactly solvable Dirac potential, including x1/3 pseudoscalar interaction. Phys. Scr. 2023, 98, 075229. [Google Scholar] [CrossRef]
- Flügge, S. Practical Quantum Mechanics I; Springer: Berlin/Heidelberg, Germany, 1971. [Google Scholar]
- Post, G.; Turbiner, A.V. Quasi-solvability of Calogero-Sutherland model. Russ. J. Math. Phys. 1995, 3, 113. [Google Scholar]
- Turbiner, A.V. Quasi-Exactly Solvable Hamiltonians related to Root Spaces. J. Nonlin. Math. Phys. 2005, 12 (Suppl. S1), 660–675. [Google Scholar] [CrossRef]
- Brink, L.; Turbiner, A.V.; Wyllard, N. Hidden algebras of the (super) Calogero and Sutherland models. J. Mathe. Phys. 1998, 39, 1285–1315. [Google Scholar] [CrossRef]
- Boreskov, K.G.; Vieyra, J.C.L.; Turbiner, A.V. Solvability of the F4 integrable system. Int. J. Mod. Phys. A 2001, 16, 4769–4801. [Google Scholar] [CrossRef]
- Humphreys, J.E. Reflection Groups and Coxeter Groups; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Coxeter, H.S.M. Regular Polytopes, 3rd ed.; Dover Publications: New York, NY, USA, 1973. [Google Scholar]
- Available online: https://commons.wikimedia.org/wiki/File:Disdyakis_6_spherical.png (accessed on 27 November 2023).
- Available online: https://en.wikipedia.org/wiki/File:Tetrakishexahedron.jpg (accessed on 27 November 2023).
- Available online: https://commons.wikimedia.org/wiki/File:Disdyakis_6_in_rhombic_6.png (accessed on 27 November 2023).
- Brink, L.; Hansson, T.H.; Vasiliev, M. Explicit solution to the N body Calogero problem. Phys. Lett. B 1992, 286, 109–111. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).