Abstract
In this work, we determine the maximum general Randić index (a general symmetric function of vertex degrees) for among all n-vertex unicyclic graphs with a fixed maximum degree and the maximum and the second maximum general Randić index for among all n-vertex unicyclic graphs, where . We establish sharp inequalities and identify the graphs attaining the inequalities. Thereby, extremal graphs are obtained for the general Randić index, and certain open gaps in the theory of extremal unicyclic graphs are filled (some open problems are provided). We use computational software to calculate the Randić index for the chemical trees up to order 7 and use the statistical (linear regression) analysis to discuss the various applications of the Randić index with the physical properties of drugs on the said chemical trees. We show that the Randić index is better correlated with the heat of vaporization for these alkanes.
MSC:
05C07; 05C15
1. Introduction
Consider a simple graph with a set of vertices and a set of edges . The degree of a vertex u, denoted by , is the number of edges incident with u. The neighbor set of u, denoted by , is the set of all vertices that are connected to u by an edge, and the maximum degree of vertices in G is denoted by . denotes the graph that is obtained from G by adding an edge , and denotes the subgraph of G that is obtained by deleting an edge from G. Consider the path and cycle graphs on vertices, denoted by and , respectively. To attach to a vertex u in G means to add an edge from u and any endpoint of . For , we attach a vertex of degree 1 to u. denotes the neighborhood of
In [1], Randić introduced one of the most widely used molecular descriptors (topological index) in structure–activity and structure–property relationship studies, which was called the Randić index [2,3,4,5]. Moreover, the product-connectivity index is another way to refer to this index, and it is defined as follows:
The authors in [6] generalized by introducing the general Randić index as
where is real.
Determining the upper and lower bounds for the general Randić index and the characterization of the corresponding extremal graphs have received increasing attention. Several results related to extremal graphs have been published for various topological indices among the different classes of graphs, since for general graphs extremal problems are very hard. Most of the time, these extremal problems are studied for classes of graphs so that a deep analysis can be carried out and thereby some extremal families with respect to a topological index can be identified. In this study, we consider the general Randić index for the class of unicyclic graphs with order n and fix their invariants like the maximum degree.
In [7,8], two variants of were studied along with lower and upper bounds for connected graphs, trees, and chemical trees. Also, in [9], Li and Yang found the maximum and the minimum general Randić indices of graphs for any value of . Researchers have recently made progress on several open problems related to the general Randić index. Rada and Cruz [10] studied an unsolved case, while Cavers et al. [11] established a relationship between the general Randić index and the normalized eigenvalues of the Laplacian matrix of a graph. Guji and Vumar [12] determined, for , the maximum general Randić index of bicyclic graphs, and in [13] the minimum was found for chemical trees with a given number of pendent vertices for any . Hu et al. [14,15] determined the maximum and minimum general Randić indices of trees for certain ranges of . An extensive survey of the Randi index was carried out by Li and Shi in [16]. Dalfó [17] obtained interesting results related to the Randić of graphs. Recently, some new results related to the Randić index were given in [18]. Zhand and Wu [19] and Liang and Wu [20] obtained results for the Randić index of line graphs. The Randić index and the Randić energy of graphs is a well studied branch of theory (see the recently published [21] and the references cited therein).
For the n-vertex trees with pendent vertices with , Liu et al. [22] found bounds for . Cui and Zhong [23] determined the maximum general Randić indices of n-vertex trees and chemical trees with k pendent vertices for and , where . Liu et al. [24] characterized the trees with extremal for trees with the maximum degree. See [25,26,27,28,29,30,31,32] for more mathematical properties of the general Randić index. There are several other well-known indices and spectral invariants like in [33,34].
In this paper, we start with some lemmas and use them to determine the maximum general Randić index for among all n-vertex unicyclic graphs with a fixed maximum degree and characterize the extremal graphs attaining the bounds (see Theorem 1). Moreover, in Theorem 2, we find the maximum and the second maximum general Randić index for among all n-vertex unicyclic graphs, where is a solution of the equation , and some unique maximal graphs are identified with respect the mentioned invariants. At the end of Section 2, some open problems are given. In Section 3, we carry out QSPR/QSAR analysis of the Randić index and its linear regression analysis, with the help of computational software. We were able to successfully show that the Randić index is better correlated with the heat of vaporization for these chemical tress of orders up to 7 (alkanes).
2. Unicyclic Graphs with Maximum General Randić Index
Next, we give some lemmas, which will be applied in the main results.
Lemma 1.
Consider a connected graph Q of order . If and are the graphs obtained from Q by attaching and to and attaching u to a path , respectively, where a and b are positive integers, then
where is a solution of the equation .
Proof.
since , , for and .
In fact, let ; then,
and
if and only if . We note that , , , and . So, , and , which implies the result.
Let and . We have three cases.
- (i)
- If , then
- (ii)
- If and , then
- (iii)
- If , then
Clearly, the function is decreasing, since , and if and only if , and , for and . Thus,
provided . So, we have
for .
The proof is complete. □
Lemma 2.
Consider a connected graph M such that . Let be a degree 2 vertex with its two neighbors and . If , is the graph obtained from M by attaching a path to u and , then
where is a solution of the equation .
Proof.
Note that is decreasing for and .
If , i.e., , then, for , we have
If , i.e., , then, for , we have
as , for . □
Next, we consider the maximum of unicyclic graphs with a given maximum degree.
For , let be a class of simple unicyclic graphs with n vertices and a maximum degree of . Specifically, for .
For , denotes the unicyclic graph obtained by attaching paths of a length of at least one to a vertex of and pendant vertices.
In the following, we will determine the maximum value of of graphs in along with identifying corresponding extremal graphs. Consequently, for , we find the unicyclic graph with the first and the second maximum .
Theorem 1.
Let be a unicyclic graph and . Then,
with equality if and only if for , and G is a unicyclic graph obtained from a cycle by attaching paths of a length of at least one to a vertex for .
Proof.
Let G be a graph that belongs to with a maximum general Randić index, v be a vertex in G with degree , and C be the unique cycle of G.
The case is trivial since in this case . In the following, we assume that .
If and there exists a vertex of degree 3 outside the cycle C, then Lemma 1 implies that we can obtain a graph that belongs to with a greater general Randić index, and this gives a contradiction. If C has at least two vertices of degree 3, then, using Lemma 2, the same conclusion is obtained. Thus, the unique vertex of degree 3 in G is .
Now, if v has a neighbor of degree 1, then
But if v has no neighbors of degree 1, then
By subtracting the two values, we obtain
Hence, is a graph obtained by adding a vertex, which is a pendant to (triangle) for , and G is a graph that is obtained by attaching a cycle for to a path of a length of at least 2.
Let . Similar to the case where , it can be concluded that v is the unique vertex with the maximum degree in G. We will show that . Otherwise, consider a vertex w on the cycle C where is equal to . If there is a vertex different from v of a degree greater than 2 outside C, or if there is a vertex different from w of a degree greater than 2 on C, then, using Lemmas 1 and 2, we can obtain a graph in with a greater , and this leads to a contradiction. Therefore, w and v are vertices of a degree higher than 2 in G. Moreover, and . Now, consider the path connecting v and w, say Q, and let be the neighbors of v outside Q and for . Then, . Otherwise, we can obtain a graph in with a higher using Lemma 1. Now, let
Then, , , , and
since the function is strictly decreasing for for .
Note that . Using Lemma 1 again, we can obtain a graph with and such that , a contradiction. Hence, v is on C.
If a vertex of a degree higher than 2 exists outside cycle C or a vertex different from v of a degree greater than 2 exists on C, then, using the same proof as before, we can obtain a graph that belongs to with a greater general Randić index, and this is a contradiction. Therefore, G is obtained from C by attaching v to paths. Now, suppose that v has k neighbors of degree 2. Thus, . When , i.e., , we have . When , that is, , we have . From the definition of the general Randić index,
As the function is strictly increasing for with , we have and
It follows that
with equality if and only if ; that is, for , and . G is unicyclic and obtained by adding paths of a length of at least one to a common vertex on C for . □
The following result characterizes the extremal graphs with the first and the second maximum general Randić index for among all n-vertex unicyclic graphs.
Theorem 2.
Let . Then, for all unicyclic graphs with at least four vertices, we have the following:
(i) is a unique graph attaining the maximum , and ;
(ii) In the case where , then is a unique graph with the second largest , and ;
(iii) For , the graphs with the second maximum are the graphs that are obtained by attaching a vertex on a cycle to a path of a length of at least one, and their general Randić indices are equal to .
Proof.
For , there are only two unicyclic graphs and such that
The result is true.
Now, let and G be an n-vertex unicyclic graph with the maximum degree , where .
Let .
If , then using Theorem 3,
since , and the function is strictly decreasing for and .
If , then, using Theorem 3, we have with equality if G is a unicyclic graph that is obtained by attaching a unique vertex of a cycle to paths of a length of at least one.
In what follows, we shall prove that is strictly decreasing for by showing that . Therefore, we calculate
Let
Then,
i.e., is strictly decreasing for , and this implies that .
So,
Consider . We have , and is strictly convex. Since , we have for , and for every . Hence, is strictly decreasing for .
It follows that
and
Thus, among all n-vertex simple unicylic graphs, the maximum general Randić index is and the corresponding extremal graph is . Moreover, the second maximum general Randić index is , and the corresponding extremal graphs are these graphs with the maximum among all n-vertex unicyclic graphs with , i.e., n-vertex graphs that are obtained by attaching a vertex on a cycle to a path of a length of at least one. □
We know that Li et al. [29] found, for , the graphs with the maximum among all n-vertex unicyclic graphs, and Liu et al. [24] characterized the trees with maximal and minimal , respectively, among all trees with . In connection with these results, the following problems are still open:
Problem 1.
For , determine the graphs with the maximum among all unicyclic graphs with n vertices.
Problem 2.
Characterize the graphs with minimal and maximal , respectively, among all unicyclic graphs with a given Δ.
Problem 3.
Characterize the graphs with minimal and maximal , respectively, among all bicyclic graphs with a given Δ, more generally, for c-cyclic graphs.
3. QSPR/QSAR of Randić Index
Topological indices are used for translating the chemical properties into numbers that can be applied for statistical analysis like correlation with physical properties in QSPR/QSAR (quantitative structure–property/activity relationship) studies. In recent years, the topological indices have become one of the major research topics in QSPR and QSAR analysis. For some applications of topological indices, see [33,35,36,37,38,39]. The use of graph entities in QSPR/QSAR analysis has attracted attacted many researchers in recent years. Topological indices have a wide range of application in non-empirical quantitative structure–property relationships (QSPRs) and quantitative structure–activity relationships (QSARs) like in [35,38,40,41,42]. These chemical properties are studied since they have a direct impact on drug transits and bioactivity in the human body. Thus, with the help of topological indices, we can design better drugs.
We will use the Randić index for modeling physical properties of 67 alkanes (n-butanes to nonanes). The well-known physical properties are molar volumes (mv’s) at 20 C, heats of vaporization (hv’s) at 25 C, molar refractions (mr’s) at 20 C, the boiling point (bp), and surface tensions (st’s) at 20 C. The data are taken from [39] (see also [43]). The values of were calculated using the AutoGraphiX III system [44].
We consider the following linear regression model:
where is a physical property and is a topological index. Using (1), we carry out the analysis for the Randić index with the bp, mv’s, mr’s, hv’s, and st’s.
The following table gives the correlation of the Randić index with the boiling point (bp), the molar volumes (mv’s) at 20 C, the molar refractions (mr’s) at 20 C, the heats of vaporization (hv’s) at 25 C, and the surface tensions (st’s) 20 C for chemical graphs up to order 7.
From Table 1, we see that all the physical properties are very well correlated with the Randić index . Heats of vaporization (hv’s) at 25 C give the best correlation with . This gives us a good sign for modeling physical properties of alkanes with the Randić index.

Table 1.
Correlation of with bp, mv, mr, hv, and st for chemical graphs up to order .
The Table 2 gives the (coefficient of determination) of with the bp, mv, mr, hv, and st for chemical graphs up to order 7.

Table 2.
Correlation of with bp, mv, mr, hv, and st for chemical graphs up to order .
The best coefficient of determination for is achieved by heats of vaporization (hv’s).
Figure 1 shows the linear regression between and the boiling point (bp), with the rounded equation
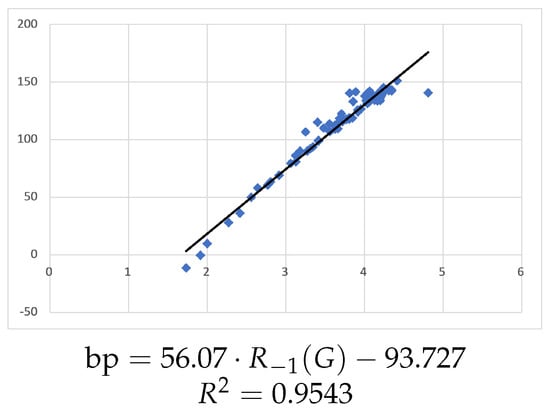
Figure 1.
Linear regression for bp vs. .
Figure 2 shows the linear regression between and the molar volumes (mv’s), with the rounded equation
The linear regression illustrates that the correlation of the boiling point is better with , where , than with molar volumes, where .
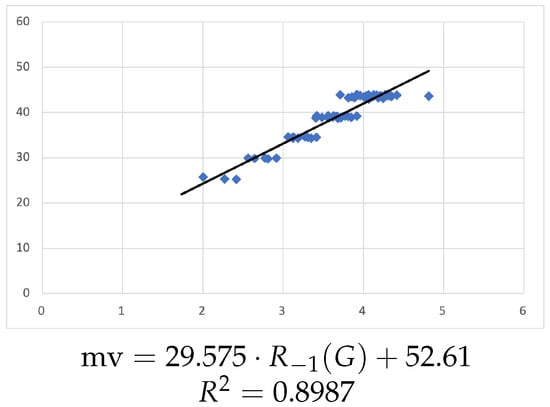
Figure 2.
Linear regression for mv vs. .
Figure 3 shows the linear regression between and the molar refractions (mr’s), with the rounded equation
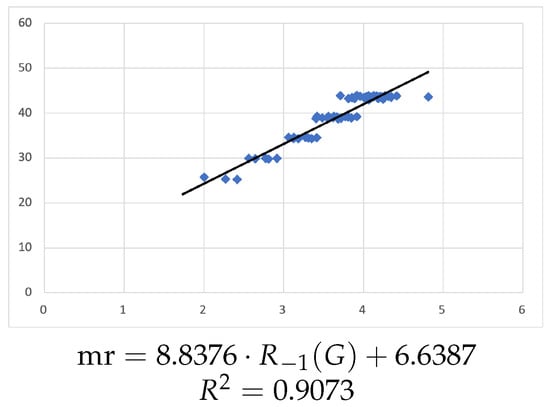
Figure 3.
Linear regression for mr vs. .
Figure 4 shows the linear regression between and the heats of vaporization (hv’s), with the rounded equation
The linear regression illustrates that the correlation of the heats of vaporization is better with , where , than with molar refractions, where .
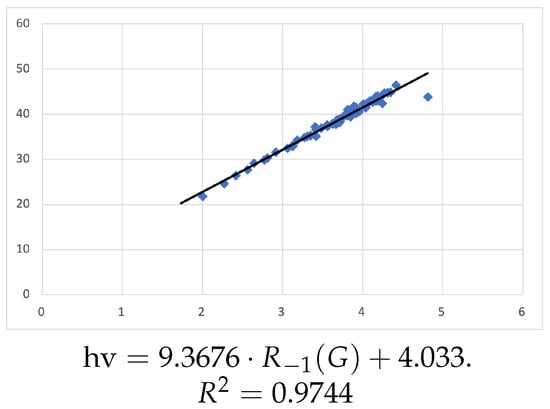
Figure 4.
Linear regression for hv vs. .
Figure 5 shows the linear regression between and the surface tension (st), with the rounded equation
and .
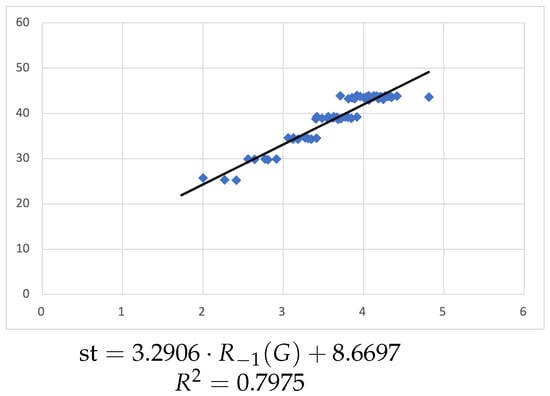
Figure 5.
Linear regression for st vs. .
The overall significant observation is that the Randić index gives a very high correlation with the heats of vaporization of alkanes, and thereby it will help in designing better models for the applicability of with such physical properties.
4. Conclusions
In this paper, some extremal results are presented that are related to the general Randić index among classes of unicyclic graphs in terms of different parameters, like the maximum degree and order n of the graph. In addition, we find the maximum and the second maximum general Randić index for for classes of unicyclic graphs with Furthermore, we carried out statistical analysis of the Randić index with physical properties of chemical graphs of alkanes up to order We observed that the Randić index is highly correlated with the heats of vaporization of alkanes. A similar type of analysis can be studied for the general Randić index for the class of bicyclic graphs and for c-cyclic graphs in general, though we need some more advanced tools and techniques for handling extremal problems related to the general Randić index.
Author Contributions
Conceptualization, A.A. and M.I.; software, M.I.; writing—original draft preparation, A.A. and M.I.; writing—review and editing, A.A. and M.I.; formal analysis, A.A. and M.I.; validation, A.A. and M.I.; methodology, A.A. and M.I.; investigation, A.A. and M.I.; resources, A.A. and M.I.; project administration, A.A. and M.I.; funding acquisition, A.A. All authors have read and agreed to the published version of this manuscript.
Funding
This research work was funded by Institutional Fund Projects under grant no. (IFPDP-151-22). Therefore, the authors gratefully acknowledge technical and financial support from the Ministry of Education and Deanship of Scientific Research (DSR), King Abdulaziz University (KAU), Jeddah, Saudi Arabia.
Data Availability Statement
The data used to support the findings of this study are available within this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Randić, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Garcia-Domenech, R.; Gálvez, J.; de Julixaxn-Ortiz, J.V.; Pogliani, L. Some new trends in chemical graph theory. Chem. Rev. 2008, 108, 1127–1169. [Google Scholar] [PubMed]
- Gutman, I.; Furtula, B. (Eds.) Recent Results in the Theory of Randić Index; University Kragujevac: Kragujevac, Serbia, 2008. [Google Scholar]
- Kier, L.B.; Hall, L.H. Molecular Connectivity in Structure-Activity Analysis; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Li, X.; Gutman, I. Mathematical Aspects of Randić-Type Molecular Structure Descriptors; University Kragujevac: Kragujevac, Serbia, 2006. [Google Scholar]
- Bollobás, B.; Erdos, P. Graphs of extremal weights. Ars Combin. 1998, 50, 225–233. [Google Scholar] [CrossRef]
- Knor, M.; Lužar, B.; Škrekovski, R. Sandwiching the (generalized) Randić index. Discret. Appl. Math. 2015, 181, 160–166. [Google Scholar] [CrossRef]
- Shi, Y. Note on two generalizations of the Randić index. Appl. Math. Comput. 2015, 265, 1019–1025. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y. Sharp bounds for the general Randić index. MATCH Commun. Math. Comput. Chem. 2004, 51, 155–166. [Google Scholar]
- Rada, J.; Cruz, R. Vertex-degree-based topological indices over graphs. MATCH Commun. Math. Comput. Chem. 2014, 72, 603–616. [Google Scholar]
- Cavers, M.; Fallat, S.; Kirkland, S. On the normalized Laplacian energy and general Randić index R−1 of graphs. Linear Algebra Appl. 2010, 433, 172–190. [Google Scholar] [CrossRef]
- Guji, R.; Vumar, E. Bicyclic graphs with maximum general Randić index. MATCH Commun. Math. Comput. Chem. 2007, 58, 683–697. [Google Scholar]
- Li, X.; Shi, Y.; Zhong, L. Minimum general Randić index on chemical trees with given order and number of pendent vertices. MATCH Commun. Math. Comput. Chem. 2008, 60, 539–554. [Google Scholar]
- Hu, Y.; Li, X.; Yuan, Y. Trees with minimum general Randić index. MATCH Commun. Math. Comput. Chem. 2004, 52, 119–128. [Google Scholar]
- Hu, Y.; Li, X.; Yuan, Y. Trees with maximum general Randić index. MATCH Commun. Math. Comput. Chem. 2004, 52, 129–146. [Google Scholar]
- Li, X.; Shi, Y. A survey on the Randi index. MATCH Commun. Math. Comput. Chem. 2008, 59, 127–156. [Google Scholar]
- Dalfó, C. On the Randić index of graphs. Discret. Math. 2019, 342, 2792–2796. [Google Scholar] [CrossRef]
- Atapour, M.; Jahanbani, A.; Khoeilar, R. New bounds for the Randi index of graphs. J. Math. 2021, 2021, 9938406. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, B. Randi index of a line graph. Axioms 2022, 11, 210. [Google Scholar] [CrossRef]
- Liang, Y.; Wu, B.H. General Randić index of a chain graph and its line graph. Open Math. 2023, 21, 20220611. [Google Scholar] [CrossRef]
- Rather, B.A.; Pirzada, S.; Imran, M.; Chishti, T.A. On Randić eigenvalues of zero divisor graphs of n. Commun. Comb. Optim. 2023, 8, 103–113. [Google Scholar]
- Liu, H.; Lu, M.; Tian, F. Trees of extremal connectivity index. Discret. Appl. Math. 2006, 154, 106–119. [Google Scholar] [CrossRef]
- Cui, Q.; Zhong, L. The general Randić index of trees with given number of pendent vertices. Appl. Math. Comput. 2017, 302, 111–121. [Google Scholar]
- Liu, H.; Yan, X.; Yan, Z. Bounds on the general Randić index of trees with a given maximum degree. MATCH Commun. Math. Comput. Chem. 2007, 58, 155–166. [Google Scholar]
- Chen, X.; Qian, J. Conjugated trees with minimum general Randić index. Discret. Appl. Math. 2009, 157, 1379–1386. [Google Scholar]
- Fischermann, M.; Hoffmann, A.; Rautenbach, D.; Volkmann, L. A linear-programming approach to the generalized Randić index. Discret. Appl. Math. 2003, 128, 375–385. [Google Scholar]
- Li, F.; Ye, Q. The general connectivity indices of fluoranthene-type benzenoid systems. Appl. Math. Comput. 2016, 273, 897–911. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Zhong, L. Trees with a given order and matching number that have maximum general Randić index. Discret. Math. 2010, 310, 2249–2257. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Shi, Y.; Xu, T. Unicyclic graphs with maximum general Randić index for η > 0. MATCH Commun. Math. Comput. Chem. 2006, 56, 557–570. [Google Scholar]
- Li, X.; Zheng, J. Extremal chemical trees with minimum or maximum general Randić index. MATCH Commun. Math. Comput. Chem. 2006, 55, 381–390. [Google Scholar]
- Vukičević, D. Which generalized Randić indices are suitable measures of molecular branching? Discret. Appl. Math. 2010, 158, 2056–2065. [Google Scholar] [CrossRef][Green Version]
- Zhong, L. General Randić index on trees with a given order and diameter. MATCH Commun. Math. Comput. Chem. 2009, 62, 177–187. [Google Scholar]
- Rather, B.A.; Aouchiche, M.; Imran, M.; Pirzada, S. On arithmetic–geometric eigenvalues of graphs. Main Group Metal Chem. 2022, 45, 111–123. [Google Scholar] [CrossRef]
- Rather, B.A.; Imran, M. A note on the energy and Sombor energy of graphs. MATCH Commun. Math. Comput. Chem. 2023, 89, 467–477. [Google Scholar] [CrossRef]
- Altassan, A.; Imran, M.; Rather, B.A. On ABC energy and its application to anticancer drugs. Aims Math. 2023, 8, 21668–21682. [Google Scholar]
- Altassan, A.; Rather, B.A.; Imran, M. Inverse sum indeg index (energy) with application as anticancer drugs. Mathematics 2022, 10, 4749. [Google Scholar] [CrossRef]
- Aouchiche, M.; Ganesan, V. Adjusting geometric-arithmetic index to estimate boiling point. MATCH Commun. Math. Comput. Chem. 2020, 84, 483–497. [Google Scholar]
- Hosamani, S.M.; Kulkarni, B.B.; Boli, R.G.; Gadag, V.M. QSPR analysis of certain graph theoretical matrices and their corresponding energy. Appl. Math. Nonlinear Sci. 2017, 2, 131–150. [Google Scholar] [CrossRef]
- Hosamani, S.; Perigida, D.; Jamagoud, S.; Maled, Y.; Gavade, S. QSPR Analysis of Certain Degree Based Topological Indices. J. Stat. Appl. Pro. 2017, 6, 361–371. [Google Scholar] [CrossRef]
- Kirmani, S.A.K.; Ali, P.; Azam, F.; Alvi, P.A. On Ve-Degree and Ev-Degree Topological Properties of Hyaluronic Acid? Anticancer Drug Conjugates with QSPR. J. Chem. 2021, 2021, 3860856. [Google Scholar] [CrossRef]
- Nasir, S.; Awan, N.U.H.; Farooq, F.B.; Parveen, S. Topological indices of novel drugs used in blood cancer treatment and its QSPR modelling. AIMS Math. 2022, 7, 11829–11850. [Google Scholar] [CrossRef]
- Shanmukha, M.C.; Basavarajappa, N.S.; Shilpa, K.C.; Usha, A. Degree-based topological indices on anticancer drugs with QSPR analysis. Heliyon 2020, 6, e04235. [Google Scholar] [CrossRef]
- Rücker, G.; Rxuxcker, C. On topological indices, boiling points and cycloalkanes. J. Chem. Inf. Comput. Sci. 1999, 39, 788–802. [Google Scholar] [CrossRef]
- Caporossi, G. Variable neighborhood search for extremal vertices: The AutoGraphiX-III system. Comput. Oper. Res. 2017, 78, 431–438. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).