Abstract
We analyze a mathematical model of the effects of soil contamination by heavy metals, which is expressed as systems of nonlinear ordinary differential equations (ODEs). The model is based on the symmetry dynamics of heavy metals soil–plant interactions. We aim to study this symmetric process and its long-term behavior, as well as to discuss the role of two crucial parameters, namely the flux of the hydrogen protons to the soil in rainfall events , and the available water for roots . We study the boundedness and positivity of the solution. Further, a parameter identification analysis of the model is presented. Numerical experiments with synthetic and realistic data of honeybee population are discussed.
Keywords:
symmetry of the heavy metals soil–plant dynamics; existence of nonnegative solutions; time-dependent parameter identification analysis MSC:
34A12; 34A55; 65L09; 82D35
1. Introduction
Heavy metal elements are inherently present in both soils and various liquids. However, the more concerning issue arises from heavy metal contamination, which is introduced into the environment through human-induced activities. These activities include industrial production processes, household waste, and other waste materials. When heavy metals are present in the soil in elevated levels, they disrupt the balance of natural land ecosystems due to their toxicity and inability to degrade. This is documented in several studies [1,2,3,4].
In soils contaminated with heavy metals, the growth of plants can be negatively affected as they absorb these metals. Some species of plants have the capability to accumulate significant quantities of heavy metals without apparent signs of damage. In a symmetric way, this poses a potential threat to both wildlife and humans [1,2,3,5]. The uptake of heavy metals by plants grown in polluted soils is a significant concern for human health, as these metals can enter the food chain, leading to potential health risks [1,2,3,6].
The process of bioaccumulation of heavy metals is akin to a complex system, impacting various physiological aspects including plant growth, lifespan, nutritional value, biomass accumulation, and the transfer or movement of these metals within the organism. The mathematical model introduced in this paper considers various influencing factors, emphasizing the role of environmental elements in plant life. Such models play a pivotal role in enhancing the sustainability of experimental research related to environmental and ecological systems. They help in reducing expenses, shortening project timelines, and offer insights into the bioaccumulation of pollutants in the environment and other areas.
Mathematical modeling has increasingly become a vital tool across numerous scientific disciplines in recent years. With the escalating costs of experimental research, in a symmetric way there has been a growing reliance on mathematical models as a more cost-effective approach to advance research. This trend has been ongoing for several decades, occasionally leading to forced attempts to fit real-world phenomena into theoretical frameworks, resulting in some failures at certain levels of complexity. However, these models have been effectively used to describe and optimize biological processes, like plant growth and development. They are also employed in simulating intricate environmental processes, such as bioremediation.
Numerical simulation techniques and statistical modeling employ advanced tools capable of creating highly complex mathematical models. Nevertheless, these models require a degree of experimental validation before they can be effectively utilized. The complexity inherent in these models often necessitates costly and elaborate experiments for their validation and further development.
In the realm of biomathematics, the mathematical modeling of biological materials often seeks to enhance or optimize various processes by utilizing economic parameters as key performance indicators. This approach primarily aids in the management of these processes, which can, in turn, partially fund scientific research. From this perspective, practices like plant cultivation or animal husbandry typically terminate the life cycle of these biological entities at an age deemed most suitable for harvest. However, the continuation of life in plants and animals beyond this predetermined age, and the effects of aging on them, have seldom been a subject of extensive study.
This background underlines our efforts to develop a mathematical model for the bioaccumulation of heavy metals in plants, and to utilize this model in the development and refinement of phytoremediation techniques. The accumulation of heavy metals in plants (and animals) has become increasingly prevalent in the post-industrial world. Bioremediation, a field that has evolved through research in biology and environmental science, has emerged as one of humanity’s solutions to mitigate the environmental damage caused by industrial activities.
The purpose of mathematical modeling in this context is to identify the underlying mechanisms of heavy metal bioaccumulation and to explore strategies to either limit or enhance the processes of bioaccumulation and bioremediation conducted by plants in contaminated soils. Researchers are actively searching for methods, techniques, or resources that could boost the efficiency of heavy metal absorption from polluted soils through phytoremediation. They aim to maximize the use of these plants, whose ability to absorb heavy metals, depending on the species of plants and the types of metals, may surpass known maximum absorption capacities.
As stated before, the increased application of mathematical models has become a vital tool for understanding complex systems. These models can enhance the significance of experimental research, streamline development processes, lower costs, and provide deeper insight into the inner workings of the system. The growing reliance on modeling has led to numerous advancements but also some setbacks. Given the inherent complexity of reality, the models designed to represent it have also become sophisticated. However, complexity in a model does not automatically guarantee accuracy, particularly if it lacks proper calibration. It is important to note that the more complex a model is, the more elaborate and sometimes impractical its calibration process may become. Therefore, a balance needs to be struck between the model’s complexity and its practical robustness in a symmetric form.
Despite numerous experimental studies conducted to investigate the harmful effects of heavy metal accumulation in plants, there has been relatively little focus on developing mathematically-based models that can broadly correlate the concentration of heavy metals in soil’s liquid phase with the levels found in plants. In this study, we have adopted a model that delineates this relationship and have corroborated it using experimental results that have been recently published.
In [2], a mathematical model is introduced that effectively simulates the relationship between soil temperature and the concentration of Zinc (Zn), along with its subsequent bioaccumulation in lettuce (Lactuca sativa L.). This model also examines the response of lettuce to Zn contamination. The core findings of this paper include three distinct mathematical models, all founded on systems of ordinary differential equations, and their validation through comparison with existing data.
Honey bees, known for their wide-ranging foraging habits, are capable of gathering contaminants from their environment, as detailed in various studies [7,8,9,10,11,12]. As they collect plant materials like nectar, pollen, and propolis and bring them back to their hives, they inadvertently accumulate substantial amounts of toxic contaminants. The paper discusses specific instances of metal concentrations, such as cadmium, copper, lead, and selenium, found in bee products across the globe [7,8,11,12,13].
Furthermore, the article delves into the numerical modeling and analysis of the transfer of aluminum in rape, a primary food source for honey bees, providing tangible results. It also emphasizes the importance of studying the reaction kinetics of honey bee populations as a critical phase in modeling the dynamics of honey bee behavior within the hive. This comprehensive approach aids in better understanding the intricate interactions and responses of honey bees to environmental contaminants, particularly within the context of their hive behavior.
In our paper [14], we have discussed the heavy metals soil–plant transfer, while our focus was the concentration of lead in the soil and its bioaccumulation in rape and sunflower. We have presented an analysis to recover five constant parameters in the fundamental model - upon finite time measurements of the metal concentrations.
In the present work we are focused on the recovery of the rate at which the hydrogen protons are introduced to the soil during rainfall events and the amount of water accessible to plant roots. The rest of the paper is organized as follows. In Section 2, we introduce the mathematical model. Section 3 presents main analytical results, concerning the model solution. The time-dependent coefficient inverse problem is formulated and solved in Section 4. The numerical simulations are presented in Section 5, while the last section concludes the paper.
2. Model Development
Initially, the focus of study was on forest decline due to concerns about its potential for sudden and significant collapse, both in scale and impact. However, recent research suggests that the same model used for trees could be applicable to non-arboreal plants like lettuce and rape (Brassica napus). This approach conceptualizes plants as a series of somewhat independent, repeating units, including branches, leaves, and flowers. This framework allows for modeling the interaction of these plants with contaminants in a manner akin to that of trees.
Central to this model is the general reaction that underpins the transfer of any heavy metal (Me) into plants, particularly addressing how these metals maintain their mobility in soils with standard pH levels. The reaction can be represented by the following symmetric chemical equation (please see [3]):
where n denotes the ion charge of the metal.
Me(OH)n + nH+ ⟷ Men+ + nH2O,
This equation crucially illustrates the balance and the symmetry between heavy metal hydroxides and their corresponding ionic forms in the presence of hydrogen ions, a key process in understanding the bioavailability of heavy metals to plants in various soil conditions.
As described earlier, we adopt the general mathematical model, initially suggested by [3]:
where
T is the biomass of plant (kg/m2),
S is the concentration of Men+ in plant (mg/kg),
A is the concentration of Men+ in the soil (mg/L),
H is the concentration of H+ in the soil solution (mg/L), respectively [14].
In the model (1)–(6), the variable t represents time (in years), while denotes the rate at which protons are introduced to the soil during rainfall events, expressed in milligrams per square meter per year (mg/(m2·year)). The parameter signifies the amount of water accessible to plant roots, measured in millimeters (mm). The coefficients , , and correspond to the rates of absorption (in liters per kilogram per year, L/(kg·year)), leakage (per year, 1/year), and reaction (per year, 1/year), respectively.
The function is utilized to model the net growth of biomass, while represents the function that accounts for plant mortality or metabolic inefficiency caused by the concentration of Men+ within the plants.
The initial version of the model (1)–(6) primarily dealt with the detrimental impact of aluminum ions, which become more active when soil pH drops below 4.2, as indicated in [3]. Within the range typically referred to as the aluminum buffer zone, the predominant reaction (as a special case) is expressed as follows:
Al(OH)3 + 3H+ ⟷ Al3+ + 3H2O.
Following the principles of chemical kinetics, Equations (3) (excluding the third term) and (4) are derived directly. The denominator of the coefficient in these equations is attributed to the atomic weight of aluminum, which is 27 atomic mass units (u), divided by the aluminum ion charge, which is 3.
Equation (1) is formulated considering the net primary production per unit of biomass, reduced by the mortality rate of the plant, , which is typically considered constant when excluding the effects of acidification. However, when accounting for the toxicity of aluminum, exhibits a sharp increase once S, the concentration of aluminum, surpasses a specific threshold.
Subsequently, the soil submodel incorporates the concentration of aluminum S that is immobilized within the tree biomass. The behavior of this compartment is detailed in (2), where symbolizes the uptake rate of aluminum per unit biomass. Naturally, this necessitates a revision of the aluminum balance in the soil. In Equation (3), an additional term is introduced to account for the aluminum absorption by trees.
The model (1)–(6) suggests that plant growth net rate, under the assumption that it escalates with T, is defined in the study [3] by the function
where the coefficients (1/year) and (m2/kg) are fixed constants. Moreover, a bimodal growth function is proposed in [6] as
with r representing the growth rate and k the carrying capacity.
In the study [3], the formula for metabolic inefficiency or potential mortality is expressed as
where (1/year), (mg/kg), (1/year), and . The critical survival threshold is at . It is important to note that plants cannot endure up to unless until that point. This would imply that plants are completely unaffected by any concentration below e, a scenario that is not typically observed in reality.
3. Mathematical Analysis
In this section we show that model (1)–(4) is mathematically and physically well-posed in a bounded domain .
Theorem 1.
If the initial data , then the solution of the system (1)–(4) are non-negative for all , while , , , and are bounded on each finite interval . Moreover, the feasible compact is given by
where and , and are defined accordingly.
Proof.
From the fourth Equation (4), we have
Therefore, .
The key of this study is the first Equation (1). First, let us note the cases behaviour of function . From (6), we have
which leads to the cases
- when , where ,
- when ,
- when .
In case 1, we have and then
Next,
Hence,
Note that is bounded for all if , otherwise it is bounded on a finite interval .
In case 2, we have and then
Next,
and then
Therefore, since , is bounded on each finite interval .
In case 3 the situation is similar, we can confirm that is bounded on a finite interval and .
Further, solving the Equation (3), we get
Then
which implies that is bounded for all .
Finally, from Equation (2), we find
Using the above established properties for the functions , one could obtain
which implies the boundedness of for all . □
4. Parameter Identification
4.1. Formulation of the Inverse Problem
The mathematical functions , , , and comply with what is known as the direct problem when the values of the functions W and p are predetermined. However, in practical scenarios, these functions W and p are typically unknown, as they cannot be directly measured, and thus require determination [14]. Once we accurately estimate these values, the model (1)–(4) becomes applicable for further analysis and predictions.
The primary challenge lies in identifying the correct values for the time-dependent parameter set in relation to the soil–plant transfer processes. This is especially relevant when the measurable system functions are available at certain time intervals, expressed as
This process of deducing the parameter is termed an inverse modeling problem. It involves the fine-tuning of a mathematical model’s parameters to align with the empirical data observed.
The data points specified in (7) are referred to as point observations. The task of determining the parameter values generally involves minimizing a functional, represented as
In this minimization process, the objective is to adjust the model such that it most accurately reflects the observed data, thus enhancing the model’s predictive and analytical accuracy for the specific infection being studied.
4.2. Numerical Solution to the Inverse Problem
In this subsection, we delve into the computational algorithm designed for the numerical resolution of inverse problems as defined by (1)–(4), (7) in a detailed manner.
For temporal reference points, we adopt distinct notations. The time mesh, denoted as and described in (8), is illustrated in Figure 1.

Figure 1.
The mesh for .
Here, represents each specific time point where the values of the system functions S, A and H are ascertainable. In the real world, the time instances, at which data is collected, are not standardized. However, the probes are expensive and measuring is performed as rarely as possible. The proposed algorithm could work with scarce data, as we will demonstrate later. For computational convenience, it is beneficial for the observation points to align with the discretization nodes. If this is not a case, it is not a problem—then, a simple interpolation might be of help. However, we have the flexibility to choose a mesh as fine as needed, as our algorithm does not necessitate data at every single node (the observation points form a subset of these discrete time nodes).
The algorithm we propose is designed to reconstruct the unknown dynamic parameters as piecewise linear functions over time in a symmetric form. This reconstruction is carried out progressively. Iterating over the measurements would result in functions with smooth undulations but at a significant computational expense. Conversely, using minimal measurements, like one or two points, quickly leads to a mere linear representation. Therefore, we strike a balance between the accuracy of the fit and computational efficiency.
For this purpose, we introduce ‘main’ observations, labeled , as shown in (8) and Figure 1. In practical terms, it is advantageous to space these main observations at intervals of two to four weeks. For the sake of clarity in this explanation, we assume a constant time step and equal values for , and , denoted as K.
In the context of observation definition (7), the indices correspond to the indices in the following manner:
where the numbers , is a subset of .
This correspondence in a symmetric manner ensures that the primary observations are effectively integrated into the algorithm, enabling a more efficient and accurate reconstruction of the dynamic parameters.
Earlier, we described the process of stepwise recovery of the unknown parameters and , using k as an iterator. At each iteration k, information available up to is utilized. There are many methods for parameter identification; see, e.g., [15,16]. The minimization procedure is of least-square type [17,18]. The computational algorithm unfolds as follows:
Step 1.1: Begin by minimizing the cost function:
At this juncture, represents the optimal values that minimize . It is presumed here that the parameter functions remain constant in the interval to avoid the ambiguity associated with a local minimum that might arise if a linear function were employed. The algorithm is structured as a predictor–corrector type, meaning that the eventual coefficient values in will be expressed as linear functions of time, an outcome to be realized in the subsequent step.
Step 1.2: The current parameter values are set as follows:
Step 2.1: The next phase involves minimizing another cost function:
This progression of steps is designed to refine the parameter estimation, ensuring a more accurate representation and understanding of the system dynamics. The algorithm’s iterative nature allows for continuous improvement of parameter accuracy over successive steps.
In case the optimal values minimizing are identified as , we then presume these parameters to exhibit linear behavior within the interval . To construct these linear functions, specific rules are employed: is set to and to , where is defined as the midpoint between and for . Similar rules are applied to . More precisely, to calculate these with symmetry, we use
It is important to note that the adjustments made in this step impact the entire interval from the first step.
Step 2.2: The parameters derived at this stage are defined as
The following is then iteratively applied from to .
Step k.1: The following step involves minimizing the cost functional:
where is chosen so that is the nearest observation point to .
If the minimum values of are , we again assume linear behavior for these coefficients in the interval . The rules dictate that equals and equals , and this applies equally to .
The calculation of the coefficients for each step involves the following equations with symmetry:
In this stage, the corrective aspect of the process impacts primarily the most recent half-step interval .
Step k.2: The parameters ascertained at this stage are defined as follows:
The final output of the algorithm is synthesized in the following manner with symmetry.
Step (K + 1): The final computation is carried out as
This results in the reconstruction of the parameters as time-variant piecewise linear functions within the interval .
At every iterative step, the nonlinear estimators are short vectors whose length is contingent on the number of parameters being recovered (in this case, there are two). This compactness contributes to the algorithm’s rapid convergence. The efficiency and applicability of this method in processing real data will be demonstrated subsequently.
5. Computational Simulations
In this section, we focus on extensive numerical simulations to showcase the effectiveness of the algorithm we have proposed.
The experimental procedure is structured in several steps. Initially, we fabricate values for and and utilize these to address the direct problem, as defined in (1)–(4). We then generate what we term quasi-real measurements, as outlined in (7), derived from the solutions of the direct problem. In the following phase, these quasi-real measurements are fed into the process for solving the inverse problem. The outcome of this algorithm is represented by the inferred values of and , which can then be contrasted with the original values used in solving the direct problem.
To evaluate the algorithm’s efficiency, we propose re-solving the direct problem, this time using the ‘implied’ parameters. The next step involves comparing the ‘real’ data values of , and against the solutions derived from these ‘implied’ functions. For a comprehensive assessment of the algorithm’s performance, we employ ‘goodness-of-fit’ metrics, which will be detailed later. This rigorous evaluation will not only validate the algorithm’s accuracy but also its applicability in practical scenarios, ensuring that it can reliably be used in real-world contexts where precise modeling of such dynamics is crucial.
We commence with the direct problem (1)–(4). The nodes of the mesh are equidistantly distributed with constant step size 0.005, and the ‘main’ observations are separated by approximately five weeks, i.e., we need to probe the functions less than once a month. For the initial conditions, we assume the seed mass to start at kg/m2 and an initial concentration of aluminium ions in the plant mg/kg. The concentration of Al ions in the soil is considered to be mg/L, while the concentration of H ions in the soil solution is set at mg/L.
Regarding the model parameters, the absorption coefficient is established at L/(kg·year), while the leakage coefficient is year, and the reaction coefficient is chosen as year. The rate of proton flux to the soil, , is maintained at a constant value of mg/(m2·year). The available water for roots is defined by a periodic function that reflects seasonal variation, expressed as mm.
The constants of the model, which dictate the net growth of plant biomass () and the metabolic inefficiency function (), are set as follows: year for the growth rate, m2/kg for the biomass coefficient, year for the metabolic rate, mg/kg as the critical concentration threshold, and year for the inefficiency factor. These parameters are crucial in modeling the dynamics of plant growth and their interaction with the heavy metal contaminants in the soil, providing a detailed simulation of the environmental processes at play.
The results are given on Figure 2.
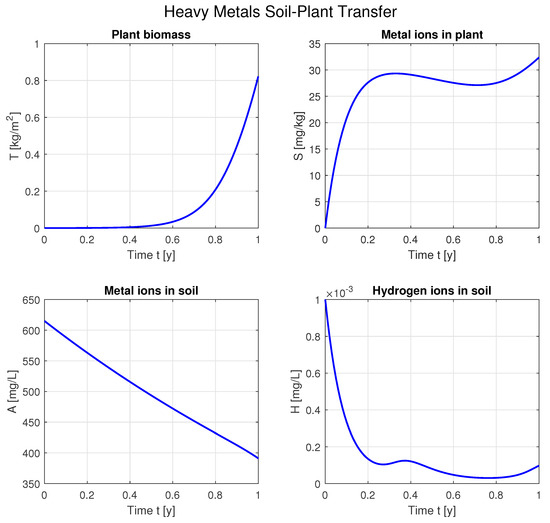
Figure 2.
Plant–soil interaction dynamics with quasi-real data.
Further, we proceed with the inverse problem (1)–(4), (7). As discussed, we assume that the parameters are unknown, and aim to reconstruct them in a piecewise-linear manner. The first test is performed with exact, i.e., non-perturbed, observations. The results are given in Figure 3 and Figure 4.
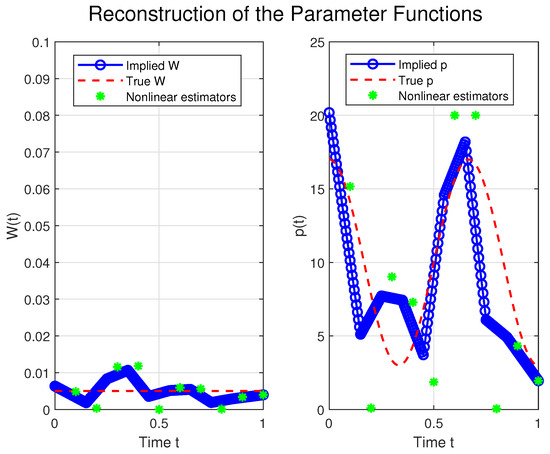
Figure 3.
Reconstructed parameters and .
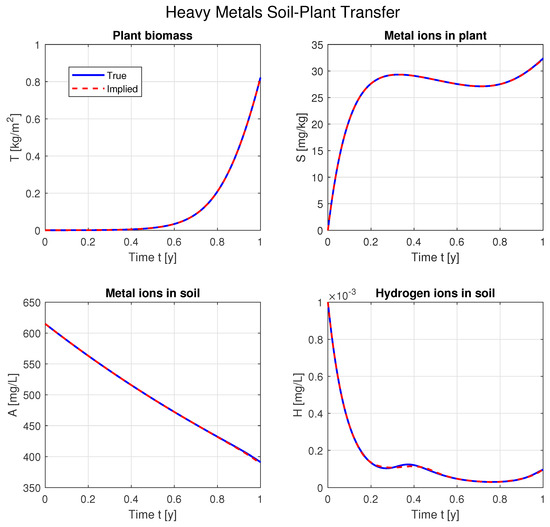
Figure 4.
Implied plant–soil interaction dynamics.
A satisfactory fit is observed, and consequently the real and implied system functions match as well. To quantify the latter, we introduce the residual norm
For this case, .
Moving forward, our focus shifts to experiments involving observations that have been intentionally perturbed. In the real world, measurement devices inevitably possess some degree of instrumental error. Therefore, conducting tests with measurements that include noise is not only relevant but also essential for practical applications. To simulate this, we introduce Gaussian noise to the observations as described in (7). When we refer to noise, it implies that the relative error in these altered observations is confined within of the actual value, with a confidence level of . This approach aims to mimic the uncertainties and inaccuracies commonly encountered in actual data-collection processes, thereby enhancing the robustness and reliability of our testing framework. By incorporating this level of noise, we can more accurately assess the effectiveness of our methods in real-world conditions, where perfect data are seldom available.
We proceed with a noise level as high as to demonstrate the robustness of the algorithm. The results are plotted on Figure 5 and Figure 6.
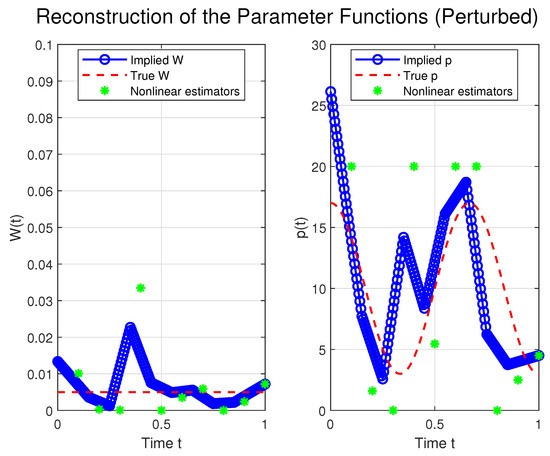
Figure 5.
Reconstructed parameters and with perturbed measurements.
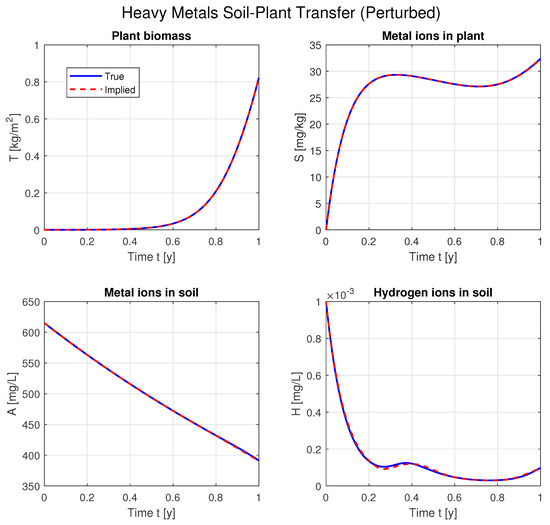
Figure 6.
Implied plant–soil interaction dynamics with perturbed measurements.
Although the recovered parameters are more distant than the real ones, the reconstruction is still acceptable. The level of the residual is .
6. Conclusions
In recent decades, the issue of heavy metal contamination has become increasingly prevalent. Substantial research efforts have been directed towards finding solutions, notably through the modeling of heavy metal dynamics in soil–plant interactions. The model presented here is a culmination of years of research and is fundamental to our understanding of this issue. It has been corroborated by numerous experimental studies, providing a comprehensive understanding of how plants interact with heavy metals.
The impact of heavy metals on plant growth varies significantly based on different soil types, plant species, and metal types. This research primarily focuses on presenting a comprehensive algorithm for reconstructing parameters that vary over time. This is achieved through a predictor–corrector methodology, which stands out for its speed, robustness, and ability to handle actual data effectively. The algorithm introduced in this study enables the reconstruction of proton flow in the soil during rainfall and the available water to plant roots as functions of time. This is crucial for understanding the vulnerability of specific ecosystems to various metal pollutants. The reconstructed data are instrumental in assessing the risk of contaminants transferring to honey and other elements of the food chain. Furthermore, this model helps to determine if pollution levels have reached critical thresholds where catastrophic ecological decline becomes inevitable. The insights gained from this approach are invaluable for further investigations into the complex dynamics of these interactions and will significantly contribute to strategies aimed at mitigating and preventing large-scale ecological disasters.
Building on this research and utilizing experimental data, our future objective is to develop models for lead accumulation. The potential effects of bioaccumulation in plants are particularly relevant for honey bee nutrition. Specifically, we aim to apply the findings of this study to model the concentration of lead in the soil and its subsequent bioaccumulation in crops like rape and sunflower. This will also include an analysis of how these plants respond to varying levels of lead concentration. This research is pivotal for understanding and mitigating the impacts of heavy metal pollution on crucial pollinators like honey bees and the broader ecological systems they support.
The methodology outlined here is not confined to the context of soil–plant interactions. In fact, the calibration of inverse problems is a common challenge across numerous fields, often presenting more complexity and bearing greater significance than the direct problems from which they are derived. The computational techniques developed can be employed in the fitting and analysis of a broad spectrum of dynamic systems, encompassing both natural phenomena and human-induced activities.
These numerical algorithms, when validated with real-world data, have the potential for widespread application across various scientific disciplines. Their versatility and adaptability make them suitable for a range of scenarios, from environmental studies to engineering applications, and even in complex fields like epidemiology or climate modeling. The adaptability and efficacy of these methods in practical scenarios underscore their importance and utility in advancing scientific understanding and problem-solving across a multitude of domains.
Author Contributions
Conceptualization, A.A. and L.V.; methodology, S.G. and L.V.; software, S.G.; validation, S.G.; formal analysis, L.V.; investigation, S.G. and L.V.; resources, A.A. and S.G.; data curation, A.A. and S.G.; writing—original draft preparation, S.G.; writing—review and editing, S.G. and L.V.; visualization, S.G.; supervision, L.V.; project administration, A.A.; funding acquisition, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bulgarian National Science Fund under Project KP-06-PN 46-7 “Design and research of fundamental technologies and methods for precision apiculture”.
Data Availability Statement
The data presented in this study are openly available in [2,14].
Acknowledgments
The authors are grateful to the anonymous referees for the useful suggestions and comments.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Guala, S.D.; Vega, F.A.; Covelo, E.F. The dynamics of heavy metals in plant–soil interactions. Ecol. Model. 2010, 221, 1148–1152. [Google Scholar]
- Cârdei, P.; Tudora, C.; Vlăduț, V.; Pruteanu, M.A.; Gădeanu, I.; Cujbescu, D.; Bordean, D.-M.; Ungureanu, N.; Ipate, G.; Cristea, O.D. Mathematical model to simulate the transfer of heavy metals from soil to plant. Sustainability 2021, 13, 6157. [Google Scholar] [CrossRef]
- De Leo, G.; Del Furia, L.; Gatto, M. The interaction between soil acidity and forest dynamics: A simple-model exhibiting catastrophic behavior. Theor. Popul. Biol. 1993, 43, 31–51. [Google Scholar] [CrossRef]
- van Genuchten, M.T.; Wagent, R.J. Two-site/region models for pesticidies transport and degradiation: Theoretical development and analytical solutions. Soil Sci. Soc. Am. J. 1989, 53, 1303–1310. [Google Scholar]
- Cârdei, P.; Tudora, C. Theoretical research on evolution of health of plants affected by heavy metal absorption process. In Proceedings of the 17th International Scientific Conference Engineering for Rural Development, Jelgava, Latvia, 23–25 May 2018; pp. 893–897. [Google Scholar]
- Guala, S.D.; Vega, F.A.; Covelo, E.F. Modification of a soil-vegetation nonlinear interaction model with acid deposition for simplified experimental applicability. Ecol. Model. 2009, 220, 2137–2141. [Google Scholar] [CrossRef]
- Goretti, E.; Pallottini, M.; Rossi, R.; La Porta, G.; Gardi, T.; Goga, B.T.C.; Elia, A.C.; Galletti, M.; Moroni, B.; Petroselli, C.; et al. Heavy metal bioaccumulation in honey bee matrix, an indicator to assess the contamination level in terrestrial environments. Environ. Pollut. 2020, 256, 113388. [Google Scholar] [CrossRef] [PubMed]
- Hladun, K.R.; Di, N.; Liu, T.-X.; Trumble, J.T. Metal contaminant accumulation in the hive: Consequences for whole-colony health and brood production in the honey bee (Apis mellifera L.). Environ. Toxicol. Chem. 2016, 39, 322–329. [Google Scholar] [CrossRef] [PubMed]
- Hristov, P.; Shumkova, R.; Palova, N.; Neov, B. Factors associated with honey bee colony losses: A mini-review. Vet. Sci. 2020, 7, 166. [Google Scholar] [PubMed]
- Hristov, P.; Shumkova, R.; Palova, N.; Neov, B. Honey bee colony losses: Why are honey bees disappearing? Sociobiology 2021, 68, e-5851. [Google Scholar] [CrossRef]
- Lazor, P.; Tomáš, J.; Tóth, T.; Tóth, J.; Čéryová, S. Monitoring of air pollution and atmospheric deposition of heavy metals by analysis of honey. J. Microbiol. Biotechnol. Food Sci. 2012, 1, 522–533. [Google Scholar]
- Scivicco, M.; Nolasco, A.; Esposito, L.; Ariano, A.; Squillante, J.; Esposito, F.; Cirillo, T.; Severino, L. Effects of COVID-19 pandemic lockdown and environmental pollution assessment in Campania region (Italy) through the analysis of heavy metals in honeybees. Environ. Pollut. 2022, 307, 119504. [Google Scholar] [PubMed]
- Demaku, S.; Aliu, A.; Sylejmani, D.; Ahmetaj, B.; Halili, J. Determination of heavy metals in bee honey as a bioindicator in the Istog, Drenas and Kastriot regions. J. Ecol. Eng. 2023, 24, 191–200. [Google Scholar] [CrossRef]
- Atanasov, A.Z.; Georgiev, S.G.; Vulkov, L.G. Parameter identification analysis of heavy metals soil–plant transfer with applications to honey bees food. AIP Conf. Proc. 2023, 2953, 050001. [Google Scholar]
- Abdulla, U.G.; Poteau, R. Identification of parameters in systems biology. Math. Biosci. 2018, 305, 133–145. [Google Scholar] [CrossRef] [PubMed]
- Abdulla, U.G.; Poteau, R. Identification of parameters for large-scale kinetic models. J. Comput. Phys. 2021, 429, 110026. [Google Scholar]
- Hasanoğlu, A.H.; Romanov, V.G. Introduction to Inverse Problems for Differential Equations; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Kabanikhin, S.I. Inverse and Ill-Posed Problems; De Gruyter: Leipzig, Germany, 2012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).