Further Stability Criteria for Sampled-Data-Based Dynamic Positioning Ships Using Takagi–Sugeno Fuzzy Models
Abstract
1. Introduction
2. Problem Formulation
3. Main Results
3.1. Construction of the Lyapunov Function
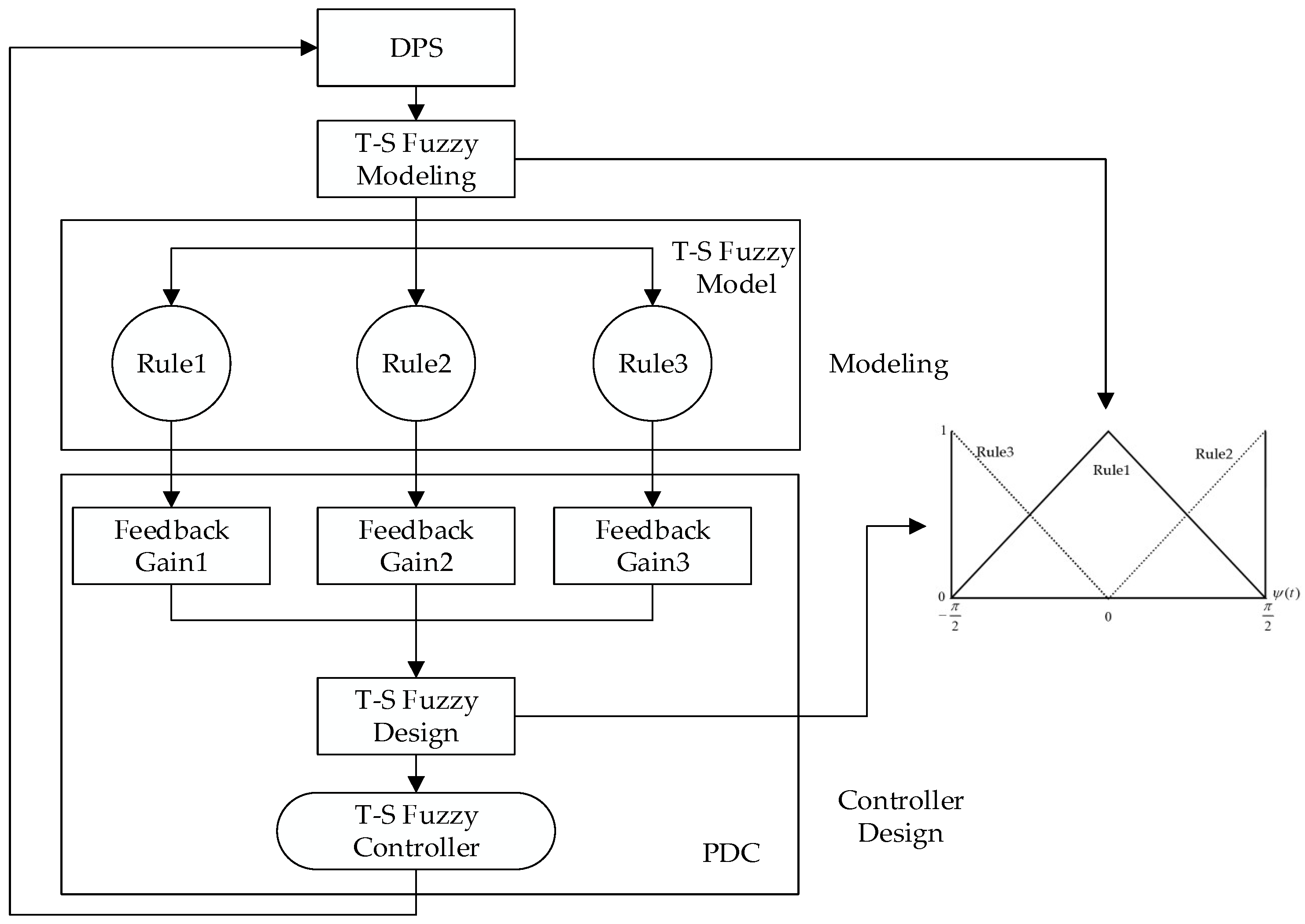
3.2. Introduction of Fuzzy Framework
3.3. Design of Sampled-Data Controller
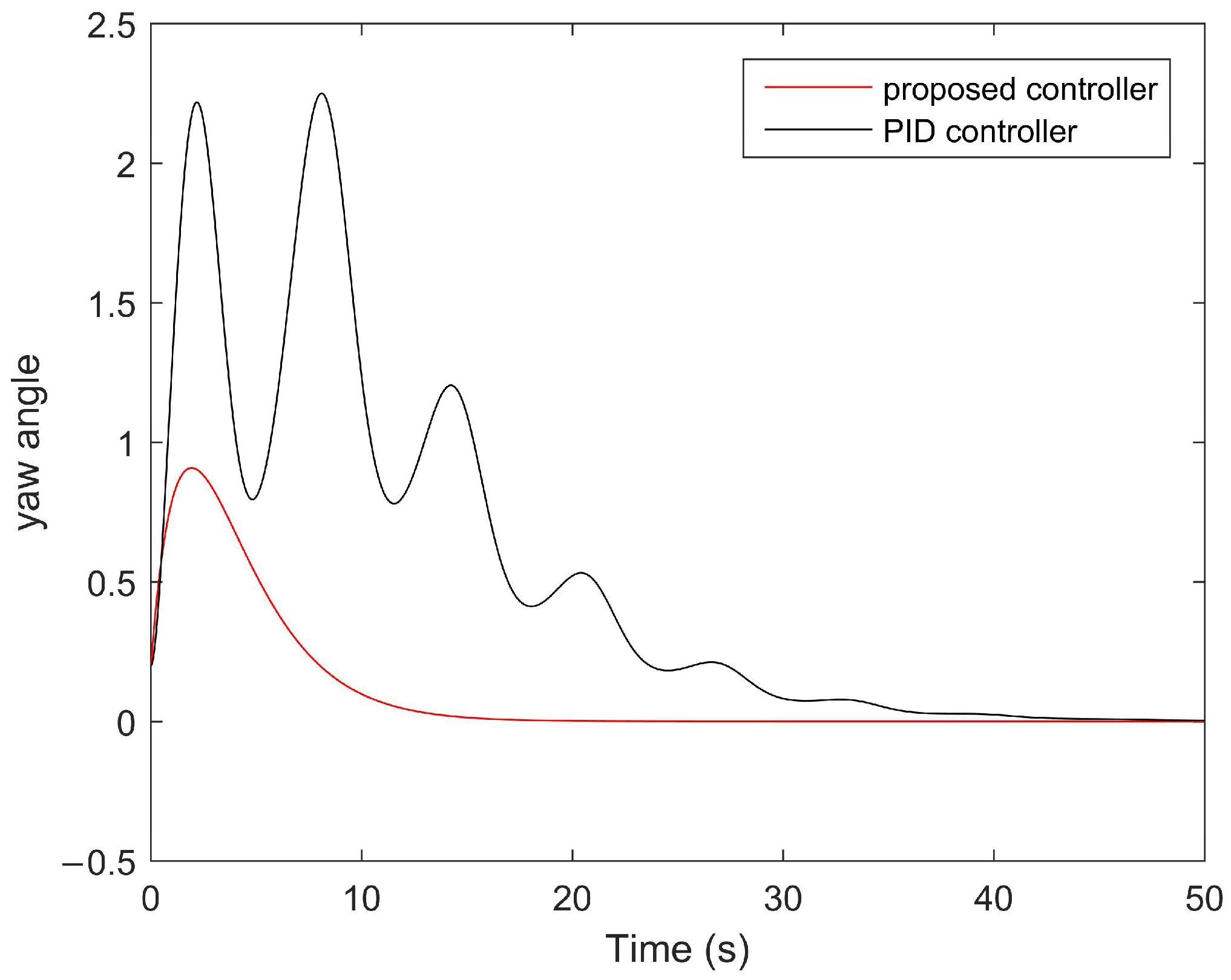
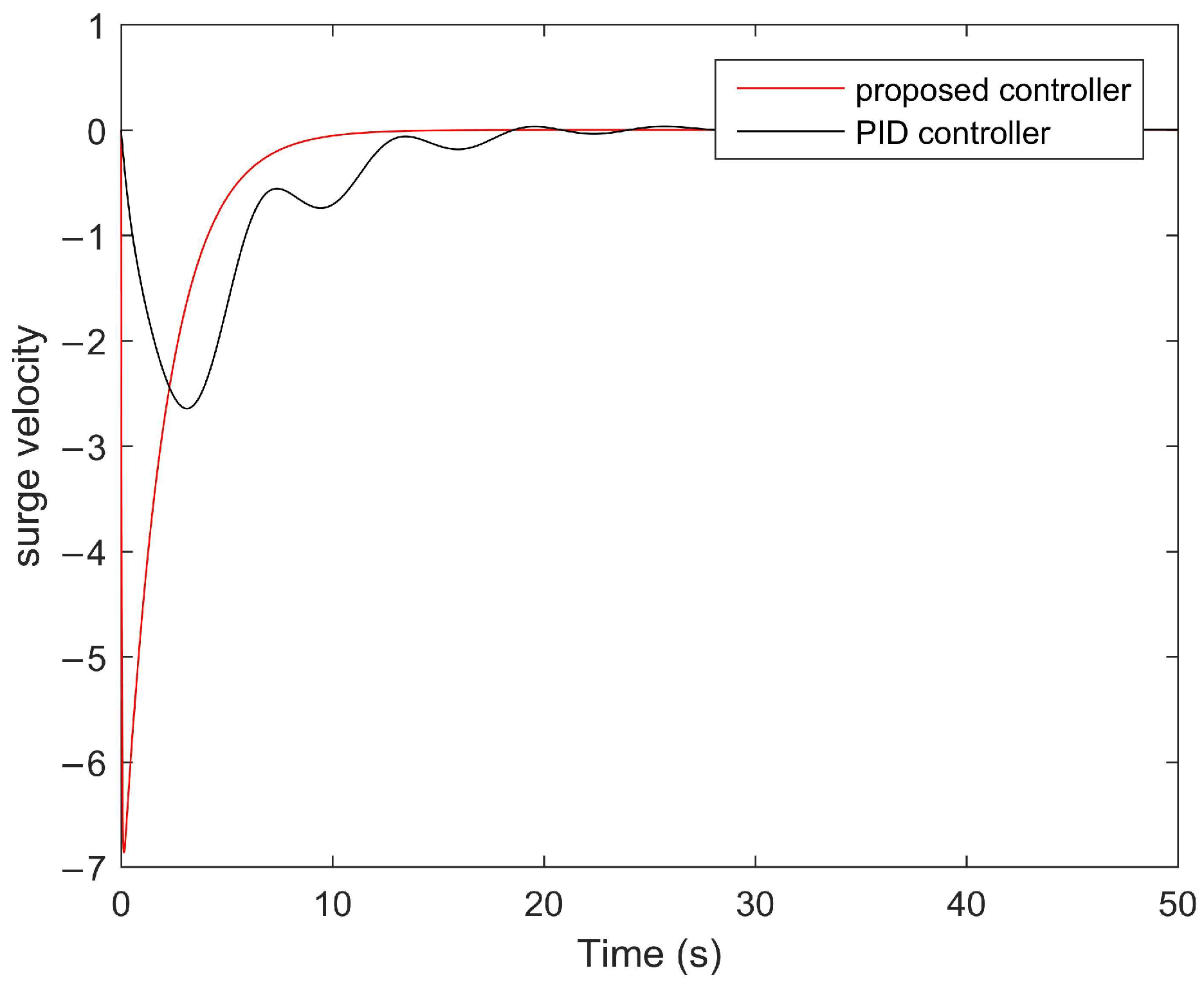
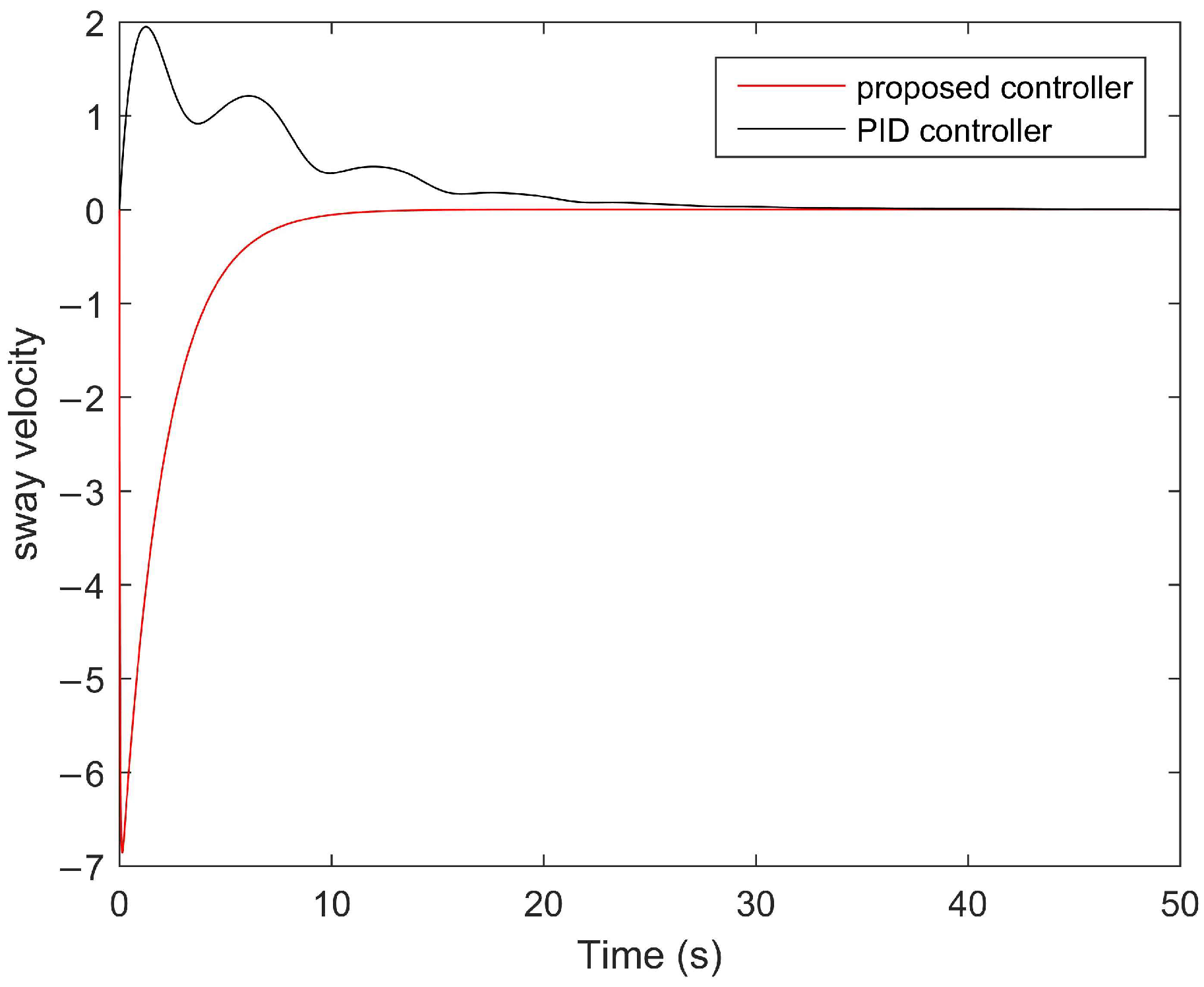
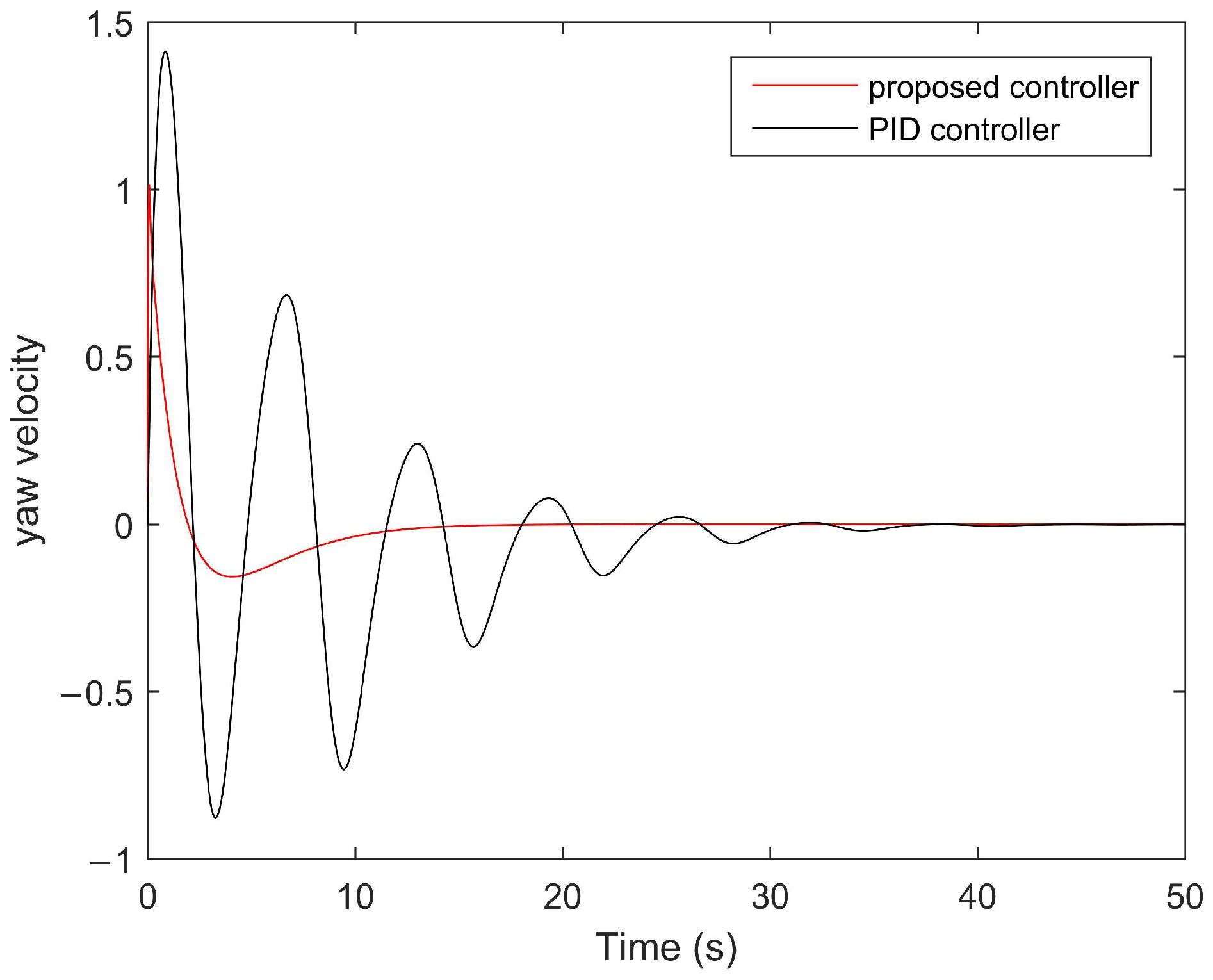
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fossen, T.I. Guidance and Control of Ocean Vehicles; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Wang, Y.L.; Han, Q.L.; Fei, M.R.; Peng, C. Network-based T-S fuzzy dynamic positioning controller design for unmanned marine vehicles. IEEE Trans. Cybern. 2018, 48, 2750–2763. [Google Scholar] [CrossRef]
- Hao, L.Y.; Zhang, H.; Li, T.S.; Lin, B.; Chen, C.P. Fault tolerant control for dynamic positioning of unmanned marine vehicles based on T-S fuzzy model with unknown membership functions. IEEE Trans. Veh. Technol. 2021, 70, 146–157. [Google Scholar] [CrossRef]
- Veksler, A.; Johansen, T.A.; Borrelli, F.; Realfsen, B. Dynamic positioning with model predictive control. IEEE Trans. Control Syst. Technol. 2016, 24, 1340–1353. [Google Scholar] [CrossRef]
- Nguyen, V.S. Investigation of a multitasking system for automatic ship berthing in marine practice based on an integrated neural controller. Mathematics 2020, 8, 1167. [Google Scholar] [CrossRef]
- Benetazzo, F.; Ippoliti, G.; Longhi, S.; Raspa, P. Advanced control for fault-tolerant dynamic positioning of an offshore supply vessel. Ocean Eng. 2015, 106, 472–484. [Google Scholar] [CrossRef]
- Karimi, H.R.; Lu, Y. Guidance and control methodologies for marine vehicles: A survey. Control Eng. Pract. 2021, 111, 104785. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X.; Yan, H. Reliable fuzzy tracking control of near-space hypersonic vehicle using aperiodic measurement information. IEEE Trans. Ind. Electron. 2019, 66, 9439–9447. [Google Scholar] [CrossRef]
- Karimi, H.R. Robust H∞ filter design for uncertain linear systems over network with network-induced delays and output quantization. Nor. Foren. Autom. 2009, 30, 27–37. [Google Scholar] [CrossRef]
- Kiruthika, R.; Krishnasamy, R.; Lakshmanan, S.; Prakash, M.; Manivannan, A. Non-fragile sampled-data control for synchronization of chaotic fractional-order delayed neural networks via LMI approach. Chaos Solitons Fractals 2023, 169, 113252. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, Y.; Zhou, P. Fuzzy-model-based sampled-data control of chaotic systems: A fuzzy time-dependent Lyapunov–Krasovskii functional approach. IEEE Trans. Fuzzy Syst. 2016, 25, 1672–1684. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, P. On master-slave synchronization of Chaotic Lur’e systems using sampled-data control. IEEE Trans. Circuits Syst. II Express Briefs 2016, 85, 981–992. [Google Scholar] [CrossRef]
- Chen, W.-H.; Wang, Z.; Lu, X. On sampled-data control for masterslave synchronization of chaotic Lur’e systems. IEEE Trans. Circuits Syst. II Express Briefs 2012, 59, 515–519. [Google Scholar]
- Wu, Z.-G.; Shi, P.; Su, H.; Chu, J. Local synchronization of chaotic neural networks with sampled-data and saturating actuators. IEEE Trans. Cybern. 2014, 44, 2635–2645. [Google Scholar]
- Wu, Z.G.; Shi, P.; Su, H.Y. Stochastic Synchronization of Markovian Jump Neural Networks with Time-Varying Delay Using Sampled Data. IEEE Trans. Cybern. 2013, 43, 796–1806. [Google Scholar] [CrossRef] [PubMed]
- Karimi, H.R.; Gao, H. Mixed H2/H∞ output-feedback control of second-order neutral systems with time-varying state and input delays. ISA Trans. 2008, 47, 311–324. [Google Scholar] [CrossRef]
- Wei, Y.; Karimi, H.R.; Yang, S. New results on sampled-data output-feedback control of linear parameter-varying systems. Int. J. Robust Nonlinear Control 2022, 32, 5070–5085. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Li, K.; Gao, Z. Robust sampled-data cruise control scheduling of high speed train. Transp. Res. Part C Emerg. Technol. 2014, 46, 274–283. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Q.; Zhou, P.; Duan, D. Robust H∞ directional control for a sampled-data autonomous airship. J. Cent. South Univ. 2014, 21, 1339–1346. [Google Scholar] [CrossRef]
- Zheng, M.; Zhou, Y.; Yang, S.; Li, L. Robust H∞ control of neutral system for sampled-data dynamic positioning ships. IMA J. Math. Control Inf. 2019, 36, 1325–1345. [Google Scholar] [CrossRef]
- Zou, Z.; Zheng, M. Design and stabilization analysis of luxury cruise with dynamic positioning systems based on sampled-data control. Math. Biosci. Eng. 2023, 20, 14026–14045. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.; Su, Y.; Yang, S.; Li, L. Reliable fuzzy dynamic positioning tracking controller for unmanned surface vehicles based on aperiodic measurement information. Int. J. Fuzzy Syst. 2023, 25, 358–368. [Google Scholar] [CrossRef]
- Castro, M.F.; Seuret, A.; Leite, V.J.; Silva, L.F. Robust local stabilization of discrete time varying delayed state systems under saturating actuators. Automatica 2020, 122, 109266. [Google Scholar] [CrossRef]
- Ge, G.; Lei, D.; Han, Q. A distributed event-triggered transmission strategy for sampled-data consensus of multi-agent systems. Automatica 2014, 50, 1489–1496. [Google Scholar]
- Zhang, X.; Han, Q.; Zhang, B. An overview and deep investigation on sampled-data-based event-triggered control and filtering for networked systems. IEEE Trans. Ind. Inform. 2017, 13, 4–16. [Google Scholar] [CrossRef]
- Yan, L.; Wang, Z.; Zhang, M.; Fan, Y. Sampled-data control for mean-square exponential stabilization of memristive neural networks under deception attacks. Chaos Solitons Fractals 2023, 174, 113787. [Google Scholar] [CrossRef]
- Yerudkar, A.; Chatzaroulas, E.; Del Vecchio, C.; Moschoyiannis, S. Sampled-data control of probabilistic boolean control networks: A deep reinforcement learning approach. Inf. Sci. 2023, 619, 374–389. [Google Scholar] [CrossRef]
- Wang, Y.; Karimi, H.R.; Lam, H.K.; Shen, H. An improved result on exponential stabilization of sampled-data fuzzy systems. IEEE Trans. Fuzzy Syst. 2018, 26, 3875–3883. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. Adaptive memory-event-triggered static output control of T–S fuzzy wind turbine systems. IEEE Trans. Fuzzy Syst. 2021, 30, 3894–3904. [Google Scholar] [CrossRef]
- Cai, X.; Shi, K.; She, K.; Zhong, S.; Tang, Y. Quantized sampled-data control tactic for TS fuzzy NCS under stochastic cyber-attacks and its application to truck-trailer system. IEEE Trans. Veh. Technol. 2022, 71, 7023–7032. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, Y.; Ahn, C.K.; Zhu, Y. Exponential stabilization of takagi–sugeno fuzzy systems with aperiodic sampling: An aperiodic adaptive event-triggered method. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 444–454. [Google Scholar] [CrossRef]
- Sheng, Z.; Lin, C.; Chen, B.; Wang, Q.-G. Stability and Stabilization of TS Fuzzy Time-delay Systems under Sampled-data Control via New Asymmetric Functional Method. IEEE Trans. Fuzzy Syst. 2023, 31, 3197–3209. [Google Scholar] [CrossRef]
- Velmurugan, G.; Joo, Y.H. Sampled-Data Control Design for T-S Fuzzy System via Quadratic Function Negative Determination Approach. IEEE Trans. Fuzzy Syst. 2023, 31, 3197–3209. [Google Scholar] [CrossRef]
- Katayama, H. Nonlinear Sampled-Data Stabilization of Dynamically Positioned Ships. IEEE Trans. Control Syst. Technol. 2010, 18, 463–468. [Google Scholar] [CrossRef]
- Katayama, H.; Aoki, H. Straight-line trajectory tracking control for sampled-data underactuated ships. IEEE Trans. Control Syst. Technol. 2014, 22, 1638–1645. [Google Scholar]
- Zheng, M.; Zhou, Y.; Yang, S.; Suo, Y.; Li, L. Robust H∞ Control for Sampled-data Dynamic Positioning Ships. J. Control Eng. Appl. Inform. 2017, 19, 84–92. [Google Scholar] [CrossRef]
- Yang, S.; Zheng, M. H-infinity Fault-Tolerant Control for Dynamic Positioning Ships based on Sampled-data. J. Control Eng. Appl. Inform. 2018, 20, 32–39. [Google Scholar]
- Zheng, M.; Yang, S.; Li, L. Stability analysis and T-S fuzzy dynamic positioning controller design for autonomous surface vehicles based on sampled-data control. IEEE Access 2020, 8, 148193–148202. [Google Scholar] [CrossRef]
- Chen, G.; Suo, Y.; Zheng, M.; Yang, S.; Li, L. Reliable tracking control of dynamic positioning ships based on aperiodic measurement information. J. Control Eng. Appl. Inform. 2022, 24, 80–89. [Google Scholar]
- Sun, J.; Liu, G.P.; Chen, J. Delay-dependent stability and stabilization of neutral time-delay systems. Int. J. Robust Nonlinear Control 2009, 19, 1364–1375. [Google Scholar] [CrossRef]
- Tannuri, E.; Agostinho, A.; Morishita, H.; Moratelli, L. Dynamic positioning systems: An experimental analysis of sliding mode control. Control Eng. Pract. 2010, 18, 1121–1132. [Google Scholar] [CrossRef]
- Garai, A.; Mandal, P.; Roy, T.K. Multipollutant air quality management strategies: T-Sets based optimization technique under imprecise environment. Int. J. Fuzzy Syst. 2017, 19, 1927–1939. [Google Scholar] [CrossRef]
- Garai, A.; Mondal, B.; Roy, T.K. Optimisation of multi-objective commercial bank balance sheet management model: A parametric T-set approach. Int. J. Math. Oper. Res. 2019, 15, 395–416. [Google Scholar] [CrossRef]
- Garai, A.; Mandal, P.; Roy, T.K. Intuitionistic fuzzy T-sets based optimization technique for production-distribution planning in supply chain management. Opsearch 2016, 53, 950–975. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.; Shi, J. Adaptive fuzzy controller design for dynamic positioning system of vessels. Appl. Ocean Res. 2015, 53, 46–53. [Google Scholar] [CrossRef]
- De la Sen, M. Robust stability of a class of linear time-varying systems. IMA J. Math. Control Inf. 2002, 19, 399–418. [Google Scholar] [CrossRef]

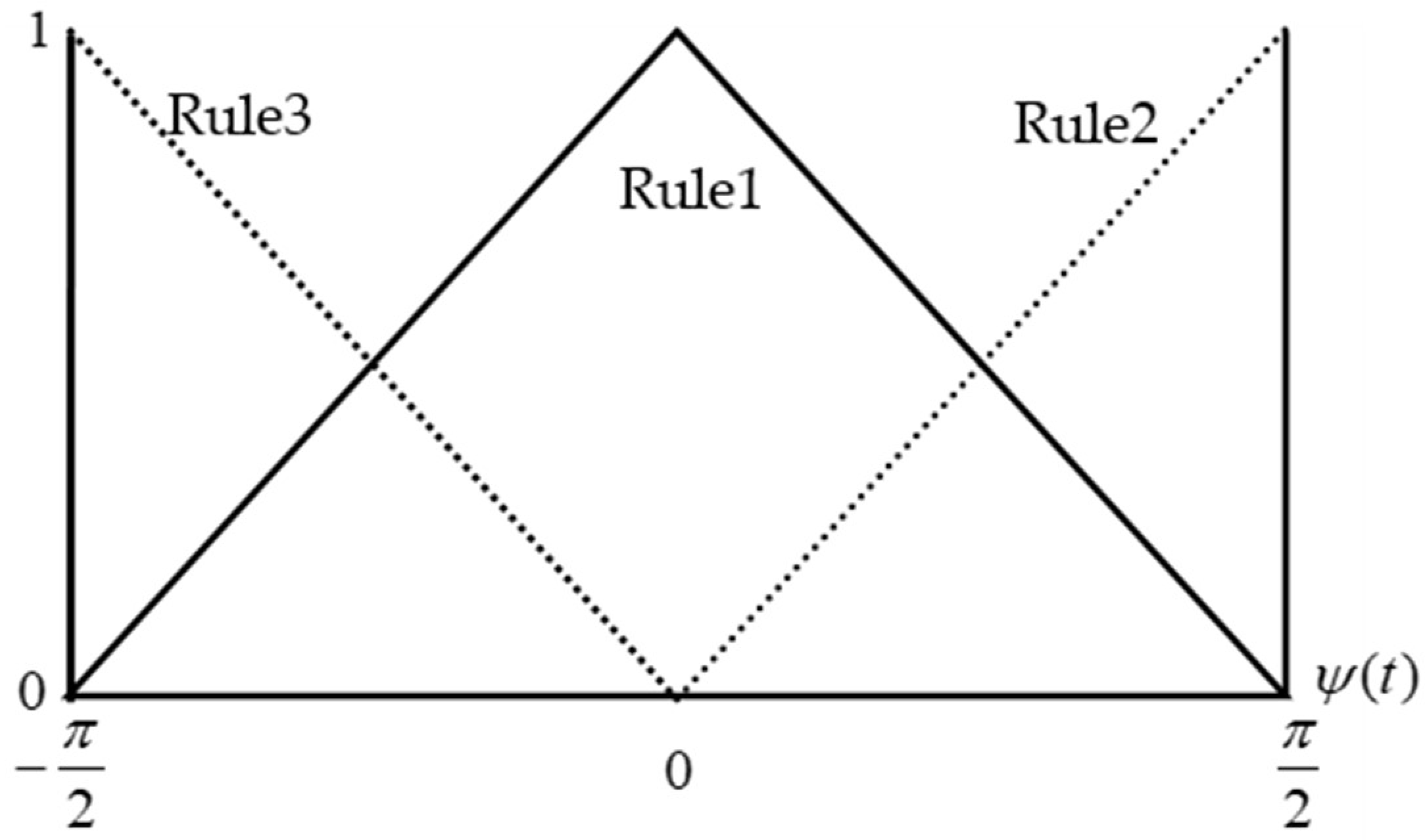
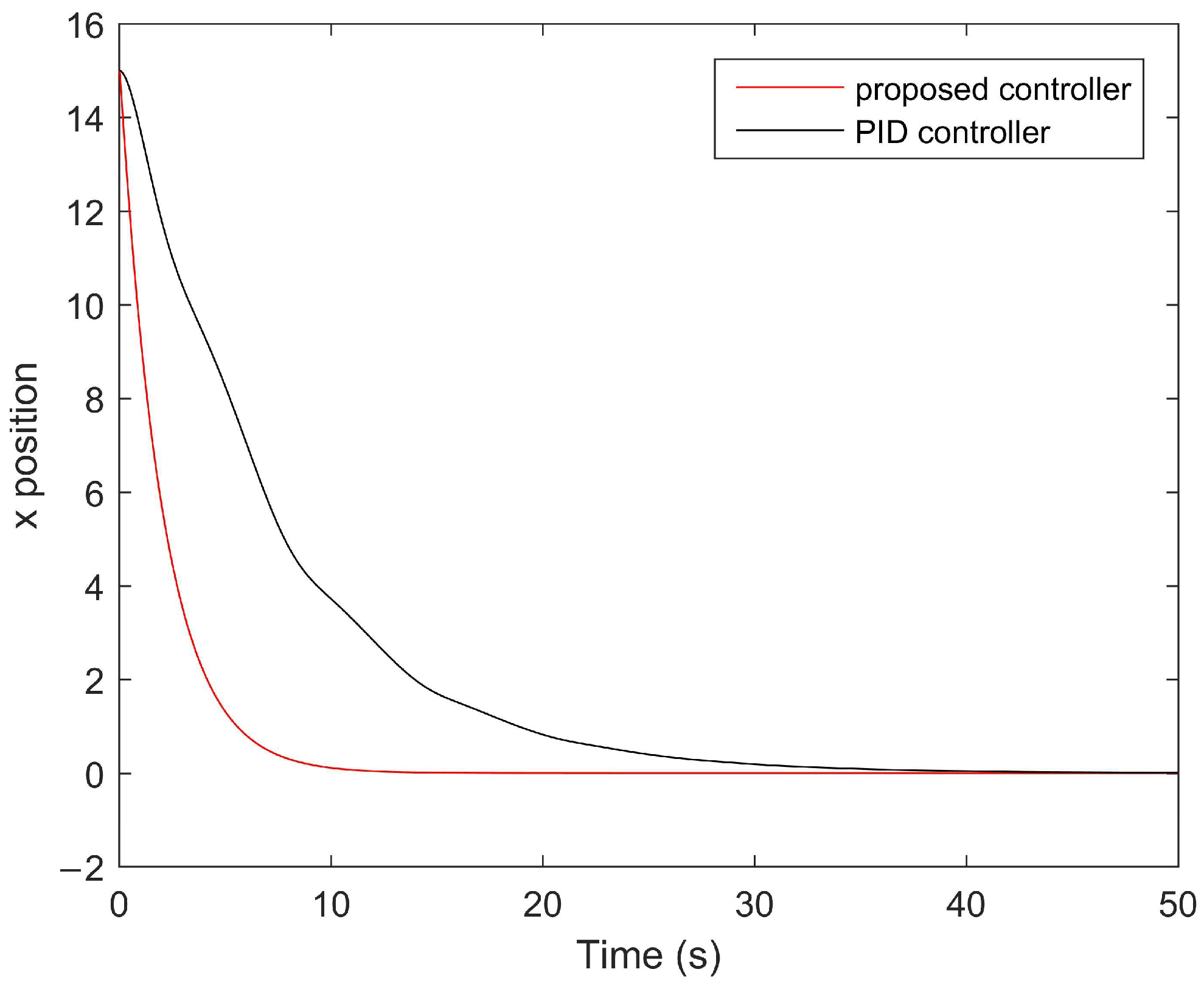
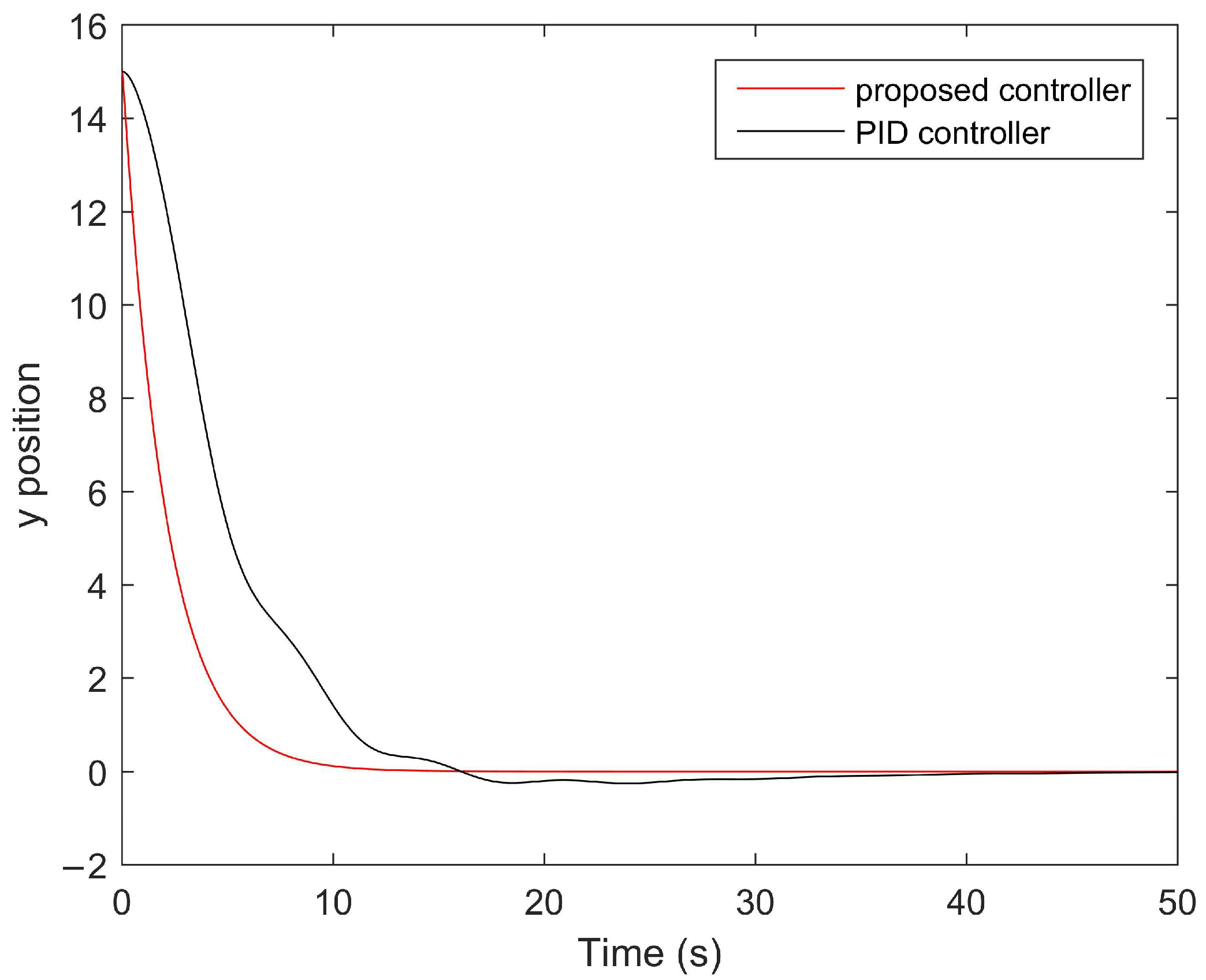
| Method | [37] | [38] | [39] | Theorem 1 |
|---|---|---|---|---|
| d2 | 0.25 | 0.264 | 0.532 | 0.681 |
| Technologies | Maximum Sampling Internal |
|---|---|
| T-set | 0.583 |
| Pareto optimality under T-set | 0.624 |
| Intuitionistic fuzzy T-set | 0.652 |
| Proposed method | 0.681 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, M.; Su, Y.; Yan, C. Further Stability Criteria for Sampled-Data-Based Dynamic Positioning Ships Using Takagi–Sugeno Fuzzy Models. Symmetry 2024, 16, 108. https://doi.org/10.3390/sym16010108
Zheng M, Su Y, Yan C. Further Stability Criteria for Sampled-Data-Based Dynamic Positioning Ships Using Takagi–Sugeno Fuzzy Models. Symmetry. 2024; 16(1):108. https://doi.org/10.3390/sym16010108
Chicago/Turabian StyleZheng, Minjie, Yulai Su, and Changjian Yan. 2024. "Further Stability Criteria for Sampled-Data-Based Dynamic Positioning Ships Using Takagi–Sugeno Fuzzy Models" Symmetry 16, no. 1: 108. https://doi.org/10.3390/sym16010108
APA StyleZheng, M., Su, Y., & Yan, C. (2024). Further Stability Criteria for Sampled-Data-Based Dynamic Positioning Ships Using Takagi–Sugeno Fuzzy Models. Symmetry, 16(1), 108. https://doi.org/10.3390/sym16010108





