Laplace-Domain Hybrid Distribution Model Based FDIA Attack Sample Generation in Smart Grids
Abstract
:1. Introduction
- -
- We propose an efficient FDIA attack sample generation method. Our method can quickly construct large-scale attack training samples for FDIA detection models, thereby solving the problem of sparse attack samples.
- -
- By analyzing the measured data changes of each node of the power system, individual Laplacian distribution can be established sequentially according to the change of the sensing measurement data of each node. A Laplace-domain hybrid distribution can be constructed to generate FDIA attack samples by combining multiple symmetric Laplace distribution models, which can better improve the concealment of the attack sample.
- -
- We conduct a large number of experiments by different detection models to verify that our attack samples are more deceptive than other attack samples. The experimental results demonstrate that our method outperforms traditional FDIA attack sample construction schemes in terms of attack strength and covert capability, while guaranteeing a low computational complexity.
2. False Data Injection Attack
3. Proposed Method
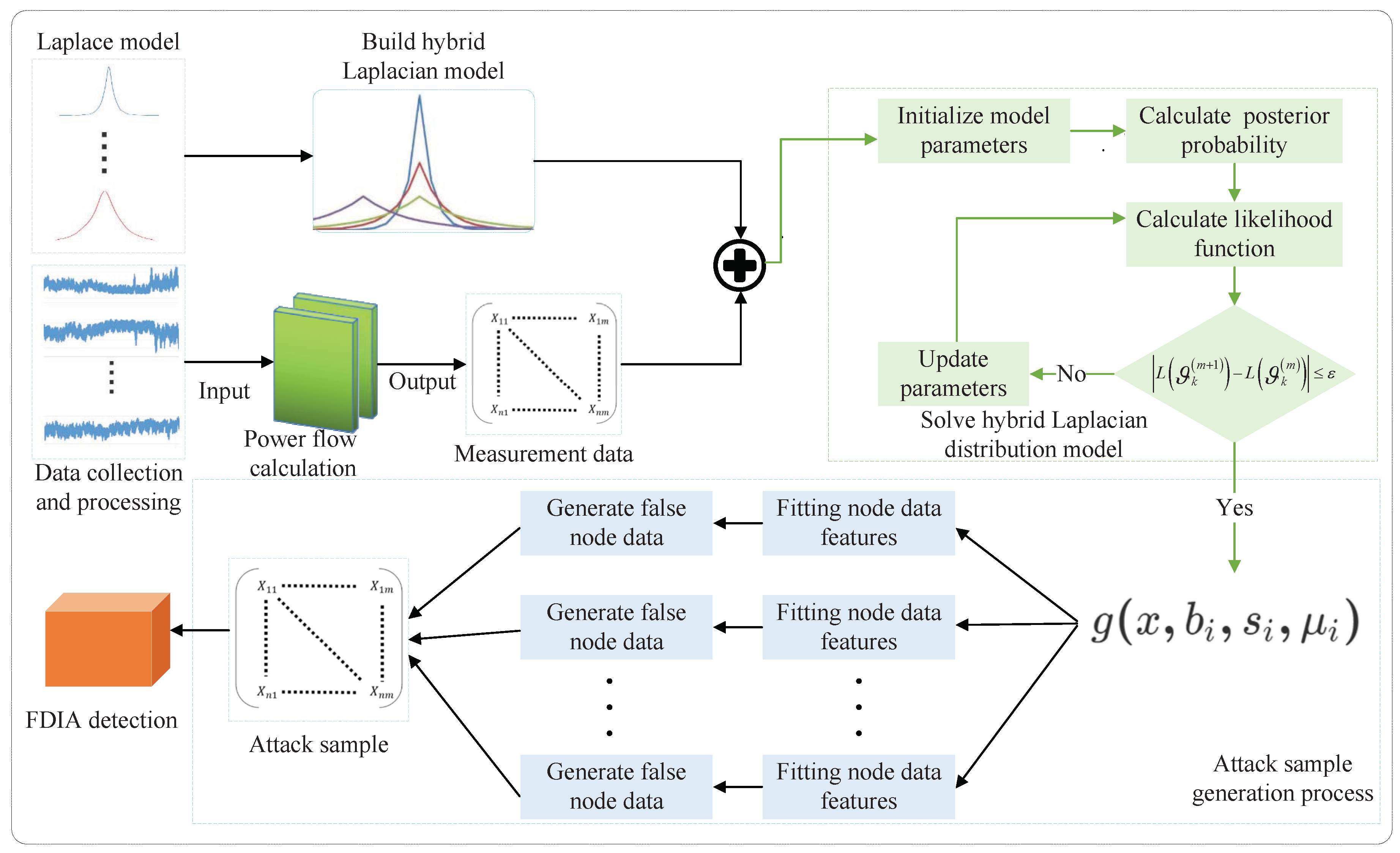
3.1. The Framework of Proposed Scheme
3.2. Laplace Distribution and Observation
3.3. Hybrid Laplace Distribution Model
- (1)
- Firstly, determine the initial values of the model parameters according to the characteristics of the sensing measurement data, then the model parameter vector is . Correspondingly, the posterior probability of sample (where ) under this initial condition can be expressed as:Considering that the posterior probability of each component of the linear component is calculated circularly: For each component, the probability density of the sample data belonging to the component is calculated by using the initialized parameters and , where the posterior probability can be calculated by matrix multiplication with the prior probability , and the posterior probability meets the normalization condition, that is, . For any group of , the assignment of samples to k components with can be completed sequentially under the initial value . Subsequently, the parameters of each component distribution can be obtained by the expectation algorithm.where , and are the component weights, component mean values and component scales updated in the first iteration, respectively. Meanwhile, is a known estimation , not the maximum likelihood estimation of hybrid distribution, and is the expected result of the first iterative separation.
- (2)
- In order to find the best model parameters, we need to introduce the maximum likelihood estimation (MLE) on sample .In order to maximize the likelihood function under the conditions of formula , we use the derivative method and make the derivative zero to solve the corresponding and .
- (3)
- Finally, after m rounds of iteration, the result of rounds can be obtained, that is, the solution of , , .In the iterative algorithm for maximum likelihood estimation of hybrid model parameters, the likelihood function is monotonically increasing, i.e., . This means that an maximum point can always be found in the iteration process, and the corresponding threshold can be given generally. When , the Likelihood function is the largest, and accordingly the iteration should stop to obtain the maximum likelihood estimation parameters.
4. Experimental Results and Discussions
4.1. Attack Data Generation
4.2. Experimental Setup
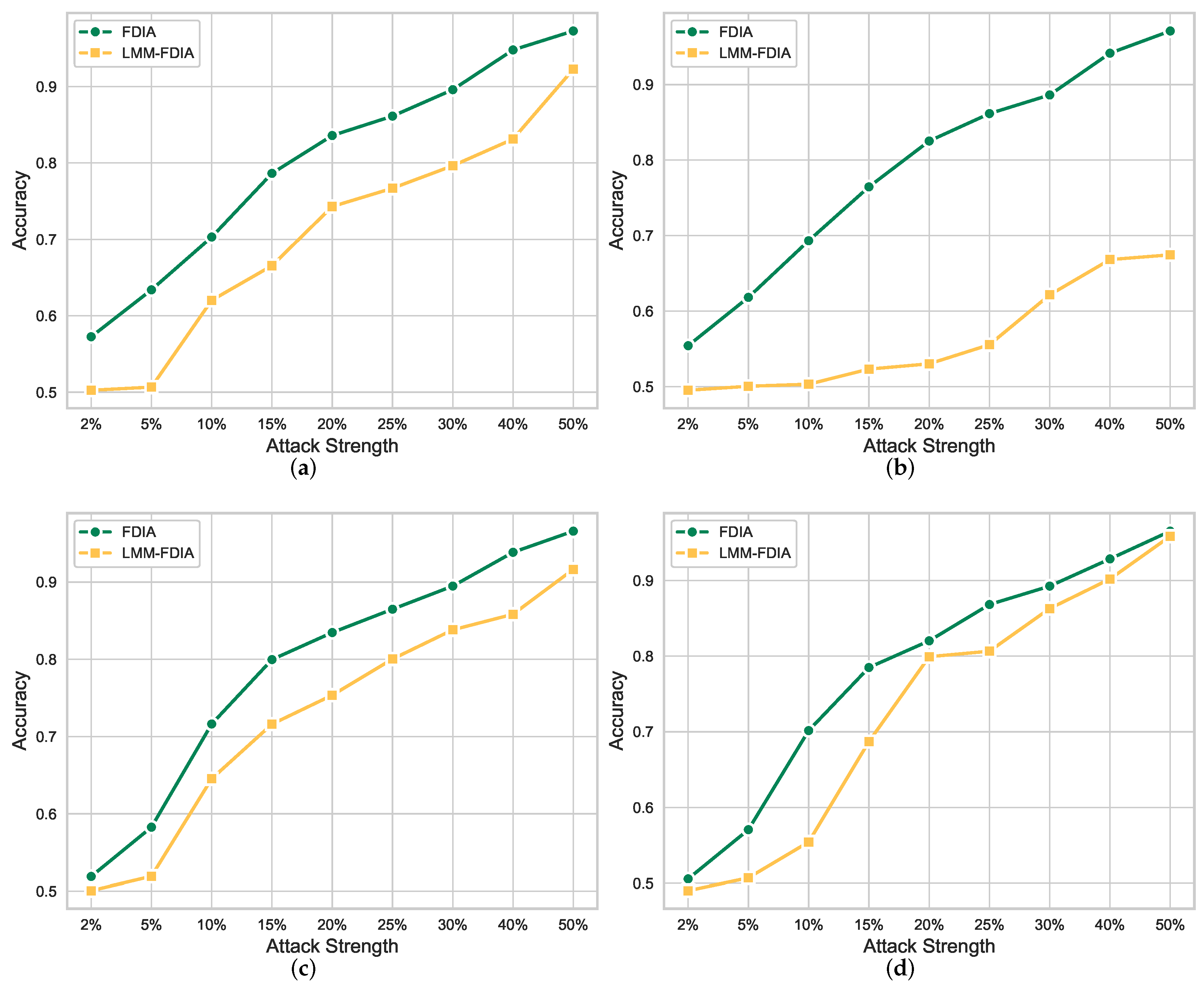
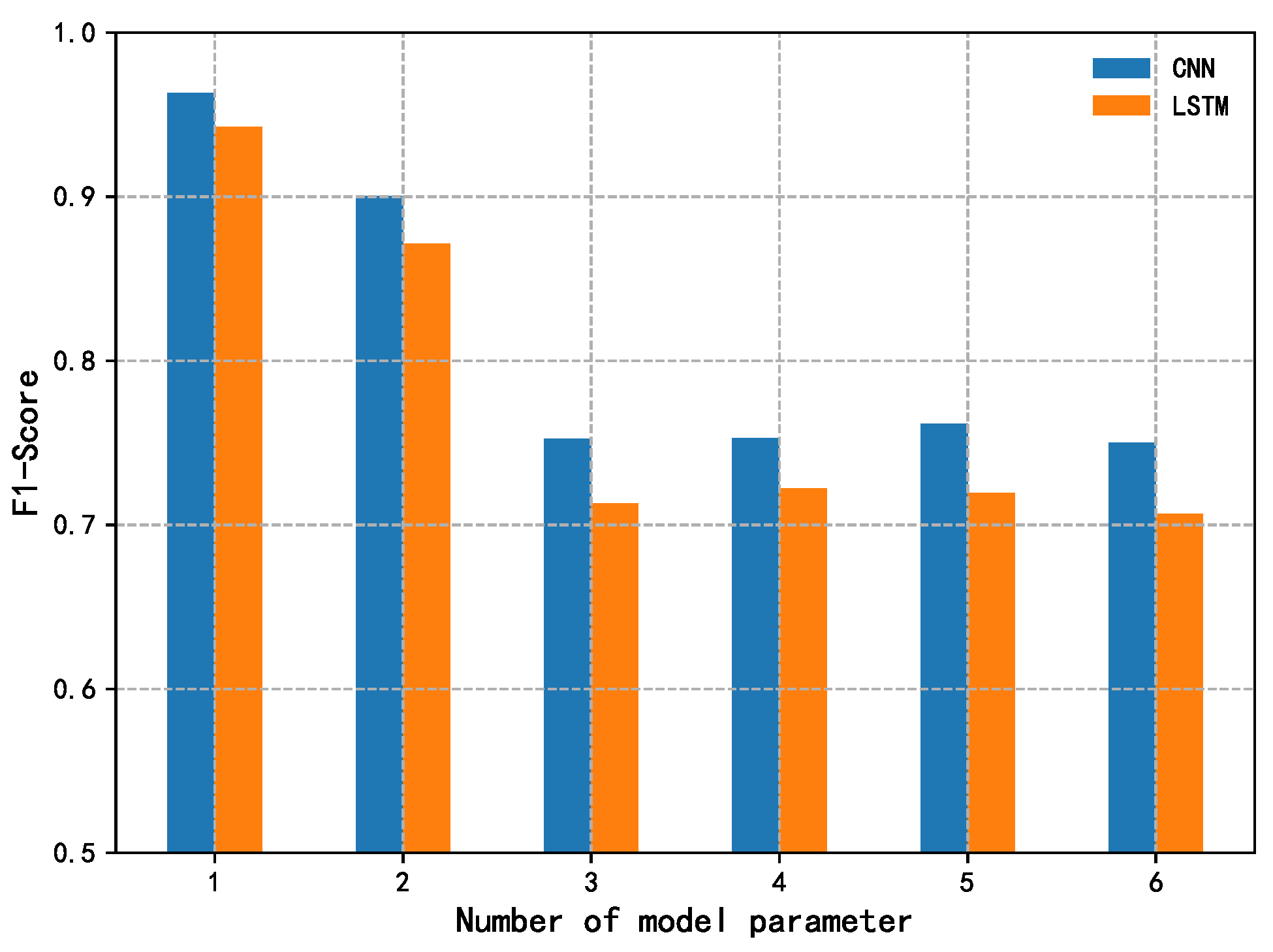
4.3. Experimental Results and Discussions
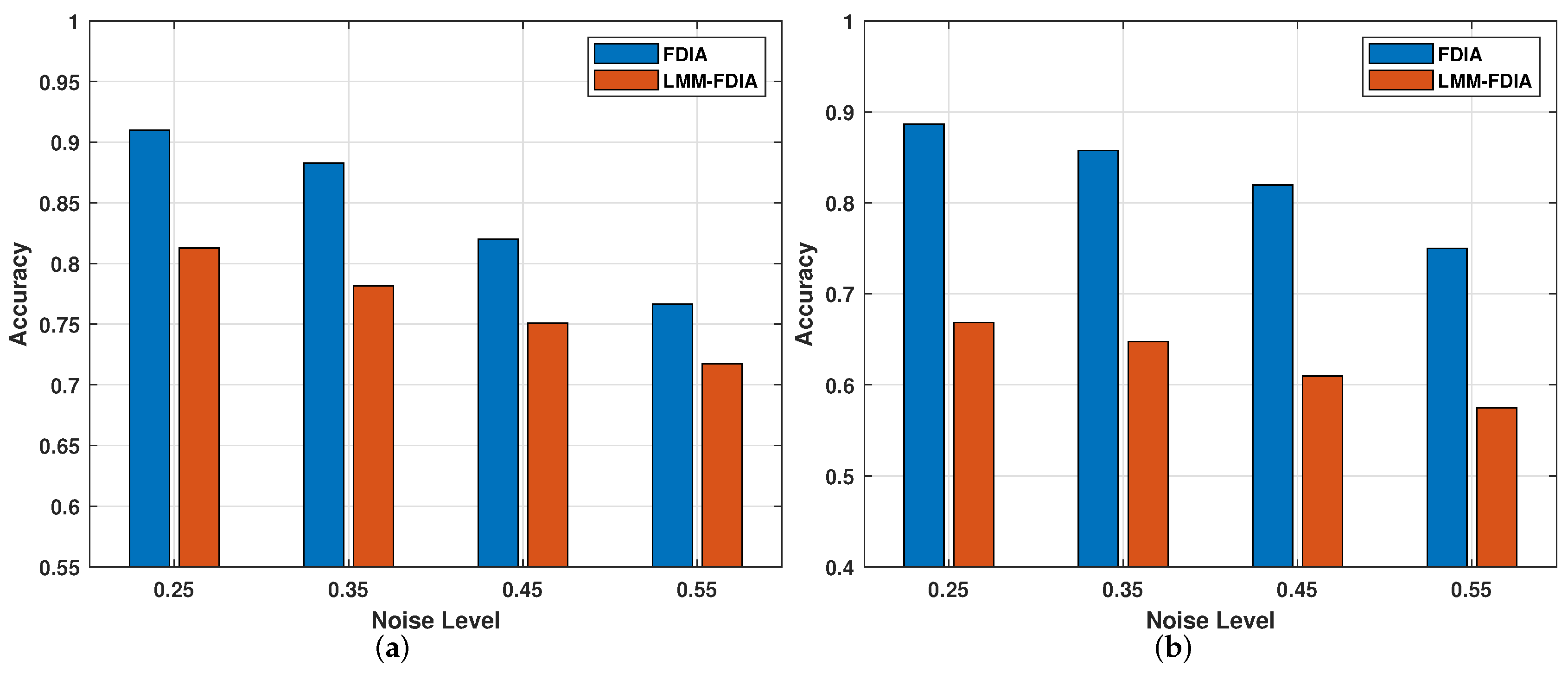
4.4. Impact of Noise Error
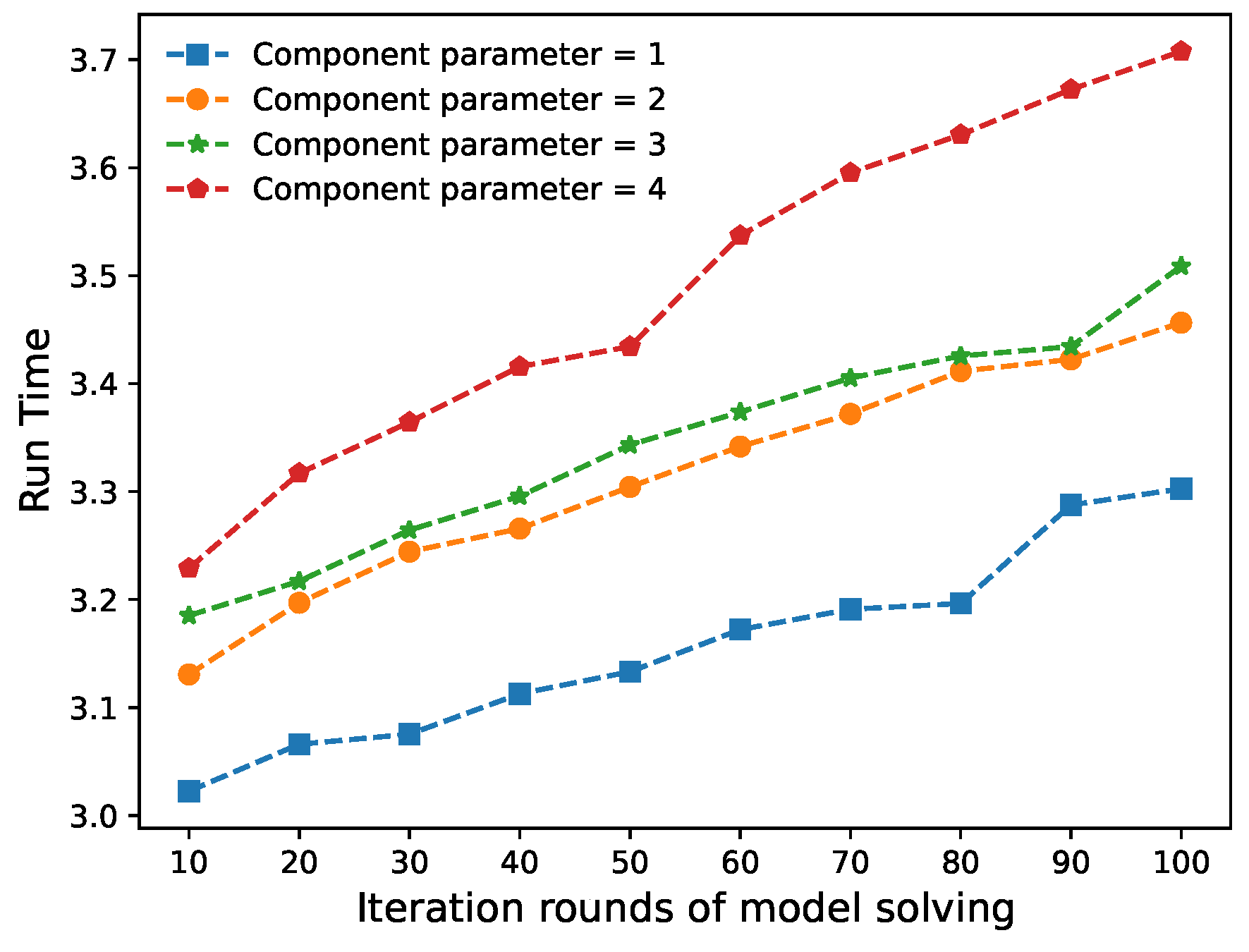
4.5. Time Complexity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Victor, C.; Harindra, S.; Brady, J.; Bjorn, V.; Vivek, K. A Review of Visualization Methods for Cyber-Physical Security: Smart Grid Case Study. IEEE Access 2023, 11, 1. [Google Scholar]
- Thakur, N.; Han, C.Y. An Intelligent Ubiquitous Activity Aware Framework for Smart Home. In Human Interaction, Emerging Technologies and Future Applications III: Proceedings of the 3rd International Conference on Human Interaction and Emerging Technologies: Future Applications (IHIET 2020), Paris, France, 27–29 August 2020; Ahram, T., Taiar, R., Langlois, K., Choplin, A., Eds.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2021; Volume 1253. [Google Scholar]
- Vergutz, A.; Noubir, G.; Nogueira, M. Reliability for Smart Healthcare: A Network Slicing Perspective. IEEE Netw. 2020, 34, 91–97. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, W.; Zhao, W. Privacy Preserving Data Aggregation for Smart Grid with User Anonymity and Designated Recipients. Symmetry 2022, 14, 847. [Google Scholar] [CrossRef]
- Charalambos, K.; Saraju, P.M. Cybersecurity for the Smart Grid. Computer 2020, 53, 10–12. [Google Scholar]
- Aoufi, S.; Derhab, A.; Guerroumi, M. Survey of False Data Injection in Smart Power Grid: Attacks, Countermeasures and Challenges (Article). Inf. Secur. Appl. 2020, 54, 102518. [Google Scholar] [CrossRef]
- Qu, Z.; Yang, J.; Lang, Y.; Wang, Y.; Han, X.; Guo, X. Earth-Mover-Distance-Based Detection of False Data Injection Attacks in Smart Grids. Energies 2022, 15, 1733. [Google Scholar] [CrossRef]
- Haftu, T.; Adnan, A.; Abdun, M. Comprehensive Survey and Taxonomies of False Data Injection Attacks in Smart Grids: Attack Models, Targets, and Impacts. Renew. Sustain. Energy Rev. 2022, 163, 112423. [Google Scholar]
- Huang, R.; Li, Y.; Wang, X. Attention-Aware Deep Reinforcement Learning for Detecting False Data Injection Attacks in Smart Grids. Electr. Power Energy Syst. 2023, 147, 108815. [Google Scholar] [CrossRef]
- Mahi, A.; Hossain, F.; Anwar, A.; Azam, S. False Data Injection Attack Detection in Smart Grid Using Energy Consumption Forecasting. Energies 2022, 15, 4877. [Google Scholar] [CrossRef]
- Nafees, M.; Saxena, N.; Cardenas, A.; Grijalva, S.; Burnap, P. Smart Grid Cyber-Physical Situational Awareness of Complex Operational Technology Attacks: A Review. Assoc. Comput. Mach. 2023, 55, 10. [Google Scholar] [CrossRef]
- Tu, W.; Dong, J.; Zhai, D. Optimal ϵ-stealthy attack in cyber-physical systems. J. Frankl. Inst. 2021, 358, 151–171. [Google Scholar] [CrossRef]
- Zhang, T.; Ye, D. False Data Injection Attacks With Complete Stealthiness in Cyber-physical Systems: A Self-Generated Approach. Automatica 2020, 120, 109117. [Google Scholar] [CrossRef]
- Xiao, L. Optimal Attack Strategy Against Fault Detectors for Linear Cyber-Physical Systems. Inf. Sci. 2021, 581, 390–402. [Google Scholar]
- Sushree, P.; Ashok, K.T. Design of False Data Injection Attacks in Cyber-Physical Systems. Inf. Sci. 2022, 608, 825–843. [Google Scholar]
- Sun, K.; Li, Z. Sparse Data Injection Attacks on Smart Grid: An Information-Theoretic Approach. IEEE Sens. 2022, 22, 14553–14562. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, P.; Chen, Y.; Xun, P.; Zhang, Z. False Data Injection Attack Based on Hyperplane Migration of Support Vector Machine in Transmission Network of the Smart Grid. Symmetry 2018, 10, 165. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Lu, Z. Graph-Based Detection for False Data Injection Attacks in Power Grid. Energy 2023, 263, 125865. [Google Scholar] [CrossRef]
- Jorjani, M.; Seifi, H.; Varjani, A. A Graph Theory-Based Approach to Detect False Data Injection Attacks in Power System AC State Estimation. IEEE Trans. Ind. Inform. 2020, 17, 2465–2475. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Y.; Li, Y.; Dong, Z.; Shahidehpour, M. Detection of False Data Injection Attacks in Smart Grid: A Secure Federated Deep Learning Approach. IEEE Trans. Smart Grid 2022, 99, 1. [Google Scholar] [CrossRef]
- Jing, H.; Liu, Y.; Zhao, J. Asymmetric Laplace Distribution Models for Financial Data: VaR and CVaR. Symmetry 2022, 14, 807. [Google Scholar] [CrossRef]
- Amos, N.; Tomasz, J.K. A Uniform-Laplace Mixture Distribution. Comput. Appl. Math. 2023, 115236. [Google Scholar]
- Wu, Y.; Sheng, Y.; Guo, N.; Li, F.; Tian, Y.; Su, X. Hybrid Deep Network Based Multi-Source Sensing Data Fusion for FDIA Detection in Smart Grid. In Proceedings of the 2022 Asia Power and Electrical Technology Conference (APET), Shanghai, China, 11–13 November 2022; pp. 310–315. [Google Scholar]
- Wu, Y.; Wang, Q.; Guo, N.; Tian, Y.; Li, F.; Su, X. Efficient Multi-Source Self-Attention Data Fusion for FDIA Detection in Smart Grid. Symmetry 2023, 15, 1019. [Google Scholar] [CrossRef]
- Shen, K.; Yan, W.; Ni, H.; Chu, J. Localization of False Data Injection Attack in Smart Grids Based on SSA-CNN. Information 2023, 14, 180. [Google Scholar] [CrossRef]
- Sayghe, A.; Anubi, O.M.; Konstantinou, C. Adversarial Examples on Power Systems State Estimation. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar]
- Mukherjee, D. Data-Driven False Data Injection Attack: A Low-Rank Approach. IEEE Trans. Smart Grid 2022, 13, 2479–2482. [Google Scholar] [CrossRef]
- Jiao, R.; Xun, G.; Liu, X.; Yan, G. A New AC False Data Injection Attack Method Without Network Information. IEEE Trans. Smart Grid 2021, 12, 5280–5289. [Google Scholar] [CrossRef]
- Tian, J.; Wang, B.; Wang, Z.; Cao, K.; Li, J.; Ozay, M. Joint Adversarial Example and False Data Injection Attacks for State Estimation in Power Systems. IEEE Trans. Cybern. 2022, 52, 13699–13713. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Qi, J.; Chen, L. Robust Cubature Kalman Filter for Dynamic State Estimation of Synchronous Machines Under Unknown Measurement Noise Statistics. IEEE Access 2019, 7, 29139–29148. [Google Scholar] [CrossRef]
- Deng, G.; Qi, N.; Tang, M.; Duan, X. Constructing Dixon Matrix for Sparse Polynomial Equations Based on Hybrid and Heuristics Scheme. Symmetry 2022, 14, 1174. [Google Scholar] [CrossRef]


| Attack Level | Attack Strength | Traditional Scheme | LMM-FDIA Based Scheme | ||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | -Score | Precision | Recall | -Score | ||
| Weak Attacks | 2% | 0.5485 | 0.6137 | 0.5613 | 0.3330 | 0.4520 | 0.3689 |
| 5% | 0.6243 | 0.6869 | 0.6408 | 0.4205 | 0.6950 | 0.5179 | |
| 10% | 0.7021 | 0.7132 | 0.7004 | 0.6556 | 0.6148 | 0.5499 | |
| Moderate Attacks | 15% | 0.7813 | 0.7954 | 0.7826 | 0.6636 | 0.5541 | 0.5574 |
| 20% | 0.8372 | 0.8424 | 0.8358 | 0.7351 | 0.6776 | 0.6764 | |
| 25% | 0.8478 | 0.8732 | 0.8565 | 0.7794 | 0.7605 | 0.7595 | |
| Strong Attacks | 30% | 0.8995 | 0.9094 | 0.8998 | 0.8280 | 0.8143 | 0.7981 |
| 40% | 0.9494 | 0.9452 | 0.9462 | 0.8541 | 0.8021 | 0.8090 | |
| 50% | 0.9754 | 0.9708 | 0.9725 | 0.9281 | 0.9186 | 0.9213 | |
| Attack Level | Attack Strength | Traditional Scheme | LMM-FDIA Based Scheme | ||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | -Score | Precision | Recall | -Score | ||
| Weak Attacks | 2% | 0.5399 | 0.5417 | 0.5408 | 0.4943 | 0.4686 | 0.4811 |
| 5% | 0.6290 | 0.6000 | 0.6141 | 0.5000 | 0.4078 | 0.4492 | |
| 10% | 0.6704 | 0.6842 | 0.6959 | 0.5044 | 0.4799 | 0.4854 | |
| Moderate Attacks | 15% | 0.7481 | 0.8063 | 0.7761 | 0.5244 | 0.4859 | 0.5045 |
| 20% | 0.8208 | 0.8307 | 0.8257 | 0.5249 | 0.6261 | 0.5054 | |
| 25% | 0.8409 | 0.9023 | 0.8705 | 0.5662 | 0.4706 | 0.5140 | |
| Strong Attacks | 30% | 0.8586 | 0.9189 | 0.8877 | 0.6058 | 0.5787 | 0.6041 |
| 40% | 0.9509 | 0.9421 | 0.9465 | 0.6742 | 0.6495 | 0.6616 | |
| 50% | 0.9831 | 0.9569 | 0.9698 | 0.7843 | 0.5867 | 0.5960 | |
| Attack Level | Attack Strength | Traditional Scheme | LMM-FDIA Based Scheme | ||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | -Score | Precision | Recall | -Score | ||
| Weak Attacks | 2% | 0.5176 | 0.5485 | 0.4952 | 0.4372 | 0.5854 | 0.4360 |
| 5% | 0.5818 | 0.5714 | 0.5650 | 0.5933 | 0.4132 | 0.3958 | |
| 10% | 0.7241 | 0.6903 | 0.7005 | 0.7976 | 0.4121 | 0.5355 | |
| Moderate Attacks | 15% | 0.8023 | 0.7874 | 0.7912 | 0.8586 | 0.5338 | 0.6525 |
| 20% | 0.8364 | 0.8263 | 0.8281 | 0.8619 | 0.6291 | 0.7165 | |
| 25% | 0.8746 | 0.8481 | 0.8583 | 0.9072 | 0.6810 | 0.7730 | |
| Strong Attacks | 30% | 0.8926 | 0.8952 | 0.8917 | 0.9464 | 0.7250 | 0.8162 |
| 40% | 0.9374 | 0.9376 | 0.9364 | 0.9189 | 0.7970 | 0.8504 | |
| 50% | 0.9621 | 0.9693 | 0.9651 | 0.9272 | 0.9047 | 0.9157 | |
| Attack Level | Attack Strength | Traditional Scheme | LMM-FDIA Based Scheme | ||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | -Score | Precision | Recall | -Score | ||
| Weak Attacks | 2% | 0.5328 | 0.1870 | 0.2769 | 0.4966 | 0.6444 | 0.5610 |
| 5% | 0.5718 | 0.6027 | 0.5869 | 0.5062 | 0.9808 | 0.6678 | |
| 10% | 0.7518 | 0.6126 | 0.6751 | 0.6737 | 0.2288 | 0.3417 | |
| Moderate Attacks | 15% | 0.8008 | 0.7654 | 0.7827 | 0.8398 | 0.4703 | 0.6029 |
| 20% | 0.8728 | 0.7549 | 0.8096 | 0.9037 | 0.6748 | 0.7726 | |
| 25% | 0.8672 | 0.8735 | 0.8703 | 0.8817 | 0.7130 | 0.7884 | |
| Strong Attacks | 30% | 0.9129 | 0.8708 | 0.8914 | 0.8338 | 0.9102 | 0.8703 |
| 40% | 0.8995 | 0.9670 | 0.9320 | 0.9499 | 0.8509 | 0.8977 | |
| 50% | 0.9555 | 0.9769 | 0.9661 | 0.9800 | 0.9373 | 0.9581 | |
| Attack Method | Characteristics | Challenges |
|---|---|---|
| FDIA [20] | Effectively avoiding BDD detection Low model complexity | Easy to detect by DL model Simple construction of attack vector |
| AFDIA [26] | Effectively avoiding BDD detection High success rate | Poor robustness Easy to detect by DL model Large amount of model parameters |
| D-FDIA [27] | Effectively avoiding BDD detection Low computational burden | Easy to detect by DL model Poor concealment of attack vector |
| SG-FDIA [28] | Effectively avoiding BDD detection High time efficiency | Easy to detect by DL model Poor robustness |
| M-AFDIA [29] | Effectively avoiding DL model detection Strong concealment of attack vectors | Easy to detect by BDD Long running time |
| S-AFDIA [29] | Effectively avoiding BDD and DL model detection | High model complexity High operation cost Obtain comprehensive system information |
| LMM-FDIA | Effectively avoiding BDD and DL model detection Low model complexity and running time Strong concealment of attack vector | Poor performance on small samples |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Zu, T.; Guo, N.; Zhu, Z.; Li, F. Laplace-Domain Hybrid Distribution Model Based FDIA Attack Sample Generation in Smart Grids. Symmetry 2023, 15, 1669. https://doi.org/10.3390/sym15091669
Wu Y, Zu T, Guo N, Zhu Z, Li F. Laplace-Domain Hybrid Distribution Model Based FDIA Attack Sample Generation in Smart Grids. Symmetry. 2023; 15(9):1669. https://doi.org/10.3390/sym15091669
Chicago/Turabian StyleWu, Yi, Tong Zu, Naiwang Guo, Zheng Zhu, and Fengyong Li. 2023. "Laplace-Domain Hybrid Distribution Model Based FDIA Attack Sample Generation in Smart Grids" Symmetry 15, no. 9: 1669. https://doi.org/10.3390/sym15091669
APA StyleWu, Y., Zu, T., Guo, N., Zhu, Z., & Li, F. (2023). Laplace-Domain Hybrid Distribution Model Based FDIA Attack Sample Generation in Smart Grids. Symmetry, 15(9), 1669. https://doi.org/10.3390/sym15091669







